DOI:
10.1039/C1SC00276G
(Minireview)
Chem. Sci., 2011,
2, 2086-2093
Mechanochemistry of F1motor protein†‡
Received
7th May 2011
, Accepted 20th June 2011
First published on 18th July 2011
Abstract
Although a variety of physical perturbations are utilised to control chemical reactions or bias chemical equilibria, mechanical force is not generally an option for controlling chemical reactions due to technical complexity. However, upon attaching handles to a responsive moiety and pulling, twisting or pushing it, unique means of controlling chemistry are permitted because mechanical force is intrinsically anisotropic for chemical structures. One remarkable example in natural systems is F1-ATPase, the water-soluble part of FoF1-ATP synthase. F1-ATPase is a rotary motor protein in which the rotor subunit rotates against the surrounding catalytic stator ring, hydrolysing ATP. A unique feature of F1-ATPase is that it synthesises ATP against the large chemical potential of ATP hydrolysis when its rotation is mechanically reversed. This mini-review will introduce the latest findings about the mechanochemical properties of F1-ATPase, and summarise the common concepts of mechanochemistry it shares with synthetic molecular systems.
Introduction: Molecular machines in cells
Living matter is dynamic; every cell moves and/or transforms its own shape actively and continuously. Even in apparently static cells, upon a closer look, one will observe that many intracellular structures are constantly moving and transforming. Although many motions do not exhibit clear directionality, implying that they are due to thermal agitation, many unidirectional motions or drastic structural changes are not attributable to thermal agitation. These dynamics are supported by molecular machines comprising proteins or RNA/protein conjugates. Myosin, kinesin, dynein and flagellar motor proteins are termed molecular motor proteins that exert force to support intracellular transportation or the large-scale transformation of cells or organelles, such as muscle fibre contraction, bacterial flagella rotation, and flagella beating in eukaryotic cells. In a limited sense, ‘molecular motor’ is the term used for proteins wherein their physiological roles are directly relevant to force generation. However, many proteins that were originally classified as enzymes have been reclassified as force-generating molecular machines. Prominent examples are enzymes involved in the central dogma of cell biology, such as DNA polymerase, RNA polymerase, and ribosome, whose principal physiological role is biopolymer production. A state-of-the-art single-molecule technique revealed that these molecules are also able to work against external forces to perform their functions.1–6 In some cases, such non-molecular motor proteins generate much larger forces than do molecular motor proteins.7,8 Thus, dynamics and force generation are common features of biology even at the molecular level.
Mechanochemical coupling of molecular machines
Most biomolecular machines consume adenosine triphosphate (ATP), hydrolysing it into adenosine diphosphate (ADP) and inorganic phosphate (Pi) as chemical fuel for functionality. Driven by the energy liberated by the ATP hydrolysis reaction, these proteins change their conformation and exert force. Unlike manmade combustion engines that convert chemical energy into mechanical work via air expansion, biomolecular machines directly convert energy derived from ATP hydrolysis into mechanical work. Thereby, they achieve high-energy conversion efficiency. Another remarkable feature of biomolecular machines that should be emphasised more, and will be a focus of this review, is that they can also convert energy in the reverse manner, i.e. they can modulate the chemical reaction equilibrium or rate constant upon external mechanical force input. One prominent example is FoF1-ATP synthase. This enzyme synthesises ATP against the large free energy of ATP hydrolysis (∼48 kJ mol−1 under physiological conditions) upon mechanical manipulation by reverse rotation as discussed later in the text. In this review, we will focus on F1-ATPase, the catalytic core of FoF1-ATP synthase, and provide a brief review about what we have learned about the mechanochemical coupling mechanism of F1-ATPase mainly from single-molecule experiments using F1-ATPase from thermophilic Bacillus PS3 (TF1) whose mechanochemical properties are the best characterised among F1-ATPases. For comparison, studies on another model system, F1 from Escherichia coli, (EF1) are also introduced arbitrarily.
FoF1-ATP synthase
FoF1-ATP synthase is found widely in the biological world, including in thylakoid membranes, the mitochondrial inner membrane, and the plasma membrane of bacteria. This enzyme synthesises ATP from ADP and Pi by using the electrochemical potential of protons across the membrane, i.e. it converts electrochemical potential into chemical energy. Under aerobic conditions, most ATP is synthesised by FoF1-ATP synthase. This enzyme also functions in the reverse direction when the electrochemical potential becomes insufficient; it catalyses proton pumping to generate electrochemical potential by hydrolysing ATP into ADP and Pi. FoF1-ATP synthase is a super-complex enzyme with a molecular weight of more than 500 kDa and consists of two rotary motors. One motor is F1 (∼380 kDa), which is the water-soluble part of ATP synthase. When isolated from the membrane portion, it acts as an ATP-driven motor; it rotates its inner subunit, resulting in ATP hydrolysis, and it is therefore termed F1-ATPase. The other rotary motor of ATP synthase is Fo (∼120 kDa), which is embedded in the membrane and generates rotary torque upon proton translocation that is driven by proton electrochemical potential (Fig. 1).9 Bacterial F1 is composed of α3β3γδε subunits. The minimum complex of F1 as a motor is the α3β3γ subcomplex. The three α and three β subunits form the hexameric stator ring in which the α and β subunits are alternately arranged. The rotor shaft is the γ-subunit, which is accommodated in the central cavity of the α3β3 ring. Upon ATP hydrolysis of the catalytic sites, F1 rotates the γ subunit in the anticlockwise direction when viewed from the Fo side. The δ and ε subunits act as connectors between F1 and Fo, each connecting the stator and rotor parts, respectively. Fo consists of ab2c8–15 subunits. The number of c-subunits varies among species. The c subunits form the rotor ring complex by aligning in a circle. The c-ring and a-subunit form a proton pathway.10 With the downhill proton flow through the proton channel, the c-ring rotates against the ab2 subunits in the direction opposite that of the γ subunit of the F1motor.11 Thus, in the FoF1 complex, Fo and F1 push each other in the opposite direction. Under physiological conditions where the electrochemical potential of the protons is sufficiently large, Fo generates larger torque than does F1 and then forcibly rotates the γ subunit in the clockwise direction. As a result, F1 catalyses the reverse reaction, i.e.ATP synthesis, and this reaction is the principle physiological function of ATP synthase.
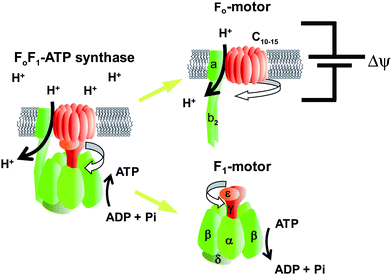 |
| | Fig. 1
Fo and F1 motors of ATP synthase. Schematic images of FoF1-ATP synthase. The rotor and stator parts are shown in red and green, respectively. The subunit composition of F1 and Fo are α3β3γδε and ab2c10–15, respectively. Fo is embedded in the cell membrane and rotates the c-ring against the ab2 stator, which is driven by proton translocation down the proton electrochemical potential across the membrane. Isolated F1 acts as the ATPase, and therefore, is referred to as F1-ATPase. Hydrolysing ATP, F1 rotates the γ subunit against the α3β3-cylinder ring. In the full complex of FoF1, Fo exerts a larger torque, reverses the rotation of F1, and leads to ATP synthesis from ADP and Pi. | |
F1-ATPase
Catalytic
reaction centres for ATP hydrolysis/synthesis reside at the three α–β interfaces, which are on the anticlockwise side of the β subunit as indicated with red circles in Fig. 2A. F1 also has non-catalytic ATP-binding sites at the three α–β interfaces, but at the opposite side of β (blue circles in Fig. 2A). Whereas the catalytic site is formed mainly with amino acid residues from the β subunit, the non-catalytic sites are primarily located within the α subunit. The three catalytic sites on the β subunits work cooperatively during catalysis. The classic working model for F1 is the ‘binding change mechanism’ proposed by Boyer.12 One important feature of this model is that the affinity for nucleotides at each catalytic site is different from each other at any given time, and the statuses of the three β subunits cooperatively change in one direction accompanying γ rotation. This hypothesis is strongly supported by the X-ray crystallographic studies on bovine mitochondrial F1 performed by Walker's group.13 The first resolved crystal structure of F113 revealed many essential structural features of F1 at atomic resolution. Importantly, the catalytic β subunits differ from each other in conformation and in the catalytic state; one subunit binds to an ATP analogue, adenosine-5′-(β,γ-imino)triphosphate (AMP-PNP); the second binds to ADP; and the third is empty (Fig. 2A). Therefore, these sites are termed βTP, βDP and βempty, respectively. Whereas βTP and βDP have a closed conformation wrapping bound nucleotides on the catalytic sites, βempty has an open conformation swinging the C-terminal domain away from the binding site to open the cleft of the catalytic site (Fig. 2B). From these structural features, it is widely thought that the open-to-closed transition of the β subunits upon ATP binding pushes γ,14 and the sequential conformational change among β subunits facilitates the unidirectional γ rotation, which was recently visualised in simultaneous imaging of the conformational change in the β subunit and γ rotation.15 It should be mentioned that although the structural features found in the first crystal structure of F1 were well conserved in the other crystal structures generated with different nucleotides or ligand analogues, there is a distinct exception16—when crystallised with a transition-state analogue complex (ADP-AlF4−), βempty is also occupied with nucleotide, and adopts a half-closed conformation. This is assumed to represent a transition state before ADP release.
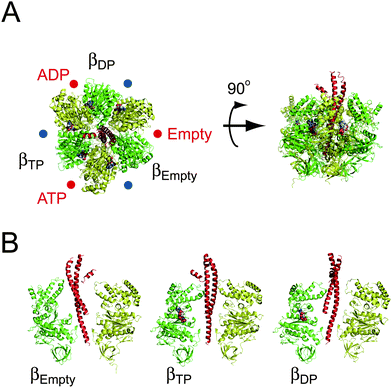 |
| | Fig. 2 Crystal structure of the α3β3γ subcomplex of F1. The crystal structure of F1 from bovine mitochondria (PDB code; 1BMF). The α, β and γ subunits are shown in yellow, green and red, respectively. (A) The left figure is viewed from the membrane side (Fo side), and is rotated 90° in the anticlockwise direction of the black arrow (right figure). The protruding part of γ is directed toward the Fo side. The catalytic sites are located at the α–β interface, and are indicated by red circles, primarily on the β subunit. Each site carries AMP-PNP, ADP, or is empty, and is designated as βTP, βDP or βempty, respectively. The other interfaces are non-catalytic sites (blue circles), all of which are occupied with AMP-PNP. (B) Conformational states of the β subunit. Three α–β pairs with the γ subunit are shown. The α and β subunits are composed of the N-terminal domain, nucleotide-binding domain, and C-terminal domain (from bottom to top). βempty has an open conformation in which the α-helical C-terminal domain rotates upwards to open the cleft of the nucleotide-binding pocket. Both βATP and βADP have a closed conformation entrapping the nucleotide within the closed pocket. | |
Single-molecule observation of F1
Since the publication of the crystal structure, many studies have attempted to demonstrate the rotation of F1. Crosslink exchange experiment between the β and γ subunits of EF117 and the polarised absorption relaxation of F1 from spinach chloroplasts18 have proven the rotational motion of the γ subunit during catalysis. The unidirectional rotation of the γ subunit upon ATP hydrolysis was demonstrated with the direct observation of F1 rotation under the microscope.19 To suppress rotary Brownian motion, F1 was immobilised on a glass surface modified with Ni-nitrilotriacetic acid (Ni-NTA) through the interaction between Ni-NTA and the His-tag, which was introduced at the N-terminus of the β subunit. In addition, a fluorescently labelled actin filament with a length of 0.6–4 μm and a diameter of 10 nm was attached to the γ subunit as the rotation marker to magnify the small motion of the γ subunit, whose radius is only 1 nm, which is much smaller than the spatial resolution (∼200 nm) of a conventional microscope (Fig. 3A). Note that in recent studies, other types of probes such as polystyrene beads, gold colloidal beads, gold nanorods and magnetic beads have been used instead of actin filaments because the imaging of fluorescently labelled actin filaments suffers from photobleaching. Currently, this rotation assay is a simple and so established technique that even 8 years old children can execute this experiment. The rotational direction was always anticlockwise when viewed from the Fo side, and importantly, it was consistent with the expected rotary direction from the crystal structure. Assuming that the β subunit undergoes the conformational transition from βempty to βTP, and then βDP, each catalytic state must propagate in the anticlockwise direction, accompanying the anticlockwise γ rotation. The rotational velocity was far slower than the rate expected from bulk ATPase measurements because of the large hydrodynamic friction exerted on the rotating actin filament. However, this allows us to estimate the torque generated by individual F1 molecules from the hydrodynamic friction in equilibrium with the torque of F1. The torque was determined to be approximately 40 pN nm. Although this is a rough estimation without consideration of the viscosity increment in the immediate vicinity of glass surfaces, the value was recently confirmed to be valid using more precise torque measurements based on the fluctuation theorem, which estimates the entropy generation upon the rotation without assuming the friction coefficient.20 Comparable or slightly higher torque values (33–50 pN nm) were reported for EF121–24 and chloroplast F1 (CF1).25 Among them, the estimation by Junge's group, 50 pN nm, would be more accurate because it was determined from the curvature of the rotating actin filament as the torque indicator to avoid the surface effect. Considering that the step size upon a single turnover of ATP hydrolysis is 120° as introduced in the following section, the work done by F1 upon a single ATP hydrolysis is 80 pN nm or more, which essentially corresponds to the free energy released from the hydrolysis of a single ATP molecule under physiological conditions, suggesting 100% energy conversion efficiency for F1.
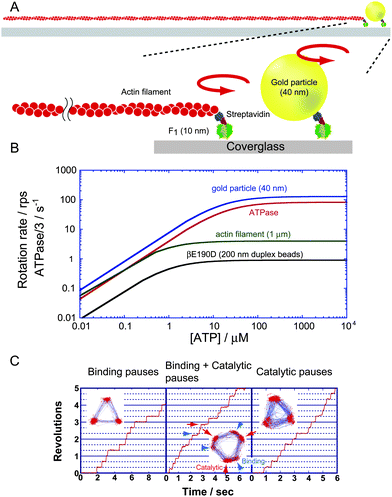 |
| | Fig. 3 Single-molecule rotation assay of F1. (A) A schematic image of the experimental setup. The α3β3 ring is fixed on the glass surface. A rotation probe, fluorescently labelled actin filament, or a gold particle is attached to the γ subunit to visualise the rotary motion under an optical microscope. (B) Rotational velocity vs.ATP concentration. Each line represents the experimentally obtained Michaelis–Menten curve for the rotation of wild-type F1 visualised with 40-nm gold particles (blue)28 and 1-μm actin filaments,28 and for rotation of a mutant F1 (βE190D) probed with 200-nm duplex beads (black)30 whose hydrodynamic friction is comparable to that of the 1-μm actin filament. ATPase turnover rates determined in solution measurement that were corrected to equal the rotational rate by dividing by 3, are also shown (red).28 To suppress the effect of the ADP-inhibited form, the solution contained lauryldimethylamine oxide, which relieves ADP inhibition. (C) Time courses of rotation and the trajectory of the centroid of the probe (insets). The left panel represents the rotation of the wild-type F1 under ATP-limiting conditions (60 nM ATP). The middle panel shows the rotation of the mutant F1-ATPase F1 (βE190D), around the KM region (2 μM ATP). The 120° step splits into 0 and 80° substeps, each intervened with a binding dwell and catalytic dwell, respectively. Arrowheads (blue) and arrows (red) indicate the positions of ATP binding and catalytic dwell, respectively. The right panel shows the rotation of F1 (βE190D) at saturating ATP (2 mM). Rotation is paused at catalytic dwell. | |
Stepping rotation
Many attempts have been made to resolve rotary motion into discrete steps to clarify how the rotation is coupled with each elementary catalytic step of ATP hydrolysis: ATP binding, hydrolysis and the release of ADP and Pi. The stepping rotation was first observed in the rotation assay with actin filaments under ATP-limiting conditions, where the ATP-binding process limits the overall turnover rate of the catalysis. When [ATP] is well below the Michaelis–Menten constant (KM) of the rotation (∼1 μM), F1 displayed discrete 120° steps, each intervened with pauses as expected from the pseudo-three-fold symmetry of the α3β3-ring (Fig. 3B and C). The mean dwell time of the pause was inversely proportional to [ATP], suggesting that the single ATP-binding event triggers individual 120° steps.26 The coupling ratio of a single 120° step per ATP was directly confirmed in a later study.27 Under ATP-saturating conditions, the stepping nature of F1 rotation was undetectable due to the damping effect of high viscous friction against the rotating actin filament. When 40-nm gold colloid, which is comparable in size to F1, was employed as the probe, the temporal resolution was largely improved so that 120° steps terminated by a 2-ms pause were observed even in saturating conditions. Later, the pause was revealed to be the waiting state for hydrolysis and Pi release (see below). The rotational velocity reached the maximum rate, which is determined not by mechanical rotation but by catalytic reaction. The observed rate slightly exceeded the expected rate from ATP hydrolysis activity measured in bulk solution.28 The discrepancy in the rates is attributed to some fraction of F1 being in an inactive state, the so-called ADP-inhibited form,29 in the ensemble solution measurement. Near the KM, where time constants for the ATP-binding step and catalysis are comparable, the rotation was further resolved into 90 and 30° substeps,28 which were later revised to be 80 and 40° substeps.30 The dwell time before the 80° substep is [ATP]-dependent, and therefore, ATP binding was identified as a trigger reaction of the 80° substep. When the catalytically critical glutamic acid termed the ‘general base’ (βE190 inTF1) was substituted with aspartic acid, the time constant of pause before the 40° substep was significantly slowed, implying that the 40° substep is triggered by ATP hydrolysis. The time constant of hydrolysis on the mutant F1 is 300 ms. The long pause permits observation of the stepping motion even using large probes such as 200-nm plastic beads (Fig. 3B and C). Near KM, the mutant F1 displays clear 80 and 40° substeps (Fig. 3C). Recent elaborated kinetic analyses of the substeps revealed that the 80° substep is triggered by ATP binding and ADP release, whereas the 40° substep is triggered by ATP hydrolysis and Pi release.28,30,31 The angular dwelling positions before the 80 and 40° substeps are termed the binding angle and catalytic angle (Fig. 3C), respectively. For EF1 rotation, although 120° stepping rotation was detected, clear 80 and 40° substeps have not been reported.24,32 This would be at least partially due to the more compliant γ shaft of EF1,33 which obscures the dwelling state between substeps.
Reaction scheme
All of the elementary reaction steps were found to occur at the binding or catalytic angle. However, because there are three positions for the binding and catalytic angles during a turn, determining the angle at which each reaction occurs is required to establish the complete reaction scheme. The angle for hydrolysis was determined using a hybrid F1 carrying a single copy of the aforementioned mutant β subunit βE190D.34 This hybrid enables the identification of the hydrolysis angle because the incorporated mutant β subunit exhibits distinctly long pauses at two positions: one pause occurs at the ATP-binding angle of the mutant β subunit (0°), and the other occurs at +200° from the binding angle. Thus, the hydrolysis angle was determined to be 200°. Simultaneous imaging of fluorescently labelled ATP and γ rotation revealed that ADP release occurs at 240°.31,35 The timing of Pi release has recently been determined to be at 320° in another type of experiment36 where F1 was stalled with magnetic tweezers during hydrolysis dwell. On the basis of the observation that bound ATP undergoes hydrolysis and synthesis in a reversible manner, it was revealed that Pi (or thiophosphate) is not released immediately after hydrolysis at 200°. Because Pi release has to occur after hydrolysis and at a catalytic angle, it was concluded that Pi release occurs at 320°. Thus, the present reaction scheme of rotation and catalysis was established as follows: ATP binding at 0°, hydrolysis at 200°, ADP release at 240°, and Pi release at 320° (Fig. 4). In this reaction scheme, the average occupancy of the catalytic sites with nucleotide is around two. On the other hand, biochemical measurements on nucleotide titration suggest the catalytic sites are fully filled with nucleotides. The explanation on the apparent discrepancy is that the catalytic site of 320° state can bind to ATP under ATP-saturating condition. It should be mentioned that there is a controversy about the timing of Pi release. Several groups proposed that Pi is released at 200° immediately after hydrolysis due to the simplicity, or based on the biochemical titrations of catalytic site occupancy with a nucleotide.37,38
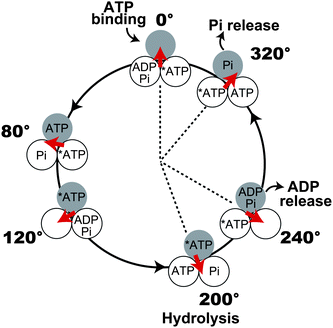 |
| | Fig. 4 Mechanochemical coupling scheme of F1. Each circle represents the chemical state of the catalytic sites on the β subunit. 0° is defined as the ATP-binding angle for the catalytic site represented as the gray circle. At 200°, the catalytic site hydrolyses ATP into ADP and Pi, which are released at 240 and 320°, respectively. Other catalytic sites also obey the same reaction scheme, and the reaction phase is different from the gray one by ±120°. Another model for Pi release is also proposed (see text). At ATP-saturating conditions, the catalytic site of 320° state can bind to ATP, and thus the occupancy of catalytic sites with nucleotide reaches 3. | |
ATP synthesis upon reverse rotation
The essential properties and basic mechanochemical coupling scheme of F1 as an ATP-driven motor have been nearly established. However, the physiological role of FoF1-ATP synthase, i.e.ATP synthesis, has not been sufficiently studied in single-molecule experiments. If ATP synthesis is a simple reverse reaction of hydrolysis, forcibly reversing the rotation of F1 should lead to efficient ATP synthesis. To verify this hypothesis, two lines of experiments have been performed. In the first type of experiment,39 a large number of F1 molecules were enclosed in an observation chamber and forcibly rotated in the reverse direction with a magnetic tweezer system. The synthesised ATP was detected as bioluminescence using the luciferin–luciferase system. Although ATP synthesis upon reverse rotation was clearly demonstrated, the uncertainty of the number of active F1 molecules in the chamber did not allow quantitative estimation of the mechanochemical coupling ratio. Therefore, the following experiment focused on a single active F1 molecule to determine the coupling ratio.27 The technical issue to be addressed was the detection of a very small number of ATP molecules generated from a single F1 molecule. Even if we assume that F1 synthesises three ATP molecules per revolution at 10 Hz for 1 min, the total number of ATP molecule is only 1800 molecules (3.0 × 10−21 mole), which is far below the detection limit of the luciferase assay. To address this issue, a microscopic reaction chamber system was developed using a microfabrication technique. The developed system has identically shaped reaction chambers, each of which is a few microns in scale and has a volume of 6 fL.40 Because the extremely small reaction volume results in high concentration, it is possible to detect the small amount of reaction product yielded from a single enzyme molecule. A single F1 molecule was encapsulated in a microchamber (Fig. 5A and B). After forcible reverse rotation with magnetic tweezers, F1 was released from the tweezers. Because the rotational rate of ATP-driven rotation is proportional to [ATP] under the experimental conditions, one can measure the increment of [ATP] as that of the ATP-driven rotation rate (Fig. 5C). It was found that F1 undergoes highly efficient ATP synthesis of ∼80% (2.3 ATP molecules per turn). The high reversibility of mechanochemical coupling is the remarkable feature of F1 that distinguishes it from other molecular motors; other motor proteins such as kinesin and myosin do not synthesise ATP when the movements are reversed by external force. Single-molecule manipulation for the elucidation of mechanochemical properties has not been attempted for EF1, although optical tweezers were developed for the manipulation.41 Therefore, in the following sections as well as this section, all of the introduced works describe TF1.
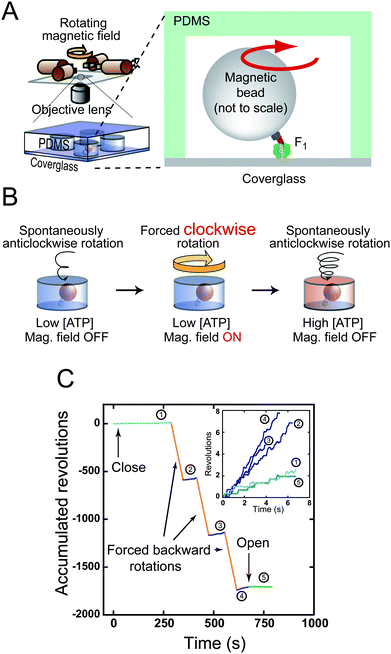 |
| | Fig. 5
ATP synthesis upon reverse rotation of F1. (A) Schematic drawing of experimental setup. (B) Experimental procedure of ATP synthesis. Active single F1 is enclosed in a micron-sized reaction chamber (left). A magnetic bead attached to the γ subunit is forcibly rotated by magnetic tweezers (centre). Newly synthesised ATP is accumulated in the chamber. The number of synthesised ATP molecules is determined from the increments in the ATP-driven rotational speed of released F1 (right). (C) Time courses of the ATP synthesis experiment. A typical data set is shown. After entrapping, the rotational velocity under the initial condition was recorded (1), and then a rotating magnetic field was applied. After forcible rotation, F1 was released to record the velocity (2). This procedure was repeated (3, 4), and was terminated by opening the chamber to confirm that F1 resumed its original velocity (5). Insets show the closed-up time course of spontaneous rotation. Velocity increment shows the ATP synthesis during forced backward rotation (orange lines). | |
ATP binding enhanced by forcible forward rotation
The aforementioned finding that the reverse rotation leads to the reverse chemical reaction is conceptually simple, and is the expected result for the verification of F1 rotation. However, the chemical equilibrium of ATP hydrolysis/synthesis is significantly inclined to hydrolysis by a factor of 1 × 108 without external perturbation. Furthermore, proteins have a large number of degrees of freedom in their conformations. Considering these facts, it is fascinating that only by manipulating the sole degree of freedom of F1, the rotary angle of the γ subunit, one can synthesise ATP against the large chemical potential of ATP hydrolysis. There is no other catalyst exhibiting such a feature in natural systems or manmade catalysts. To achieve highly efficient mechanochemical coupling, individual catalytic steps—ATP-binding, hydrolysis and product release—should be tightly coupled with γ rotation in F1. In other words, these reactions should be modulated upon γ rotation. To elucidate the mechanical modulation of the ATP-binding process, the microchamber system was again used.42 In this experiment, the F1 molecule was enclosed in a similar chamber as used for the ATP synthesis experiment. However, the molecules were rotated in the ‘forward’ direction. Only a limiting amount of ATP was added to the solution to monitor ATP consumption as the decrement in the velocity of spontaneous rotation. Because only the ATP-binding step has a long time constant compared with other reaction steps under this experimental condition, the efficiency of ATP binding during forcible rotation was determined as the net coupling efficiency. After each forcible rotation, F1 resumed its spontaneous rotation and its velocity decreased, suggesting that the forcible rotation is well coupled with ATP hydrolysis. Surprisingly, even while rotating at a much faster rate than that of spontaneous rotation, F1 still couples the rotation with hydrolysis. This implies that the mechanical forward rotation largely enhances the ATP-binding rate. Numerical analysis of this result suggests that the rate constant of ATP binding increases significantly, at least by a factor of 10 during the 80° substep.
Additional evidence for mechanical modulation of the reaction
Another implication regarding the mechanical modulation of catalysis came from the manipulation of F1 in an inhibitory state. During catalytic turnover in ATP hydrolysis, F1 stochastically lapses into an inhibitory state, pausing rotation by tightly holding ADP that has to be released to continue the reaction.29,43 This inhibitory state is termed the ADP-inhibited form. When mechanically manipulated, F1 readily resumes the active rotation, releasing the tightly bound ADP into solution.44 This mechanical activation highly depends on the direction of manipulation and duration of manipulation; when rotated in the forward direction and held for a longer time, the activation probability drastically increases. It was demonstrated that the rate constant of mechanical activation triggered by ADP release increases exponentially. Recently, we performed similar experiments to investigate how ATP binding and hydrolysis are modulated upon γ rotation by stalling F1 in the ATP-binding or hydrolysis-waiting state.45 It was found that the ATP-binding rate and association constant of ATP are also exponentially enhanced upon γ rotation (by a factor of 1 × 104 or more for the association constant during the 80° substep), but hydrolysis exhibits weak angle dependence. These findings indicate that the ATP-binding process is the major torque-generating step. All of the reaction steps examined thus far are accelerated upon γ subunit rotation. Since these reactions occur on different β subunits, each β subunit accelerates other reactions on different β subunits by pushing the γ subunit. This would be one of the principal bases of cooperativity among β subunits. Although ATP synthesisvia the reverse rotation is a unique feature of F1, the core structural element around the catalytic site of F1 shares common and well-conserved structural features with other ATP-driven motors and ATPases.46 Considering this point, the ability to mechanically modulate catalysis would be shared by other molecular machines, although the degree of sophistication of mechanochemical coupling would be largely different. In fact, several reports demonstrated that the catalytic reaction rate of myosin or kinesin motor could be enhanced or suppressed by external manipulation.47–50 These properties are discussed in the context of cooperativity between the 2 catalytic head domains of the motors.
Implications for synthetic molecular systems
The important implications we learned from F1-ATPase are as follows. (1) Mechanical force can regulate and modulate the rate and equilibrium constants of chemical reactions; (2) mechanical modulation enables programming of cooperativity among catalytic reaction centres and leads to the unidirectional motion of molecular machines; and (3) the mechanical connection of two motors allows novel energy conversion. The same concepts should be applicable to synthetic chemical molecules. Although this has not been attempted frequently, the mechanical control of chemical reactions has been reported. Moore and co-workers successfully demonstrated mechanochemistry in synthetic molecules by using a polymeric gel.51 Tensile force on the polymer gel induced the structural isomerisation of a mechanophore moiety introduced in the polymer chain. Similar attempts were made using a different method;52,53 a responsive moiety was linked to polymer chains, and the solution of the conjugate was subjected to an ultrasonic wave that stretched the polymer and thus exerted tensile force on the moiety. Moore’s group reported that a geometrically specific reaction of a cyclobutene ring opening was induced under tensile force.53 Initiation of the catalytic reaction52 by ultrasonically induced stretching was also demonstrated by the Sijbesma group.52 Once the state-of-the-art single-molecular manipulation and analysis are applied to such synthetic molecular systems, new experimental approaches for more quantitative and precise control of mechanophores will be enabled, leading to the rational design of mechanosensitive moieties or molecular systems.
There are also reports on the development of unidirectionally moving synthetic molecular motors54 such as the overcrowded alkenes developed by Feringa55 and the multistation catenanes and molecular walkers developed by Leigh.56,57 We are very interested in these works. However, although their chemical properties were extensively studied, the mechanical properties of synthetic motors such as torque or force and step size remain to be elaborated. In addition, to our knowledge, the mechanical linkage of two molecular motors for energy conversion as observed in FoF1-ATP synthase has not yet been conducted. We do not consider this a fancy technique. Rather, it appears feasible to connect existing motors, for example, F1-ATPase and a light-driven synthetic motor54 (Fig. 6). When linked with consideration of the step size and the torque of two motors, the hybrid motor realises the photosynthesis that directly converts light energy into chemical energy viaATP synthesis. The assembly of biomolecular and synthetic molecular motors would pave the way for new energy conversion technologies.
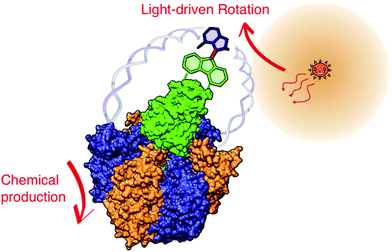 |
| | Fig. 6 Light-driven ATP synthesis by combination of light-driven artificial motor and F1-ATPase. Schematic image of the artificial hybrid system composed of two different motors: synthetic light-driven motor and F1-ATPase. Rotor parts are directly linked, and stator parts are connected via a flexible joint (DNA strand). The chemical structure of the synthetic motor does not show the reality. The expectation is that the light-driven motor functions similarly as Fo in ATP synthase to reverse F1 and induce ATP synthesis. | |
Acknowledgements
We thank all members of the Noji Laboratory.
References
- A. Goel, M. D. Frank-Kamenetskii, T. Ellenberger and D. Herschbach, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 8485–8489 CrossRef CAS.
- B. Maier, D. Bensimon and V. Croquette, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 12002–12007 CrossRef CAS.
- G. J. Wuite, S. B. Smith, M. Young, D. Keller and C. Bustamante, Nature, 2000, 404, 103–106 CrossRef.
- R. V. Dalal, M. H. Larson, K. C. Neuman, J. Gelles, R. Landick and S. M. Block, Mol. Cell, 2006, 23, 231–239 CrossRef CAS.
- M. H. Larson, W. J. Greenleaf, R. Landick and S. M. Block, Cell, 2008, 132, 971–982 CrossRef CAS.
- M. D. Wang, M. J. Schnitzer, H. Yin, R. Landick, J. Gelles and S. M. Block, Science, 1998, 282, 902–907 CrossRef CAS.
- Y. R. Chemla, K. Aathavan, J. Michaelis, S. Grimes, P. J. Jardine, D. L. Anderson and C. Bustamante, Cell, 2005, 122, 683–692 CrossRef CAS.
- D. E. Smith, S. J. Tans, S. B. Smith, S. Grimes, D. L. Anderson and C. Bustamante, Nature, 2001, 413, 748–752 CrossRef CAS.
- M. Yoshida, E. Muneyuki and T. Hisabori, Nat. Rev. Mol. Cell Biol., 2001, 2, 669–677 CrossRef CAS.
- W. Junge, H. Lill and S. Engelbrecht, Trends Biochem. Sci., 1997, 22, 420–423 CrossRef CAS.
- M. Diez, B. Zimmermann, M. Borsch, M. Konig, E. Schweinberger, S. Steigmiller, R. Reuter, S. Felekyan, V. Kudryavtsev, C. A. Seidel and P. Graber, Nat. Struct. Mol. Biol., 2004, 11, 135–141 CrossRef CAS.
- P. D. Boyer, Annu. Rev. Biochem., 1997, 66, 717–749 CrossRef CAS.
- J. P. Abrahams, A. G. Leslie, R. Lutter and J. E. Walker, Nature, 1994, 370, 621–628 CrossRef CAS.
- G. Oster and H. Wang, J. Bioenerg. Biomembr., 2000, 32, 459–469 CrossRef CAS.
- T. Masaike, F. Koyama-Horibe, K. Oiwa, M. Yoshida and T. Nishizaka, Nat. Struct. Mol. Biol., 2008, 15, 1326–1333 CrossRef CAS.
- R. I. Menz, J. E. Walker and A. G. Leslie, Cell, 2001, 106, 331–341 CrossRef CAS.
- T. M. Duncan, V. V. Bulygin, Y. Zhou, M. L. Hutcheon and R. L. Cross, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 10964–10968 CrossRef CAS.
- D. Sabbert, S. Engelbrecht and W. Junge, Nature, 1996, 381, 623–625 CrossRef CAS.
- H. Noji, R. Yasuda, M. Yoshida and K. Kinosita, Jr., Nature, 1997, 386, 299–302 CrossRef CAS.
- K. Hayashi, H. Ueno, R. Iino and H. Noji, Phys. Rev. Lett., 2010, 104, 218103 CrossRef.
- H. Noji, K. Hasler, W. Junge, K. Kinosita, Jr., M. Yoshida and S. Engelbrecht, Biochem. Biophys. Res. Commun., 1999, 260, 597–599 CrossRef CAS.
- H. Omote, N. Sambonmatsu, K. Saito, Y. Sambongi, A. Iwamoto-Kihara, T. Yanagida, Y. Wada and M. Futai, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 7780–7784 CrossRef CAS.
- O. Panke, D. A. Cherepanov, K. Gumbiowski, S. Engelbrecht and W. Junge, Biophys. J., 2001, 81, 1220–1233 CrossRef CAS.
- D. Spetzler, J. York, D. Daniel, R. Fromme, D. Lowry and W. Frasch, Biochemistry, 2006, 45, 3117–3124 CrossRef CAS.
- T. Hisabori, A. Kondoh and M. Yoshida, FEBS Lett., 1999, 463, 35–38 CrossRef CAS.
- R. Yasuda, H. Noji, K. Kinosita, Jr. and M. Yoshida, Cell, 1998, 93, 1117–1124 CrossRef CAS.
- Y. Rondelez, G. Tresset, T. Nakashima, Y. Kato-Yamada, H. Fujita, S. Takeuchi and H. Noji, Nature, 2005, 433, 773–777 CrossRef CAS.
- R. Yasuda, H. Noji, M. Yoshida, K. Kinosita, Jr. and H. Itoh, Nature, 2001, 410, 898–904 CrossRef CAS.
- Y. Hirono-Hara, H. Noji, M. Nishiura, E. Muneyuki, K. Y. Hara, R. Yasuda, K. Kinosita, Jr. and M. Yoshida, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 13649–13654 CrossRef CAS.
- K. Shimabukuro, R. Yasuda, E. Muneyuki, K. Y. Hara, K. Kinosita, Jr. and M. Yoshida, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14731–14736 CrossRef CAS.
- K. Adachi, K. Oiwa, T. Nishizaka, S. Furuike, H. Noji, H. Itoh, M. Yoshida and K. Kinosita, Jr., Cell, 2007, 130, 309–321 CrossRef CAS.
- B. Zimmermann, M. Diez, N. Zarrabi, P. Graber and M. Borsch, EMBO J., 2005, 24, 2053–2063 CrossRef CAS.
- H. Sielaff, H. Rennekamp, S. Engelbrecht and W. Junge, Biophys. J., 2008, 95, 4979–4987 CrossRef CAS.
- T. Ariga, BioSystems, 2008, 93, 68–77 CrossRef CAS.
- T. Nishizaka, K. Oiwa, H. Noji, S. Kimura, E. Muneyuki, M. Yoshida and K. Kinosita, Jr., Nat. Struct. Mol. Biol., 2004, 11, 142–148 CrossRef CAS.
- R. Watanabe, R. Iino and H. Noji, Nat. Chem. Biol., 2010, 6, 814–820 CrossRef CAS.
- W. Junge, H. Sielaff and S. Engelbrecht, Nature, 2009, 459, 364–370 CrossRef CAS.
- R. Shimo-Kon, E. Muneyuki, H. Sakai, K. Adachi, M. Yoshida and K. Kinosita, Jr., Biophys. J., 2010, 98, 1227–1236 CrossRef CAS.
- H. Itoh, A. Takahashi, K. Adachi, H. Noji, R. Yasuda, M. Yoshida and K. Kinosita, Nature, 2004, 427, 465–468 CrossRef CAS.
- Y. Rondelez, G. Tresset, K. V. Tabata, H. Arata, H. Fujita, S. Takeuchi and H. Noji, Nat. Biotechnol., 2005, 23, 361–365 CrossRef CAS.
- T. Pilizota, T. Bilyard, F. Bai, M. Futai, H. Hosokawa and R. M. Berry, Biophys. J., 2007, 93, 264–275 CrossRef CAS.
- Y. Iko, K. V. Tabata, S. Sakakihara, T. Nakashima and H. Noji, FEBS Lett., 2009, 583, 3187–3191 CrossRef CAS.
- J. M. Jault, C. Dou, N. B. Grodsky, T. Matsui, M. Yoshida and W. S. Allison, J. Biol. Chem., 1996, 271, 28818–28824 CrossRef CAS.
- Y. Hirono-Hara, K. Ishizuka, K. Kinosita, Jr., M. Yoshida and H. Noji, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4288–4293 CrossRef CAS.
-
R. Watanabe and D. Okunoet al., to be submitted.
- H. Noji, T. Amano and M. Yoshida, J. Bioenerg. Biomembr., 1996, 28, 451–457 CrossRef CAS.
- Y. Oguchi, S. V. Mikhailenko, T. Ohki, A. O. Olivares, E. M. De La Cruz and S. Ishiwata, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7714–7719 CrossRef CAS.
- Y. Oguchi, S. V. Mikhailenko, T. Ohki, A. O. Olivares, E. M. De La Cruz and S. Ishiwata, Nat. Chem. Biol., 2010, 6, 300–305 CrossRef CAS.
- S. Uemura and S. Ishiwata, Nat. Struct. Biol., 2003, 10, 308–311 CrossRef CAS.
- S. Uemura, K. Kawaguchi, J. Yajima, M. Edamatsu, Y. Y. Toyoshima and S. Ishiwata, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5977–5981 CrossRef CAS.
- D. A. Davis, A. Hamilton, J. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martinez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72 CrossRef CAS.
- A. Piermattei, S. Karthikeyan and R. P. Sijbesma, Nat. Chem., 2009, 1, 133–137 CrossRef CAS.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423–427 CrossRef CAS.
- E. R. Kay, D. A. Leigh and F. Zerbetto, Angew. Chem., Int. Ed., 2007, 46, 72–191 CrossRef CAS.
- N. Koumura, R. W. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Nature, 1999, 401, 152–155 CrossRef CAS.
- D. A. Leigh, J. K. Wong, F. Dehez and F. Zerbetto, Nature, 2003, 424, 174–179 CrossRef CAS.
- M. von Delius, E. M. Geertsema and D. A. Leigh, Nat. Chem., 2009, 2, 96–101.
Footnotes |
| † Funding: This work was partially supported by Grants-in-Aid for Scientific Research (No. 18074005 to H. N.) and by special education and research expenses (to H. N.) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan. |
| ‡ Conflict of Interest: None declared. |
|
| This journal is © The Royal Society of Chemistry 2011 |
Click here to see how this site uses Cookies. View our privacy policy here. 





