Exploiting single-ion anisotropy in the design of f-element single-molecule magnets
Jeffrey D.
Rinehart
and
Jeffrey R.
Long
*
Department of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: jrlong@berkeley.edu
First published on 7th September 2011
Abstract
Scientists have long employed lanthanide elements in the design of materials with extraordinary magnetic properties, including the strongest magnets known, SmCo5 and Nd2Fe14B. The properties of these materials are largely a product of fine-tuning the interaction between the lanthanide ion and the crystal lattice. Recently, synthetic chemists have begun to utilize f-elements—both lanthanides and actinides—for the construction of single-molecule magnets, resulting in a rapid expansion of the field. The desirable magnetic characteristics of the f-elements are contingent upon the interaction between the single-ion electron density and the crystal field environment in which it is placed. This interaction leads to the single-ion anisotropies requisite for strong single-molecule magnets. Therefore, it is of vital importance to understand the particular crystal field environments that could lead to maximization of the anisotropy for individual f-elements. Here, we summarize a qualitative method for predicting the ligand architectures that will generate magnetic anisotropy for a variety of f-element ions. It is hoped that this simple model will serve to guide the design of stronger single-molecule magnets incorporating the f-elements.
The rise of f-elements in single-molecule magnetism
It has been nearly twenty years since the discovery that a discrete molecule could possess an energy barrier to the reorientation of its molecular spin that was large enough to observe magnetic hysteresis.1 Such single-molecule magnets can have magnetic relaxation times that are more than 108 times slower than normal molecular paramagnets. Their synthesis, characterization, and implementation has flourished as a lively crossroads for chemistry, physics, and materials science. Single-molecule magnets offer the intriguing possibility of creating switchable, molecular-scale devices that store or manipulate information using the orientation of their molecular spin.2 Their quantum coherent properties have sparked further interest, as the possibility of applications in quantum computing is becoming apparent.3 Although the majority of research in this area has been performed on large ensembles of molecules, recent advances have shown that single-molecule magnets can be successfully transferred to surfaces with retention of their magnetic behavior4 and potentially exploited as spintronic devices.5 However, any application is limited by the extremely low temperatures or fast timescale required for observation of slow magnetic relaxation.The vast majority of single-molecule magnets have anisotropy barriers to spin reversal lower than 60 cm−1 (86 K), which corresponds to a 4 K relaxation time of approximately 2 s.6 Thus, from the beginning of the field of single-molecule magnetism, a major goal for chemists has been to design and synthesize molecules that retain functionality in a more readily accessed temperature regime. Progress toward this goal can be measured in several ways. First, the anisotropy barrier, Ueff, as defined by the Arrhenius relationship for relaxation time, τ = τ0exp(Ueff/kBT), dictates the high-temperature dynamics of single-molecule magnets. This is because at higher temperatures relaxation can occur via excitation to a low-lying excited state and subsequent de-excitation to either of the orientations of the ground state spin. However, given a low enough temperature, single-molecule magnets will deviate from Arrhenius behavior as alternate relaxation processes that shortcut the barrier begin to dominate. In this low-temperature regime, hysteresis in a plot of magnetization vs. field is often used as a measure of the long-timescale dynamics of a complex. If a potential application requires only very brief magnetization times, then the anisotropy barrier is key to measuring the utility of a molecule; however, if a measurement timescale of 1 s or longer is required, magnetic hysteresis is a more apt measure.
Fig. 1 and Table 1 display the highest measured hysteresis temperature and anisotropy barrier for the strongest f-element and transition metal single-molecule magnets.7 From the data, it is evident that the f-elements have a lot to offer toward enhancing the strength of molecular magnets. For instance, from the first single-molecule magnet discovered in 1993 to present, the largest anisotropy barrier and highest hysteresis temperature have increased approximately 60% and 70%, respectively, for transition metal clusters and approximately 1200% and 370% respectively for f-elements. Their properties are even more impressive given that nearly all of the results in Fig. 1 have been published in the last several years. In fact, although the f-elements figured prominently in the unravelling of the physics of paramagnetic relaxation,9 their weak magnetic exchange coupling initially made them undesirable targets for single-molecule magnetism. Based on the first single-molecule magnet discovered, Mn12O12(O2CMe)16(H2O)4,1 high-spin, strongly-coupled transition metal clusters were considered to be the most promising targets and still comprise the majority of the research in the field. However, the discovery in 2003 that lanthanide phthalocyanine sandwich complexes, [LnPc2]n (LnIII = Tb, Dy, Ho; H2Pc = phthalocyanine; n = −1, 0, +1), could display unprecedented relaxation behavior7l led to the gradual acceptance of the lanthanides in single-molecule magnetism.
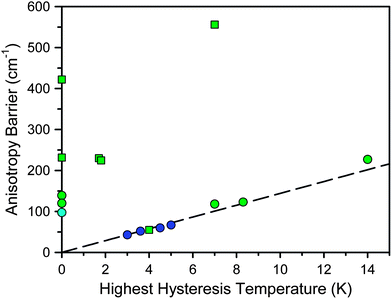 | ||
| Fig. 1 Plot of the highest recorded hysteresis temperature vs. the anisotropy barrier for selected single-molecule magnets. Here, hysteresis is defined as showing a measurable coercive field in a plot of field vs. magnetization. Molecules not reporting hysteresis are placed along the y-axis. Blue, green, and cyan symbols represent transition metal-, lanthanide-, and actinide-based single-molecule magnets, respectively. Squares and circles represent single-ion and multinuclear clusters, respectively. The dashed line represents the parameters leading to 1 s relaxation, assuming Arrhenius behavior with τ0 = 10−9 s. | ||
| Moleculea | U eff /cm−1 | Hysteresis T /K | Ref. |
|---|---|---|---|
| a H2(Pc(OEt)8) = 2,3,9,10,16,17,23,24-octaethoxyphthalocyanine; saoH2 = 2-hydroxybenzaldehyde oxime; hfpip = 1,1,1,5,5,5-hexafluoro-4-(4-tert-butylphenylimino)-2-pentanonate; D2py2(TBA) = 4,4′-(5-(3,3-dimethylbut-1-ynyl)-1,3-phenylene)bis(diazomethylene)dipyridine; THF = tetrahydrofuran; H2bmh = 1,2-bis(2-hydroxy-3-methoxybenzylidene) hydrazine; H2msh = 3-methoxysalicylaldehyde hydrazine; H3L = [(2-hydroxy-3-methoxyphenyl)methylene] hydrazide; H(L1) = o-vanillin; H2(L2) = 2-hydroxymethyl-6-methoxyphenol; H2COT = cyclooctatetraene; H2Pc = phthalocyanine; Hsal = salicylaldehyde; H3(L3) = 6,6′-(1E,1′E)-(2,2-dimethylpropane-1,3-diyl)bis(azan-1-yl-1-ylidene)bis(methan-1-yl-1-ylidene)bis(2-methoxyphenol); HR = 1-isopropoxydodecane; H2iPc = 2,3,9,10,16,17,23,24-octa(isopropylidenedioxy)phthalocyanine. | |||
| Mn12O12(O2CMe)16(H2O)4 | 43 | 3 | 1b |
| Mn12O12(O2CCH2Br)16(H2O)4 | 52 | 3.6 | 7a |
| [Dy(Pc(OEt)8)2]+ | 55 | 4 | 7b |
| Mn6O2(sao)6(O2CPh)2(EtOH)4 | 60 | 4.5 | 7c |
| [Co(hfpip)2(D2py2(TBA))]2 | 67 | 5 | 7d |
| [NpO2Cl2][NpO2Cl(THF)3]2 | 97 | 7e | |
| Dy4(OH)2(bmh)2(msh)4Cl2 | 118 | 7 | 7f |
| [Dy4(L)4(MeOH)6] | 120 | 7g | |
| [{[(Me3Si)2N]2(THF)Dy}2N2]− | 123 | 8.3 | 7h |
| [Dy6(OH)4(L1)4(L2)2(H2O)9Cl]5+ | 139 | 7i | |
| (C5Me5)Er(COT) | 225 | 1.8 | 7j |
| [{[(Me3Si)2N]2(THF)Tb}2N2]− | 227 | 14 | 7k |
| [TbPc2]− | 230 | 1.7 | 7l |
| Dy(sal)(NO3)(MeOH)Zn(L3) | 234 | 7m | |
| Tb((RO)8Pc)2 | 422 | 7n | |
| TbiPc2 | 566 | 7 | 7o |
Paramount amongst the factors distinguishing the f-elements as spin-carriers for single-molecule magnets is their unparalleled single-ion anisotropy. Although the physical understanding of this effect is by no means a new concept, a simple methodology for targeting highly anisotropic single-molecule magnets without complex calculations or labor-intensive empirical characterization of the crystal field could be very beneficial to exploratory research. This perspective attempts to lay out a simple model for predicting ligand field environments that should be amenable to single-molecule magnet behavior.
Complexity of the f-element electronic structure
While strong single-ion anisotropy makes the f-elements enticing targets for single-molecule magnet research, it also leads to an extremely complex electronic structure. The simplifications and assumptions made for interpreting the magnetism of most transition metal complexes can lead to gross inaccuracies when applied to f-elements. This is because electronic spin is no longer the only significant source of angular momentum in the system. The near (but not complete) degeneracy of the f orbitals leads to a large unquenched orbital moment that must be considered. Thus, for an ion of interest for single-molecule magnetism, such as Dy(III), simply defining the electronic structure by the number of valence electrons (4f9) is far less descriptive than the term symbol for the spin–orbit coupled ground state: 6H15/2 (S = 5/2; L = 5; J = 15/2) (see Fig. 2). The spin–orbit coupled quantum number, J, is of utmost importance, since the spin–orbit coupling energy is generally larger than the effect of the crystal field for f-elements. Therefore, instead of the spin–orbit interaction acting as a perturbation on the crystal field, the reverse is usually a more accurate description.![Low energy electronic structure of the Dy(iii) ion with sequential perturbations of electron-electron repulsions, spin–orbit coupling, and the crystal field. The crystal field splitting is constructed from a model for the complex, Dy[(Me3Si)2N]3.8 Energy is measured relative to the ground crystal field (mJ) state. Further complications due to mixing between states have been neglected in favor of clarity.](/image/article/2011/SC/c1sc00513h/c1sc00513h-f2.gif) | ||
| Fig. 2 Low energy electronic structure of the Dy(III) ion with sequential perturbations of electron-electron repulsions, spin–orbit coupling, and the crystal field. The crystal field splitting is constructed from a model for the complex, Dy[(Me3Si)2N]3.8 Energy is measured relative to the ground crystal field (mJ) state. Further complications due to mixing between states have been neglected in favor of clarity. | ||
This subordination of the crystal field to the spin–orbit interaction makes it a minor factor in the overall electronic structure, yet it turns out to be a key factor in creating single-molecule magnets with f-elements. The interaction of the ground spin–orbit coupled J state with the crystal field generates the magnetic anisotropy barrier separating opposite orientations of the spin ground state. To continue with the Dy(III) ion example, the ground J state of the free-ion is sixteen-fold degenerate (2JDy + 1 states) and composed of magnetic substates, mJ, characterized by mJ = ±15/2, ±13/2, ±11/2, ±9/2, ±7/2, ±5/2, ±3/2, ±1/2 (+J, J − 1, J − 2,…, −J). These projections of the total angular momentum quantum number can be affected differently by the surrounding crystal field, thereby removing the (2J + 1)-fold degeneracy of the ground state.10 This splitting, in combination with the strong spin–orbit interaction, links the orientation of the spin to the strength and symmetry of the ligand field. The implication to single-molecule magnets is that we can increase single-ion anisotropy simply by judiciously choosing the coordination environment of the lanthanide ion.
While the magnitude of the crystal field splitting is difficult to calculate ab initio and time-consuming to determine empirically, several empirical methodologies can be employed to do so. These methods include the simultaneous least squares fitting of paramagnetic NMR shifts and magnetic susceptibility data,11 low-temperature spectroscopic analysis of high-symmetry single crystals,12 and computational fitting of magnetic susceptibility data to a Hamiltonian with terms accounting for interelectronic repulsion, spin–orbit coupling, ligand field effects, isotropic exchange interactions, and the applied magnetic field.13 These methods are all able to characterize compounds that have shown interesting behavior, but are unable to predict which molecules will have the requisite electronic structure for showing single-molecule magnet behavior. The following section takes a model that has long been used to explain single-ion anisotropy and applies it to the specific application of designing single-molecule magnets.
Exploiting single-ion anisotropy in the design of f-element single-molecule magnets
The search for electronic structures leading to strong f-element single-molecule magnetism has two underlying imperatives. First, the ground state should be doubly-degenerate and of a high magnitude ±mJ quantum number. This ensures that a high magnetic moment is maintained at temperatures where only the ground state is significantly populated. Double degeneracy is imperative because single-molecule magnets are defined by the bistability of their ground state; a singlet ground state would be of little interest magnetically. In the absence of a magnetic field, breaking the ±mJ degeneracy is forbidden for Kramers (odd electron count) ions due to time-reversal symmetry considerations.15 Thus, Dy(III) ions will always maintain a degenerate ground state while Tb(III) ions must have a strictly axial crystal field symmetry to do so.The second requirement for strong single-ion anisotropy is a large separation between the bistable ground ±mJ state and the first excited ±mJ state. This separation defines the energy required to relax the spin, assuming a temperature-dependent relaxation mechanism.16 If these two conditions are satisfied, we should maintain a magnetic ground state and severely slow the magnetic relaxation at temperatures below the first excitation energy.
To judge whether these conditions will be satisfied for a particular molecule, the simplest form of the electronic Hamiltonian can be used: ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ion +
ion + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cf (where
cf (where ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ion is the free ion Hamiltonian and
ion is the free ion Hamiltonian and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cf is the crystal field symmetry Hamiltonian. First, let us consider the single-ion contributions. Given an axial frame of reference,17 the basic shapes of the lowest J states can be described mathematically by the quadrupole moment of the f-electron charge cloud, which is prolate (axially elongated), oblate (equatorially expanded), or isotropic (spherical). This shape variation of the f-electron charge cloud arises from the strong angular dependence of the f orbitals. For example, the 4fx(x2 − 3y2) orbital is strongly oblate (see Fig. 3), so an ion possessing only an f-electron in this orbital, such as a Ce(III) ion, will retain an oblate-shaped electron density. Because orbital occupations are simply determined by Hund's rules, we can easily approximate the distribution of the free-ion f-electron density for each ion. The shapes of the 4f electron densities are depicted in Fig. 4, and provide a simple yet powerful visualization of the free-ion contribution to the 4f electronic structure.
cf is the crystal field symmetry Hamiltonian. First, let us consider the single-ion contributions. Given an axial frame of reference,17 the basic shapes of the lowest J states can be described mathematically by the quadrupole moment of the f-electron charge cloud, which is prolate (axially elongated), oblate (equatorially expanded), or isotropic (spherical). This shape variation of the f-electron charge cloud arises from the strong angular dependence of the f orbitals. For example, the 4fx(x2 − 3y2) orbital is strongly oblate (see Fig. 3), so an ion possessing only an f-electron in this orbital, such as a Ce(III) ion, will retain an oblate-shaped electron density. Because orbital occupations are simply determined by Hund's rules, we can easily approximate the distribution of the free-ion f-electron density for each ion. The shapes of the 4f electron densities are depicted in Fig. 4, and provide a simple yet powerful visualization of the free-ion contribution to the 4f electronic structure.
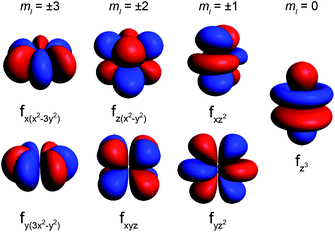 | ||
| Fig. 3 Representations of the 4f orbitals from highest magnitude ml (most oblate shape) to lowest magnitude ml (most prolate shape). | ||
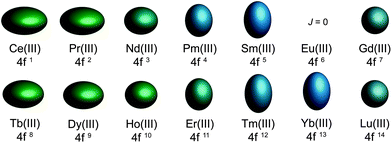 | ||
| Fig. 4 Quadrupole approximations of the 4f-shell electron distribution for the tripositive lanthanides. Values are calculated using the total angular momentum quantum number (J), the Stevens coefficient of second order (α) and the radius of the 4f shell squared 〈r2〉.14Europium is not depicted due to a J = 0 ground state. | ||
With the free-ion electron densities in hand, we can next consider the type of crystal field that will lead to a highly anisotropic ground state for a given f-element. There are two general optimum ligand architectures depending on whether the basic overall shape of free-ion electron density is oblate, as for Ce(III), Pr(III), Nd(III), Tb(III), Dy(III), and Ho(III), or prolate, as for Pm(III), Sm(III), Er(III), Tm(III), and Yb(III). To maximize the anisotropy of an oblate ion, we should place it in a crystal field for which the ligand electron density is concentrated above and below the xy plane, as, for example, is the case with a sandwich-type ligand geometry. In such a crystal field, the ground state will have bistable orientations of mJ parallel and antiparallel to the molecular axis (large mJ) because these configurations minimize repulsive contacts between ligand and f-electron charge clouds (see Fig. 5, left). Conversely, low magnitude mJ orientations will force the f-electron charge cloud into direct contact with the ligands, creating a high-energy state. For a prolate ion, an equatorially-coordinating geometry is preferable so as to minimize charge contact with the axially-located f-element electron density, as shown at the right in Fig. 5.
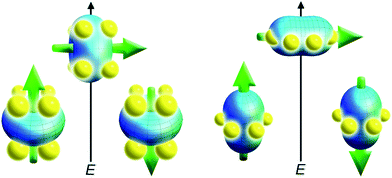 | ||
| Fig. 5 Depictions of low- and high-energy configurations of the f-orbital electron density with respect to the crystal field environment for a 4f ion of oblate (left) and prolate (right) electron density. The green arrow represents the orientation of the spin angular momentum coupled to the orbital moment. For the oblate electron density, an axial “sandwich”-type crystal field minimizes the energy of the mJ = J (high moment) state, making it a desirable target for single-molecule magnet design. In the prolate electron density case, an equatorial electron configuration minimizes the energy of the mJ = J state. | ||
This very simple model offers a surprising amount of information about how to approach single-molecule magnet design for the f-elements. First of all, it explains why the majority of systems studied thus far have involved axially-coordinated ligand environments (because the most used ion, Dy(III), has an oblate electron density). In fact, the Dy(III) ion may represent the ideal ion for single-molecule magnetism: it is a Kramers ion, so a doubly degenerate mJ ground state is ensured. It combines a large-moment 6H15/2 ground state18 with significant anisotropy of the 4f shell. The Tb(III) ion offers similar properties with an even greater electronic anisotropy, however a bistable ground state requires that rigorous axial symmetry be maintained,7l or that magnetic coupling be employed to create an exchange bias,7k,o since bistability is not guaranteed for a non-Kramers ion. This model also suggests a less explored method of generating strong single-ion anisotropy for single-molecule magnet synthesis involving strongly prolate ions like Tm(III) and Yb(III). Here, an equatorial ligand coordination environment can be paired with an ion of prolate electron density to generate the anisotropy barrier.
Examples of single-ion anisotropy in f-element single-molecule magnets
Lanthanide bisphthalocyanine complexes
The series of mononuclear complexes [LnPc2]n (LnIII = Tb, Dy, Ho; H2Pc = phthalocyanine; n = −1, 0, +1), adopting the sandwich structure depicted in Fig. 6, were the first lanthanide single-molecule magnets to be identified.7l The anisotropy barriers measured for the terbium complex and its derivatives remain among the very highest yet discovered. Its low-lying electronic structure was determined by the simultaneous least squares fitting of paramagnetic NMR shifts and magnetic susceptibility data (see Fig. 7).21 From the model of f-element single-ion anisotropy laid out in the preceding section, it is easy to see that as the 4f electron density changes from highly oblate (Tb(III)) to highly prolate (Yb(III)), the ground state shifts from higher magnitude mJ states to lower magnitude mJ states due to the sandwich-type ligand environment of the Pc2− ligands. Also, the total energy splitting varies by almost 200 cm−1 from the ions with the most aspherical electron densities to those with the most spherical. This is simply a confirmation that the oblate electron densities of Tb(III) and Dy(III) ions will promote strongly axial single-ion anisotropies and thus function as single-molecule magnets in this type of environment.![Representations of f-element structures displaying strong single-ion anisotropy. (Upper left) Structure of [TbPc2]− (Pc2− = phthalocyanine) with red, blue, and gray spheres represent terbium, nitrogen, and carbon respectively. Hydrogen atoms have been removed for clarity. (Upper right) Structure of An(COT)2 ((COT)2− = cyclooctatetraene; An = U(iv), Np(iv), and Pu(iv)) with orange, gray, and white spheres representing An, carbon, and hydrogen, respectively. (Lower) Structure of SmCo5 with purple and green spheres representing samarium and cobalt respectively. Layers above and below the one depicted contain only cobalt in a similar arrangement of hexagons rotated by 30°.](/image/article/2011/SC/c1sc00513h/c1sc00513h-f6.gif) | ||
| Fig. 6 Representations of f-element structures displaying strong single-ion anisotropy. (Upper left) Structure of [TbPc2]− (Pc2− = phthalocyanine) with red, blue, and gray spheres represent terbium, nitrogen, and carbon respectively. Hydrogen atoms have been removed for clarity. (Upper right) Structure of An(COT)2 ((COT)2− = cyclooctatetraene; An = U(IV), Np(IV), and Pu(IV)) with orange, gray, and white spheres representing An, carbon, and hydrogen, respectively. (Lower) Structure of SmCo5 with purple and green spheres representing samarium and cobalt respectively. Layers above and below the one depicted contain only cobalt in a similar arrangement of hexagons rotated by 30°. | ||
![Splitting of the spin–orbit coupled (J) ground state by the crystal field for [LnPc2]− compounds.21](/image/article/2011/SC/c1sc00513h/c1sc00513h-f7.gif) | ||
| Fig. 7 Splitting of the spin–orbit coupled (J) ground state by the crystal field for [LnPc2]− compounds.21 | ||
While this explains the general features of the diagram there are a number of interesting subtleties that require a more detailed version of the model. For instance, why is there such a noticeable separation between the ground state and first excited state for the Tb(III) complex but not for the Dy(III) complex, and why are the mJ states of the Yb(III) complex not ordered from lowest to highest as might be expected for a strongly prolate ion? The answer to these questions lies in the anisotropy of individual mJ states. As depicted in Fig. 8, a graphical representation of the angular dependence of the 4f charge density of the various mJ states can be constructed to further rationalize the results in Fig. 7.19 A cursory consideration of the anisotropy of these states reveals that the mJ = ±6 state of the Tb(III) ion has an extremely oblate electron density, making it ideal for the bis-phthalocyanine sandwich-type geometry. In contrast to this, the mJ = ±5, ±4, ±3, ±2, ±1, and 0 states all have prolate electron densities making them extremely unfavorable for the sandwich-type geometry. This extreme contrast leads to a large separation of the ground mJ = ±6 state from the lowest excited state—exactly the requisite conditions for strong single-molecule magnet behavior.
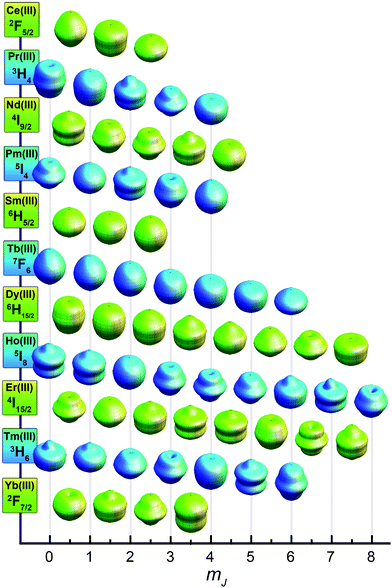 | ||
| Fig. 8 Approximations of the angular dependence of the total 4f charge density for mJ states composing the lowest spin–orbit coupled (J) state for each lanthanide. In the absence of a crystal field, all mJ states for each lanthanide ion are degenerate. Values are calculated from parameters derived in ref. 19. | ||
While most of the ions show some general progression from highest to lowest mJ state or vice versa, ytterbium has a more complicated energy splitting. Tellingly, the shapes of the mJ states for the Yb(III) ion displayed in Fig. 8 defy the general classification of oblate or prolate and take on a more varied angular dependence. However, once again the splitting shown in Fig. 7 can be rationalized in terms of the interaction between the free ion charge densities and the ligand field. The mJ = ±7/2 state has almost no oblate density, making it clearly the highest energy state, whereas the mJ = ±5/2 state is mostly composed of oblate density, with only small lobes extending along the z-axis. Considering that the Pc2− ligands have a central cavity along the z-axis, this should not create too much of an unfavorable interaction. However, the mJ = ±3/2 and ±1/2 states have considerable prolate lobes that should form an intermediate interaction between the favorable one of the mJ = ±5/2 state and the extremely unfavorable one of mJ = ±7/2 state. Interestingly, these charge densities also suggest that in an equatorial coordination environment the Yb(III) ion should have a highly favorable, well-separated mJ = ±7/2 ground state. Empirical electronic structure studies have shown this, but as of yet no single-molecule magnet behavior has been demonstrated.20
SmCo5
While not a molecular species, it is interesting to apply the above model of anisotropy to an intermetallic compound wherein lanthanide single-ion anisotropy generates one of the strongest magnets known. Because the high coercive field of SmCo5 is largely due to the magnetic anisotropy created by the delocalized band structure of cobalt interacting with the localized electrons on the Sm(III) ions, we can approximate its anisotropy in terms of a localized electronic model. The crystal structure is composed of sheets of Sm(III) ions surrounded by six equatorially-coordinated cobalt atoms (see Fig. 6). Above and below these planes are sheets of cobalt atoms that form a cylinder of charge density enclosing the Sm(III) ions. The strongly prolate shape of the mJ = ±5/2 state for Sm(III), as shown in Fig. 8, is well suited to form a low energy combination with this type of ligand charge density. This contrasts sharply with the oblate shapes of the mJ = ±3/2 and ±1/2 states that are both extremely unfavorable in this crystal field environment. This creates a highly anisotropic f-electron moment that is coupled to the delocalized cobalt moment, thus enforcing hard magnet behavior.It is interesting to note that all strong classical lanthanide magnets utilize only the early lanthanides (4fn, n < 7). This is due to the fact that the 4f electrons of less than half filled f-shells will couple ferromagnetically to the delocalized transition metal electrons leading to a higher moment and stronger magnetism, despite the lower contribution from the lanthanide ion.22 In single-molecule magnets, however, the late lanthanides can be used since magnetic coupling is either irrelevant (for mononuclear systems) or determined by the particular exchange pathway present. Thus molecular magnets can take advantage of the high moments of the later lanthanides while still exploiting the same properties that make magnets like SmCo5 so strong.
Actinocenes
The previous examples have focused on lanthanide systems. This is because, to a first approximation, the ground spin–orbit coupled state can be considered well-isolated and any mixing of states is negligible for the lanthanide ions of interest. This approximation tends to hold up reasonably well, since the generally weak interaction of the lanthanides with a crystal field is about an order of magnitude smaller than the spin–orbit coupling interaction.23 Thus, interactions between mJ states are minimized, and mJ remains a fairly good quantum number for describing the system. Deviations from this are well known and account for many of the subtleties of lanthanide spectroscopy,24 but they go beyond the scope of the simple model presented here. Such state-mixing deviations tend to be much more pronounced in the actinides, where stronger metal–ligand interactions are frequently observed. Although actinide single-molecule magnetism remains far less developed, these complications could eventually prove to be assets: greater metal–ligand interactions could provide greater excited state separation and enhanced magnetic coupling for multinuclear assemblies. The model described above still retains some predictive quality for understanding actinide single-ion anisotropy, but only in limited cases.For example, Np(COT)2 (neptunocene; (COT)2− = cyclooctatetraene dianion) contains the Np(IV) ion with three unpaired 5f-electrons. By analogy to Nd(III), which has an equivalent 4f3 electron count, Np(IV) has an oblate electron density that should be amenable to the sandwich-type ligand environment of the (COT)2− ligands. Recently, single-molecule magnet behavior was demonstrated in this compound, confirming the presence of significant single-ion anisotropy.25 The 5f4 species, Pu(COT)2 (plutonocene; (COT)2− = cyclooctatetraene dianion), also presents an interesting case since it shows only temperature-independent paramagnetism, despite having a paramagnetic 5I4 spin–orbit ground state.26 By comparison with Pm(III) (see Fig. 8), Pu(IV) should have a prolate electron density ground state. In the sandwich-type crystal field environment of the (COT)2− ligands, this leads to a lowering of the energy of the nonmagnetic mJ = 0 state. In agreement with this picture, the magnetic behavior observed for plutonocene is due to mixing between the non-magnetic ground state and low-lying excited states.
Conclusions
The above examples illustrate how a simple model of the f-element electronic structure can be applied to diverse situations to predict the presence of significant single-ion anisotropy. In many cases, this can lead to strong single-molecule magnet behavior. Interestingly, many of the molecules in Table 1 have ill-defined crystal field environments. Such low-symmetry molecules can also lead to strong anisotropy, but their behavior is difficult to predict. It is our hope that consideration of the factors leading to axial anisotropy in different f-elements will give rise to effective targeting of new single-molecule magnets with high anisotropy barriers, thus further spurring this promising and rapidly-developing branch of molecular magnetism.Acknowledgements
This research was funded by NSF Grant No. CHE-0617063.Notes and references
- (a) R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, High-spin molecules: [Mn12O12(O2CR)16(H2O)4], J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Magnetic bistability in a metal-ion cluster, Nature, 1993, 365, 141–143 CrossRef CAS.
- (a) A. R. Rocha, V. M. García-Suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Towards molecular spintronics, Nat. Mater., 2005, 4, 335–339 CrossRef CAS; (b) L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186 CrossRef CAS; (c) M. Affronte, Molecular nanomagnets for information technologies, J. Mater. Chem., 2009, 19, 1731–1737 RSC.
- (a) M. N. Leuenberger and D. Loss, Quantum computing in molecular magnets, Nature, 2001, 410, 789–793 CrossRef CAS; (b) A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Will spin-relaxation times in molecular magnets permit quantum information processing?, Phys. Rev. Lett., 2007, 98, 057201-1–057201-4; (c) P. C. E. Stamp and A. Gaita-Ariño, Spin-based quantum computers made by chemistry: hows and whys, J. Mater. Chem., 2009, 19, 1718–1730 RSC.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic memory of a single-molecule quantum magnet wired to a gold surface., Nat. Mater., 2009, 8, 194–197 CrossRef CAS.
- A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Graphene spintronic devices with molecular nanomagnets, Nano Lett., 2011, 11, 2634–2639 CrossRef.
- It is important to distinguish between the term anisotropy barrier and the somewhat nebulous term blocking temperature. The anisotropy barrier is the Arrhenius activation energy for the process of spin reversal. Assuming Boltzmann statistics, the anisotropy energy expressed in Kelvin indicates the temperature at which the relaxation time will equal Euler's number multiplied by the attempt time. Attempt times for paramagnets are usually 10−8 to 10−10 s, so a molecule at a temperature equal to its anisotropy barrier will have a relaxation time of approximately 3 ns. The blocking temperature can refer to (a) the temperature at which a peak is observed in the out-of-phase susceptibility (χ′′) at a given frequency, (b) the first temperature at which hysteresis is observed in a plot of field vs. magnetization, or (c) the temperature at which a maximum is observed in the zero-field cooled magnetization. Since the measurement times of these techniques can span seven orders of magnitude, one must be careful when comparing blocking temperatures between single-molecule magnets.
- (a) N. E. Chakov, S.-C. Lee, A. G. Harter, P. L. Kuhns, A. P. Reyes, S. O. Hill, N. S. Dalal, W. Wernsdorfer, K. A. Abboud and G. Christou, The properties of the [Mn12O12(O2CR)16(H2O)4] single-molecule magnets in truly axial symmetry: [Mn12O12(O2CCH2Br)16(H2O)4]·4CH2Cl2, J. Am. Chem. Soc., 2006, 128, 6975–6989 CrossRef CAS; (b) N. Ishikawa, Y. Mizuno, S. Takamatsu, T. Ishikawa and S.-y. Koshihara, Effects of chemically induced contraction of a coordination polyhedron on the dynamical magnetism of bis(phthalocyaninato)dysprosium, a single-4f-ionic single-molecule magnet with a Kramers ground state, Inorg. Chem., 2008, 47, 10217–10219 CrossRef CAS; (c) C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, A record anisotropy barrier for a single-molecule magnet, J. Am. Chem. Soc., 2007, 129, 2754–2755 CrossRef CAS; (d) D. Yoshihara, S. Karasawa and N. Koga, Cyclic single-molecule magnet in heterospin system, J. Am. Chem. Soc., 2008, 130, 10460–10461 CrossRef CAS; (e) N. Magnani, E. Colineau, R. Eloirdi, J.-C. Griveau, R. Caciuffo, S. M. Cornet, I. May, C. A. Sharrad, D. Collison and R. E. P. Winpenny, Superexchange coupling and slow magnetic relaxation in a transuranium polymetallic complex, Phys. Rev. Lett., 2010, 104, 197202-1–197202-4; (f) P.-H. Lin, T. J. Burchell, L. Unger, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, A polynuclear lanthanide single-molecule magnet with a record anisotropic barrier, Angew. Chem., Int. Ed., 2009, 48, 9489 CrossRef CAS; (g) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, Two-step relaxation in a linear tetranuclear dysprosium(III) aggregate showing single-molecule magnet behavior, J. Am. Chem. Soc., 2010, 132, 8538–8539 CrossRef CAS; (h) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Strong exchange and magnetic blocking in N23− radical-bridged lanthanide complexes, Nat. Chem., 2011, 3, 538–542 CrossRef CAS; (i) I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Coupling Dy3 triangles enhances their slow magnetic relaxation, Angew. Chem., Int. Ed., 2010, 49, 6352–6356 CrossRef CAS; (j) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, An organometallic single-ion magnet, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS; (k) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, A N23− radical-bridged terbium complex exhibiting magnetic hysteresis at 14 K, J. Am. Chem. Soc. DOI:10.1021/ja206286h; (l) N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Lanthanide double-decker complexes functioning as magnets at the single-molecular level, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS; (m) A. Watanabe, A. Yamashita, M. Nakano, T. Yamamura and T. Kajiwara, Multi-path magnetic relaxation of mono-dysprosium(III) single-molecule magnet with extremely high barrier, Chem.–Eur. J., 2011, 17, 7428–7432 CrossRef CAS; (n) M. Gonidec, F. Luis, À. Vílchez, J. Esquena, D. B. Amabilino and J. Veciana, A liquid-crystalline single-molecule magnet with variable magnetic properties, Angew. Chem., Int. Ed., 2010, 49, 1623–1626 CAS; (o) M. Gonidec, R. Biagi, V. Corradini, F. Moro, V. De Renzi, U. del Pennino, D. Summa, L. Muccioli, C. Zannoni, D. B. Amabilino and J. Veciana, Surface supramolecular organization of a terbium(III) double-decker complex on graphite and its single molecule magnet behavior, J. Am. Chem. Soc., 2011, 133, 6603–6612 CrossRef CAS.
- S. Jank, H. Reddmann and H.-D. Amberger, Electronic structures of highly symmetrical compounds of f elements XLIII: Parametric analysis of the absorption spectrum of tris(bis(trimethylsilylamido))dysprosium(III) (Dy(btmsa)3), Inorg. Chim. Acta, 2008, 361, 2154–2158 CrossRef CAS.
- R. Orbach, Spin–lattice relaxation in rare-earth salts, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484 CrossRef CAS and references therein.
- In lanthanide chemistry, the splitting of the mJ states due to the weak crystal field is often referred to as the Stark splitting, and the states themselves are referred to as Stark sublevels. However, Stark's claim on the nomenclature is dubious at best. His Nobel prize was awarded for study of the splitting of hydrogen electronic states in the presence of an external electric field and never dealt with the f-elements or crystal field environments. Reference to the splitting of the mJ degeneracy of the ground state in lanthanides can be traced to J. Becquerel's work “Introduction to a Theory of Magneto-optical Phenomena in Crystals” ( J. Becquerel, Einleitung in eine Theorie der magneto-optischen Erscheinungen in Kristallen, Z. Phys., 1929, 58, 205–216 Search PubMed ), wherein he compares the effect of the electric field created by the environment of the lanthanide to a sort of inhomogeneous Stark effect. In doing so he references W. Pauli's description of the anomalous spectral lines observed in some compounds of mercury ( W. Pauli, Quantentheorie, Handbuch der Physik, 1922, 23, 248 Search PubMed). Given Stark's tangential connection to the subject, it seems somewhat superfluous to rename an effect that is essentially crystal field splitting after him. When one considers Stark's rejection of quantum mechanics due to its conflicts with his Nazi ideology, his case is weakened even further ( J. Stark, Nationalsozialismus und Wissenschaft, München, 1934 Search PubMed). Therefore, in this manuscript the microstates of spin–orbit coupled J states are simply referred to as mJ states. For further information on Stark see M. Leone, A. Paoletti and N. Robotti, A simultaneous discovery: the case of Johannes Stark and Antonino Lo Surdo, Phys. Perspect., 2004, 6, 271–294 Search PubMed.
- N. Ishikawa, Simultaneous determination of ligand-field parameters of isostructural lanthanide complexes by multidimensional optimization, J. Phys. Chem. A, 2003, 107, 5831–5835 CrossRef CAS.
- H.-D. Amberger, H. Reddmann, T. J. Mueller and W. J. Evans, Parametric analysis of the crystal field splitting pattern of Pr(η5-C5Me5)3, Organometallics, 2010, 29, 1368–1373 CrossRef CAS (and references therein).
- H. Schilder and H. Lueken, Computerized magnetic studies on d, f, d–d, f–f, and d–s, f–s systems under varying ligand and magnetic fields, J. Magn. Magn. Mater., 2004, 281, 17–26 CrossRef CAS.
- R. Skomski, Simple Models of Magnetism, Oxford University Press, Oxford, 2008 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed.
- There are numerous mechanisms whereby a shortcut can be found for this barrier, even in highly symmetric Kramers ion systems where state mixing is formally forbidden. These mechanisms include long-range dipolar interactions and nuclear coupling, however, their discussion goes beyond the scope of this perspective (see ref. 15).
- While imposing an axial reference frame on a free-ion has little physical meaning by itself, its utility will become evident upon the introduction of the crystal field.
- Only the Ho(III) ground state (5I8) has a higher total angular momentum, however the Ho(III) ion lacks a Kramers ground state and has significantly less propensity for magnetic anisotropy (see Fig. 4).
- J. Sievers, Asphericity of 4f-shells in their Hund's rule ground states, Z. Phys. B: Condens. Matter Quanta, 1982, 45, 289–296 Search PubMed.
- S. Janka, H. Reddmann, C. Apostolidis and H.-D. Amberger, Electronic Structures of Highly Symmetrical Compounds of f Elements. 42 [1] Derivation and Simulation of the Crystal Field Splitting Pattern of Tris(bis(trimethylsilyl)amido)ytterbium(III), Z. Anorg. Allg. Chem., 2007, 633, 398–404 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Mononuclear lanthanide complexes with a long magnetization relaxation time at high temperatures: a new category of magnets at the single-molecular level, J. Phys. Chem. B, 2004, 108, 11265–11271 CrossRef CAS.
- K. H. J. Buschow and F. R. De Boer, Physics of Magnetism and Magnetic Materials, Kluwer Academic, New York, 2003 Search PubMed.
- Notable exceptions include Sm(III) and Eu(III) ions.
- (a) B. G. Wybourne, Spectroscopic Properties of Rare Earths, Wiley, New York, 1965 Search PubMed; (b) G. H. Dieke, Spectra and Energy Levels of Rare Earth Ions in Crystals, Wiley, New York, 1968 Search PubMed.
- N. Magnani, C. Apostolidis, A. Morgenstern, E. Colineau, J.-C. Griveau, H. Bolvin, O. Walter and R. Caciuffo, Magnetic Memory Effect in a Transuranic Mononuclear Complex, Angew. Chem., Int. Ed., 2011, 50, 1696–1698 CrossRef CAS.
- D. G. Karraker, J. A. Stone, E. R. Jones Jr. and N. Edelstein, Bis(cyclooctatetraenyl)neptunium(IV) and bis(cyclooctatetraenyl)plutonium(IV), J. Am. Chem. Soc., 1970, 92, 4841–4845 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2011 |
