Merging the chemistry of electron-rich olefins with imidazolium ionic liquids: radicals and hydrogen-atom adducts†
Cody N.
Sherren
a,
Changhua
Mu
b,
Michael I.
Webb
b,
Iain
McKenzie
b,
Brett M.
McCollum
b,
Jean-Claude
Brodovitch
b,
Paul W.
Percival
b,
Tim
Storr
b,
Kenneth R.
Seddon
c,
Jason A. C.
Clyburne
*a and
Charles J.
Walsby
*b
aMaritime Centre for Green Chemistry, Department of Chemistry, Saint Mary's University, Halifax, NS B3H 3C3, Canada. E-mail: Jason.Clyburne@smu.ca
bDepartment of Chemistry, Simon Fraser University, Burnaby, BC V5A 1S6, Canada. E-mail: cwalsby@sfu.ca
cThe QUILL Research Centre, School of Chemistry and Chemical Engineering, The Queen's University of Belfast, Belfast, BT9 5AG, Northern Ireland, UK
First published on 17th August 2011
Abstract
To probe the reactivity of ionic liquids relevant to their use in electrochemical applications, the ionic liquid 1-ethyl-3-methylimidazolium tetrachloroaluminate(III) was reacted with metallic lithium to produce a persistent radical, which can be considered a hydrogen-atom adduct of an electron-rich olefin (ERO). Reaction of tetrakis(dimethylamino)ethene, a bona fide ERO, with muonium, produces a structurally similar radical.
1,3-Dialkylimidazolium ions have found numerous applications in modern chemistry, notably as components of ionic liquids.1 These unique solvents exhibit industrially appealing properties such as low volatility, low flammability, and high thermal stability.2 Recently, ionic liquids have attracted particular attention in a variety of electron-rich applications, including batteries3 and solar cells.4 Further development of these types of applications for ionic liquids, particularly with regards to their long-term stability, is affected by processes that may generate other reactive species.
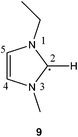
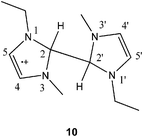
Electron transfer to 1,3-dialkylimidazolium ions 1 leads to the formation of radicals, such as 3 and 4. The chemistry of such species is largely uncharted, but is likely to be important in the future development of ionic liquids as electrolytes; for example, they could potentially be generated by anodic reduction in battery applications.5 A particularly interesting property of these radicals is the relationship of their coupling products, 4, to electron-rich olefins (EROs) such as 5 and 6; addition of a hydrogen atom to an ERO generates the corresponding radical species. EROs possess chemistry that is unique among alkenes, and have found applications as strong nucleophiles and reducing agents.6 They were also important in the early understanding of N-heterocyclic carbenes (NHCs).7 It has been shown that unstable NHCs dimerise to give enetetramines,8 indicating that EROs such as 5 could be generated from NHCs such as 2. The interrelationship between these chemical species is further highlighted by noting that deprotonation of imidazolium ions, such as 1,3-dialkylimidazolium, 1, generates an NHC, 2 (Fig. 1),7 and that NHCs are also valuable precursors to known, and perhaps novel, halide-free ionic liquids.9
 | ||
| Fig. 1 Imidazolium ions, N-heterocyclic carbenes, electron-rich olefins and related radicals. | ||
To study these related imidazolium-based species, two distinct systems were selected. In the first, a generic imidazolium ionic liquid was treated with lithium, and the generation of the coupling product 4 was observed; it was characterised by spectroscopic and modelling studies. This species is likely to have been generated from radical 3 (Scheme 1), and is the hydrogen-atom adduct of the unknown ERO, 5. Reactivity of this type, where the imidazolium radical reacts with the parent cation from the ionic liquid to form a dimer radical cation, through a “charge trapping” mechanism, has been indicated in studies of the radiolysis of imidazolium ionic liquids.10,11 In the second system, the related radical species, 7, was generated by treatment of ERO 6 with muonium, a hydrogen-atom surrogate. The radicals identified in these studies may be important in the long-term electrochemical use of ionic liquids, and demonstrate the relationship between 1,3-dialkylimidazolium ions, 1, NHCs, 2, and EROs, 5.
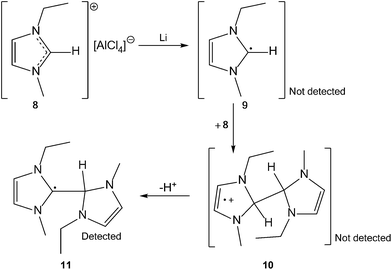 | ||
| Scheme 1 The postulated reaction mechanism of “charge trapping” that can potentially produce three radical species following reaction of lithium with 1,3-dialkylimidazolium ionic liquids. | ||
The ionic liquid selected for the first study was composed of 1-ethyl-3-methyimidazolium chloride mixed with 40 mol% aluminium(III) chloride. This material is a liquid at room temperature and has a relatively wide electrochemical window.12 The presence of aluminium(III) chloride ensures that the system is anhydrous and the stoichiometry ensures that the mixture is basic, with an excess of chloride ion relative to aluminium(III) chloride. Addition of lithium beads to the solution and subsequent stirring for one hour resulted in the formation of a transparent, rusty red–brown solution. The unreacted lithium beads were removed by filtration. The colour of the solution was persistent over several weeks, with decay of the colour occurring only with exposure to moist air. A portion of this material was placed inside a sealed quartz tube, and electron paramagnetic resonance (EPR) measurements of the solution gave the spectrum shown in Fig. 2.13
 | ||
| Fig. 2 Experimental (top) and simulated (bottom) EPR spectra of the solution formed after treatment of the 1-ethyl-3-methyimidazolium ionic liquid with lithium. Experimental spectral parameters: frequency = 9.8383 GHz, modulation amplitude = 0.1 mT, time constant = 5.12 ms, sweep time = 20 s, average of 200 scans. Simulation parameters: g = 2.00279, 2 × a(14N) = 0.54 mT, a(14N) = 0.53 mT, a(14N) = 0.16 mT, a(1H) = 0.84 mT, a(1H) = 0.56 mT, a(1H) = 0.54 mT, 2 × a(1H) = 0.28 mT, a(1H) = 0.27 mT. Peak-to-peak linewidth = 0.13 mT, Lorentzian line shapes. | ||
Complex chemistry for radicals generated in ionic liquids has been reported previously.11,14 In this case, to determine which of the radical products 9, 10 or 11 (Scheme 1) was present after treatment of the imidazolium ionic liquid with lithium required a combination of spectral fitting and density functional theory (DFT) calculations. The EPR spectrum (Fig. 2) was simulated using the MATLAB-based simulation package, EasySpin.15
Accurate simulation of the spectrum was challenging due to contributions from several partially resolved hyperfine couplings. Furthermore, it was hard to assess using traditional manual simulation methods whether a particular model for the hyperfine structure was significantly better than any other. To address these problems we used the iterative fitting procedures available in EasySpin to find the optimum set of g-value, linewidth and hyperfine coupling constants for simulation of the spectrum. This was performed in two stages using a genetic algorithm initially, followed by further refinement using a simplex least-squares method. The fitting procedure produces a value of the RMSD between the experimental and simulated spectra, which enabled unbiased comparison of different models. This was used to exclude radical 9 as the observed species, since the best simulation possible with two 14N atoms gives an RMSD more than double that of the best fitting with four 14N nuclei. A qualitative comparison of the best fitting spectra for a coupled product (10 or 11) showed that the two-14N model produces spectral line shapes, defined by partially resolved hyperfine splittings, that do not match the EPR data, whereas the four 14N model agrees very well with the experimental spectrum. The EasySpin fitting procedures not only give an unbiased assignment of the spectrum but also allow simulation with a minimal set of hyperfine interactions. Potentially, a large number of 1H nuclei could contribute to the hyperfine structure seen in the EPR spectrum. Simply counting lines to determine multiplicity in this case is not sufficient due to the complexity arising from partially-resolved structure. By using iterative spectral fitting to analyse the effect of small 1H hyperfine couplings on the RMSD, it was determined that, in addition to four 14N hyperfine interactions, only five 1H hyperfine couplings provide resolvable contributions to the spectrum (Fig. 2). Furthermore, based on the excellent simulation of the experimental EPR data possible with this limited set of parameters, it is clear that a single radical species is present in the solution.
To determine which of the possible radicals gave the observed EPR spectrum, we performed DFT calculations of the EPR hyperfine couplings of radicals 9, 10 and 11. Geometry optimisations (opt = tight) were performed using the Gaussian 09 program (Revision A.02),16 the B3LYP functional,17 and the 6-311+g* basis set on all atoms. Frequency calculations at the same level of theory confirmed that the optimised structures were located at a minimum on the potential energy surface. Single-point calculations of hyperfine coupling constants were completed with the B3LYP functional and the EPR-III basis set of Barone18 on all atoms. The largest 1H hyperfine couplings, for the monomeric radical 9 and the protonated dimer 10, were calculated to be 2.68 and 2.26 mT respectively, consistent with the large couplings expected for the proton attached to the 2-position of the spin-bearing imidazolium ring in each case (Table 1). These values are incompatible with the EPR spectrum, which is simulated with a largest 1H coupling of only 0.84 mT. By contrast, the hyperfine couplings calculated for the dimer radical 11 (Table 1) are in good agreement with experiment, with the largest 1H hyperfine coupling calculated to be 0.85 mT, suggesting that the neutral radical 11 is formed by deprotonation of 10. As demonstrated by spin-density calculations, the absence of a large hyperfine coupling is due to the lack of a proton at the principal spin-bearing carbon. The DFT-optimised geometry of radical 11 is shown in Fig. 3 along with its SOMO, which illustrates the delocalised nature of the radical, and is consistent with the number of hyperfine coupling interactions observed in the EPR spectrum. Deprotonation of radical 10 seems reasonable given the basicity of the ionic liquids, and such reactions of imidazolium dimer radical cations has been suggested in irradiated ionic liquids.11
|
|
|
|
|
|||
|---|---|---|---|---|---|---|
| C2–H/Å | 1.077 | 1.091 | 1.096 | 1.095 | 1.117 | |
| C2–N1/Å | 1.334 | 1.420 | 1.428 | 1.427 | 1.413 | 1.487 |
| C2–N3/Å | 1.335 | 1.417 | 1.426 | 1.425 | 1.435 | 1.482 |
| C1–N5/Å | 1.380 | 1.396 | 1.386 | 1.380 | 1.376 | 1.411 |
| C3–N4/Å | 1.380 | 1.391 | 1.387 | 1.379 | 1.403 | 1.413 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/Å C/Å |
1.359 | 1.348 | 1.351 | 1.356 | 1.349 | 1.337 |
| N–C–N/° | 108.93 | 104.84 | 104.33 | 103.58 | 104.58 | 102.12 |
| C2–C2′/Å | N/A | N/A | 1.726 | 1.496 | ||
| a X/mT | N/A | H: 2.68, 0.60, 0.50, 0.25, 0.10 | H: 2.26, 2.10, 0.81, 0.54, 0.44, 0.28, 0.25, 0.23, 0.14 | H: 0.85, 0.48, 0.47, 0.15, 0.13, 0.12 | ||
| N1: 0.27, N3: 0.24 | N1: 2.65, N3: 0.78 | N1: 0.30, N3: 0.30 | ||||
| N1′: 2.56, N3′: 1.38 | N1′: 0.16, N3′: 0.59 | |||||
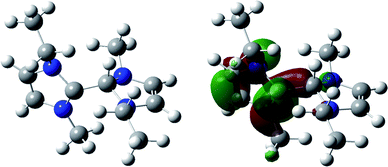 | ||
| Fig. 3 Optimised structure of 11 (left) and diagram of its SOMO (right). Energy minimised geometries calculated at the DFT B3LYP 6-311+g* level. | ||
Most interesting is the potential of 11 to behave as a hydrogen atom source, as a base, and as an oxidant or a reductant. Furthermore, 1,3-dialkylimidazolium ionic liquids are important electrolytes in secondary batteries, and generation of species such as those described above may lead to unwanted cathodic decomposition.19 It is also possible that the delocalised nature of the radical detected in this work could lead to the formation of the resistive cell coatings that can occur when imidazolium-based ionic liquids are used in electrochemical cells.20
In principle, a radical such as 11 could be generated by adding a hydrogen atom to the as yet unknown ERO 5. The hydrogen atom is an exceptional probe of reactivity because its small size minimises steric obstruction and its simple structure avoids additional electronic effects. However, the hydrogen atom is not a familiar reagent for solution studies, largely because of complications inherent in its generation. Photolysis or radiolysis of water, or other protic solvents, is typically used to produce hydrogen atoms but this can result in the production of additional radical species or simple diamagnetic addition products.21
Rather than use hydrogen atoms to generate a radical from ERO 6 we have employed muonium (Mu = [μ+e−]), which is a single-electron atom whose nucleus is the positive muon.22 Muonium is chemically equivalent to the hydrogen atom, but has only one-ninth the mass. The utility of muonium as a probe of chemistry at electron-rich sites is well-documented,23 with radicals generated by addition of muonium characterised by techniques collectively known as muon spin rotation and resonance (μSR).24–26 In principle, a radical compound reminiscent of 11 could be prepared by hydrogen atom (or its surrogate Mu) addition to an ERO such as 6 (see Scheme 2). Transverse-field muon spin rotation (TF-μSR) is used to characterise muoniated radicals, via determination of their muon hyperfine constants.26 In this technique, a beam of spin-polarised muons is injected into the sample. A fraction of the muons stopping in the sample can pick up an electron to form muonium, which can then react with unsaturated compounds to form muoniated radicals (Scheme 2). Other muons (typically 65% in organic materials) become incorporated in diamagnetic molecules through radiolysis. The two fractions are distinguished by their spin precession frequencies. The muon hyperfine coupling constant associated with a given muoniated radical is readily determined from the separation of the pair of radical peaks, which occur on either side of the diamagnetic peak.
As illustrated in Fig. 4, the TF-μSR spectrum obtained from neat tetrakis(dimethylamino)ethene, 6, exhibits radical frequencies ν12 and ν43 that are equally spaced about the diamagnetic frequency, νD. This corresponds to a muon hyperfine coupling constant of Aμ = 59.86 ± 0.01 MHz. The equivalent proton hyperfine coupling constant, calculated by scaling the muon hyperfine coupling constant by the ratio of the proton and muon magnetic moments (μp/μp = 0.3141) is a(1H) ∼18.8 MHz (or 0.67 mT).25 DFT calculations of the geometry and spin density of the hydrogen-atom adduct, 7 (Fig. 5), were performed as described for species 8–11 and predict a 1H hyperfine coupling of 0.58 mT, roughly 15% smaller than measured. The muon hyperfine coupling constant of 7 depends on the dihedral angle, θ, between the C–Mu bond and the axis of the p-orbital containing the unpaired electron, and the amount of unpaired electron spin density on the carbon atom, ρ: Aμ = [L + M〈cos2(θ)〉]ρ, where L is a small negative constant and M is a large positive constant. The proton hyperfine constant is calculated for a given geometry (fixed value of θ), but the measured hyperfine constant corresponds to a vibrationally averaged value. Enhanced zero-point vibration in the muoniated radical generally results in larger 〈cos2(θ)〉 and hence larger Aμ than predicted. Our findings are consistent with this. The small coupling to the proton (muon) beta to the radical centre demonstrates the structural similarity between the muoniated radical, 7, and the deprotonated radical dimer, 11, generated in the ionic liquid. In both cases, the C–Mu(H) bond is almost perpendicular to the π symmetry orbital of the radical centre and some spin density is delocalised onto the orbitals of nitrogen atoms, as illustrated in Fig. 3 and 5.
 | ||
| Fig. 4 TF-μSR spectrum of neat tetrakis(dimethylamino)ethene, 6, at 298 K. The radical frequencies ν12 and ν43 are equally spaced about the diamagnetic frequency, νD. The diamagnetic frequency has been truncated to make the radical frequencies more visible. The muon hyperfine coupling constant was determined from the difference between ν12 and ν43 and is 59.86 ± 0.01 MHz. | ||
 | ||
| Fig. 5 Structure of ERO 6 (left), its hydrogen (muonium) adduct 7 (centre), and its SOMO (right). Energy minimised geometries calculated at the DFT B3LYP 6-311+g* level. | ||
Conclusions
It has been shown that, under basic conditions, an imidazolium ion can react, through a C–C bond-forming reaction and deprotonation, to give a neutral radical adduct, 11. This species is the hydrogen-atom adduct of an ERO. An analogous radical species, 7, was generated directly from an ERO, 6, by addition of muonium. These results suggest that, in 1,3-dialkylimidazolium ionic liquids, not only must chemistry related to NHC reactivity be anticipated, but also that radical chemistry related to EROs could occur. The formation of radicals such as 11, which are capable of facile protonation and deprotonation reactions, as well as electrochemical behaviour, indicates that long-term use of simple 1,3-dialkylimidazolium ionic liquids in electron-rich applications may produce even more complex mixtures than previously anticipated. The production of these ERO-derived radicals may in some cases, favourably or unfavourably, affect the electrochemical properties of these materials.Acknowledgements
Funding was provided by the Natural Sciences and Engineering Council of Canada (NSERC) to C. J. W., J. A. C. C., P. W. P. and T. S. C. J. W. and J. A. C. C. acknowledge support from the Canadian Foundation for Innovation (CFI). C. J. W. and T. S. thank Westgrid for access to computational resources. J. A. C. C. also acknowledges support from the Canada Research Chairs Program and the Nova Scotia Research and Innovation Trust.Notes and references
- (a) A. Stark and K. R. Seddon, in Kirk-Othmer Encyclopaedia of Chemical Technology, ed. A. Seidel, John Wiley & Sons, Inc., Hoboken, NJ, 2007, vol. 26, p. 836 Search PubMed; (b) M. Freemantle, An Introduction to Ionic Liquids, RSC Publications, Cambridge, UK, 2010 Search PubMed.
- N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123 RSC.
- (a) J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS; (b) S. Seki, Y. Kobayashi, H. Miyashiro, Y. Ohno, A. Usami, Y. Mita, N. Kihira, M. Watanabe and N. Terada, J. Phys. Chem. B, 2006, 110, 10228 CrossRef CAS.
- (a) H. Choi, C. Baik, S. O. Kang, J. Ko, M. S. Kang, M. K. Nazeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2008, 47, 327 CrossRef CAS; (b) D. Kuang, S. Uchida, R. Humphry-Baker, S. M. Zakeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2008, 47, 1923 CrossRef CAS.
- H. Ohno, Electrochemical Aspects of Ionic Liquids, 2nd edn, Wiley, Hoboken, NJ, 2011 Search PubMed.
- (a) R. W. Hoffmann, Angew. Chem., Int. Ed. Engl., 1968, 7, 754 CrossRef CAS; (b) J. Hocker and R. Merten, Angew. Chem., Int. Ed. Engl., 1972, 11, 964 CrossRef CAS.
- W. Kirmse, Angew. Chem., Int. Ed., 2010, 49, 8798 CrossRef CAS.
- (a) H. W. Wanzlick and H. J. Kleiner, Angew. Chem., 1961, 73, 493 CrossRef CAS; (b) H. W. Wanzlick, Angew. Chem., 1962, 74, 129 CrossRef CAS; (c) H. W. Wanzlick, F. Esser and H. J. Kleiner, Chem. Ber., 1963, 96, 1208 CrossRef CAS; (d) F. E. Hahn, L. Wittenbecher, R. Boese and D. Blaser, Chem.–Eur. J., 1999, 5, 1931 CrossRef CAS; (e) R. W. Alder, M. E. Blake, L. Chaker, J. N. Harvey, F. Paolini and J. Schutz, Angew. Chem., Int. Ed., 2004, 43, 5896 CrossRef CAS.
- (a) A. J. Carmichael, M. Deetlefs, M. J. Earle, U. Fröhlich and K. R. Seddon, in Ionic Liquids as Green Solvents, ed. M. J. Earle and K. R. Seddon, ACS Symposium Series, Vol. 856, American Chemical Society, Washington, DC, 2003, p. 14 Search PubMed; (b) M. J. Earle and K. R. Seddon, Preparation of imidazole carbenes and the use thereof for the synthesis of ionic liquids, World Pat., WO 01 77081, 2001.
- I. A. Shkrob and J. F. Wishart, J. Phys. Chem. B, 2009, 113, 5582 CrossRef CAS.
- (a) I. A. Shkrob, J. Phys. Chem. B, 2010, 114, 368 CrossRef CAS; (b) I. A. Shkrob, T. W. Marin, S. D. Chemerisov and J. F. Wishart, J. Phys. Chem. B, 2011, 115, 3872 CrossRef CAS.
- (a) A. J. Pearce, Part II Thesis, Oxford University, 1983; (b) The electrochemical window for this ionic liquid is 2.9 V, as discussed by: T. Schubert, S. Zein, E. Abedin, A. P. Abbott, K. J. McKenzie, K. S. Ryder and F. Endres, in Electrodeposition from Ionic Liquids, 2nd edn, ed. F. Endres, D. MacFarlane, and A. Abbott, Wiley-VCH, Weinheim, 2008, p. 83 Search PubMed; H. Matsumoto, in Electrochemical Aspects of Ionic Liquids, ed. H. Ohno, Wiley, Hoboken, NJ, 2011, p. 43 Search PubMed.
- Attempts were made to improve spectral resolution by warming the sample in the hope of reducing the viscosity, and thus reducing the molecular correlation time, in order to give narrower line widths. However, heating of the sample to 45 °C led to irreversible broadening of the EPR signal, indicating a radical degradation process. The viscosity of the ionic liquid was relatively low at room temperature and was not reduced significantly at the elevated temperature.
- G. Le Rouzo, C. Lamouroux, V. Dauvois, A. Dannoux, S. Legand, D. Durand, P. Moisy and G. Moutiers, Dalton Trans., 2009, 6175 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. FarkasJ. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- V. Barone, in Recent Advances in Density Functional Methods, ed. D. P. Chong, World Scientific, Singapore, 1995, p. 287 Search PubMed.
- M. Galinski, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567 CrossRef CAS.
- J. Mun, Y. S. Jung, T. Yim, H. Y. Lee, H. J. Kim, Y. G. Kim and S. M. Oh, J. Power Sources, 2009, 194, 1068 CrossRef CAS.
- P. Neta, Chem. Rev., 1972, 72, 533 CrossRef CAS.
- A muon (or mu meson) is an elementary particle (a lepton), 209 times heavier than an electron, with a mean lifetime of 2.2 μs.
- (a) D. C. Walker, J. Chem. Soc., Faraday Trans., 1998, 94, 1 RSC; (b) C. J. Rhodes, J. Chem. Soc., Perkin Trans. 2, 2002, 1379 RSC; (c) R. West and P. W. Percival, Dalton Trans., 2010, 39, 9209 RSC.
- TRIUMF in Vancouver, Canada, is one of only four accelerators in the world that has intense beams of spin-polarized muons that are necessary for μSR spectroscopy.
- S. J. Blundell, Chem. Rev., 2004, 104, 5717 CrossRef CAS.
- I. McKenzie and E. Roduner, Naturwissenschaften, 2009, 96, 873 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures for sample preparation, experimental details of EPR and μSR measurements, optimised XYZ coordinates for species 6–10. See DOI: 10.1039/c1sc00408e |
| This journal is © The Royal Society of Chemistry 2011 |