The mixed cyanide halide Au(I) complexes, [XAuCN]⁻ (X = F, Cl, Br, and I): evolution from ionic to covalent bonding

Abstract

We report a combined experimental and theoretical investigation of [XAuCN]⁻ (X = F, Cl, Br, I) to examine the chemical bonding in the mixed cyanide halide Au(I) complexes. Photoelectron spectra are obtained for [XAuCN]⁻, yielding electron affinities of 5.38 ± 0.05, 5.14 ± 0.05, and 4.75 ± 0.05 eV for XAuCN (X = Cl, Br, I), respectively. Relativistic quantum chemical calculations based on wavefunction theory and density functional theory are carried out to help interpret the photoelectron spectra and elucidate the electronic structures and chemical bonding in the [XAuCN]⁻ complexes. Spin–orbit coupling is found to be important in all the complexes, quenching the Renner–Teller distortion in the neutral molecules. Ab initio calculations including spin–orbit effects allow quantitative assignments of the observed photoelectron spectra. A variety of chemical bonding analyses based on the charge population, bond orders, and electron localization functions have been carried out, revealing a gradual transition from ionic behavior between F–Au in [FAuCN]⁻ to relatively strong covalent bonding between I–Au in [IAuCN]⁻. Both relativistic effects and electron correlations are shown to enhance the covalency in the gold iodide complex.

---

Introduction

Gold halides and their mixed-ligand complexes (LAuX: X = halides, L = neutral ligands) are important gold compounds and play a key role in gold chemistry.¹ Mixed-ligand gold complexes, such as PPh₃AuCl and N-heterocyclic carbene–AuCl (NHCs–AuCl), are extensively used in organometallic syntheses and homogenous catalysis.² Due to the strong relativistic effects, gold atoms and clusters display many unique chemical bonding properties, such as aurophilicity³ and covalent bonding characters in gold-containing molecules.⁴ The Au(I) ion in most cases prefers to be coordinated by two ligands in a linear geometry⁵ with general structures of [LAuL]⁺, [LAuX] or [XAuX]⁻. The low coordination of Au(I) along with its ubiquitous aurophilic property makes LAuX an important building block in gold nanomaterials.⁶ Accurate theoretical calculations of Au-containing molecules are computationally intensive due to complicated electron correlations and the relativistic effects.⁷Experimental data are essential to verify theoretical methods aimed at treating Au-containing compounds. Photoelectron spectroscopy (PES) combined with high-level ab initio calculations has been a powerful approach for probing the electronic and structural properties of metal complexes without the complication of condensed-phase environments.⁸ In the current paper, we combine PES and ab initio calculations to investigate a series of cyanide-halide mixed-ligand Au(I) complexes, [XAuCN]⁻ (X = F, Cl, Br, I).

In aqueous solution, the dicyanide anion, Au(CN)₂⁻, is the most stable and soluble Au(I) species, which has been used to extract gold since ancient time. In a recent PES and theoretical study, we have shown that there is significant covalent character in the Au–CN bond in Au(CN)₂⁻.⁹ Covalent bonding in the AuCN molecule was also predicted computationally,¹⁰ as borne out in a recent photoelectron imaging study of AuCN⁻.¹¹ Beside AuCN, gold oxides and sulfides have been shown to exhibit relatively strong covalent characters.¹² More interestingly, an Au atom has been found to behave like an H atom in Au–Si and Au–B clusters.¹³ While an early PES study on gold halide complexes emphasized the generation of divalent Au(II) species,¹⁴ a very recent joint PES and theoretical study on gold dihalide complexes has revealed relatively strong covalent character between gold and iodine in AuI₂⁻ compared with its lighter halogen analogues.¹⁵ The covalent bonding character found in an increasing number of gold-containing molecules has stimulated us to investigate the gold halide and cyanide mixed-ligand complexes, [XAuCN]⁻ (X = F, Cl, Br, I). Although they are important building blocks in coordination polymers,¹⁶ these mixed-ligand complexes have not been observed in the gas phase so far. In the current article, we systematically investigate the evolution of chemical bonding between the Au and halogen atoms in the mixed-ligand complexes, [XAuCN]⁻ (X = F, Cl, Br, I). Density functional and ab initio wavefunction calculations are carried out on the four [XAuCN]⁻ species to help spectral interpretation and chemical bonding analyses.

Experimental method

The experiment was carried out using a magnetic-bottle type PES apparatus equipped with an electrospray ionization (ESI) source and an ion trap time-of-flight mass spectrometer. Details of the apparatus have been described elsewhere¹⁷ and only a brief description is given here. All the [XAuCN]⁻ anions (X = Cl, Br, I) were produced by ESI from 0.1 mM solutions of KAu(CN)₂ mixed with the corresponding potassium halides (KX) in a methanol/water (90/10) solvent. The anions of interest were selected by a mass gate and decelerated before being intercepted by a probe laser beam. The photodetached electrons were analyzed by a 2.5-meter long magnetic-bottle time-of-flight tube, modified from the original design.¹⁷ As shown below, the shortened flight tube does not affect the electron energy resolution significantly. Similar experiments using KF did not produce the [FAuCN]⁻ anion and no experimental data was obtained for this species. In general, it appears that Au(I) does not form complexes with F⁻ ligands. For example, we were not able to observe AuF₂⁻ complexes previously while AuX₂⁻ complexes with heavier halides were readily observed.^14,15

Two laser systems were used for photodetachment in the current investigation. An F₂ excimer laser (157 nm: 7.866 eV) was used to obtain spectra at high electron binding energies. A dye laser equipped with a frequency-doubling unit provides tunable laser wavelengths from 600 to 206 nm. Because the resolution of the magnetic-bottle type PES analyzer depends on the photoelectron kinetic energies, the dye laser wavelengths are usually chosen to enhance the resolution for low binding energy features. Because of the relatively high electron binding energies of the [XAuCN]⁻ species, a wavelength of 206.19 nm (6.013 eV) was used in the current experiment to obtain higher resolution spectra, which yielded more accurate adiabatic electron binding energies. Time-of-flight photoelectron spectra were collected and converted to kinetic energy spectra calibrated with the known spectra of Au⁻ and I⁻. The electron binding energy spectra reported were obtained by subtracting the kinetic energy spectra from the respective detachment photon energies. The kinetic energy resolution (ΔE/E) of the magnetic-bottle electron analyzer was ∼3%, i.e., 30 meV for 1 eV electrons.

Computational methods

The theoretical studies were performed using both density functional theory (DFT) and ab initio wavefunction theory (WFT) methods. DFT calculations were done on [XAuCN]⁻ (X = F, Cl, Br, I) and their neutrals using the generalized gradient approximation (GGA) with the PBE exchange–correlation functional¹⁸ implemented in the Amsterdam Density Functional (ADF 2009.01) program.¹⁹ The Slater basis sets with the quality of triple-ζ plus two polarization functions (TZ2P) were used, with the frozen core approximation applied to inner shells [1s²-4f¹⁴] for Au, [1s²] for C, N, and F, [1s²-2p⁶] for Cl, [1s²-3d¹⁰] for Br, and [1s²-4d¹⁰] for I. The scalar relativistic (SR) and spin–orbit (SO) coupling effects were taken into account by the zero-order-regular approximation (ZORA).²⁰ Geometries were fully optimized at the SR-ZORA level and single-point energy calculations were performed with the inclusion of the SO effects. Vibrational frequency calculations were carried out at the SR-ZORA level to verify that the anion species were minima on the potential energy surface. The B3LYP hybrid functional²¹ was also used to optimize [XAuCN]⁻ with the Gaussian 03 program²² to compare with the PBE results that used the pure GGA results. The comparison of GGA and hybrid functionals tends to provide a useful evaluation of the accuracy of DFT results.

We further performed high-level ab initioWFT calculations for [XAuCN]⁻ (X = F, Cl, Br, I) using more sophisticated electron correlation methods implemented in the MOLPRO 2008 program.²³ In these calculations, we used both the CCSD(T) (coupled-cluster with single and double and perturbative triple excitations)²⁴ and CASSCF (complete-active-space self-consistent field) methods.²⁵ The geometries of [XAuCN]⁻ were optimized at the level of CCSD(T) with scalar relativistic effects included; single-point CCSD(T) energies of the ground and excited states of the neutrals were calculated at the geometries of the anions, which accurately generate the state-specific scalar relativistic energies of all the states. The electron binding energies corresponding to one-electron transitions from the closed-shell ground states of [XAuCN]⁻ to the ground and excited states of the XAuCN neutrals were obtained using the CASSCF/CCSD(T)/SO approach that we used previously for Au(CN)₂⁻ and AuI₂⁻.^9,15 In this approach, the SO splittings were treated as a perturbation to the scalar relativistic state energies and were calculated on the basis of CASSCF wave functions with the diagonal matrix elements replaced by the individual CCSD(T) state energies. The SO coupling effect was included by using a state-interacting method²⁶ with SO pseudopotentials.²⁷ The theoretical PES spectra were simulated using Gaussian functions with a line width of 0.035 eV. The simulated PES intensities were simply scaled according to the experimental observation. In the MOLPRO and Gaussian 03 calculations, we used the Stuttgart energy-consistent relativistic pseudopotentials ECP60MDF (Au) and ECP28MDF (I) and the corresponding valence triple-ζ basis sets cc-pVTZ-PP for Au²⁸ and I.²⁹ The all-electron basis sets cc-pVTZ were used for C, N, F,³⁰Cl,³¹ and Br.³² The cc-pVTZ-PP and cc-pVTZ basis sets are abbreviated as VTZPP and VTZ hereafter.

Experimental results

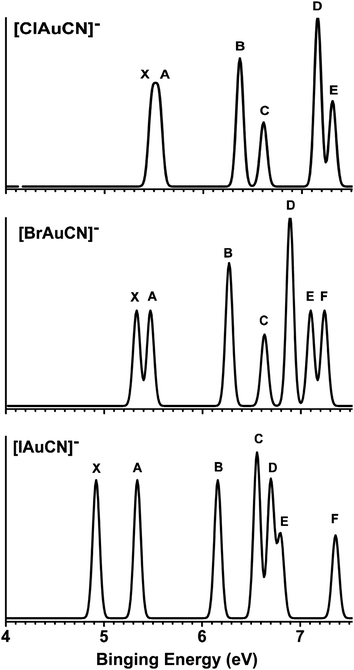
The photoelectron spectra of [XAuCN]⁻ (X = Cl, Br, I) are shown in Fig. 1 and 2 at 157 and 206.19 nm, respectively. The spectra for the three species are similar and their binding energies decrease systematically from X = Cl to I. The vertical detachment energies (VDEs) of all the observed features are given in Table 1, where they are compared with theoretical calculations (vide infra). Five major electron detachment bands are observed for [ClAuCN]⁻ (Fig. 1), where the bands X and A are overlapping and are partially resolved in the 206 nm spectrum (Fig. 2). Because of the overlap, the VDE of the X band can only be estimated to be ∼5.5 eV. From the detachment threshold in the 206 nm spectrum, an adiabatic detachment energy (ADE) for [ClAuCN]⁻ is estimated as 5.36 ± 0.05 eV. Vibrational structures are resolved for the A band with a spacing of 390 ± 40 cm⁻¹. The C band in the spectrum of [ClAuCN]⁻ is relatively weak, whereas the E band appears as a shoulder to the D band.

Fig. 1 Photoelectron spectra of [XAuCN]⁻ (X = Cl, Br and I) at 157 nm (7.866 eV).

Fig. 2 Photoelectron spectra of [XAuCN]⁻ (X = Cl, Br and I) at 206.19 nm (6.013 eV).

Table 1 Observed and calculated vertical detachment energies (VDEs) for [XAuCN]⁻ (X = Cl, Br and I) anion and final-state assignments

	Feature	Final state	VDE (eV)
			Exp^a	Theo^c
a The uncertainty for the measured VDEs is ± 0.05 eV. b A vibrational frequency of 390 ± 40 cm^−1 was observed for the first excited state of ClAuCN. c The first VDE for each anion is calculated using CCSD(T) method without including SO effects for the neutral and anionic ground states. The SO effects are included in the CASSCF/CCSD(T)/SO calculations of excitation energies for the neutral species. The higher VDEs are obtained by adding the first VDE to the neutral excitation energies calculated at the geometry of the anions.
[ClAuCN]^−	X	^2Π3/2	∼5.5	5.47
	A	^2Π1/2	5.59^b	5.54
	B	^2Σ^+1/2	6.18	6.36
	C	^2Δ5/2	∼6.7	6.60
	D	^2Σ^+1/2	7.05	7.15
	E	^2Π3/2	7.21	7.30
		^2Π1/2		7.35
[BrAuCN]^−	X	^2Π3/2	5.27	5.32
	A	^2Π1/2	5.55	5.46
	B	^2Σ^+1/2	6.07	6.26
	C	^2Δ5/2	∼6.6	6.62
	D	^2Σ^+1/2	6.79	6.88
	E	^2Π3/2	6.97	7.09
	F	^2Π1/2	7.11	7.23
[IAuCN]^−	X	^2Π3/2	4.83	4.91
	A	^2Π1/2	5.34	5.33
	B	^2Σ^+1/2	5.97	6.15
	C	^2Σ^+1/2	6.51	6.55
	D	^2Δ5/2	6.65	6.69
	E	^2Π3/2	6.82	6.79
	F	^2Π1/2	7.11	7.35

---

The energy separation between features X and A increases from X = Cl to I, hinting that they may be partly derived from the halide ligand as a result of SO splitting. The band B is relatively sharp and its binding energy is similar for all three species (Fig. 1), suggesting that this band is derived from either Au or the CN ligand. The C and D bands in the spectrum of [BrAuCN]⁻ are similar to those in the spectrum of [ClAuCN]⁻, except their binding energies are decreased in the former. An extra band F at a VDE of 7.11 eV is observed in the spectrum of [BrAuCN]⁻. The higher binding energy part of the [IAuCN]⁻spectrum is somewhat different from those of the two lighter halide complexes: four well-separated bands (C, D, E, F) are observed, where the intensity of band E is relatively weak.

From the 206 nm spectra (Fig. 2), we are able to estimate the ADEs for [BrAuCN]⁻ and [IAuCN]⁻ as 5.25 ± 0.05 and 4.75 ± 0.05 eV, respectively. The X bands for all three species are broad, suggesting significant geometry changes from the ground states of the [XAuCN]⁻ anions to the [XAuCN] neutrals. In the 206 nm spectra of [ClAuCN]⁻ and [BrAuCN]⁻, weak spectral features near 5.8 eV (labelled as “*”) are observed for both species. These features are discernible in the 157 nm spectra (Fig. 1), but they seem enhanced at 206 nm. These weak features are most likely due to shakeup transitions.

Theoretical results

We optimized various structures of the [XAuCN]⁻ (X = F, Cl, Br, I) anions and found they are all linear X–Au–CN species with C_∞v symmetry and ¹Σ⁺ ground state. These structures are confirmed to be minima through frequency analyses at the PBE level, as implemented in the ADF program. The optimized bond lengths of these anions at PBE, B3LYP, and CCSD(T) levels of theory are listed in Table 2 and compared with the homogeneous AuX₂⁻ species. The bond lengths from the three levels of theory are consistent with each other within 0.04 Å or better for all the species. The optimized geometry parameters for [Au(CN)₂]⁻ are also listed in Table 2 for direct comparison with the halide-substituted analogues.

Table 2 Optimized bond lengths of [XAuCN]⁻ (C_∞v) at the levels of PBE, B3LYP, and CCSD(T) compared with those of the homogeneous species, AuX₂^−a

	R(X–Au)/Å	R(Au–C)/Å					R(C–N)/Å
	PBE	B3LYP	CCSD(T)	PBE	B3LYP	CCSD(T)	PBE	B3LYP	CCSD(T)
a The PBE results are from ADF calculations using SR-ZORA PBE/TZ2P. The B3LYP (Gaussian 03) and CCSD(T) (MOLPRO) results are calculated with Stuttgart pseudopotentials and cc-pVTZ-PP basis sets for Au and I, and cc-pVTZ basis sets for other elements (see text).
[FAuCN]^−	2.008	1.996	1.978	1.927	1.939	1.923	1.175	1.162	1.169
[ClAuCN]^−	2.319	2.337	2.307	1.955	1.968	1.950	1.173	1.161	1.169
[BrAuCN]^−	2.466	2.464	2.425	1.960	1.976	1.957	1.173	1.160	1.169
[IAuCN]^−	2.624	2.629	2.589	1.972	1.987	1.969	1.173	1.160	1.168
[FAuF]^−	1.997	1.983	1.962
[ClAuCl]^−	2.305	2.325	2.291
[BrAuBr]^−	2.454	2.452	2.410
[IAuI]^−	2.611	2.622	2.576
[NCAuCN]^−				1.995	2.006	1.994	1.172	1.160	1.172

---

The total energy difference at the CCSD(T) level between the anionic and neutral ground states at the anion geometry gives the first VDE (i.e. VDE₁) for each complex. The higher VDEs were calculated by adding the vertical excitation energies of the neutral molecule calculated at the anion geometry to the first VDE. The calculated VDEs and the final spectroscopic states are compared with the experimental data in Table 1 and plotted in Fig. 3 by fitting a Gaussian of 0.035 eV width to each VDE to yield the simulated spectra.

Fig. 3 Simulated PES spectra using the theoretical VDEs calculated with the CASSCF/CCSD(T)/SO approach.

The ADEs calculated at the CCSD(T) level are listed in Table 3 and compared with the experiments. The neutral ground states (²Π) of XAuCN (X = F, Cl, Br, I) all have the bent structures with C_s symmetry at the SR-ZORA level of theory due to the Renner–Teller vibronic coupling effect.³³ However, when SO coupling is included at the SO-ZORA PBE level all the XAuCN (X = F–I) species become linear. For IAuCN, the linear structure is also confirmed with CCSD(T) single-point calculations at the B3LYP optimized geometry when corrected by PBE/SOC results. The SR- and SO-ZORA geometry structures of the four neutral species optimized with PBE functional are given in Table 4. The Renner–Teller distortion energies are relatively small for these species. With the inclusion of SO coupling effects, the ²Π ground states of XAuCN split into ²Π_1/2 and ²Π_3/2, which eliminates the degeneracy of the ground states and thus quenches the Renner–Teller distortion.

Table 3 Experimental and theoretical adiabatic detachment energies (ADEs) for [XAuCN]⁻ (X = F, Cl, Br, I)^a

	Expt.	Calcd.^b
a The ADEs also represent the electron affinities for the corresponding neutral XAuCN species. b The ADEs are calculated at the CCSD(T)/VTZ level with the optimized B3LYP/VTZ geometries.
[FAuCN]^−	—	5.59
[ClAuCN]^−	5.38 ± 0.05	5.40
[BrAuCN]^−	5.14 ± 0.05	5.25
[IAuCN]^−	4.75 ± 0.05	4.89

---

Table 4 The optimized SO- and SR-ZORA (in parentheses) geometries of neutral XAuCN species using the PBE/TZ2P approach in the ADF code^a

a Without SO coupling, the neutral XAuCN species are slightly bent due to Renner–Teller effect, which is quenched by the differential SO effects of halogennp and Au 5d orbitals (see text).
R(Au–X)/Å	1.932 (1.944)	2.238 (2.249)	2.390 (2.400)	2.559 (2.566)
R(Au–C)/Å	1.912 (1.907)	1.943 (1.940)	1.949 (1.947)	1.959 (1.958)
R(C–N)/Å	1.183 (1.182)	1.180 (1.178)	1.178 (1.176)	1.176 (1.175)
∠XAuC/°	180.00 (172.17)	180.00 (167.33)	180.00 (167.21)	180.00 (167.68)
∠AuCN/°	180.00 (173.93)	180.00 (175.14)	180.00 (175.60)	180.00 (176.55)

---

The isocontour surfaces of the Kohn–Sham orbitals of [XAuCN]⁻ (X = F, Cl, Br, I) calculated using SR-ZORA are shown in Fig. 4. The SO splittings of the scalar-relativistic Kohn–Sham MO levels from the ADF/PBE calculations are shown in Fig. 5 in order to qualitatively illustrate the trend of the SO splittings in the [XAuCN]⁻ (X = F, Cl, Br, I) series.

Fig. 4 The isocontour surfaces of the Kohn–Sham orbitals of [XAuCN]⁻ (X = F, Cl, Br, I) (isocontour = 0.05 a.u.).

Fig. 5 The SO splitting of the SR-ZORA Kohn–Sham MOs of [XAuCN]⁻ (X = F, Cl, Br and I).

Discussion

As shown in Fig. 3 and Table 1, the theoretical results are in good agreement with the experimental data. The HOMOs of the anion species all have π-symmetry (Fig. 4) and consist of the anti-bonding combination of the (p_x, p_y) lone-pair orbitals on the halogen, the Au (d_xz, d_yz) orbitals, and the π-orbitals of CN. Electron detachment from the HOMO results in a ²Π final state. SO splitting gives rise to the ²Π_3/2 ground state and the ²Π_1/2 excited state of neutral XAuCN, which correspond to the X and A bands observed in the PES spectra, respectively. The calculated VDEs for these two transitions are in excellent agreement with the experimental data for all three species observed (Table 1 and Fig. 3). The calculated ADEs for the ground state transition of all the species of Cl, Br, and I are also in good agreement with the experimental data (Table 3). Our CCSD(T) calculations predict the ADE of [FAuCN]⁻ or the electron affinity of FAuCN to be 5.59 eV, the largest among all the species studied, even though this species was not observed experimentally. Upon electron detachment from the HOMO, the X–Au bond lengths decrease by 0.074 Å (F), 0.078 Å (Cl), 0.072 Å (Br), and 0.064 Å (I) as a result of the reduced antibonding interactions. These geometry changes between the neutral and anion ground states are consistent with the broad ground-state band observed for all three species, in particular, for [ClAuCN]⁻ and [BrAuCN]⁻.

As shown in Fig. 4 and 5, the HOMO-1 is a σ-orbital primarily of Au s-d_z² character. The calculated VDEs for all the Cl, Br, I species for this detachment channel are also in good agreement with the experimental data (band B in Fig. 1). The HOMO-2 for all the four species is the degenerate, quasi-atomic δ orbitals from the Au5d (xy, x²−y²) pair. The band C of [ClAuCN]⁻ and [BrAuCN]⁻ and band D of [IAuCN]⁻ correspond to one SO component (²Δ_5/2) from detachment from this orbital. As expected, the observed VDEs of this feature are almost the same (within 6.6 ∼ 6.7 eV) for the Cl, Br, and I species (Table 1). It is interesting to note that the detachment cross section for this feature is unusually low at 157 nm (Fig. 1).

The HOMO-3 of [ClAuCN]⁻ and [BrAuCN]⁻ is a π-orbital primarily from the (p–d)π X–Au bonding orbitals with contribution from the CN ligand. Electron detachment from this orbital of [BrAuCN]⁻ results in the E and F bands in the PES spectra due to the large SO effects of Au5d and halogennp orbitals. For [ClAuCN]⁻, detachment from HOMO-3 gives rise to band E as the ²Π_3/2 component. The ²Π_1/2 component is calculated to be close to ²Π_3/2 and may correspond to the shoulder on the E band (Fig. 1). For [IAuCN]⁻, the HOMO-4 has the same character and detachment from this orbital results in bands E and F in the PES spectra as well. The calculated SO splittings (Table 1) for the detachment from this orbital are in good agreement with the observed values and the trend is consistent with the (p–d)π X–Au bonding nature for this orbital.

The D bands of [ClAuCN]⁻ and [BrAuCN]⁻ correspond to detachment from HOMO-4, which is essentially a non-bonding combination between the halogen p_z orbital and the σ lone pair on CN. The HOMO-3 orbital of [IAuCN]⁻ has the same nature, corresponding to the C band in the PES spectrum. It should be noted that the detachment cross section from this orbital is particularly high for all three species. Overall, the calculated VDEs from the CASSCF/CCSD(T)/SO approach are in excellent agreement with the experimental data, allowing quantitative interpretation of the PES spectra. The accuracy of this approach for excited-states energies is also verified in other heavy-element systems.^34,35

To understand the chemical bonding in the [XAuCN]⁻ complexes, we carried out population analyses and calculated bond orders using a variety of theoretical approaches.^36–45 The calculated atomic charges and Au–X bond orders are given in Table 5. All methods show that the Au atom carries little charge, while the negative charge is mainly distributed between the X and CN ligands. The calculated Wiberg, Mayer, and Gopinathan–Jug (G–J) bond orders of the Au–X bonds all show that the F–Au bond is much weaker than the other X–Au bonds, with the I–Au bond order being the highest. The F–Au bond can be considered to be ionic due to the more polarized charge distribution. The calculated electron localization functions (ELFs) (Fig. 6) show that there is nearly no electron pairing density between the Au and F atoms, whereas strong electron paring density exists between Au and CN in all four species regardless of the halogen ligands in [XAuCN]⁻. Apparent electron pairing density exists between Au and the heavier halogen atoms, indicating that the latter all have weak covalency. The electron pairing density increases from F to I and the I–Au bond has the highest covalent character. The current observations are consistent with our recent studies of the AuI₂⁻ and Au(CN)₂⁻ complexes,^9,15 and reveal the evolution from mainly ionic bonding between F–Au in [FAuCN]⁻ to relatively strong covalent bonding between I–Au in [IAuCN]⁻.

Table 5 Theoretical atomic charges on Au and halogen atoms and the calculated bond orders of X–Au

		Net charge
	Atom	Mulliken^36	Hirschfeld^39	Voronoi^40	Bader^38	MDC-q ^41
[FAuCN]^−	Au	0.100	−0.002	0.066	0.273	0.155
	F	−0.626	−0.461	−0.498	−0.699	−0.525
[ClAuCN]^−	Au	0.003	−0.018	0.050	0.174	0.097
	Cl	−0.544	−0.458	−0.496	−0.608	−0.508
[BrAuCN]^−	Au	0.084	−0.016	−0.043	0.153	0.050
	Br	−0.631	−0.467	−0.497	−0.588	−0.483
[IAuCN]^−	Au	−0.024	−0.028	0.003	0.057	−0.003
	I	−0.523	−0.462	−0.466	−0.479	−0.461

---

		Bond order
	Bond	Wiberg^42	Mayer^43	G–J^44	N–M(3)^45
[FAuCN]^−	F–Au	0.337	0.545	0.366	0.840
[ClAuCN]^−	Cl–Au	0.404	0.813	0.449	0.877
[BrAuCN]^−	Br–Au	0.420	0.724	0.448	0.872
[IAuCN]^−	I–Au	0.457	0.864	0.480	0.886

---

Fig. 6 The electron localization functions for [XAuCN]⁻.

Conclusions

We have carried out a joint experimental and computational study on a series of mixed halide cyanide Au(I) complexes, [XAuCN]⁻ (X = F, Cl, Br, I). Photoelectron spectra are measured at 206 and 157 nm for the anions with X = Cl, Br, I. The well-resolved spectra are compared with relativistic quantum calculations, revealing ionic bonding in F-Au and increased covalent bonding from Cl–Au to I–Au. The calculations show that without spin–orbit coupling all the neutral XAuCN (X = F, Cl, Br, I) species have bent geometries due to Renner–Teller effect. Differential spin–orbit coupling effects of halogennp orbitals and Au 5d orbitals are large enough to quench the Renner–Teller effect, leading to linear structures for all neutral XAuCN in their ground state. Calculated bond orders and ELFs are all consistent with covalent bonding between Au and CN and increased covalency between Au and the heavy halogen ligands.

Acknowledgements

The experimental work done at Brown University was supported by the National Science Foundation (CHE-1049717). The theoretical work done at Tsinghua University was supported by NKBRSF (2011CB932400) and NSFC (20933003, 11079006, 91026003) of China. The calculations were done using the DeepComp 7000 Supercomputer at the Computer Network Information Center, Chinese Academy of Sciences and the Shanghai Supercomputing Center.

References

1. G. J. Hutchings, M. Brust and H. Schmidbaur, Chem. Soc. Rev., 2008, 37, 1759.
2. (a) D. J. Gorin, B. D. Sherry and F. D. Toste, Chem. Rev., 2008, 108, 3351; (b) J. C. Y. Lin, R. T. W. Huang, C. S. Lee, A. Bhattacharyya, W. S. Hwang and I. J. B. Lin, Chem. Rev., 2009, 109, 3561; (c) M. Pazicky, A. Loos, M. J. Ferreira, D. Serra, N. Vinokurov, F. Rominger, C. Jakel, A. S. K. Hashmi and M. Limbach, Organometallics, 2010, 29, 4448; (d) M. Alcarazo, T. Stork, A. Anoop, W. Thiel and A. Furstner, Angew. Chem., Int. Ed., 2010, 49, 2542; (e) N. Marion and S. P. Nolan, Chem. Soc. Rev., 2008, 37, 1776.
3. H. Schmidbaur, Gold Bull., 2000, 33, 3.
4. L. S. Wang, Phys. Chem. Chem. Phys., 2010, 12, 8694.
5. H. Schmidbaur, S. Cronje, B. Djordjevic and O. Schuster, Chem. Phys., 2005, 311, 151.
6. (a) W. J. Hunks, M. C. Jennings and R. J. Puddephatt, Inorg. Chem., 2002, 41, 4590; (b) M. J. Katz and D. B. Leznoff, J. Am. Chem. Soc., 2009, 131, 18435.
7. (a) P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412; (b) O. Dietz, V. M. Rayon and G. Frenking, Inorg. Chem., 2003, 42, 4977.
8. T. Waters, X. B. Wang and L. S. Wang, Coord. Chem. Rev., 2007, 251, 474.
9. X. B. Wang, Y. L. Wang, J. Yang, X. P. Xing, J. Li and L. S. Wang, J. Am. Chem. Soc., 2009, 131, 16368.
10. P. Zaleski-Ejgierd, M. Patzschke and P. Pyykkö, J. Chem. Phys., 2008, 128, 224303.
11. X. Wu, Z. B. Qin, H. Xie, R. Cong, X. H. Wu, Z. C. Tang and H. J. Fan, J. Phys. Chem. A, 2010, 114, 12839.
12. H. J. Zhai, C. Burgel, V. Bonacic-Koutecky and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 9156.
13. (a) B. Kiran, X. Li, H. J. Zhai and L. S. Wang, J. Chem. Phys., 2006, 125, 133204; (b) H. J. Zhai, L. S. Wang, D. Y. Zubarev and A. I. Boldyrev, J. Phys. Chem. A, 2006, 110, 1689.
14. D. Schroder, R. Brown, P. Schwerdtfeger, X. B. Wang, X. Yang, L. S. Wang and H. Schwarz, Angew. Chem., Int. Ed., 2003, 42, 311.
15. Y. L. Wang, X. B. Wang, X. P. Xing, F. Wei, J. Li and L. S. Wang, J. Phys. Chem. A, 2010, 114, 11244.
16. (a) J. S. Ovens, A. R. Geisheimer, A. A. Bokov, Z. G. Ye and D. B. Leznoff, Inorg. Chem., 2010, 49, 9609; (b) J. S. Ovens and D. B. Leznoff, Dalton Trans., 2011, 40, 4140.
17. L. S. Wang, C. F. Ding, X. B. Wang and S. E. Barlow, Rev. Sci. Instrum., 1999, 70, 1957.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
19. ADF 2009.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands (http://www.scm.com).
20. E. vanLenthe, R. vanLeeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281.
21. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) P. J. Stephens, F. J. Devlin, M. J. Frisch and C. F. Chabalowski, J. Phys. Chem., 1994, 98, 11623.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision D.02), Gaussian, Inc., Wallingford, CT, 2004.
23. H.-J. Werner MOLPRO, Version 2008.1 Ed. A package of ab initio programs; see: http://www.molpro.net.
24. (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910; (b) G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382.
25. B. O. Roos and P. R. Taylor, Chem. Phys., 1980, 48, 157.
26. A. Berning, M. Schweizer, H. J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
27. (a) D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227; (b) T. R. Cundari, M. T. Benson, M. L. Lutz and S. O. Sommerer, Rev. Comput. Chem., 1996, 8, 145.
28. K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283.
29. K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877.
30. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
31. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358.
32. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 1999, 110, 7667.
33. R. Renner, Z. Phys., 1934, 92, 172.
34. (a) F. Wei, G.-S. Wu, W. H. E. Schwarz and J. Li, Theor. Chem. Acc., 2011, 129, 467; (b) F. Wei, G.-S. Wu, W. H. E. Schwarz and J. Li, J. Chem. Theory Comput., 2011 DOI:10.1021/ct2000233.
35. J. Su, Y.-L. Wang, F. Wei, W. H. E. Schwarz and J. Li, J. Chem. Theory Comput., 2011 DOI:10.1021/ct200419x.
36. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833.
37. R. Bader, Chem. Rev., 1991, 91, 893.
38. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
39. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129.
40. C. F. Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189.
41. M. Swart, P. T. v. Duijnen and J. G. Snijders, J. Comput. Chem., 2001, 22, 79.
42. K. B. Wiberg, Tetrahedron, 1968, 24, 1083.
43. I. Mayer, Int. J. Quantum Chem., 1984, 26, 151.
44. M. S. Gopinathan and K. Jug, Theor. Chim. Acta, 1983, 63, 497.
45. (a) A. Michalak, R. L. DeKock and T. Ziegler, J. Phys. Chem. A, 2008, 112, 7256; (b) R. F. Nalewajski and J. Mrozek, Int. J. Quantum Chem., 2004, 51, 187; (c) R. F. Nalewajski and J. Mrozek, Int. J. Quantum Chem., 1997, 61, 589; (d) R. F. Nalewajski, J. Mrozek and A. Michalak, Polish J. Chem., 1998, 72, 1779; (e) R. F. Nalewajski, J. Mrozek and G. Mazur, Can. J. Chem., 1996, 74, 1121.

---