Differentiating intrinsic SERS spectra from a mixture by sampling induced composition gradient and independent component analysis†
Justin L.
Abell‡
*a,
Joonsang
Lee‡
b,
Qun
Zhao
b,
Harold
Szu
c and
Yiping
Zhao
d
aNanoscience and Engineering Center, Department of Biological and Agricultural Engineering, University of Georgia, Athens, GA 30602, USA. E-mail: jabell@uga.edu
bDepartment of Physics and Astronomy, University of Georgia, Athens, GA 30602, USA
cArmy NVESD MS/Human Signature Exploitation Ft., Belvoir, VA 22060, USA
dNanoscience and Engineering Center, Department of Physics and Astronomy, University of Georgia, Athens, GA 30602, USA
First published on 2nd November 2011
Abstract
By generating a composition gradient on a highly uniform SERS substrate and applying independent component analysis, we demonstrate that one can extract the intrinsic SERS spectrum of individual components from SERS spectra obtained from a two-component mixture.
Surface-enhanced Raman scattering (SERS) has attracted a great deal of attention due to its powerful merits as an ultra-sensitive, label-free trace chemical sensing platform. The ability of SERS spectra to provide sharp, highly resolved spectral fingerprints allows for superior chemical and biological sensing.1,2 Traditionally, SERS has been employed for analysis of relatively pure samples in a well defined medium; however, biologically-relevant samples, such as blood or sputum, contain a mixture of components, and the resulting SERS spectra can be very complicated compared to those of pure analytes. The conventional practice is to combine SERS with other techniques, such as magnetic beads,3–6 microfluidic or electric-field devices,7–9 or centrifugation.10 These approaches usually require the use of capture probes, specialized devices, continuous consumption of SERS-active colloids, and/or multiple processing steps.
Obtaining information about individual analyte(s) from SERS spectra of a mixture is a very challenging yet very urgent task for the SERS community. So far, most reports in the literature use direct visual observation or statistical methods such as principal component analysis (PCA) to analyze SERS mixture signals.11–16 However, to obtain information of individual spectral components, higher order statistics, e.g. kurtosis beyond the 2nd order Gaussian statistics is needed in a class of algorithms called blind source separation (BSS) method or independent component analysis (ICA).17ICA is a statistical method that extracts individual source signals from the measured mixture signals by means of their joint density factorization. For example, if the measured signal results from a mixture of two analytes with source signal sj (j = 1, 2), the mixture signal xi (i = 1, 2), can be expressed as a linear combination of s1 and s2,
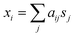 | (1) |
For real samples such as blood or sputum, the composition ratios of different analytes are typically fixed once the samples are received. Thus, it is a challenge to obtain two SERS spectra from samples with different compositions. One approach to address this challenge is to utilize the intrinsic, nonuniform distribution of analyte molecules that results when a liquid mixture is applied to a SERS-active surface. The resulting distribution of analytes onto the sensing surface can be significantly affected by the analyte's diffusivity and adsorption capability, as well as the drying process of the sample solvent. Because the measured SERS signal is proportional to the number of molecules within the measurement area, the resulting spatial distribution of each species onto the surface can be mapped by acquiring multiple measurements at different locations on the substrate. In this Communication, we utilize the intrinsic sampling-induced nonuniform distribution of two different analytes within a mixture sample, coupled with ICA, to demonstrate a proof-of-principle application for unsupervised separation of SERS source spectra from measurements obtained from a mixture sample.
To demonstrate the principle, two Raman probes, trans-1,2- bis(4-pyridyl) ethylene (BPE) and 4-hydroxy thiophenol (i.e.mercaptophenol, MPh), are selected because they both produce strong yet distinct SERS spectra. Furthermore, BPE and MPh both adsorb strongly to Ag surfaces but through different chemical constituents, i.e. a lone-pair nitrogen and a thiol, respectively, and therefore are expected to adsorb to the surface at different rates and with different binding strengths. Thus, applying a droplet containing a dilute mixture of these analytes to a SERS surface should simultaneously generate a non-uniform distribution of the two analytes with varying and spatially-dependent surface coverage ratios after the sample solvent dries as shown in Fig. 1A.
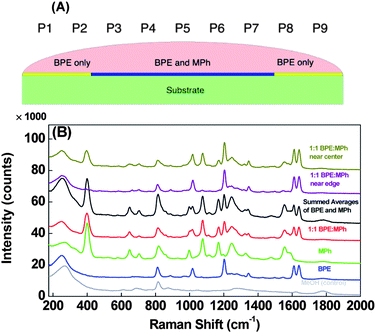 | ||
Fig. 1 A) Cross sectional diagram of the BPE: MPh droplet spreading on the AgNR substrate and the possible spatial distribution of the resulting films of analyte BPE and MPh. The approximate locations P1 through P9 are labelled here as a reference. B) Average SERS spectra for methanol, BPE, MPh, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 BPE:MPh mixture. The artificially summed SERS spectrum of MPh and BPE and the SERS spectra of the mixture sample at different substrate location are also shown. Spectra are offset for clarity. 1 BPE:MPh mixture. The artificially summed SERS spectrum of MPh and BPE and the SERS spectra of the mixture sample at different substrate location are also shown. Spectra are offset for clarity. | ||
BPE and MPh were dissolved in methanol to yield 5 × 10−5 mol L−1 solutions. A mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 BPE:MPh, with each analyte present at 5 × 10−5 mol L−1 was also prepared. The SERS measurements were performed by dispensing a 4 μl volume of the mixture at the center of a small 1 × 1 cm2silver nanorod (AgNR) SERS substrates.23,24 The droplet immediately spread across the entire surface of the AgNR substrate and the methanol completely evaporated in ∼1 min. SERS spectra were obtained using a portable Raman system (Enwave Optronics, model 10HT-HRC) with a λ = 785 nm laser, at 30 mW power and 2 s integration time. Approximately 9 measurements were mapped along a line across the substrate using ∼1 mm steps as shown in Fig. 1A.
1 BPE:MPh, with each analyte present at 5 × 10−5 mol L−1 was also prepared. The SERS measurements were performed by dispensing a 4 μl volume of the mixture at the center of a small 1 × 1 cm2silver nanorod (AgNR) SERS substrates.23,24 The droplet immediately spread across the entire surface of the AgNR substrate and the methanol completely evaporated in ∼1 min. SERS spectra were obtained using a portable Raman system (Enwave Optronics, model 10HT-HRC) with a λ = 785 nm laser, at 30 mW power and 2 s integration time. Approximately 9 measurements were mapped along a line across the substrate using ∼1 mm steps as shown in Fig. 1A.
Fig. 1B shows the SERS spectra of pure BPE, MPh, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 BPE:MPh mixture acquired from an average of 9 points measured in a grid-like pattern across the 1 × 1 cm2AgNR substrates. The figure also includes a representative spectrum of the MeOH as well as an artificial spectrum generated by summing the pure MPh and pure BPE spectra together. The measured BPE signal (used as s1) demonstrates sixteen observable peaks at Δν ≈ 254, 691, 811, 888, 969, 1016, 1068, 1203, 1231, 1245, 1277, 1344, 1430, 1495, 1546, 1611, and 1640 cm−1 with the primary BPE peaks being Δν ≈ 1016, 1203, 1611, and 1640 cm−1, which correspond to the pyridine ring breathing, C
1 BPE:MPh mixture acquired from an average of 9 points measured in a grid-like pattern across the 1 × 1 cm2AgNR substrates. The figure also includes a representative spectrum of the MeOH as well as an artificial spectrum generated by summing the pure MPh and pure BPE spectra together. The measured BPE signal (used as s1) demonstrates sixteen observable peaks at Δν ≈ 254, 691, 811, 888, 969, 1016, 1068, 1203, 1231, 1245, 1277, 1344, 1430, 1495, 1546, 1611, and 1640 cm−1 with the primary BPE peaks being Δν ≈ 1016, 1203, 1611, and 1640 cm−1, which correspond to the pyridine ring breathing, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C ethylene stretch, C
C ethylene stretch, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C pyridine stretch, and C
C pyridine stretch, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C ethylene stretch, respectively.25 Fifteen peaks are distinguishable in the measured MPh spectrum (used as s2), Δν ≈ 273, 330, 400, 582, 649, 704, 820, 996, 1076, 1115, 1169, 1250, 1342, 1482, and 1555 cm−1. Of these, the primary peaks observed for MPh are Δν ≈ 400, 1076, and 1169 cm−1, which corresponds to ring vibrations of the benzene constituent.26BPE and MPh therefore appear to have fairly distinct spectra, with the only significantly overlapping peaks at Δν ≈ 996 and 1016 cm−1, respectively. Furthermore, comparing these spectra to those acquired from the control sample (methanol only) we can see the large, defined peaks at Δν ≈ ∼270 and ∼800 cm−1 common in all the spectra which likely result from adsorbed contaminants. The measured spectrum of the BPE:MPh mixture is virtually identical to the artificial spectrum generated by adding the SERS spectra of pure BPE and pure MPh together, confirming that a mixture spectrum is a linear combination of the individual SERS spectra of the two probes. Finally, the spectral cross-correlation coefficient r of the BPE and MPh are quantitatively estimated as r = −0.005, which demonstrates the independence of SERS spectra of the two source analytes. Thus, we can apply ICA algrithm to the SERS spectra of this mixture.
C ethylene stretch, respectively.25 Fifteen peaks are distinguishable in the measured MPh spectrum (used as s2), Δν ≈ 273, 330, 400, 582, 649, 704, 820, 996, 1076, 1115, 1169, 1250, 1342, 1482, and 1555 cm−1. Of these, the primary peaks observed for MPh are Δν ≈ 400, 1076, and 1169 cm−1, which corresponds to ring vibrations of the benzene constituent.26BPE and MPh therefore appear to have fairly distinct spectra, with the only significantly overlapping peaks at Δν ≈ 996 and 1016 cm−1, respectively. Furthermore, comparing these spectra to those acquired from the control sample (methanol only) we can see the large, defined peaks at Δν ≈ ∼270 and ∼800 cm−1 common in all the spectra which likely result from adsorbed contaminants. The measured spectrum of the BPE:MPh mixture is virtually identical to the artificial spectrum generated by adding the SERS spectra of pure BPE and pure MPh together, confirming that a mixture spectrum is a linear combination of the individual SERS spectra of the two probes. Finally, the spectral cross-correlation coefficient r of the BPE and MPh are quantitatively estimated as r = −0.005, which demonstrates the independence of SERS spectra of the two source analytes. Thus, we can apply ICA algrithm to the SERS spectra of this mixture.
Also, a large variation in SERS spectra at different locations of the mixture was obtained for MPh, indicating a non-homogenous distribution of the analyte onto the surface. The spectra of the BPE:MPh mixture acquired near the center (xP5) and near the edge (xP1) of the substrate are also presented in Fig. 1B. Cursory examination of these spectra show that the BPE peak intensity is relatively insensitive to position, indicating a uniform BPE surface coverage across the SERS substrate; meanwhile the MPh peak intensities at Δν ≈ 400, 1076, 1169, and 1555 cm−1 decrease significantly as the measurement position approaches the edge of the substrate. This indicates that the surface coverage of MPh decreases from center to edge, implying that there is a spatial gradient of the BPE and MPh on the substrate surface. This result is expected due to the capillary spreading of the droplet and the interfactial interaction nature of BPE and MPh. The MPh appears to adsorb to the Ag surface with a much faster rate compared to that of BPE, and because there is only a limited amount of each analyte in the solution, the MPh molecules in solution will be depleted before the wetting front reaches the edge of the substrate. However, because BPE may be adsorbing more slowly on the AgNR, there will still be sufficient BPE molecules to access (and adsorb to) the AgNRs near the wetting front before being depleted. Therefore, a gradient of MPh and BPE coverage from the center to the edge will be established as shown in Fig. 1A. Such spatial variation of the analyte intensity ratio is key to demonstrate the principle of separation in this work. Finally, the spectral features resulting from the background show very little variation.
In fact, quantitative information of the BPE:MPh ratio across the substrate can be obtained from ICA. Various combination of the SERS data, e.g., xP1 and xP2, xP1 and xP3,,…,, xP1 and xP9, or xP5 and xP6,, xP5 and xP9 were used as the mixture signals x1 and x2 to perform ICA analysis shown in Fig. 2, where xP1 and xP5 were used as reference spectra. We performed pre-processing steps, including detrending, centering and whitening of the mixture signals to make the ICA estimation simpler and better conditioned. First, the baselines of the all data were removed. The removal procedure estimates the baseline through multiple windows followed by regressing the baseline to the estimates with a spline approximation. Next, we performed the centering process by subtracting its mean value from the original mixture signals so that the mixture signals and the independent components have zero mean. Then, we performed the whitening process so that the source signals are uncorrelated and their variances equal unity. In this paper, we have carried out ICA by maximization of non-Gaussianity. According to the central limit theorem, a sum of two independent random variables (i.e. source signals) usually has a distribution that is closer to Gaussian than any of the two original random variables. To use non-Gaussianity for the ICA estimation, we need a quantitative measurement such as the kurtosis, entropy, or negentropy. Here, we have employed FastICA which uses a fixed point algorithm and the negentropy as a quantitative measurement for the non-Gaussianity to estimate the original spectra.8 To improve the accuracy of the estimated ICA spectra, the measured spectra were truncated below 360 cm−1 to remove the large peak resulting from the background. Fig. 2 shows the rescaled ICA-separated spectra of BPE and MPh compared to the measured spectra. Qualitatively, the simulated ICA spectra capture the main characteristics of the pure BPE and MPh spectra. The cross-correlation coefficient r between the ICA-separated spectrum and the measured BPE spectrum was calculated to be r > 0.9, while for MPh, r ≈ 0.7. The result demonstrates that one can use the sampling induced composition gradient and ICA to obtain a good approximation of the pure analyte spectra from the mixture. After a close examination of Fig. 2, we find that negative peaks appear near Δν ≈ 810 and 1020 cm−1 in the estimated MPh spectra (Fig. 2B) which appear to correspond to the intense BPE or background features; there is also a small inverted peak near 400 and negative peak at 1076 cm−1 for the ICA spectra of BPE, which correspond to the intense MPh peaks at these locations.
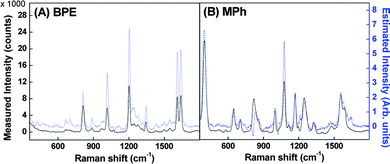 | ||
| Fig. 2 Comparison of the measured spectra (dark) and ICA-estimated spectra (light) for (A) BPE and (B) MPh SERS at P5 using P1 as a reference. | ||
Since the SERS spectra of the mixture are linear combinations of s1 and s2, the weighting coefficients in eqn (1) should follow ai1 ∝ NBPE and ai2 ∝ NMPh, respectively, where NBPE and NMPh are the number of BPE and MPh molecules within the measurement area. Thus, by fixing x1 as the spectrum at a specific location (i.e. the weighting coefficients a11 and a12 are fixed) while varying x2 with the spectrum from different locations, the location-dependent weighting coefficients a21 and a22 can be estimated. These two coefficients a21 and a22 can be used to represent the relative coverage ratio of BPE and MPh at different locations. As highlighted in Fig. 1B, the measured SERS spectra at P1 and P5 are significantly different, we have used either of them as the reference measurement x1, and obtained the ratio of a21/a11 and a22/a12 as a function of different locations. Fig. 3 shows the normalized ratio of the weighting coefficients a2j/a1j, (normalized to the maximum ratio value) for A) BPE and B) MPh using P1 (squares) or P5 (circles) as a reference point. As a comparison, Fig. 3A and B also show the peak intensities (triangles) of BPE (Δν ≈ 1200 cm−1; I1200) and MPh (Δν ≈ 1076 cm−1; I1076), respectively, which were also normalized to the maximum intensity obtained for each analyte. Because ICA does not generate weighting coefficients when the reference location is referenced to itself (i.e. x2 = x1), we assume that a2j/a1j is equal to unity at this location; therefore, we artificially set a2j/a1j = 1.
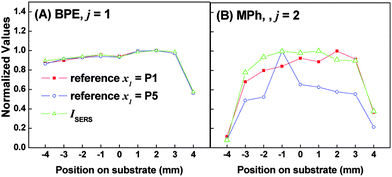 | ||
| Fig. 3 Plot of the normalized weighting coefficients and normalized SERS intensity for A) BPE and B) MPh. Each figure shows three plots: i) the normalized ratio of a2j/a1j, where 1 and 2 represent the weighting coefficient estimated for the reference point (P1, edge of substrate) and some other location, respectively, and j = 1 or 2 for BPE and MPh, respectively; ii) same as i) but using P5 (center of substrate) as the reference location; and iii) the intensity of I1200 (BPE) and I1076 (MPh) normalized to the highest value. For i) and ii) the a2j/a1j ratio is normalized to the maximum ratio value obtained. | ||
As shown in Fig. 3A, the spatially-dependent normalized a21/a11 ratio demonstrates a nearly perfect match to the spatially-dependent normalized I1200, regardless the reference locations. Both I1200 and the ratio a21/a11 show a fairly flat spatial dependence, with less than ∼ 50% drop in value at the right edge of the substrate, indicating that the BPE is evenly distributed onto the AgNR substrate. Fig. 3B, on the other hand, shows that the I1076 drops by >90% and >60%, for the left and right edge points respectively. This indicates that the MPh surface coverage is significantly decreased closer to the edge of the substrate. The normalized a22/a12 ratio in Fig. 3B appears to match very closely to the normalized I1076 profile with respect to position on the substrate. We also point out that the plot with P1 as a reference shows a better match to the I1076 profile than the one with P5 as a reference. This result demonstrates that ICA can be used to quantitatively map the relative analyte distribution.
Since the coefficients a21 and a22 are proportional to the number of particular molecules measured, the ratio a21/a22 should be proportional to the BPE:MPh ratio at a specific location, i.e., in principle one can map the BPE:MPh ratio at different locations from Fig. 3. To do so, we first need to establish a calibration curve of a21/a22versusBPE:MPh ratio. Mixture solutions with fixed BPE:MPh ratios were prepared and applied to different substrates and average SERS spectra was determined for each ratio (see ESI† for details). Again, FastICA was used to generate aij for each mixture relative to the reference. Fig. S5A (ESI†) shows the calibration curve of a21/a22versusBPE:MPh. Therefore, the BPE:MPh ratio map in our experiment can be obtained as shown in Fig. 4. Because the ICA does generate a weighting coefficient at the reference location (P1, x = −4 mm) is referenced with itself, we omitted this value from the plot. For comparison, using the measured SERS intensity we can obtain another ratio mapping with IBPE/IMPh as shown with the calibration curve Fig. S5B. This result demonstrates that the ICA plus composition gradient can be used to predict and map the mixture's composition ratio quantitatively.
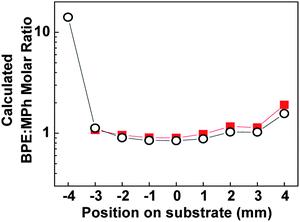 | ||
| Fig. 4 The calculated BPE:MPh ratio using the a21/a22 (squares) calibration curve in Fig. S5A, and IBPE/IMPh calibration curve in Fig. S5B (circles). The calculated BPE:MPh ratio using a21/a22 at x = − 4 mm has been omitted. The y-axis is presented in logarithmic scale for easier visualization. | ||
In conclusion, we have successfully implemented ICA anlaysis to separate the intrinsic SERS spectra of the components in a mixture by obtaining a spatially distributed SERS spectra of a single mixture. The weighing coefficients obtained from the ICA analysis can be used to quantitatively map the relative spatial distribution of each component. This proof-of-principle demonstrates that one can potentially separate mixture SERS spectra using only one mixture sample. However, for practical clinical samples, this technique needs further refinement due to the constraints of ICA, especially the requirement for spectral independence of the analytes of interest. Many biomolecules of interest such as proteins are composed of similar molecular constituents, i.e. the same 20 amino acids, and therefore may not show significant signal independence ultimately disqualifying them for ICA analysis. Smaller biologically relevant molecules, however, have been investigated with SERS8,10,27 and may demonstrate the requisite signal independence. Thus, to further improve ICA for correlated signal analysis is needed. Furthermore, traditional approaches for multiplexing analysis (e.g.fluorescent labeling) can also be utilized for SERS and ICA analysis. For example, one can use an extrinsic-label SERS multiplexing approach, labeling the analytes with pre-selected molecules that show spectral independence. In this case, the current ICA method should be well suited to separate the source signals of the labels from complex mixture spectra.
Acknowledgements
JA and YPZ are supported by USDA CSREES Grant # 2009-35603-05001.Notes and references
- K. Hering, D. Cialla, K. Ackermann, T. Dorfer, R. Moller, H. Schneidewind, R. Mattheis, W. Fritzsche, P. Rosch and J. Popp, Anal. Bioanal. Chem., 2008, 390, 113 CrossRef CAS.
- S. D. Hudson and G. Chumanov, Anal. Bioanal. Chem., 2009, 394, 679 CrossRef CAS.
- S. A. Chen, J. L. Yao, S. Y. Han and R. A. Gu, Acta Chim. Sinica, 2151, 68 Search PubMed.
- S. A. Chen, Y. X. Yuan, J. L. Yao, S. Y. Han and R. A. Gu, Chem. Commun., 2011, 47, 4225 RSC.
- L. L. He, B. Deen, T. Rodda, I. Ronningen, T. Blasius, C. Haynes, F. Diez-Gonzalez and T. P. Labuza, J. Food Sci., 2011, 76, N49 CrossRef CAS.
- L. L. He, C. L. Haynes, F. Diez-Gonzalez and T. P. Labuza, J. Raman Spectrosc., 2011, 42, 1428 CrossRef CAS.
- I. F. Cheng, H. C. Chang and D. Hou, Biomicrofluidics, 2007, 1, 021503 CrossRef.
- A. Marz, B. Monch, P. Rosch, M. Kiehntopf, T. Henkel and J. Popp, Anal. Bioanal. Chem., 2011, 400, 2755 CrossRef.
- V. Ranc, A. Stanova, J. Marak, V. Maier, J. Sevcik and D. Kaniansky, J. Chromatogr., A, 2011, 1218, 205 CrossRef CAS.
- P. H. Hsu and H. H. K. Chiang, J. Raman Spectrosc., 2010, 41, 1610 CrossRef.
- E. Blackie, E. C. Le Ru, M. Meyer, M. Timmer, B. Burkett, P. Northcote and P. G. Etchegoin, Phys. Chem. Chem. Phys., 2008, 10, 4147 RSC.
- P. G. Etchegoin, M. Meyer, E. Blackie and E. C. Le Ru, Anal. Chem., 2007, 79, 8411 CrossRef CAS.
- E. Koglin, A. Tarazona, S. Kreisig and M. J. Schwuger, Colloids Surf., A, 1997, 123, 523 CrossRef.
- R. Stevenson, R. J. Stokes, D. MacMillan, D. Armstrong, K. Faulds, R. Wadsworth, S. Kunuthur, C. J. Suckling and D. Graham, Analyst, 2009, 134, 1561 RSC.
- J. Thornton and R. K. Force, Appl. Spectrosc., 1991, 45, 1522 CrossRef CAS.
- G. F. Wang, H. Y. Park and R. J. Lipert, Anal. Chem., 2009, 81, 9643 CrossRef CAS.
- Q. Zhao, J. Langley, J. Lee, J. L. Abell and Y. Zhao, Proc. SPIE–Int. Soc. Opt. Eng., 2011, 80580E CrossRef.
- C. Gobinet, V. Vrabie, M. Manfait and O. Piot, IEEE Trans. Biomed. Eng., 2009, 56, 1371 CrossRef.
- X. G. Shao, Z. C. Liu and W. Cai, Analyst, 2009, 134, 2095 RSC.
- L. Silveira, A. R. De Paula, C. A. Pasqualucci and M. T. T. Pacheco, Instrum. Sci. Technol., 2008, 36, 134 CrossRef CAS.
- V. Vrabie, C. Gobinet, O. Piot, A. Tfayli, P. Bernard, R. Huez and M. Manfait, Biomed. Signal Proc., 2007, 2, 40 CrossRef.
- L. Fang, M. Lin and Y. Zheng, IEEE Computer Society Fourth International Conference on Natural Computation, 2008, 429 Search PubMed.
- S. B. Chaney, S. Shanmukh, R. A. Dluhy and Y. P. Zhao, Appl. Phys. Lett., 2005, 87, 031908 CrossRef.
- J. D. Driskell, S. Shanmukh, Y. Liu, S. B. Chaney, X. J. Tang, Y. P. Zhao and R. A. Dluhy, J. Phys. Chem. C, 2008, 112, 895 CAS.
- W. H. Yang, J. Hulteen, G. C. Schatz and R. P. VanDuyne, J. Chem. Phys., 1996, 104, 4313 CrossRef CAS.
- H. M. Lee, M. S. Kim and K. Kim, Vib. Spectrosc., 1994, 6, 205 CrossRef CAS.
- T. L. Wang, H. K. Chiang, H. H. Lu and F. Y. Peng, Opt. Quantum Electron., 2005, 37, 1415 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c1an15623c |
| ‡ Co-first author: These authors contributed equally to this study. |
| This journal is © The Royal Society of Chemistry 2012 |
