Evidence for atomic mixingvia multiple intermediates during the dynamic interconversion of silicate oligomers in solution†
Kim E.
Jelfs
a,
Edwin
Flikkema
b and
Stefan T.
Bromley
*cd
aDepartment of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK
bInstitute of Mathematics and Physics, Aberystwyth University, Penglais, Aberystwyth, Ceredigion, SY23 3BZ, UK
cDepartment de Química Física & Institut de Química Teòrica i Computacional, Universitat de Barcelona, C/Martí i Franquès 1, E-08028 Barcelona, Spain. E-mail: s.bromley@ub.edu
dInstitució Catalana de Recerca i Estudis Avançats (ICREA), E-08010 Barcelona, Spain
First published on 14th October 2011
Abstract
We investigate Si8- and Si16-based silicate species via global optimisation searches and ab initio calculations and propose a new multi-mechanism interpretation of the experimentally observed atomic mixing of silicate oligomers in solution.
Silicate oligomers, (SiO2)N(H2O)M, play a critical role in mineral nucleation, growth and dissolution. These species also lay at the heart of the debate concerning the pre- and post-nucleated regime of technologically important zeolite materials during hydrothermal synthesis. Knowing the structure and reactions of zeolite precursor species in solution is vital in determining whether nucleation proceeds via the growth of particles through the addition of small precursors, or whether aggregation of larger Secondary Building Units (SBUs) dominates.1,2 In order to address this issue 29Si NMR spectroscopy3–6 and Mass Spectroscopy (MS)7 have been employed to help characterize (SiO2)N(H2O)M clusters. However, reliable structure assignments are for the most part only available for species with N ≤ 8, with a few tentative assignments beyond this size. The reactions of some clusters in this relatively small size range have also been theoretically studied.8,9 Recently, an elegantly designed ESI (Electrospray Ionisation) MS experiment by Schüth et al., using isotopically labeled Si atoms, has shown that (SiO2)8(H2O)4 cubic octamer oligomers (hereafter termed double four-rings (D4Rs) following the zeolite nomenclature) in solution are a highly dynamic species which can rapidly and reversibly interconvert with an associated interchange of atoms.10 Assuming a single route for D4R interconversion, a specific mechanism based on a concerted exchange of cubic faces (or single four-rings—S4Rs) was put forward as being most compatible with the kinetic modeling. We present a systematic theoretical study of the free energy landscape of silicate (SiO2)N(H2O)M clusters in solution (for N = 8, 16 for a relevant range of M). Our detailed investigation allows us to propose an additional range of possible alternative routes for D4R interconversion based on substantially more stable intermediates than that needed for the concerted S4R exchange mechanism. Furthermore, we argue that our enriched multi-mechanism perspective is more consistent with the kinetic analysis of the ESI-MS data and is chemically more reasonable than the interpretation based on a single concerted mechanism.
Employing a three-step approach, we first extensively searched the complex potential energy landscape (PEL) of (SiO2)N(H2O)M clusters for low energy clusters using the basin hopping global optimisation algorithm11 and specifically parameterized interatomic potentials.12,13 Secondly, the energies and geometries of the 10–15 lowest energy clusters from step one were further refined using density functional theory (DFT) with the GAMESS-UK14 code, employing the B3LYP hybrid functional15 and a 6-31G(d,p) basis set with no symmetry constraints. This level of DFT theory has been established to be relatively accurate and computationally efficient for treating silicate oligomers with respect to very high level methods.16 We note that these two steps have also been previously successfully applied to find the ground states of bare and partially hydroxylated silica clusters.17,18 Finally, following previous studies8,9,16 we calculate the free energy of solution of the clusters, and any necessary water molecules to maintain the same chemical composition of all considered systems, by extracting the relevant thermodynamic terms (at 20 °C) from DFT evaluations of their (harmonic) vibrational frequency spectra (including zero point vibrations) and solvation energies using the polarisable continuum model (PCM).19 See ESI† for further details.
The most stable (SiO2)8(H2O)4 oligomer found by our method corresponds to the D4R which is known to be a dominant species in solution for a range of alkaline pH values.20 In particular D4Rs are known to be the majority species in tetramethylammonium cation (TMA+) solutions,21 possibly assisted by TMA+ acting as an external scaffold protecting the D4Rs against hydrolysis.22 In Fig. 1 we show the relative free energies of solution of a range of (SiO2)N(H2O)M oligomers for N = 8, 16 with respect to two isolated D4Rs. Blue diamonds correspond to OH condensation and hydroxylation reactions of a D4R (i.e. leading to (SiO2)8(H2O)4−x and (SiO2)8(H2O)4+x respectively). We see that the D4R occupies a minimum free energy point on this series indicating that it is stable against reactions which tend to open or contract its symmetric cubic structure (see Fig. 2, S1). This intrinsic stability of the D4R may further help to explain the observed dominance of D4Rs in solution. The asymmetry of the blue data points about the D4R minimum, also shows that the hydroxylation of the D4R is considerably more facile, energetically, than condensation of its OH groups. The red square points are a selection of low energy Si16-based clusters that we find for an OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio ranging from one (i.e. that of a D4R) to increasingly condensed oligomers. The corresponding green triangular points specifically relate the gradual linking of two initially non-interacting D4Rs via one, two, and three shared Si–O–Si linkages. The singly Si–O–Si-linked double D4R oligomer has been assigned to an observed (SiO2)16 species in NMR23 and MS7spectra, and has been put forward as a likely way in which D4Rs initially start to condense.10 The points corresponding to doubly and triply linked D4Rs follow the route for such a reaction to continue.
Si ratio ranging from one (i.e. that of a D4R) to increasingly condensed oligomers. The corresponding green triangular points specifically relate the gradual linking of two initially non-interacting D4Rs via one, two, and three shared Si–O–Si linkages. The singly Si–O–Si-linked double D4R oligomer has been assigned to an observed (SiO2)16 species in NMR23 and MS7spectra, and has been put forward as a likely way in which D4Rs initially start to condense.10 The points corresponding to doubly and triply linked D4Rs follow the route for such a reaction to continue.
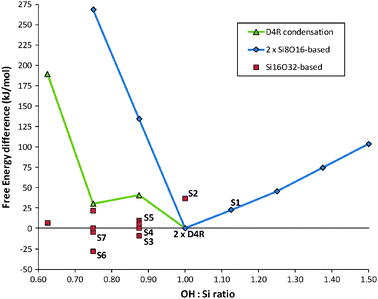 | ||
| Fig. 1 Free energies of solution of silicate oligomers: (a) blue diamonds relate to two (SiO2)8(H2O)M oligomers, (b) green triangles relate to (SiO2)16(H2O)M oligomers based on Si–O–Si linked D4Rs, (c) red squares relate to other (SiO2)16(H2O)M based oligomers. Labelled points refer to structures in Fig. 2 and 3. | ||
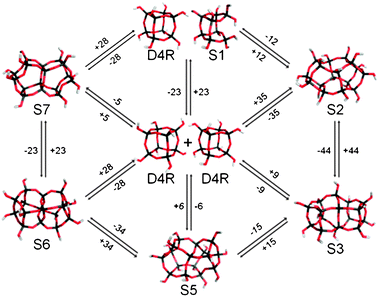 | ||
| Fig. 2 A selection of chemically plausible interconversion reactions involving two D4Rs and other oligomeric species. Arrows denote reaction pathways with differences in free energies of solution in kJ mol−1. | ||
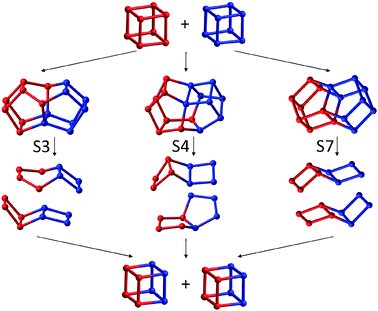 | ||
| Fig. 3 A variety of possible one step interconversion processes whereby two D4Rs swap four Si atoms via the S3, S4 and S7 intermediates (see also Fig. 1 and 2). Only the silicon atoms are shown. | ||
For an OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio of one we find a number of low energy (SiO2)16(H2O)8 clusters with either cage-like or complex amorphous geometries. Of these, a cage-like isomer with the same topology as the 16 Si-atom building unit of the zeolite RTE was found to be most stable, lying 35 kJ mol−1 above two isolated D4Rs (see Fig. 2, S2). Upon decreasing the OH
Si ratio of one we find a number of low energy (SiO2)16(H2O)8 clusters with either cage-like or complex amorphous geometries. Of these, a cage-like isomer with the same topology as the 16 Si-atom building unit of the zeolite RTE was found to be most stable, lying 35 kJ mol−1 above two isolated D4Rs (see Fig. 2, S2). Upon decreasing the OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio to 0.875, however, we find the lowest free energy (SiO2)16(H2O)7 oligomer to be 9 kJ mol−1 more stable than two isolated D4Rs (see Fig. 2, S3). For this composition we also find a number of oligomers having free energies in a narrow range (20 kJ mol−1) above the most stable oligomer (see, for example, Fig. 2, S5). In contrast, the initial linking of two D4Rs by a Si–O–Si bridge costs 41 kJ mol−1 (i.e. 50 kJ mol−1 less stable than S3). Continuation of the Si–O–Si link-forming process between two D4Rs results in a doubly-linked oligomer being 31 kJ mol−1 higher in energy than two isolated D4Rs. Although less energetically disfavoured with respect to the D4R reagents than the singly linked oligomer, it is 59 kJ mol−1 less favourable than the lowest energy (SiO2)16(H2O)6 oligomer we find. This latter oligomer (see Fig. 2, S6), which represents an energetically downhill D4R coalescence process (−28 kJ mol−1), appears to be the most stable Si16-based oligomer relative to condensation and hydroxylation. As in the (SiO2)16(H2O)7 case we also find a number of other (SiO2)16(H2O)6 oligomers that are lower in free energy than the doubly-linked double D4R (see e.g.Fig. 2, S6 and S7). For further condensation, the lowest free energy (SiO2)(H2O)5 oligomer found is 7 kJ mol−1 less stable than two D4Rs, but is over 180 kJ mol−1 more stable than the triply linked D4R oligomer.
Si ratio to 0.875, however, we find the lowest free energy (SiO2)16(H2O)7 oligomer to be 9 kJ mol−1 more stable than two isolated D4Rs (see Fig. 2, S3). For this composition we also find a number of oligomers having free energies in a narrow range (20 kJ mol−1) above the most stable oligomer (see, for example, Fig. 2, S5). In contrast, the initial linking of two D4Rs by a Si–O–Si bridge costs 41 kJ mol−1 (i.e. 50 kJ mol−1 less stable than S3). Continuation of the Si–O–Si link-forming process between two D4Rs results in a doubly-linked oligomer being 31 kJ mol−1 higher in energy than two isolated D4Rs. Although less energetically disfavoured with respect to the D4R reagents than the singly linked oligomer, it is 59 kJ mol−1 less favourable than the lowest energy (SiO2)16(H2O)6 oligomer we find. This latter oligomer (see Fig. 2, S6), which represents an energetically downhill D4R coalescence process (−28 kJ mol−1), appears to be the most stable Si16-based oligomer relative to condensation and hydroxylation. As in the (SiO2)16(H2O)7 case we also find a number of other (SiO2)16(H2O)6 oligomers that are lower in free energy than the doubly-linked double D4R (see e.g.Fig. 2, S6 and S7). For further condensation, the lowest free energy (SiO2)(H2O)5 oligomer found is 7 kJ mol−1 less stable than two D4Rs, but is over 180 kJ mol−1 more stable than the triply linked D4R oligomer.
Although the calculated relative free energies for the incremental link-forming condensation of two D4Rs are not insurmountable, the fact that there are energetically preferred oligomers in each step of this proposed process strongly suggests that other condensation/hydroxylation reactions will also compete and/or perhaps dominate. Following the temporal development of mass spectra Schüth et al. found that in order to best match the evolution of the D4R isotope distribution over time required a kinetic model involving the exchange of four Si atoms at a time.10 Based upon this model an interpretation was proposed which required a concerted face-on reaction of D4Rs with S4R-exchange.10 The combinatorial kinetic analsis does not rely on specific geometric arrangements of exchanged atoms (e.g. it doesn’t assume that the exchanged atoms should lie on a face of the D4R), nor does it make assumptions about the geometry of the linked/fused D4R intermediate(s). Furthermore, the kinetic model only involves atoms which are exchanged between D4Rs in a statistically prescribed way (via an undescribed intermediate mechanism) and no other species i.e. it assumes that all atoms are accounted for in the D4Rs and their interactions and no atoms are lost or gained.
In Fig. 2 we highlight a few of the plausible D4R interconversion reactions that could occur based on our calculations. As other calculations have shown that oligomerisation barriers for smaller silicate clusters are low9,16 (typically <40 kJ mol−1), and tend to decrease for larger condensed species, we can reasonably expect that these reactions have barriers equal to or less than the reported experimental value of 136 ± 5 kJ mol−1.10 Our data suggest that a rich and complex dynamic equilibrium between many structurally distinct silicate oligomers occurs in the D4R system in solution, which is consistent with experimental observations for smaller species.3 Interestingly our data are also fully compatible with many routes involving direct (or indirect) D4R interconversions with the final result that four atoms are interchanged. In Fig. 3 we show three ways of exchanging four silicon atoms based on D4R interconversion with oligomers S3, S4 and S7, all of which have small free energy differences with a pair of D4Rs. In these one-step direct mechanisms a pair of D4Rs combine to form a new pair, with four silicon atoms exchanged. Evidently, based on our findings, we can imagine more complex indirect pathways with the same end result. We note that these mechanisms differ from the concerted face-on mechanism in which two D4Rs form only one further D4R by the combination of two faces from the parent D4Rs, while two S4Rs are released. Here, the D4Rs do not form a closed system but gradually disappear (reflected in the need for a 50% scaling of the rate constant). As the D4R population does not seem to diminish with time in the experiment, such a picture must assume that it is somehow replenished in an undefined way from the “silicate pool”. This uncontrolled extra process (e.g. formation of D4Rs from random S4R combinations) is not present in the kinetic model. In our proposed four-atom exchange mechanisms, however, every two D4Rs combine to form two new D4Rs, thus forming a closed system that fits the kinetic modelling.
The concerted exchange mechanism initially proceeds via the singly linked D4R oligomer which has been assigned to be as a low intensity species in a TMA solution by Pelster et al. from ESI-MS.7 We note that this assignment might equally be made using any lower energy structure found here of the same mass. With respect to the similarly assigned (SiO2)16(H2O)7 species from 29Si NMR by Kinrade et al.,23 we also note that our lowest energy (SiO2)16(H2O)7 oligomer (Fig. 2 and 3, S3) has, like the singly bridged D4R oligomer, two Q4 species and 14 Q3 species and can be regarded as a symmetric coalescence of two D4Rs (i.e. it maintains many structural motifs of two separate D4Rs). Due to these strong similarities we feel that it is quite probable that the NMR data may be consistent with other, more stable, oligomers than the singly-linked D4R. We note that our findings do not necessarily also hold for Ge-containing silicate systems24 as germanium is known to specifically promote D4R formation.25
Our study reveals new insights into the structures and stabilities of Si8-based and Si16-based oligomers in solution. Our results are particularly relevant to understanding processes in the hydrothermal synthesis of zeolites and more generally provides useful insights into the rich and complex structural chemistry of relatively large silicate oligomers. Based on our findings we propose a new interpretation of the observed atomic mixing of D4R oligomers in solution. Rather than via a single concerted reaction route as previously suggested, we propose that a multitude of relatively low energy interconversion reactions involving complex fused intermediates significantly contribute to this process. Our multi-mechanism perspective: (i) is consistent with what is known for smaller silicate species in solution, (ii) involves the lowest free energy hydroxylated oligomers yet reported in the literature, and (iii) allows for many chemically plausible routes for D4R four atom exchanges which are compatible with the known kinetics of this process.
We acknowledge funding from projects FIS2008-02238, 2009SGR1041 XRQTC, and computer time from Barcelona Supercomputer centre. KJ acknowledges support from HPC-EUROPA2. EF holds a RCUK Academic Fellowship.
Notes and references
- A. Aerts, C. E. A. Kirschhock and J. A. Martens, Chem. Soc. Rev., 2010, 39, 4626 RSC.
- C. S. Cundy and P. A. Cox, Microporous Mesoporous Mater., 2005, 82, 1 CrossRef CAS.
- C. T. G. Knight, R. J. Balec and S. D. Kinrade, Angew. Chem., Int. Ed., 2007, 46(43), 8148 CrossRef CAS.
- M. Haouas and F. Taulelle, J. Phys. Chem. B, 2006, 110, 3007 CrossRef CAS.
- H. Cho, A. R. Felmy, R. Craciun, J. P. Keenum, N. Shah and D. A. Dixon, J. Am. Chem. Soc., 2006, 128, 2324 CrossRef CAS.
- C. T. G. Knight and S. D. Kinrade, J. Phys. Chem. B, 2002, 106, 3329 CrossRef CAS.
- S. A. Pelster, W. Schrader and F. Schüth, J. Am. Chem. Soc., 2006, 128, 4130 CrossRef.
- M. J. Mora-Fonz, C. R. A. Catlow and D. W. Lewis, J. Phys. Chem. C, 2007, 111, 18155 CAS.
- T. T. Trinh, A. P. Jansen, R. A. van Santen and E. J. Meijer, J. Phys. Chem. C, 2009, 113, 2647 CAS.
- S. A. Pelster, B. Weimann, B. B. Schaack, W. Schrader and F. Schüth, Angew. Chem., 2007, 119, 6794 CrossRef.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111 CrossRef CAS.
- E. Flikkema and S. T. Bromley, Chem. Phys. Lett., 2003, 378, 622 CrossRef CAS.
- A. Hassanali and S. J. Singer, J. Phys. Chem. B, 2007, 111, 11181 CrossRef CAS.
- GAMESS-UK is a package of ab initio programs. M. F. Guest, I. J. Bush, H. J. J. van Dam, P. Sherwood, J. M. H. Thomas, J. H. van Lenthe, R. W. A. Havenith and J. Kendrick, Mol. Phys., 2005, 103(6–8), 719 CrossRef CAS.
- A. D. J. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. L. Schaffer and K. T. Thomson, J. Phys. Chem. C, 2008, 112, 12653 CAS.
- E. Flikkema and S. T. Bromley, J. Phys. Chem. B, 2004, 108, 9638 CrossRef CAS.
- S. T. Bromley and E. Flikkema, J. Chem. Phys., 2005, 122, 114303 CrossRef CAS.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef CAS.
- S. Sjöberg, J. Non-Cryst. Solids, 1996, 196, 51 CrossRef.
- D. Hoebbel, G. Garzo, G. Engelhardt and A. Vargha, Z. Anorg. Allg. Chem., 1982, 494, 3 CrossRef.
- S. Caratzoulas, D. G. Vlachos and M. Tsapatsis, J. Am. Chem. Soc., 2006, 128, 596 CrossRef CAS.
- S. Kinrade, J. C. H. Donovan, A. S. Schach and C. T. G. Knight, J. Chem. Soc., Dalton Trans., 2002, 1250 RSC.
- B. B. Schaack, W. Schrader and F. Schüth, J. Phys. Chem. B, 2009, 113, 11240 CrossRef CAS.
- M. A. Zwijnenburg, S. T. Bromley, J. C. Jansen and T. Maschmeyer, Microporous Mesoporous Mater., 2004, 73, 171 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of theoretical methods and oligomers. See DOI: 10.1039/c1cc14674b |
| This journal is © The Royal Society of Chemistry 2012 |
