Frustrated magnetism in the S = 1 kagomé lattice BaNi₃(OH)₂(VO₄)₂

Abstract

Frustrated magnets with integer spin are predicted to have exotic physical properties including spin nematicity, yet few are known to exist. We report a new, frustrated S = 1 magnet, BaNi₃(OH)₂(VO₄)₂, which is the structural analogue of the mineral vesignieite. Magnetic frustration arises from a competition between ferromagnetic and antiferromagnetic ordering leading to a glassy transition at 19 K.

---

Magnetic frustration prevents the emergence of a unique ground state configuration, thus allowing for unusual states to arise. Some of these unusual states can be attributed to strongly correlated electrons, i.e., electrons that cannot be modeled as individual particles but rather are better described collectively. Magnetically frustrated systems are of interest to the physics community, partially due to their potential connection to superconductivity¹ but also because they can engender new phases of matter when strong correlation is confined to low dimension. Theoretical treatments of these enticing systems predict properties ranging from a spin liquid state² to spin nematicity.³ Despite an extensive theoretical literature of strongly correlated, low dimensional systems, experimental confirmation of theoretical predictions has yet to be achieved owing to a paucity of real systems for exploration. Several years ago, we reported a 2-D magnetically frustrated S = ½ system⁴ that recent measurements suggest is the best candidate for a 2-D spin liquid.^5–8 For structurally similar 2-D kagomé lattice systems of higher spin, S = [/] and S = [/], interesting magnetic properties derived from spin frustration are circumvented by long-range magnetic order.^9–13 The intermediate spin regime defined by S = 1 has yet to be investigated, and is of particular interest because it lies between the quantum (S = ½) and more classical S = ([/], [/]) regimes. Additionally, integer spin states have been shown from a theoretical standpoint¹⁴ to behave differently than half-integer spin states in some systems.

Only three S = 1 kagomé lattices have heretofore been reported. A vanadium analogue of jarosite, KV₃(OH)₆(SO₄)₂, displays antiferromagnetically-stacked ferromagnetic layers. Vanadium centers comprising the kagomé intralayer couple ferromagnetically via a V–O–V exchange pathway.¹⁵ Nearest-neighbor ferromagnetic coupling, which was not expected based on Goodenough-Kanamori rules, was explained by a tilt in the oxygen p-orbitals out of alignment with the magnetic coupling axis. Another kagomé compound based on vanadium(III), YCa₃(VO)₃(BO₃)₄, has very recently been reported, and it too displays ferromagnetic coupling in the kagomé plane with antiferromagnetic coupling between layers.¹⁶ The only other S = 1 kagomé lattice, [C₆N₂H₈][NH₄]₂[Ni₃F₆(SO₄)₂], is indeed magnetically frustrated.¹⁷ Detailed magnetic studies suggest that a 3-D magnetic ordering transition at 10 K is due to the integer nature of the spin,¹⁸ though the interlayer organic molecules may also play a role as a conduit for long range magnetic order.

We sought to synthesize a Ni²⁺ kagomé lattice with larger interlayer spacing and no obvious interlayer coupling pathway. Such a system is difficult to realize owing to the chemical stability of Ni(OH)₂ and the proclivity for Ni²⁺ to reside in a square planar ligand field, and consequently assume a low spin, S = 0 magnetic configuration. We targeted the previously unknown nickel analogue of the copper mineral vesignieite, BaCu₃(OH)₂(VO₄)₂.^19,20 The Ba²⁺ ions may serve as ideal non-magentic spacers of the 2-D kagomé planes and a nearly octahedral environment around the Cu²⁺ centers, facilitated by rigid VO₄ tetrahedra of vesignieite, would be expected to hinder distortion to a square planar geometry. Here we report the synthesis of a new 2-D magnetically frustrated Ni²⁺ kagomé lattice, BaNi₃(OH)₂(VO₄)₂.

Synthesis of Ni-vesignieite proceeds with the addition of Ni(OH)₂ (0.15 g 1.6 mmol) to an excess of 28% ammonium hydroxide (250 mL) in a round bottom flask. The solution was capped and stirred for 24 h until all of the green Ni(OH)₂ powder dissolved and the solution turned blue. Stoichiometric amounts of V₂O₅ (0.39 g, 0.53 mmol) and Ba(O₂CCH₃) (0.136 g 0.53 mmol) were then added to the solution and the mixture was heated at reflux for 4 h. The ammonia gas produced as the reaction proceeded was vented from the reaction vessel. During the course of the reaction, a yellow precipitate forms at the bottom of the reaction vessel. Filtration of the yellow precipitate was performed when the reaction mixture was hot so as to increase the solubility of any residual Ni(OH)₂ starting material. The yellow precipitate was collected and then soaked in ammonium hydroxide for 12 h to remove any last vestiges of Ni(OH)₂, as indicated by the disappearance of Ni(OH)₂ peaks from the powder X-ray diffraction (PXRD) of the yellow precipitate. Repetitive soaking of the product did not alter its magnetic properties.

Polycrystalline samples of the final product were examined by PXRD on an X'Pert PANalytical diffractometer with a Cu source. Data were acquired for 2θ = 5° to 80°. Vesignieite was employed as an initial structural model.²¹ The structure was refined using the HighScore Plus software package and standard Rietveld refinement techniques. The structure was solved in the monoclinic space group C2/m.§ Ni-vesignieite can best be described by kagomé planes spaced by 7.2 Å owing to the presence of Ba²⁺ ions that reside between the layers. The Ni²⁺ ions are bridged by two types of metal–oxygen interactions shown in Fig. 1. A μ²-oxo, which is provided by a VO₄ tetrahedra, bridges Ni²⁺ and sets Ni–O–Ni bond angles at 84.6(2)° and 94.06(3)°. μ³ hydroxide resides within the interior of the Ni₃ triangle with Ni–O–Ni angles of 101.6(4)° and 97.7(3)°. The low symmetry space group leads to three different Ni–O bonding distances: 1.930(1), 2.005(2) and 2.161(1) Å. The Ni²⁺⋯Ni²⁺ distances are more symmetric at 2.908(2) and 2.938(2) Å.

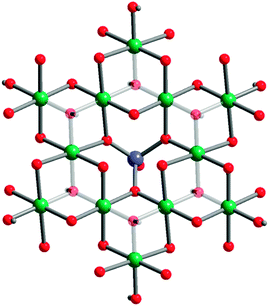Fig. 1 Crystal structure of BaNi₃(OH)₂(VO₄)₂. Green, purple, and red spheres represent Ni, V, and O atoms, respectively. Hydrogen and barium atoms have been removed for clarity and the central hydroxides faded to emphasize the kagomé lattice and demonstrate the two coupling pathways, through the μ³-hydroxide (at the center of the Ni₃ triangles) and through the μ²-oxo (along the edges of the Ni₃ triangles).

The different Ni–O bond distances and Ni–O–Ni bond angles are determinants of the nearest neighbor exchange interactions. An angular dependence to magnetic coupling is expected based on Goodenough-Kanamori rules for superexchange through oxygen orbitals. A switch from strong antiferromagnetic coupling to strong ferromagnetic coupling should occur between metal spins that are connected through aligned metal–oxygen orbitals (180°) versus orthogonal metal–oxygen orbitals (90°) for M–O–M coupling in which M is a single metal in the same chemical environment. Empirical evidence indicates that the sign of magnetic coupling for octahedral Ni²⁺ switches at 97°.²² Thus, coupling of nickel spins through the μ³ hydroxide is expected to produce strong antiferromagnetic coupling, on the order of J ∼ −100 cm⁻¹, and coupling through μ² oxos is expected to produce strong ferromagnetic coupling on the order magnitude of J ∼ +100 cm⁻¹.

Magnetic susceptibility data were acquired at a range of applied dc fields ranging from 20 Oe to 20 kOe. Data are linear from 300 K to 20 K with a value of 1 cm³K mol⁻¹ per Ni²⁺ ion, the expected contribution for an S = 1 ion with g = 2.0. At 20 K the magnetic susceptibility rapidly increases, indicating the onset of magnetic ordering. At 15 K, whereas the χT product sharply decreases towards zero, χ levels off and does not decrease, indicating an absence of three-dimensional antiferromagnetic ordering, as observed in Ni(OH)₂ (Fig. 2).²³ The Curie–Weiss temperature of +10 K, which was determined from high temperature inverse susceptibility data (Fig. 3), is indicative of weak ferromagnetic coupling. The Curie–Weiss temperature in the copper vesignieite analogue is −77 K.¹⁹ The negative Curie–Weiss temperature is ascribed to coupling dominated by the antiferromagnetic coupling pathway owing to a slight Jahn–Teller distortion of the Cu orbitals. The significantly smaller Curie–Weiss temperature in the nickel analogue is attributed to the increased electron density in the ferromagnetic coupling pathway, and not to a decrease in the magnitude of antiferromagnetic exchange, thus leading to a situation of competing exchange. The existence of two strong coupling pathways as opposed to one weak pathway is supported by the observation of curvature of the inverse susceptibility at high temperature. The curvature suggests the spins are not fully uncoupled at 300 K.

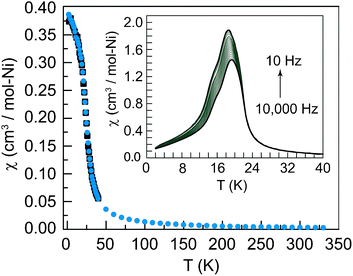Fig. 2 Dc susceptibility data acquired at an applied field of 5000 Oe. Black squares (■) are zero-field cooled data, cyan circles () are field-cooled data. Inset: ac susceptibility data at a frequency range of 10 Hz to 10 000 Hz in logarithmic increments, with a total of 20 frequencies measured.

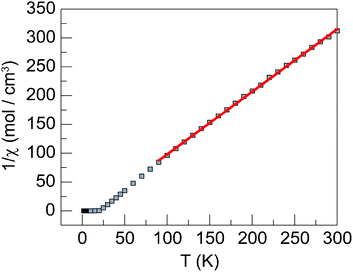Fig. 3 Inverse susceptibility data calculated from data acquired at 20 Oe. A linear fit gives a Curie–Weiss temperature of +10 K.

Ac susceptibility data were collected across the maximum of the peak in the χT data (Fig. 2, inset) to probe the nature of the low temperature behavior and ordering transition. The frequency dependence of the data indicates a spin-glass ordering transition. Additionally the data display the characteristic asymmetry and curvature of a spin glass transition. The different domain sizes created during glassy ordering lead to a continuum of relaxation times, which are manifested in a curved peak in the out-of-phase ac susceptibility.²⁴ Based on simple orbital considerations, and empirical evidence of magnetic exchange, the magnitude of the Curie–Weiss temperature is extremely small for the given Ni–O–Ni bond angles and the Ni²⁺⋯Ni²⁺ distance. The low Curie–Weiss temperature and the spin glass transition point to glassy order caused by a competition between two magnetic coupling pathways, an antiferromagnetic coupling pathway through the μ³ hydroxide bridge, and an ferromagnetic coupling through the μ² oxo bridges, leading to magnetic frustration. Magnetic frustration is further enhanced by the geometric frustration inherent to antiferromagnetic coupling within the kagomé triangle. We believe that the competing interactions between the two coupling pathways lead to magnetic frustration which results in a glassy ordering transition. Despite the glassy behavior at low temperatures, it would be most interesting to probe this compound for evidence of spin nematicity.

Research was supported by NSF Grant CHE-1041863. D.E.F. acknowledges the NSF for an ACC fellowship. Research involved the MRSEC Shared Experimental Facilities at MIT, which are supported in part by the NSF under Award DMR-0819762. Y.S.L. acknowledges support from the DOE-BES under Grant No. DE-FG02-07ER46134. The authors thank Dr Scott Speakman for invaluable X-ray diffraction assistance. The authors thank Dr Shaoyan Chu for assistance with the MPMS-XL and magnetism assistance.

Notes and references

1. P. W. Anderson, Science, 1987, 235, 1196.
2. L. Balents, Nature, 2010, 464, 199.
3. K. Damle and T. Senthil, Phys. Rev. Lett., 2006, 97, 067202.
4. M. P. Shores, E. A. Nytko, B. M. Bartlett and D. G. Nocera, J. Am. Chem. Soc., 2005, 127, 13462.
5. J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Qiu, D. G. Nocera and Y. S. Lee, Phys. Rev. Lett., 2010, 104, 147201.
6. J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. J. H. Chung, D. G. Nocera and Y. S. Lee, Phys. Rev. Lett., 2007, 98, 107204.
7. D. E. Freedman, T. H. Han, A. Prodi, P. Muller, Q.-Z. Huang, Y.-S. Chen, S. M. Webb, Y. S. Lee, T. M. McQueen and D. G. Nocera, J. Am. Chem. Soc., 2010, 132, 16185.
8. M. de Vries and A. Harrison, Nature, 2010, 468, 908.
9. K. Matan, B. M. Bartlett, J. S. Helton, V. Sikolenko, S. Mat'as, K. Prokes, Y. Chen, J. W. Lynn, D. Grohol, T. J. Sato, M. Tokunaga, D. G. Nocera and Y. S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 214406.
10. B. M. Bartlett and D. G. Nocera, J. Am. Chem. Soc., 2005, 127, 8985.
11. T. Inami, T. Morimoto, M. Nishiyama, S. Maegawa, Y. Oka and H. Okumura, Phys. Rev. B: Condens. Matter, 2001, 64, 054421.
12. D. Grohol, K. Matan, J. H. Cho, S. H. Lee, J. W. Lynn, D. G. Nocera and Y. S. Lee, Nat. Mater., 2005, 4, 323.
13. D. Grohol, D. G. Nocera and D. Papoutsakis, Phys. Rev. B: Condens. Matter, 2003, 67, 064401.
14. S. K. Pati and C. N. R. Rao, J. Chem. Phys., 2005, 123, 234703.
15. D. Papoutsakis, D. Grohol and D. G. Nocera, J. Am. Chem. Soc., 2002, 24, 2647.
16. W. Miller, M. Christensen, A. Khan, N. Sharma, R. B. Macquart, M. Avdeev, G. J. McIntyre, R. O. Piltz and C. D. Ling, Chem. Mater., 2011, 23, 1315.
17. J. N. Behera and C. N. R. Rao, J. Am. Chem. Soc., 2006, 128, 9334.
18. J. N. Behera, A. Sundaresan, S. K. Pati and C. N. R. Rao, ChemPhysChem, 2007, 8, 217.
19. Y. Okamoto, H. Yoshida and Z. Hiroi, J. Phys. Soc. Jpn., 2001, 78, 033701.
20. R. H. Colman, F. Bert, D. Boldrin, A. D. Hillier, L. C. Chapon, P. Manuel, P. Mendels and A. S. Wills, arXiv:1104.2558v3 [cond-mat.str-el].
21. Z. Ma, R. He and X. Zhu, Acta Geol. Sinica, 1990, 64, 302.
22. K. K. Nanda, L. K. Thompson, J. N. Bridson and K. Nag, J. Chem. Soc., Chem. Commun., 1994, 1337.
23. T. Takada, Y. Bando, M. Kiyama and H. Miyamoto, J. Phys. Soc. Jpn., 1966, 21, 2745.
24. J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional experimental details and crystallographic information. CCDC 837685. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c1cc14731e

‡ Current address Department of Chemistry and Department of Physics and Astronomy The Johns Hopkins University Baltimore, MD 21218 USA.

§ Crystallographic data for BaNi₃(OH)₂(VO₄)₂: Ni₆Ba₂V₄O₂₀H₄, FW = 577.27, monoclinic, C2/c, a = 10.2129(62), b = 5.8155(35), c = 7.8882(40), β = 117.01(4), V = 417.41(905), Z = 1, T = 295 K, R = 0.0953, wR = 0.1325, reflections measured = 155, unique reflections = 147, R_int = 0.1306.

---