In situ characterization of infra red femtosecond laser ablation in geological samples. Part B: the laser induced particles
François-Xavier
D'Abzac
*a,
Anne-Magali
Seydoux-Guillaume
a,
Jérôme
Chmeleff
a,
Lucien
Datas
b and
Franck
Poitrasson
a
aGET, UMR 5563 CNRS, Université de Toulouse, IRD, OMP, 14 avenue Edouard Belin, 31400, Toulouse, France. E-mail: dabzac@lmtg.obs-mip.fr
bTEMSCAN, CIRIMAT, Université de Toulouse, 118 route de Narbonne, 31400, Toulouse, France
First published on 26th October 2011
Abstract
The analytical study of infra red femtosecond laser induced particles has been performed using Transmission Electron Microscopy (TEM) and Low Pressure Impaction (ELPI). Various natural and synthetic matrices have been tested: monazite (phosphate), zircon (silicate), NIST610 (glass), spinel (oxide), quartz (silicate structure), silicon (semiconductor) and Nordic gold (metallic alloy). Three types of particles are systematically observed: very rare large round spherical particles (dp ≈ 1 μm) whose composition is close to the initial sample, spherical particles of smaller size (dp ≤ 250 nm) and agglomerates of dp ≈ 10 nm particles. Chemical compositions of the latter two are complementary with respect to the ablated sample. Isolated occurrence of hydrodynamic sputtering may explain the creation of rare large droplets. Other particles are probably generated from the irradiated matter in the supercritical state during the cooling process and plasma expansion. A recent model provides a strong basis to describe vapour to particle conversion and further condensation/coalescence processes for simple systems (single component). Additional assumptions must be included to apply the model to our observations of complex multi-elemental systems. A qualitative interpretation may be proposed on the basis of fractionated condensation/coalescence and further agglomeration of particles, depending on plasma pressure and the ablated elements properties (mainly density and melting period) as well as the thermal evolution of the plume. This interpretation is discussed and validated for each sample type. Previous results concerning ablation mechanisms using the same system are included in our model. The generation of particles from a vapour phase confirms that vaporization is the main ablation mechanism in the femtosecond regime. Moreover, the possible presence of molecular sized clusters in the initial plasma, which can accelerate the nucleation process, strongly suggests that fragmentation is the secondary ablation mechanism. Finally, the present study is an experimental validation for recent femtosecond laser ablation simulation, and it brings new insights for interpreting particles generation processes for complex systems. Correlations between laser ablation ICP-MS measurements must now be made with the present results.
Introduction
The worldwide expansion of LA-ICP-MS analysis and its needed constant improvement asks for a better understanding of the recurrent limitations associated with solid sample in situ analysis.1–5 Since its introduction, capabilities of such a technique have increased and issues such as chemical fractionation6,7 and matrix dependency for sample calibration8 have been well known. The possibility of using femtosecond instead of nanosecond pulses has brought numerous advantages and the previous limitations were considerably reduced.7,9–11 Nevertheless, it has taken some time before these promising first results lead to widespread development of femtosecond lasers in analytical laboratories. Recent attempts to link the characteristics of laser ablation products with LA-ICP-MS measurements have been very promising,12,13 yet showing that there is still a need to understand the fundamental processes occurring during ablation and particle generation.In previous works, we studied ablation mechanisms in the infra red femtosecond regime.14,15 Natural monazite samples were submitted to a femtosecond laser beam under variable conditions, in order to characterize the ablated structures. Comparisons were made with existing analytical studies on different matrices which used similar observation tools.16–18 Thermal and mechanical effects were observed during the ablation. Molecular dynamic simulations of femtosecond laser ablation19 were used as references in order to identify the underlying mechanisms responsible for the different damaged structures.20,21 Using high fluence (F ≈ 12.7 J cm−2) ultra short pulses (τ = 60 fs), traces of spallation and homogeneous nucleation of gaseous phases were identified as damaging processes, yet never causing the ablation of the sample. Consequently, higher fluence related mechanisms were proposed to be the main ablation processes: fragmentation and vaporization. Nevertheless, this assumption needs to be validated and it is partly the goal of the present study.
This article (part B) aims at achieving the in situ characterization of IR-femtosecond laser induced particles, and determining the processes involved in their generation and growth. In the same perspective as our above cited previous study (part A), our analytical results will be compared to the current models of particles generation in the laser induced plasma. For this purpose, simulations and models established by Hergenröder et al.22–24 will be used, as they mainly refer to the LA-ICP-MS problems. The influence of the initial target matrix will be qualified and a general model will be synthesized from our interpretations. These results will help to determine whether or not chemical fractionation can be induced in the femtosecond regime.
Experimental
Laser ablation
We used a commercial Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sapphire femtosecond system (Pulsar 10, Amplitude Technologies, Evry/Seine, France). Specifications may be found in Freydier et al. (2008). The laser was operated at the fundamental wavelength (λ = 800 nm), using a Chirped Pulse Amplification system,25 with output pulse duration and maximum pulse energy of τ = 60 fs and E0 = 12 mJ per pulse respectively. Repetition rate, up to 10 Hz, was controlled by a mechanic shutter placed between the regenerative amplifier and the multipassage amplifier. Energy is controlled by a combination of a rotative half wave plate and twin polarisers. Pulse duration can be optimized by moving the second grating of the compressor stage, via a micrometric screw. Laser specifications and operating conditions are described in Table 1. The beam is focused through a modified optical microscope (BX51, Olympus, Hamburg, Germany), equipped with an XYZ motorized sample stage. The beam is focused on the target by a 50 mm focusing coated lens. Craters reach a diameter of about 90 μm after some dozens of shots. We used a cylindrical 25 cm3 ablation cell, mounted with a quartz window. All samples are enclosed in an accustomed compound during ablation. Sample viewing can be made through the microscope binoculars or via a CCD camera placed at the top of the microscope. Aerosols are flushed off the cell by a 0.5 L min−1helium flow. The laser was set at τ = 60 fs, E0 = 1 mJ per pulse and f = 5 Hz for all samplings. The fluence on the sample surface thus reaches 15.7 J cm−2. Ablations were conducted on three separated single spot ablations of 120 s each in order to collect a sufficient amount of particles. In the case of silicon (see section Samples), the sample was not thick enough to undergo a 120 s ablation. We thus conducted multiple runs of 20 s in order not to ablate through the sample.
sapphire femtosecond system (Pulsar 10, Amplitude Technologies, Evry/Seine, France). Specifications may be found in Freydier et al. (2008). The laser was operated at the fundamental wavelength (λ = 800 nm), using a Chirped Pulse Amplification system,25 with output pulse duration and maximum pulse energy of τ = 60 fs and E0 = 12 mJ per pulse respectively. Repetition rate, up to 10 Hz, was controlled by a mechanic shutter placed between the regenerative amplifier and the multipassage amplifier. Energy is controlled by a combination of a rotative half wave plate and twin polarisers. Pulse duration can be optimized by moving the second grating of the compressor stage, via a micrometric screw. Laser specifications and operating conditions are described in Table 1. The beam is focused through a modified optical microscope (BX51, Olympus, Hamburg, Germany), equipped with an XYZ motorized sample stage. The beam is focused on the target by a 50 mm focusing coated lens. Craters reach a diameter of about 90 μm after some dozens of shots. We used a cylindrical 25 cm3 ablation cell, mounted with a quartz window. All samples are enclosed in an accustomed compound during ablation. Sample viewing can be made through the microscope binoculars or via a CCD camera placed at the top of the microscope. Aerosols are flushed off the cell by a 0.5 L min−1helium flow. The laser was set at τ = 60 fs, E0 = 1 mJ per pulse and f = 5 Hz for all samplings. The fluence on the sample surface thus reaches 15.7 J cm−2. Ablations were conducted on three separated single spot ablations of 120 s each in order to collect a sufficient amount of particles. In the case of silicon (see section Samples), the sample was not thick enough to undergo a 120 s ablation. We thus conducted multiple runs of 20 s in order not to ablate through the sample.
| Laser system | Amplitude technologies “Pulsar 10” |
|---|---|
| Wavelength | 800 nm (fundamental) |
| Repetition rate | 5 Hz |
| Pre-ablation laser warm up | 45 min |
| Pulse duration | 60 fs |
| Beam diameter | 10 mm |
| Focusing objective | 50 mm coated lens |
| Spot diameter | 90 μm |
| Maximum pulse energy | 12 mJ per pulse |
| Ablation cell | Cylindrical, 25 cm−3 |
| Carrier gas | Helium, 0.5 L min−1 |
Particle collection
Particles were collected using an in-house built trapping system (Fig. 1), consisting of a modified 5 mL syringe containing an aluminium stub (12 mm diameter), usually used as sample holder in Scanning Electron Microscopy. A TEM Cu or Ni grid (3 mm diameter) was placed on the stub, as the effective particle trap. Before use, all syringes were cleaned for 24 h in a dilute HCl solution (1 mol L−1) and rinsed for 24 more hours in Milli-Q water. Final mounting was realized in a clean room to avoid contamination on the collecting surfaces by any in-air pollutants.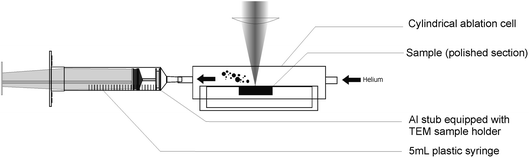 | ||
| Fig. 1 Description of the home made particle collector attached to the cylindrical ablation cell. | ||
Counting
Particle counting and sizing were achieved using a Low Pressure Impactor (ELPI, DEKATI, Tampere, Finland) similar to that used by Koch et al.26 Neutral aerosols go through a charging cell before being counted through a cascade impactor (12 stages). Particles are measured according to their charge, related to their effective surface. The system applies a conversion based on a spherical shape of particle and delivers data in terms of aerodynamic diameter (da). According to DeCarlo et al.,27da considers a standard particle density of ρp = 1 g cm−3 and can be converted to a more representative volume equivalent diameter (dve) that takes into account the particle density (ρp) and the shape factor (χ) which illustrates the deviation from the spherical shape (χ = 1). Acquisitions initially range from da = 0.03 μm to 10 μm under a 30 L min−1 gas flow rate. In our case, a filter stage, provided with the ELPI device, was added before the cascade impactor. A shifting of the range of detection from da = 0.007 μm to 6 μm under a reduced gas flow rate of 10 L min−1 is expected, following the device technical specifications. Our ablation cell can support a maximum of 1 L min−1 gas flow rate and is used throughout all the experiment at 0.5 L min−1 to fit the usual LA-ICP-MS acquisition settings. A free filtered ambient air entrance has then been added to reach the ELPI operating flow rate. A dilution factor equal to 20 has then been taken into account for data conversion.Measurements are conducted after completing a 40 s background suppression, automatically driven by the system. Experiments were performed over 10 min of ablation on a single spot, fitting all other laser settings and samples constraints of previously obtained particle collections (see section Laser).
Samples
The Moacyr monazite (LREE(PO4)) from Itambe pegmatite (Brazil) has been used for particles collection, counting and crater study. This monoclinic orthophosphate28 is of great interest in geology because of its concentration of U and Th, making it a reliable geochronometer.29,30Monazite has been previously studied for its defect healing properties and its particular response to auto-irradiation,31 which make it a potential efficient phase for nuclear waste storage.32 The crystalline structure of the Moacyr monazite has been precisely characterized, and its chemical homogeneity has been demonstrated. Previous work used the Moacyr monazite as an analytical reference for developing LA-ICP-MS dating of various monazites.33 In addition to monazite, a wide variety of other sample types were used for particles collection and size distribution measurements. We attempted to cover as many different structures and chemical compositions as possible, in order to look for any eventual matrix-dependent behaviour of laser induced aerosols. Whenever possible, reference or at least previously well characterized materials were studied:-NIST610 glass standard reference material34 has been chosen because of its widespread use as a synthetic standard in LA-ICP-MS and its transparent, amorphous matrix.
-Synthetic quartz (SiO2) (Crystal Laser) has been used as the most reliable reference for hard transparent crystallized material. Preliminary analytical results about femtosecond ablation efficiency with near infra red wavelengths have been performed recently and give access to experimentally determined ablation properties.35
-A synthetic silicon wafer (pure Si) has been used to illustrate the opaque metallic silicon matrix (cubic system), in comparison to quartz (trigonal silicate) and NIST610 (glass).
-Zircon 91500 (ref. 36) (ZrSiO4) is a natural reference sample commonly used for geochronological purposes. It is a tetragonal silicate with a density of ∼4.
-Nordic gold alloy coin (Cu = 89 wt%, Al = 5 wt%, Zn = 5 wt% and Sn = 1 wt%) is a good example of metal alloy, opaque and composed of dense elements.
-Finally, oxides were tested using a natural spinel (MgAl2O4), from Wutu Town Chungle County, Shandong Province, China, optically opaque and previously characterized at the GET by Electron Microprobe (EPMA) (SX50, Cameca).
Sample compositions are reported in Table 2. Concentrations under 0.1 wt% are not given because they are undetectable by Energy Dispersive X-ray analyses.
| Monazite (Seydoux et al., 2002) | NIST610 (Pearce et al., 1997) | Zircon (Wiedenbeck et al., 1995) | Spinela | |
|---|---|---|---|---|
| wt% | ||||
| a x > 15 wt%: RSD ≤ 1%; x ≈ 1 wt%: RSD ≈ 3%; x < 1 wt%: RSD ≥ 15%. | ||||
| P2O5 | 27.81 | — | — | — |
| Na2O | — | 13.79 | — | — |
| MgO | — | — | — | 15.48 |
| Al2O3 | — | 2.10 | — | 55.35 |
| TiO2 | — | — | — | 1.19 |
| MnO | — | — | — | 0.14 |
| FeO | — | — | — | 26.34 |
| CaO | 0.44 | 11.82 | — | — |
| ZrO2 | — | — | 62.87 | — |
| SiO2 | 1.42 | 72.27 | 32.27 | 0.13 |
| Y2O3 | 0.71 | — | 0.29 | — |
| HfO2 | — | — | 0.66 | — |
| La2O3 | 14.51 | — | — | — |
| Ce2O3 | 30.59 | — | — | — |
| Pr2O3 | 3.14 | — | — | — |
| Nd2O3 | 10.20 | — | — | — |
| Sm2O3 | 2.05 | — | — | — |
| Gd2O3 | 0.94 | — | — | — |
| PbO | 0.16 | — | — | — |
| ThO2 | 6.92 | — | — | — |
| UO2 | 0.13 | — | — | — |
| ZnO | — | — | — | 0.10 |
| Total | 99.02 | 99.98 | 96.09 | 98.63 |
Results
1 Morphology
Fig. 2 shows a TEM large scale picture of the collected aerosols, in the case of Moacyr monazite. The overview reveals complex structures building either very small (<30 nm) or much larger (>1 μm) agglomerates, as well as dark round particles. These particle types are observed for all samples. Close ups of particles are shown for monazite in Fig. 2b and c and for other samples in Fig. 3. Two types of particles stand out.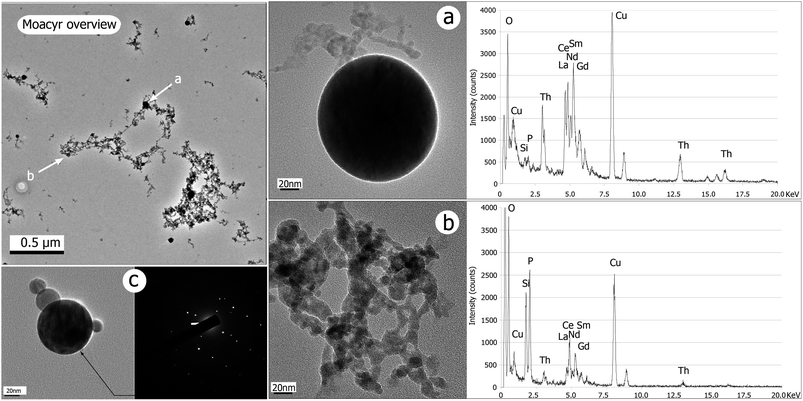 | ||
| Fig. 2 Images of particles (TEM/BF) collected from Moacyr monazite ablation (E0 = 1 mJ per pulse, τ = 60 fs, f = 5 Hz, t = 120 s × 3). The overview picture shows complex structures of clusters and the contrasted sizes of beads. Close up on bead (a) and cluster (b) with the associated EDX spectrum reveals that both particles are chemically different. Copper is from the TEM grid. (c) Occurrence of crystallized bead: fringes of Bragg are visible as variable contrasts within the bead; the SAED image almost shows a regular pattern, but scattered spots indicate either another crystal domain or a bad orientation of the electron beam through the lattice. | ||
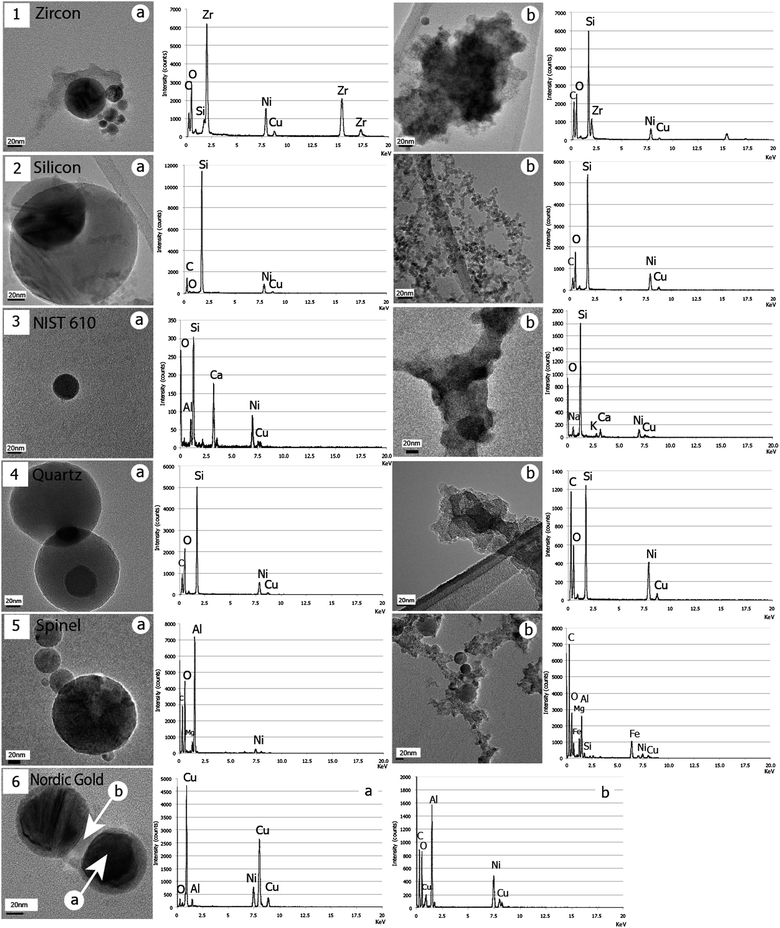 | ||
| Fig. 3 BF/TEM illustrations of the two types of particles for all samples: zircon (1), silicon (2), NIST610 (3), quartz (4), spinel (5) and Nordic gold (6). The corresponding EDX spectra associated with each image show a strong chemical partitioning of initial sample elements, except for quartz for which this is less obvious between Si and O. Note that no cluster could be observed in (6) but only a systematic thick coating of beads, wherein O is detected. Intensities of peaks depend on the volume of emitting matter. | ||
(i) The first population is made of variably sized clusters (Fig. 2b and 3.1b–6b), composed of ultra fine dp = 10–20 nm particles. Clusters size ranges from several dozens of nanometres to several micrometres. Some variations can be noticed with their morphology: zircon, NIST610 and quartz clusters (Fig. 3.1b, 3b and 4b respectively) show “hard bonding”37 compared to monazite, silicon, and spinel (Fig. 2b and 3.2b and 5b respectively) for which individual ∼10 nm components can be well distinguished (“soft bonded clusters”). We could not detect any of these among the particles induced by the Nordic gold alloy laser ablation. Instead, a thick coating of clear amorphous matter is observed on the other type of particles (Fig. 3.6b).
(ii) The second population is composed of single rounded particles (Fig. 2a and 3.1a–6a), with observed sizes from dp ≈ 10 nm with very rare occurrences of dp ≈ 1200 nm. The major part of these beads is amorphous, but we have noticed occurrences of crystalline structures in rare cases. Fig. 2c shows an agglomerate of four beads generated from the monazite sample. The largest (dp = 73 nm) shows Bragg diffraction contrasts, characteristic of a crystalline structure; this is confirmed by the associated SAED pattern (clear spots).
2 Chemical compositions
Significant differences of composition are shown in EDX spectra associated with TEM images (Fig. 2 and 3) and depend on the morphology of the analyzed particles. In most samples, chemical elements composing the initial target are partitioned between the two types of particles (clusters or beads). We will consider an empirical limit of detection of 1 wt%, since [Gd] = 0.94 wt% is the lowest concentrated element detected. Systematic copper and nickel peaks result from the TEM grid X-ray emission. Particles collected from monazite ablation show clusters enriched with phosphorus and silicon, and beads enriched with thorium and light rare earth elements, but depleted in phosphorus and silicon (Fig. 2). In the case of zircon, zirconium is concentrated in beads and silicon in clusters (Fig. 3.1). For spinel, Al is concentrated within beads while clusters preferentially contain Fe and Mg (Fig. 3.5). Analyses using EDX on particles from silicon and synthetic quartz reveal that, apart from the silicon response, clusters seem to be enriched with oxygen. Analyses made on Nordic gold beads reveal that the chemical difference appears between the beads and their contrasted coatings, with Cu and Al complementary between beads and coating (Fig. 3.6). Repeated measurements of NIST 610 show apparently that Al and Ca are present in beads, while Na and K are enriched with clusters (Fig. 3.3). A more detailed study of beads composition has been conducted in monazite since the observed sizes are very widespread. Thus, Fig. 4 shows TEM images of the two extreme reported sizes of beads, with the associated EDX spectra. A clear difference can be noticed with phosphorus. Indeed, the response within the 1.2 μm bead is clear (Fig. 4.2) and the spectrum is even close to the bulk monazite reported in the previous study.14 However, the smallest bead is totally depleted in phosphorus (Fig. 4.1), and thus complements very well with the cluster composition to fit the bulk monazite.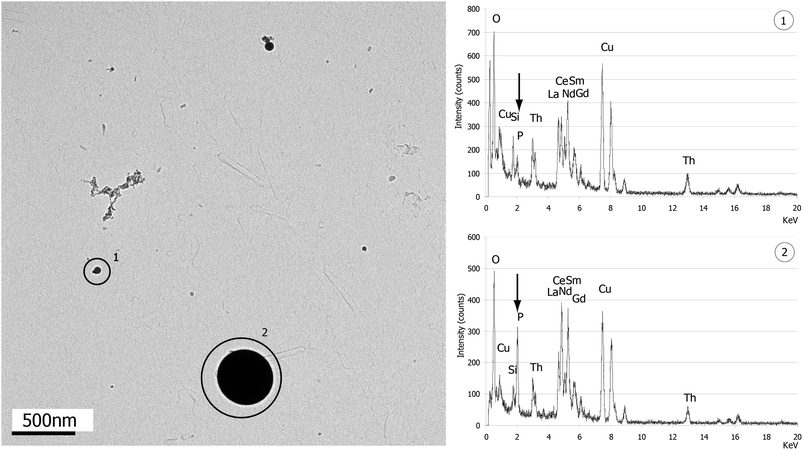 | ||
| Fig. 4 BF/TEM image of particles from Moacyr monazite ablation (E0 = 1 mJ per pulse, τ = 60 fs, f = 5 Hz, t = 120 s × 3). The picture shows the coexistence of clusters, (1) a small bead (dp ≈ 50 nm) totally depleted in phosphorus (arrow in EDX spectrum) and (2) a large bead (dp ≈ 450 nm) wherein phosphorus is much more concentrated. | ||
3 Counting
Fig. 5 (inset) shows the mean size distribution of NIST610 particles obtained over a campaign of 8 days, recording one acquisition per day. We used this sample as reference as it is usually used in LA-ICP-MS analysis as external standard. Table 3 reports the numerical data. To be comparable, data are normalized following eqn (1):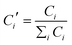 | (1) |
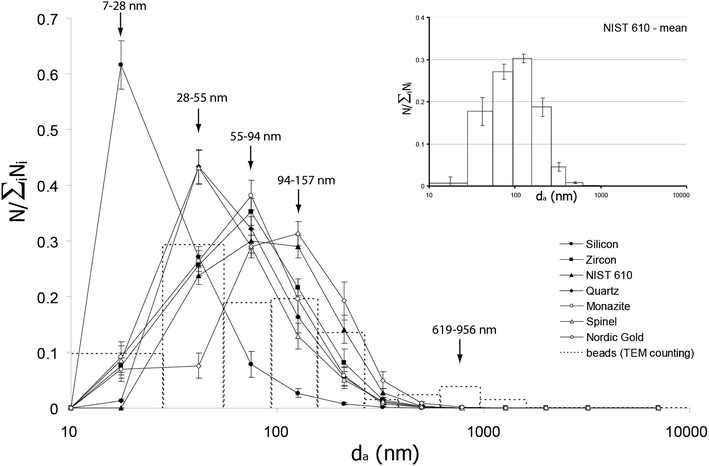 | ||
| Fig. 5 Size distribution of aerosols for all samples studied. Intensities (Ci′) are normalized to the total particles density for each acquisition. Values of da correspond to the median size of each class (see Table 3). Error bars are plotted as a function of reproducibility obtained on NIST610 (inset) over 8 acquisitions (1 per day during 8 days), and are dependent on the intensity of the signal. Note that the initial matrix seems to play a role in the broadening of the particle size distribution: black arrows indicate the central size class of the four distinguished sorts of distribution patterns (see section Results). The dashed histogram represents the TEM beads counting statistics realized over the 8 samples, from 133 specimens, corresponding to 11 days of experiment. Note that the main size distribution is well correlated to the ELPI data, and that another small peak appears on the 619–956 nm size class. | ||
| d a a/μm | 0.021 | 0.039 | 0.072 | 0.121 | 0.204 | 0.320 | 0.489 | 0.769 | 1.241 | 1.970 | 3.116 | 6.345 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The given values of da correspond to the median diameter of each particles size class. b Mean values calculated from 8 measurements performed over 8 consecutive days. c C i ′ > 0.2: 7%RSD; 0.1 < Ci′ < 0.2: 18%RSD; Ci′ < 0.1:30%RSD. | ||||||||||||
| C i ′c | ||||||||||||
| Zircon | 0.076 | 0.256 | 0.352 | 0.216 | 0.082 | 0.015 | 0.003 | 4 × 10−4 | 6 × 10−5 | 2 × 10−5 | 9 × 10−6 | 6 × 10−6 |
| Silicon | 0.616 | 0.271 | 0.078 | 0.027 | 0.007 | 0.001 | 0.000 | 2 × 10−5 | 8 × 10−6 | 4 × 10−6 | 2 × 10−6 | 2 × 10−6 |
| NIST610 | 2 × 10−4 | 0.238 | 0.299 | 0.290 | 0.141 | 0.027 | 0.004 | 4 × 10−4 | 1 × 10−4 | 6 × 10−5 | 3 × 10−5 | 2 × 10−5 |
| Monazite | 0.092 | 0.264 | 0.382 | 0.196 | 0.057 | 0.008 | 0.001 | 8 × 10−5 | 3 × 10−5 | 1 × 10−5 | 4 × 10−6 | 3 × 10−6 |
| Nordic gold | 0.069 | 0.076 | 0.290 | 0.313 | 0.192 | 0.050 | 0.009 | 0.001 | 2 × 10−4 | 1 × 10−4 | 6 × 10−5 | 4 × 10−5 |
| Quartz | 0.014 | 0.433 | 0.321 | 0.164 | 0.055 | 0.010 | 0.002 | 3 × 10−4 | 5 × 10−5 | 2 × 10−5 | 8 × 10−6 | 5 × 10−6 |
| Spinel | 0.085 | 0.432 | 0.290 | 0.128 | 0.050 | 0.011 | 0.003 | 4 × 10−4 | 7 × 10−5 | 2 × 10−5 | 7 × 10−6 | 4 × 10−6 |
| NIST (meanb) | 0.007 | 0.177 | 0.272 | 0.303 | 0.187 | 0.045 | 0.008 | 0.001 | 2 × 10−4 | 8 × 10−5 | 4 × 10−5 | 2 × 10−5 |
| RSD (%) | 207.7 | 18.7 | 6.7 | 3.3 | 11.7 | 21.7 | 29.7 | 26.7 | 12.4 | 12.0 | 13.5 | 13.1 |
| TEM counting | 0.097 | 0.293 | 0.187 | 0.195 | 0.135 | 0.015 | 0.022 | 0.037 | 0.015 | 0 | 0 | 0 |
Experiments show that size distribution of NIST610 particles is monomodal, centered on da = 94–157 nm, and quite large as the 4 main class size contributions are above 15% (∼94% of the total density). The main part of Fig. 5 shows the compilation of the particles size distribution of all samples, and Table 3 reports the numerical values of Ci′. Every distribution is monomodal. Nevertheless, they are not all centered on the same mean size. Four groups can be distinguished, each of them gathering samples with similar distributions regarding the error bars. Silicon is the narrowest distribution, centered on da = 7–28 nm as two stages gather ∼89% of the total amount of particles. Spinel and quartz distributions are broader and centered on da = 28–55 nm. Monazite and zircon are centered on da = 55–94 nm and show the same broadening as the precedent group, for which ∼80% of analyzed material is contained within 3 stages. Finally, as described above, NIST610 distribution is so much broader that the central peak is spread over two size classes (within error bars): da = 55–94 nm and da = 94–157 nm.
As exposed in the Experimental section, da ≠ dve. With respect to ρp and χ, the particle diameter will be either over- or underestimated by the ELPI. Moreover and unfortunately, the precise conversion from da to dve is hazardous in our case because of the different morphologies (≠χ) and chemical compositions (≠ρp) of particles within a single measurement. However, a qualitative estimation can be made using experimental results from DeCarlo et al.27 Our approximation is based on the electrical mobility diameter (dm). This value represents the size of a spherical particle with the same velocity as the particle of interest (characterized by da and χ ≥ 1) in a constant electric field. For nonspherical particles, or particles such as ρp > ρ0, we find dm > da. Then, we refer to the results from DeCarlo et al. showing the dependence of χ to ρp as a function of dm. Given a particle density (ρp) mostly higher than 3, and considering that the major part of them are not spherical (χ > 1), we find that for most of our samples ρp > χ. The only exception is silicon (ρp = 2.3), for which there is a probability for this ratio to be close to 1 (ρp = χ) or below (ρp < χ). Given this, it is possible to estimate a qualitative ratio of da out of the volume equivalent dm. Hence, we find that all particles are probably shifted towards larger sizes (da/dve) before correction, except for silicon for which there can be a possible negative shifting. In other words, our results of particle size distribution are overestimated, except in the case of silicon for which it is underestimated. The scattering of the distributions observed in Fig. 5 should then be reduced and result in a similar monomodal distribution within uncertainties. The narrower distribution of silicon aerosols and the larger one of the NIST610 may however be conserved and remain significant.
It would be helpful to evaluate the proportion of each population in the global size distribution. Unfortunately, as said above, ELPI is unable to detect such variations, and the exploitation of data can be made only with considering a single density for the whole measurement. Then we conducted a visual counting and sizing of beads using TEM. We measured 133 specimens over 8 different samples and 11 sessions. Data are reported as Ci′ values in Table 3 and added in Fig. 5 (dashed histogram). Results show that the major part of beads (∼90%) is included in the monomodal distribution and has a diameter dp ≤ 250 nm. Given the above developed qualification of the distribution shifting, we can estimate that the beads size distribution estimated by TEM counting is similar to the global aerosol size distribution measured by ELPI. In the case of monazite, this fraction corresponds to beads which are totally depleted in phosphorus (smallest specimen in Fig. 4). The remaining fraction (dp > 250 nm) is visible with our visual counting, but is negligible regarding ELPI counting. In the case of monazite (Fig. 4, largest specimen), this fraction corresponds to beads whose composition approaches that of the bulk mineral.
Discussion
Ablated matter and generation of particles from the plasma
a Generation of large particles (>1 μm) via hydrodynamic sputtering. According to previous studies, large round shaped particles that we observe would be generated by ejection of melt droplets from the superficial layer22,37–40 of the crater. The dynamics of such mechanisms is explained by Kelvin–Helmholtz instabilities at the interface of plasma and melt.22 This interpretation is in agreement with the previously observed melted/recrystallized layer occurring at the bottom of the ablation pit.14 The chemical composition of such beads (Fig. 4.2) differs from that of the bulk sample, but it is probable that diffusion of volatile elements during cooling, such as phosphorus in monazite, has happened within the droplets as soon as they have been ejected, as Horn and von Blanckenburg41 would suggest for an incomplete ionization through heating process in a plasma torch. Nevertheless, comparisons between ELPI and TEM particle counting underline the fact that this population is very limited and even negligible compared to the main size distribution, as shown in counting statistics (Table 3). The analytical gap between ELPI and TEM counting is explained by our collection technique (Fig. 1). It is basically an impactor stage, which will preferentially collect the largest particles in the gas flow, because of their higher inertia.42 In consequence, as shown by our TEM counting statistics (Fig. 5), large particles are observed around dp = 1 μm which are not counted with ELPI. They probably result from hydrodynamic sputtering, as shown by Koch et al.26 Hence, TEM counting emphasizes such small fractions, pointing out their very rare occurrence. Nevertheless, if their contribution in number density is very poor, the equivalent mass accounts for a large fraction of the total amount of produced aerosol. However, such objects are more affected by gravity and are very likely to be lost along transport.43 Consequently, in terms of LA-ICP-MS measurements, their impact should be very limited.
b Generation of round particles via gas to particle conversion. On the other hand, the small size fraction of the counted beads (<250 nm) which is the larger portion may hardly be associated to any form of hydrodynamic sputtering. This is highlighted by:
(i) The particles size distribution: as shown in Fig. 5 and Table 3, ∼90% of the beads measured with TEM are smaller than 250 nm. This fraction is well correlated to the systematic monomodal size distribution measured by ELPI and corresponds to the smaller fraction of particles measured by Koch et al.,26 the origin of which was already excluded to be the ejection of melt.
(ii) Minimum required stable size: Fig. 5 and Table 3 show that more than 50% of the counted beads are smaller than 100 nm, which has been defined in other studies22,23 as a minimal stable size for particles generated by hydrodynamic sputtering.
(iii) Complementary chemical compositions: small beads (<250 nm) and clusters are very complementary relative to the bulk composition of the ablated material. This is verified in every sample (Fig. 2 and 3). These chemical variations cannot be explained by fractionation due to diffusion of volatiles in a melt, as for hydrodynamic sputtering products, because the associated EDX analyses show here a complete exclusion of some elements depending on the particle morphology. Finally, each type seems to carry a part of the original chemical content of the bulk starting sample.
Taken together, these arguments allow us to reject the hypothesis of hydrodynamic sputtering as the mechanism responsible for the generation of beads smaller than 250 nm. Therefore, and considering the high chemical complementarity with clusters regarding the bulk sample, we suggest that these beads may be produced through gas to particle conversion within the same event as agglomerates. Nevertheless, the difference in shape and size between the two types of particles goes against this. Moreover, the hypothesis seems to be in disagreement with the results obtained by Hergenröder,23 notably because of the maximum growth size of 100 nm according to this author. Yet, particles observed over all our TEM foils indicate that beads are rigorously identical with one another within the range 10–250 nm. The existing gap between this maximum computed condensation/coalescence size reported by Hergenröder23 and our experimental results must be discussed as well as the difference observed in shape and size with agglomerates, by taking a closer look at the different mechanisms implied in particle growth and also at the laser induced plasma evolution:
(i) Early condensation: the simulation23 considers homogeneous nucleation as the triggering mechanism for condensation processes. It is defined as the creation of a critical size cluster from molecules in a supersaturated gas. These become nuclei for further growth. This is modelled for plasma containing only one element. Nucleation takes place when the saturation vapour pressure of this element is reached, as shown by results on Si, Fe and Cu. In plasma containing more than one element, this critical state is difficult to define. We can speculate that vapour pressure is controlled by the most concentrated species, but the latter may not always be strongly dominant. In any case, it is likely that some elements will be forced to condense earlier than their theoretical nucleation start if the plasma consists exclusively of them.
(ii) Heterogeneous nucleation: it describes the growth of a condensation nucleus with a critical size from an already existing particle in the vapour plume. The simulation23 does not take this mechanism into account because of high instabilities and high cooling rate of the plasma. Nevertheless, our previous results on laser induced damage under similar conditions consider fragmentation as a probable ablation mechanism.14,15 This photo-mechanical process is defined as the splitting of the target into small sized clusters. If we consider that such matter breakdown products can be included in the expanding plume, it would favour a less energetic growth process than homogeneous nucleation (the nuclei already exist) and accelerate the coarsening of particles from early condensation start.
(iii) This coarsening is then governed by a coalescence mechanism, itself depending on the probability of collision between liquid particles. The numerous multi-particle agglomerates observed (Fig. 2 and 3) confirm that the rate of collision is always high enough for this condition to be fulfilled. Afterwards, the growth time depends on the cooling rate and the melting period. As we cannot make out precise time scales relative to the considered phenomena, we will only restrict the melting interval to the temperature state between boiling temperature and fusion temperature: ΔT = Tboil − Tfus. Considering that plasma plume thermal evolution is similar from one sample to another, the melting period will mainly depend on ΔT. Even if pressure inside the plasma certainly induces variations of this ΔT, there are probably still differences between growing species. Some elements may then probably undergo a longer coalescence state relative to lower ΔT elements. Our results show that in most of the cases (Fig. 2, 3 and Table 4) elements with high ΔT are more concentrated in beads (Th and La for monazite, Zr for zircon, Al for spinel).
| Element | Mass/g mol−1 | Density/g cm−3 | T fus/K | T boil/K | ΔT |
|---|---|---|---|---|---|
| O | 16 | 0.001 | 54 | 90 | 36 |
| Na | 23 | 0.97 | 373 | 1173 | 800 |
| Mg | 24 | 1.70 | 923 | 1363 | 440 |
| Al | 26 | 2.70 | 933 | 2773 | 1840 |
| Si | 28 | 2.30 | 1673 | 3473 | 1800 |
| P | 31 | 1.80 | 317 | 553 | 236 |
| K | 39 | 0.86 | 333 | 1033 | 700 |
| Ca | 40 | 1.50 | 1113 | 1773 | 660 |
| Ti | 47 | 4.50 | 1973 | 3573 | 1600 |
| Fe | 55 | 7.80 | 1773 | 3073 | 1300 |
| Cu | 63 | 9.00 | 1273 | 2773 | 1500 |
| Zr | 91 | 6.50 | 2073 | 4673 | 2600 |
| Sn | 118 | 5.70 | 503 | 2873 | 2370 |
| La | 139 | 6.10 | 1193 | 3673 | 2480 |
| Th | 232 | 11.70 | 1973 | 5073 | 3100 |
(iv) The time dependency is then even more important in this discussion. A higher ΔT implies a longer liquid state for the concerned elements. Simulations23 hardly consider plasma conditions and evolution beyond 1 μs. The reported maximum grown particles (dp ≈ 100 nm) are based on this limit. However, in situ experiments on femtosecond laser induced plasmas44–47 report calculated electronic temperatures of ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K 400 ns after the plasma creation, before falling down to ∼5000 K after 10 μs (ten times the simulated growth), which is far higher than fusion temperatures of every studied element at room pressure. These results are based on a self-similar expansion fitting to metal plasma and consider that pulse duration is the main parameter controlling the plasma cooling rate. Nevertheless, our results on different matrices (including metallic ones) are very similar so we assume that the temperature evolution is similar or at least does not involve conditions close to the fusion point.
000 K 400 ns after the plasma creation, before falling down to ∼5000 K after 10 μs (ten times the simulated growth), which is far higher than fusion temperatures of every studied element at room pressure. These results are based on a self-similar expansion fitting to metal plasma and consider that pulse duration is the main parameter controlling the plasma cooling rate. Nevertheless, our results on different matrices (including metallic ones) are very similar so we assume that the temperature evolution is similar or at least does not involve conditions close to the fusion point.
(v) At these late times of the plasma evolution (>1 μs), the pressure state is locally close to the ambient gas pressure because plasma has passed into a shock wave regime. This latter regime is by definition very prone to particle collision (and so coalescence if in the liquid state) because of the higher particle density at the front of the expanding plume. On the opposite, particles at the back of the shock wave may rather stop growing because of the resulting local low pressure state. This may explain the broadening of beads size distribution. Indeed, the latter is presently centered on 28 nm < dp < 55 nm (Fig. 5), which is still well correlated to the simulation.
Finally, the above mentioned conditions seem favourable to the growth of a substantial fraction of spherical beads above dp = 100 nm through gas to particle conversion, early condensation and further coalescence and above all, high collision rate. Fig. 6 illustrates the particle growth along plasma expansion and cooling, showing the different processes involved in the condensation and coarsening which possibly end up in the presently observed particles (Fig. 2 and 3). A correlation with the existing simulation23 is thus feasible. Yet the growth of agglomerates within the same event still has to be explained and confronted to our hypothesis of a single complex gas to particle conversion mechanism.
 | ||
| Fig. 6 Illustration of the proposed model for particles growth in the expanding plasma plume, established on the basis of previous simulation of gas to particle conversion,23 and in situ observations from ablation of different initial samples in this study. Time is not indicated because it depends on different parameters, themselves dependent on the elements properties constituting the plasma as well as their combinations (see Discussion). | ||
a Monazite . This sample perfectly illustrates the chemical complexity of natural samples, and at the same time it is a very good example to validate our model. In the supercritical state, high pressure/temperature plasma contains fragmentation products that high density elements like thorium and rare earth elements can use as nuclei to start condensing. Their high ΔT (relative to phosphorus which is the other major element) allows coalescence to proceed until particles reach maximal sizes of dp ≈ 250 nm before solidification. This occurs in the context of a high collision rate at the shock wave front with very long plasma lifetime above the fusion point (>1 μs). This stage relaxes the plasma surrounding pressure so that other elements such as phosphorus cannot reach saturation until a very late stage when they eventually condense massively. Phosphorus, with its small ΔT, does not allow the condensed particles to coalesce beyond observed sizes of dp ≈ 10 nm. Phosphorus solidifies and agglomeration is assured by collision processes favoured by the high particle density. This interpretation is supported by the great gap existing between the properties of the different elements. Accordingly, generation and growing steps proceed without massive overlapping of the different processes. In addition, oxygen, which massively composes not only monazite but nearly all of the samples, must be included in this model. Observations show that it is always in high concentration within particles. According to this, we must conclude that oxygen takes part in particles growing from the very first condensation stage until the last particle has solidified. Yet, we cannot conclude whether it is totally consumed in particles growth or partially lost if it maintains as a gaseous phase. This statement and interpretation remains valuable for all the samples containing oxygen. Specific features such as crystalline structures are observed in rare cases in spherical particles (Fig. 2c). These are unlikely to be a consequence of another ablation mechanism, only because of their negligible occurrence (4 particles over our whole set of samples). This may rather be a consequence of the annealing properties of the mineral, provided it gains a sufficient amount of energy (cooling plasma) to crystallize after coalescence. This could also simply happen because of the energy brought by the electron beam during TEM observations.
b Zircon . In this system two main components can be considered: zirconium and silicon. Their density, ΔT and concentration differences are strong enough to figure out a process very similar to that of monazite of fractionated condensation/coalescence. Zirconium is twice more concentrated in the plasma and its density is three times that of silicon. It is likely to condense first and coalesce along with plasma cooling. Beads density is high enough so that collision rate is efficient enough after solidification to create beads agglomerates (Fig. 3.1a). Silicon condenses at a later stage. The “hard bonding” structure formed by the latter could result from an unachieved coalescence process, or agglomeration close to the fusion point, probably during the shock wave stage of plasma expansion.
c NIST610 . The complex chemical composition of this system, with close concentrations (Na and Ca), contrasting with very low concentrated high density elements (Al) makes it difficult to figure out a sequential condensation process. Nevertheless, observations highlight constant parameters such as those presented in Fig. 3.3. A plausible scenario can then be envisioned. Silicon accounts for ∼70 wt% of the total amount of matter, bringing the highest contribution to the total pressure. Moreover, its high nominal density and ΔT (Table 4) probably imply that it takes part in particles growing all along plasma expansion, which is confirmed by the chemical composition of aerosols (Fig. 3). Aluminium has about the same density as silicon so condenses early in beads. It is probably totally consumed at this early condensation stage, which may explain that we do not detect any trace of this element in agglomerates (Fig. 3.3b). Calcium has lower density and ΔT, but due to its high concentration (∼11.8%), it probably reaches saturation early so takes part in beads coalescence. Sodium and potassium have about twice lower density than calcium. It is then logical from our model to find them condensing in agglomerates, probably using silicon condensed particles (dp ≈ 10 nm) as nuclei. Their low fusion point can explain why these latter particles rather show a “hard” structure.
d Spinel. In this case, three elements must be considered: Al, Mg and Fe. Aluminium is the main constituting element (55%) and its properties make it condensing all along plasma cooling (like silicon in NIST610). We thus measure it in both types of particles, yet in higher content in beads relative to other elements (Fig. 3.5). Magnesium has the lowest density, concentration and ΔT. It should then condense at later stages, forming agglomerates on aluminium nuclei bases. We do observe such particles, in their “hard” shape, indicating that agglomeration probably occurs close to the fusion point. Iron is very specific in this scenario. It has by far the highest density but it is paradoxically detected in agglomerates. This may be explained by the pressure relaxation inside the plume after massive condensation of Al, which keeps iron saturation vapour pressure way above the system pressure until temperature is low enough for it to condense.
e Nordic gold. In this system, copper is by far the most concentrated and the most dense element. It should then produce a large amount of coalescing particles. Aluminium is much less concentrated and dense. Its saturation pressure should be kept away from the system pressure by the strong copper condensation, and delay its own phase transition. In the end, nuclei (i.e. copper particles) are numerous in the plume and aluminium is probably likely to condense at their surface, creating the observed embedding morphology (Fig. 3.6). Even if not reported above for other systems, this phenomenon is visible on every sample: zircon beads show a clear silicon coating, monazite beads often show a thin phosphorus layer at their surface and in spinel; beads of aluminium are often embedded in magnesium agglomerates. Nordic gold may simply present specific extreme conditions (concentrations and density differences) for this process to occur massively.
f Synthetic quartz and silicon. These two samples are composed of silicon. Both of them generate beads of the same texture and contrast (Fig. 3.2a and 4a). It is possible to figure out an expanding plume wherein silicon nucleates and condenses into small particles (dp ≈ 10 nm) and collision rate inhomogeneities broaden the size distribution by coalescence.23 Yet, agglomerates are different between quartz and silicon wafer. In the latter case, they are “soft” structured, indicating that agglomeration mainly occurs in the solid state, contrary to quartz in which ablation induces “hard” structured agglomerates, rather showing that collision occurs close to the fusion point. This difference could be explained by different ablation mechanisms. However, these have previously been found identical whatever the matrix given the similar ablated structures.14–18 An alternative explanation is the presence of oxygen in quartz. As explained in the previous cases, the latter is difficult to quantify because of its recurrence and high intensity on EDX spectra. For pure silicon, it is surprisingly high as well. As the sample surface is polished just before ablation, oxidation of the target is unlikely to be at the origin of it. We then suspect that the collected particles are oxidized after, during stocking time, which could also explain the higher amount of oxygen in agglomerates because of their larger contact surface to ambient air. In the end, oxygen cannot take part in particle growth for silicon as it may for quartz. Hence, the comparison between quartz and silicon brings an interesting hint of the role played by oxygen. In this case, it may contribute to the system pressure evolution, involving variations of silicon saturation points. The impact may be important as a change between liquid and solid state agglomeration stages, thus triggering the earlier condensation of Si for quartz, allowing agglomeration close to the fusion point.
Conclusion
We have performed an analytical study of infra red femtosecond laser induced aerosols through qualitative (morphology and chemical composition) and quantitative (particle counting) aspects using Transmission Electron Microscopy and Low Pressure Impaction. Three morphologies were defined: (i) very limited occurrences of large spherical particle (dp ≈ 1 μm) chemically close to sample composition, (ii) spherical particles (dp ≤ 250 nm) and (iii) more or less developed agglomerates of dp ≈ 10 nm particles showing hard or soft structures depending on the initial target. A specific generation process can be attributed to each type of particle: (i) rare large beads probably result from hydrodynamic sputtering occurring from the superficial modified layer of the crater pit;14 (ii) small beads may be generated from gas to particle conversion, condensation and coalescence under specific conditions: early nucleation (high density elements) and favoured coalescence (high collision rate and high ΔT); (iii) agglomerates are probably generated from late condensation and limited coalescence respectively due to low density of the elements of concern and low ΔT, more likely to result in a collision stage close to the fusion point (cooling plasma) or under solid state. Depending on elements properties and the different combination of these elements in our samples, particle generation scenarios can be deduced in accordance with the existing model.The results also provide arguments for identifying ablation mechanisms. Thus, the proposed model is in good agreement with our previous result pointing out vaporization and fragmentation as the main processes of IR-femtosecond laser ablation.
Implications for LA-ICP-MS analysis are currently addressed in a subsequent study, and are particularly focused on the consequences about chemical fractionation associated with ICP-MS response.
Acknowledgements
The authors would like to thank Rémi Freydier for his motivating never-ending implication in this project. Frédéric Candaudap, Aurélie Lanzanova, Sophie Gouy and Thierry Aigouy for their availability, Philippe de Parseval and Damien Guillaume for providing the natural spinel and the synthetic quartz sample. David le Dur from ECOMESURE (Janvry, France) is thanked for his great help during the ELPI campaign of measurements, and Christian Dominici at the CP2M, Université Paul Cézanne (Marseille) for performing FIB milling. Luc Vigroux, Pierre Marie Paul and Pierrick Leroy are thanked for their technical support and advising in femtosecond laser handling. Many thanks are addressed to the anonymous reviewers for their helpful and constructive comments. This work was funded by CNRS, Amplitude Technologies and a PPF from the Ministry of Research.References
- B. J. Fryer, S. E. Jackson and H. P. Longerich, Chem. Geol., 1993, 109, 1–8 CrossRef CAS.
- D. Günther and B. Hattendorf, TrAC, Trends Anal. Chem., 2005, 24, 255–265 CrossRef.
- C. A. Heinrich, T. Pettke, W. E. Halter, M. Aigner-Torres, A. Audétat, D. Günther, B. Hattendorf, D. Bleiner, M. Guillong and I. Horn, Geochim. Cosmochim. Acta, 2003, 67, 3473–3497 CrossRef CAS.
- K. Niemax, Fresenius' J. Anal. Chem., 2001, 370, 332–340 CrossRef CAS.
- R. E. Russo, X. Mao, H. Liu, J. Gonzalez and S. S. Mao, Talanta, 2002, 57, 425–451 CrossRef CAS.
- E. F. Cromwell and P. Arrowsmith, Appl. Spectrosc., 1995, 49, 1652–1660 CAS.
- C. C. Garcia, H. Lindner, A.v. Bohlen, C. Vadla and K. Niemax, J. Anal. At. Spectrom., 2008, 23, 470–478 RSC.
- Q. Bian, C. C. Garcia, J. Koch and K. Niemax, J. Anal. At. Spectrom., 2005, 21, 187–191 Search PubMed.
- R. Freydier, F. Candaudap, F. Poitrasson, A. Arbouet, B. Chatel and B. Dupré, J. Anal. At. Spectrom., 2008, 23, 702–710 RSC.
- T. Hirata and Y. Kon, Anal. Sci., 2008, 24, 345–353 CrossRef CAS.
- F. Poitrasson, X. Mao, S. S. Mao, R. Freydier and R. E. Russo, Anal. Chem., 2003, 75, 6184–6190 CrossRef CAS.
- D. Fliegel, M. Klementova and J. Kosler, Anal. Chem., 2010, 82, 4272–4277 CrossRef CAS.
- R. Glaus, R. Kaegi, F. Krumeich and D. Gunther, Spectrochim. Acta, Part B, 2010, 65, 812–822 CrossRef.
- F. X. D'Abzac, A. M. Seydoux-Guillaume, J. Chmeleff, L. Datas and F. Poitrasson, J. Anal. At. Spectrom. 10.1039/c1ja10153f.
- A. M. Seydoux-Guillaume, R. Freydier, F. Poitrasson, F. X. D'Abzac, R. Wirth and L. Datas, Eur. J. Mineral., 2010, 22, 235–244 CrossRef CAS.
- A. Borowiec, M. Couillard, G. A. Botton and H. K. Haugen, Appl. Phys. A: Mater. Sci. Process., 2004, 79, 1887–1890 CAS.
- M. Couillard, A. Borowiec, H. K. Haugen, J. S. Preston, E. M. Griswold and G. A. Botton, J. Appl. Phys., 2007, 101, 033519 CrossRef.
- E. Coyne, J. P. Magee, P. Mannion, G. M. O′Connor and T. J. Glynn, Appl. Phys. A: Mater. Sci. Process., 2005, 81, 371–378 CrossRef CAS.
- R. F. W. Herrmann, J. Gerlach and E. E. B. Campbell, Appl. Phys. A: Mater. Sci. Process., 1998, 66, 35–42 CrossRef CAS.
- P. Lorazo, L. J. Lewis and M. Meunier, Phys. Rev. Lett., 2003, 91, 225502 CrossRef.
- D. Perez and L. J. Lewis, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 184102 CrossRef.
- R. Hergenröder, J. Anal. At. Spectrom., 2006, 21, 517–524 RSC.
- R. Hergenröder, J. Anal. At. Spectrom., 2006, 21, 1016–1026 RSC.
- R. Hergenröder, O. Samek and V. Hommes, Mass Spectrom. Rev., 2006, 25, 551–572 CrossRef.
- D. Strickland and G. Mourou, Opt. Commun., 1985, 56, 219–221 CrossRef.
- J. Koch, A.v. Bohlen, R. Hergenröder and K. Niemax, J. Anal. At. Spectrom., 2004, 19, 267–272 RSC.
- P. F. DeCarlo, J. G. Slowik, D. R. Worsnop, P. Davidovits and J. L. Jimenez, Aerosol Sci. Technol., 2004, 38, 1185–1205 CAS.
- Y. Ni, J. M. Hughes and A. M. Mariano, Am. Mineral., 1995, 80, 21–26 CAS.
- J.-M. Montel, S. Foret, M. Veschambre, C. Nicollet and A. Provost, Chem. Geol., 1996, 131, 37–53 CrossRef CAS.
- R. R. Parrish, Can. J. Earth Sci., 1990, 27, 1431–1450 CAS.
- A. Meldrum, L. A. Boatner, W. J. Weber and R. C. Ewing, Geochim. Cosmochim. Acta, 1998, 62, 2509–2520 CrossRef CAS.
- A.-M. Seydoux-Guillaume, R. Wirth, A. Deutsch and U. Scharer, Geochim. Cosmochim. Acta, 2004, 68, 2517–2527 CrossRef CAS.
- J. L. Paquette and M. Tiepolo, Chem. Geol., 2007, 240, 222–237 CrossRef CAS.
- N. J. G. Pearce, W. T. Perkins, J. A. Westgate, M. P. Gorton, S. E. Jackson, C. R. Neal and S. P. Chenery, Geostand. Newsl., 1997, 21, 115–144 CrossRef CAS.
- C. Courtieu, F.-X. D'Abzac, J. Chmeleff, D. Guillaume and A.-M. Seydoux-Guillaume, Eur. J. Mineral., 2011, 23, 391–400 CrossRef CAS.
- M. Wiedenbeck, P. Allé, F. Corfu, W. L. Griffin, M. Meier, F. Oberli, A. Von Quadt, J. C. Roddick and W. Spiegel, Geostand. Geoanal. Res., 1995, 19, 1–23 CrossRef CAS.
- J. J. Gonzalez, C. Liu, S.-B. Wen, X. Mao and R. E. Russo, Talanta, 2007, 73, 567–576 CrossRef CAS.
- R. P. Camata, M. Hirasawa, K. Okuyama and K. Takeuchi, J. Aerosol Sci., 2000, 31, 391–401 CrossRef CAS.
- M. Miclea, C. C. Garcia, I. Exius, H. Lindner and K. Niemax, Spectrochim. Acta, Part B, 2006, 61, 361–367 CrossRef.
- A. Ben-Yakar, A. Harkin, J. Ashmore, R. L. Byer and H. A. Stone, J. Phys. D: Appl. Phys., 2007, 40, 1447–1459 CrossRef CAS.
- I. Horn and F. von Blanckenburg, Spectrochim. Acta, Part B, 2007, 62, 410–422 CrossRef.
- C. Y. Liu, X. L. Mao, J. Gonzalez and R. E. Russo, J. Anal. At. Spectrom., 2005, 20, 200–203 RSC.
- D. Bleiner, P. Lienemann and H. Vonmont, Talanta, 2005, 65, 1286–1294 CrossRef CAS.
- X. Zeng, X. L. Mao, R. Greif and R. E. Russo, Appl. Phys. A: Mater. Sci. Process., 2005, 80, 237–241 CrossRef CAS.
- O. Barthelemy, J. Margot, M. Chaker, M. Sabsabi, F. Vidal, T. W. Johnston, S. Laville and B. Le Drogoff, Spectrochim. Acta, Part B, 2005, 60, 905–914 CrossRef.
- O. Barthélémy, Caractérisation d’un plasma d’aluminium créé par interaction laser-matière à bas flux sous environnement atmosphérique, Université de Montréal, 2004 Search PubMed.
- B. Le Drogoff, J. Margot, F. Vidal, S. Laville, M. Chaker, M. Sabsabi, T. W. Johnston and O. Barthelemy, Plasma Sources Sci. Technol., 2004, 13, 223–230 CrossRef CAS.
- C. Liu, X. L. Mao, S. Mao, X. Zeng, R. Greif and R. E. Russo, Anal. Chem., 2004, 76, 379–383 CrossRef CAS.
- J. Kosler, M. Wiedenbeck, R. Wirth, J. Hovorka, P. Sylvester and J. Mikova, J. Anal. At. Spectrom., 2005, 20, 402–409 RSC.
- S. Tsantilis and S. E. Pratsinis, Langmuir, 2004, 20, 5933–5939 CrossRef CAS.
- F. X. D'Abzac, F. Poitrasson, R. Freydier and A. M. Seydoux-Guillaume, J. Anal. At. Spectrom., 2010, 25, 681–689 RSC.
| This journal is © The Royal Society of Chemistry 2012 |
