C⋯π interaction of non-hydrogen bond type

Abstract

An unusual C⋯π interaction of non-hydrogen bond type has been found for the first time in ethyl (2Z)-2-cyano-3-[(3-fluoro-4-methoxyphenyl)amino]prop-2-enoate and is rationalized by ab initio computations as being the result of electrostatic interactions. The database analysis has shown its scarcity.

---

Noncovalent interactions, such as hydrogen bonding, aromatic stacking and cation⋯π interactions, play a dominant role in many forefront areas of modern chemistry, from materials design to molecular biology.^1–7 Wherever present, they often strongly influence many chemical and biochemical phenomena; therefore, a complete understanding of these chemical and biochemical processes will often demand a complete understanding of the interactions too. It is not surprising that a great deal of interest has been generated in the study of such interactions. Under the class of the X⋯π interactions, where the π-cloud of the benzene interacts with an electropositive atom X, the H⋯π and cation⋯π systems form two separate classes, and have received a great deal of attention in recent times. By contrast, the N⋯π, O⋯π, S⋯π etc. interactions^7,8 involving the benzene π-electrons have been significantly underrated due to their rarity.

The C⋯π interactions of non-hydrogen bond type are more rare for two reasons. First, unlike the H atom in the H⋯π system or the cation in the cation⋯π unit, atom C is usually not sufficiently electron-deficient (electropositive) to serve as the π-electrons acceptor. Second, atom C is not often situated in sterically-unhindered positions. This communication shows that in spite of these limitations, an electropositive olefinic C atom forms an electrostatic acceptor–donor interaction with an electron-rich aromatic ring, thus contributing to crystal stability.

A striking example of such an C⋯π interaction is found in the crystal structure of ethyl (2Z)-2-cyano-3-[(3-fluoro-4-methoxyphenyl)amino]prop-2-enoate, 1 (Fig. 1). The planar sp² vinyl atom C1 lied nearly vertically (<5°) over or under the phenyl ring centroid of the neighboring molecule. The distance of C1 to the centroid of the C5*–C10* ring is only 3.425(2) Å, which is markedly shorter than the upper limit of the sum of van der Waals radii, 3.6 Å (the phenyl ring half-thickness, taken as 1.7–1.9 Å, being half the centroid–centroid distance in parallel phenyl rings).⁹ The geometric parameters suggest a stronger C⋯π interaction. Here the electron-deficient atom C1 acts as a π-electron acceptor and the π-cloud of the electron-rich phenyl ring acts as a π-electron donor. Though the anilino group is bonded to the vinyl atom C2, atom C1 still exhibits relatively lower electron density due to the presence of two strong electron-withdrawing substituents with substantial negative electrostatic potential held by the C2–N1, C3≡N2 and ester carbonyl groups, respectively, around the “positively charged C1 atom”. This can be verified by the shorter C2–N1, C3≡N2 and C4=O1 bonds [1.324, 1.143 and 1.221 Å, respectively]. The feature in charge distribution is similar to some extent to that of the perfluorobenzene,¹⁰ with reduced electron-density on the centroid of the phenyl ring and high electron-density on the edge (perfluorobenzene model). As such, here the feature of charge distribution facilitates the formation of the intermolecular C⋯π interaction between the electron-deficient C1 atom and the electron-rich C5–C10 ring.

Fig. 1 Part of the packing diagram of ethyl (2Z)-2-cyano-3-[(3-fluoro-4-methoxyphenyl)-amino]prop-2-enoate, 1, showing the formation of the double C⋯π interactions between C1 and C5–C10 ring with a C1⋯Cg distance of 3.425 Å (Cg is the centroid of the C5–C10 ring). Atoms marked with an asterisk (*) are at the symmetry position: −x, 1 − y, −z.

Recent studies have shown the existence of cation⋯π interactions between an electron-deficient cation and an electron-rich arene. Systems hosting such interactions have been found in the CSD and have been the subject of recent papers.^11–13 However, most of the work on this subject still remain theoretical.^14–16 Computational study shows that the interactions between cations such as Li⁺, Na⁺, K⁺, NH₄⁺, Al⁺, Ag⁺etc. and π-systems such as C₆H₆, C₆H₅CH₃ or C₆H₅OH were found to be energetically favourable,⁷ and that energy minima were found to lie along the principal symmetry axis of the molecule and the binding energy increases with the increase of π-electron density.

A model of the C⋯π interaction can be reasoned out from the cation⋯π interactions, though the systems differ in parameters such as the distance of the C atom with respect to the principal axis (or rather the pseudo axis considering the loss of symmetry in our system) of the aromatic ring. As such, the C⋯π interaction can be predicted to be energetically favorable between an electron-deficient C atom and a π-electron-rich benzene ring. Interestingly, such a prediction comes true for the first time in compound 1.

To further seek theoretical evidence for the C⋯π, the density functional theory (DFT) calculations at the BLYP^17,18/6-31+G(d) level with the long-range correction scheme of Hirao and coworkers¹⁹ (LCBLYP/6-31+G(d)) were performed on compound 1. The monomer and the dimers formed by C⋯π interaction were studied. All the calculations were carried out using the GAUSSIAN 09 package.²⁰ According to our DFT calculations, atom C1 carries the largest Mulliken positive charge (0.747, Fig. 2) and the benzene ring as a whole carries high negative charge (−0.266). The feature in charge distribution is in good accordance with our crystallographically induced conclusion, therefore, from which it is demonstrated again that the interaction between the electron-deficient C1 and the electron-rich C5–C10 ring is attractive in nature and the formation of the C⋯π interaction should be mainly attributed to electrostatic interactions. The calculated attractive force for dimer I, including the zero-point energy corrections, is −12.9 kcal mol⁻¹. The calculation also shows that the C⋯π interaction geometry (Fig. 2) is in good accordance with that found in the crystal structure; the distance between C1 atom and the centroid of C5–C10 ring is 3.422 Å, and atom C1 is within 5° of being directly above the centroid. Therefore, the DFT calculations have presented compelling theoretical evidence for the C⋯π interaction, and simultaneously given us valuable insight into the nature and energetic profiles of the interaction.

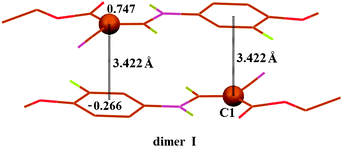Fig. 2 The dimeric structure I of compound 1 optimized within the DFT method, LC-BLYP/6-31+G(d) level of theory, showing the Mulliken charge distribution on C1 and the benzene ring as a whole, and the resulting C⋯π interaction. For the sake of clarity, some hydrogen atoms have been omitted.

We have also probed the vibrational characteristics of the C=C bond in an attempt to observe this interaction in solution and the solid state. IR spectroscopic measurements of the ν_C=C stretching frequency in the solid crystalline material and in solution of CH₂Cl₂ show dramatic changes; the FTIR spectra of the crystalline sample in KBr showed ν_C=C at 1650 cm⁻¹, and a significant red shift (1635 cm⁻¹) was observed in CH₂Cl₂. This indicated that the intermolecular C⋯π interaction in 1 does have a significant effect on the vibrational frequency of the C=C bond.

In order to further probe the generality of the novel C⋯π interaction, a systematic search of CSD (version 5.32 2011) was performed. Considering the requirement of the steric hindrance, the ‘above ring’ carbon atom is constrained to be sp² hybridized, lie within 10° of being above the phenyl ring center and no more than 3.6 Å far away from the center. The angle parameter of 10° for the database search seems to be too restrictive, however, when the search angle is beyond the scope, such as in the range of 10–25°, all the hits give common examples of offset π⋯π interactions; the 3.6 Å cut-off was chosen based on the van der Waals radius of carbon, taken as 1.7 Å, and the phenyl ring half-thickness of 1.7–1.9 Å.⁹ Under the constraints, a total of 135 hits were retained; these hits were always scrutinized manually; and those obviously inappropriate compounds including disordered structures were eliminated. With these stipulations, only thirteen unambiguous C⋯π interactions were found (Table 1), out of which three are present in organic crystals, and ten in metal complexes. Though these systems differ from our studied structure 1, the C⋯π interactions in nature are identical to each other. The database analysis also reveals that, for those C⋯π systems, the ‘above ring’ carbon atom is located within about 7° of being vertically above or under the centroid of the aromatic ring, and the average distance to the centroid is 3.44 Å. Obviously, the average C⋯π bond geometry is consistent with that found in 1. Therefore, the results from the CSD search, the crystallographic study, theoretical calculation and IR spectra analysis of structure 1 have confirmed that C⋯π interaction, though rare, can actually occur between an adequately electron-deficient C atom and an electron-rich aromatic ring, and is structurally significant when it does occur.

Table 1 Results of database analysis of C⋯π interactions

	No. of entries	Mean geometric parameters
		d ^b/Å	α ^c/°
a Refcodes: BEFRUA, BEGCEW, FAKBID, HIVQEI, PARKAU, SADPUJ, QIHPUS, VAPNEF, BUTVAO, GUYZIK, FOSWOA, PIZCEH, VIVKIV. b The distance from the ‘above ring’ carbon to the ring centroid. c The angle between the ‘above ring’ carbon–ring centroid vector and the vector perpendicular to the C6–aromatic ring.
C⋯π interactions	13^a	3.44	7.1

---

The crystal structure also exhibits an intramolecular hydrogen bond of N–H⋯O type (Fig. 1), the distance H1⋯O1 being 2.06 Å, and the associated angle N1–H1⋯O1 133°. This strong intramolecular H-bond fixes the Z configuration of the C1=C2 bond and contributes to maintain a planar conformation to the molecule's main skeleton, thus allowing the p-electrons of the sp²-hybridized N1 to localize sufficiently and finally in favor of the formation of the ‘perfluorobenzene model’ in charge distribution. This sets the stage for the C⋯π, as well as the following O⋯π interactions observed within the crystal lattice.

Besides the C⋯π interaction, the structure also exhibits geometric characters once expected for an O⋯π interaction of non-hydrogen bond type (Fig. 3).^8a The ethoxy atom O2 is found to locate vertically above or under the centre, and 3.486 Å away from the centre. The distance is slightly longer than the upper limit of Σvdw radii, 3.42 Å. Despite this, the O⋯π interaction is still shown to be attractive in nature by the density functional theory (DFT) calculations at the BLYP^17,18/6-31+G(d) level with the long-range correction scheme of Hirao and coworkers¹⁹ (LCBLYP/6-31+G(d)). The calculated interacting energy for dimer II (Fig. 4), including the zero-point energy corrections, is −11.0 kcal mol⁻¹. In addition, the calculated O⋯π geometry closely resembles that in the crystal structure (Fig. 3 and 4); the distance between atom O2 and the C5–C10 ring centroid is 3.372 Å, and O2 is located within 5° of being directly above the centroid. The ethoxy atom O2 serves as a p-electron acceptor and the p-cloud of the aromatic ring acts as an electron donor. The reduced p-electron density on O2, due to the resonance of a lone pair over the bonded ester carbonyl group, favors the formation of electrostatic acceptor–donor interactions of O⋯π type. Like C⋯π interaction, the O⋯π interaction is also uncommon in the literature, though a number of C=O⋯π types have been reported recently,^21–26 the nature of which is nothing but a lone-pair⋯π interaction. In the case of compound 1, the O⋯π interaction, however, occurs between the electron-density-reduced alkoxy oxygen and the aromatic π-electrons, the former distinctly NOT being an electron-rich carbonyl O atom.

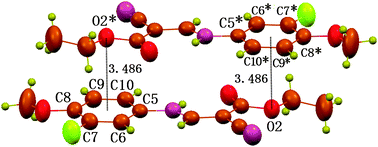Fig. 3 Part of packing diagram of compound 1, showing the double O⋯π interactions between O2 and C5–C10 ring with a O2⋯Cg distance of 3.486 Å (Cg is the centroid of the C5–C10 ring). Atoms marked with an asterisk (*) are at the symmetry position: 1 − x, 1 − y, −z.

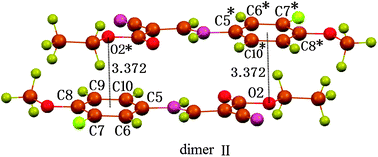Fig. 4 The dimeric structure II of compound 1 optimized within the DFT method, LC-BLYP/6-31+G(d) level of theory, showing theoretically the formation of the O⋯π interaction.

In addition to the C⋯π and O⋯π interactions, the aromatic C6–H and the olefinic C2–H cooperatively form a pair of conventional bifurcated C–H⋯N hydrogen bonds to the cyano nitrogen atom of the neighboring molecule related by centrosymmetry (Fig. 5), the distances H2⋯N2 and H6⋯N2 being 2.51 and 2.61 Å, respectively, and the associated angles C2–H2⋯N2 and C6–H6⋯N2 being 153 and 161°, respectively. These noncovalent interactions, including C⋯π, O⋯π, C–H⋯N and N–H⋯O, assist each other synergistically and constitute a two-dimensional sheet (Fig. 5).

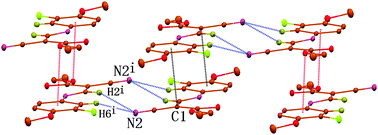Fig. 5 Part of crystal structure of compound 1, showing the formation of a two-dimensional sheet via combination of C⋯π, O⋯π interactions and C–H⋯N hydrogen bonds. For the sake of clarity, H atoms not involved in the motif shown have been omitted, and selected atoms are labeled. Symmetry code: −x, 2 − y, −z.

In conclusion, the detailed structural analysis has revealed an unusual C⋯π interaction occurring between an electron-deficient C atom and an electron-rich aromatic ring. Ab initio computations performed at the LC-BLYP/6-31+G(d) level and IR spectra gave effective supporting data for the C⋯π interaction. The database analysis has shown its scarcity. We believe that the present work may be the first systematic study on the C⋯π interaction.

Experimental

Synthesis of ethyl (2Z)-2-cyano-3-[(3-fluoro-4-methoxyphenyl)amino]prop-2-enoate, 1

A mixture of 3-fluoro-4-methoxyaniline (0.02 mol), ethyl 2-cyano-3-ethoxyacrylate (0.02 mol) and toluene (10 ml) was heated at reflux for ca. 10 min. The reaction mixture was then cooled to room temperature. The precipitate was collected by filtration and washed with ethanol. Crystals suitable for an X-ray analysis were obtained by slow cooling of a hot toluene solution of the crude product.

X-Ray structure determination

The selected crystal was mounted in inert oil on glass fibers. Data were measured using Mo-Kα radiation on a Bruker SMART 1000 CCD diffractometer. Data collection at 296 K and reduction were performed using SMART and SAINT software.²⁷ Absorption correction was applied using the multi-scan method (SADABS).²⁸ The crystal structure of 1 was solved by direct methods and refined by full matrix least-squares on F² using the SHELXTL program package.²⁹ All non-hydrogen atoms were subjected to anisotropic refinement, and all H atoms were placed in geometrically idealized positions and constrained to ride on their parent atoms.

Crystal data

C₁₃H₁₃FN₂O₃, M = 264.25, triclinic, P1̄, a = 7.145(1), b = 7.580(1), c = 13.441(1) Å, α = 83.394(2), β = 78.094(2), γ = 70.208(2)°, V = 669.3(1) ų, Z = 2, T = 296(2) K, D_c = 1.311 g cm⁻³; 4583 reflections collected, 2309 unique (R_int = 0.017), 1681 observed with I > 2(I); final R = 0.0340, wR₂ = 0.0975, goodness-of-fit S = 1.01.

Notes and references

1. L. A. Hardegger, B. Kuhn, B. Spinnler, L. Anselm, R. Ecabert, M. Stihle, B. Gsell, R. Thoma, J. Diez, J. Benz, J.-M. Plancher, G. Hartmann, D. W. Banner, W. Haap and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 314–318.
2. K. E. Schwiebert, D. N. Chin, J. C. MacDonald and G. M. Whitesides, J. Am. Chem. Soc., 1996, 118, 4018–4029.
3. J. A. Zerkowski, J. P. Mathias and G. M. Whitesides, J. Am. Chem. Soc., 1994, 116, 4305–4315.
4. J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319.
5. G. A. Jeffrey and W. Saenger, Hydrogen bonding in biological structures, Springer, New York, 1991.
6. G. R. Desiraju, Crystal Engineering: The Design of Organic Solids,Elsevier, Amsterdam, 1989.
7. J. C. Maa and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324.
8. (a) Z. Zhang, Y. Wu and G. Zhang, CrystEngComm, 2011, 13, 4496–4499; (b) J. B. O. Mitchell, C. L. Nandi, S. Ali, I. K. Mcdonald, J. M. Thornton, S. L. Price and J. Singh, Nature, 1993, 366, 413; (c) J. Lewinski, W. Bury and I. Justyniak, Eur. J. Inorg. Chem., 2005, 4490–4492.
9. C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896.
10. (a) B. W. Gung and J. C. Amicangelo, J. Org. Chem., 2006, 71, 9261–9270; (b) J. H. Williams, Acc. Chem. Res., 1993, 26, 593–598; (c) A. P. West, S. Mecozzi and D. A. Dougherty, J. Phys. Org. Chem., 1997, 10, 347–350; (d) M. L. Waters, Curr. Opin. Chem. Biol., 2002, 6, 736–741.
11. C. M. Older, R. McDonald and J. M. Stryker, J. Am. Chem. Soc., 2005, 127, 14202–14203.
12. C. Elschenbroich, E. Schmidt, B. Metz and K. Harms, Organometallics, 1995, 14, 4043–4045.
13. E. R. T. Tiekink and J. Zukerman-Schpector, CrystEngComm, 2009, 11, 1176–1186.
14. R. A. Kumpf and D. A. Dougherty, Science, 1993, 261, 1708–1710.
15. S. Mecozzi, A. P. West and D. A. Dougherty, J. Am. Chem. Soc., 1996, 118, 2307–2308.
16. J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 4177–4178.
17. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
18. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789.
19. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
21. J. E. Gautrot, P. Hodge, D. Cupertinob and M. Helliwell, New J. Chem., 2006, 30, 1801–1807.
22. M. G. B. Drew, S. Nag and D. Datta, Inorg. Chim. Acta, 2009, 362, 610–613.
23. X.-L. Gao, L.-P. Lu and M.-L. Zhu, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, o123–o127.
24. S. R. Choudhury, P. Gamez, A. Robertazzi, C. Y. Chen, H. M. Lee and S. Mukhopadhyay, Cryst. Growth Des., 2008, 8, 3773–3784.
25. S. K. Seth, B. Dey, T. Kar and S. Mukhopadhyay, J. Mol. Struct., 2010, 973, 81–88.
26. C. Biswas, M. G. B. Drew, D. Escudero, A. Frontera and A. Ghosh, Eur. J. Inorg. Chem., 2009, 2238–2246.
27. SMART 5.0 and SAINT 4.0 for Windows NT, Area Detector Control and Integration Software, Bruker Analytical X-Ray Systems Inc., Madison, WI, 1998.
28. G. M. Sheldrick, SADABS: Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Germany, 1996.
29. G. M. Sheldrick, SHELXTL 5.1 for Program for Windows NT: Structure Determination Software Programs, Bruker Analytical X-Ray Systems, Inc., Madison, WI, 1997.

---

Footnote

† CCDC reference number 837545. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c2nj20903a

---