Lubrication mechanism of concentrated polymer brushes in solvents: effect of solvent viscosity
Akihiro
Nomura
a,
Kohji
Ohno
a,
Takeshi
Fukuda
a,
Takaya
Sato
bc and
Yoshinobu
Tsujii
*ac
aInstitute for Chemical Research, Kyoto University, Uji, Kyoto 611-0011, Japan. E-mail: tsujii@scl.kyoto-u.ac.jp
bDepartment of Chemical and Biological Engineering, Tsuruoka National College of Technology, Inooka, Tsuruoka, Yamagata 997-8511, Japan
cJST, CREST, Uji, Kyoto 611-0011, Japan
First published on 14th November 2011
Abstract
We investigated the frictional properties of concentrated polymer brushes (CPBs) of poly(methyl methacrylate) (PMMA) immersed in two highly viscous ionic liquids (ILs) that are good solvents for PMMA: N,N-diethyl-N-methyl-N-(2-methoxyethyl)ammonium bis(trifluoromethanesulfonyl)imide (DEME-TFSI) and 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide (EMI-TFSI). These ILs could swell the CPB of PMMA to the same degree as toluene, a more commonly used good solvent of much lower viscosity. The CPB of PMMA effectively reduced the interaction between surfaces in these ILs and hence developed otherwise hidden hydrodynamic lubrication, which was characterized by the dependence of the frictional coefficient μ on shear velocity v. In the hydrodynamic-lubrication regime, the linear relationship was obtained between them in the double logarithmic plot, giving a slope close to unity, which is expected for a Newtonian fluid, in the solvents studied even though the viscosity differed by nearly two orders of magnitude. More interestingly, the μ values in this regime of lubrication were found to be scaled by the viscosity of the solvent. These results not only enable us to discuss the details of the effect of solvent viscosity on lubrication properties of the CPB systems but also demonstrated their ability to act as an excellent lubrication system in combination with ILs as lubricating fluids.
Introduction
The polymer brush, an assembly of polymer chains densely end-grafted on surfaces or at interfaces, has been attracting much attention in many areas of science and technology, e.g., adhesion, colloid stabilization, rheology, and tribology.1–5 Recently, surface-initiated living radical polymerization was successfully employed to directly grow polymer chains from various solid surfaces in a living-polymerization process. This success enabled us to arbitrarily and easily control both the chain length and chain length distribution of grafted polymers.6–8 A more significant breakthrough provided by this technique is the exceptional increase in graft density, more than one order of magnitude higher than that of typical semi-dilute polymer brushes (SDPBs).9 Such high-density polymer brushes reasonably fall in the regime of “concentrated” polymer brushes (CPBs), in which the excluded-volume effect is screened, in a solvent, over whole chains, as in a “concentrated” solution of free chains. We previously reported that the CPBs possess dramatically different structures and properties owing to high osmotic pressure in a good solvent balanced by the exceptionally high elastic stress of graft chains.7,10,11One of the most prominent and promising properties is super lubrication established between confronted CPBs in a solvent.12,13 Our recent study on the dependency of shear velocity v on the frictional coefficient μ revealed that two lubrication mechanisms exist.13 In the first mechanism, boundary lubrication, in which the interaction between brushes determines the friction, it can be seen that μ values are less dependent on v. In a good solvent, such an interaction can be ascribed to the interpenetration of polymer brushes. When the confronted SDPBs are compressed to a certain degree, they can mix with each other, showing a frictional transition to values of μ on the order of 10−1. In contrast, the CPB showed compression-independent super lubrication on the order of 10−4 in μ, which is due to CPBs never mixing with each other at high compressions because of the conformational entropic properties of highly extended CPB chains. Such low μ values have been achieved for polyelectrolyte systems of polymer brushes and gels in water with the aid of electrostatic repulsion or hydration forces. It is interesting that the CPB can achieve such super lubrication without these effects, e.g., even by a non-ionic polymer system in a non-aqueous solvent, which may serve to broaden the scope of its application in lubrication.
The second mechanism of lubrication is hydrodynamic lubrication, in which the viscosity resistance of the lubricating layer determines the friction. The reduced friction of CPBs in the above-mentioned boundary lubrication enabled us to observe otherwise hidden hydrodynamic lubrication. In this lubrication regime, the viscosity resistance between and/or in the solvent-swollen polymer brushes dominates the friction, and hence the μ value increases exponentially with increasing v, as was previously observed for the CPBs of PMMA and PS in toluene in a region beyond a certain v value. We previously studied the CPB of PS in a mixture of good/non-solvents, in which the degree of swelling of the brushes was controlled. We demonstrated that under the hydrodynamic-lubrication regime, the confronted polymer brushes still had some interaction and that the frictional property could be scaled by the degree of swelling. This is a new mechanism characteristic to the CPB, in contrast to the usual hydrodynamic lubrication forming a pure-solvent layer. It may be expected that the hydrodynamic lubrication will be affected by the viscosity and brush height concurrently. In order to test this assumption and also to clarify the mechanism of hydrodynamic lubrication for the CPB, we investigated the frictional property of the CPB of PMMA in ionic liquids (ILs) which have higher viscosities than typical organic solvents such as toluene.
Recently, ILs have attracted much attention as green solvents because of their characteristic properties such as nonvolatility, noncombustibility, wide solvent-temperature ranges, and electrochemical stability.14–16 ILs can dissolve various kinds of chemical additives, including some polymers, by suitably designing the molecular structure of anionic and cationic species.17–20 ILs usually have higher viscosities than general organic solvents of equivalent molecular weight because of enhanced intermolecular interaction.21–24 It has been reported that some organic solvents affect the clustering of IL molecules so much so that a dramatic decrease in the viscosity can be observed by the addition of a small amount of the solvent.25,26 In recent years, efforts have been made to employ ILs as lubricants especially at high temperatures and/or under vacuum.27–32 Under these conditions the evaporation of organic solvents is problematic. Hao et al. grafted IL-type polymers on carbon nanotubes to confirm their excellent friction-reducing and antiwearing properties as additives in IL lubricants.31 Takahara et al. also studied the friction of an IL-type polymer brush immersed in an IL solvent. They claimed that the high affinity of the brush component to the solvent led to a reduction in the interaction between the friction surfaces and hence a low μ.32
Fig. 1 shows the chemical structures of the ILs studied: N,N-diethyl-N-methyl-N-(2-methoxyethyl)ammonium bis(trifluoromethanesulfonyl)imide (DEME-TFSI) and 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide (EMI-TFSI). Here, we discuss their ability to solubilize the CPB of PMMA and also investigate the relationship between solvent viscosity and frictional data in hydrodynamic lubrication. This work should provide a guideline for novel designs of friction/lubrication-controlled materials by taking advantage of unique properties of the CPBs and ILs. The CPB can exhibit excellent lubrication in a good solvent.
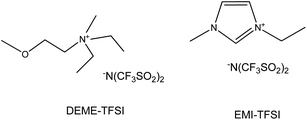 | ||
| Fig. 1 Chemical structures of DEME-TFSI and EMI-TFSI. | ||
Experimental section
Materials
Methyl methacrylate (MMA, 99%, Nacalai Tesque, Japan) was passed through a column of basic alumina to remove inhibitors. Cu(I)Cl (99.9%, Wako Pure Chemical, Japan), ethyl 2-bromoisobutylate (EBIB, 99%, Wako), 4,4′-dinonyl-2,2′-bipyridine (dNbipy, 97%, Sigma-Aldrich Co., USA), and hexamethyldisilazane (HMDS, Tokyo Chemical Industry Co., Ltd., Japan) were used as received. (2-Bromo-2-methyl)propionyloxyhexyltriethoxysilane (BHE) was prepared as previously reported.33 All other reagents were used as received from commercial sources.A silicon wafer (Ferrotec Corp., Japan, one side chemically/mechanically polished, a thickness of 525 μm) was cleaned by ultrasonication in CHCl3 for 15 min and ultraviolet (UV)/ozone-treatment for 10 min before fixation of BHE. A silica particle (SiP, HIPRESICA SP, diameter 10 μm,) was obtained from Ube Nitto Kasei Co., Ltd., and was used as a probe for the AFM measurement.
Synthesis of concentrated PMMA brushes via surface-initiated ATRP
Well-defined CPBs of PMMA were prepared by surface-initiated atom transfer radical polymerization (SI-ATRP), as previously reported. Briefly, a silicon wafer was immersed in an ethanol solution of BHE (1 wt%) and 28%-aqueous NH3 (5 wt%) for 12 h at room temperature and washed with ethanol. Thus obtained, BHE-immobilized silicon wafer was immersed in a degassed MMA (in bulk) containing EBIB (3 mM), Cu(I)Cl (16 mM), and dNbipy (37 mM), sealed under an argon atmosphere in a Schlenk flask, and heated at 70 °C for 2 h. EBIB was added as a free initiator not only to control the polymerization but also to yield free polymers which is a good measure of the molecular weights of graft polymers (see below).34,35 After polymerization, the solution was subjected to gel permeation chromatographic (GPC) measurements to determine the molecular weights of free polymer and monomer conversions. The PMMA-grafted silicon wafer was copiously rinsed and then washed by ultrasonication in CHCl3 to remove physisorbed free polymers and impurities. The dry thickness, Ld, of the PMMA-brush layer was determined using a spectroscopic ellipsometer (M-2000U, J.A. Woollam, Lincoln, NE). For the synthesis of the CPB of PMMA on a SiP, the same procedure was followed except that the SiP concentration maintained at ∼0.5 wt% for all steps. Table 1 lists the characteristics of the CPBs of PMMA studied in this paper. The number-average molecular weight, Mn, and the polydispersity index, Mw/Mn, are those of the free polymer analyzed by GPC calibrated with PMMA standards. It is reasonable to assume that these values should well approximate those of the graft chains.34,35 The graft density σ was calculated from Mn, Ld, the bulk density of a PMMA film ρ (=1.19 g cm−3),36 and the Avogadro constant NA, using σ = ρLdNA/Mn.| Substrate | M n | M w/Mn | L d/nm | σ/chains nm−2 |
|---|---|---|---|---|
| Wafer | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.24 | 41 | 0.52 |
| Probe | 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.21 | — | — |
Hydrophobic treatment of silicon wafer and SiP
Hydrophobic treatment of a silicon wafer was performed according to the method of Chen et al.:37 a silicon wafer was immersed in a mixture of HMDS (10 wt%) and toluene (90 wt%), heated at 110 °C for 5 h, and then rinsed with chloroform. The same treatment was applied to a SiP with a concentration as low as ∼0.3 wt%. After the treatment, the modified SiP was repeatedly washed with chloroform and stored in it prior to use.AFM force measurements
Normal and frictional forces were measured by an atomic force microscope (AFM) (JPK Instruments Inc., Germany, NanoWizard) equipped with a rectangular-shaped cantilever (Olympus Optical Co., Ltd., Japan, OMCL-RC800, normal spring constant, kn = 0.1 N m−1). The procedures are given in detail elsewhere13 and are described briefly as follows. A brush-modified or hydrophobized SiP was attached on the cantilever with a two-component epoxy resin adhesive. The normal and lateral displacements (Δz and Δx, respectively) of the cantilever were simultaneously monitored in approaching/retracting modes, while the substrate was slid back and forth in the horizontal plane normal to the cantilever by applying a triangular-wave oscillation on a piezo actuator via a function generator (Wave Factory 1945, NF Corp, Japan). The normal and frictional forces (Fn and Fs) were evaluated according to eqn (1) and (2), respectively:| Fn = knΔz | (1) |
| Fs = ksΔx | (2) |
| ks = GWT3/3L | (3) |
Other measurements
The viscosities of DEME-TFSI and EMI-TFSI (Table 2) were determined with a rheometer (Malvern Instruments, UK, CVOR 150) equipped with a temperature control unit (Malvern Instruments, Melts Oven) and a cone/plate geometry with a diameter of 25 mm. The viscosity of toluene was referred to in ref. 40 (0.6 mPa s at room temperature). GPC was carried out at 40 °C on a Shodex GPC-101 high-speed liquid chromatography system equipped with a guard column (Shodex GPC KF-G), two 30 cm mixed columns (Shodex GPC KF-804L, exclusion limit = 4 × 105), and a differential refractometer (Shodex RI-101). Tetrahydrofuran (THF) was used as an eluent at a flow rate of 0.8 mL min−1. PMMA standards were used to calibrate the GPC system. Ellipsometric measurements were made on a compensator rotating, spectroscopic ellipsometer (M-2000U, J.A. Woollam, Lincoln, NE) equipped with D2 and QTH lamps. The thickness of the dry PMMA-brush layer was calculated using the refractive index of PMMA in bulk (1.19 g cm−3).Results and discussion
The AFM measurement of the equilibrium thicknesses Le revealed that ILs could swell the CPB of PMMA to similar levels as when toluene, a good solvent for PMMA, is employed. The Le/Lc,w value reached about 60 ± 10% in all cases, where Lc,w is the contour chain length calculated from the Mw value. This suggests that the studied ILs are solvents of similar quality to toluene from the viewpoint of the similarity in their values for all the systems. Sufficiently good solvent-quality was also confirmed by Fig. 2, which shows the Fa value between the studied lubricating surfaces estimated from the retracting force profile in the AFM measurement. The CPB-modified surface gave little adhesion in all the solvents. This indicates that these solvents including the ILs are good enough to suppress the attractive interaction between polymer segments and that the graft density is high enough to effectively reduce the interpenetration between brushes, as was previously observed for SDPBs. In contrast, a value of Fa of 0.2–1.0 nN was detected between the hydrophobized silica surfaces (unmodified with the CPB) in DEME-TFSI and toluene. Any adhesive interaction will, of course, increase the friction to destroy the hydrodynamic lubrication layer and enter the boundary lubrication regime.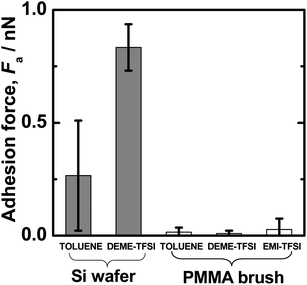 | ||
| Fig. 2 Adhesion forces Fa observed at 30 °C by AFM in the retracting mode between hydrophobized silica surfaces and between PMMA-brush surfaces in ILs and toluene. | ||
Fig. 3 and 4 illustrate the results of the properties of friction/lubrication in these three solvents. For the silica surfaces without brushes, the μ value increased with increasing Fn, approaching almost a constant value of ca. 0.1 in ILs and in toluene. It was assumed that at a low Fn, a lubricating layer of a solvent as a fluid was formed. This can be rationalized by the fact that the μ value at a lower Fn is dependent on v (as shown by the triangle symbol in Fig. 4a). Unfortunately, this lubricating layer was not maintained up to high Fn values because of high adhesive interactions. This breakdown caused the system shift to boundary lubrication. This regime of lubrication was characterized by Fs being approximately proportional to Fn and thus an almost constant value of μ (Amonton–Coulomb's law41) independent of v. Interestingly, approximately the same μ value was obtained both in toluene and DEME-TFSI, regardless of the differences in viscosity. This is due to the fact that the system is in the regime of boundary lubrication.
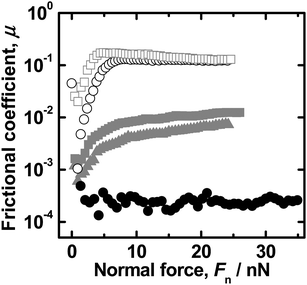 | ||
| Fig. 3 Plot of normal force Fnvs. frictional coefficient μ measured at 30 °C at a shear velocity v of 6 μm s−1 between the hydrophobized silica surfaces in DEME-TFSI (open squares) and toluene (open circles) and between the PMMA-brush surfaces in DEME-TFSI (gray filled squares), EMI-TFSI (gray filled triangles) and toluene (black filled circles). | ||
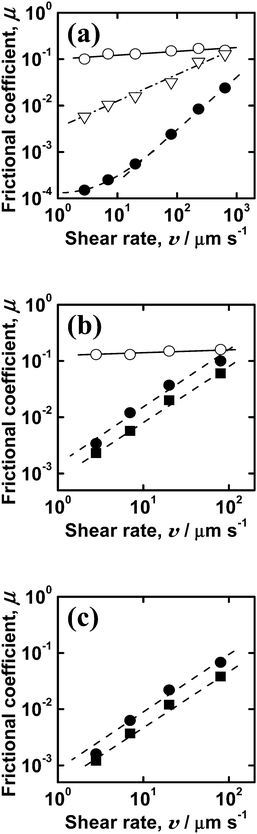 | ||
| Fig. 4 Plots of frictional coefficient μ vs. shear velocity v measured between the hydrophobized silica surfaces (open symbols) and between the PMMA-brush surfaces (closed symbols) in (a) toluene, (b) DEME-TFSI, and (c) EMI-TFSI. The temperature was 30 °C (circles and triangles) and 57 °C (squares), and the Fn value was 20 nN (circles) and 40 nN (squares) as a saturated value against v except for 2 nN (triangles). | ||
The addition of the CPB on the surfaces greatly improved the lubrication. As discussed previously,12 the CPB of PMMA showed a compression-independent super lubrication in toluene, which was described by two lubrication mechanisms: boundary lubrication giving μ values on the order of 10−4 (observed in a lower-v region) and hydrodynamic lubrication having v-dependent μ values. This is also the case even with ILs. As observed in the system without brushes, the μ value increased with increasing Fn, approaching a constant value. This may imply the formation of a solvent-lubricating layer between the two CPB-modified surfaces at a lower Fn region. However, it is difficult to unequivocally confirm this conclusion with the present data. Fig. 4 shows the μ data at Fn = 20 nN for 30 °C and at Fn = 40 nN for 57 °C (as almost saturated values) as a function of v. The v-dependency of μ indicates hydrodynamic lubrication. The suppression of attractive interactions effectively lowered the friction in the boundary lubrication, possibly to the same levels of μ as in toluene, allowing hydrodynamic lubrication to dominate.
The temperature had a slight impact on the frictional property in the two ILs. It should be noted that approximately the same slope of the line in Fig. 4 was obtained under all conditions, even though the μ value of the ILs was about 100 times greater than that in toluene. Here, we discuss the relationship between μ and v in hydrodynamic lubrication according to the following power-law equation generally expected for the viscosity-determining lubrication:
| μ = βvα | (4) |
| β = η/h | (5) |
The effect of solvent viscosity on friction was subsequently analyzed according to eqn (5). Fig. 5 plots β = μv−α (with α = 1 as discussed above) as a function of viscosity of the solvent in bulk. The parameter β can be interpreted as the local viscosity in a solvent-swollen brush layer. Good correlation was obtained between β and μ; the slope of the line in Fig. 5 is almost unity. This implies that the local viscosity of the brush layer is linearly related to the solvent viscosity. The viscosity of a liquid can be determined by the size of the molecules and the intermolecular interactions (leading to clustering of molecules in some cases). In a polymer solution especially of a dilute concentration, the viscosity is proportional to the solvent viscosity,43 unless a polymer segment affects the intermolecular interaction. From this point of view, the observed proportionality is a special case, presumably due to the solvent-swollen CPB possessing a highly stretched-chain conformation. The above-mentioned data do not show clustering to have a significant effect. The formation of a lubricating layer in concert with the solvent-swollen CPB layer in the IL system can be readily explained in terms of the hydrodynamic-lubrication mechanism.
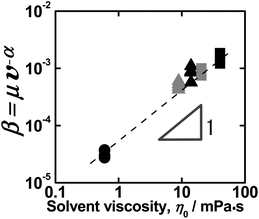 | ||
| Fig. 5 Plot of β parameter (=μv−α) vs.solvent viscosity η0 measured in toluene at 30 °C (black circles), DEME-TFSI at 30 °C (black squares) and 57 °C (black triangles), and EMI-TFSI at 30 °C (grey squares) and 57 °C (grey triangles). | ||
Conclusions
The AFM-microtribologic technique was used to investigate the frictional properties of the CPB of PMMA in highly viscous ILs (DEME-TFSI and EMI-TFSI) and toluene, which are all good solvents for PMMA. In the ILs, little adhesive interaction between the brush surfaces was observed (as was the case in toluene), which caused a dramatic decrease in the frictional coefficient μ in the boundary-lubrication regime to values less than 10−3. This decrease allowed the hydrodynamic-lubrication mechanism to dominate. In this regime, the v-dependence of μ followed power-law scaling with an α value close to unity. It was suggested that the thus produced lubricating layers should have similar thicknesses in toluene as well as ILs and that the frictional property could be simply related to the solvent viscosity. These friction/lubrication properties can be attributed to the unique features of the CPBs in a good solvent: the polymer chains are highly stretched due to high osmotic pressure. We have suggested that the local viscosity of the lubricating layer on or in the brushes is proportional to that of the solvent in bulk. Finally, we concluded that the addition of the CPB layer improved the friction even in ILs, where the hydrodynamically lubricating layer was successfully produced and maintained under all the conditions studied. The combination of ILs and CPBs may open up novel routes toward the control of lubrication in practical applications.Acknowledgements
This work was partly supported by a Grant-in-Aid for Scientific Research (grant-in-aid 17002007 and 21245031) from the Ministry of Education, Culture, Sports, Science, and Technology, Japan.Notes and references
-
Polymeric Stabilization of Colloidal Dispersions, ed. D. H. Napper, Academic Press, London, 1983 Search PubMed
.
- E. Raphael and P. G. Gennes, J. Phys. Chem., 1992, 96, 4002–4007 CrossRef CAS
.
- J. Klein, Annu. Rev. Mater. Sci., 1996, 26, 581–612 CrossRef CAS
.
- J. Klein and E. Kumacheva, Science, 1995, 269, 816–819 CAS
.
- R. C. Parnas and Y. Cohen, Rheol. Acta, 1994, 33, 485–505 CrossRef CAS
.
- S. Edmondson, V. L. Osborne and W. T. S. Huck, Chem. Soc. Rev., 2004, 33, 14–22 RSC
.
- Y. Tsujii, K. Ohno, S. Yamamoto, A. Goto and T. Fukuda, Adv. Polym. Sci., 2006, 197, 1–45 CAS
.
- R. Barbey, L. Lavanant, D. Paripovic, N. Schuwer, C. Sugnaux, S. Tugulu and H. A. Klok, Chem. Rev., 2009, 109, 5437–5527 CrossRef CAS
.
- M. Ejaz, S. Yamamoto, K. Ohno, Y. Tsujii and T. Fukuda, Macromolecules, 1998, 31, 5934–5936 CrossRef CAS
.
- S. Yamamoto, M. Ejaz, Y. Tsujii, M. Matsumoto and T. Fukuda, Macromolecules, 2000, 33, 5602–5607 CrossRef CAS
.
- S. Yamamoto, M. Ejaz, Y. Tsujii and T. Fukuda, Macromolecules, 2000, 33, 5608–5612 CrossRef CAS
.
- Y. Tsujii, A. Nomura, K. Okayasu, W. Gao, K. Ohno and T. Fukuda, J. Phys.: Conf. Ser., 2009, 184, 012031 CrossRef
.
- A. Nomura, K. Okayasu, K. Ohno, T. Fukuda and Y. Tsuji, Macromolecules, 2011, 44, 5013–5019 CrossRef CAS
.
- J. Dupont, R. F. de Souza and P. A. Z. Suarez, Chem. Rev., 2002, 102, 3667–3691 CrossRef CAS
.
-
Ionic Liquids, ed. B. Kirchner, Springer, Heidelberg, 2007 Search PubMed
.
-
M. Freemantle, An Introduction to Ionic Liquids, Royal Society of Chemistry, London, 2010 Search PubMed
.
- A. J. Carmichael, D. M. Haddleton, S. F. A. Bon and K. R. Seddon, Chem. Commun., 2000, 14, 1237–1238 RSC
.
- T. Biedron and P. Kubisa, Macromol. Rapid Commun., 2001, 22, 1237–1242 CrossRef CAS
.
- P. Kubisa, Prog. Polym. Sci., 2004, 29, 3–12 CrossRef CAS
.
- M. A. Susan, T. Kaneko, A. Noda and M. Watanabe, J. Am. Chem. Soc., 2005, 127, 4976–4983 CrossRef CAS
.
- W. R. Carper, J. L. Pflug, A. M. Elias and J. S. Wilkes, J. Phys. Chem., 1992, 96, 3828–3833 CrossRef CAS
.
- J. Fuller, R. T. Carlin, H. C. Delong and D. Haworth, Chem. Commun., 1994, 3, 299–300 RSC
.
- A. Elaiwi, P. B. Hitchcock, K. R. Seddon, N. Srinivasan, Y. M. Tan, T. Welton and J. A. Zora, J. Chem. Soc., Dalton Trans., 1995, 2, 3467–3472 RSC
.
- P. A. Z. Suarez, S. Einloft, J. E. L. Dullius, R. F. Souza and J. Dupont, J. Chim. Phys. Phys.-Chim. Biol., 1998, 95, 1626–1639 CrossRef CAS
.
- K. R. Seddon, A. Stark and M. J. Torres, Pure Appl. Chem., 2000, 72, 2275–2287 CrossRef CAS
.
- J. G. Huddleston, A. E. Visser, W. M. Reichert, H. D. Willauer, G. A. Broker and R. D. Rogers, Green Chem., 2001, 3, 156–164 RSC
.
- H. Z. Wang, Q. M. Lu, W. M. Ye and Z. J. Cui, Wear, 2004, 256, 44–48 CrossRef CAS
.
- H. Kamimura, T. Kubo, I. Minami and S. Mori, Tribol. Int., 2007, 40, 620–625 CrossRef CAS
.
- J. Sanes, F. J. Carrion, M. D. Bermudez and G. M. Nicolas, Tribol. Lett., 2006, 21, 121–123 CrossRef CAS
.
- B. Bhushan, M. Palacio and B. Kinzig, J. Colloid Interface Sci., 2008, 317, 275–287 CrossRef CAS
.
- X. W. Pei, Y. Q. Xia, W. M. Liu, B. Yu and J. C. Hao, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 7225–7237 CrossRef
.
- T. Ishikawa, M. Kobayashi and A. Takahara, ACS Appl. Mater. Interfaces, 2010, 2, 1120–1128 CAS
.
- K. Ohono, T. Morinaga, K. Koh, Y. Tsujii and T. Fukuda, Macromolecules, 2005, 38, 2137–2142 CrossRef
.
- Y. Tsujii, M. Ejaz, K. Sato, A. Goto and T. Fukuda, Macromolecules, 2001, 34, 8872–8878 CrossRef CAS
.
- T. Morinaga, M. Ohkura, K. Ohno, Y. Tsujii and T. Fukuda, Macromolecules, 2007, 40, 1159–1164 CrossRef CAS
.
-
W. Wunderlich, in Polymer Handbook, ed. J. Brandrup, E. H. Immergut and E. A. Grulke, John Wiley & Sons Inc, New York, 4th edn, 1999, ch. 5, pp. 87–90 Search PubMed
.
- Y. K. Chen, K. C. Chang, K. Y. Wu, Y. L. Tsai, J. S. Lu and H. Chen, Appl. Surf. Sci., 2009, 255, 8634–8642 CrossRef CAS
.
- G. Meyer and N. M. Amer, Appl. Phys. Lett., 1990, 57, 2089–2091 CrossRef CAS
.
- C. P. Green, H. Lioe, J. P. Cleveland, R. Proksch, P. Mulvaney and J. E. Sader, Rev. Sci. Instrum., 2004, 75, 1988–1996 CrossRef CAS
.
- F. Santos, C. de Castro, J. Dymond, N. Dalaouti, M. Assael and A. Nagashima, J. Phys. Chem. Ref. Data, 2006, 35, 1–8 CrossRef CAS
.
- G. Amonton, Mem. del'Academie Royale A, 1699, 275–282 Search PubMed
.
-
H. A. Barnes, J. F. Hutton and K. Walters, An Introduction to Rheology, Elsevier, Amsterdam, 1989, ch. 1, pp. 1–10 Search PubMed
.
-
P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 9th edn, 2010, ch. 18, pp. 659–694 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2012 |
