A site energy distribution function for the characterization of the continuous distribution of binding sites for gases on a heterogeneous surface†
K. Vasanth
Kumar
*,
A. Maria
Silvestre-Albero
and
F.
Rodriguez-Reinoso
Laboratorio de Materiales Avanzados, Departamento de Química Inorgánica, Universidad de Alicante, Apartado 99, 030080, Alicante, Spain. E-mail: vasanth@ua.es
First published on 21st November 2011
Abstract
A binding site energy distribution function for a Jensen-Seaton isotherm and its limiting cases was proposed and successfully applied to the adsorption of several gas molecules on different essentially microporous carbons. According to the proposed model the studied carbon materials exhibit two energetic states where the site energy is exponentially or unimodaly distributed depending on the adsorption pressure. Carbons with a larger contribution from micropores seem to be in general more heterogeneous, with a wider binding site energy distribution, than less microporous carbons.
High pressure adsorption of supercritical gases has received much attention in recent years due to applications that include storage of hydrogen and natural gas on porous materials. In spite of the importance of this process, the fundamentals are not well understood as most of the existing theoretical isotherms such as Langmuir, Freundlich, Toth, etc., that were derived for adsorption on vacant sites, do not consider the gas compressibility in micropores at high pressure.1 Considering the limitations of the existing theoretical isotherms, Jensen and Seaton1 proposed a useful empirical equation for type I adsorption isotherms in microporous solids which accounts for the compressibility of the adsorbed phase.
Several researchers had shown that the JS isotherm is more adequate than Langmuir or Toth isotherms at high pressure.2–4 On the other hand, a site energy distribution function for the JS isotherm is important since this isotherm considers both the compressibility of the gas (at higher pressure) and the binding site heterogeneity.
Furthermore, such a function would implicitly reflect the underlying thermodynamic assumptions of this isotherm that have not been discussed previously. We have already developed a series of site energy distribution functions based on different theoretical isotherms.5–9 In this work we propose a new mathematical function based on the JS isotherm that could identify simultaneously the heterogeneity of the adsorbent and also the affinity of the binding sites for the gas molecules of interest. To the best of our knowledge no site energy distribution functions are available for adsorption systems following this isotherm, which is flexible with four parameters and can accurately represent most of the experimental equilibrium data at both low and high pressures. A successful attempt is made in this study to propose a site energy distribution of an adsorbent following the JS isotherm, based on a site energy distribution function defined by a condensation approximation method. The proposed model is used to determine the site energy distribution of BPL activated carbon for the supercritical adsorption of ethane at high pressure and two more activated carbons obtained in our laboratory for N2 molecules at 77 K (the boiling point of N2).
The Jensen and Seaton1 adsorption isotherm involving four isotherm parameters is given by:
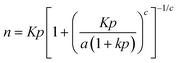
| (1) |
Eqn (1) is based on a function that interpolates between two asymptotes, Henry's low pressure and an asymptote reflecting the compressibility at high pressure given by:1
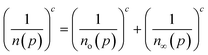 | (2) |
The site energy distribution of an adsorbent can be easily determined from the theoretical isotherm by solving the adsorption integral (eqn (3)) to generate the corresponding affinity distribution:10
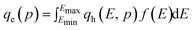 | (3) |
Eqn (3) assumes the adsorption of gas molecules, qe, by a heterogeneous surface to be the integral of an energetically homogeneous isotherm (qh) multiplied by a site energy frequency distribution, f(E). Emin and Emax are the energy limits that are directly related to the maximum and minimum pressure in the adsorption isotherm. Eqn (3), the Fredholm integral equation of first kind, is difficult to solve and it has no general analytical solution. Considering the importance of this expression, several approximate solutions have been developed and are described elsewhere.11 The condensation approximation method, developed by Cerofolini12 and further developed or applied by Rudzinski and Everett,11 and Jaroniec13 for different adsorption systems is used in this study. This method was successfully applied recently to predict the distribution of binding site energies of different adsorbents for different target molecules following different theoretical isotherms with three to five isotherm parameters.5–10 According to the condensation approximation method the true kernel is replaced by a condensation isotherm; in the present study this corresponds to the JS isotherm. This method defines the site energy distribution function directly from the isotherm equation applied and, thus, the range of pressure used in the experimental isotherm controls the energy distribution. The area under the distribution curve is controlled by the maximum adsorption capacity and the spread of the distribution is controlled by the heterogeneity factor. The equilibrium pressure can be related to the energy of adsorption using the Polanyi potential theory given by:10
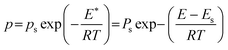
| (4) |
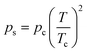 | (5) |
Incorporation of eqn (4) into eqn (3) will lead to an approximate site energy distribution, f(E*), which is the differentiation of the isotherm, q(E*), with respect to E*:10
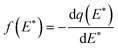 | (6) |
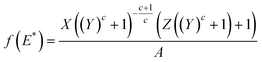 | (7) |
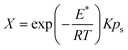 | (8) |
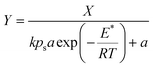 | (9) |
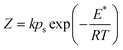 | (10) |
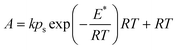 | (11) |
In order to show the applicability of the proposed energy distribution function, the site energy distribution of BPL activated carbon for ethane at 212.7 K is described here. The isotherm constants were obtained from the work of Jensen and Seaton.1 Since the site energy distribution function proposed in this study needs the value of ps, the expression of Ozawa et al.14 (eqn (5)) was used for theoretical convenience to determine this value at the temperature used and the approximate value was estimated to be 23.7 bar at 212.7 K. The isotherm parameters and the empirically determined saturation vapor pressure are substituted in eqn (7) to predict the site energy distribution of the studied activated carbon, as shown in Fig. 1. Although the site energy distribution function (eqn (7)) has no mathematical restrictions, this equation will produce negative energy values when E < Es. Further, since the isotherm parameters that were used to obtain f(E) are sensitive to the pressure range studied, only the energy distribution curve within the range of pressures used in the experimental isotherm can be considered valid. Thus, no attempts should be made to extrapolate over the pressure range in the experimental isotherm. Thus, the limits E*max and E*min (see eqn (4)) in a site energy distribution curve correspond to RTln(pmin/ps) and RTln(pmax/ps). The terms pmin and pmax should be the lowest and highest pressures in the experimental isotherm. Fig. 1 shows the energy distribution according to the JS isotherm ranging from 19.1 to 4.6 kJ mol−1, that corresponds to the pressure range 0.01–3.53 bar in the experimental isotherm. The experimental isotherm is not shown in this work as it was described elsewhere.1Fig. 1 shows that, according to the JS isotherm, the site energy is exponentially and unimodally distributed over the energy range E* < 6747 J mol−1 and 6747 < E* < 19133 J mol−1, respectively. It can be further observed from Fig. 1, that the unimodal site energy distribution is characterized by two energetic sites: (i) an unimodal peak corresponding to low-energy binding sites (6747 < E* < 12157 J mol−1) and (ii) an asymptotically decaying region corresponding to high-energy binding sites (12157 < E* < 19133 J mol−1). This observation suggests that BPL activated carbon has more than one energetic state for the uptake of ethane molecules within the studied pressure range. The exponential site energy distribution corresponds to sites with lower binding energy that are accessible to the adsorbing molecules only at higher pressure. The complexity in the spread of site energy distribution is expected in such an adsorbent due to the presence of pores of different size and depth within a heterogeneous surface. The shape of the energy distribution curve can also be related to the mathematical structure of the JS isotherm, which looks like a hybrid expression due to the addition of an exponential isotherm to a heterogeneous isotherm. From the concepts of thermodynamics, any isotherm with such a mathematical structure should typically exhibit two different energy states (as in the present case): exponential and quasi-Gaussian distributions at low and high pressure, respectively.
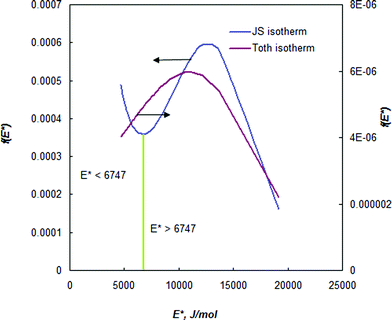 | ||
| Fig. 1 Binding-site energy distribution of BPL carbon for ethane at 212.7 K. | ||
The proposed model was further applied to estimate the site energy distributions of two established activated carbons AC0 and AC60 developed in our laboratory by chemical activation using olive stones as a precursor for N2 gas molecules at 77 K. We have already estimated the distributions of the binding site energies in these carbon adsorbents using a Sips isotherm.8 We estimate here the f(E*) according to the JS isotherm and compare it with the distribution estimated using a Sips isotherm. The detailed physicochemical characteristics of these adsorbents are not presented here and readers are suggested to refer to the detailed work of Silvestre-Albero et al.15 However, we would like to mention here that the sample AC60 was obtained by the physical activation of AC0 with CO2 (100 cm3 min−1) at 1098 K for a time period of 60 h. The experimental equilibrium data of N2 adsorption at 77 K were fitted to the JS isotherm by a non-linear regression analysis. The non-linear regression analysis involves a trial and error method that involves a process of minimizing the error distribution between the experimental data and the JS isotherm.
The error minimization was done by maximizing the coefficient of determination, r2, using Solver, add-in, Microsoft Spreadsheet, Microsoft Excel, Microsoft corporation. Fig. 2, shows the experimental data and the fitted JS isotherm for the adsorption of N2 by AC0 and AC60. Fig. 2 also includes the fitted isotherm parameters and the r2 values and it shows that the experimental data are well represented by the JS isotherm, with r2 values > 0.97. This indicates that the JS isotherm can be reasonably used to describe the characteristic adsorption behavior of N2 molecules in the studied materials at 77 K. Thus, the JS isotherm can reliably generate the energy distribution spectra of these adsorbents in the studied pressure and temperature ranges.
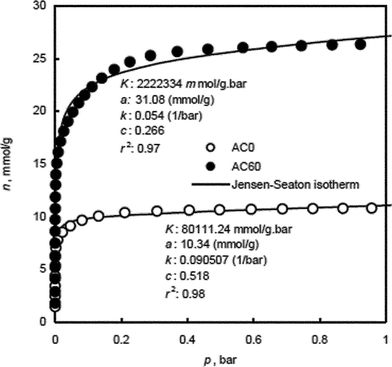 | ||
| Fig. 2 Experimental and Jensen–Seaton isotherms for N2 adsorption by activated carbons, AC0 and AC60. | ||
The determined JS isotherm parameters were used to determine the binding site energy distributions of the carbons AC0 and AC60 using eqn (7) and these are shown in Fig. 3. It can be realized from eqn (7) that this expression does not have any mathematical restrictions for the binding site energy values. However, this expression will predict negative energy values that do not have any physical meaning for the conditions E* < Es. Thus, it is important to mention that any site energy distribution curve obtained using eqn (7) is valid only for the range of pressures in the adsorption isotherm. Thus, the site energy distribution spectra shown in Fig. 3 cover only the range of pressures studied in the isotherm. The highest binding site energy corresponds to the amount adsorbed at the lowest pressure measured experimentally. Fig. 3 shows that the site energy in carbon AC60 is exponentially and unimodally distributed over the energy range E* < 1000 J mol−1 and 1000 < E* < 6000 J mol−1, respectively. It can be further observed from Fig. 3 that in carbon AC60 the unimodal site energy distribution is characterized by two energetic sites: (i) an unimodal peak corresponding to low-energy binding sites (3966 < E* < 6376 J mol−1) and (ii) an asymptotically decaying region corresponding to high-energy binding sites (1000 < E* < 3966 J mol−1). The exponentially decaying (3966–6376 J mol−1 in AC60) portion corresponds to the low pressure region of the experimental isotherm, where the high affinity binding sites are preferentially sampled. In this region the isotherm is far away from saturation and usually a Henry or Freundlich isotherm can reliably predict the actual binding process.
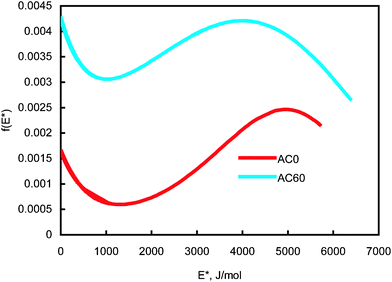 | ||
| Fig. 3 Binding-site energy distributions of activated carbons AC0 and AC60 for N2 molecules at 77 K. | ||
In the case of carbon AC0 we noticed a similar site energy spectrum; however, the affinity of both high and low energy binding sites for N2 molecules in AC60 is significantly higher than the reference carbon AC0. A comparison of this unimodal region for AC60 and AC0 clearly indicates that carbon AC0 has a widened left hand side, indicating that most of the adsorption sites have energies lower than a statistical mean value. In the case of carbon AC60 we noticed that the binding site energies are unimodal and widely distributed between 1000–6376 J mol−1. This implies that the activation process significantly increased the binding affinity of sites with higher energies and the mean binding affinity of the adsorption sites for N2 molecules.
All these observations obviously indicate that both of these carbons have two different energetic states for the adsorption of N2 molecules at 77 K. Apart from this trend, the main difference appears to be that the carbon AC60, with well developed microporosity, is more heterogeneous than AC0, as measured by the value of the heterogeneity index (c). The greater heterogeneity in fact increases the affinity of both low and high energy binding sites. This obviously indicates that the heterogeneity is a characteristic feature of the activation process rather of than the carbon material itself.
In our earlier experimental work15 we noticed that the physical activation of AC0 altered the porous structure, with an increase in micropore volume. The increase in pore volume was attributed to the simultaneous opening of new pores and deepening of the existing ones. The experimentally observed facts could be deduced from the site energy spectrum of carbonAC60, which is wide when compared to carbon AC0. Thus, the shape and intensity of the site energy spectra can be used to estimate quantitatively the opening and deepening of pores during the activation process.
The shape and intensity of the site energy distribution curve will vary depending on the isotherm model applied. Our earlier theoretical study based on a Sips isotherm8 implies that the binding site energies in the studied activated carbons AC0 and AC60 were unimodally distributed instead of showing two different energetic states as in the present case with the JS isotherm. This is not a surprising observation since the site energy distribution spectra obtained by any of the isotherm models are unique and will represent the basic thermodynamic assumption of the model. In the case of the Freundlich isotherm this corresponds to an exponential distribution of binding sites, whereas in the case of the Toth isotherm, this corresponds to a quasi-Gaussian distribution. Selection of binding model is primarily based on its ability to accurately reproduce the experimental isotherms. The accuracy of the theoretical isotherm in representing the experimental equilibrium data can be easily determined from the error functions used to minimize the error distribution between the experimental and theoretical isotherms. In this study we assume that the JS isotherm could represent the experimental data, which is further confirmed by the relatively higher r2 value that measures the difference in errors minimized between experimental data and the JS isotherm.
It is important to point out that the JS isotherm can be reduced to Langmuir and Toth isotherms upon applying the limiting conditions of these isotherms: (i) k = 0 and c = 1 and (ii) k = 0, respectively. For the first limiting condition, eqn (1) reduces to a Langmuir isotherm given by:
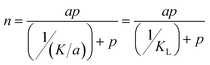 | (12) |
Then by the theory (of the Langmuir isotherm), the constant a represents the number of binding sites with binding affinity KL. The binding affinity KL can be used to determine the approximate energy of the binding sites using the expression: KL = exp(−Eads/RT). For example: in the case of the adsorption of ethane by BPL activated carbon at 212.7 K, the isotherm parameters K and a were found to be 267.86 mmol g−1.bar and 6.610 mmol g−1, respectively.1 Thus, the binding affinity, KL can be determined using the expression: KL = K/a as 0.0247 bar−1. From the binding affinity value, the approximate energy of the binding site can be determined as: −Eads = ln(KL)/RT = 6546 J mol−1.bar. The site energy of the BPL activated carbon for ethane molecules was predicted in this work using the Langmuir isotherm only for demonstration purposes and thus, the value predicted should not be considered real as the assumption of a homogeneous surface for an activated carbon with different pores of different shape and depth is meaningless. A more realistic model such as given by the JS or Toth isotherms that can explain the site heterogeneity should be considered.
For the second limiting condition, the site energy distribution function can be obtained by applying the conditions: k = 0 and p = psexp(−E*/RT) in eqn (1) and differentiating the resulting expression with respect to E*:
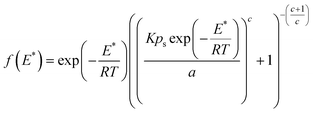
| (13) |
To demonstrate the applicability of eqn (13), the Toth isotherm parameters for the ethane/BPL activated carbon system were fitted to this expression to obtain the corresponding site energy distribution as shown in Fig. 1. The isotherm constants were obtained from the work of Jensen and Seaton.1 According to eqn (13) (which is based on a Toth isotherm), the site energies are distributed unimodally within the pressure range considered, which is different to the curve predicted by the site energy distribution function based on the JS isotherm. The differences in site energy distribution are expected as they implicitly reflect the basic thermodynamic assumptions of both models. In the case of the Toth isotherm, the distribution of site energy follows a quasi-Gaussian curve with a widened left hand side, thus indicating that most of the adsorption sites have an energy lower than a statistical mean value, which was the assumption of this isotherm model. It is worth noting that the shape and intensity of the site energy distribution curve calculated using the condensation approximation method will vary depending on the isotherm applied. In the present case, in addition to the difference in the shape of the site energy distribution curve, the intensity of the site energy determined by Toth and JS isotherms also differs by a magnitude of 102. As mentioned earlier, the complexities in using theoretical isotherms in predicting the binding site energy can be eliminated by selecting a particular binding model based on its reliability to predict the affinities of the binding sites for a particular gas molecule.16 In the present case, the site energy distribution predicted using the JS isotherm can be assumed to represent the actual site energy distributions considering the relatively better fit of this isotherm with respect to the Toth isotherm, especially at high pressure. The JS isotherm fits the experimental data better than the Toth isotherm due to its flexibility, with an additional parameter b to represent experimental equilibrium data at both low and high pressure.
In summary, we confirmed that the proposed site energy distribution function based on the JS and its limiting case isotherms can predict the different energetic states of microporous carbon materials for any gas molecule of interest. For practical applications the proposed models based on the JS or Toth isotherms can be useful as they can rapidly generate the site energy distribution curves without using any complicated or sophisticated computer programs that may be difficult for most users. The present study clearly indicates that the JS isotherm and its limiting case isotherms can be used as a tool in determining the binding site energy distributions of any porous materials that may differ by physicochemical characteristics. Thus these proposed models can complement any adsorption system to characterize both heterogeneity and the binding site energies of the adsorbent and they only need the isotherm parameters that can be obtained by a simple regression analysis.
The binding site energy is conventionally estimated by a single-site or multiple-site Langmuir isotherm. In the former we need to assume that there is only one type of binding site with equal affinity, but this does not seem to be practically correct as it ignores the heterogeneity of binding sites, especially for the case of heterogeneous materials such as activated carbons. On the other hand, a multiple-site Langmuir model that assumes more than one site appears to be an empirical approach and it needs human assumption while deciding the number of binding sites from the experimental isotherm. The JS and its limiting case isotherm can serve as an alternative to these conventional approaches since they assume a continuous distribution of binding sites rather than discrete. In addition, since the intensity and shape of binding energy spectra obtained by this mathematical function are sensitive to the heterogeneity and the pressure, they will allow us to measure quantitatively the extent of heterogeneity and the affinity of binding sites for target molecules in the pressure and temperature ranges of interest. This will directly allow us to compare the performance of different adsorbents with different physicochemical characteristics and to obtain a rational optimization of the activation process with improved binding characteristics for a given gas molecule. In this work, as a case study, we demonstrated the applicability of the JS isotherm in characterizing the heterogeneity of carbon based materials, nevertheless, the applicability of the proposed mathematical function is not limited only for this purpose. It can serve as an excellent tool for characterizing molecularly imprinted polymers, molecular organic frameworks, etc. In the field of catalysis, such tools are desperately required where the reactions are highly dependent on the heterogeneity of the catalyst surface.17 Measuring the heterogeneity of the adsorbent will also play an important role in screening adsorbents for energy storage applications.18–19
Acknowledgements
Support from the Ministerio de Ciencia e Innovacion (Project PLE2009-0052) and the Genaralitat Valenciana (Project PROMETEO/2009/002-FEDER) are acknowledged. KVK would like to thank the Ministerio de Ciencia e Innovacion for the Juan de la Cierva contract. ASA acknowledges a PhD fellowship from MEC, Spain.References
- C. R. C. Jensen and N. A. Seaton, Langmuir, 1996, 12, 2866–2867 CrossRef CAS.
- A. Goj, D. S. Sholl, E. D. Akten and D. Kohen, J. Phys. Chem. B, 2002, 106, 8367–8375 CrossRef CAS.
- M. Heuchel, R. Q. Snurr and E. Buss, Langmuir, 1997, 13, 6795–6804 CrossRef CAS.
- Y. He, J.-H. Yun and N. A. Seaton, Langmuir, 2004, 20, 6668–6678 CrossRef CAS.
- K. V. Kumar, M. Monteiro de Castro, M. Martinez-Escandell, M. Molina-Sabio, J. Silvestre-Albero and F. Rodriguez-Reinoso, Chem. Phys. Lett., 2010, 492, 187–192 CrossRef.
- K. V. Kumar, M. C. M. de Castro, M. Martinez-Escandell, M. Molina-Sabio and F. Rodriguez-Reinoso, J. Phys. Chem. C, 2010, 114, 13759–13765 CAS.
- K. V. Kumar, M. C. M. de Castro, M. Martinez-Escandell, M. Molina-Sabio and F. Rodriguez-Reinoso, Phys. Chem. Chem. Phys., 2011, 13, 5753–5759 RSC.
- K. V. Kumar, J. C. Serrano-Ruiz, H. K. S. Souza, A. M. Silvestre-Albero and V. K. Gupta, J. Chem. Eng. Data, 2011, 56, 2218–2224 CrossRef CAS.
- K.V. Kumar, M. C. M. de Castro, M. Martinez-Escandell, M. Molina-Sabio and F. Rodriguez-Reinoso, ChemPhysChem, 2010, 11, 2555–2560 CrossRef CAS.
- M. C. Carter and J. E. Kilduff, Environ. Sci. Technol., 1995, 29, 1773–1780 CrossRef CAS.
- W. Rudzinski and D. H. Everett, Adsorption of Gases on Heterogeneous Surfaces, Academic Press Ltd., London, UK, 1992 Search PubMed.
- G. F. Cerofolini, Thin Solid Films, 1975, 26, 53–59 CrossRef.
- M. Jaroniec, Surf. Sci., 1975, 50, 553–564 CrossRef CAS.
- S. Ozawa, S. Kusumi and Y. J. Ogino, J. Colloid Interface Sci., 1976, 56(1), 83–91 CrossRef CAS.
- A. Silvestre-Albero, J. Silvestre-Albero, A. Sepúlveda-Escribano and F. Rodríguez-Reinoso, Microporous Mesoporous Mater., 2008, 115, 603–608 CrossRef.
- R. J. Umpleby, S. C. Baxter, A. M. Rampey, G. T. Rushton, Y. Chen and K. D. Shimizu, Characterization of the heterogeneous binding site affinity distributions in molecularly imprinted polymers, J. Chromatogr., B: Anal. Technol. Biomed. Life Sci., 2004, 804, 141–149 CrossRef CAS.
- A. Borodziński and A. Gołębiowski, Langmuir, 1997, 13, 883–887 CrossRef.
- J. Llorens and M. Pera-Titus, Colloids Surf., A, 2009, 350, 63–72 CrossRef CAS.
- K. V. Kumar, M. C. Monteiro de Castro, M. Martinez-Escandell, M. Molina-Sabio and F. Rodriguez-Reinoso, Chem. Eng. J., 2011, 168, 972–978 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The complete derivation of the site energy distribution function based on the Jensen-Seaton isotherm. See DOI: 10.1039/c1ra00564b |
| This journal is © The Royal Society of Chemistry 2012 |
