Dynamic recovery in silicate-apatite structures under irradiation and implications for long-term immobilization of actinides

Abstract

The irradiation responses of Ca₂La₈(SiO₄)₆O₂ and Sr₂Nd₈(SiO₄)₆O₂ with the apatite structure are investigated to predict their long-term behaviour as host phases for immobilization of actinide elements from the nuclear fuel cycle. Different ions and energies are used to study the effects of dose, temperature, atomic displacement rate and ionization rate on irradiation-induced amorphization and recrystallization. The dose for amorphization increases with temperature in two stages, below and above 150 K. In the high temperature stage relevant to actinide immobilization, the increase of amorphization dose with temperature exhibits a strong dependence on the ratio of ionization rate to displacement rate for the different ions. Data analysis using a dynamic model for amorphization reveals that ionization-induced processes, with activation energy of 0.15 ± 0.02 eV, dominate dynamic recovery for ions from Ne through Xe. For heavier Au ions or for alpha-recoil nuclei emitted in alpha decay of actinides, ionization becomes less dominant and dynamic recovery is controlled primarily by thermally-driven processes. In post-irradiation annealing studies of amorphous samples, epitaxial thermal recrystallization is observed at 1123 K, and irradiation-enhanced nucleation of nanocrystallites is observed under irradiation with heavier ions. The recrystallization temperature under irradiation decreases with increasing ion mass to a value of ∼823 K, which also defines the thermally-driven critical temperature for amorphization under irradiation with heavy ions. Some partial recovery due to alpha particle irradiation at 300 K is observed that suggests a self-healing mechanism in apatite phases containing actinides. Based on the results and dynamic model, the temperature and time dependences of amorphization in silicate-apatite host phases for actinide immobilization are predicted.

---

Introduction

Irradiation-induced amorphization (the transition from a crystalline to an aperiodic or amorphous state) is one of the more technologically relevant phase transitions under extreme environments that has long intrigued scientists. The crystalline-to-amorphous transition in natural (metamict) minerals as a result of alpha decay of trace quantities of U and Th has been a subject of investigation by mineralogists for over a century.¹ Systematic studies of ion-beam-induced amorphization in Si over several decades have led to significant scientific breakthroughs and to development of the technology associated with modern ion-beam processing of semiconductor devices.² The increased development and deployment of advanced ceramics have generated fundamental and technological interest in the irradiation-induced crystalline-to-amorphous transition in ceramic materials and related minerals. Understanding and modelling the processes of irradiation damage and recovery in ceramics and minerals is essential to: 1) the use and reliability of advanced ceramics in nuclear fission and fusion power applications, including the nuclear fuel cycle; 2) the safe immobilization of high-level nuclear wastes (HLW), plutonium, and other actinides; 3) the modification and tailoring of ceramic structures, compositions and properties by energetic ion beams; and 4) geologic age-dating and thermochronology. While irradiation-induced amorphization has been investigated in many different complex oxide structures and compositions,^3-11 the exact nature of the amorphization process is not well defined for most ceramics, and numerous models^12–26 have been developed to explain various aspects of the amorphization process. In general, amorphization in ceramics occurs homogeneously or heterogeneously, becomes more difficult with increasing temperature, and occurs only below a critical temperature where the rate of recovery or recrystallization equals the amorphization rate.^3,24 This critical temperature has been observed to depend on ion mass and dose rate in silicon,^13,18 intermetallic compounds,^27,28silicon carbide,^29,30 and complex oxides.^4,11,20,31

Natural apatites, Ca₁₀(PO₄)₆(OH,Cl,F)₂, are the most abundant of the phosphate minerals³² and are often used for age dating because of incorporated uranium. The durability of natural apatites is well demonstrated by apatites from the Oklo natural reactor site in the Republic of Gabon, Africa; these apatites have retained significant ²³⁵U enrichment³³ and high fission-product concentrations in their structure,^33,34 despite exposure to self-radiation damage and the geologic environment for nearly 2 billion years. Rare-earth phosphate-silicate phases with structures analogous to natural apatite have been observed in glass-ceramic waste forms³⁵ and as recrystallized alteration products on the surfaces of HLW glasses as a result of aqueous corrosion.^36,37 The latter data indicate the inherent stability of these apatite phases relative to HLW glasses.³⁵ Rare-earth silicates with the apatite structure also have been observed as actinide host phases in a devitrified borosilicate HLW glass,³⁸ a multiphase ceramic waste form,³⁹ a glass-ceramic waste form,⁴⁰ and a cement waste form.⁴¹ These particular apatite-structured phases, which are also related to britholite minerals, are generally of the composition, Ca_4-xRE₆₊x(SiO₄)_6-y(PO₄)_y(F,OH,O)₂ (where RE = La, Ce, Pr, Nd, Pm, Sm, Eu, and Gd).

The long-term immobilization of actinide elements from past and future processing of used nuclear fuel requires geologically stable host phases whose performance and response to self-radiation damage can be predicted with some degree of reliability for thousands to hundreds of thousands of years or more. Due to its chemical durability in geologic environments and ability to accommodate a number of chemical elements, apatite structures have attracted considerable attention as host phases for the immobilization of transuranic actinides (Np, Pu, Am, Cm) and high-actinide nuclear waste,^33,42–46 and they have also been of interest as host phase for fission products, such as Cs.⁴⁷ Such apatite structures with incorporated actinides will be subject to collisional and ionizing irradiation from the radioactive decay of the radionuclides, and this may lead to changes of microstructure and the degradation of the chemical durability, which can affect the performance of apatite-based waste forms for actinide immobilization. Valid models of long-term behaviour must, by necessity, be developed based on accelerated irradiation testing over laboratory time scales using short-lived actinides, such as ²³⁸Pu or ²⁴⁴Cm, or ion irradiation methods.³

One of the earliest studies of the irradiation-induced crystalline-to-amorphous transition in apatite structures was initiated over 30 years ago on polycrystalline Ca₂Nd₈(SiO₄)₆O₂ doped with 1.24 wt% ²⁴⁴Cm.^48–52 In this silicate apatite, amorphization under ambient conditions appears to occur directly within the collision cascade of the ²⁴⁰Pu recoil nucleus emitted during alpha decay of ²⁴⁴Cm. The fully amorphous state is reached at a dose of 2.6 × 10¹⁸ alpha-decays/g,⁵² which is equivalent to an atomic displacement dose of about 0.12 dpa (displacements per atom). This crystalline-to-amorphous transformation is accompanied by a 9.4% increase in macroscopic volume,⁵² an order of magnitude increase in aqueous dissolution rate,⁴⁹ and increases in fracture toughness.⁵⁰ Thermal recrystallization of the fully amorphous state in this Cm-containing Ca₂Nd₈(SiO₄)₆O₂ occurs in a single recovery stage with an activation energy of 3.1 ± 0.2 eV.⁴⁹ In another study of polycrystalline Ca₂Nd₈(SiO₄)₆O₂,⁵³ irradiation with 3 MeV Ar⁺ ions at about 473 K to a dose exceeding 10 dpa resulted in saturation swelling of about 1.5% due to defect accumulation, but no evidence for amorphization was observed. Post-irradiation annealing of the Ar-irradiated samples revealed a defect recovery stage at about 623 K with an activation energy of 1.3 ± 0.1 eV. In order to understand this behaviour and contribute to the basic understanding of irradiation-induced phase instability and amorphization in silicate apatites and other complex ceramics, a systematic study of ion-irradiation-induced amorphization in single crystals of Ca₂La₈(SiO₄)₆O₂ and Sr₂Nd₈(SiO₄)₆O₂ was undertaken to investigate the dependence of amorphization on dose, temperature, ion mass and energy. Based on advances in understanding and models in recent years, this paper provides new data and broader interpretation of previous results^20,54 that leads to a more comprehensive understanding of the role of ionization on the crystalline-to-amorphous transition in silicate-apatite structures. The effects of ion mass on irradiation-induced recrystallization of pre-amorphized Ca₂La₈(SiO₄)₆O₂ are also presented. Finally, these results and model provide the basis for predicting the temperature and time dependence of amorphization in silicate-apatite host phases for actinides, and these predictions provide boundaries for performance assessments.

Experimental procedures

Single crystals of Ca₂La₈(SiO₄)₆O₂ were grown from a stoichiometric melt by Airtron Corporation,²⁰ and single crystals of Sr₂Nd₈(SiO₄)₆O₂ were grown by the floating zone method.⁵⁵ These orthosilicate apatites have a very open hexagonal (P6₃/m) structure in which the SiO₄ tetragonal monomers are isolated from one another and then linked by various metal cations. The edge sharing 7-fold sites (6h) are occupied primarily by La or Nd; the 8-fold cation sites (4f) are occupied by both Ca and La or Sr and Nd,⁵⁶ as shown in Fig. 1.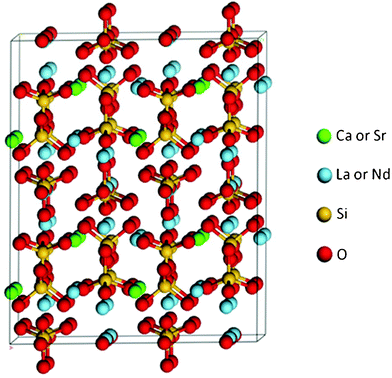

Fig. 1 Structure of (Ca,Sr)₂(La,Nd)₈(SiO₄)₆O₂.

Specimens of Ca₂La₈(SiO₄)₆O₂ with [0001] orientations were cut as thin sections from the crystals and prepared as TEM specimens by Ar⁺ ion milling prior to irradiation. Special care was taken (i.e., reduction in accelerating voltage and milling angle before perforation) to minimize possible Ar⁺ ion damage. Irradiations of Ca₂La₈(SiO₄)₆O₂ were carried out, using the HVEM-Tandem and IVEM-Tandem Facilities at Argonne National Laboratory,^57,58 with 0.8 MeV Ne⁺ ions (2.4 × 10⁻² ions nm⁻² s⁻¹), 1.0 MeV Ar⁺ (1.2 × 10⁻² ions nm⁻² s⁻¹), 1.5 MeV Kr⁺ ions (3.4 × 10⁻³ ions nm⁻² s⁻¹), and 1.5 MeV Xe⁺ ions (3.4 × 10⁻³ ions nm⁻² s⁻¹) over the temperature range from 15 K to 773 K. All irradiations were performed at 5 to 10° off the zone axis of the oriented specimens. Structural changes and the ion fluence for complete amorphization in the electron transparent thickness (∼200 nm) of the specimens were determined in situ by intermittent transmission electron microscopy (TEM) and selected area electron diffraction (SAED) following each irradiation step. Except as noted, the TEM electron beam was off during the actual ion irradiations to minimize the effects of ionization and subthreshold energy transfers from the electrons. The high-energy ions used in this study penetrate well beyond the electron transparent thickness, thus minimizing ion-implantation effects, which may impact the critical amorphization dose in ceramics,⁵⁹ as well as any uncertainties in determining the critical amorphization dose due to thickness variations.⁶⁰ Post irradiation annealing studies of fully amorphous Ca₂La₈(SiO₄)₆O₂ samples were performed in situ to investigate the effects of 0.8 MeV Ar⁺ and 1.5 MeV Xe⁺ ion irradiation during annealing on recrystallization processes.

Specimens of Sr₂Nd₈(SiO₄)₆O₂ with [0001] orientations were cut as thick sections from the crystal and subsequently polished prior to irradiation. The samples were irradiated at 160 and 300 K with 1.0 MeV Au⁺ ions (1.0 × 10⁻³ ions nm⁻² s⁻¹) at ∼7° off the [0001] axis using a 3.0 MV tandem accelerator within the Environmental Molecular Sciences Laboratory (EMSL) at the Pacific Northwest National Laboratory.⁶¹ The accumulation of damage and the dose for amorphization were determined by in situRutherford backscattering spectrometry in channelling geometry (RBS/C) along the [0001] direction using 2.0 MeV He⁺ ions with a scattering angle of 150°.

The local ionization and atomic displacement densities per ion as a function of depth in Ca₂La₈(SiO₄)₆O₂ and Sr₂Nd₈(SiO₄)₆O₂ under these irradiation conditions, as well as those in previous studies, were determined from full cascade Monte Carlo calculations using the SRIM-2003 (S̲topping and R̲ange of I̲ons in M̲atter) code,^62,63 with an assumed average displacement energy for each element of 50 eV, which is reasonably estimated from theoretical calculations on a related britholite composition.⁶⁴ In order to compare the results for the different ions, the cumulative ion fluences for complete amorphization are normalized to the local displacement dose, in units of displacements per atom (dpa). Based on previous cross-sectional TEM results,⁵⁴ the displacement dose for the in situTEM studies is determined at a depth of 30 nm, since it is in this depth regime where complete amorphization is expected to last occur because of the damage gradient and enhanced surface amorphization. For the in situRBS/C work, the displacement dose is determined at the depth corresponding to the peak in the damage profile. The SRIM code was also used to calculate the local energy loss to ionization processes by the incident ion and secondary ion recoils and the local ratio of ionization rate to displacement rate.

Results and discussion

Dose dependence of amorphization

Quantitative analysis of RBS/C spectra at different ion fluences has been previously reported for Sr₂Nd₈(SiO₄)₆O₂ irradiated with 1.0 MeV Au⁺ ions at 160 K to determine the relative disorder of Nd at the damage peak as a function of local dose.⁶⁵ Similar analysis of RBS/C spectra has been carried out for irradiations at 300 K. The dose dependence of irradiation-induced disordering in Sr₂Nd₈(SiO₄)₆O₂ irradiated at 160 and 300 K with 1.0 MeV Au⁺ ions is shown in Fig. 2. Complete amorphization corresponds to a relative disorder of 1.0 and occurs at a dose of 0.06 ± 0.006 dpa for irradiation at both 160 and 300 K, indicating minimal temperature dependence under these irradiation conditions. Using in situTEM and SAED, the progression of the amorphization process at intermediate doses is less quantitative; however, the dose for complete amorphization is determined quantitatively by the complete loss of diffraction maxima in the SAED patterns, as illustrated previously for Ca₂La₈(SiO₄)₆O₂ irradiated with 1.5 MeV Kr⁺ ions.⁵⁴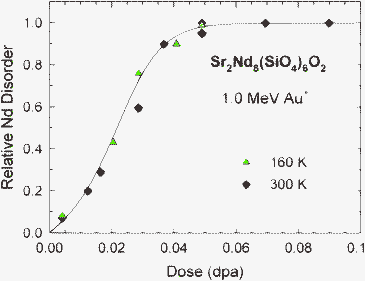

Fig. 2 Relative Nd disorder at the damage peak as a function of local dose in Sr₂Nd₈(SiO₄)₆O₂ irradiated at 160 and 300 K with 1.0 MeV Au⁺ ions.

Temperature dependence of amorphization

High-resolution TEM has previously detailed the atomic-scale amorphous structure produced directly within the atomic collision cascades or tracks of individual energetic ions in Ca₂La₈(SiO₄)₆O₂, as well as the dependence of amorphous cascade size on incident ion mass and irradiation temperature.⁵⁴ This previous work also demonstrated that both electron-irradiation and thermal annealing decrease the size of the amorphous cascade structures. Thus, irradiation temperature and local ionization are expected to affect the rate of irradiation-induced amorphization and the dose required for complete amorphization. The effects of temperature on the dose for complete amorphization of Ca₂La₈(SiO₄)₆O₂ under 0.8 MeV Ne⁺, 1.0 MeV Ar⁺, 1.5 MeV Kr⁺, and 1.5 MeV Xe⁺ ion irradiations are shown in Fig. 3, along with the results for Sr₂Nd₈(SiO₄)₆O₂ under 1.0 MeV Au⁺ irradiation from Fig. 2. The lowest critical amorphization dose in Ca₂La₈(SiO₄)₆O₂ at 15 K is 0.16 dpa and, within experimental error (± 10%), is identical for both 1.5 MeV Kr⁺ and 1.5 MeV Xe⁺ ions. Under 0.8 MeV Ne⁺ irradiation, the critical amorphization dose is slightly higher at this temperature, suggesting that Ne⁺ may be less effective in producing amorphization. The dose for complete amorphization increases with temperature in two distinct stages. The dynamic recovery in Stage I (15 to ∼150 K) is probably associated with close-pair recombination. In Stage II (above ∼150 K), the increase in amorphization dose with temperature is associated with increased defect mobility and epitaxial recrystallization at the crystalline-amorphous interface of amorphous cascade structures, similar to that observed during thermal annealing.⁵⁴ The more rapid increase in amorphization dose with temperature for Ne⁺ was previously thought to be due to the lower energy of its recoils,²⁰ but the results presented here indicate that this is more likely due to the much higher-rate of in-cascade ionization for Ne ions, as suggested by the high value of the ratio, R, of ionization rate to displacement rate in Table 1. At 300 K, the dose for amorphization increases with decreasing ion mass. In the case of the Ne⁺ irradiation at 300 K, an additional irradiation at a factor of 5 lower ion flux resulted in the same dose for amorphization, indicating no effect of damage rate on amorphization dose at 300 K under Ne⁺ irradiation, despite the strong temperature dependence. This is consistent with an irradiation-assisted recovery process being dominant under these conditions.²⁴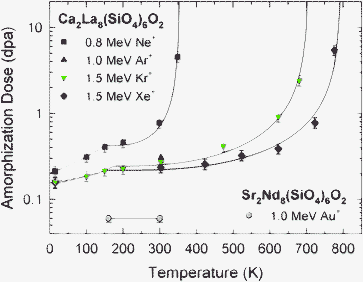

Fig. 3 Temperature dependence of the critical dose for complete amorphization in Ca₂La₈(SiO₄)₆O₂ and Sr₂Nd₈(SiO₄)₆O₂.

Table 1 Model parameters determined from fit of Eqn (1) to Stage II behavior (Fig. 3) for Ca₂La₈(SiO₄)₆O₂ irradiated with Ne, Kr and Xe, predicted parameters for Ar irradiated Ca₂La₈(SiO₄)₆O₂ and Au and He irradiated Sr₂Nd₈(SiO₄)₆O₂, the ratio, R, of ionization to displacement rates for the irradiation conditions, and the critical temperatures for amorphization, T_c

Incident particle	Do (dpa)	σ r/σd	R (Gy/dpa)	E irr (eV)	T c (K)
a Predicted based on R from Fig. 4. b Predicted based on Eqn (2) and the predicted values for σr/σd (Fig. 4) and Eirr.
0.8 MeV Ne^+	0.42 ± 0.03	136.0 ± 5.0	6.3 × 10^9	0.15 ± 0.02	355 ± 10
1.0 MeV Ar^+	0.3 ± 0.03	39.1^a	2.1 × 10^9		450^b
1.5 MeV Kr+	0.24 ± 0.02	11.6 ± 2.0	6.7 × 10^8	0.15 ± 0.02	705 ± 10
1.5 MeV Xe^+	0.22 ± 0.01	9.1 ± 2.0	4.5 × 10^8	0.15 ± 0.02	800 ± 10
1.0 MeV Au^+	0.06 ± 0.006	4.6^a	2.3 × 10^8		1140^b
2.0 MeV He^+		5820^a	2.7 × 10^11		201^b

---

For all incident ions, the dose for complete amorphization increases with decreasing ion mass and with increasing temperature. The increase with temperature is also more rapid with decreasing ion mass. These results suggest that there is an increased efficiency of simultaneous dynamic recovery with decreasing ion mass. As already noted, this shift in temperature dependence (i.e., decrease in critical temperature) with decreasing ion mass is similar to behaviour reported previously for amorphization in other materials.^{13,18,27–30} Ionization-enhanced defect diffusion and recrystallization, due to increases in the electronic to nuclear stopping ratio with decreasing mass, may play a role in the temperature dependence, and this process is well known to retard irradiation-induced amorphization in Si^66–68 and Si₃N₄,⁵⁹ as well as suppress dislocation loop formation in MgAl₂O₄ and Al₂O₃ under irradiation.⁶⁹

In general, the observed increase in amorphization dose with increasing temperature is due to simultaneous dynamic recovery processes with activation energies, E_a, that are associated with defect migration/recombination in the crystal structure or epitaxial recrystallization at the crystalline/amorphous interface. Several models have been used to describe the temperature dependence of amorphization in ceramics and semiconductors in terms of a single activated process.^{13,14,18,20,21,24}

The most general expression for amorphization dose, D, at temperature, T, has the form:^24,70

D = D_o/[1 − {σ_rφ exp(–E_irr/kT) + ν_th exp(–E_th/kT)}/σ_dφ] (1)

where D_o is the amorphization dose at 0 K associated with a single temperature stage, σ_r and σ_d are the cross sections for irradiation-induced recovery and damage production, respectively, E_irr and E_th are the activation energies for irradiation-induced and thermal recovery processes, respectively, ν_th is the thermal jump frequency, k is the Boltzmann constant, and φ is the ion flux. While Eqn (1) can be used to fit data over a wide temperature region for a single activated process, simultaneous radiation-induced and thermal recovery makes model fitting challenging due to the large number of fit parameters and limited data. Nonetheless, Eqn (1) can be used to explore the dominance of radiation-induced recovery or thermal recovery by setting one or the other term to zero. This approach has been used to describe the increase in amorphization dose with increased ionization-induced recovery in electron-irradiated 6H–SiC,⁷¹ the increase in amorphization rate with increasing damage rate near the critical temperature in ion-irradiated 4H–SiC,⁷⁰ and dynamic recovery in ion-irradiated SrTiO₃.¹¹

There are insufficient data to model the Stage I behaviour; however, by assuming only irradiation-induced recovery, Eqn (1) provides a good fit to the Stage II data in Fig. 3 (above 150 K), as shown by the solid curves. The fit parameters, D_o, σ_r/σ_d and E_irr, are summarized in Table 1. The activation energy, 0.15 ± 0.02 eV, is similar to the value (0.13 ± 0.02 eV) estimated previously for Ne⁺ and Xe⁺ using a different approach.²⁰ In contrast, Eqn (1) with only the thermal recovery term (irradiation term set to zero) does not yield an acceptable fit to the data for any reasonable values of ν_th and E_th, which suggests that the temperature dependence over this range is dominated by irradiation-induced recovery processes with an activation energy of ∼0.15 eV. This low activation energy is similar to that measured for ionization-enhanced recrystallization in amorphous SrTiO₃,¹¹ which suggests that ionization-induced processes may play a similar role in recrystallizing the amorphous cascade structures under these irradiation conditions. Such low activation energies are typical of athermal processes or electronic excitation processes. Localized electronic excitations produced by ionization can significantly affect local bonding and may effectively lower the energy barriers to defect recovery and recrystallization processes, as discussed previously.^11,65

Some insights into the nature of irradiation-induced recovery processes can be gained by examining the dependence of σ_r/σ_d (Table 1) on the ratio, R, of the local ionization rate to displacement rate determined from SRIM calculations, as shown in Fig. 4. The results indicate a linear dependence of σ_r/σ_d on the ratio of ionization to displacement rates that goes to zero as the ionization to displacement ratio goes to zero, which suggests that ionization is the dominant contributor to the dynamic recovery processes represented by σ_r; however, additional data at intermediate values of R would be useful in future studies to confirm the linear dependence.

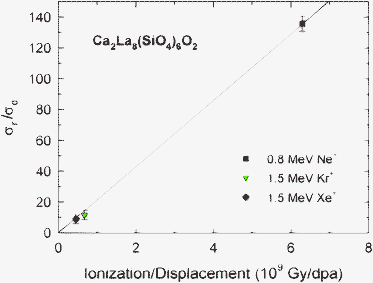Fig. 4 Values of σ_r/σ_d from model fits for Ca₂La₈(SiO₄)₆O₂ as a function of the local ratio, R, of ionization rate to displacement rate.

Values of the critical temperature, T_c, for the Ne⁺, Kr⁺ and Xe⁺ irradiations are determined from extrapolation of the curve fits in Fig. 3 and are included in Table 1. If irradiation-induced recovery processes are dominant, T_c(irr) is given by the expression:²⁴

T _c(irr) = E_irr/[k ln (σ_r/σ_d)] (2)

Under these conditions, T_c(irr) is independent of ion flux and is inversely dependent on the ratio, σ_r/σ_d. Using the results from Table 1, a plot of the experimentally-determined values of T_c as a function of 1/ln(σ_r/σ_d), as shown in Fig. 5, exhibits an excellent linear relationship and yields an activation energy of 0.14 ± 0.02 eV, which is consistent with the activation energies (Table 1) determined by the model fits to the data in Fig. 3 over a wide temperature range. Using Eqn (1), the value of E_irr, and the predicted values of σ_r/σ_d (Table 1) for the Ar⁺, Au⁺ and He⁺ ions, the values of T_c(irr) for the Ar⁺, Au⁺ and He⁺ irradiations can be estimated and are included in Table 1. The T_c(irr) value of 450 K predicted for 1.0 MeV Ar⁺ irradiation of Ca₂La₈(SiO₄)₆O₂ is consistent with the observation that amorphization is not observed in Ca₂Nd₈(SiO₄)₆O₂ irradiated at ∼475 K with 3.0 MeV Ar⁺ to 10 dpa.⁵³ The predicted T_c(irr) value of 201 K for He⁺ irradiated Sr₂Nd₈(SiO₄)₆O₂ is also consistent with the observation that amorphization is not observed in Ca₂Nd₈(SiO₄)₆O₂ irradiated with alpha particles at 300 K;⁵³ this also demonstrates that additional He⁺ irradiation during RBS/C does not contribute to the observed amorphization, but may contribute to recovery, as discussed in more detail below.

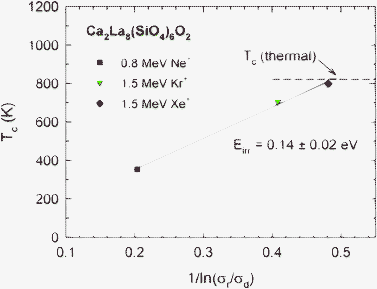Fig. 5 Critical temperature, T_c, in Ca₂La₈(SiO₄)₆O₂ as a function of 1/ln(σ_r/σ_d).

The role of thermal recovery on T_c is explored by examining damage-rate effects. When thermal recovery processes are dominant, T_c is given by the expression:²⁴

T _c(th) = E_th/[k ln(ν_th/σ_dφ)] (3)

Under these conditions, T_c is dependent on damage rate, σ_dφ. Since the absolute value of ν_th and σ_d are not known, Eqn (3) can be rewritten as:

1/T_c(th) = (k/E_th) [ln(ν_th) − ln(σ_dφ)] (4)

Both ν_th and E_th are constants for a single recovery process, and a plot of 1/T_c as a function of ln(σ_dφ) should yield a slope of −k/E_th. Using values of σ_dφ given by the local SRIM displacement rate, the experimental values for 1/T_c exhibit a poor linear dependence on ln(σ_dφ), as shown in Fig. 6, and the deduced activation energy, 0.067 eV, is unrealistic for thermal recovery processes near T_c in this material, which suggests that thermal recovery processes do not contribute significantly to determining T_c in this material under these irradiation conditions.

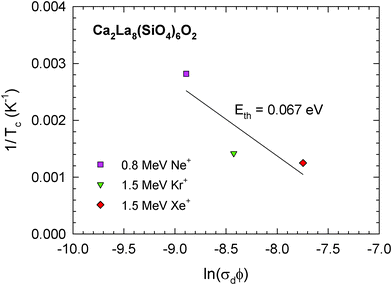Fig. 6 Inverse critical temperature, 1/T_c, in Ca₂La₈(SiO₄)₆O₂ as a function of ln(σ_dφ).

At temperatures sufficiently below T_c, thermal recovery processes are negligible. From Eqn (1), the inverse amorphization dose, 1/D, under these conditions can be written as:

1/D = [1 − (σ_r/σ_d) exp(–E_irr/kT)]/D_o (5)

which at constant temperature is proportional to σ_r/σ_d. If ionization-induced recovery processes are dominant, σ_r/σ_d should be proportional to the local ratio, R, of ionization to displacement rates (Fig. 4). As shown in Fig. 7, the inverse amorphization dose for irradiations at 15 and 300 K (from Fig. 2) exhibits a linear dependence on the SRIM calculated R values, consistent with Eqn (5) and the results in Fig. 4. These results demonstrate a systematic increase in amorphization dose with an increase in the local ratio of ionization to displacement rates, providing further evidence of the role of ionization in dynamic recovery processes.

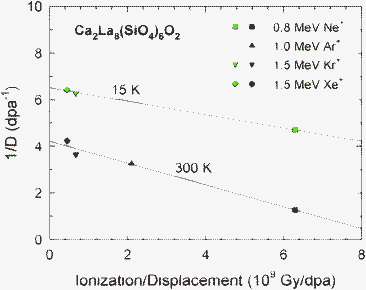Fig. 7 Inverse amorphization dose in Ca₂La₈(SiO₄)₆O₂ at 15 and 300 K as a function of the local ratio, R, of ionization rate to displacement rate.

The above results suggest that dynamic recovery in Ca₂La₈(SiO₄)₆O₂ under ion irradiation is dominated by ionization-induced processes, except at higher temperatures approaching T_c(th), where thermal recovery will begin contributing. These results and interpretation are consistent with the increased dynamic recovery induced in ion-irradiated Ca₂La₈(SiO₄)₆O₂ by simultaneous electron irradiation^54,72 and the electron-irradiation induced recrystallization at room temperature observed for isolated amorphous cascades in Ca₂La₈(SiO₄)₆O₂,⁵⁴ as well as for the recrystallization of a buried amorphous layer induced in Sr₂Nd₈(SiO₄)₆O₂ by electron irradiation.⁷³

Recrystallization

Post-irradiation recrystallization should occur at the amorphous-crystalline interface (epitaxial recrystallization) in partially amorphous materials or by nucleation and growth processes in fully amorphous material. In siturecrystallization of fully amorphous specimens was studied as a function of temperature, with and without simultaneous ion irradiation. Isochronal anneals were conducted in situ in the electron microscope, without the electron beam, for 30 min, starting at 823 K. Selected area electron diffraction was conducted periodically to monitor the annealing. Without electron or ion beams, recrystallization was not observed during 30 min annealing at temperatures up to 1073 K; however, at 1123 K, full epitaxial recrystallization to the original single crystal structure occurred after only 10 min, with the recrystallization initiated at the buried crystalline-amorphous interface in thicker regions of the specimen. Under 800 keV Ar⁺ ion irradiation, some random nucleation of a few nanocrystallites was observed following 30 min anneals at 1023 and 1073 K, as shown in Fig. 8, but the amorphous structure remains dominant. Under 1.5 MeV Kr⁺ ion irradiation, no recrystallization was observed following 30 min annealing at 823 and 873 K; however, rapid recrystallization to a polycrystalline structure was observed at 923 K. After 2 min at 923 K with 1.5 MeV Kr⁺ ions, fine crystallites of ∼50 nm diameter were observed in the bright-field image, and crystalline diffraction spots were observed in the electron diffraction pattern. This irradiation-enhanced recrystallization process continued over a 38 min period, producing a randomly-oriented polycrystalline structure with crystallites of ∼300 nm diameter, as shown in Fig. 9.

Fig. 8 Random crystallites in amorphous Ca₂La₈(SiO₄)₆O₂ after 30 min at 1023 K under 800 keV Ar⁺ irradiation.

Fig. 9 TEM image of pre-amorphized Ca₂La₈(SiO₄)₆O₂ after recrystallization at 923 K under 1.5 MeV Kr⁺ irradiation.

The activation energy for these recrystallization processes can be estimated, as shown previously,⁴⁹ following the method of analysis of Primak,⁷⁴ where the most probable activation energy, E_a, for an annealing or recrystallization process occurring at a particular temperature, T_r, and time, t, is given by the expression:

E _a = kT_r ln(ν_tht) (6)

where ν_th is the thermal jump frequency, as defined above. The thermal jump frequency for recrystallization of the radiation-induced amorphous state in Ca₂Nd₈(SiO₄)₆O₂ has been previously determined to be 5 × 10¹⁴ s⁻¹.⁴⁹ Using this value, the recrystallization temperature and time above (923 K, 38 min), and Eqn (6), the activation energy for epitaxial thermal recrystallization in Ca₂La₈(SiO₄)₆O₂ is estimated to be 3.8 eV. Under 1.5 MeV Kr⁺ irradiation, the activation energy for the observed nucleation and growth recrystallization is 3.3 eV, which is within the experimental uncertainty of the value (3.1 ± 0.2 eV) rigorously determined for recrystallization of amorphous Cm-doped Ca₂Nd₈(SiO₄)₆O₂ to a polycrystalline structure,⁴⁹ which also occurred in the presence of heavy ²⁴⁰Pu alpha-recoil particles at a temperature of 823 K.

While the critical temperature for amorphization, T_c, exhibits a strong dependence on ratio of ionization to displacement cross sections, the recrystallization temperature, T_r, decreases with increasing ion mass, which suggests a dependence on the damage (collisional) energy density, and there may even be a threshold for this effect, since recrystallization under Ar⁺ irradiation is largely incomplete below the temperature for thermal epitaxial recrystallization. This polycrystalline recrystallization process under irradiation is probably associated with the high damage energy density within the ballistic collision cascade that provides sufficient energy to overcome the nucleation barrier for crystallization. The dependence of T_r and T_c on the damage energy density calculated from SRIM for each ion is shown in Fig. 10. Interestingly, T_r approaches T_c at high damage energy densities, and both approach the T_r value of 823 K determined previously for amorphous Cm-doped Ca₂Nd₈(SiO₄)₆O₂,⁴⁹ with a damage energy density of 2750 eV nm⁻¹/ion for the alpha-recoil nucleus. Thus, for heavy ions with high damage energy densities, such as 1.0 MeV Au⁺ (damage energy density of 3030 eV nm⁻¹/ion at the damage peak), the values of T_c and T_r become identical and equal to 823 K, which defines the value of T_c(th) at comparable ion-beam damage rates that can be used to determine T_c(th) at the much lower dose rates expected for similar silicate-apatite phases used for the immobilization of actinides.

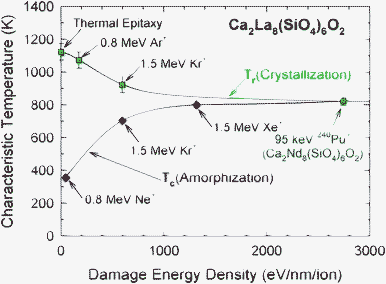Fig. 10 Comparison of critical temperature for amorphization, T_c, and irradiation-enhanced recrystallization temperature, T_r, in Ca₂La₈(SiO₄)₆O₂ as a function of the average damage energy density.

A buried amorphous layer, ∼250 nm thick, was formed in Sr₂Nd₈(SiO₄)₆O₂ by irradiation with 1.0 MeV Au⁺ ions at 300 K to 0.5 ions nm⁻² (0.2 dpa at the damage peak). The initial damage state was investigated at 300 K by RBS/C using 2.0 MeV He⁺ ions, which is above the T_c(irr) for the He⁺ ions (Table 1). To investigate whether irradiation at 300 K with 2.0 MeV He⁺ ions induced any recovery of the buried amorphous layer, irradiation of this sample with He⁺ ions (alpha particles) was continued, with periodic RBS/C measurements of the amorphous thickness in the sample, to an ion fluence equivalent to 40 RBS/C measurements. The results in Fig. 11 show that alpha particle irradiation induces recovery at the crystalline-amorphous interface that causes a relative decrease in the thickness of the amorphous layer. Since the ratio, R, of ionization rate to displacement rate for the alpha particles at this depth is 5820 Gy/dpa, this recovery is driven by ionization-induced processes. While the relative recovery of this highly damaged state is just over 7% for the maximum ion fluence, such alpha-particle induced recovery could be more significant for early stages of damage accumulation or during simultaneous irradiation with heavy ions and alpha particles (as in alpha-decay), similar to the enhanced recovery of amorphous cascade structures observed in Ca₂La₈(SiO₄)₆O₂ under electron-irradiation and under simultaneous electron and ion irradiation.⁵⁴ This observed alpha-particle enhanced recovery is also similar to that induced by alpha particles (0.8 to 3.2 MeV) in natural fluoroapatite predamaged by 220 keV Pb⁺ ion irradiation.⁷⁵

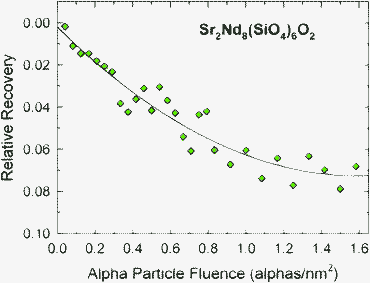Fig. 11 Relative recovery in thickness of buried amorphous layer in Sr₂Nd₈(SiO₄)₆O₂ under irradiation with 2.0 MeV alpha particles at 300 K.

Implications for actinide immobilization

The two quantities most useful for predicting the long-term amorphization behaviour in materials for the immobilization of actinides are the baseline amorphization dose, D_o, under ambient temperature conditions, preferably determined in studies employing short-lived actinides, and the critical temperature, T_c(th), due to thermal recovery processes. As shown in the present study, neither D_o nor T_c(th) are readily determined from ion-irradiation experiments involving a range of ion species. It is evident from the range of D_o and T_c values for different ions in Table 1 that employing a single ion species in irradiation studies can be insufficient to provide valid parameters for long-term predictions of the radiation response of actinide host phases.

Based on studies of ²⁴⁴Cm-doped Ca₂Nd₈(SiO₄)₆O₂, the value for D_o is 2.6 × 10¹⁸ alpha-decays g⁻¹,⁵² which is equivalent to 0.12 dpa and is not derivable from the current ion-irradiation data. This dpa value is about twice that measured at room temperature (0.06 dpa) in Sr₂Nd₈(SiO₄)₆O₂ irradiated with Au⁺ ions (Fig. 3), which have a very low R value (Table 1) that is comparable to the value (1.1 × 10⁸Gy/dpa) for the alpha-recoil nucleus, ²⁴⁰Pu, emitted by the alpha decay of ²⁴⁴Cm in Ca₂Nd₈(SiO₄)₆O₂. While this difference in amorphization dose could be attributed to compositional differences, it is considered unlikely. A more likely explanation is that the 5.8 MeV alpha particles emitted by the decay of ²⁴⁴Cm induce some recovery of existing alpha-recoil damage along their 18 μm track length. This interpretation is consistent with the alpha-particle induced recovery in Sr₂Nd₈(SiO₄)₆O₂ reported here (Fig. 11), as well as with the ionization-enhanced annealing induced by alpha particles in predamaged natural fluoroapatite.⁷⁵ These results highlight the challenge of using ion beams to determine values of D_o due to alpha-decay processes in actinide-host phases, as well as the critical self-healing role that ionization-enhanced recovery from alpha particles may play in the performance of actinide-bearing waste forms.

While it would be preferable to determine T_c(th) from the temperature dependence of amorphization in samples containing short-lived actinides, such as ²⁴⁴Cm or ²³⁸Pu, the necessary data do not currently exist, and it would require 5 to 10 years to obtain the necessary T_c(th) data, if long-term funding could be committed. In the absence of such data, T_c(th) must be determined from detailed analysis of data from ion-irradiation and thermal annealing experiments, as illustrated here for the case of Ca₂La₈(SiO₄)₆O₂ and shown in Fig. 10. Even then, T_c(th) must be corrected for changes in dose rates using Eqn (3). From the results in Fig. 10, the critical temperature at typical ion-irradiation dose rates, but for actinide damage energy densities, is 823 K. Based on this T_c(th) value and Eqn (3), the critical temperatures are predicted, as summarized in Table 2, for Ca₂(La,Nd)₈(SiO₄)₆O₂ containing 1.33 wt% ²⁴⁴Cm, as in previous Cm-doped experiments,^48–52 as well as in Ca₂(La,Nd)₈(SiO₄)₆O₂ actinide host phases containing 10 wt% ²³⁹Pu or 2 and 5 wt% minor actinides from reprocessed commercial nuclear waste.⁷⁶ A significant decrease in T_c(th) of several hundred degrees is observed at the dose rates representative of conditions for actinide-host phases. Because of changing alpha activity with time, the critical temperatures in Table 2 should be considered as upper boundaries. The value of T_c(th) for 10 wt% ²³⁹Pu is much higher than that previously estimated, which was incorrectly based on the critical temperature for 1.5 MeV Kr⁺ ion irradiation and a much lower estimate for the activation energy;⁷⁷ this highlights the point about possible invalid predictions from irradiation data based on a single ion species.

Table 2 Critical temperature, T_c(th), for Ca₂(La,Nd)₈(SiO₄)₆O₂ under heavy ion irradiation and for different actinide contents and dose rates

Irradiation condition	Dose rate (dpa s^−1)	Initial alpha activity (Bq g^−1)	T c(th) (K)
Heavy ions	4.2 × 10^−4	Not applicable	823
1.24 wt% ^244Cm	1.5 × 10^−9	3.6 × 10^10	632
5 wt% minor actinides	8.8 × 10^−11	2.3 × 10^9	601
2 wt% minor actinides	3.5 × 10^−11	9.5 × 10^8	591
10 wt% ^239Pu	8.5 × 10^−12	2.3 × 10^8	577

---

One prediction that can be provided for performance assessment is the temperature dependence of the amorphization dose for actinide host phases with different actinide content. This can be predicted from the model given by Eqn (1), assuming thermally dominated recovery processes, and the data in Table 2. The predicted temperature dependence for amorphization in the Ca₂(La,Nd)₈(SiO₄)₆O₂ system for different types and concentrations of actinides is shown in Fig. 12. These results are a somewhat conservative prediction, but one that may be sufficient for some engineering assessments. The predictions clearly show that the critical temperature for Ca₂(La,Nd)₈(SiO₄)₆O₂ is above the expected repository temperatures for all cases considered; thus, amorphization in this phase will occur at the dose previously determined for Cm-doped Ca₂La₈(SiO₄)₆O₂, 2.6 × 10¹⁸ alpha-decays g⁻¹ (0.12 dpa),⁵² without significant influence of dynamic recovery processes.

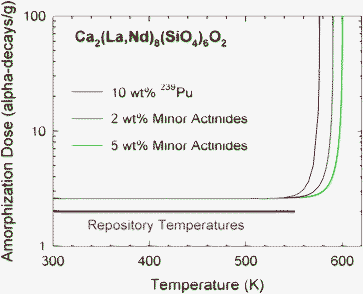Fig. 12 Predicted temperature dependence of amorphization in Ca₂(La,Nd)₈(SiO₄)₆O₂ with different actinide content. Also shown is the range of expected repository temperatures.

Because the amorphization dose in actinide-containing Ca₂(La,Nd)₈(SiO₄)₆O₂ is largely independent of temperature in this temperature regime, the amorphization process should be independent of dose rate, but the time for amorphization will depend on dose rate. Thus, based on the previously determined dose dependence of amorphous fraction in Cm-doped Ca₂Nd₈(SiO₄)₆O₂,⁵² it is possible to predict the time dependence of amorphization in Ca₂(La,Nd)₈(SiO₄)₆O₂ for different actinide contents with corresponding differences in dose rates (Table 2), as illustrated in Fig. 13. While Ca₂(La,Nd)₈(SiO₄)₆O₂ containing 5 wt% minor actinides will require only about 100 years to become amorphous under these conditions, amorphization for 10 wt% ²³⁹Pu will take nearly 1000 years due to the order of magnitude lower dose rate.

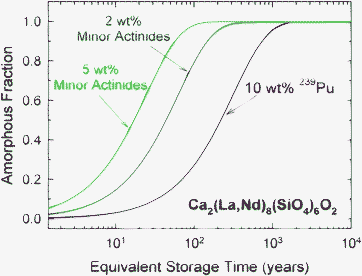Fig. 13 Predicted time dependence of amorphization in Ca₂(La,Nd)₈(SiO₄)₆O₂ with different actinide content and corresponding dose rates (Table 2).

Conclusions

The temperature dependence of irradiation-induced amorphization in Ca₂La₈(SiO₄)₆O₂ has been analyzed using a dynamic model for amorphization. The results indicate that the amorphization dose increases and the critical amorphization temperature decreases as the ratio of in-cascade ionization to displacement rates increases. Model fits yield the ratio of irradiation-induced recovery cross section to damage cross section, σ_r/σ_d, for each ion irradiation condition and an activation energy of 0.15 ± 0.01 eV for irradiation-induced recovery. The critical temperature exhibits a linear dependence on 1/ln(σ_r/σ_d), consistent with the model. Epitaxial thermal recrystallization is observed at 1123 K with an activation energy of ∼3.8 eV. Irradiation-induced recrystallization of a polycrystalline structure is observed at lower temperatures with an activation energy of ∼3.2 eV, which is consistent with that (3.1 ± 0.2 eV) previously measured in Cm-doped Ca₂Nd₈(SiO₄)₆O₂.⁴⁹ The temperature for recrystallization decreases with increasing damage energy density to a saturation value of about 823 K, which suggests that high damage energy densities assist in overcoming the nucleation barrier for crystallization. Partial recrystallization of a buried amorphous layer in Sr₂Nd₈(SiO₄)₆O₂ is observed under irradiation with alpha particles at 300 K, which suggests that alpha particles from actinide decay can promote self-healing in silicate-apatite waste forms. Based on these results, the temperature and time dependence of amorphization in silicate-apatite host phases containing different relevant actinide concentrations are predicted. Finally, this work has demonstrated both the complexity involved in using ion-irradiation methods to predict long-term behaviour and the potential pitfalls of using a narrow range of irradiation results in such predictions; the approaches and results described here provide insights and roadmap to experimental studies to develop similar performance boundaries for other actinide host phases.

Acknowledgements

Research supported by the U. S. Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division and performed in part at the HVEM/IVEM-Tandem Facility, a DOE-BES user facility at Argonne National Laboratory. A portion of research was also performed at the Environmental Molecular Sciences Laboratory (EMSL), a national scientific user facility sponsored by the Department of Energy's Office of Biological and Environmental Research at Pacific Northwest National Laboratory.

References

1. R. C. Ewing, B. C. Chakoumakos, G. R. Lumpkin and T. Murakami, MRS Bull., 1987, 7(4), 58.
2. J. S. William, MRS Bull., 1992, 17(6), 47.
3. W. J. Weber, R. C. Ewing, C. R. A. Catlow, T. Diaz de la Rubia, L. W. Hobbs, C. Kinoshita, Hj. Matzke, A. T. Motta, M. Nastasi, E. K. H. Salje, E. R. Vance and S. J. Zinkle, J. Mater. Res., 1998, 13, 1434.
4. R. C. Ewing, W. J. Weber and J. Lian, J. Appl. Phys., 2004, 95, 5949.
5. A. Meldrum, L. A. Boatner and R. C. Ewing, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141, 347.
6. A. Meldrum, L. A. Boatner, L. M. Wang and R. C. Ewing, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 127(128), 160.
7. K. L. Smith, M. G. Blackford, G. R. Lumpkin and N. J. Zaluzec, J. Nucl. Mater., 2000, 277, 159.
8. R. C. Ewing, A. Meldrum, L. M. Wang, W. J. Weber and L. R. Corrales, Rev. Mineral. Geochem., 2003, 53, 387.
9. Y. Zhang, W. J. Weber, W. Jiang, C. M. Wang, V. Shutthanandan and A. Hallén, J. Appl. Phys., 2004, 95, 4012.
10. I.-T. Bae, Y. Zhang, W. J. Weber, M. Ishimaru, Y. Hirotsu and M. Higuchi, J. Mater. Res., 2008, 23, 962.
11. Y. Zhang, J. Lian, C. M. Wang, W. Jiang, R. C. Ewing and W. J. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 094112.
12. J. F. Gibbons, Proc. IEEE, 1972, 60, 1062.
13. F. F. Morehead and B. L. Crowder, Radiation Effects, 1970, 6, 27.
14. J. R. Dennis and E. B. Hale, J. Appl. Phys., 1978, 49, 1119.
15. R. P. Webb and G. Carter, Radiation Effects, 1981, 59, 69.
16. G. Carter, Radiat. Eff., 1986, 100, 281.
17. N. Hecking, K. F. Heidemann and E. te Kaat, Nucl. Instrum. Methods Phys. Res., Sect. B, 1986, 15, 760.
18. K. A. Jackson, J. Mater. Res., 1988, 3, 1218.
19. G. Carter and M. J. Nobes, J. Mater. Res., 1991, 6, 2103.
20. W. J. Weber and L. M. Wang, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 91, 63.
21. W. J. Weber, R. C. Ewing and L. M. Wang, J. Mater. Res., 1994, 9, 688.
22. A. Meldrum, S. J. Zinkle, L. A. Boatner and R. C. Ewing, Phys. Rev. B: Condens. Matter, 1999, 59, 3981.
23. S. X. Wang, L. M. Wang and R. C. Ewing, Phys. Rev. B: Condens. Matter, 2000, 63, 024105.
24. W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 166–167, 98.
25. Y. Zhang, W. J. Weber, V. Shutthanandan, R. Devanathan, S. Thevuthasan, G. Balakrishnan and D. M. Paul, J. Appl. Phys., 2004, 95, 2866.
26. Y. Zhang, W. J. Weber, W. Jiang, A. Hallén and G. Possnert, J. Appl. Phys., 2002, 91, 6388.
27. J. Koike, P. R. Okamoto, L. E. Rehn and M. Meshii, J. Mater. Res., 1989, 4, 1143.
28. A. T. Motta, J. Nucl. Mater., 1997, 244, 227.
29. W. J. Weber, L. M. Wang, N. Yu and N. J. Hess, Mater. Sci. Eng., A, 1998, 253, 62.
30. W. J. Weber, L. M. Wang, Y. Zhang, W. Jiang and I.-T. Bae, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 2793.
31. S. X. Wang, L. M. Wang, R. C. Ewing, G. S. Was and G. R. Lumpkin, Nucl. Instrum. Methods Phys. Res., Sect. B, 1999, 148, 704.
32. D. McConnell, Apatite, Springer-Verlag, New York, 1973.
33. R. Bros, J. Carpena, V. Sere and A. Beltritti, Radiochimica Acta, 1996, 74, 277.
34. H. Hidaka, K. Takahashi and P. Holliger, Radiochim. Acta, 1994, 66(67), 463.
35. D. J. Wronkiewicz, S. F. Wolf and T. S. Di Santo, in Scientific Basis for Nuclear Waste Management XIX, ed. W. M. Murphy and D. A. Knecht, Mater. Res. Soc. Symp. Proc. Vol. 412, Pittsburgh, 1996, p. 345.
36. W. L. Ebert, J. K. Bates and W. L. Bourcier, Waste Manage., 1991, 11, 205.
37. W. L. Gong, R. C. Ewing, L. M. Wang, E. Vernaz, J. K. Bates and W. L. Ebert, in Scientific Basis for Nuclear Waste Management XIX, ed. W. M. Murphy and D. A. Knecht, Mater. Res. Soc. Symp. Proc. Vol. 412, Pittsburgh, 1996, p. 197.
38. W. J. Weber, R. P. Turcotte, L. R. Bunnell, F. P. Roberts and J. W. Westsik, Jr., in Ceramics in Nuclear Waste Management, ed. T. D. Chikalla and J. E. Mendel, CONF-790420, National Technical Information Services, Springfield, VA, 1979, p. 294.
39. R. P. Turcotte, J. W. Wald, F. P. Roberts, J. M. Rusin and W. Lutze, J. Am. Ceram. Soc., 1982, 65, 589.
40. A. K. Dé, B. Luckscheiter, W. Lutze, G. Malow and E. Schiewer, Ceramic Bulletin, 1976, 55, 500.
41. C. M. Jantzen and F. P. Glasser, Ceramic Bulletin, 1979, 58, 459.
42. R. C. Ewing, W. J. Weber and W. Lutze, in Disposal of Weapon Plutonium, ed. E. R. Merz and C. E. Walter, Kluwer Academic Publishers, The Netherlands, 1996, p. 65.
43. F. Audubert, J. Carpena, J. L. Lacout and F. Tetard, Solid State Ionics, 1997, 95, 113.
44. L. Boyer, J. Carpena and J. L. Lacout, Solid State Ionics, 1997, 95, 121.
45. R. C. Ewing and L. M. Wang, Rev. Mineral. Geochem., 2002, 39, 673.
46. W. J. Weber, A. Navrotsky, S. Stefanovsky, E. R. Vance and E. Vernaz, MRS Bull., 2009, 34, 46.
47. A. Chartier, C. Meis and J. D. Gale, Phys. Rev. B: Condens. Matter, 2001, 64, 085110.
48. W. J. Weber, J. Am. Ceram. Soc., 1982, 65, 544.
49. W. J. Weber, Radiation Effects, 1983, 77, 295.
50. W. J. Weber and Hj. Matzke, Mater. Lett., 1986, 5, 9.
51. W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 1992, 65, 88.
52. W. J. Weber, J. Am. Ceram. Soc., 1993, 76, 1729.
53. W. J. Weber, R. K. Eby and R. C. Ewing, J. Mater. Res., 1991, 6, 1334.
54. L. M. Wang and W. J. Weber, Philos. Mag. A, 1999, 79, 237.
55. Y. Masubuchi, M. Higuchi, H. Katase, T. Takeda, S. Kikkawa, K. Kodaira and S. Nakayama, Solid State Ionics, 2004, 166, 213.
56. J. A. Fahey, W. J. Weber and F. J. Rotella, J. Solid State Chem., 1985, 60, 145.
57. C. W. Allen, L. L. Funk, E. A. Ryan and A. Taylor, Nucl. Instrum. Methods Phys. Res., Sect. B, 1989, 40-41, 553.
58. C. W. Allen and E. A. Ryan, Microsc. Res. Tech., 1998, 42, 255.
59. S. J. Zinkle and L. L. Snead, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 116, 92.
60. L. M. Wang, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 141, 312.
61. S. Thevuthasan, C. H. F. Peden, M. H. Engelhard, D. R. Baer, G. S. Herman, W. Jiang, Y. Liang and W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 420, 81.
62. J. F. Ziegler, J. P. Biersack, U. Littmark, The Stopping and Range of Ions in Solids, Pergamon Press, New York, 1985.
63. J. F. Ziegler, J. P. Biersack and M. D. Ziegler, The Stopping and Range of Ions in Solids, SRIM Co., 2008.
64. C. Meis, J. Nucl. Mater., 2001, 289, 167.
65. Y. Zhang, I.-T. Bae and W. J. Weber, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 2828.
66. H. J. Stein, Appl. Phys. Lett., 1963, 2, 235.
67. D. N. Seidman, R. S. Averback, P. R. Okamoto and A. C. Baily, Phys. Rev. Lett., 1987, 58, 900.
68. I. Jencic and I. M. Robertson, J. Mater. Res., 1996, 11, 2153.
69. S. J. Zinkle, J. Nucl. Mater., 1995, 219, 113.
70. Y. Zhang, W. J. Weber, W. Jiang, C. M. Wang, A. Hallen and G. Possnert, J. Appl. Phys., 2003, 93, 1954.
71. I.-T. Bae, W. J. Weber, M. Ishmaru and Y. Hirotsu, Appl. Phys. Lett., 2007, 90, 121910.
72. R. Devanathan, K. E. Sickafus, W. J. Weber and M. Nastasi, J. Nucl. Mater., 1998, 253, 113.
73. I.-T. Bae, Y. Zhang and W. J. Weber, Appl. Phys. Lett., 2007, 90, 021912.
74. W. Primak, The Compacted States of Vitreous Silica, Gordon and Breach, New York, 1975.
75. S. Ouchani, J.-C. Dran and J. Chaumont, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 132, 447.
76. W. J. Weber and F. P. Roberts, Nucl. Technol., 1983, 60, 178.
77. W. J. Weber, R. C. Ewing and A. Meldrum, J. Nucl. Mater., 1997, 250, 147.

---