Use of digital image processing of microscopic images and multivariate analysis for quantitative correlation of morphology, activity and durability of electrocatalysts

Abstract

Building structure-to-property relationships is one of the most often attempted research tasks in today's material chemistry. In this report, we present a universal methodology for building structure-to-property relationship models based on statistical correlations between image parameters extracted from microscopic images and the property of interest. The methodology presented consists of conversion of SEM images into useful quantitative morphological descriptors, such as roughness and texture, by digital image processing, separating images into high- and low-frequency components reflecting roughness in meso- and macro- regimes, and applying principal component analysis (PCA) to correlate morphological parameters with other performance characteristics used to evaluate electrocatalysts’ catalytic activity and durability.

---

Introduction

Building structure-to-property relationships is one of the most often attempted research tasks in today's chemistry of materials. Often, relationships are directly dependent and easy to identify. In complex, highly correlated systems, those correlations are intertwined and multi-directional. Predicting the macroscopic property of interest, such as activity, wettability, stability, etc., based on correlation with materials morphology is challenging, but is still achievable when quantitative treatment by multivariate analysis is employed.

One of the most important issues to be solved before commercialization of polymer electrolyte fuel cells (PEFCs) is their long-term durability.¹ It has long been recognized that the morphology, structure and surface properties of carbon materials strongly affect their tendency to electrochemical corrosion. The morphology of the support, such as the surface area, roughness and porosity, is one of the contributing factors to catalytic efficiency and stability, governing the overpotential and the rate controlling steps of the electrode reactions.² The transport behavior of gases within the support, accessibility of reactive ions to the active sites and conductivity of the support are among the parameters affected by the morphology of the support that have not been studied in great detail.¹ One of the main reasons is that structural/morphological changes are not particularly easy to correlate with degradation.

In recent reports, pore size distributions (PSD) extracted from HRTEM microscopic images and adsorption data demonstrated complementary results that can be used independently to characterize porous carbons.^3,4 The relevant scale that promotes formation of an effective double-layer or the transfer of ions into the pore structure includes pores of 5–100 nm in size. Secondary Electron Microscopy (SEM) therefore is more a efficient way than HRTEM to access these lateral dimensions of mesoporosity. SEM is being used very extensively in the characterization of electrocatalysts.^5–7 Quantitative information, contained in SEM images is being largely under-utilized in most of the studies, as qualitative analysis by means of a visual inspection of images is often the dominating approach used for analytical correlation of morphology with electrocatalytic activity and/or stability. The goal of Digital Image Processing (DIP) is to find a representation of the intensity distribution of a given image and to convert 2-D images into 1-D image descriptors (values) that can be utilized for quantitative morphology representation and description.

One of the most important parameters which can be extracted from images by DIP is surface roughness, which is the first order statistics calculated from image intensity histogram.⁸ The average roughness (R_a) is the arithmetic mean of the absolute values of the surface departure from the mean plane. R_sk, the skewness of the roughness profile, is very important as it describes the asymmetry of the roughness, pointing to the domination of valleys (pores) or peaks in the micrograph. R_sk increases as the relative amount of pores, captured as dark values of intensity in images, increases.

Texture being a second order statistic is another important feature used in DIP. It arises from the repetition of local patterns. Textural features, such as based on a grey scale co-occurrence matrix, provide measures of contrast, randomness or directionality, which are important descriptors of materials morphology.^9,10 Textural measures describe important morphological features of materials, such as uniformity of pores and/or particles distribution, orderliness of structures (pores), repetitiveness vs. randomness of features, etc.

DIP of SEM images will result in large number of statistical parameters extracted (roughness and texture), which need to be correlated with the property of interest, in this case durability and performance of electrocatalysts. Dealing with a large number of variables and finding correlations between them for the purpose of classification of samples is an important challenge. Multivariate statistical methods of data analysis (MVA) become of critical importance in structure-to-property relationship modeling.¹¹ Principal Component Analysis (PCA) is used herein as an analysis tool to find samples that are globally correlated or anti-correlated and to facilitate visualization of the variables responsible for the correlations.

Herein, we demonstrate methodology for extracting quantitative morphological information from microscopic images by digital image processing and correlating this information with the activity and durability of electrocatalysts for building structure-to-property relationships using Principal Component Analysis. The presented methodology can be extended to any research involving targeted material design, where a set of microscopic images (SEM or TEM) and properties of interest, i.e. activity, solubility, wettability, etc., are measured for set of materials ranging in their properties.

Materials and methods

Materials

The electrocatalysts evaluated in this research work are 55 wt% PtCo supported on carbon blacks prepared by spray pyrolysis.¹² The carbons used for support are modified Ketjen Black (KB) carbons supplied by Cabot Corporation. Because of its large surface area (∼6X compared to VULCAN XC72), good conductivity, high structure and high hydrophilicity, KB is a viable candidate for low temperature fuel cell applications when modified to increase crystallinity and other morphological characteristics.

Instrumentation

Electrochemical evaluation of electrocatalysts. In electrochemical evaluation the materials are tested in a half-cell consisting of a three electrode system with liquid electrolyte (2M H₂SO₄) and a passive air supply. The working electrode is an air breathing gas diffusion electrode (GDE) with the gas diffusion and catalytic layers pressed on to a Ni (or Pt) mesh. Pt was used as the counter and Hg/Hg₂SO₄ as the reference electrode. In the electrochemical evaluation of carbon blacks, ECSA of the working electrode is calculated for all of the carbons subjected to half-cell evaluation by obtaining a cylic voltammogram at a scan rate of 5 mV s⁻¹ in the 0–200 mV range. A specific capacitance of 10 μF cm⁻² is conservatively assumed for all carbon blacks and the ECSA is obtained.

Chronoamperometry technique was used to provide short-term transient (current measured 15 s after voltage is applied) and pseudo steady-state (current measured 30 min after voltage is applied). With the potentiostat operating in the potentiostatic mode, the following potentials were applied: 0.8, 1.0, 1.2, 1.4 and 1.5 V and the corrosion currents were recorded vs. time for transient and steady-state conditions.

The durability of the cathode electrocatalyst was also obtained in a single membrane-electrode assembled (MEA) of PEMFC, air/nitrogen and Nafion® system. A 50 cm² MEA was prepared using the catalyst under investigation by a standard Cabot procedure, which is then assembled into a fuel cell and conditioned for 12–16 h. Initial measurements, such as hydrogen cross-over current and electrochemical surface area, were obtained followed by a polarization curve at a cell temperature of 80 °C with 50% relative humidity and a back pressure of 7.1 psig. Polarization curves provided open circuit potential (OCP) and current densities at 0.8 V and 0.7 V, representing ohmic and mass-transport regimes.

Scanning electron microscopy. The SEM used in this research work is a Hitachi S-5200 Nano SEM. It has a magnification ranging from 100×–2 000 000×. Resolution is 2 nm at 1 kV and 0.5 nm at 30 kV. Sample preparation for this SEM in this research work was comparatively very simple because of the powder nature of the carbon blacks. The candidate electrocatalyst powders were mounted onto a 200 mesh carbon-coated copper grid, which was then mounted onto a standard sample holder. The holder is then shaken vigorously but firmly to get rid of any extraneous material from the grid. All experimental parameters, i.e. voltage, magnification, current and gain, were kept constant from sample to sample to ensure that intensity variability in images is caused only by the sample variability and not instrumental factors. 5 replicate SEM images at 5 kV and 10 000× magnification from various areas on the sample were acquired. Pt loading was kept constant for all samples and it was assumed that the distribution of Pt particles and their size, which may vary due to support effects, will be reflected in the final morphology of the SEM image.

Brunauer-Emmett-Teller (BET) surface areas were determined from nitrogen adsorption/desorption measurements performed on a Quantochrome Autosorb-I-MP instrument.

Image processing

SEM images. Digital Image Processing of SEM images, including roughness and texture analysis, was done in in-house written GUI¹³ in Matlab using Image Processing Toolbox.¹⁴ 5 SEM images for each sample were processed and the resulting statistical parameters were averaged.

Multivariate analysis

Multivariate analysis of data was done using PLS Toolbox 5.0 for Matlab.¹⁵ Principal Component Analysis, using autoscaling as a preprocessing option (mean centering and scaling to unit variance), was the default method of data analysis. PCA extracts the key mathematical principal components (PC) from a large data matrix, by converting it into two smaller matrices that are easier to examine and interpret. The first PC accounts for the largest part of the variance in the data, the second PC accounts for the second-largest part of the variance, and so forth. The results of PCA are usually displayed as score plots (reflecting the significance of each sample in a principal component), loading plots (reflecting the significance of each variable in a principal component) and biplots (showing both samples and variables for two principal components). Biplots will be used herein as they provide a more instructive visualization of the clustering of samples for identification of variables that are the most or least important for a specific sample grouping. Correlated variables and samples will be located in the same regions on a biplot.

A PCA model was built from the data for samples 1,3,4,5,6,7,8 and 9, and then this model was applied to data for sample 2 as a validation step. This sample is displayed using a different color/symbol on biplots in the Results and Discussion section.

Results and discussion

Electrochemical testing of electrocatalysts

For each of the samples, corrosion data, i.e. corrosion currents for different voltages at transient and steady-state conditions in a gas diffusion electrode set-up, were obtained. Durability of the cathode electrocatalyst was also obtained in a single membrane-electrode assembled (MEA) of PEMFC. Polarization curves provided open circuit potential (OCP) and current densities at 0.8 V and 0.7 V, representing ohmic and mass-transport regimes. ECSA was calculated for estimation of the potential performance of the catalyst when dispersed on the support. Table 1 shows the results of MEA testing, while Fig. 1 plots GDE corrosion currents.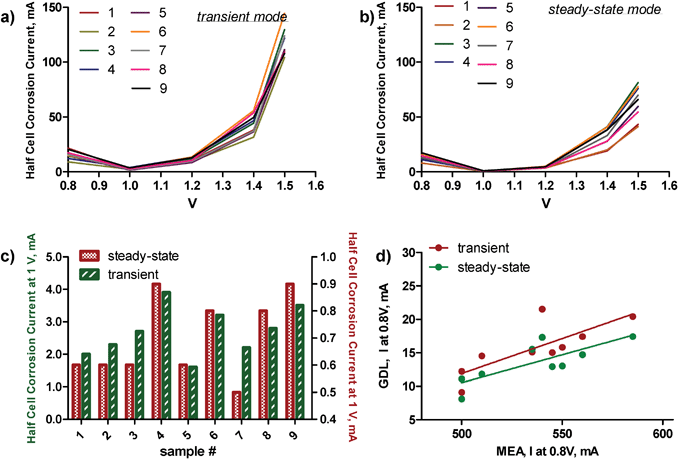

Fig. 1 Corrosion currents for a) transient, b) steady-state conditions for all samples. c) A comparison of currents at 1 V polarization for both conditions. d) A comparison of MEA data at 0.8 V to GDL corrosion data at 0.8 V.

Table 1 MEA performance data for all electrocatalyst samples along with BET surface area and ECSA

	MEA performance			Surface area
Sample	OCP, mV	I 0.8, mA	I 0.7, mA	BET	ECSA
1	946	540	1015	143	46.0
2	939	500	940	161	40.3
3	939	510	950	149	46.3
4	951	500	940	143	40.8
5	948	545	978	141	43.2
6	946	535	970	143	48.2
7	954	550	1000	149	47.4
8	975	560	1003	152	43.0
9	965	585	955	143	47.4

---

As a measure of the corrosion resistance, we used Kinoshita's definition as the current at 1 V polarization, the potential close to operating potential of a low temperature fuel cell.² It is clearly evident that sample numbers 4, 6 8 and 9 are the least oxidation resistant at potentials close to the operating potentials of a low temperature fuel cell (Fig. 1c). The electrochemical oxidation of carbon blacks in acidic electrolyte solutions is a combination of two processes. Below 1.23 V, carbon oxidizes to CO₂. Above 1.23 V, corrosion due to oxygen evolution contributes to the total corrosion current. Samples 3 and 4 have larger corrosion currents at higher voltages (1.4 and 1.5 V) than the rest of the samples. Fig. 1d compares MEA performance data at 0.8 V to the GDE corrosion data at the same potential at steady-state and transient regimes. The linear relationship between data from these two independent methods points towards good predictive ability of durability tests, such as was done in the half-cell in the GDE set-up of the performance of electrocatalysts in the MEA system.

Though large differences and trends between GDE corrosion data (Fig. 1) and MEA performance data, as well as BET surface area (Table 1) can be discerned from inspection of the original data, it is hard to visualize the similarities and differences between samples and the voltages responsible for them. Principal Component Analysis of all of the electrochemical data shown in Table 1 and Fig. 1 was used to analyze the similarities and differences between samples and the electrochemical properties responsible for them, as discussed below.

Digital image processing of SEM images

Fig. 2 shows a subset of SEM images acquired for 4 samples. Different sizes of carbon black particle agglomerations and pores are evident. Correlation of morphology with durability and performance of electrocatalysts through visual inspection of these images is very cumbersome, as well as subjective to the analyst's perception. Direct quantitative correlations are possible through the conversion of images into quantitative descriptors by DIP, such as roughness and texture. BET and ECSA provide integral surface area originating from porosity from the bulk of the material. SEM images, even though they represent the surface of the material, contain more morphological information than just porosity, such as will be discussed below. It is also important to understand how surface porosity is different from that in the bulk of the material.

Fig. 2 SEM images for samples a) 1, b) 4, c) 8, d) 9.

A typical surface exhibits roughness superimposed over waviness. Waviness is due to the more widely spaced repetitive deviations (low-frequency component of images) and roughness is due to the finer, random irregularities of surface texture (high-frequency component of images). Waviness and roughness are responsible for different phenomena and processes related to the electrocatalyst performance, mainly because they correspond to different diffusion regimes, i.e. the interplay between configurational and Knudsen diffusion in mesopores (10 s of nanometers) with high-frequency roughness and regular diffusion in macropores (100 s of nanometers) with low-frequency waviness. It is, thus, important to separate and evaluate waviness and roughness parameters individually. For this purpose, we have applied a high-pass filter to remove the low-frequency component and a low-pass filter to remove the high-frequency component from images to produce roughness and waviness image components, respectively. Fig. 3 shows typical original and filtered SEM image components from one of the catalysts, along with line profiles. As one can see, spacing of features in the high-frequency component images is in the order of tens of nanometers (referred to as meso-), while that for the low-frequency component is in the order of hundreds of nanometers (referred to as macro-). Roughness parameters (average roughness and skewness) can then be calculated from the low (R_a^L and R_sk^L) and high (R_a^H and R_sk^H) frequency image components separately.

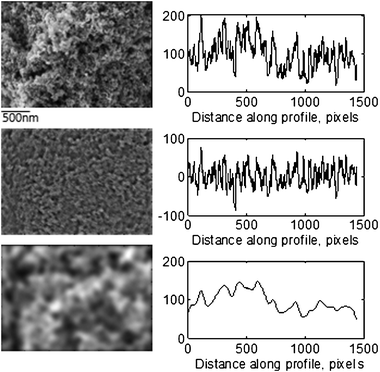Fig. 3 Original (top), high-frequency (middle) and low-frequency (bottom) component images for sample 1 with corresponding line profiles.

Grey-Level Co-occurrence Matrix (GLCM) texture measurements have been the workhorse of image texture. The GLCM is a tabulation of how often different combinations of pixel intensity values (grey levels) occur in an image. The GLCM described here is used for a series of “second order” texture calculations. First order texture measures are statistics calculated from the original image values, like roughness and skewness discussed above, and do not consider pixel neighbor relationships. Second order measures consider the relationship between groups of two (usually neighboring) pixels in the original image.

Four GLCM texture parameters, in particular, homogeneity, contrast, correlation and angular second momentum were also evaluated for images. Homogeneity is a measure of statistical stationarity, i.e. a measure of the probability that the pixels of each region have the same values. This property relates directly to self-similarity and inverse of contrast. Homogeneous images contain ideal repetitive structures, and such uniformity produces idealized patterns. Contrast (also called the sum of squares variance) represents the amount of local variation and represents the degree of differences between bright (particles) and dark (pores) values of intensity in images. Correlation measures the linear dependency of grey levels of neighboring pixels, with values of 0 for uncorrelated (a perfectly uniform image) and 1 for perfectly correlated pixels. Angular second moment (ASM, also called uniformity) measures the orderliness of an image. Higher values of ASM will be for more orderly images.

Both roughness and texture parameters are statistical measures calculated from intensity values within images, which are dependent not only on the material properties, but also microscope settings, such as magnification, acceleration voltage and current. To ensure that intensity variability is a function of the sample itself, all of the samples reported within this study were analyzed within several hours with microscope settings kept unchanged, as discussed in the Experimental section. Images acquired at different times, by different operators and at different settings cannot be included into this particular structure-to-property model as intensity within SEM images will be variable due to instrumental parameters as well. To represent the morphological properties for such heterogeneous samples, as carbon black-supported electrocatalysts, 5 areas on each sample were analyzed to obtain average statistical parameters. The Pt loading was kept constant for all samples to eliminate this effect on the morphology. The overall morphology, which is sampled by SEM, and, as consequence, roughness and texture parameters representing it, have contributions from the morphology of the carbon support itself, as well as from Pt nanoparticles, which may have different distributions and sizes on various types of carbon supports.

Table 2 shows the average statistical parameters extracted by DIP of 5 SEM images for all of the electrocatalysts. Though large differences and trends can be discerned from an inspection of Table 2, it is hard to find similarities and differences between samples and the morphological features responsible for them. In order to do so, PCA was applied to data contained within Table 2, as discussed below.

Table 2 Statistical parameters extracted from SEM images

	Roughness				Texture
Sample	R a ^L	R sk ^L	R a ^H	R sk ^H	Contr.	Corr.	ASM	Homog.
1	17.2	0.73	84.6	1.09	0.39	0.77	0.14	0.82
2	22.1	0.53	93.3	1.12	0.49	0.82	0.10	0.79
3	19.7	0.75	87.8	1.07	0.41	0.77	0.15	0.81
4	17.7	0.91	90.7	1.07	0.35	0.78	0.19	0.84
5	19.4	0.71	89.0	1.11	0.39	0.83	0.13	0.82
6	20.5	0.60	90.5	1.08	0.49	0.76	0.12	0.79
7	21.3	0.60	90.6	1.13	0.46	0.83	0.10	0.80
8	19.5	0.65	95.3	1.06	0.40	0.78	0.14	0.82
9	24.0	0.46	95.6	1.08	0.55	0.79	0.10	0.77

---

Structure-to-property relationship via PCA

As we have discussed above, it is possible to discern major differences between samples and electrochemical and morphological parameters from visual inspection of Tables 1, 2 and Fig. 1. However, it is virtually impossible to find correlations between samples and variables in this way. Multivariate analysis methods can be used to reduce the dimensionality of the data and help interpret data. PCA is mathematically defined as an orthogonal linear transformation that transforms the data to a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on. The results of a PCA are usually discussed in terms of component scores (the transformed variable values corresponding to a particular sample in the data) and loadings (the weight by which each standardized original variable should be multiplied to get the component score). PCA biplots, as shown in Fig. 4, display scores or relationships between samples and loading or relationships between variables for 2 principal components on one plot. Samples that have values of parameters (variables) close to the mean of all samples are located near the x and y axes intersection. Variables that have zero or low contribution into principal components also lie along the zero axes. The further the samples or variables are from the zero intersection in any direction, the more different the sample is from the mean and the more significant the variable is. Similar samples lie close to each other in the same quadrant of the biplot with variables having the highest contribution to these samples in the same quadrant.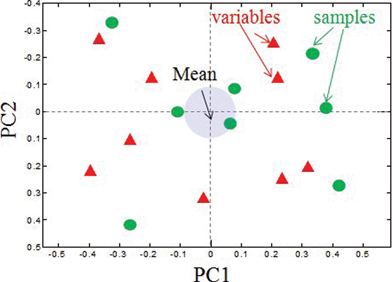

Fig. 4 A PCA biplot showing the relationship between loadings and variables. Correlated variables and samples will be located in the same quadrant on a biplot.

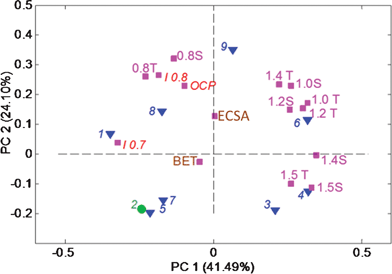
First, we will discuss correlations identified among a set of catalysts based on electrochemical data including single MEA performance (open circuit potential (OCP), I0.7 and I0.8 (currents at 0.7 and 0.8 V, respectively), chronoamperometry in gas-diffusion electrode (currents at different potentials are noted by corresponding value of potential and S and T stands for either steady-state, i.e. 1.4S, or transient regimes, i.e. 1.4T, as discussed in experimental section) and surface areas, BET and electrochemically accessible (ECSA) (data shown in Table 1 and Fig. 1). Fig. 5 shows a biplot of these data. First principal component (PC1) captures 41.5% of variance in data and separates samples based on durability. Samples on the positive side of the x-axis, i.e. 3, 4, 6 and 9, have higher corrosion currents at all overpotentials (OPs), while samples on the negative side of the x-axis, i.e. 1, 5, 7 and 8, have lower corrosion currents. PC2 separates samples by electrocatalytic activity. Open circuit potential (OCP) and currents measured at 0.7 and 0.8 V all contribute positively to PC2. Samples 1, 6, 8 and 9, correlating with these electrochemically measured performance parameters, have better catalytic activity than the group of samples 3, 4, 5 and 7, within which samples 5 and 7 are relatively poor initial catalysts with modest catalytic activity at higher OPs. Samples 1, 8 and 9 comprise the optimal group that combines high activity and moderate durability. Values of currents at 0.8 V determined by chronoamperometry in gas diffusion electrode and MEA testing lie very closely on the biplot due to high correlation, confirming that the durability test, such as that done in a half-cell in the GDE set-up, is a very good predictor of performance in the complete MEA test system. BET surface area has a low contribution to both principal components, indicating that the changes in the bulk porosity do not have any correlation with MEA performance or corrosion behavior.

Fig. 5 The PCA biplot for electrochemical performance and durability data (Table 1 and Fig. 1).

Furthermore, PC2 separates samples by type of corrosion, i.e. corrosion due to evolution of oxygen (dominant at OPs higher than 1.23 V) and electrochemical corrosion, occurring at OPs below 1.23 V). In samples 3 and 4, corrosion due to evolution of oxygen is dominating in comparison with samples 6 and 9. Data for validation sample 2 were excluded from the model and the model created from the data for the rest of the samples was then applied to data for this sample. Validation shows that sample 2 belongs to the group of samples 5 and 7.

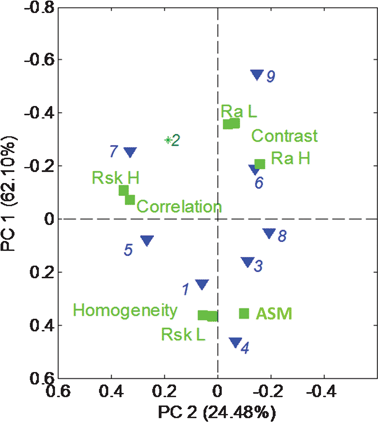
Fig. 6 shows the PCA biplot for morphological parameters (roughness and texture) extracted from SEM images (in Table 2) (note that PC1 is plotted vs. PC2 and axes are reversed for easier comparison with Fig. 5). Classification of samples based on morphological parameters extracted from SEM images is very similar to that obtained from electrochemical performance. Samples 3, 4, 6 and 9, being more corrosive, are also very different from the other samples in their morphology, having a higher contrast and overall roughness in both macro- and meso-regimes as well as ASM (order). Sample 8 has the same morphology as all of these samples, but is much more durable, indicating that surface composition and chemistry should also be taken into consideration (ongoing work). Homogeneity of the image which is larger for repetitive uniform structures (such as ordered pores) is correlated with skewness in macro-regime R_sk^L, which is indicative of a larger amount of pores of hundreds of nanometers. Correlation, on the other hand, which is higher for perfectly correlated pixels (less uniform images) is correlated with skewness on meso-regime R_sk^H, which is indicative of larger amounts of smaller 10 s nms pores. It might indicate that mesopores are non-uniformly distributed, while macropores are uniformly ordered.

Fig. 6 The PCA biplot for SEM statistics (Table 2).

Fig. 7 shows the PC biplot for the data table combining roughness and texture parameters (Table 2) with the electrochemical data shown in Fig. 1 and Table 1. As one can see, the grouping of samples based on a combination of performance and morphology (Fig. 7) is similar to the grouping determined based on performance only (Fig. 6). Combining the performance data with morphology, however, brings an understanding of the effect that morphology has on performance. Specifically, the highest ECSA and electrocatalytic activity is correlated with the highest roughness in both meso- and macro-regimes and high contrast or heterogeneity in images. BET, on the other hand which shows overall bulk porosity does not contribute to either of the principal components, showing that bulk surface area is not the factor responsible for electrocatalytic activity and stability of these electrocatalysts. Electrochemically accessible surface area, on the other hand, along with heterogeneity of the morphology, which is determined by roughness and contract parameters from SEM images, are directly related to the performance of the electrocatalysts in a real fuel-cell environment. High overall meso- and macro-roughness also contribute to the corrosion process (a positive contribution into PC1). Similarly to what has been seen from the PCA of just morphological parameters, it is evident that skewness from high-frequency regime (mesopores) and skewness from low-frequency mode (macropores) are anti-correlated. Lots of mesopores (high R_sk^H) and high correlation (more disordered morphology) in images is contributing to electrocatalytic activity, especially at 0.7 V, indicating larger accessibility of sites, while lots of larger pores (high R_sk^L) and more homogeneous and ordered features contribute to high corrosion currents. Sample 9 is a sample with optimal morphological parameters resulting in the largest electrocatalytic activity and moderate durability. Large roughness in both meso- and macro regimes, as well as a large amount of disordered small pores provides better access to smaller active particles, which might not be as accessible through larger macropores resulting in better performance. At the same time, a larger amount of mesopores versus a larger amount of macropores also results in smaller corrosion currents. Larger pores create larger surface area access for the corrosion process.

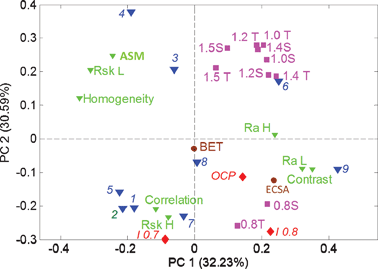Fig. 7 The PCA biplot for combined SEM statistics (Table 2) and electrochemical performance (Table 1) and durability (Fig. 1) data.

Conclusions

The methodology presented in this work focused on 1) conversion of microscopic images into a useful quantitative morphological descriptor, 2) separating roughness in meso- and macro-regimes and 3) using PCA to correlate morphological parameters with electrochemical performance as very useful tool for understanding the properties of carbon black samples that should be targeted to achieve an optimally performing electrocatalyst. An electroactive and durable electrocatalyst should have a balanced morphology, where high roughness in both tens and hundreds of nanometers dimension of features provides high ECSA, lots of small pores (tens of nm) result in more accessible sites and limited large porosity (hundreds of nm) leads to higher durability.

We would like to acknowledge the support of DOE-EPSCoR DE-FG02-08ER46530 New Mexico Implementation Program.

References

1. R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J. E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K. I. Kimijima and N. Iwashita, Chem. Rev., 2007, 107(10), 3904–3951.
2. K. Kinoshita, Carbon: Electrochemical and Physicochemical Properties, Wiley, John & Sons Inc., New York, NY, 1988.
3. Z. H. Huang, F. Y. Kang, W. L. Huang, J. B. Yang, K. M. Liang, M. L. Cui and Z. Y. Chen, J. Colloid Interface Sci., 2002, 249(2), 453–457.
4. D. Lozano-Castello, D. Cazorla-Amoros, A. Linares-Solano, K. Oshida, T. Miyazaki, Y. J. Kim, T. Hayashi and M. Endo, J. Phys. Chem. B, 2005, 109(31), 15032–15036.
5. E. Slavcheva, G. Ganske, G. Topalov, W. Mokwa and U. Schnakenberg, Appl. Surf. Sci., 2009, 255(13–14), 6479–6486.
6. S. Ang and D. Walsh, Appl. Catal., B, 2010, 98, 49–56.
7. J. Aragane and H. Urushibata, Nippon Kagaku Kaishi, 1995,(9), 736–742.
8. K. A. Alshibli and M. I. Alsaleh, J. Comput. Civ. Eng., 2004, 18(1), 36–45.
9. R. B. VonDreele, J. Appl. Crystallogr., 1997, 30, 517–525.
10. J.-P. D. Costa, C. Germain and P. Baylou, in 2001 - GRETSI - Actes de Colloques, 2001.
11. K. Artyushkova, S. Pylypenko, T. S. Olson, J. E. Fulghum and P. Atanassov, Langmuir, 2008, 24(16), 9082–9088.
12. D. A. Konopka, S. Pylypenko, P. Atanassov and T. L. Ward, ACS Appl. Mater. Interfaces, 2010, 2(1), 86–95.
13. K. Artyushkova, GUI for calculating 1st and 2nd order statistics from images http://me.lt/9eN76.
14. Matlab 2008, MathWorks, Natick, Massachusetts.
15. PLS Toolbox 5.0 Eigenvector Research, Wenatchee, WA.

---