On the electronic structure and conflicting d-orbital aromaticity in the Re3O3− cluster†
Hua-Jin
Zhai
a,
Wen-Jie
Chen
b,
Xin
Huang
*b and
Lai-Sheng
Wang
*a
aDepartment of Chemistry, Brown University, Providence, Rhode Island 02912, USA. E-mail: Lai-Sheng_Wang@brown.edu
bDepartment of Chemistry, Fuzhou University, Fuzhou, Fujian 350108, P. R. China and State Key Laboratory of Structural Chemistry, Fuzhou, Fujian 350002, P. R. China. E-mail: xhuang@fzu.edu.cn
First published on 22nd February 2012
Abstract
The structure and chemical bonding in the Re3O3− cluster are investigated using photoelectron spectroscopy and density-functional theory calculations. Vibrationally-resolved photoelectron spectra were obtained, yielding an accurate electron affinity (2.54 ± 0.02 eV) and a ground-state Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequency (960 ± 30 cm−1) for the Re3O3 neutral cluster. It is shown that the Re3O3− cluster possesses a C2v (1A1) ground-state structure consisting of a Re3 triangle with one bridging and two terminal oxygens. Molecular orbital analysis reveals that the Re3 core in Re3O3− possesses conflicting d-orbital aromaticity (π-antiaromatic and σ-aromatic), consistent with its C2v symmetry. Well-resolved photodetachment transitions from the Re 5dz2 δ orbitals allow the bond strength and resonance energy of a delocalized δ-bond to be estimated.
O stretching frequency (960 ± 30 cm−1) for the Re3O3 neutral cluster. It is shown that the Re3O3− cluster possesses a C2v (1A1) ground-state structure consisting of a Re3 triangle with one bridging and two terminal oxygens. Molecular orbital analysis reveals that the Re3 core in Re3O3− possesses conflicting d-orbital aromaticity (π-antiaromatic and σ-aromatic), consistent with its C2v symmetry. Well-resolved photodetachment transitions from the Re 5dz2 δ orbitals allow the bond strength and resonance energy of a delocalized δ-bond to be estimated.
There has recently been increasing interest in free transition-metal oxide clusters, primarily aiming for a molecular-level understanding of oxide catalysts using well-defined and controllable model systems.1–6 Characterization of the structures and electronic properties of oxide clusters is a prerequisite to assess their suitability as models for catalytic active centers. Photoelectron spectroscopy (PES),5 among other gas-phase experimental techniques including infrared multiple photon dissociation (IR-MPD) spectroscopy,2 has emerged as a powerful tool to probe the intrinsic geometric and electronic properties of oxide clusters. Furthermore, the oxidation states of the metal centers in oxide clusters can be tuned by controlling the composition, providing opportunities to explore novel chemical bonding in transition-metal-containing systems. For example, d-orbital aromaticity7 and δ-aromaticity8 owing to multi-center d–d bonding have been discovered recently in transition metal oxide clusters.9,10 In the current communication, we report vibrationally resolved PES spectra for the Re3O3− cluster. Combined PES and density-functional theory (DFT) calculations show that the Re3O3− cluster adopts a C2v (1A1) global minimum with one bridging and two terminal oxygens. Molecular orbital analysis reveals conflicting d-orbital aromaticity (σ-aromatic and π-antiaromatic) for this cluster, consistent with the C2v structural distortion of the Re3 core. The PES spectra also allow us to evaluate the strength and resonance energy of the delocalized Re 5dz2 δ-bond on the basis of well-resolved detachment transitions from the δ orbitals.
The Re3O3− clusters were produced in a laser vaporization supersonic cluster source and mass-selected for the photodetachment PES experiment (see the Experimental Section). The PES spectra at 193 nm (6.424 eV) and 355 nm (3.496 eV) photon energies are shown in Fig. 1. The ground-state band X is well-resolved at 355 nm with a short vibrational progression (960 ± 30 cm−1). The 0–0 transition yields an accurate value for the electron affinity of the Re3O3 neutral cluster as 2.54 ± 0.02 eV (Table 1), which also defines the first adiabatic (ADE) and vertical detachment energy (VDE) for the Re3O3− anion cluster. The 355 nm spectrum also reveals a relatively weak and sharp band A at 3.04 eV, which defines the first excited state of Re3O3. The sharp peak is followed by a broad weak feature, which will be shown below to be due to shake-up transitions. Band A displays a strong dependence on photon energies and its relative intensity is greatly enhanced at 193 nm (Fig. 1b). The weak band B at a VDE of 3.43 eV is better defined at 193 nm. Numerous broad bands are revealed at higher binding energies. Band C (VDE: 4.34 eV) has an estimated ADE of 3.95 eV. The spectrum is essentially continuous beyond 4.6 eV, and bands D (∼4.8–5.2 eV) and E (∼5.7 eV) are tentatively labeled for the sake of discussion.
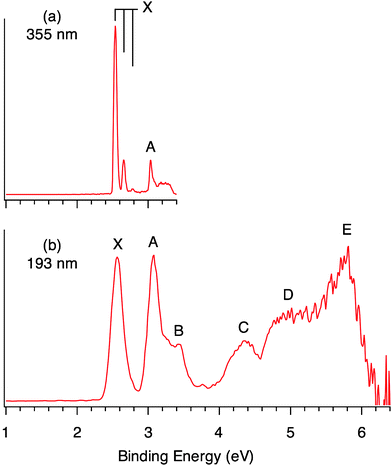 | ||
| Fig. 1 Photoelectron spectra of Re3O3− at (a) 355 nm (3.496 eV) and (b) 193 nm (6.424 eV). The vertical lines in (a) represent the resolved vibrational structures. | ||
| Feature | ADE (exptl)a | VDE (exptl)a | Channel | VDE (theor) |
|---|---|---|---|---|
| a Numbers in parentheses represent experimental uncertainties in the last digit. b The ground-state vibrational frequency for the Re3O3 neutral species is measured to be 960 ± 30 cm−1 from the observed vibrational progression of Re3O3− (band X, Fig. 1a). c Electron affinity of the neutral species. d Due to shake-up processes (see text). | ||||
| Xb | 2.54 (2)c | 2.54 (2) | HOMO (4a1) | 2.39 |
| A | 3.04 (2) | 3.04 (2) | HOMO−1 (2b2) | 2.99 |
| Bd | 3.43 (5) | |||
| C | 3.95 (5) | 4.34 (5) | HOMO−2 (3a1) | 4.31 |
| D | ∼4.8–5.2 | HOMO−3 (1a2) | 4.65 | |
| HOMO−4 (2a1) | 4.78 | |||
| HOMO−5 (1b1) | 5.19 | |||
| E | ∼5.7 | HOMO−6 (1b2) | 5.52 | |
Structural searches were conducted at the B3LYP level of theory (see the Computational Methods section). Candidate structures for Re3O3− and Re3O3 with a wide variety of initial geometries and different spin multiplicities are considered and all the optimized structures are summarized in the ESI† (Figs. S1 and S2). The global minima of Re3O3− and Re3O3 and selected low-lying structures (within ∼0.5 eV) are shown in Fig. 2. The global minimum of Re3O3− is a C2v (1A1) structure (Fig. 2a), in which the Re3 trimer is coordinated with one bridging and two terminal O atoms. The bridging O exhibits typical single Re–O bond distances (1.920 Å), while the terminal O atoms give Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bonds (1.728 Å). The Re atom that is not bonded with O gives two very short Re–Re distances (2.309 Å);11 the third Re–Re bond is elongated (2.808 Å). The low-lying anion structures (Fig. 2b and 2c) show similar atomic connectivities and bond distances, but possess lower symmetry relative to the global minimum. Alternative anion structures (Fig. S1, ESI†) are at least ∼0.5 eV higher in energy. In particular, the highly symmetric tri-terminal D3h (3A1′) and tri-bridged D3h (1A1′) anion structures are 3.06 and 5.36 eV above the global minimum, respectively. The Re3O3 neutral cluster possesses a C2v (2A1) global minimum (Fig. 2d), which closely resembles that of the anion (Fig. 2a). Three low-lying quartet Cs or C2v neutral structures are within ∼0.5 eV (Fig. 2e–2g). Additional neutral structures turn out to be at least ∼0.8 eV above the global minimum (Fig. S2, ESI†). To ensure the reliability of the energetics of the B3LYP calculations, the relative energies for the low-lying structures of Re3O3− were further evaluated via coupled cluster [CCSD(T)] single-point calculations at the B3LYP geometries. As shown in Table 2 the B3LYP and CCSD(T) results are coherent, firmly showing that the C2v (1A1) structure is the global minimum for the Re3O3− anion cluster.
O double bonds (1.728 Å). The Re atom that is not bonded with O gives two very short Re–Re distances (2.309 Å);11 the third Re–Re bond is elongated (2.808 Å). The low-lying anion structures (Fig. 2b and 2c) show similar atomic connectivities and bond distances, but possess lower symmetry relative to the global minimum. Alternative anion structures (Fig. S1, ESI†) are at least ∼0.5 eV higher in energy. In particular, the highly symmetric tri-terminal D3h (3A1′) and tri-bridged D3h (1A1′) anion structures are 3.06 and 5.36 eV above the global minimum, respectively. The Re3O3 neutral cluster possesses a C2v (2A1) global minimum (Fig. 2d), which closely resembles that of the anion (Fig. 2a). Three low-lying quartet Cs or C2v neutral structures are within ∼0.5 eV (Fig. 2e–2g). Additional neutral structures turn out to be at least ∼0.8 eV above the global minimum (Fig. S2, ESI†). To ensure the reliability of the energetics of the B3LYP calculations, the relative energies for the low-lying structures of Re3O3− were further evaluated via coupled cluster [CCSD(T)] single-point calculations at the B3LYP geometries. As shown in Table 2 the B3LYP and CCSD(T) results are coherent, firmly showing that the C2v (1A1) structure is the global minimum for the Re3O3− anion cluster.
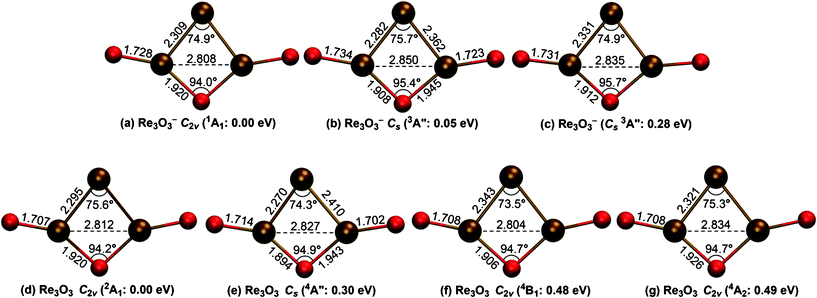 | ||
| Fig. 2 Optimized global minima and low-lying structures (within ∼0.5 eV) for Re3O3− and Re3O3 clusters at the B3LYP/Re/Stuttgart+2f1g/O/aug-cc-pVTZ level. Bond distances (in Å) and selected bond angles (°) are shown. | ||
To facilitate comparison with the experiment, we have simulated the PES spectra of Re3O3− on the basis of the C2v global minimum (Fig. 2a), the low-lying Cs structures (Fig. 2b and 2c), and selected D3h structures (Figs. S3 and S4, ESI†). The highly-symmetric and higher energy D3h structures are included because these are tempting candidates to account for the observed simple vibrational progression in the ground-state PES band (Fig. 1a). All simulated spectra are compared with the 193 nm experimental spectrum in Fig. 3. It is immediately clear that the two higher-energy D3h structures do not agree with the experiment (Fig. 3d and 3e) and they can be safely ruled out. The two low-lying Cs (3A′′) structures are both triplet states and they display slightly lower electron binding energies.12,13 The observed PES spectra of Re3O3− are very clean on the lower binding energy side, which suggests that there are no contributions from any low-lying isomers or even any vibrational hot bands, and a single isomer is responsible for the observed spectra.
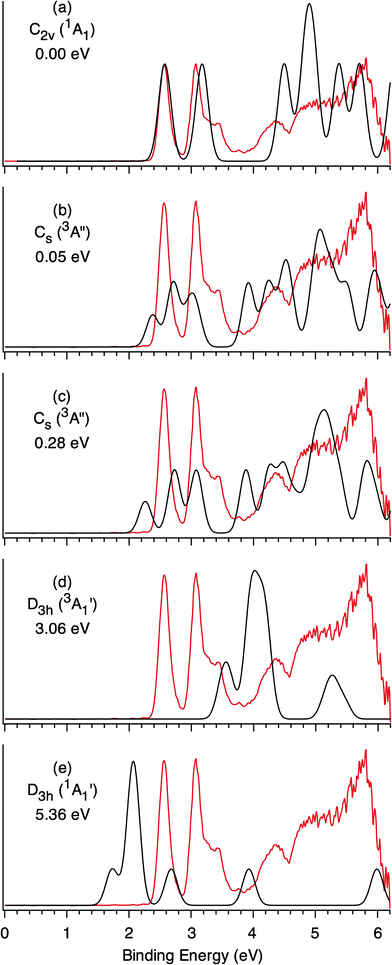 | ||
| Fig. 3 Simulated photoelectron spectra (black curves) for the C2v (1A1) global minimum (a), low-lying Cs structures (b and c), and selected D3h structures (d and e) of Re3O3−, compared to the experimental 193 nm spectrum (red curve). Relative energies at the B3LYP level are shown. The simulations are done by fitting the distribution of calculated vertical detachment energies with unit-area Gaussian functions of 0.1 eV width. The simulated spectrum in (a) has been shifted to the blue by 0.15 eV to show its overall agreement with experiment. | ||
The simulated spectrum of the C2v (1A1) global minimum well reproduces the observed PES spectral features (Fig. 3a). The C2v (1A1) global minimum is closed shell with the valence electron configuration 1a121b221b122a121a223a122b224a12. Detachment from the 4a1 highest occupied molecular orbital (HOMO) results in the neutral C2v (2A1) ground state with a predicted VDE of 2.39 eV, which is in good agreement with the experimental value of 2.54 eV (Table 1). B3LYP appears to underestimate the ground-state electron binding energy by ∼0.15 eV. The VDE for detachment from HOMO−1 (2b2) is predicted as 2.99 eV, in excellent agreement with the experimental band A (VDE: 3.04 eV). Both the 4a1 and 2b2 orbitals (Fig. 4) are primarily nonbonding Re 5dz2 lone pairs (or more strictly speaking, slightly antibonding orbitals), consistent with the observed sharp PES bands X and A, which suggest no or little geometry changes upon electron detachment. The next detachment channel is from HOMO−2 (3a1) with a calculated VDE of 4.31 eV, which is in excellent agreement with band C (VDE: 4.34 eV). The 3a1 HOMO−2 is a Re–Re bonding orbital, consistent with the broad PES band observed. Detachment channels from HOMO−3 through HOMO−6 are predicted within the 4.6–5.6 eV binding energy range and all involve bonding or antibonding orbitals, consistent with the broad and nearly continuous spectral features (D and E). The above assignments leave band B unaccounted for. This relatively weak band is assigned to shake-up processes, due to the availability of low-lying unoccupied 5d orbitals. Indeed, B3LYP calculations predict a shake-up transition (2B1 ← 1A1) at 3.27 eV, which involves detaching an electron from the HOMO and simultaneously promoting another from the HOMO to the lowest unoccupied molecular orbital (LUMO). Another shake-up transition, 2A2 ← 1A1, is predicted at 3.34 eV, where an electron is detached from the HOMO and another is promoted from the HOMO to LUMO+1. These shake-up transitions are in excellent agreement with band B (3.43 eV), demonstrating strong electron correlation effects in the Re3O3− cluster.
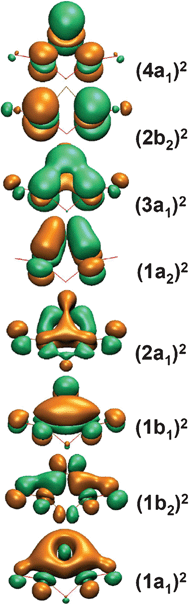 | ||
| Fig. 4 Molecular orbital pictures for the C2v (1A1) global minimum of Re3O3−. | ||
The well-resolved and simple vibrational progression in the ground-state transition (Fig. 1a) is remarkable, suggesting that both the Re3O3− anion and Re3O3 neutral cluster are of relatively high symmetry with little geometry change between them. The high frequency (960 ± 30 cm−1) suggests that the vibrational mode should involve a totally symmetric Re–O stretching. Vibrational analysis for the neutral C2v (2A1) global minimum reveals a totally symmetric Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequency of 1003.5 cm−1 (unscaled) for the terminal oxygens, in good agreement with the experimental measurement. The HOMO (4a1) of C2v (1A1) anion is an antibonding δ* orbital with minor contributions from the terminal O 2p atomic orbitals. Our calculations show that indeed very little anion-to-neutral structural changes take place regarding the Re–Re and Re–O–Re bond distances and the bond angles (Fig. 2aversus2d). The most obvious geometric change is the shortening of the terminal Re
O stretching frequency of 1003.5 cm−1 (unscaled) for the terminal oxygens, in good agreement with the experimental measurement. The HOMO (4a1) of C2v (1A1) anion is an antibonding δ* orbital with minor contributions from the terminal O 2p atomic orbitals. Our calculations show that indeed very little anion-to-neutral structural changes take place regarding the Re–Re and Re–O–Re bond distances and the bond angles (Fig. 2aversus2d). The most obvious geometric change is the shortening of the terminal Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances by 0.021 Å, in excellent agreement with the observed vibrational progression. Therefore, the observed vibrational structures provide further structural proof for the anion C2v (1A1) and neutral C2v (2A1) global minima.
O distances by 0.021 Å, in excellent agreement with the observed vibrational progression. Therefore, the observed vibrational structures provide further structural proof for the anion C2v (1A1) and neutral C2v (2A1) global minima.
The C2v global minimum structure for Re3O3− is interesting, and it is very different from the highly symmetric D3h aromatic W3O92− and Ta3O3− clusters.7,8 The origin of the reduced symmetry in Re3O3− can be understood from an analysis of its valence electronic structure. The Re atom possesses an electron configuration of 5d56s2. All eight occupied valence orbitals in the Re3O3− (C2v, 1A1) ground state are Re-based s–d orbitals, as shown in Fig. 4. The HOMO (4a1), HOMO−1 (2b2), and HOMO−2 (3a1) are δ* and δ orbitals composed of Re 5dz2 atomic orbitals from each Re atom. These three orbitals can be effectively localized as three dz2 lone-pairs, and they do not contribute to net bonding in the Re3O3− cluster. The HOMO−4 (2a1), HOMO−6 (1b2), and HOMO−7 (1a1) are all delocalized σ orbitals from combinations of Re 6s/5d hybrid atomic orbitals. The six delocalized σ electrons render Re3O3− σ aromatic. The HOMO−3 (1a2) and HOMO−5 (1b1) are delocalized π orbitals from Re 5d atomic orbitals. The four π electrons indicate that the Re3O3− cluster can be considered as π-antiaromatic according to the Hückel rule, which is the origin for the C2v global minimum structure. Thus, the Re3O3− cluster is an unusual case of conflicting d-orbital aromaticity. Note that the shorter Re–Re distances (2.309 Å) in C2v (1A1) are in between typical Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Re (2.38 Å) and Re
Re (2.38 Å) and Re![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Re (∼2.2 Å) bonds,11 suggesting enhanced Re–Re bonding due to the electronic delocalization in the Re3 core.
Re (∼2.2 Å) bonds,11 suggesting enhanced Re–Re bonding due to the electronic delocalization in the Re3 core.
Conflicting aromaticity is known in molecules composed of main group elements,9,14–16 but has not been observed for transition-metal systems to date. In fact, the idea of d-orbital aromaticity is fairly new,7–10,17–23 and there are no previously known d-orbital antiaromatic species. A previous suggestion of a “potentially” d-orbital antiaromatic Ti3(CO)3 cluster24 has recently been shown to be an aromatic species after all.10,25 The conflicting d-orbital aromaticity observed in Re3O3− hints that there may potentially be a wide variety of transition-metal aromatic compounds with multiple aromaticity and/or antiaromaticity. It is noted that the well-known 12e Re3Cl9 compound possesses three localized Re![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Re double bonds and the 14e Re3Cl92− dianion is a 2π aromatic system.26
Re double bonds and the 14e Re3Cl92− dianion is a 2π aromatic system.26
The δ-bond in transition metal compounds is known to be much weaker than either the σ- or π-bond.27 Delocalized multi-center δ-bond (δ-aromaticity)8 represents a new mode of chemical bonding, which should exert additional resonance stabilization. The unique electronic structure of the Re3O3− cluster offers an opportunity to experimentally quantify the resonance energy for a delocalized δ-bond. As shown in Fig. 4, the HOMO (δ*), HOMO−1 (δ*), and HOMO−2 (δ) of Re3O3− (C2v, 1A1) are the bonding and antibonding combinations composed of the Re dz2 atomic orbitals, which correspond to the observed PES bands X, A, and C, respectively (Fig. 1). These orbitals are fully occupied, resulting in negligible net bonding contribution, that is, three dz2 lone-pairs. If we take the centroid of the three observed PES bands as a reference (Fig. 5b), it is possible to estimate the stabilization energy of the bonding dz2 δ orbital and the destabilization energies of the dz2 δ* orbitals, using the differences of the measured ADEs as shown in Fig. 5a.28,29 The bonding δ orbital is stabilized by 0.77 eV, giving rise to an electronic stabilization energy for the delocalized δ-bond of 1.54 eV (∼35 kcal mol−1). This stabilization energy is substantially higher than that of a typical localized δ-bond as established for transition metal dimer complexes via electronic absorption spectroscopy (upper limit: 20 kcal mol−1).29 The difference of ∼15 kcal mol−1 can be attributed to the resonance energy of the delocalized δ-bond, which is quite significant and nearly comparable to the strength of a localized δ-bond itself. It is stressed that the above values for bond strength and resonance energy of a delocalized δ-bond are based on the distorted C2v structure and should be considered qualitative estimates.30 For an ideally delocalized δ-bond the resonance energy is expected to be even larger. Evaluation of the resonance energy of an aromatic molecule has been a notoriously difficult and complex task in general, relying largely on the choice of an appropriate reference system.31 Our PES study of Ta3On− (n = 1–5) clusters provides a hint that the delocalization indeed has an observable stabilization effect on the δ orbital, but quantification of this effect was not possible previously.32 It is instructive to compare the resonance energy of the delocalized δ-bond with those of the π-aromatic benzene (36 kcal mol−1)31 and the d-orbital σ-aromatic W3O92− cluster (∼24 kcal mol−1),7 which suggests that the resonance energy correlates closely with the type of bond, as anticipated.
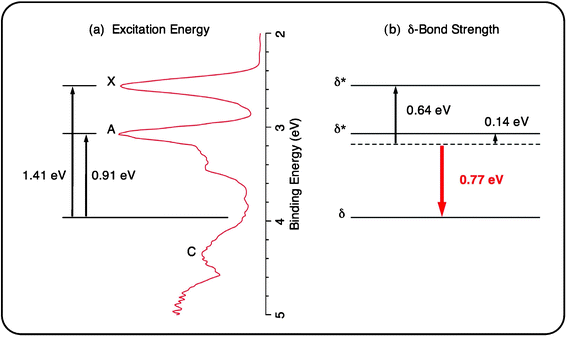 | ||
| Fig. 5 The measured X–C and A–C adiabatic excitation energies from the photoelectron spectra (a) allow the evaluation of energetic stabilization of the delocalized δ orbital and destabilization of the δ* orbitals (b). The strength of a delocalized δ-bond thus amounts to 1.54 eV (∼35 kcal mol−1). | ||
In conclusion, we have investigated the electronic properties and chemical bonding of the Re3O3− cluster via vibrationally-resolved photoelectron spectroscopy and density-functional theory calculations, showing that the Re3O3− anion cluster adopts a C2v (1A1) global minimum structure. Bonding analysis reveals a conflicting d-orbital aromaticity (σ-aromaticity and π-antiaromaticity). The experimental data also facilitates the evaluation of the strength (∼35 kcal mol−1) and resonance energy (∼15 kcal mol−1) of a delocalized δ-bond.
Experimental and computational section
Photoelectron spectroscopy
The experiment was carried out using a magnetic-bottle PES apparatus equipped with a laser vaporization supersonic cluster source.33 Briefly, RemOn− cluster anions were produced by laser vaporization of a pure Re disk target in the presence of a helium carrier gas seeded with 0.01% O2 and were analyzed using a time-of-flight mass spectrometer. Re3O3− clusters were mass-selected and decelerated before being photodetached. Photoelectrons were collected at nearly 100% efficiency by the magnetic bottle and analyzed in a 3.5 m long electron flight tube. The PES spectra were calibrated using the known spectra of Rh− and Au−, and the resolution of the apparatus was ΔEk/Ek ≈ 2.5%, that is, ∼25 meV for 1 eV electrons.Computational methods
The DFT calculations were carried out using the hybrid B3LYP functional.34–36 The global minimum searches were performed using analytical gradients with the Stuttgart relativistic small core basis set and effective core potential37,38 augmented with two f-type and one g-type polarization function for Re [ζ(f) = 0.327, 0.955; ζ(g) = 0.636] as recommended by Martin and Sundermann39 and the aug-cc-pVTZ basis set for oxygen.40,41 Scalar relativistic effects, that is, the mass velocity and Darwin effects, were taken into account via the quasi-relativistic pseudo-potentials. Vibrational frequency calculations were performed to verify the nature of the stationary points. The VDEs were calculated using the generalized Koopmans' theorem by adding a correction term to the eigenvalues of the anion.42 The correction term was calculated as δE = E1 − E2 − εHOMO, where E1 and E2 are the total energies of the anion and neutral, respectively, in their ground states at the anion equilibrium geometry and εHOMO corresponds to the eigenvalue of the HOMO of the anion. All B3LYP calculations were performed using the Gaussian 03 package.43 Additional single-point calculations at the coupled cluster [CCSD(T)]44 level with the Re/Stuttgart+2f1g/O/aug-cc-pVTZ basis sets at the B3LYP geometries were performed to evaluate the relative energies of the three low-lying anion cluster structures. For open-shell systems, the R/UCCSD(T) approach was used, where a restricted open-shell Hartree–Fock (ROHF) calculation was initially performed and the spin constraint was relaxed in the correlation treatment. The CCSD(T) calculations were performed using the MOLPRO 2010.1 package.45Acknowledgements
This work was supported by the Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, U. S. Department of Energy under grant No. DE-FG02-03ER15481 (catalysis center program). X. H. gratefully acknowledges support from the Natural Science Foundation of China (21071031 and 90922022) and the Natural Science Foundation of Fujian Province of China (No. 2008J0151).References
- D. K. Bohme and H. Schwarz, Angew. Chem., Int. Ed., 2005, 44, 2336 CrossRef.
- K. R. Asmis and J. Sauer, Mass Spectrom. Rev., 2007, 26, 542 CrossRef CAS.
- G. E. Johnson, R. Mitric, V. Bonacic-Koutecky and A. W. Castleman Jr., Chem. Phys. Lett., 2009, 475, 1 CrossRef CAS.
- Y. Gong, M. F. Zhou and L. Andrews, Chem. Rev., 2009, 109, 6765 CrossRef CAS.
- H. J. Zhai and L. S. Wang, Chem. Phys. Lett., 2010, 500, 185 CrossRef CAS.
- Y. X. Zhao, X. N. Wu, J. B. Ma, S. G. He and X. L. Ding, Phys. Chem. Chem. Phys., 2011, 13, 1925 RSC.
- X. Huang, H. J. Zhai, B. Kiran and L. S. Wang, Angew. Chem., Int. Ed., 2005, 44, 7251 CrossRef CAS.
- H. J. Zhai, B. B. Averkiev, D. Yu. Zubarev, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2007, 46, 4277 CrossRef CAS.
- D. Yu. Zubarev, B. B. Averkiev, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 257 RSC.
- T. R. Galeev and A. I. Boldyrev, Annu. Rep. Prog. Chem., Sect. C, 2011, 107, 124 RSC.
- For recommended covalent radii for single, double, triple bonds, see: P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 12770 Search PubMed.
- Recent experimental and computational study of ReOn− and ReOn (n = 3, 4) clusters shows that the B3LYP calculations with the current basis sets can yield relatively accurate ground-state VDEs for Re oxide clusters. See: W. J. Chen, H. J. Zhai, X. Huang and L. S. Wang, Chem. Phys. Lett., 2011, 512, 49 Search PubMed.
- The two Cs (3A′′) Re3O3− anion structures (Fig. 2b and 2c) can be ruled out from experimental observation for numerous reasons: (i) These isomers are consistently higher in energy at both the B3LYP and CCSD(T) levels of theory (Table 2); (ii) The observed PES pattern (Fig. 1) strongly suggests a closed-shell Re3O3− anion cluster, rather than an open shell; (iii) The simulated PES spectra for the Cs (3A′′) anion structures disagree with experiment (Fig. 3b and 3c); (iv) Other arguments are based on the calculated first VDEs and the vibrational information, as described in the text.
- A. I. Boldyrev and L. S. Wang, Chem. Rev., 2005, 105, 3716 CrossRef CAS.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811 CrossRef CAS.
- A. Ugrinov, A. Sen, A. C. Reber, M. Qian and S. N. Khanna, J. Am. Chem. Soc., 2008, 130, 782 CrossRef CAS.
- C. A. Tsipis, E. E. Karagiannis, P. F. Kladou and A. C. Tsipis, J. Am. Chem. Soc., 2004, 126, 12916 CrossRef CAS.
- C. S. Wannere, C. Corminboeuf, Z. X. Wang, M. D. Wodrich, R. B. King and P. v. R. Schleyer, J. Am. Chem. Soc., 2005, 127, 5701 CrossRef CAS.
- B. B. Averkiev and A. I. Boldyrev, J. Phys. Chem. A, 2007, 111, 12864 CrossRef CAS.
- X. X. Chi and Y. Liu, Int. J. Quantum Chem., 2007, 107, 1886 CrossRef CAS.
- B. Wang, H. J. Zhai, X. Huang and L. S. Wang, J. Phys. Chem. A, 2008, 112, 10962 CrossRef CAS.
- A. C. Tsipis, C. E. Kefalidis and C. A. Tsipis, J. Am. Chem. Soc., 2008, 130, 9144 CrossRef CAS.
- A. P. Sergeeva and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2010, 12, 12050 RSC.
- Q. Xu, L. Jiang and N. Tsumori, Angew. Chem., Int. Ed., 2005, 44, 4338 CrossRef CAS.
- C. Foroutan-Nejad, S. Shahbazian and P. Rashidi-Ranjbar, Phys. Chem. Chem. Phys., 2011, 13, 4576 RSC.
- A. P. Sergeeva and A. I. Boldyrev, Comments Inorg. Chem., 2010, 31, 2 CrossRef CAS.
- F. A. Cotton, C. A. Murillo and R. A. Walton, Multiple Bonds Between Metal Atoms, 3rd ed.Springer, New York, 2005 Search PubMed.
- The PES bands not only reflect the occupation of molecular orbitals in the anion, but also represent the ground state and excited states of the neutral species. In the PES spectra of the Re3O3− anion cluster, bands X, A, and C correspond to the ground state and excited states of the Re3O3 neutral cluster, whose electron configurations are …δ(3a1)2δ*(2b2)2δ*(4a1)1, …δ (3a1)2δ*(2b2)1δ*(4a1)2, and …δ(3a1)1δ*(2b2)2δ*(4a1)2, respectively. The ADE differences for X–C and A–C, as shown in Fig. 5a, are thus equivalent to the δ to δ* promotion energies. Two-thirds of the average of these δ to δ* promotion energies represents the stabilization energy of the delocalized δ orbital (0.77 eV; Fig. 5b). The central idea here is to ensure that the net bonding for the δ2δ*2δ*2 framework in Re3O3− is negligible (that is, three dz2 lone-pairs), where the stabilization of the delocalized δ orbital is effectively compensated by the destabilization of the δ* orbitals (0.64 and 0.14 eV; Fig. 5b). Consequently, the strength of a delocalized δ bond is estimated as 1.54 eV (∼35 kcal mol−1). The above procedure to evaluate the strength of delocalized δ bond is essentially the same as that used for a localized δ bond in the transition metal dimer complexes (ref. 29), which is associated with the electronic excitation from the δ to δ* orbital.
- W. C. Trogler and H. B. Gray, Acc. Chem. Res., 1978, 11, 232 CrossRef CAS.
- It is appropriate to state explicitly here that the value of the resonance energy of the δ-bond (∼15 kcal mol−1) is qualitative due to the following approximations made. First, ideally the resonance energy of a delocalized δ-bond in a triangular cluster should be evaluated as the difference in energy between the triangular cluster with a delocalized δ-bond and the triangular cluster with a localized δ-bond. It is chosen in our evaluation to replace the latter value with that of a localized δ-bond in a non-triangular cluster (ref. 29), although the error thus introduced is expected to be small. A localized δ-bond in a triangular cluster should not differ much from a localized δ-bond in a non-triangular cluster. Second, in our evaluation the bond strength of the localized δ-bond is taken from the upper limit estimated for the Tc–Tc or Mo–Mo δ-bond (ref. 29), rather than that from an appropriate localized Re–Re δ-bond. It is believed that the Tc–Tc bond should be similar to the Re–Re bond, in particular for the weak δ-bonding. We are not aware of any specific mention of the Re–Re δ-bond strength in the literature. It may be stressed that the upper limit of the bond strength of 20 kcal mol−1 for a localized δ-bond is a general notion for the transition metal complexes, not specifically limited to Tc–Tc or Mo–Mo bonds. We think the upper limit value is good enough for the current discussion.
- M. K. Cyrański, Chem. Rev., 2005, 105, 3773 CrossRef CAS.
- H. J. Zhai, B. Wang, X. Huang and L. S. Wang, J. Phys. Chem. A, 2009, 113, 9804 CrossRef CAS.
- L. S. Wang, H. S. Cheng and J. Fan, J. Chem. Phys., 1995, 102, 9480 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123 CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, Pseudopotentials of the Stuttgart/Dresden Group 1998, revision August 11, 1998 (http://www.theochem.uni-stuttgart.de/pseudopotentials) Search PubMed.
- J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 10180 CrossRef CAS.
- M. J. Frisch et al., Gaussian 03, revision D.01, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schützet al., MOLPRO, version 2010.1, a package of ab initio programs. See http://www.molpro.net Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Alternative optimized cluster structures for Re3O3− and Re3O3 at the B3LYP level and their Cartesian coordinates, and molecular orbital pictures for the high-lying D3h structures of Re3O3−. See DOI: 10.1039/c2ra00753c |
| This journal is © The Royal Society of Chemistry 2012 |
