Structure, molecular motion, and phase transition of a highly disordered crystal [Co(NH3)6](ClO4)3†
Natalia
Górska
*a,
Akira
Inaba
a,
Yasukazu
Hirao
b,
Edward
Mikuli
c and
Krystyna
Hołderna-Natkaniec
d
aResearch Center for Structural Thermodynamics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan. E-mail: gorska@chem.sci.osaka-u.ac.jp
bDepartment of Chemistry, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
cDepartment of Chemical Physics, Faculty of Chemistry, Jagiellonian University, Ingarden 3, 30-060, Kraków, Poland
dInstitute of Physics, A. Mickiewicz University, Umultowska 85, 61-614, Poznań, Poland
First published on 28th March 2012
Abstract
Four crystalline phases of the coordination compound [Co(NH3)6](ClO4)3 are identified by adiabatic calorimetry. An order–disorder phase transition (II→I) occurs at TC1 = 334.2 K with an entropy change of 6.4 J K−1 mol−1. The X-ray single-crystal diffraction at 340 K demonstrates that phase I is cubic (Z = 4) and that two types of anions exist with different types of disorder. In phase II at 200 K, five anions (out of twelve) become ordered and three cations (out of four) are deformed to give a lower symmetry, still in a cubic system (Z = 32). This is attributed to orientational ordering of the anions triggered by NH⋯O hydrogen-bonding interactions. The 1H-NMR study suggests that some NH3 ligands are oriented because of hydrogen bonding, whereas some cations reorient isotropically like in phase I. The energy required to reorient an ordered anion in the crystal lattice of phase II is estimated from the excess heat capacity below TC1 to be 40 kJ mol−1, which corresponds to the energy needed to break the hydrogen bond, 8 kJ mol−1. While the transitions at 111.7 K (III→II) and 97.6 K (IV→II), with an entropy change of 5.7 J K−1 mol−1, do not substantially affect the dynamics, they are attributed to further orientational ordering of the anions still disordered in phase II.
1. Introduction
The hexaammine cobalt(III) complex cation has an octahedral symmetry with nearly freely rotating ammonia ligands around their three-fold axes in a wide temperature range. Except for many other diverse applications previously reported,1–4 it can act as a potential anion receptor and a building block for the construction of 3D networks as it has a suitable framework for assembling the anionic components and contains hydrogen bond donor groups.5,6 Interestingly, [M(NH3)6]3+ complexes with trivalent metals crystallize in the same space group and have comparable unit cell parameters to the analogical [M(NH3)6]2+ complexes with divalent metals,7–9 but surprisingly their phase behavior is significantly different.10,11 Although the thermal behavior of both types of the compounds has been widely characterized in the literature through the decades, there is still not enough information about the molecular dynamics and the nature of the hydrogen bond like interactions occurring in these systems, depending on the temperature. One of the reasons can be the general difficulty in investigating the highly disordered materials, and the other a necessity to use complementary physico-chemical methods for their proper examination.The thermal behavior of the coordination compound [Co(NH3)6](ClO4)3 has previously been studied by Mikuli et al.12 While a phase transition was observed at 103 K by differential scanning calorimetry (DSC), the Fourier transform far- and middle-infrared (FT-FIR and FT-MIR) spectra did not show any drastic change at the transition, indicating that this transition is not connected to a significant change in the crystal structure. Only a subtle change in molecular motion from the characteristic behavior of the spectral width of the ρr(NH3)F1u mode at 820 cm−1 was observed. It was suggested that the NH3 ligands perform a fast stochastic reorientation on a picosecond time scale around the Co–N axis, and the motion becomes significantly slower below the transition temperature.12
At room temperature, the crystal was considered to be isostructural with three other compounds of the same type: [Cr(NH3)6](ClO4)3, [Cr(NH3)6](BF4)3, and [Co(NH3)6](BF4)3.7,13 The X-ray powder diffraction pattern was consistent with a cubic system (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group; No. 225; O5h)7 with 4 formula units in the unit cell with the lattice parameter a = 11.384 Å. However, the distinct difference between [Co(NH3)6](ClO4)3 and the other compounds13–15 is that there is no phase transition near room temperature. This encouraged us to carefully reinvestigate the phase behavior and crystal structure in detail.
m space group; No. 225; O5h)7 with 4 formula units in the unit cell with the lattice parameter a = 11.384 Å. However, the distinct difference between [Co(NH3)6](ClO4)3 and the other compounds13–15 is that there is no phase transition near room temperature. This encouraged us to carefully reinvestigate the phase behavior and crystal structure in detail.
As described below, by adiabatic calorimetry, we observed another phase transition at 334.2 K and determined the crystal structure at 200 K and 340 K by X-ray single-crystal diffraction (XRSCD). We also utilized 1H-NMR to investigate the dynamics.
2. Experimental
A powder sample was prepared and characterized as described in a previous paper.12 Single crystals for XRSCD measurements were obtained by slow evaporation from the aqueous solution.Heat capacity measurements were conducted between 10 K and 350 K using a laboratory-made adiabatic calorimeter. The powder sample was placed in a gold-plated copper cell with an inner volume of 2.77 cm3. The mass of the loaded sample was 0.99753 g (2.1711 mmol). Helium exchange gas was used to attain equilibrium within the cell. The temperature was measured by a rhodium–iron alloy resistance thermometer, whose temperature scale is based on ITS-90. The heat capacity of the empty cell was measured in advance and subtracted from the total heat capacity. More details can be found in previous papers.16,17
The XRSCD data were collected on two different diffractometers with filtered Mo-Kα radiation. A good-quality orange crystal with dimensions 0.4 × 0.4 × 0.4 mm3 was investigated by a Rigaku R-AXIS RAPID diffractometer. The crystal-to-detector distance was 127.0 mm. The measurements were first conducted at 340 K and then at 140 K. After a preliminary investigation of the low temperature data that indicated a large unit cell, we used a Rigaku R-AXIS VII diffractometer. The crystal-to-detector distance was 200.0 mm. A crystal with dimensions 0.2 × 0.2 × 0.2 mm3 was investigated. After measurement at 200 K, the crystal was re-examined at 340 K to confirm its stability. All data were collected with a temperature accuracy of ±2 K. Full analysis of the crystal structures at 340 K and 200 K was conducted by direct methods (SHELX-97 and SIR2004)18,19 using Yadokari-XG 2009.20 The details of these measurements are listed in Table 1.
| Crystallographic method | Single-crystal diffraction | Single-crystal diffraction |
| Diffractometer | Rigaku R-AXIS RAPID | Rigaku R-AXIS VII |
| Radiation | μ(Mo-Kα) (λ = 0.71075 Å) | μ(Mo-Kα) (λ = 0.71075 Å) |
| Empirical formula | [Co(NH3)6](ClO4)3 | [Co(NH3)6](ClO4)3 |
| Formula weight | 459.48 g mol−1 | 459.48 g mol−1 |
| Temperature | 340 K | 200 K |
| Crystal system | Cubic | Cubic |
| Space group |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 225) m (No. 225) |
Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (No. 206) (No. 206) |
| Lattice parameters | a = 11.455(3) Å | a = 22.7660(6) Å |
| Volume | 1503.0(7) Å3 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799.4(5) Å3 799.4(5) Å3 |
| Z | 4 | 32 |
| D calc | 2.031 g cm−3 | 2.069 g cm−3 |
| F 000 | 936.00 | 7488.00 |
| 2θmax | 69.8° | 55.0° |
| No. of reflections measured | Total: 5305 | Total: 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241 241 |
| Unique: 208 (Rint = 0.0253) | Unique: 2267 (Rint = 0.0394) | |
| Exposure rate | 90.0 s/° | 80.0 s/° |
| Data images | 44 exposures | 180 exposures |
| Structure solution | Direct Methods | Direct Methods |
| Refinement method | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 |
| Reflection/Parameter Ratio | 10.40 | 15.11 |
| Goodness of Fit on F2 | 1.285 | 1.181 |
| R indices | R1 = 0.0665; wR2 = 0.2097 | R1 = 0.0957; wR2 = 0.2785 |
1H-NMR measurements were conducted using the powder sample in the temperature range 80–345 K. A laboratory-made continuous-wave spectrometer operating at a frequency of 25 MHz in a double-modulation system was used. The first derivative of the absorption signal was recorded by changing the frequency of the autodyne generator to either 130 or 250 kHz to obtain the line width (δB) and the second moment (M2).
3. Results and discussion
3.1 Calorimetry
Before the precise measurement by adiabatic calorimetry, the thermal stability of the compound was investigated by thermogravimetry with simultaneous differential thermal analysis. The mass reduction at 360 K amounted to less than 0.5% of its initial mass. In addition, a phase transition at 334 K with no thermal hysteresis was detected by DSC.Fig. 1 illustrates the molar heat capacity of the rapidly cooled sample (about −10 K min−1) determined by adiabatic calorimetry. This was the first series of measurements. The compound exhibits a phase transition at TC1 = 334.2 K (from phase II to I), where the low temperature tail of the heat capacity is characteristic. The enthalpy of transition was evaluated by estimating a “normal” heat capacity curve as indicated in Fig. 1. The enthalpy was 2.07 ± 0.05 kJ mol−1 and the corresponding entropy of transition was 6.4 ± 0.2 J K−1 mol−1.
3.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f1.gif) | ||
| Fig. 1 The molar heat capacities obtained for a rapidly cooled sample of [Co(NH3)6](ClO4)3. | ||
An anomaly was observed at around 100 K, not only in the heat capacity, but also in the temperature drift, due to a spontaneous warming effect, indicating that stabilization from a metastable state is involved here. The sample was then annealed at 98.3 K for 10 h and the second series of measurements was conducted. For the third series of measurements, the sample was annealed at 90.9 K for 30 h for further stabilization. The results are shown in Fig. 2. With annealing, the peak at 97.6 K became smaller, whereas the peak at 111.7 K simultaneously became larger. The transition observed at TC2 = 111.7 K is therefore between two stable phases, III and II, whereas the transition at TC3 = 97.6 K is from the metastable phase IV to the supercooled phase II. The inset to Fig. 2 shows a schematic phase relation with Gibbs energy. Since the transformation to the stable phase was very slow, it was not fully completed. The entropy change associated with the anomalies for the well-annealed sample amounted to 5.7 ± 0.2 J K−1 mol−1. We did not observe any glassy behavior over the whole temperature region.
3. Inset: a schematic diagram of the Gibbs energy to show the phase relation.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f2.gif) | ||
| Fig. 2 The annealing effect on the heat capacity of the [Co(NH3)6](ClO4)3. Inset: a schematic diagram of the Gibbs energy to show the phase relation. | ||
3.2 Crystal structure of phase I
The crystal structure of phase I obtained at 340 K is depicted in Fig. 3. It belongs to a cubic system (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, No. 225) with 4 formula units in the unit cell with a lattice parameter a = 11.455(3) Å. It is isostructural with three other compounds of the same type: [Co(NH3)6](BF4)3, [Cr(NH3)6](ClO4)3, and [Cr(NH3)6](BF4)3, investigated at room temperature.7,13 The Fm
m space group, No. 225) with 4 formula units in the unit cell with a lattice parameter a = 11.455(3) Å. It is isostructural with three other compounds of the same type: [Co(NH3)6](BF4)3, [Cr(NH3)6](ClO4)3, and [Cr(NH3)6](BF4)3, investigated at room temperature.7,13 The Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group is not compatible with the three-fold symmetry of NH3 ligands, and because of their fast rotation, the hydrogen atoms were ignored and only the positional and thermal parameters of Co, Cl, O, and N atoms were refined. The crystal structure consists of coordination cations of Co(NH3)63+, having a regular octahedral symmetry with all Co–N bond lengths equal to 1.976 Å, and with two types of ClO4− anions that differ in orientational disorder.
m space group is not compatible with the three-fold symmetry of NH3 ligands, and because of their fast rotation, the hydrogen atoms were ignored and only the positional and thermal parameters of Co, Cl, O, and N atoms were refined. The crystal structure consists of coordination cations of Co(NH3)63+, having a regular octahedral symmetry with all Co–N bond lengths equal to 1.976 Å, and with two types of ClO4− anions that differ in orientational disorder.
3 in phase I. The two types of the orientational disorder of the ClO4− anions are indicated.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f3.gif) | ||
| Fig. 3 The arrangement of the polyhedral blocks in the unit cell of [Co(NH3)6](ClO4)3 in phase I. The two types of the orientational disorder of the ClO4− anions are indicated. | ||
The first type of anions, hereafter designated as “cubic” anions, are disordered between two possible orientations in such a way that eight half-oxygen atoms occupy the vertices of a cube with a Cl atom located at the center. All six planes of this cube are symmetrically surrounded on each side by Co(NH3)63+ units and are orthogonal to the four-fold symmetry axes of these cations. The ClO4− anions of this type are located at the center of the unit cell and at the middle of the edges. The shortest N⋯Cl distance is 3.752 Å. The anions of the second type have adamantane geometry, hereafter designated as “adamantane-like” anions, and fill up the channels formed between the sandwiched Co(NH3)63+ and ClO4− groups of the first type. These anions are also disordered, but have more than two different orientations. There are eight (out of twelve) anions of the second type in the unit cell. The greater freedom of rotation of these anions can be explained by much weaker hydrogen bonds being created, because the N⋯Cl distance (4.146 Å) is significantly longer than that of the cubic anions. Exactly the same two types of anion orientational disorder have been previously observed in [Ru(NH3)6](BF4)3.21
3.3 Crystal structure of phase II
Table 2 lists the positional parameters with standard deviations and equivalent isotropic displacement coefficients obtained at 340 K and 200 K. A comparison of the selected interatomic distances and angles is given in Table 3.| Atom | x | y | z | U |
|---|---|---|---|---|
| 340 K | ||||
| Co | 0.0000 | 0.0000 | 0.0000 | 0.028(5) |
| Cl(1) | 0.5000 | 0.0000 | 0.0000 | 0.036(1) |
| Cl(2) | 0.2500 | 0.2500 | 0.2500 | 0.050(1) |
| N | 0.1725(4) | 0.0000 | 0.0000 | 0.043(1) |
| O(1) | 0.4270(5) | 0.0730(5) | 0.0730(5) | 0.063(3) |
| O(2) | 0.1196(13) | 0.2500 | 0.2500 | 0.083(5) |
| O(3) | 0.1814(8) | 0.1814(8) | 0.1814(8) | 0.101(4) |
| 200 K | ||||
| Co(1) | 0.5000 | 0.0000 | 0.0000 | 0.014(1) |
| Co(2) | 0.2592(1) | 0.0000 | 0.2500 | 0.011(1) |
| Cl(1) | 0.2500 | 0.2500 | 0.2500 | 0.016(1) |
| Cl(2) | 0.2500 | 0.0072(1) | 0.0000 | 0.017(1) |
| Cl(3) | 0.1275(1) | 0.1275(1) | 0.1275(1) | 0.019(1) |
| Cl(4) | 0.3768(1) | 0.1286(1) | 0.1204(1) | 0.040(1) |
| N(1) | 0.4133(2) | 0.0006(2) | 0.0005(2) | 0.024(1) |
| N(2) | 0.3459(3) | 0.0000 | 0.2500 | 0.022(1) |
| N(3) | 0.1728(3) | 0.0000 | 0.2500 | 0.020(1) |
| N(4) | 0.2588(2) | 0.0871(2) | 0.2504(2) | 0.020(1) |
| N(5) | 0.2590(2) | −0.0010(2) | 0.3367(2) | 0.021(1) |
| O(1) | 0.2824(3) | 0.2851(3) | 0.2105(3) | 0.022(2) |
| O(2) | 0.2098(4) | 0.2098(4) | 0.2098(4) | 0.028(3) |
| O(3) | 0.2137(2) | 0.0422(2) | 0.0373(2) | 0.035(1) |
| O(4) | 0.2870(2) | −0.0311(2) | 0.0363(2) | 0.031(1) |
| O(5) | 0.0900(2) | 0.1606(2) | 0.1647(2) | 0.037(1) |
| O(6) | 0.0903(2) | 0.0903(2) | 0.0903(2) | 0.039(2) |
| O(7) | 0.3738(6) | 0.1920(6) | 0.1147(6) | 0.053(3) |
| O(8) | 0.3715(5) | 0.0630(6) | 0.1157(5) | 0.059(4) |
| O(9) | 0.4418(4) | 0.1289(4) | 0.1161(4) | 0.044(3) |
| O(10) | 0.3120(8) | 0.1244(8) | 0.1152(8) | 0.070(6) |
| O(11) | 0.3677(8) | 0.1234(8) | 0.0512(9) | 0.062(7) |
| O(12) | 0.3738(4) | 0.1269(4) | 0.1870(4) | 0.041(3) |
| O(13) | 0.3433(8) | 0.1697(8) | 0.0936(8) | 0.052(6) |
| O(14) | 0.4150(20) | 0.1650(20) | 0.1520(20) | 0.080(20) |
| O(15) | 0.4075(10) | 0.0964(10) | 0.0888(10) | 0.043(8) |
| O(16) | 0.3495(10) | 0.0984(10) | 0.1565(10) | 0.042(8) |
| 340 K | 200 K | ||
|---|---|---|---|
| a Description of the symbols at 340 K: Cl(1): derived from disordered ClO4− of cubic type; Cl(2): disordered ClO4− of adamantane type. b Description of the symbols at 200 K: Cl(1): derived from disordered ClO4− of cubic type; Cl(2): ordered ClO4− (from cubic type); Cl(3): ordered ClO4− (from adamantane type); Cl(4): disordered ClO4− of adamantane type. | |||
| Distances / Å | |||
| Co–N | 1.976(4) | Co(1)–N(1) | 1.973(5) |
| Co(2)–N(2) | 1.975(7) | ||
| Co(2)–N(3) | 1.967(6) | ||
| Co(2)–N(4) | 1.982(4) | ||
| Co(2)–N(5) | 1.974(5) | ||
| N–Cl(1) | 3.752 | N(4)–Cl(1) | 3.714 |
| N(1)–Cl(2) | 3.721 | ||
| N(2)–Cl(2) | 3.673 | ||
| N(3)–Cl(2) | 3.769 | ||
| N(5)–Cl(2) | 3.726 | ||
| N–Cl(2) | 4.146 | N(1)–Cl(3) | 4.206 |
| N(3)–Cl(3) | 4.156 | ||
| N(1)–Cl(4) | 4.053 | ||
| N(3)–Cl(4) | 4.108 | ||
| N(4)–Cl(4) | 3.979 | ||
| N(5)–Cl(4) | 4.073 | ||
| Cl(1)–O(1) | 1.448(9) | Cl(1)–O(1) | 1.412(8) |
| Cl(1)–O(2) | 1.584(15) | ||
| Cl(2)–O(3) | 1.426(5) | ||
| Cl(2)–O(4) | 1.469(5) | ||
| Cl(3)–O(5) | 1.420(5) | ||
| Cl(1)–Cl(2) | 4.960 | Cl(3)–Cl(1) | 4.832 |
| Cl(4)–Cl(1) | 4.968 | ||
| Cl(3)–Cl(2) | 4.868 | ||
| Cl(4)–Cl(2) | 4.845 | ||
| Cl(4)–Cl(2) | 4.893 | ||
| Cl(4)–Cl(2) | 5.108 | ||
| Angles / ° | |||
| N–Co–N | 90 | N(1)–Co(1)–N(1) | 90.0(2) |
| N–Co–N′ | 180 | N(1)–Co(1)–N(1′) | 180.000(2) |
| N(4)–Co(2)–N(5′) | 89.64(19) | ||
| N(3)–Co(2)–N(5) | 89.91(14) | ||
| N(5)–Co(2)–N(5) | 179.8(3) | ||
| N(4)–Co(2)–N(4′) | 179.5(3) | ||
| N(3)–Co(2)–N(2) | 180 | ||
| N(5)–Co(2)–N(2) | 90.09(14) | ||
| N(5)–Co(2)–N(4) | 90.35(19) | ||
| O(1)–Cl(1)–O(1) | 70.5 | O(1)–Cl(1)–O(1) | 66.5(3) |
| O(1)–Cl(1)–O(1′) | 109.5 | O(1)–Cl(1)–O(1′) | 113.5(3) |
| O(2)–Cl(1)–O(1) | 105.1(3) | ||
| O(2)–Cl(1)–O(1′) | 74.9(3) | ||
A view of the unit cell of phase II (at 200 K) is shown in Fig. 4. It belongs to a cubic system (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group, No. 206), but with 32 formula units in the unit cell with the lattice parameter a = 22.7660(6) Å. Identical to the structure at 340 K, the Ia
space group, No. 206), but with 32 formula units in the unit cell with the lattice parameter a = 22.7660(6) Å. Identical to the structure at 340 K, the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group could be determined assuming fast rotations of the hydrogen atoms around the Co–N bonds. Similar coordination compounds with such a large unit cell at room temperature have been reported previously.22,23 The crystals of [Co(NH3)5H2O](ClO4)3 with one NH3 ligand replaced by one water molecule in the coordination sphere of the Co3+ cation exhibit dimorphism. Some crystallize in the orthorhombic system (Pmn21 space group; a = 11.37(5) Å, b = 16.74(5) Å, c = 7.79(5) Å; Z = 4) and some in a cubic system (Pn3n space group; a = 22.68(2) Å, Z = 32). The [Co(NH3)6](CuCl5) compound crystallizes in a cubic system with a Fd3c space group with a = 22.992(3) Å and Z = 32.
space group could be determined assuming fast rotations of the hydrogen atoms around the Co–N bonds. Similar coordination compounds with such a large unit cell at room temperature have been reported previously.22,23 The crystals of [Co(NH3)5H2O](ClO4)3 with one NH3 ligand replaced by one water molecule in the coordination sphere of the Co3+ cation exhibit dimorphism. Some crystallize in the orthorhombic system (Pmn21 space group; a = 11.37(5) Å, b = 16.74(5) Å, c = 7.79(5) Å; Z = 4) and some in a cubic system (Pn3n space group; a = 22.68(2) Å, Z = 32). The [Co(NH3)6](CuCl5) compound crystallizes in a cubic system with a Fd3c space group with a = 22.992(3) Å and Z = 32.
3 in phase II. The two types of cations and three types of anions are indicated.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f4.gif) | ||
| Fig. 4 The arrangement of the polyhedral blocks in the unit cell of [Co(NH3)6](ClO4)3 in phase II. The two types of cations and three types of anions are indicated. | ||
Because of the interactions through the NH⋯O hydrogen bonds, two types of coordination cations are created in phase II (see Fig. 5). One type of Co(NH3)63+ (red) remains regular with all the Co–N distances equal to 1.973 Å. The other type (blue) is slightly deformed, with the N–Co–N bond angle ranging from 89.64 to 90.35° and from 179.5 to 180° and with two pairs of Co–N bonds being the same and equal to 1.974 Å and 1.982 Å, respectively, thus preserving a two-fold symmetry axis (see Table 3). The ratio of these two types of octahedral units, one regular and one deformed, is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.
3.
![Left: The arrangement of Co(NH3)63+ blocks in phase II viewed along the [001] direction. Right: Two types of octahedral cations exist, one regular and the other deformed. The different colors denote the different Co–N bond lengths.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f5.gif) | ||
| Fig. 5 Left: The arrangement of Co(NH3)63+ blocks in phase II viewed along the [001] direction. Right: Two types of octahedral cations exist, one regular and the other deformed. The different colors denote the different Co–N bond lengths. | ||
The NH⋯O hydrogen bonds are also responsible for the orientational ordering of the anions. Three types of ClO4− anions, one ordered and two dynamically disordered, can be distinguished, as illustrated in Fig. 6. Three-fourths of the cubic anions (Fig. 6a) and one-fourth of the adamantane-like anions (Fig. 6b) are ordered in their orientation, as represented by green tetrahedra. The ratio of ordered, cubic, and adamantane-like anions is thus 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The Cl(1)–O bond lengths and O–Cl(1)–O angles listed in Table 3 indicate that the disordered anions of the cubic type, which remain in phase II, are fairly deformed.
6. The Cl(1)–O bond lengths and O–Cl(1)–O angles listed in Table 3 indicate that the disordered anions of the cubic type, which remain in phase II, are fairly deformed.
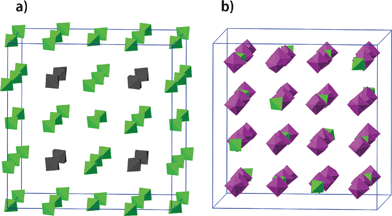 | ||
| Fig. 6 The arrangement and dynamics of the ClO4− anions of (a) cubic geometry and (b) adamantane geometry in phase II. Three-fourths of all the cubic anions and one fourth of all the adamantane-like anions, which are marked in green, are ordered in their orientation. | ||
3.4 Nearest surrounding of ClO4− in phase II
Fig. 7 illustrates the four different nearest surrounding anion types in phase II. As shown in Fig. 7a, the disordered anion of cubic type Cl(1)O4− is encapsulated in the center of octahedral- and cubic-shaped cavities formed by Co(NH3)63+ cations and ClO4− anions, respectively. All six deformed cations symmetrically surround the hosted anion from each side, with the shortest N⋯Cl(1) distances being the same and equal to 3.714 Å. This cavity is still large enough for the anion to continue its reorientation. The cubic anion is also surrounded by eight anions, six of them are disordered, while the remaining two are ordered. The distances between Cl(1) and Cl(4) (Cl from the disordered anion of cubic geometry⋯Cl from the disordered anion of adamantane geometry) and between Cl(1) and Cl(3) (Cl from the disordered anion of cubic geometry⋯Cl from the ordered anion) are 4.968 Å and 4.832 Å, respectively. Therefore, the two ordered anions are shifted closer to the hosted anion in the anionic cavity.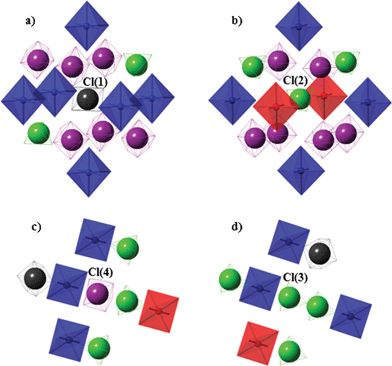 | ||
| Fig. 7 Nearest surrounding of ClO4− anions in phase II: (a) disordered anion of cubic type, (b) ordered anion (from the cubic type in phase I), (c) disordered anion of adamantane type, and (d) ordered anion (from the adamantane type in phase I). | ||
Four cations (one regular and three deformed) and four anions (one disordered and three ordered) in a tetrahedral arrangement around the hosted anion are the nearest neighbors of the ordered anion Cl(3)O4− (Fig. 7d), which is adamantane-type disordered in phase I. The shortest Cl(3)⋯N(3) distance between this anion and the deformed cation is 4.156 Å, whereas the shortest Cl(3)⋯N(1) distance between the anion and the regular cation is longer, with a value of 4.206 Å. Furthermore, there are three ordered anions equidistant from the hosted anion (Cl(2)⋯Cl(3) = 4.868 Å) and one disordered anion, at a shorter distance (Cl(1)⋯Cl(3) = 4.832 Å). Thus, the described anion is not located symmetrically in any of these two cavities. It is evident that hydrogen bonds are created between the three deformed cations and the hosted anion, resulting in the orientational ordering of the anion and shifting it closer to the disordered anion with cubic geometry, causing its deformation.
Fig. 7b shows the nearest cations and anions surrounding the ordered anion Cl(2)O4−, which is cubic-type disordered in phase I. There are six coordination cations (four deformed and two regular) and eight anions (six disordered and two ordered) distributed around the hosted anion. Interestingly, the shortest distances between the Cl and N atoms derived from each adjacent cation are not the same in this case. Five are in the range 3.726–3.769 Å, but the sixth is notably shorter (the Cl(2)⋯N(2) distance is equal to 3.673 Å). Thus, the intermolecular Cl(2)O⋯HN(2) hydrogen-bonding interactions between the hosted anion and one out of the six surrounding cations are the reasons for the ordering of this anion.
Fig. 7c shows the nearest cations and anions surrounding the disordered anion of the adamantane type Cl(4)O4−. Four cations (three deformed and one regular) as well as four anions (one disordered and three ordered) are the nearest neighbors, arranged tetrahedrally around the hosted anion. The shortest Cl⋯N and Cl⋯Cl distances range from 3.979 to 4.108 Å and from 4.845 to 5.108 Å, respectively. The two cavities in which the disordered anion is placed provide sufficient space for its reorientation.
A schematic diagram, which focuses on the Cl⋯N and Cl⋯Cl distances obtained at 200 K, is presented in Fig. 8. Specifically, the interactions marked in red are crucial for orientational ordering of the relevant anions in phase II. It should be noted here that some deformed cations and the ordered anions are close enough to orient some NH3 ligands. For instance, the distance N(3)H⋯O(5) is 2.894 Å.
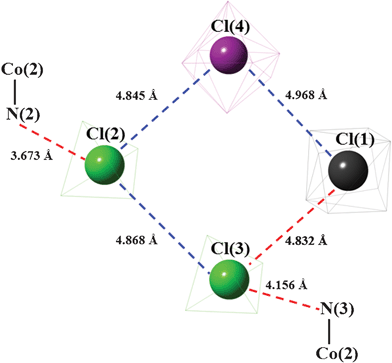 | ||
| Fig. 8 A schematic diagram showing the relevant interatomic distances obtained in phase II. The distances marked in red are assumed to be crucial for the change in geometry below TC1. | ||
3.5 Molecular motion in Co(NH3)63+
Fig. 9 illustrates representative line-shape derivatives of the 1H-NMR signal obtained at different temperatures. There is only one very narrow component visible in phase I. At low temperatures below TC1, two new components (one broad and the other intermediate) appear and the narrow component still remains at 170 K. However, no appreciable change was observed across the low-temperature transitions at TC2 and TC3. The complex line shape reflects the complexity of the structure as described above. δB of each component is plotted in Fig. 10a as a function of temperature. Fig. 10b shows the temperature dependence of M2 obtained from the spectra. At 80 K, M2 is 18.1 × 10−8 T2 and decreases gradually on heating to level off when it reaches the value of 15.8 × 10−8 T2 between 220 K and 300 K. It then decreases at the transition at TC1 to 1.1 × 10−8 T2 in phase I. A similar study was performed previously by Murray and Waugh15 for compounds of the [Co(NH3)6]X3 type, where X = Cl−, Br−, I−, NO3−, BF4−, and PF6−. Except for [Co(NH3)6](BF4)3, all these compounds have complex line shapes at low temperatures.3.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f9.gif) | ||
| Fig. 9 The line-shape derivatives of the 1H-NMR signal recorded at different temperatures for [Co(NH3)6](ClO4)3. | ||
3. The arrows denote the transition temperatures.](/image/article/2012/RA/c2ra01184k/c2ra01184k-f10.gif) | ||
| Fig. 10 The temperature dependencies of (a) line width δB and (b) second moment M2 of the 1H-NMR signal for [Co(NH3)6](ClO4)3. The arrows denote the transition temperatures. | ||
For the rigid structure, M2 was calculated according to the Van Vleck formula24 as a sum of the dominant H–H and H–N intramolecular interactions and the intermolecular contribution. Given the structural parameters from our X-ray study, where the NH3 ligands are octahedrally coordinated with respect to the Co–N bonds with an average distance of 1.976 Å, and assuming the N–H average distance as 1.00 Å and the H–N–H angle as 107°,25M2 may be calculated as 48.8 × 10−8 T2. This value is much larger than the value we obtained at 80 K, indicating that most of the NH3 ligands perform fast reorientational motions, as suggested by a previous IR study.1 We then calculated M2 with some dynamical models by considering the effects of various molecular motions.26–28 The results are presented in Table 4.
| Molecular motions | M 2 / 10−8 T2 | |||
|---|---|---|---|---|
| Intramolecular interactions H–H in Co(NH3)63+ | Intramolecular interactions H–N in Co(NH3)63+ | Intermolecular interactions | Sum 1+2+3 | |
| 1 (average) | 2 | 3 | 4 | |
| Rigid structure | 45.3 | 2.3 | 1.2 | 48.8 |
| NH3 reorientations around Co–N | 13.3 | 0.9 | 1.2 | 15.4 |
| Co(NH3)63+ reorientations around the four-fold axis | 12.8 | 0.9 | 1.2 | 14.9 |
| Co(NH3)63+ reorientations around the three-fold axis | 9.8 | 0.9 | 1.2 | 11.9 |
| Isotropic reorientations | 0 | 0.8 | 0.8 | |
The reorientations of all the NH3 ligands cause M2 to decrease to 15.4 × 10−8 T2, which meets the experimental value of 15.8 × 10−8 T2 at the temperature between 220 K and 300 K in phase II. At this temperature, however, other modes related to the whole cations are already excited, indicating that some NH3 ligands are still oriented during the time scale of the NMR measurement (ca. 10 μs). This is consistent with our X-ray results as described in Section 3.4. Some of the hydrogen bonds connecting the cations and anions are strong enough to make the former deformed and the latter ordered in the orientation. The NH3 ligands located in between can be oriented within the relevant time scale. Indeed, above 170 K, the situation becomes very complicated. The existence of the narrow component suggests that some cations, probably the ones with a regular shape, perform isotropic reorientation. The anisotropic reorientation of the cations around the four-fold axis or three-fold axis can also be excited. On the other hand, some NH3 ligands may still be oriented. Various types of dynamics are mixed in phase II, reflecting the complex structure. In contrast, for phase I, we can safely say that all cations perform isotropic reorientations. Phase I is therefore highly disordered.
3.6 Mechanism of phase transitions
With all the information available on the phase transitions in this crystal, we can discuss the possible mechanism. There is a possibility that the NH3 ligands are disordered with distinct orientations at high temperatures and ordered in one of them at low temperatures. In fact, this cannot be ruled out exclusively. At this stage, however, we have no such experimental evidence. A careful neutron diffraction study can resolve this problem. The space groups determined from our X-ray diffraction study may or may not be changed. Here, we assume that all the transition entropies come from the anions.From our structural study, it is evident that the phase transition at TC1 is of the order–disorder type. The stochastic reorientational motion of the NH3 ligands can only contribute to the normal part (or baseline) heat capacity. The entropy change that we obtained (6.4 J K−1 mol−1) has to be explained by the orientational disordering of the relevant anions. There are three anions in the formula unit and five out of twelve anions are ordered in phase II, where three anions come from the cubic-type in phase I and two from the adamantane-type. If we suppose that those anions become disordered independently from each other in phase I, then we simply get an entropy value of (3/12) × 3 × R ln2 = 4.3 J K−1 mol−1 for the cubic-type anions. For the adamantane-type anions, we have a value somewhat larger than (2/12) × 3 × R ln2 = 2.9 J K−1 mol−1. The experimental value is slightly smaller than the total (7.2 J K−1 mol−1), which can be justified by the fact that there is a hydrogen-bonding network in the crystal, and the anions cannot be disordered independently. There must be some weak restriction preventing independent disordering in phase I, which gives a smaller value of entropy.
For the low temperature transitions at TC2 and TC3, little can be said about the mechanism. We do not know the crystal structures of phases III and IV. However, one can imagine that the disordered anions remaining in phase II may be ordered in the orientation at low temperatures. If all anions are ordered well below TC3, we get a total entropy value of 3R ln 2 = 17.3 J K−1 mol−1, which is significantly larger than the experimental value of 12.1 J K−1 mol−1. This can also be justified by the same reason when we assume that the system has no residual entropy. The disordered anions in phase II are not perfectly independent of each other. Some correlation exists among those disordered anions.
Assuming the third law of thermodynamics, we can define the “orientational” entropy for the anions. The experimental values, 12.1 J K−1 mol−1 for phase I and 5.7 J K−1 mol−1 for phase II, are significantly smaller than those expected by assuming independent disordering, 3R ln2 (= 17.3 J K−1 mol−1) and (7/12) × 3R ln2 (= 10.1 J K−1 mol−1), respectively. The discrepancies are explained by the restricted disordering of the anions in both phases.
3.7 Energy to reorient an anion in phase II
From the low-temperature tail of the heat capacity immediately below TC1, it is possible to estimate the energy required to rotate an ordered ClO4− anion in phase II. Assuming that the number of ClO4− anions in the wrong orientation, n, is very small compared with the total number of the ordered anions, N, we have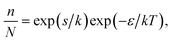 | (1) |
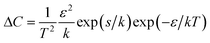 | (2) |
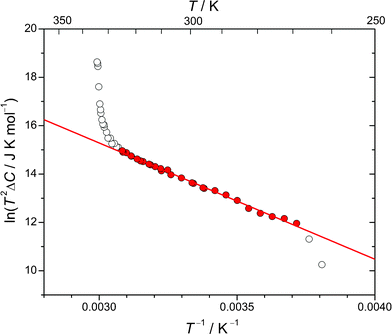 | ||
| Fig. 11 An evaluation of the energy required to reorient an ordered ClO4− anion in the crystal lattice of phase II. The filled marks denote the data used for fitting. | ||
4. Conclusions
A combination study of the highly disordered crystal [Co(NH3)6](ClO4)3 by calorimetry, XRSCD, and NMR gave precise information on the phase transition, crystal structure, and molecular motion.1. The compound exhibits three solid–solid phase transitions at TC1 = 334.2 K, TC2 = 111.7 K, and TC3 = 97.6 K. The one at TC1 (II→I) is the order–disorder type with a transition entropy of 6.4 J K−1 mol−1. The transition at TC2 (III→II) and the one at TC3 (IV→II) from the metastable phase IV to the supercooled phase II are also the order–disorder type with a transition entropy of 5.7 J K−1 mol−1. These entropies are explained by the orientational disorder of the anions.
2. In phase I at 340 K, the compound crystallizes in the cubic system, with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group with a = 11.455(4) Å and Z = 4. There is only one type of coordination cation of Co(NH3)63+ with a perfectly octahedral symmetry and two types of tetrahedral ClO4− ions, which differ in the degree of dynamic disorder. In phase II at 200 K, the compound crystallizes in the cubic system having an Ia
m space group with a = 11.455(4) Å and Z = 4. There is only one type of coordination cation of Co(NH3)63+ with a perfectly octahedral symmetry and two types of tetrahedral ClO4− ions, which differ in the degree of dynamic disorder. In phase II at 200 K, the compound crystallizes in the cubic system having an Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group with a = 22.7660(6) Å and Z = 32. There are three types of anions varying in degree of both dynamic and static disorders and two types of cations (one deformed and one regular). The orientational ordering of the anions is triggered by the NH⋯O hydrogen-bonding interactions.
space group with a = 22.7660(6) Å and Z = 32. There are three types of anions varying in degree of both dynamic and static disorders and two types of cations (one deformed and one regular). The orientational ordering of the anions is triggered by the NH⋯O hydrogen-bonding interactions.
3. Various types of dynamics are mixed in phase II, reflecting the complex structure. Some NH3 ligands are oriented during the time scale of the NMR measurement, whereas some cations perform isotropic reorientations identical to phase I. In contrast, phase I, an orientationally disordered crystalline phase, is highly disordered.
4. The energy required to reorient an ordered anion in phase II is estimated from the excess heat capacity observed immediately below TC1, which in turn gives the energy to break the NH⋯O hydrogen bond, 8 kJ mol−1.
Acknowledgements
This work is Contribution No. 17 from the Research Center for Structural Thermodynamics.References
- Z. Zhao, F. Liang, P. Hu, L. Guo, Q. Zhong, L. He and C. Chen, Phys. E., 2007, 39, 99–102 CrossRef CAS.
- A. S. Naura, N. R. Kalla, R. P. Sharma and R. Sharma, Biol. Trace Elem. Res., 2007, 119, 147–165 CrossRef CAS.
- L. D'Souza, J. R. Regalbuto and J. T. Miller, J. Catal., 2008, 254, 157–169 CrossRef CAS.
- S. He, P. G. Arscott and V. A. Bloomfield, Biopolymers, 2000, 53, 329–341 CrossRef CAS.
- R. P. Sharma, R. Bala, R. Sharma and V. Ferretti, Inorg. Chim. Acta, 2005, 358, 3457–3464 CrossRef CAS.
- R. P. Sharma, R. Bala, R. Sharma, U. Rychlewska and B. Warżajtis, J. Fluorine Chem., 2005, 126, 967–975 CrossRef CAS.
- R. G. W. Wyckoff, Crystal Structures, Wiley/Interscience, New York, 1965, vol. 3 Search PubMed.
- K. B. Nilsson, L. Eriksson, V. G. Kessler and I. Persson, J. Mol. Liq., 2007, 131–132, 113–120 CrossRef CAS.
- A. Migdał-Mikuli, E. Mikuli, S. Wróbel and Ł. Hetmańczyk, Z. Naturforsch. A, 1999, 54, 590–594 Search PubMed.
- J. Hetmańczyk, Ł. Hetmańczyk, A. Migdał-Mikuli, E. Mikuli and I. Natkaniec, J. Alloys Compd., 2011, 509, 6545–6550 CrossRef.
- K. Parliński, Phys. Status Solidi B, 1980, 98, 487–494 CrossRef.
- E. Mikuli, A. Migdał-Mikuli, N. Górska, S. Wróbel, J. Ściesiński and E. Ściesińska, J. Mol. Struct., 2003, 651–653, 519–524 CrossRef CAS.
- E. Mikuli, N. Górska, S. Wróbel, J. Ściesiński and E. Ściesińska, J. Mol. Struct., 2004, 692, 231–236 CrossRef CAS.
- E. Mikuli, N. Górska, S. Wróbel, J. Ściesiński and E. Ściesińska, Z. Naturforsch. A, 2007, 62, 179–186 CAS.
- G. R. Murray and J. S. Waugh, J. Chem. Phys., 1958, 29, 207–213 CrossRef CAS.
- T. Matsuo, K. Kohno, A. Inaba, T. Mochida, A. Izuoka and T. Sugawara, J. Chem. Phys., 1998, 108, 9809–9816 CrossRef CAS.
- H. Suzuki, A. Inaba, J. Krawczyk and M. Massalska-Arodź, J. Chem. Thermodyn., 2008, 40, 1232–1242 CrossRef CAS.
- SHELX-97: G. M. Sheldrick, Acta Crystallogr. A, 2008, 64, 112–122 CrossRef.
- SIR2004: M. C. Burla, R. Caliandro, M. Camalli, G. L. Cascarano, L. De Caro, C. Giacovazzo, G. Polidori and R. Spagna, J. Appl. Crystallogr., 2005, 38, 381–388 CrossRef CAS.
- K. Wakita, Yadokari-XG, Software for Crystal Structure Analyses, 2001; CrossRefRelease of Software (Yadokari-XG 2009) for Crystal Structure Analyses, C. Kabuto, S. Akine, T. Nemoto and E. Kwon, J. Cryst. Soc. Jpn., 2009, 51, 218–224 CrossRef.
- H. C. Stynes and J. A. Ibers, Inorg. Chem., 1971, 10, 2304–2308 CrossRef CAS.
- R. O. W. Fletcher and I. A. McDoom, Acta Crystallogr., 1967, 23, 436–438 CrossRef CAS.
- I. Bernal, J. D. Korp, E. O. Schlemper and M. S. Hussain, Polyhedron, 1982, 1, 365–369 CrossRef CAS.
- J. H. Van Vleck, Phys. Rev., 1948, 74, 1168–1183 CrossRef.
- A. W. Hewat and C. Riekel, Acta Crystallogr. A, 1979, 35, 569–571 CrossRef.
- G. W. Smith, J. Chem. Phys., 1962, 36, 3081–3093 CrossRef CAS.
- G. W. Smith, J. Chem. Phys., 1965, 42, 4229–4243 CrossRef CAS.
- G. W. Smith, J. Chem. Phys., 1969, 50, 3595–3605 CrossRef CAS.
- R. H. Beaumont, H. Chihara and J. A. Morrison, Proc. Phys. Soc., 1961, 78, 1462–1481 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical data of the molar heat capacity and X-ray crystallographic data (CIF) obtained at 340 K and 200 K. CCDC reference numbers 853069 and 853070. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2ra01184k |
| This journal is © The Royal Society of Chemistry 2012 |
