Quantum sieving: feasibility and challenges for the separation of hydrogen isotopes in nanoporous materials
Jinjun
Cai
,
Yanlong
Xing
and
Xuebo
Zhao
*
Qingdao Institute of Bioenergy and Bioprocess Technology, Chinese Academy of Sciences, Qingdao, 266101, China. E-mail: zhaoxb@qibebt.ac.cn; Fax: +86-532-80662728; Tel: +86-532-80662729
First published on 13th June 2012
Abstract
Quantum effects on the molecular adsorption and migration in confined porous materials can not be ignored if the difference between the pore size and molecular hard core is no longer large compared to the de Broglie wavelength of gas molecules. Extensive studies of the quantum sieving have been focused on nanoporous materials due to their potential applications in separating hydrogen (H2) isotopes. This article reviews state-of-the-art research activities in the field of separation, discussing the feasibility of separating H2 isotopes by quantum sieving in nanoporous materials including zeolites, carbons and organic framework materials. The overall results indicate that an effective separation of H2 isotopes is possible via combining the equilibrium and kinetic selectivity of adsorption induced by a quantum sieving effect. A fundamental understanding of the factors that affect the quantum molecular sieving is discussed. We hope to outline a clear insight into the perspectives and challenges on this novel separation technique for H2 isotopes in the subsequent course of researches.
 Jinjun Cai | Jinjun Cai is a PhD candidate under the supervision of Prof. Xuebo Zhao at the Qingdao Institute of Bioenergy and Bioprocess Technology, Chinese Academy of Sciences. He was born in Hunan Province, China. He received his BS degree in Jishou University in 2008 and received his MS degree in Wuyi University in 2011. His current research concentrates both on the separation of various gas mixtures and exploration of the quantum sieving mechanism. |
 Yanlong Xing | Yanlong Xing was born in Shandong Province, China. She received her B.S & M.S degree in 2005 and 2008 from the Shandong Normal University, China. In 2008, she joined the Qingdao Institute of Bioenergy and Bioprocess Technology as a Research Assistant. Her scientific interests focus on the separation of hydrogen isotopes. |
 Xuebo Zhao | Xuebo Zhao is a Professor of Qingdao Institute of Bioenergy and Bioprocess Technology, Chinese Academy of Sciences. He received his PhD degree in 2005 from the Newcastle University. He is the member of Royal Society of Chemistry and the winner of The Derek Ezra Award 2004 for outstanding achievement in combustion engineering research. His papers have been cited more than 800 times so far. His research interests focus on nanoporous materials: synthesis, adsorption and separation properties. |
Introduction
H2 has been recognized as the most attractive energy carrier and fuel in the near future due to its clean combustion which creates neither air pollution nor greenhouse-gas emissions.1–3 The separation of H2 isotopes is a significant research subject in the nuclear industry because deuterium (D2) is an important raw material for nuclear fusion and also a key element for the neutron moderator of heavy water in nuclear reactor. Moreover, D2 is of great importance due to its wide applications in medical treatment and detection as a tracer.4 Since the natural content of D2 is only 0.015% and the consumption of D2 and tritium (T2) is less than 10% in a nuclear fusion reactor, they must be recycled effectively from the wastes of nuclear fusion, considering environmental safety and durable economy. With an increasing demand for environmental protection from the current usage of fossil fuel, the energy situation is becoming more and more serious. There is no doubt that fusion energy will eventually play an important role in future. In order to better exploit the fusion energy from D2 and T2, the separation of H2 isotopes has triggered great attention since it is one of key technologies for recycling the fuel from a nuclear fusion reactor and the operating exhaust gases in the fusion reaction. The existing methods for the separation of H2 isotopes such as cryogenic distillation and thermal diffusion suffer from high energy consumption and low efficiency.5–7 It is necessary for relevant researchers around the world to exploit an efficient and low-cost method for an industrial application of D2 and T2.Adsorptive separation has many advantages and the most important is that the adsorbent can be used repeatedly, therefore inhibiting the production of radioactive wastes and environmental pollution. Generally, the cost of adsorptive separation is relatively low and molecular sieving is successfully applied to the industrial applications for the air separation.8–11 Zeolite, activated carbon and organic framework materials are representatives of nanoporous materials that have been widely used in various technologies and can separate gas molecules based on different sizes and shapes.12 However, traditional molecular sieving will be invalid in the separation of isotopes due to their similar properties. Quantum sieving, a novel separation method for H2 isotopes, has aroused great interest recently in the area of separation. The heavier isotopes exhibit a strong isotope effect in adsorption at low temperature, in which T2 displays a stronger adsorption strength than D2 and H2. Although the isotope effect in adsorption has been known for many years, the conception of quantum sieving was first proposed in 1995 by Beenakker et al.13 based on the simple model of hard spheres in a hard cylindrical well. It has been proposed that if the difference between the pore size and molecular hard core become comparable to the de Broglie wavelength, quantum effects on the molecular adsorption and transport become important. Compared with the traditional separation methods for H2 isotopes, quantum molecular sieving is considered promising. Although large numbers of papers on the storage of H2 have been published in the literature,14–19 to the best of our knowledge, there is no comprehensive report on separating H2 isotopes. This review article summarizes the main recent achievements in the areas of separating H2 isotopes via quantum sieving and highlights the relevance of crucial issues which should be noted in the future course of research.
Strategies for separating H2 isotopes
The isotopes of H2, D2 and T2 are important raw materials in the nuclear industry. With an increasing demand for fusion energy from the current usage of D2 and T2, the separation of H2 isotopes is one of key issues for realizing the industrial applications of fusion energy using D2 and T2 as fusion reactor fuels. Since the chemical properties of isotopes are almost identical, their separation is only possible through small difference in their mass and other physical properties. So far, several separation methods for H2 isotopes such as cryogenic distillation, electrolysis, proton exchange, centrifugation, thermal diffusion, chromatography and metal hydride absorption are being investigated.5–7,20–24 Among the methods mentioned above, proton exchange between H2O and H2 or H2S shows a higher separation factor although the process needs special catalysts which greatly increase the cost, and it is very difficult to obtain the pure components directly. Cryogenic distillation was used in the early stages but its complex processes led to high costs. Centrifugation has the great advantage of requiring the simplest device but the efficiency is rather low. Chromatography has the ability to determine the amount of H2 isotopes while its intermittent operation and low-processing capacity make it difficult to achieve the requirements of industrial application. Thermal diffusion needs simpler processes and devices but the small-scale and high-energy consumption result in great difficulty in achieving the multi-level series connection. In addition, the method of metal hydride absorption for separating H2 isotopes has triggered great concerns in recent years for its high separation factor and cost-effectiveness,25–28 in addition, the regeneration of metals requires higher temperatures.Clearly, most of the conventional methods have low selectivity and high energy requirements for the separation of H2 isotopes. Therefore, an alternative efficient method should be exploited as soon as possible. One of the most promising processes is the adsorptive separation in specific confined systems at low temper-atures by quantum molecular sieving, utilizing differences in the adsorptive capacities or kinetic characteristics between isotopes induced by quantum effects.
Equilibrium simulation of quantum sieving
Since the phenomenon of quantum sieving was first predicted by Beenakker et al.,13 separation of H2 isotopes via quantum sieving has attracted great attention. Wang et al.29 were the first to certify the existence of quantum sieving effects at 20 K in single-walled carbon nanotubes (SWNTs) and interstices via the path integral grand canonical Monte Carlo (PI-GCMC) simulation. The results suggest that SWNTs with a pore size of less than 7 Å will show high selectivity and T2 will adsorb in suitable nanotubes and interstices where H2 can be effectively excluded. Challa et al.30,31 also used PI-GCMC simulations to study the selectivity both in interstices and SWNTs, considering the effects of temperature, pressure and pore size. Their results exhibit that the selectivity of T2/H2 with an order of 105 in a (3, 6) tube and 104 in an (10, 10) interstice at 20 K is almost 20 times higher than D2/H2 under the same conditions (Fig. 1a). They found that the lowest selectivity occurred in a (6, 6) tube and the selectivity was greatly affected by the temperatures and pressures.31 | ||
| Fig. 1 (a) Pure fluid isotherms in the (3, 6) nanotubes (open symbol) and (10, 10) interstices (filled symbol) at 20 K from the PI-GCMC simulation. Circles for T2, diamonds for D2 and triangles for H2.31 Reprinted with permission from Ref. 31. Copyright © 2002 American Institute of Physics; (b) Zero-pressure selectivity for ortho–D2/para–H2 mixture as a function of pore width for different temperatures. Circles for 20 K, squares for 40 K, diamonds for 100 K and triangles for 300 K.33 Reprinted with permission from Ref. 33. Copyright © 2009 Springer-Verlag. | ||
Since PI-GCMC simulations are time-consuming, Garberoglio used Boltzmann bias grand canonical Monte Carlo (BMC) simulations to evaluate the selectivity in SWNTs and carbon slit pores.32,33 He found that significant quantum sieving effects exist both in SWNTs and carbon slit pores and the selectivity exhibits a strong dependence on the temperature (Fig. 1b). The selectivity of D2/H2 is about 150 in carbon slit pores with pore widths of 5.7 Å at 20 K which drops to 3 at 77 K. The authors34 also used the PI-GCMC simulations to study the effect of pressure and temperature on the selectivity in several organic framework materials. Their results indicate that the largest quantum sieving effect is for the sorbent with the narrowest pores and the selectivity has a strong dependence on temperature while a less pronounced dependence on pressure. Moreover, the selectivity of T2/H2 in these organic frameworks is orders of magnitude lower than the extraordinary values predicted for narrower nanotubes.29–33 Recently, Liu et al.35 introduced a new concept of “quantum effective pore size” (QEPS), that is, an effective pore size calculated by considering the swelling of the adsorbate–adsorbent potential size parameters caused by quantum effects and they observed good correlation between selectivity and QEPS (Fig. 2). They found that two MOFs of Cu(F-pymo)2 and CPL-1 exhibit exceptional selectivity which is higher than other MOFs as well as the porous materials such as carbon nanotubes, slit-shaped graphite and zeolites studied so far.35
 | ||
| Fig. 2 (a) Typical crystal structure of the Cu(F-pymo)2 used in simulations; (b, c, d) The selectivity of the D2/H2, T2/H2, and T2/D2 as a function of the quantum effective pore size of MOFs at 0.001 MPa.35 Reprinted with the permission from Ref. 35. Copyright © 2011 American Chemical Society. | ||
Bhatia's group36 used PI-GCMC simulations with Silvera–Goldman (SG) potentials to study the separation of a H2/D2 mixture in carbon slit pores and the optimum separation conditions were determined to be: 1.0 bar and 40 K with a pore width of 0.56 nm. It is worth noting that they also simulated a practical separation process with 0.05% D2 in mixture under the best conditions and demonstrated that the mole fraction of D2 can increase to 50.3% after three separation steps. They believe that the separation efficiency can be further improved by the faster diffusion of D2 compared to H2 which we will discuss in next section. Later, they studied the separation of a HD/H2 mixture in the carbon slit pores and discussed the effect of temperature, pressure and pore size.37 Their results suggest that the optimal pore size for separating HD and H2 is 0.56 or 0.57 nm and the optimal pressure for the 0.56 and 0.57 nm slit pore is 10.0 and 0.1 bar, respectively. Interestingly, they observed an unusual crossover effect at high densities where the selectivity in 0.85 nm slit pore exceeds the one in 0.69 nm slit pore, which is due to the enhanced quantum confinement effect with the formation of a second layer in the larger slit pore. However, they found that only a modest selectivity of HD/H2 existed in the commercial Takeda 3A carbon molecular sieve (CMST-3A) based on the slit pore models with a distribution of pore sizes.
Kaneko's group38–43 studied the selectivity of D2/H2 in SWNTs, metal–organic framework materials of CuBOTf and single-wall carbon nanohorns (SWNHs) at liquid nitrogen temperature (77 K) using grand canonical Monte Carlo simulations incorporating quantum effects via the Feynman–Hibbs approach (FH-GCMC). They found that the FH-GCMC simulation can be used effectively as an alternative to the PI-GCMC simulation for exploring the adsorptive properties of quantum H2. Their results suggest that molecules are preferentially adsorbed in the cone part of SWNHs (Fig. 3) and the zero-pressure selectivity of D2/H2 is around 1.08. As the pressure decreases, the selectivity increases because the quantum swelling of H2 is more significant than for D2 in the narrow conical part of these SWNHs (Fig. 4a).38,39 Noguchi et al.40 found that the D2/H2 selectivity in CuBOTf was around 1.3 at 77 K over the whole range of pressures and the selectivity was in good agreement with the experimental results, which we will discuss in subsequent section. The authors42 also found that the selectivity of D2/H2 in the well-bundled SWNTs is greatly lower than the one in loosely-assembled SWNTs. They ascribed the higher selectivity in the latter one to its unique structures and geometrical defects which facilitate the molecules' diffusion and introduce strong adsorption field on its surface. Tanaka et al.41 have evaluated the selectivity of D2/H2 in (10, 10) interstices at 77 K via FH-GCMC simulation. D2 molecules are preferentially adsorbed in (10, 10) interstices from the D2/H2 binary mixtures and the difference of adsorptive capacities between H2 and D2 decreases with increasing pressures. The authors43 studied the adsorption of D2/H2 and HD/H2 binary mixtures in the carbon slit pores and cylindrical pores using the PI-GCMC and FH-GCMC simulations. The results show that the two methods exhibit good consistency and the quantum effects in the cylindrical pores are larger than the quantum effects in the slit pores. The optimal pore size for the separation of the D2/H2 and HD/H2 mixtures is 0.623 and 0.625 nm respectively. The selectivity of D2/H2 at 77 K in a cylindrical pore with a pore width of 0.623 nm is 9.9 (Fig. 4b) and the selectivity of HD/H2 in a cylindrical pore with a pore width of 0.625 nm is 4.3.
 | ||
| Fig. 3 Configurational snapshots collected from the FH-GCMC simulation for hydrogen adsorption in SWNHs at 77 K.39 (a) 10−4 MPa, (b) 10−3 MPa, (c) 10−2 MPa, and (d) 0.1 MPa. Reprinted with the permission from Ref. 39. Copyright © 2005 American Chemical Society. | ||
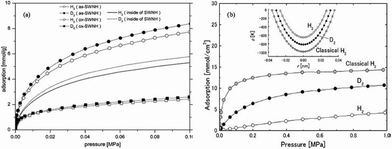 | ||
| Fig. 4 (a) The adsorption isotherms of H2 (D2) for as-SWNHs, ox-SWNHs, and the internal space of SWNHs at 77 K.39 Reprinted with permission from Ref. 39. Copyright © 2005 American Chemical Society; (b) The single-component adsorption isotherms of the quantum LJ H2 and D2 in carbon cylindrical pore of D = 0.623 nm at 77 K obtained from the FH-GCMC simulations. H2 adsorption isotherm from classical LJ potential at 77 K is also shown for comparison. The inset compares the solid-fluid interaction potentials for the quantum LJ H2 and D2 at 77 K and the classical LJ H2.43 Reprinted with permission from Ref. 43. Copyright © 2011 The Society of Chemical Engineers, Japan. | ||
Kinetic simulations of quantum sieving
Increasing attention has been focused on kinetic quantum sieving for separating H2 isotopes in recent years. In this section, we will systematically summarize the recent progress in separating H2 isotopes via kinetic quantum sieving simulations. Bhatia and co-workers44–47 are one of the representatives who recognized the effectiveness for separating H2 isotopes by the kinetic quantum sieving. Kumar et al.44–46 observed reverse kinetic molecular sieving in zeolite-ρ at low temperatures for the first time in which they applied atomistic molecular dynamic (MD) simulations, incorporating quantum effects via Feynman–Hibbs approach. The results indicate that zeolite-ρ with a window diameter of 0.596 nm does not exhibit a reverse kinetic selectivity while it will do with a window diameter of 0.543 nm (Fig. 5a) and the flux selectivity reaches the value of 22.66 at 30 K while staying rather low at higher temperature. Later, they studied the possibility of kinetic sieving for H2 isotopes by observing their dynamic properties in the one-dimensional channels of AlPO4–25 at low temperatures by transition state theory (TST) and MD simulations.47 Their calculations indicate that the reverse kinetic selectivity is observed when the temperature is around 110 K. Moreover, results from the TST and MD simulations are in good agreement, with only some minor deviation at 30 K where the kinetic selectivity is 50 in TST while 70 in the MD simulations (Fig. 5b). All results mentioned above suggest that reversal kinetic diffusion is very sensitive to the pore diameter and there may have great potential application for separating H2 isotopes via kinetic quantum sieving at low temperatures in suitable materials. | ||
| Fig. 5 (a) Temperature variation of a transport diffusivity of H2 and D2 in zeolite ρ with a narrower window. D2 begins to diffuse faster around 94 K. Kinetic D2/H2 selectivity at various temperatures is shown in the inset.45 (b) Kinetic D2/H2 selectivity in AlPO4–25 at various temperature obtained from the TST and MD simulation. Squares denote TST values and circles denote MD results.47 Reprinted with permission from Ref. 45 and Ref. 47. Copyright © 2006 and 2008 American Chemical Society. | ||
Recently, Smith and co-workers48 studied the kinetic model for the transport of H2 molecules in CMS via TST simulations to clarify the effect of the pore-mouth and cavity on kinetic sieving. The results indicate that the differences in the length and layer of pore-mouth can not affect the outcome of kinetic sieving while a small change in diameter (0.6 Å) will greatly affect the selectivity. Moreover, it is very interesting to note that the results for the diffusion barriers in the cavity are in related to the model, namely, nanotube-shaped or spherical-shaped models. The activation barrier lies in the cavity for nanotube-shaped models and in the pore-mouth for the spherical-shaped model. Therefore, researchers should consider the cavity shape and size in addition to the pore-mouth size in the future study for ensuring the rate-determining steps and achieving the quantum-mediated kinetic molecular sieving of H2 and D2 on microporous materials.
Theoretical approaches of selective adsorption
Besides equilibrium and kinetic simulations for quantum sieving processes, calculations through theoretical approaches such as the ideal adsorption solution theory (IAST) are widely used by many researchers. They have first confirmed the rationality of IAST for evaluating selectivity by FH-GCMC and/or PI-GCMC simulation and then predict the adsorptive isotherms of mixtures leading to the selectivity. Johnson's group29–31 applied the IAST to calculate the selectivity of D2 and T2 over H2 both at 20 and 77 K, showing good agreement between the theory and PI-GCMC simulation up to moderate loadings. Noguchi et al.40 also used IAST to evaluate the D2/H2 selectivity in CuBOTf, showing values around 1.3 at 77 K over a whole range of pressure while in the range 1.9 ∼ 3.0 kPa at 40 K and increases with pressure. Hattori et al.49 used IAST to evaluate the effects of fluorination on the selectivity of activated carbon fibers (ACF) at 20 K. The results show that the selectivity both in ACFs and F-ACFs increases monotonically with pressure, though the selectivity in ACFs is always larger than the one in F-ACFs. Tanaka et al.41 analyzed the D2/H2 selectivity by the IAST in (10, 10) interstices at 77 K (Fig. 6). The results suggest that the selectivity exceeds 2.9 at 0.1 MPa, almost twice the cryogenic distillation of liquid H2 isotopes mixtures at 0.25 MPa and 24 K. They also predicted the selectivity of D2 and HD over H2 both in carbon cylindrical and slit pores, indicating that the predictions for all carbon pore models at 77 K and moderate pressures agreed well with the direct FH-GCMC simulations.43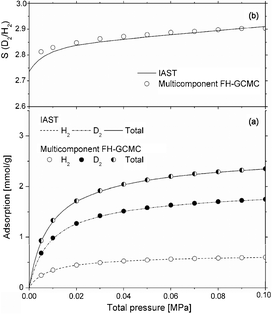 | ||
| Fig. 6 (a) Adsorption isotherms of D2/H2 mixture by using the IAST and FH-GCMC simulations in (10, 10) interstice for a bulk mixture containing 50% H2, along with the adsorption isotherm of the individual components; (b) D2/H2 selectivity obtained by using IAST and the mixture adsorption FH-GCMC simulations.41 Reprinted with the permission from Ref. 41. Copyright © 2009 Springer-Verlag. | ||
Many researchers began to consider other models for predicting the quantum sieving selectivity because early simulations always treat H2 as a sphere object and only considered the effect of the transversal zero-point energy, i.e. the rotational motion is ignored. Recently, Hathorn et al.50 found that the restricted rotational degree of freedom contributed greatly to quantum effects. They observed a large selectivity in a range of 6–8 Å for a cylinder pore, suggesting that both the translational and rotational confinements led to significant selectivity. Later, Trasca et al.51 calculated the zero-pressure selectivity of D2/H2 at 20 K in interstices of bundles of (18, 0) nanotubes and the selectivity reached the order of 109. They ascribed such a large selectivity to two reasons, one is the consideration of both the zero-point and rotational contributions and the other is the usage of a slightly deeper solid-fluid potential. The stronger the confinement, the larger differences existed in the zero-point energies of isotopes. The difference between rotational energies of isotopes is the same situation.51 Goldfield et al.52,53 evaluated the selectivity of D2 and T2 over H2 in SWNTs with three kinds of potential parameters by treating the translational and rotational degrees of freedom explicitly. Their results suggest that the selectivity for all the three potentials is only significant at low temperatures and the D2/H2 and T2/H2 selectivity in the (3, 6) tube can be the orders of 106 and 1010 at 20 K, respectively.53 Johnson's group54 studied the effects of interaction potential and rotational-translational coupling on the selectivity. Their results suggest that the selectivity is very sensitive to atomic diameters while insensitive to potential well depth. Moreover, the rotational states have large effects on the selectivity. Later, the authors55 analyzed the effects of quantized rotational degrees of freedom in various SWNTs at 20 K, indicating that the quantized rotational degrees of freedom has a dramatic effect on selectivity in the (3, 6) tube where the T2/H2 selectivity has an increases by over 7000-fold while the increase in the selectivity for other tubes is much less, being on the order of 2.3 in (2, 8) tube and nearly negligible in the case of (6, 6) tube.55
On the other hand, many researchers have done lots of work on the enthalpies for the adsorption of H2 on MOFs, graphene and carbon nanotubes,56–58 using density functional theory (DFT) and ab initio molecular orbital theory. Okamoto et al.56 used ab initio molecular orbital theory to examine the physisorption of H2 on planar and curved graphene clusters. Their results indicate that potential energy curves of H2–H2 interactions are almost repulsive and the physisorption energies for H2 molecules on curved graphene can be increased about three times more than those on planar ones. Sillar et al.58 studied the H2 adsorption in MOF-5 and confirmed that quantum effects must be taken into account when calculating adsorption enthalpies. The results show that the ab initio quantum chemistry combined with molecular statistics makes an accurate description possible of the interactions between H2 and MOF-5. Tada et al.57 studied the adsorption of H2 molecules in various kinds of SWNTs and found that potential energy barrier height (PBH) for H2 on the outer wall of nanotubes decreases as the tube diameter decreases. In contrast, the PBH for H2 penetration into an open-ended nanotube increases as the tube diameter decreases, independent on the geometry, i.e., zigzag or armchair structures. These results on the structure-dependent H2 adsorption to SWNTs can be explained reasonably with sp2–sp3 re-hybridization caused by the interactions between the adsorbed H2 and carbon atoms of SWNTs. Based on the computed results for the physisorption of H2 molecules, we firmly believe that the quantum effects can be very obvious in suitable materials which can be utilized for separating H2 isotopes. The adsorbate–adsorbate interactions are slightly lower between D2 molecules while the adsorbent–adsorbate interactions are greater for D2 because D2 has a lower zero-point energy compared with H2, which was confirmed by virial analysis in our previous works.59
In addition, Suzuki and co-workers60–62 have recently used the buckybowl-like molecules (C36H12 and C36D12), basic fragment structures of zeolite-templated carbons,63 as the model structures to evaluate the stable adsorptive sites for additional proton and deuteron (H* and D*) at room temperature by PIMD simulations including thermal and nuclear quantum fluctuation. Their results indicate that the stable adsorptive sites for D* exist on all carbon atoms while those sites for H* are not observed on the innermost carbon present inside the buckybowl. The results further confirm that the quantum sieving does exist with total adsorptive amounts for D2 larger than H2 and indicate that the isotope effect is very important for theoretical analysis of H2 adsorption even at room temperature.
Experimental studies of selective adsorption
Although there are many promising theory and simulation works on the separation of H2 isotopes via equilibrium quantum sieving introduced by Johnson's group,29–32 almost all experimental data at 77 K showed that difference of adsorptive capacity between H2 and D2 was small and did not change a lot. Stephanie–Victoire et al.64 reported the adsorptive amount of D2 over H2 (nmD2/nmH2) is 1.16 on a NaA zeolite. Kotoh et al.65 also reported the separation factor of D2/H2, HD/H2 and D2/HD on a 5A zeolite due to thermal diffusion is 1.207, 1.127 and 1.07, respectively. Our previous works59,66–69 have reported that the nmD2/nmH2 on several kinds of porous carbons and metal–organic framework materials, and the value is in the range 1.05–1.20 depending on pressures (Fig. 7b). Chu et al.70 also reported nmD2/nmH2 on various molecular sieves and the value is in the range 1.02–1.15 depending on the pore diameters (Fig. 7a). Moreover, Kaneko's group38–43,49 reported large numbers of experimental data about values of nmD2/nmH2 on SWNHs, ACFs, CuBOTf and SWNTs. They found that the value of nmD2/nmH2 on SWNHs is in the range 1.06–1.08 at 77 K and molecules are preferentially adsorbed in a conical part with pore size less than 2 nm.38,39 The nmD2/nmH2 on CuBOTf at 77 K is around 1.3 which is in good agreement with simulation works over the whole range of pressures while values at 40 K are in the range 2.6–5.8 and increase monotonically with pressure, showing larger selectivity than simulation ones.40 In addition, they have studied the effects of fluorination on nmD2/nmH2 for ACFs at 20 K and results indicate that fluorination process reduced nmD2/nmH2 although the F-ACFs sample has a narrower pore width.49 | ||
| Fig. 7 (a) The adsorptive isotherms of H2 and D2 on different zeolites at 77 K. Symbols: white denote H2 and gray denote D2.70 (b) The isotherms of H2 and D2 on HKUST-1 at 77 K,67 the nmD2/nmH2 value at 800 mbar is 1.09. Reprinted with the permission from Ref. 70 and Ref. 67. Copyright © 2006 and 2007 American Chemical Society. | ||
Compared with substantial experimental works on equilibrium quantum sieving, there are only few experimental works on the kinetic quantum sieving. We and our co-workers have observed for the first time that D2 diffuses faster than H2 at 77 K in CMST-3A with a pore size of 0.546 nm (Fig. 8).59 Chu et al.70 studied the dynamic adsorption of H2 and D2 in several zeolites with different pore widths at 77 K and indicated that the adsorptive rate of H2 is larger than D2 in mesopores while this order reverses in micropores. Although they did not refer to the concept of quantum sieving, their results confirmed the existence of quantum sieving indirectly in suitable micropores. Moreover, they find that the adsorptive rate of D2 is higher than H2 when pressure is low while the order will reverse for a higher pressure,71 namely, the ratio of D2–H2 adsorptive rate constants increases first and then decreases with increasing pressure. Recently, Bhatia's group used quasi-elastic neutron scattering to study the diffusion of H2 and D2 in CMST-3A45 and zeolite-ρ,72 showing that D2 diffuses faster than H2 below 100 K which confirmed the importance of the quantum effects below 100 K, especially the remarkable kinetic quantum sieving effects. Moreover, dynamic characteristics obtained from experiments are in good agreement with the molecular dynamic simulations.44–47
 | ||
| Fig. 8 (a, b) Adsorption and desorption kinetic profiles of H2 and D2 for different pressures on CMS T3A at 77 K. (c, d) Variation of rate constants for H2 and D2 adsorption and desorption on CMS T3A at 77 K obtained from the stretched exponential model with different pressures. Reprinted with permission from Ref. 59. Copyright © 2006 American Chemical Society. | ||
Conclusion and perspectives
In this review, we have selectively discussed and summarized the main recent achievements in the field of separation of H2 isotopes via quantum sieving. Our main aim is to reveal the key issues, challenges and opportunities facing present and future researches on kinetic quantum sieving. There are large numbers of simulated and theoretical works on the quantum sieving to analyze the adsorptive characteristics and separation mechanism of hydrogen isotopes. The adsorptive data at 77 K on various porous materials indicated that the nmD2/nmH2 is small with ranges from 1.06 to 1.50 while the kinetic selectivity of D2/H2 is much higher than the equilibrium one, indicating that the adsorptive separation of hydrogen isotopes should not be based on equilibrium but kinetic quantum sieving. Besides, it is evident that the nmD2/nmH2 decreases with increasing temperature while the effects of pressure seem uncertain for different materials. With significant fundamental knowledge already accumulated by previous research works, kinetic quantum sieving shows an encouraging prospect in realizing the separation of H2 isotopes. From an industrial point of view, however, many challenges remain in the area of separation for achieving effective kinetic quantum sieving.It can be seen from the above discussions that both equilibrium and kinetic quantum sieving are strongly dependent on pore size, temperature and pressure. Despite excellent simulations and a few experimental works of the kinetic quantum sieving, however, one should note that it is still desperately short of experimental data to confirm the presence of kinetic quantum sieving in other narrow geometries. Moreover, materials with the suitably ordered pores critical for kinetic quantum sieving are very hard to prepare in large quantities. In order to better understand kinetic quantum sieving in porous materials, there is still much research that needs to be done. Firstly, one should consider doing some more rigorous simulations to optimize the existing models on quantum-mediated kinetics in various porous materials because the results are sensitive to potential parameters applied in simulations. Secondly, experiments to answer the question of where the diffusion barrier actually occurs in molecular transport through the pores are needed. Thirdly, materials with ordered ultramicropores and narrow pore size distribution should be intentionally prepared. Last but not least, effects of surface and interface properties of materials on the kinetic quantum sieving should be extensively studied.
On the whole, irrespective of porous materials used as quantum sieves for the separation of H2 isotopes at low temperature, pore structure is the key factor and the pore size must be narrower than 0.7 nm. The properties of kinetic quantum sieving may have great potential application in developing more efficient and economical methods for separating H2 isotopes and producing heavy water. Theoretical calculations and simulations promise to promote the rapid development of this striking kinetic quantum sieving project. In view that few experimental works were done in the current stage, we suggest that the future studies should be concentrated on the parameters such as temperature, pressure, pore size and surface properties of the kinetic quantum sieving and then we will see a prosperous perspective for separating H2 isotopes via quantum sieving. In short, using quantum-induced kinetic selectivity for the separation of H2 isotopes combined with equilibrium selectivity in suitable porous materials will be less complex and more economically viable .
Acknowledgements
We greatly appreciate the financial support from the “Hundred Talents Program” of Chinese Academy of Sciences (No.KJCX2-YW-W34) and the National Natural Science Foundation of China (No.21073216 and No.21173246).References
- A. Züttel, Mater. Today, 2003, 6, 24–33 CrossRef.
- L. Zhou, Renewable Sustainable Energy Rev., 2005, 9, 395–408 CrossRef CAS.
- J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- F. Keppler, J. T. G. Hamilton, W. C. McRoberts, I. Vigano, M. Braß and T. Rockmann, New Phytol., 2008, 178, 808–814 CrossRef CAS.
- P. Kowalczyk, P. A. Gauden and A. P. Terzyk, J. Phys. Chem. B, 2008, 112, 8275–8284 CrossRef CAS.
- F. M. Richter, E. B. Watson, R. Mendybaev, N. Dauphas, B. Georg, J. Watkins and J. Valley, Geochim. Cosmochim. Acta, 2009, 73, 4250–4263 CrossRef CAS.
- I. Alekseev, S. Bondarenko, O. Fedorchenko, T. Vasyanina, K. Konoplev, E. Arkhipov, T. Voronina, A. Grushko, A. Tchijov and V. Uborsky, Fusion Eng. Des., 2003, 69, 33–37 CrossRef CAS.
- C. R. Reid and K. M. Thomas, Langmuir, 1999, 15, 3206–3218 CrossRef CAS.
- C. R. Reid and K. M. Thomas, J. Phys. Chem. B, 2001, 105, 10619–10629 CrossRef CAS.
- B. L. Newalkar, N. V. Choudary, P. Kumar, S. Komarneni and T. S. G. Bhat, Chem. Mater., 2002, 14, 304–309 CrossRef CAS.
- B. L. Newalkar, N. V. Choudary, U. T. Turaga, R. Vijayalakshmi, P. Kumar, S. Komarneni and T. S. G. Bhat, Chem. Mater., 2003, 15, 1474–1479 CrossRef CAS.
- K. Kotoh, S. Takashima and Y. Nakamura, Fusion Eng. Des., 2009, 84, 1108–1112 CrossRef CAS.
- J. J. M. Beenakker, V. D. Borman and S. Y. Krylov, Chem. Phys. Lett., 1995, 232, 379–382 CrossRef CAS.
- L. Schlapbach and A. Zuttel, Nature, 2001, 414, 353–358 CrossRef CAS.
- F. L. Darkrima, P. albrunota and G. P. Tartagliab, Int. J. Hydrogen Energy, 2002, 27, 193–202 CrossRef.
- J. Chen and F. Wu, Appl. Phys. A: Mater. Sci. Process., 2004, 78, 989–994 CrossRef CAS.
- Y. Yurum, A. Taralp and T. N. Veziroglu, Int. J. Hydrogen Energy, 2009, 34, 3784–3798 CrossRef.
- L. Wang and R. T. Yang, Catal. Rev. Sci. Eng., 2010, 52, 411–461 CAS.
- K. M. Thomas, Catal. Today, 2007, 120, 389–398 CrossRef CAS.
- T. Lueders, M. Manefield and M. W. Friedrich, Environ. Microbiol., 2004, 6, 73–78 CrossRef CAS.
- A. F. Bernhardt, Appl. Phys. A-Mater., 1976, 9, 19–34 CAS.
- G. Lis, L. Wassenaar and M. Hendry, Anal. Chem., 2008, 80, 287–293 CrossRef CAS.
- O. Degtyareva and L. Bondareva, J. Anal. Chem., 2004, 59, 442–446 CrossRef CAS.
- S. Hu, J. Hou, L. Xiong, K. Weng, T. Yang and Y. Luo, Sep. Purif. Technol., 2011, 77, 214–219 CrossRef CAS.
- W. Luo, D. F. Cowgill and R. A. Causey, J. Phys. Chem. C, 2009, 113, 20076–20080 CAS.
- F. Leardini, J. Ares, J. Fernandez, J. Bodega and C. Sanchez, Int. J. Hydrogen Energy, 2011, 36, 8351–8357 CrossRef CAS.
- S. C. James, J. Hamilton and W. G. Wolfer, Chem. Eng. Sci., 2012, 68, 250–257 CrossRef CAS.
- J. W. Phair and R. Donelson, Ind. Eng. Chem. Res., 2006, 45, 5657–5674 CrossRef CAS.
- Q. Wang, S. R. Challa, D. S. Sholl and J. K. Johnson, Phys. Rev. Lett., 1999, 82, 956–959 CrossRef CAS.
- S. R. Challa, D. S. Sholl and J. K. Johnson, Phys. Rev. B: Condens. Matter, 2001, 63, 245411–245419 CrossRef.
- S. R. Challa, D. S. Sholl and J. K. Johnson, J. Chem. Phys., 2002, 116, 814–824 CrossRef CAS.
- G. Garberoglio, J. Chem. Phys., 2008, 128, 134109 CrossRef CAS.
- G. Garberoglio, Eur. Phys. J. D, 2009, 51, 185–191 CrossRef CAS.
- G. Garberoglio, Chem. Phys. Lett., 2009, 467, 270–275 CrossRef CAS.
- D. Liu, W. Wang, J. Mi, C. Zhong, Q. Yang and D. Wu, Ind. Eng. Chem. Res., 2011, 51, 434–442 CrossRef.
- Y. Wang and S. K. Bhatia, J. Phys. Chem. C, 2009, 113, 14953–14962 CAS.
- Y. Wang and S. K. Bhatia, Mol. Simul., 2009, 35, 162–171 CrossRef.
- H. Tanaka, J. Fan, H. Kanoh, M. Yudasaka, S. Iijima and K. Kaneko, Mol. Simul., 2005, 31, 465–474 CrossRef CAS.
- H. Tanaka, H. Kanoh, M. Yudasaka, S. Iijima and K. Kaneko, J. Am. Chem. Soc., 2005, 127, 7511–7516 CrossRef CAS.
- D. Noguchi, H. Tanaka, A. Kondo, H. Kajiro, H. Noguchi, T. Ohba, H. Kanoh and K. Kaneko, J. Am. Chem. Soc., 2008, 130, 6367–6372 CrossRef CAS.
- H. Tanaka, D. Noguchi, A. Yuzawa, T. Kodaira, H. Kanoh and K. Kaneko, J. Low Temp. Phys., 2009, 157, 352–373 CrossRef CAS.
- D. Noguchi, H. Tanaka, T. Fujimori, H. Kagita, Y. Hattori, H. Honda, K. Urita, S. Utsumi, Z. Wang, T. Ohba, H. Kanoh, K. Hata and K. Kaneko, J. Phys.: Condens. Matter, 2010, 22, 334207 CrossRef.
- H. Tanaka and M. T.Miyahara, J. Chem. Eng. Jpn., 2011, 44, 355–363 CrossRef CAS.
- A. V. A. Kumar and S. K. Bhatia, Phys. Rev. Lett., 2005, 95, 245901 CrossRef.
- A. V. A. Kumar, H. Jobic and S. K. Bhatia, J. Phys. Chem. B, 2006, 110, 16666–16671 CrossRef CAS.
- A. V. A. Kumar, H. Jobic and S. K. Bhatia, Adsorption, 2007, 13, 501–508 CrossRef.
- A. V. A. Kumar and S. K. Bhatia, J. Phys. Chem. C, 2008, 112, 11421–11426 CAS.
- M. Hankel, H. Zhang, T. X. Nguyen, S. K. Bhatia, S. K. Gray and S. C. Smith, Phys. Chem. Chem. Phys., 2011, 13, 7834–7844 RSC.
- Y. Hattori, H. Tanaka, F. Okino, H. Touhara, Y. Nakahigashi, S. Utsumi, H. Kanoh and K. Kaneko, J. Phys. Chem. B, 2006, 110, 9764–9767 CrossRef CAS.
- B. C. Hathorn, B. G. Sumpter and D. W. Noid, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 022903 CrossRef.
- R. A. Trasca, M. K. Kostov and M. W. Cole, Phys. Rev. B: Condens. Matter, 2003, 67, 035410 CrossRef.
- T. Lu, E. M. Goldfield and S. K. Gray, J. Phys. Chem. B, 2003, 107, 12989–12995 CrossRef CAS.
- T. Lu, E. M. Goldfield and S. K. Gray, J. Phys. Chem. B, 2006, 110, 1742–1751 CrossRef CAS.
- G. Garberoglio, M. M. DeKlavon and J. K. Johnson, J. Phys. Chem. B, 2006, 110, 1733–1741 CrossRef CAS.
- G. Garberoglio and J. K. Johnson, ACS Nano, 2010, 4, 1703–1715 CrossRef CAS.
- Y. Okamoto and Y. Miyamoto, J. Phys. Chem. B, 2001, 105, 3470–3474 CrossRef CAS.
- K. Tada, S. Furuya and K. Watanabe, Phys. Rev. B: Condens. Matter, 2001, 63, 155405 CrossRef.
- K. Sillar, A. Hofmann and J. Sauer, J. Am. Chem. Soc., 2009, 131, 4143–4150 CrossRef CAS.
- X. Zhao, S. Villar-Rodil, A. J. Fletcher and K. M. Thomas, J. Phys. Chem. B, 2006, 110, 9947–9955 CrossRef CAS.
- K. Suzuki, M. Kayanuma, M. Tachikawa, H. Ogawa, H. Nishihara, T. Kyotani and U. Nagashima, J. Alloys Compd., 2011, 509, S868–S871 CrossRef CAS.
- K. Suzuki, M. Kayanuma, M. Tachikawa, H. Ogawa, H. Nishihara, T. Kyotani and U. Nagashima, Comput. Theor. Chem., 2011, 975, 128–133 CrossRef CAS.
- K. Suzuki, M. Tachikawa, H. Ogawa, S. Ittisanronnachai, H. Nishihara, T. Kyotani and U. Nagashima, Theor. Chem. Acc., 2011, 130, 1039–1042 CrossRef CAS.
- H. Nishihara, Q. Yang, P. Hou, M. Unno, S. Yamauchi, R. Saito, J. I. Paredes, A. Martinez-Alonso, J. M. D. Tascon, Y. Sato, M. Terauchi and T. Kyotani, Carbon, 2009, 47, 1220–1230 CrossRef CAS.
- F. Stephanie-Victoire, A.-M. Goulay and E. C. d. Lara, Langmuir, 1998, 14, 7255–7259 CrossRef CAS.
- K. Kotoh, T. Nishikawa and Y. Kashio, J. Nucl. Sci. Technol., 2002, 39, 435–441 CrossRef CAS.
- X. B. Zhao, B. Xiao, A. J. Fletcher and K. M. Thomas, J. Phys. Chem. B, 2005, 109, 8880–8888 CrossRef CAS.
- B. Xiao, S. Wheatley, X. Zhao, A. J. Fletcher, S. Fox, A. G. Rossi, I. L. Megson, S. Bordiga, L. Regli, K. M. Thomas and R. E. Morris, J. Am. Chem. Soc., 2007, 129, 1203–1209 CrossRef CAS.
- B. Chen, X. Zhao, A. Putkham, K. Hong, E. B. Lobkovsky, E. J. Hurtado, A. J. Fletcher and K. M. Thomas, J. Am. Chem. Soc., 2008, 130, 6411–6423 CrossRef CAS.
- X. Lin, J. Jia, X. Zhao, K. M. Thomas, A. J. Blake, G. S. Walker, N. R. Champness, P. Hubberstey and M. Schröder, Angew. Chem., Int. Ed., 2006, 45, 7358–7364 CrossRef CAS.
- X. Chu, Y. Zhou, Y. Zhang, W. Su, Y. Sun and L. Zhou, J. Phys. Chem. B, 2006, 110, 22596–22600 CrossRef.
- X. Chu, Y. Zhao, Y. Kan, W. Zhang, S. Zhou, Y. Zhou and L. Zhou, Chem. Eng. J., 2009, 152, 428–433 CrossRef CAS.
- T. X. Nguyen, H. Jobic and S. K. Bhatia, Phys. Rev. Lett., 2010, 105, 085901 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |
