Combined IR absorption and modeling study of nanoporous zeolite imidazolate frameworks (ZIFs) filled with hydrogen
Sergei N.
Yurchenko
*a,
Bassem
Assfour†
b,
Eduard V.
Lavrov
c and
Gotthard
Seifert
b
aDepartment of Physics and Astronomy, University College London, Gower Street, WC1E 6BT London, UK. E-mail: s.yurchenko@ucl.ac.uk
bInstitut für Physikalische Chemie, Technische Universität Dresden, 01062 Dresden, Germany
cIAP/Halbleiterphysik, Technische Universität Dresden, 01062 Dresden, Germany
First published on 15th August 2012
Abstract
A combined IR absorption and first principles modelling study of zeolite imidazolate frameworks (ZIFs) filled with hydrogen is presented. It is shown that hydrogen physisorbed in a ZIF results in a number of absorption lines at around 4131, 4121, 4480, 4700, 4880, 5100, and 5280 cm−1, which are assigned to the Q(0), Q(1), S1(0), S1(1), 2S1(0), S1(0) + S1(1), and 2S1(1) ro-vibrational transitions of physisorbed H2, respectively. The latter three modes represent simultaneous excitation of molecular pairs, which implies that hydrogen physisorbed in ZIF occurs at a density close to that of the liquid and/or solid state. The adsorption onset temperature defined as the maximum temperature at which localized adsorption occurs was found to be around 80 K.
1 Introduction
At present, zeolitic imidazolate frameworks (ZIFs)—a novel class of metal organic frameworks (MOFs)—are considered to be promising materials for hydrogen storage applications.1 The crystal structure of ZIFs is based on the aluminosilicate zeolite nets, whereby the tetrahedral Si(Al) sites are replaced by transition metals Zn(II), Co(II), or In(III) tetrahedrally coordinated by imidazolate ligands.2Molecular hydrogen consists of two protons with nuclear spin 1/2. According to the Pauli principle, the total wave function of the system has to be antisymmetric with respect to the permutations of the nuclei. Because of the symmetry requirements for the total wave function, for the nuclear spin I = 1 (ortho state, o-H2) only odd values of the rotational quantum number J are allowed, whereas for I = 0 (para state, p-H2) J has to be even.3 A large magnetic field gradient is needed to transfer ortho to para hydrogen. As a result, under ‘normal’ conditions (low pressure gaseous phase, non-paramagnetic host, etc.) the two states do not thermalize and, once formed, remain independent.
The transitions of interest here are those associated with the vibrational (Δv = 1) H–H excitation. Selection rules for Raman scattering demand that ΔJ = 0, ±2, which at low temperatures results in the appearance of only four Q(0), Q(1), S1(0), and S1(1) modes in the spectra. In the case of isolated H2, these are to be found at around 4161, 4155, 4500, and 4715 cm−1, respectively.4 The notation Q(J) denotes a transition between states with the same rotational quantum number, whereas those with ΔJ = 2 are labeled as S1(J).
Due to the symmetry of the electron distribution, an isolated hydrogen molecule has a zero dipole moment, which implies that its vibrational transitions are infrared inactive. Physisorption of H2 causes IR absorption, since the equivalence of the two protons breaks up. Interaction with the host weakens the H–H bonds, resulting in enhancement of the bond length, as well as anharmonicity of the molecular vibrations. This manifests itself in the red-shift of the vibrational transitions as compared to those of isolated H2. The Q(J) modes of H2 physisorbed in MOF-5,5 MOF-74,6,7 and CuBTC (also known as HKUST-1)8 were found to be red-shifted by 27, 65, and 64 cm−1, respectively.
Apart from the H–H vibration, physisorbed H2 is characterized by the translation motion, which can be detected in IR absorption. The translational potential is highly anharmonic and requires a numerical solution of the quantum mechanical problem.9,10 The translation frequency for H2 trapped in MOF-5 and MOF-74 was found to be 84 and 123 cm−1, respectively.5,6 This is to be compared with the translation frequency of H2 in a C60 lattice,11 127 cm−1.
Additionally, the interaction of H2 with the host raises the degeneracy of the rotational states and results in splitting of the ro-vibrational modes. The value of splitting provides a direct insight into the rotational barrier as well as the preferential alignment of physisorbed H2: either an axially symmetric orientational barrier confining the molecule to rotation in two dimensions (2D rotor) or an axially confining potential restricting the molecule from rotating (1D vibrator). Typically, H2 bound to the organic linker reveals the properties of a 2D rotor,12 whereas the metal site results in 1D vibrator behavior.13,14 The rotational barriers for H2 trapped in MOF-5 were estimated15 to be 142 and 83 cm−1.
Ro-vibrational modes of physisorbed H2 are very sensitive to the details of interaction with a specific trapping site, each of which exhibits a unique IR signature and dependence on pressure, temperature, hydrogen load etc. For example, two strong IR doublets, due to the Q(1) and Q(0) modes at around 4130 and 4140 cm−1, were observed for H2 trapped at MOF-5 and assigned to ‘primary’ and ‘secondary’ adsorption sites, respectively.5 Similar findings were reported for MOF-74 and CuBTC, providing important insight into the effect of the unsaturated metal sites on the adsorption of H2 in these materials.6,7,12
The intensities of the IR lines can also contribute to our understanding of the adsorption process. The intensity ratio of the Q(0) and Q(1) modes as a function of time reveals directly the rate of the ortho–para conversion process. For H2 in MOF-5 it was found to be several hours, whilst in MOF-74 it takes 20–30 min to convert o-H2 to p-H2.5,6 The isobaric temperature dependence of the corresponding integrated intensities is then utilized to estimate the binding energy (in terms of the binding enthalpy or enthalpy of adsorption) of the adsorption side by means of the variable temperature infra-red (VTIR) spectroscopic method.12,16,17 Employing the VTIR method for MOFs, the following values of the binding enthalpy have been obtained: −3.5 and −7.4 kJ mol−1 (for ‘primary’ and ‘secondary’ sites) in MOF-5;15 −10.1 kJ mol−1 (at the Cu2+ site) in CuBTC;12 and −8.2 kJ mol−1 (main site) in MOF-74.6
It is clear therefore that IR absorption spectroscopy is a tool that provides a wealth of important information about the details of hydrogen adsorption in porous materials, which cannot be obtained from the adsorption isotherm—typically employed in qualitative experimental analysis. IR absorption studies of H2 were reported for such porous systems as C60,10 clathrates,18 zeolites,17,19–21 MOF-5,5,12,15 MOF-74,6,7 CuBTC,8,12,22 and other MOFs,12,23,24 as well as first principles calculations of IR activity of H2 trapped at different MOF systems.23–26 In particular, an accurate theoretical description of the internal rotation–vibration–translation motion of H2 was carried out for the fullerene9–11,27 and clathrate18,28,29 hosts.
Here we report the results of a combined IR absorption and ab initio investigation of hydrogen trapped in ZIF-8. A one cage-type structure of ZIF-8 (sodalite topology) contains an organic linker 2-methylimidazolate (mIM).2 Previous studies indicate two possible adsorption sites for hydrogen (see Fig. 1A) with the imidazolate linker as the primary adsorption center.30–32
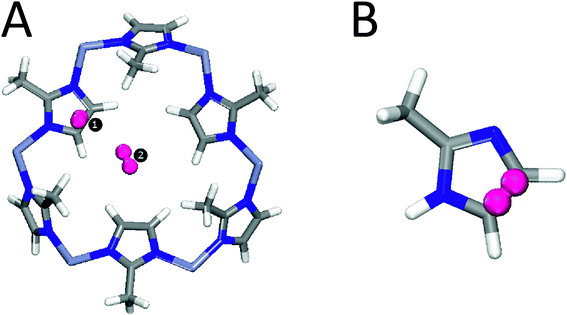 | ||
| Fig. 1 (A) Two main adsorption sites of H2 on a large fragment of ZIF-8. (B) A smaller fragment of ZIF-8 containing Site 1 (see text for details). | ||
Finally, we note that the selection rules of IR absorption and Raman scattering are complementary and that the latter can be, in principle, also applied to probe the properties of H2 in MOFs.33 However, MOFs in the form of powder employed in our study result in a strong background scattering of the excitation laser light, which makes Raman investigation of weak H2 vibrational transitions an extremely challenging task.
The paper is structured as follows. In sections 2 and 3 we describe the experimental and theoretical methods. In section 4 the experimental results of the IR study are presented, which are analyzed in section 5 on the basis of DFT and MP2 calculations. Some discussions and conclusions are offered in sections 6 and 7.
2 Experimental setup
The ZIF-8 metal organic framework (commercial name Basolite@Z1200) in the form of powder supplied by Sigma-Aldrich was employed in this study. For IR absorption measurements, the samples were placed in a precision cell made of SUPRASIL® provided by Hellma Analytics with sizes of 5 × 5 × 33 mm3. IR absorption spectra were recorded with a Bomem DA3.01 Fourier spectrometer equipped with a CaF2 beam splitter, a Globar light source, and a liquid nitrogen cooled InSb detector. The spectral resolution was 1 cm−1. The measurements were performed in an exchange-gas cryostat equipped with ZnSe windows. Three different gases or gas mixtures were studied: pure He and a mixture of He with H2 or D2 in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The pressure of the exchange gas was 0.6 bar at room temperature.
1. The pressure of the exchange gas was 0.6 bar at room temperature.
In the cases of the H2 and D2 ambients, He was employed to reach temperatures below that of the liquefaction of hydrogen.
During the measurements, the precision cell was open on the top end so that the contact gas could freely penetrate into the ZIF powder. The measurements took place as follows. First, a sample was cooled down from room temperature to 10 K, which took approximately 15 min, and an IR absorption spectrum was obtained. Subsequently, IR spectra were recorded while the sample temperature rose via natural warming up of the cryostat at a rate of approximately of 0.9 K min−1.
3 Theoretical methods
To study the full periodic ZIF-8 system using reasonably high ab initio methods is prohibitively expensive at the current technical level accessible to us. In the case of the cluster presented in Fig. 1A we could not afford to use even the MP2 level of theory. As a compromise between computational costs and accuracy we applied the MP2/CC-TZPV level of theory to the smaller cluster B (see Fig. 1) only. The MP2 method in conjunction with the CC-TZPV basis set is known to provide appropriate values for the interaction between H2 and the host in case of aromatic systems.34,35 Our previous study31 as well experimental work by Wu et al.30 showed that the interaction between the hydrogen molecules and the ZIF structure occurs mainly with the organic linker. Along these lines, in the MP2 calculations we consider only the interaction between H2 and the imidazole linker.In order to characterize the spectroscopic properties of H2 adsorbed on ZIF-8, we have performed the following calculations: (i) a DFT-based frequency analysis of two H2 molecules adsorbed on the fragment of ZIF-8 shown in Fig. 1A using the GGA DFT method in conjunction with the PBEPBE/cc-pVDZ level of theory as implemented in the GAUSSIAN-03 program package;36 (ii) a reconstruction of the interaction energies and dipole moments of the system H@ZIF-8 as functions of the rotational and vibrational (H–H) degrees of freedom with MP2/aug-cc-pVTZ for the reduced cluster shown in Fig. 1B (GAUSSIAN-03). The structure of the ZIF-8 fragment as well as the positions of H2 were taken from ref. 31, where they were obtained through molecular dynamics (MD) simulations. The DFT-based frequency analysis (i) produced all the fundamental frequencies and the corresponding intensities for the cluster shown in Fig. 1A, including the vibrational modes of the structure as well as the translational, rotational, and vibrational modes of the two H2 molecules adsorbed at two sites. In our MP2 calculations (ii) each interaction energy EH2@ZIF-8 was estimated as the difference between the total energy of the system consisting of one H2 molecule and a ZIF-8 fragment (Fig. 1B) and the sum of the energies of the corresponding fragments. The calculated interaction energies were corrected for the basis set superposition error (BSSE) using the counterpoise (CP) method.37
4 IR absorption
Fig. 2 shows sections of IR absorption spectra of ZIH-8 in the range typical for the pure vibrational Q(J) transitions of H2.4 Three types of contact gases were employed in order to obtain the spectra presented in the figure: He, H2 + He, and D2 + He. For simplicity we will refer to these as ZIH-8:He, ZIH-8:H2:He, and ZIH-8:D2:He, respectively. The lines seen in the spectra are overtones of the 2-methylimidazole linker comprising ZIH-8. No significant difference for all three ambients is visible for temperatures above 76 K. We take this as an indication that no physisorption of He, H2, and D2 on 2-methylimidazole occurs above 83 K. At lower temperatures, however, IR spectra strongly depend on the ambient employed.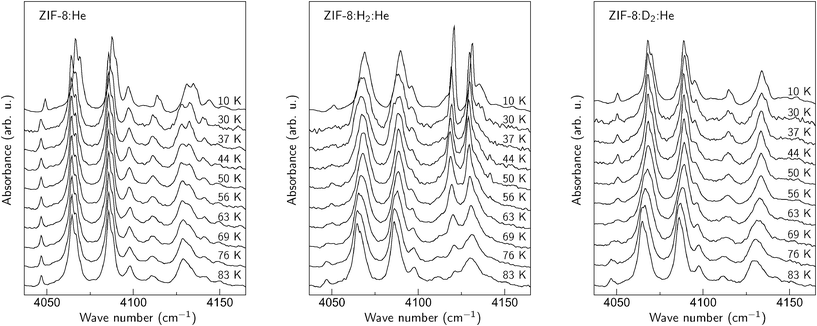 | ||
| Fig. 2 Sections of the IR absorption spectra of a ZIF-8 powder obtained in the He, H2 + He, and D2 + He ambients. | ||
In the case of He (left panel in the figure), the absorption spectra do not change substantially down to 30 K. At 10 K, however, most of the IR lines experience a blue-shift of 2–3 cm−1. We interpret this behavior as an adsorption of He onto the surface of the 2-methylimidazole linker. The shift of the overtone frequencies originates from the non-resonant interaction of the He atoms with the linker, which results in distortion of the host structure. This interpretation is supported by the drop in He pressure in the cryostat at 10 K, which correlates with the temperature at which IR absorption lines experience the blue-shift. Based on the results presented in the figure, we conclude that He adsorption under the conditions employed in our experiment takes place at 20 ± 10 K.
The results obtained for the ZIH-8:H2:He sample are presented in the middle panel of Fig. 2. Two new signals at 4131 and 4121 cm−1 appear in the spectra for temperatures below 80 K. These can be assigned to the Q(0) and Q(1) modes of H2 physisorbed on the 2-methylimidazole linker, respectively. The temperature at which these lines show up is then an ‘adsorption onset temperature’ (Ta) of hydrogen, defined as the maximum temperature at which the localized adsorption occurs (see discussion in ref. 12). Note that the value of Ta ≈ 80 K observed for ZIF-8 is comparable to those reported for MOF-5 (105 K) and CuBTC (110 K).12
In order to corroborate our suggestion about the nature of the Q(J) modes, similar experiments were performed in the mixture of D2 and He. The corresponding spectra are shown in the right panel of Fig. 2. As expected, the 4121 and 4131 cm−1 features do not appear after the replacement of hydrogen with deuterium. Nonetheless, the spectra taken at T < 83 K in the D2 + He ambient differ from those of pure He. In particular, the feature at 4130 cm−1 does not reveal a ‘camel back’ structure. We interpret this behavior as a physisorption of D2, which results in changes of the overtone frequencies of the linker.
The Q(J) modes of physisorbed D2 are expected to shift by a factor of approximately 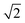 down to 2990 cm−1, compared to those of H2. We could not, however, detect any significant difference in the IR spectra taken for all contact gases in the corresponding spectral region. A possible explanation for this behavior is the overlapping of the D2 modes with the dominant absorption features of the linker related to the C–H and/or N–H units (see for example ref. 38 and 39).
down to 2990 cm−1, compared to those of H2. We could not, however, detect any significant difference in the IR spectra taken for all contact gases in the corresponding spectral region. A possible explanation for this behavior is the overlapping of the D2 modes with the dominant absorption features of the linker related to the C–H and/or N–H units (see for example ref. 38 and 39).
The ZIH-8:D2:He spectra can serve as a background signal to separate the vibrational modes of physisorbed hydrogen from those of the perturbed linker, since the adsorption process of D2 and H2 is similar (see for example ref. 23). Fig. 3 represents the result of subtraction of the ZIH-8:H2:He and ZIH-8:D2:He spectra recorded at 10 K where the Q(0) and Q(1) modes are clearly seen. The insert shows the frequencies of these modes as a function of temperature. The temperature dependences of the Q(J) modes are non-monotonic with a minimum at around 50 K. It also follows from the figure that the frequency difference between the Q(0) and Q(1) modes (ortho–para splitting) equals 10.5 cm−1 and is independent of the temperature. Note that the values of the ortho–para splitting for H2 bound onto or in different hosts reported in the literature are somewhat smaller, around 6–8 cm−1.40–42 This increase in the Q(0) and Q(1) separation can be attributed to the stronger anharmonicity of the vibrational H–H potential of the adsorbed molecule compared to that of free hydrogen. Indeed, in the first approximation the Q(0)–Q(1) separation equals 2αe, where 2αe is the rotational–vibrational coupling constant. The latter is given by43
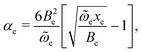 | (1) |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) e, and
e, and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) exe are the rotational, harmonic, and anharmonic constants, respectively. It follows from eqn (1) that the larger the Q(0)–Q(1) separation, the larger the αe constants and therefore the anharmonic constants
exe are the rotational, harmonic, and anharmonic constants, respectively. It follows from eqn (1) that the larger the Q(0)–Q(1) separation, the larger the αe constants and therefore the anharmonic constants ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) exe. Alternatively, this behavior of H2 in ZIH-8 can also be caused by the interaction between the ro-vibrational modes of hydrogen and the combinational modes of the linker (see section 6 for more details).
exe. Alternatively, this behavior of H2 in ZIH-8 can also be caused by the interaction between the ro-vibrational modes of hydrogen and the combinational modes of the linker (see section 6 for more details).
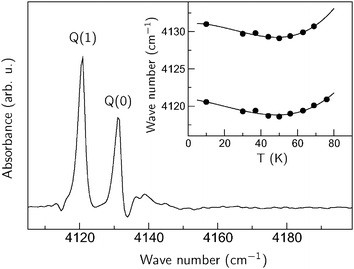 | ||
| Fig. 3 Section of the IR absorption spectrum of ZIP-8:H2:He taken at 10 K. A ZIH-8:D2:He spectrum was used as a background. The inset shows the temperate dependencies of the Q(1) and Q(0) lines. The solid lines are a guide for the eye. | ||
The Q(0) and Q(1) modes are not the only new signals observed in ZIH-8:H2:He. Fig. 4 shows extended sections of the IR spectra presented in Fig. 2. Additional groups of lines centered at approximately 4480, 4700, 4880, 5100, and 5280 cm−1 appear in the ZIH-8:H2:He sample. Note that the 5280 cm−1 feature is not shown due to its weak intensity compared to the other signals. Based on the spectral positions of these lines, we assign the 4480 and 4700 cm−1 features to the ro-vibrational transitions S1(0) and S1(1), which in the case of the free molecule occur at 4500 at 4720 cm−1.4 The frequency differences between the S1(J) and Q(J) modes are equal to 350 (J = 0) and 580 cm−1 (J = 1), which is very close to the pure rotational transitions of free H2 S0(0) and S0(1).4 The splitting of the S1(J) modes is explained by the interaction of the molecule with the ZIH-8 host, which reduces the spherical symmetry of the interatomic potential and lifts the degeneracy of the rotational states.
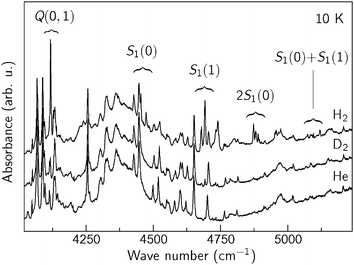 | ||
| Fig. 4 IR absorption spectra of ZIF-8 filled with He, H2 + He, and D2 + He taken at T = 10 K. | ||
We assign the bands at 4880, 5100 and 5280 cm−1 to the double rotational 2S1(0), S1(0) + S1(1), and 2S1(1) transitions of the molecular pairs, respectively. These modes are typical for the IR spectra of liquid and solid hydrogen (see for example ref. 45 and 46), which strongly indicates that hydrogen confined in the pores of ZIF-8 occurs at high densities. Similar multi-excitation transitions were also reported in the inelastic neutron scattering study of hydrogen adsorbed in C60 and CuBTC.47,48.
The Q(J) and S1(J) transitions observed in the spectra of ZIH-8:H2:He are red-shifted by approximately 20–30 cm−1 compared to the values of free H2. This is a typical behavior of physisorbed H2, which originates from the weakening of the H–H bond due to the interaction with the linker.49 These values detected for ZIH-8 can be compared to those reported for other MOFs: 27 cm−1 (MOF-5),5 65 cm−1 (MOF-74),6 and 64 cm−1 (CuBTC).8 We discuss the origin of the Q(J) and S1(J) modes in more detail in section 6.
5 Calculations
5.1 Trapping sites
There are two possible trapping sites for hydrogen on ZIF-8, both of which are indicated in Fig. 1A.30,31,50 We believe that the IR features presented in Fig. 4 are due to H2 trapped at the primary adsorption site (referred to as Site 1). Our arguments are as follows. Site 1 is the imidazolate organic linker and expected to induce stronger polarization and thus a stronger dipole moment compared to the secondary site (Site 2). This has been confirmed by our DFT-based frequency analysis (see below). Indeed, we found that H2 adsorbed at Site 1 (referred to as H2(1)@ZIF-8) is characterized by a vibrational intensity that is five times stronger than that at Site 2 (referred to as H2(2)@ZIF-8), namely 32.1 km mol−1vs. 6.5 km mol−1, respectively. This should correspond to a more than twice as strong dipole moment contribution (i.e. first derivative with respect to the H–H distance) of H2(1)@ZIF-8. Apart from this, the number of adsorption Sites 1 and 2 are in the ratio 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and each instance of Site 1 exhibits a larger contribution to the adsorption capacity than Site 2, as follows from our most recent MD simulations,31 which all point to Site 1 as the primary source of IR absorption of H2. The hydrogen molecules are weakly bonded at both sites. We estimated the adsorption energy of H2 located over the imidazolate ring to be 8.6 kJ mol−1 (Site 1), while H2 in the pore channel (Site 2) has the adsorption energy of 6.2 kJ mol−1.
1, and each instance of Site 1 exhibits a larger contribution to the adsorption capacity than Site 2, as follows from our most recent MD simulations,31 which all point to Site 1 as the primary source of IR absorption of H2. The hydrogen molecules are weakly bonded at both sites. We estimated the adsorption energy of H2 located over the imidazolate ring to be 8.6 kJ mol−1 (Site 1), while H2 in the pore channel (Site 2) has the adsorption energy of 6.2 kJ mol−1.
Relatively small shifts of the hydrogen IR features observed support our theoretical findings that the metal (Zn) site does not play an important role here (see also ref. 17).
5.2 Ro-vibrational transitions
From a DFT frequency analysis (see section 3) performed for two hydrogen molecules adsorbed at two different adsorption sites simultaneously, we obtained IR features at 4071 and 4064 cm−1 corresponding to the adsorption of H2(1)@ZIF-8 and H2(2)@ZIF-8, with vibrational intensities of 32.1 and 6.5 km mol−1, respectively. These features represent the fundamental vibrational transitions v = 0 → v = 1 and can be compared to the experimental vibrational Q(0) transition at 4131 cm−1 (see absorption spectra of ZIF-8:H2:He presented in Fig. 2). Assuming that this transition corresponds to adsorption Site 1, our theoretical prediction is off by 60 cm−1. However, the theoretical value of the red shift, ΔvQ(0) = 43 cm−1, is in a better agreement with the experiment (30 cm−1). Here ΔvQ(0) is evaluated as the difference between the frequency of H2(1)@ZIF-8 and that of free H2, computed using the same level of theory (PBEPBE/cc-pVDZ). It should also be noted that the strongest intensities obtained with DFT for this system correspond to the N–H modes of the host structure (3630–3644 cm−1, up to 657 km mol−1).In order to evaluate the dependence of the potential (interaction) energy EH2@ZIF–8 and dipole moment of the system H2(1)ZIF-8 on the vibrational and rotational modes, we performed a number of MP2/aug-cc-pVTZ calculations for the reduced cluster shown in Fig. 1B. Varying the interatomic distance H–H at the optimized position,52 we reconstructed both the potential energy V(R) and dipole moment μ(R) functions shown in Fig. 5 and 6. Here R is the H–H distance. The computed interaction energies for seven interatomic distances H–H around the equilibrium are shown in Fig. 5, also compared to the ab initio potential function of the free hydrogen molecule.51 Our MP2 potential of H2 adsorbed on ZIF-8 is only slightly more anharmonic. Assuming that the larger Q(0)–Q(1) splitting of 10.5 cm−1 in Fig. 3 is caused by the larger anharmonicity of the H–H interaction potential, from eqn (1) we obtain the anharmonic constant ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) exe ≈ 270 cm−1, which is about 2.2 times larger than that of free hydrogen,
exe ≈ 270 cm−1, which is about 2.2 times larger than that of free hydrogen, ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) exe = 121.3 cm−1 with αe = 3.062 cm−1 and
exe = 121.3 cm−1 with αe = 3.062 cm−1 and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) e = 4401 cm−1.53
e = 4401 cm−1.53
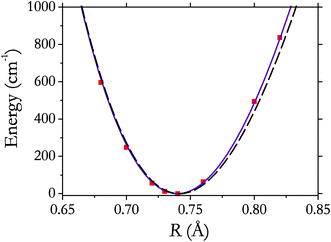 | ||
| Fig. 5 Potential energy (MP2/aug-cc-pVTZ) of the system H2(1) ZIF-8 as a function of H–H distance (squares) and its interpolation using a Morse oscillator (solid line). The potential energy curve of free hydrogen51 is shown by the dashed line. | ||
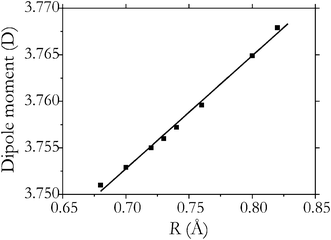 | ||
| Fig. 6 Electric dipole moment (MP2/aug-cc-pVTZ) of the system H2(1) ZIF-8 as a function of the H–H distance (squares) and its interpolation using a linear function 3.758 + 0.12(R − Re) (solid line). | ||
With the value of ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) exe we can estimate the frequency of D2 from
exe we can estimate the frequency of D2 from
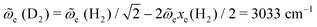 | (2) |
The induced dipole moment (Fig. 6) exhibits a rather strong dependence on R, linear to a very good approximation with the first derivative with respect to R at R = Re is equal to 0.12 D Å−1. This results in the dipole Q(J) (ΔJ = 0) transitions of H2 observed, assuming that the dipole moment of the system H2(1)@ZIF-8 can be factorized into the induced dipole moment of H2 and the dipole moment of the host.
The rotational motion of the adsorbed H2 can be described as a hindered rotation, which is illustrated in Fig. 7, where the dependence of the interaction energy on the polar angle θ is shown. Here θ = 0 corresponds to the equilibrium orientation of H2, which is approximately perpendicular to the organic linker (Fig. 1A).31,52 The rotational barrier (in terms of the polar angle θ) is found to be about 270 cm−1. This can be compared to the barriers of H2@MOF-5, 142 and 83 (of the primary and secondary absorption sites),15 and to that of H2@CuBTC, 660 cm−1.48 The dependence on the azimuthal rotation is essentially less pronounced both in our case and in cases of the systems mentioned, in the range 10–40 cm−1. The effect of the internal hindered rotation on the profile of the IR spectra is discussed below.
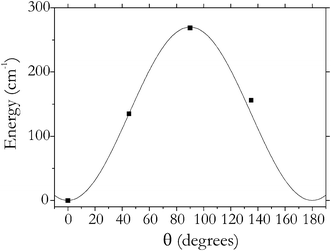 | ||
| Fig. 7 Potential energy of the system H2(1)ZIF-8 as a function of the orientation of H2 relative to the host (squares) and its interpolation using a Fourier series (solid line). | ||
The translation motion of H2 in MOFs is also known to play an important role. For example in the cases of H2@MOF-5, H2@MOF-74, and CuBTC the translational modes were found to be of about 80–120 cm−1, which resulted in the corresponding IR lines appearing blue-shifted relative to the vibrational Q(0) feature.5,6 We expect the translational mode of H2 in ZIF-8 to be of the same order of magnitude. Employing the Morse approximation to the potential functions of H2@ZIF-8 reported in ref. 52, we obtain the translation frequency of about 110 cm−1. However, we could not see any evidence of the translation–vibrational transitions in our IR spectra of H2@ZIF-8, which is probably because of the limitations of our current experimental approach.
5.3 Hindered rotation
The rotational barrier induced by the interaction with the host structure removes the m-degeneracy of the H2 rotational states. This results in splitting of the ro-vibrational levels and the transition frequencies with J > 0. In the case of H2@MOF systems, this effect is especially pronounced for the S(0) and S(1) features. Such splittings in the S(0) and S(1) bands were observed for H2@MOF-5 (42 cm−1 and 59 cm−1, respectively) associated with |m| ≤ 2.5 In fact, the Q(1) splitting (Δm = ±1) was also reported for H2@MOF-5 to be about 65 cm−1.56 Discussion
The results of our experiments and calculations reveal that H2 physisorbed on the surface of ZIH-8 gives rise to IR absorption lines which match the Q(J) and S1(J) ro-vibrational transitions of the molecule—in agreement with the IR absorption of H2 reported for different MOF materials. It should be mentioned, however, that this assignment suffers from a number of inconsistencies failing to explain the following issues. (i) The spectra presented in Fig. 4 clearly show that the intensities of the S1(J) and Q(J) modes are comparable. On the other hand, the S1(J) transitions with ΔJ = 2 are forbidden in the dipole approximation and should not be IR inactive. (ii) The ortho–para splitting between the Q(0) and Q(1) modes is significantly larger than those reported for other MOF systems: 7 cm−1 (CuBTC),12 8 cm−1 (MOF-74),6 9 cm−1 (MOF-5).15A possible solution for these puzzles could be an alternative explanation for the nature of the 4121, 4131, 4480, 4700, 4880, 5100, and 5280 cm−1 lines. Fig. 4 shows that the expected ro-vibrational transitions of H2 occur either at or very close to the combinational modes of the linker. This implies that even a weak anharmonic term coupling the two systems should result in a significant shift of both vibrational modes and, more importantly, in the appearance of forbidden IR transitions of the molecule in the IR spectra (Fermi resonance).54 The latter results from the mixing of the wave functions of physisorbed H2 and the linker so that the molecule “borrows” some intensity from the host.
It follows from here that apparent intensities of the ro-vibrational modes, as well as their positions in the spectra, also depend on the details of the interaction between the molecule and the linker, rather than on the properties of physisorbed H2 alone. Fermi resonance also implies that the number of IR lines may not coincide with the number of split-off components of a degenerate J state, which makes interpretation of the IR absorption spectra extremely challenging.
7 Conclusions
Combined IR absorption and a first principles modeling study of zeolite imidazolate frameworks (ZIFs) filled with hydrogen is presented. It is shown that hydrogen physisorbed in ZIF results in a number of absorption lines at around 4131, 4121, 4480, 4700, 4880, 5100, and 5280 cm−1, which are assigned to the Q(0), Q(1), S1(0), S1(1), 2S1(0), S1(0) + S1(1), and 2S1(1) ro-vibrational transitions of physisorbed hydrogen, respectively. The adsorption onset temperature, defined as the maximum temperature at which localized adsorption occurs, was found to be around 80 K.Acknowledgements
One of the authors (EVL) acknowledges support by the Deutsche Forschungsgemeinschaft under Grant No. LA 1397/3.References
- L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186 CrossRef CAS.
- L. D. Landau and E. M. Lifschitz, Statistical Physics, Part 1, Pergamon Press, Oxford, England, 3rd edn, 1980 Search PubMed.
- B. P. Stoicheff, Can. J. Phys., 1957, 35, 730 CrossRef CAS.
- S. A. FitzGerald, K. Allen, P. Landerman, J. Hopkins, J. Matters, R. Myers and J. L. C. Rowsell, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224301 CrossRef.
- S. A. FitzGerald, J. Hopkins, B. Burkholder, M. Friedman and J. L. C. Rowsell, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104305 CrossRef.
- S. A. FitzGerald, B. Burkholder, M. Friedman, J. B. Hopkins, C. J. Pierce, J. M. Schloss, B. Thompson and J. L. C. Rowsell, J. Am. Chem. Soc., 2011, 133, 20310–20318 CrossRef CAS.
- S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. S. Wheatley, R. E. Morris and A. Zecchina, Phys. Chem. Chem. Phys., 2007, 9, 2676–2685 RSC.
- M. Xu, F. Sebastianelli, B. R. Gibbons, Z. Bačić, R. Lawler and N. J. Turro, J. Chem. Phys., 2009, 130, 224306 CrossRef.
- R. M. Herman and J. C. Lewis, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155408 CrossRef.
- S. A. FitzGerald, S. Forth and M. Rinkoski, Phys. Rev. B: Condens. Matter, 2002, 65, 140302 CrossRef.
- J. G. Vitillo, L. Regli, S. Chavan, G. Ricchiardi, G. Spoto, P. D. C. Dietzel, S. Bordiga and A. Zecchina, J. Am. Chem. Soc., 2008, 130, 8386–8396 CrossRef CAS.
- J. Eckert and G. J. Kubas, J. Phys. Chem., 1993, 97, 2378–2384 CrossRef CAS.
- P. M. Forster, J. Eckert, B. D. Heiken, J. B. Parise, J. W. Yoon, S. H. Jhung, J.-S. Chang and A. K. Cheetham, J. Am. Chem. Soc., 2006, 128, 16846–16850 CrossRef CAS.
- S. Bordiga, J. G. Vitillo, G. Ricchiardi, L. Regli, D. Cocina, A. Zecchina, B. Arstad, M. Bjørgen, J. Hafizovic and K. P. Lillerud, J. Phys. Chem. B, 2005, 109, 18237–18242 CrossRef CAS.
- E. Garrone and C. O. Areán, Chem. Soc. Rev., 2005, 34, 846–857 RSC.
- C. O. Areán, G. T. Palomino, E. Garrone, D. Nachtigallová and P. Nachtigall, J. Phys. Chem. B, 2006, 110, 395–402 CrossRef.
- T. A. Strobel, K. C. Hester, C. A. Koh, A. K. Sum and E. D. Sloan Jr., Chem. Phys. Lett., 2009, 478, 97 CrossRef CAS.
- L. Regli, A. Zecchina, J. G. Vitillo, D. Cocina, G. Spoto, C. Lamberti, K. P. Lillerud, U. Olsbye and S. Bordiga, Phys. Chem. Chem. Phys., 2005, 7, 3197 RSC.
- E. N. Gribov, D. Cocina, G. Spoto, S. Bordiga, G. Ricchiardi and A. Zecchina, Phys. Chem. Chem. Phys., 2006, 8, 1186 RSC.
- D. Scarano, S. Bertarione, F. Cesano, J. G. Vitillo and A. Zecchina, Catal. Today, 2006, 116, 433–438 CrossRef CAS.
- C. Prestipino, L. Regli, J. Vitillo, F. Bonino, A. Damin, C. Lamberti, A. Zecchina, P. Solari, K. Kongshaug and S. Bordiga, Chem. Mater., 2006, 18, 1337–1346 CrossRef CAS.
- N. Nijem, J.-F. Veyan, L. Kong, K. Li, S. Pramanik, Y. Zhao, J. Li, D. Langreth and Y. J. Chabal, J. Am. Chem. Soc., 2010, 132, 1654–1664 CrossRef CAS.
- L. Kong, V. R. Cooper, N. Nijem, K. Li, J. Li, Y. J. Chabal and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 081407 CrossRef.
- L. Kong, Y. J. Chabal and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 121402 CrossRef.
- L. Kong, G. Román-Pérez, J. M. Soler and D. C. Langreth, Phys. Rev. Lett., 2009, 103, 096103 CrossRef.
- T. Yildirim and A. B. Harris, Phys. Rev. B: Condens. Matter, 2002, 66, 214301 CrossRef.
- M. Xu, Y. S. Elmatad, F. Sebastianelli, J. W. Moskowitz and Z. Bačić, J. Phys. Chem. B, 2006, 110, 24806–24811 CrossRef CAS.
- M. Xu, F. Sebastianelli and Z. Bačić, J. Chem. Phys., 2008, 128, 244715 CrossRef.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2007, 129, 5314 CrossRef CAS.
- B. Assfour, S. Leoni and G. Seifert, J. Phys. Chem. C, 2010, 114, 13381–13384 CAS.
- M. Zhou, Q. Wang, L. Zhang, Y.-C. Liu and Y. Kang, J. Phys. Chem. B, 2009, 113, 11049 CrossRef CAS.
- B. Panella and M. Hirscher, Phys. Chem. Chem. Phys., 2008, 10, 2910–2917 RSC.
- O. Hubner, A. Gloss, M. Fichtner and W. Klopper, J. Phys. Chem. A, 2004, 108, 3019–3023 CrossRef.
- T. Heine, L. Zhechkov and G. Seifert, Phys. Chem. Chem. Phys., 2004, 6, 980–984 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M.W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- G. Lendvay and I. Mayer, Chem. Phys. Lett., 1998, 297, 365 CrossRef CAS.
- S. R. Venna and M. A. Carreon, J. Am. Chem. Soc., 2010, 132, 76 CrossRef CAS.
- B. Wang, A. P. Cote, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Nature, 2008, 453, 207 CrossRef CAS.
- J. Vetterhöffer, J. Wagner and J. Weber, Phys. Rev. Lett., 1996, 77, 5409 CrossRef.
- E. V. Lavrov and J. Weber, Phys. Rev. Lett., 2002, 89, 215501 CrossRef CAS.
- M. Hiller, E. V. Lavrov and J. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045306 CrossRef.
- G. Herzberg, Molecular Spectra and Molecular Structure: I. Spectra of Diatomic Molecules, Krieger, Malabar, FL, 1989 Search PubMed.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- E. J. Allin, W. F. J. Hare and R. E. MacDonald, Phys. Rev., 1955, 98, 554–555 CrossRef CAS.
- M. Zoppi, L. Ulivi, M. Santoro, M. Moraldi and F. Barocchi, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, R1935–R1938 CrossRef CAS.
- S. A. FitzGerald, T. Yildirim, L. J. Santodonato, D. A. Neumann, J. R. D. Copley, J. J. Rush and F. Trouw, Phys. Rev. B: Condens. Matter, 1999, 60, 6439–6451 CrossRef CAS.
- C. M. Brown, Y. Liu, T. Yildirim, V. K. Peterson and C. J. Kepert, Nanotechnology, 2009, 20, 204025 CrossRef.
- D. G. Hamilton and R. H. Crabtree, J. Am. Chem. Soc., 1988, 110, 4126 CrossRef CAS.
- W. Zhou, H. Wu, T. J. Udovic, J. J. Rush and T. Yildirim, J. Phys. Chem. A, 2008, 112, 12602–12606 CrossRef CAS.
- J. S. Sims and S. A. Hagstrom, J. Chem. Phys., 2006, 124, 094101 CrossRef.
- B. Assfour, S. Leoni, S. Yurchenko and G. Seifert, Int. J. Hydrogen Energy, 2011, 36, 6005–6013 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules, Van Nostrand Reinhold Company, New York, 1979 Search PubMed.
- E. Fermi, Z. Phys., 1931, 71, 250 CrossRef CAS.
Footnote |
| † Present address: Department of Chemistry, Atomic Energy Commission, P.O. Box 6091, Damascus, Syria |
| This journal is © The Royal Society of Chemistry 2012 |
