Single crystal structure refinement of one- and two-layer hydrates of sodium fluorohectorite

Abstract

Crystal structures of both one- and two-layer hydrates of sodium fluorohectorite were refined against single crystal data for the first time because melt synthesis yielded a sodium fluorohectorite showing little stacking disorder as compared to natural clays. In both hydrate phases, the relative shift of adjacent 2:1 layers is fixed by hydrogen-bonding between water molecules coordinated to interlayer cations and basal oxygen atoms of tetrahedral sheets encompassing the interlayer space. Despite some apparent diffuse scattering, a decent single crystal refinement of the semi-ordered structure of the one-layer hydrate is achieved, revealing structural details of the interlayer spacing for the first time. For the two-layer hydrate the structural model proposed for vermiculites is confirmed but a different ordering pattern of interlayer [Na(H₂O)₆]⁺ is suggested. While in the two-layer hydrate sodium cations reside at the centre of the interlayer space, in the one-layer hydrate sodium is displaced from the centre of the interlayer space either towards the upper or towards the lower tetrahedral sheet. This displacement allows for coordination to the hexagonal cavity on one side while the coordination sphere of sodium is completed by three coordinating water molecules on the other side. These three water molecules in turn are involved in hydrogen bonding to the opposite tetrahedral sheet.

---

Introduction

Hydrated (swollen) clays of the 2:1 structure family (e.g. montmorillonite, saponite, hectorite, or vermiculite; for nomenclature of clay minerals see Martin et al.¹) are among the most important industrial minerals. World production of bentonites (rocks rich in montmorillonite) in 2006 amounted to 13 700 000 metric tons, which were mostly used as rheological additives for drilling fluids and civil engineering, as foundry sand binder, and as adsorptives (for instance in pet litter).² More recently, more advanced applications such as microporous hybrid materials,^3,4 functional films for optoelectronic packaging,⁵ halogen-free flame retardants,⁶ and nanofillers in composites⁷ have been established. All these applications depend crucially on the hydration state of the clays, and swelling is probably the most important feature of expandable 2:1 layered silicates.

Despite the industrial importance of hydrated clay phases, and despite intensive research over recent decades,^8–17 details of the one-layer hydrate structure are under debate. This is due to two handicaps intrinsic to natural clays: hydration is critically dependent on two factors, the hydration enthalpy of interlayer cations and the charge density. For natural 2:1 clays like montmorillonite, isomorphic substitution responsible for the layer charge clusters into domains and the charge density is inhomogeneous. As a consequence of charge heterogeneity, individual interlayers in any singular clay crystal will realize different states of hydration. It is common that at a given relative humidity (r.h.) zero-, one-, and two-layer hydrates are found concomitantly in the same crystal. The random interstratification of different basal spacings renders even a one-dimensional Fourier analysis of the electron density distribution in the interlayer space difficult.

Besides interstratification, structure solution is even more severely hampered by planar defects. Intercalated water acts as a kind of lubricant and this is why most hydrated clay phases are turbostratically disordered. Adjacent layers stacked into a crystal are randomly rotated or shifted, the phase is not fixed, a unit cell cannot be defined, and scattering is completely diffuse.

A comprehensive description of the structure of these hydrated phases would have to deliver information about the coordination of interlayer cations, the relative position/phase relationship of adjacent 2:1 layers (interlayer displacement),¹⁸ and the “interaction” pattern between the interlayer species (cations and water) and the basal oxygen atoms comprising the interlayer. Although an amazingly detailed picture of the structure of the interlayer could be derived employing one-dimensional Fourier synthesis of X-ray and neutron diffraction data, possibly in combination with NMR data and different computer simulation methods,^19–22 experimental evidence for interlayer displacement and specific interactions between interlayer species and the silicate layer require three-dimensionally or at least semi-ordered “crystals” that are only little affected by planar defects (stacking disorder). There is, however, only a limited number of “single crystal” refinements of hydrated phases available in the literature applying some rare occasions of semi-ordered vermiculites (Santa Olalla, Spain, and Carl Moss Ranch, Llano County, Texas) showing significantly less stacking faults and consequently much reduced diffuse scattering.^23,24 In addition to the remaining stacking disorder, the electron density of these natural vermiculites is, however, affected by mixed occupation of all cationic positions (octahedral, tetrahedral, and interlayer). Consequently, crystal structure refinement in all cases had to be restricted to certain classes of reflections that are least affected by the stacking disorder patterns (k = 3n). Disorder patterns and structures of two-layer hydrates of Na- and Mg-vermiculites was comprehensively discussed by Suquet and Perzerat, and de la Calle et al. after applying PXRD and Weissenberg-camera single crystal data.^10,11 In these studies, the one-layer hydrate was found to be completely disordered and details of the interlayer structure could consequently not be resolved. The two-layer hydrate was found to be semi-ordered and a structural model of the interlayer spacing was deduced. Please note, that all these “single crystal” refinements used standard programs that are incapable of taking diffuse scattering into account. Consequently, the information about disorder patterns hidden in the diffuse scattering is ignored and only the main structure of the three-dimensionally ordered volume of the crystals is refined. More recently, the Rietveld refinement of an X-ray powder diffraction (PXRD) trace of semi-ordered Santa Olalla vermiculite was refined using DIFFaX+, a program that indeed also takes stacking disorder and diffuse scattering into account.²⁵

To reduce the complexity we sought to synthesize a well ordered fluorovermiculite (vermiculite where the hydroxyl group is replaced by fluorine) of nominal composition, [Na_0.85]^inter[Mg_2.15Li_0.85]^oct[Si₄]^tetO₁₀F₂, which we prefer to refer to as highly charged fluorohectorite (Na-hect) (hectorite where the hydroxyl group is replaced by fluorine) because the material lacks the Tschermak substitution typical of vermiculites. Fortunately, for this synthetic Na-hect stacking disorder and diffuse scattering is indeed reduced to a level that allows a full crystal structure refinement of all hkl reflections, which delivers full structural details for both the one-layer and the two-layer hydrates.

Experimental section

The fluorohectorite used was synthesized via melt synthesis.^16,26,27 The high purity reagents (in total ∼4 g) of SiO₂ (Merck, fine granular, calcined), MgF₂ (Chempur, 99.99%), MgO (Alfa Aesar 99.95%), Li₂SiO₃ (Alfa Aesar 99.95%), and Na₂O–2SiO₂-glass were weighed into a molybdenum crucible in an Ar atmosphere in accordance with a stoichiometric composition of [Na_0.85]^inter[Mg_2.15Li_0.85]^oct[Si₄]^tetO₁₀F₂ (target composition). Na₂O–2SiO₂-glass was produced by melting Na₂CO₃ (Aldrich, 99.9%) and SiO₂ (Merck, fine granular, calcined) in a 1:2 molar ratio at 1050 °C for 10 h to ensure complete release of carbon dioxide. The molybdenum crucible was sealed so as to be gas-tight using the procedure described elsewhere.²⁸ The crucible was heated in a graphite furnace (Graphit HT-1900, Linn High Therm) for the synthesis. To prevent inhomogeneity of the product owing to gravity segregation in the melt, the crucible was positioned horizontally in the furnace and rotated at 50 rpm. The crucible was heated from room temperature (RT) to 1750 °C (20 °C min⁻¹), left at 1750 °C for 1 h, then cooled to 1450 °C with a cooling rate of 50 °C min⁻¹, followed by a low cooling rate of 3 °C min⁻¹ from 1450 °C to 800 °C, and finally it was quenched by switching off the power. The crucible was opened under an Ar atmosphere and the synthetic Na-hect was stored in a Glovebox.

PXRD patterns of zero-, one-, and two-layer hydrates of synthetic Na-hect were measured using a STOE Stadi P powder diffractometer (transmission geometry, CuKα₁ radiation (λ = 1.54059 Å), Ge monochromator, linear position sensitive detector). The measurement was performed in sealed glass capillaries in order to fix r.h. and to minimize texture effects. For the zero-layer hydrate Na-hect, the capillary was filled and closed in the Glovebox. For the one-layer hydrate, the synthetic Na-hect was exposed to water vapour at 43% r.h. (K₂CO₃ saturated solution). The equilibrated sample was quickly transferred into a capillary which was sealed with grease for PXRD measurement. For the two-layer hydrate, the synthetic Na-hect was placed into a capillary which was still open at both ends. Then the capillary was filled with distilled water by immersing one end of the capillary into water. After two weeks of equilibration, the capillary was sealed at both ends and the PXRD pattern was recorded.

The single crystal X-ray data of the one- and two-layer hydrates of synthetic Na-hect were collected for selected crystals showing a minimum of diffuse streaks. In order to minimize the dynamics of the interlayer water and to fix the water content, data were collected at 173 K on a STOE IPDS I diffractometer with graphite monochromated MoKα₁ radiation (λ = 0.71073 Å) using crystals of approximately 0.25 mm × 0.20 mm × 0.02 mm in size in 320 frames (0.5° step per frame, 30 min per frame). Prior to mounting, the single crystals were equilibrated at appropriate r.h., as described above for the PXRD measurements. Further details of the data collection and structure refinement are given in Table 1. The composition of the synthetic Na-hect was determined by wavelength dispersive X-ray spectroscopy (WDX) on a Joel JXA 8200 spectrometer, with acceleration voltage 15 kV, and beam spot diameter 1 μm, which was calibrated against certified mineral standards (Si-andradite Ca₃Fe₂Si₃O₁₂, Mg-synthetic Enstatit Mg₂[Si₂O₆], O-silicon dioxide SiO₂, F-fluorite CaF₂, Na-albite NaAlSi₃O₈). The counting time was 20 s at the peak position and 10 s on each side of the peak position. For microprobe analysis, the very same crystal that has been used for X-ray data collection was fixed in resin on a glass slide and coated with carbon. Because of the inability of this method to determine the lithium content, the composition of the synthetic layered silicate was normalized to Si_4.00. The lithium content was confirmed independently for the bulk material by inductively coupled plasma atomic emission spectroscopy (ICP-AES), where for Li determination two samples of about 20 mg of dry synthetic Na-hect were weighed into a clean Teflon flask of 150 mL volume. After addition of 1.5 mL 30 wt.% HCl (Merck), 0.5 mL of 85 wt.% H₃PO₄ (Merck), 0.5 mL 65 wt.% HNO₃ (Merck) and 1 mL of 48 wt.% HBF₄ (Merck) the sample was digested in a MLS 1200 Mega microwave digestion apparatus for 6.5 min and heated at 600 W (MLS GmbH, Mikrowellen-Labor-Systeme, Leutkirch, Germany). The closed sample container was cooled to room temperature and the clear solution was diluted to 100 mL in a volumetric flask.

Table 1 Crystallographic data and details of the single crystal structure refinements of 1WL and 2WL of synthetic Na-hect

Crystal data
Formula unit [Na0.7xH2O]^inter[Mg2.3Li0.7]^oct[Si4]^tetO10F2
Formula weight = 387.22 (g mol^−1) (without interlayer water)
MoKα radiation (λ = 0.71073 Å) graphite monochromator
T = 173 K
1WL	2WL
a = 5.2434(10) Å	a = 5.2432(10) Å
b = 9.0891(18) Å	b = 9.0870(18) Å
c = 12.165(2) Å	c = 15.064(3) Å
β = 93.92(3)°	β = 96.42(3)°
V = 578.4(2) Å^3	V = 713.2(2) Å^3
Monoclinic. C2/m (No. 12)	Monoclinic. C2/m (No. 12)
Z = 2	Z = 2
Plate colourless	Plate colourless
0.25 mm × 0.20 mm × 0.02 mm	0.25 mm × 0.20 mm × 0.02 mm
Data collection
STOE IPDS I diffractometer
Completeness of 2θ = 0.98	Completeness of 2θ = 0.98
2006 measured reflections	2477 measured reflections
597 independent reflections	734 independent reflections
384 reflections with I > 2σ(I)	426 reflections with I > 2σ(I)
R int = 0.181	R int = 0.226
θ max = 25.90°	θ max = 25.93°
θ min = 3.36°	θ min = 2.72
h = −5 → 6	h = −5 → 6
k = −11 → 10	k = −10 → 10
l = −14 → 14	l = −18 → 18
Refinement applying SHELXTL 5.1 (Bruker AXS).
Refinement on F^2	Refinement on F^2
R[F^2 > 2σ(F^2)] = 0.109	R[F^2 > 2σ(F^2)] = 0.1150
wR(F^2) = 0.2881	wR(F^2) = 0.2787
S = 1.110	S = 1.042
w = 1/[σ^2(Fo^2) + (0.20000P)^2 +0.000P] where P = (Fo^2 + 2 Fc^2)/3	w = 1/[σ^2(Fo^2) + (0.20000P)^2 + 0.000P] where P = (Fo^2 + 2 Fc^2)/3
Δρmax = 1.58 eÅ^3	Δρmax = 1.12 eÅ^3
Δρmin = −0.71 eÅ^3	Δρmin = −0.76 eÅ^3
61 parameters	73 parameters

---

The water content of both hydrates was determined gravimetrically. Approximately 100 mg of equilibrated one- and two-layer hydrate samples were dried at 250 °C at reduced pressure (2.2 × 10⁻² mbar) for 24 h. The weight loss during drying was attributed to interlayer water.

The cation exchange capacity (CEC) of synthetic Na-hect was determined using the barium chloride method. For this, 0.2 g of synthetic Na-hect were suspended in 25 mL of distilled water, and 25 mL of 1 M barium chloride solution were added. The mixture was shaken overnight and then centrifuged, and the supernatant solution was collected. To ensure complete exchange of sodium, the cation exchange was repeated two times. The Na⁺ content of the collected solutions was determined by Atomic Absorption Spectroscopy (AAS). Additionally, the CEC was crosschecked by analyzing the Ba-exchanged Na-hect for its Ba-content by ICP-AES after microwave digestion as described for the determination of the Li-content.

Results and discussion

Synthesis of a phase pure Na-hect

Fig. 1 shows the PXRD pattern of zero-, one-, and two-layer hydrates (0WL, 1WL, and 2WL, respectively) of synthetic Na-hect. No crystalline impurities could be detected.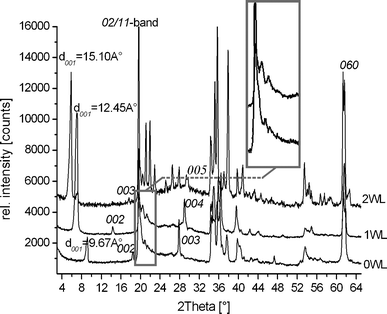

Fig. 1 Powder X-ray diffraction pattern of zero- (0WL, d₀₀₁ = 9.67 Å), one- (1WL, d₀₀₁ = 12.45 Å), and two-layer hydrates (2WL, d₀₀₁ = 15.10 Å) of synthetic sodium fluorohectorite.

The 1WL showed uniform intercrystalline reactivity as indicated by a rational 00l series (variation coefficient = 0.33%)²⁹ and a basal spacing of d₀₀₁ = 12.5 Å. Due to overlap, we were only able to unambiguously determine the positions of the 00l-series where l_max = 5 in the cases of the zero-layer hydrate and the one-layer hydrate, and l_max = 8 in the case of the two-layer hydrate. While the 1WL is uniformly hydrated, at the 2WL state some crystals remain in the 1WL state. The 00l series (variation coefficient = 0.42%) of the 2WL phase is nevertheless rational, suggesting a uniform swelling behavior within a single crystal, while some crystals are less reactive for whatever reason. The 2WL gives a basal spacing of d₀₀₁ = 15.1 Å. Judging by the number of peaks detectable in the diffraction pattern, in particular at the diffraction angle (20–23° 2θ) where the 02/11-band appears, it became quite obvious that the stacking disorder decreased significantly with increasing hydration. Please note that PXRD samples an average of the bulk material, and even an observed peak maxima superimposed on an asymmetric λ-shaped hk-band might already indicate that a few (semi-)ordered single crystals are present. In any case, the 2WL can be indexed without problems (a = 5.2310 Å, b = 9.0681 Å, c = 15.0307 Å, and β = 97.12°). Good quality crystals with little diffuse scattering can also quite easily be found for the 2WL. The disorder–order transition upon hydration is reversible. We therefore tried to improve the stacking order for 1WL by repeatedly cycling between 1WL and 2WL, but the crystallinity as judged by the PXRD trace could not be improved. Nevertheless, by screening a large number of 1WL crystals we succeeded in identifying individual crystals with much reduced diffuse scattering. In agreement with previous observations for non-hydrated [Na_0.5]^inter[Mg_2.5Li_0.5]^oct[Si₄]^tetO₁₀F₂ which is also heavily disordered,³⁰ for 0WL, all crystals checked were highly disordered and therefore no structure refinement was attempted.

The chemical composition of synthetic Na-hect was determined by WDX to be [Na_0.7]^inter[Mg_2.3Li_0.7]^oct[Si₄]^tetO₁₀F₂. Following digestion of the material and applying ICP-AES, the contents of Na⁺, Li⁺, and Mg²⁺ were 0.73 ± 0.05, 0.72 ± 0.02, and 2.25 ± 0.04, respectively. The CEC of synthetic Na-hect as determined via Na⁺ in the supernatant after Ba²⁺ exchange was 1.85 meq g⁻¹. The CEC calculated from the Ba-content of Ba-hect was 1.75 meq g⁻¹. These values are in close agreement with theoretical values calculated from the chemical formula as determined by WDX (1.81 meq g⁻¹).

The H₂O/Na molar ratio as determined gravimetrically was 3.2 and 5.6 for the 1WL and 2WL, respectively. The value for the 2WL was significantly higher than what has been reported by Beyer and von Reichenbach,³¹ who have used a phlogopite with a layer charge per formula unit (p.f.u.) of x = 0.98. They pointed out that for the 2WL, the interlayer space is densely packed with a ratio of H₂O/Na = 4 and therefore no additional water could possibly be accommodated in the interlayer space. Please note that we synthesized a much lower layer charge of x = 0.7 p.f.u., as indicated by microprobe analysis. Since the interlayer space is expected to be still densely packed, unoccupied Na-positions will yield voids to accommodate additional water.

Single crystal structure refinement

Details of the single crystal structure refinements, together with experimental details of 1WL and 2WL of synthetic Na-hect, are included in Table 1. A standard single crystal refinement program was applied that is not capable of handling diffuse (non-Bragg) scattering. As in earlier work, diffuse scattering had to be ignored but refinement was performed against the complete data set.

Further information about the structure refinement can be requested from Fachinformationszentrum Karlsruhe, Gesellschaft für wissenschaftlich-technische Information mbH, D-76344 Eggenstein-Leopoldshafen, Germany, by indicating the deposition numbers CSD-424706 and CSD-424707 for 1WL and 2WL hydrate, respectively (email: crysdata@fiz-karlsruhe.de).

The quality of the data sets, as indicated by the R_int values, is satisfactory for this class of materials since, due to the diffuse scattering, the integration profiles of affected reflections are ill-defined, which consequently leads to somewhat higher R_int values. The structures could be solved without problems by applying direct methods as implemented in SHELXTL 5.1 (Bruker AXS).³² For both hydrates, the refinement of the structure of the 2:1 layer also was straightforward and atomic displacement parameters (ADP) could even be refined anisotropically. This underlines the good quality of the data sets. Occupancies of interlayer cations and water were freely refined. The water content as obtained by the refinement is somewhat lower than the values determined by gravimetric analysis. From the occupation factors obtained in the refinement the following compositions could be calculated: [Na_0.7·2.1H₂O]^inter[Mg_2.2Li_0.8]^oct[Si₄]^tetO₁₀F₂ and [Na_0.7·4H₂O]^inter[Mg_2.2Li_0.8]^oct[Si₄]^tetO₁₀F₂ for 1WL and 2WL, respectively). Most likely this is due to the residual disorder and diffuse scattering (see Fig. S1 and S2, ESI†).

As might have been expected, interlayer water and cations were trickier to be located and refined. Na-sites could, however, be identified by looking for a sensible coordination environment. In both 1WL and 2WL, alternative positions with partial occupation were identified. As pointed out earlier, unoccupied Na-sites are generally expected to be filled by additional water molecules. However, given the complexity of the refinement, we did not attempt concomitant refinement of partially occupied water on Na-sites. Despite these difficulties, for 2WL a stable refinement was possible without restraining or even constraining atomic distances and bond angles between interlayer constituents of the 2WL structure, as done by Beyer and von Reichenbach.³¹

For 1WL, all water molecules coordinating to sodium could be identified in the difference Fourier map, however, for stable refinement the distances between water molecules and between water and sodium had to be restrained by applying DFIX. Please note that the refinements were not restricted to selected classes of reflections that are less affected by stacking faults, instead all reflections have been used. Given this, the quality of the refinement as indicated by R values of around 11% is very reliable.

Structure of 1WL and 2WL hydrate

The crystal structure of 1WL and 2WL projected along [100] are represented in Fig. 2. There is a longstanding dispute in the literature about the position of the interlayer cations in the 1WL. Some authors suggest that it resides on the central plane of the interlayer.^33,34 Computer simulations of 1WL support this view.^35,36 Some other authors claimed that the interlayer cations are displaced from the center towards tetrahedral sheets.^14,37

Fig. 2 Structure of 1WL and 2WL of Na-hect projected along [100] indicating in particular the location of the interlayer cations.

Our refinement clearly showed that in the 1WL Na⁺ interlayer cations are not residing in the middle of the interlayer space but are displaced towards the tetrahedral sheet enclosing the interlayer space. Displacement towards the upper or lower tetrahedral sheets is of course degenerate and consequently two alternative sites with differing Z values for Na⁺ could be identified during refinement. These alternative Na⁺ sites can be clearly spotted in the Fourier map (Fo-map: F(obs) Fourier with phases from F(calc)) of the interlayer space (see Fig. S3, ESI†). For 1WL, the central plane of the interlayer space is occupied by water molecules which are coordinated to the interlayer cations (see below).

Contrary to 1WL, for 2WL the interlayer cations reside at the central plane of the interlayer space as has been suggested by others,^23,31 and this is also supported by the Fo-map of the interlayer space (see Fig. S4, ESI†).

Although the close proximity of the origin of charge in saponites certainly will influence the location of interlayer cations, we still would like to compare the Z-positions of these cations and the interlayer water coordinated to them, as recently published by Ferrage et al.³⁸ for a high layer charge saponite ([Na_x]^inter[Mg₆]^oct[Si_4-xAl_x]^tetO₁₀(OH)₂, x = 0.7). For 1WL, Ferrage et al. found a strong dependence of the Na-location on the forcefield applied in the modelling study. For the S/S-FF-forcefield³⁸ the Na-sites were well located and were found to be displaced by approximately ±0.8 Å from the central plane of water molecules, which is in close agreement with 0.815 Å found in our refinement. For 2WL, Ferrage et al., with all forcefields applied, found a smaller amount of Na displaced from the central plane of the interlayer space, which is mostly related to the tetrahedral substitution. The distance between the main Na-site at the central plane and the two water layers above and below is reported by Ferrange et al. to be around 1.5 Å.³⁸ Our refinement of the single crystal data gave, however, significantly shorter distances along z of 1.32 Å and 1.37 Å. It is difficult to judge whether these differences are due to the different types of clay and charge patterns or whether it indeed would suggest that the forcefield parameters applied would have to be further refined. Part of the difference can certainly also be attributed to the different temperatures that the data were collected at.

The relative position of the lower and upper tetrahedral sheets encompassing the interlayer region (stacking order) as viewed along [001] is presented in Fig. 3A and Fig. 3B for 2WL and 1WL, respectively. The observed location of sodium cations for 1WL and 2WL relative to the lower tetrahedral sheet is depicted in Fig. 4. For 2WL, the upper and lower hexagonal cavities are stacked face to face. Contrary to mica structures where this arrangement is assured by interlayer cations in the center intruding into the hexagonal cavities on both sides, the cavities are not occupied by interlayer cations in the 2WL structure. Instead, the Na⁺ resides above the tetrahedrons (see Fig. S4, ESI†). As pointed out by Beyer and von Reichenbach³¹ two sets of Na⁺ sites depicted as m1 and m2 (in Fig. 4A) exist. With a charge density of x = 1.0 p.f.u. only half of these possible Na⁺ sites are occupied, with x = 0.7 p.f.u., as we found for Na-hect, even less than half are occupied. Not surprisingly, structure refinement results in an equal statistical occupation of both sites, m1 and m2, as is also obvious from the Fo-map (see Fig. S5, ESI†). Beyer and von Reichenbach³¹ have proposed that m1 and m2 sites are concomitantly occupied in the same interlayer space, resulting in zig-zag-chains of edge-sharing octahedral running along [100].

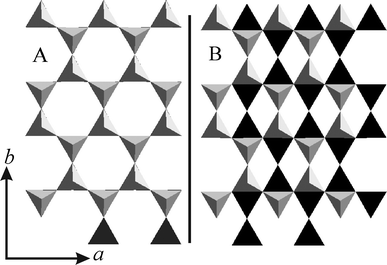Fig. 3 Comparison of the relative position of the lower (black) and upper (grey) tetrahedral sheets encompassing the interlayer region (stacking order) as viewed along c*: 2WL (A) and 1WL (B).

Fig. 4 Position of hydrated Na⁺ interlayer cations relative to the lower hexagonal cavity; A: 2WL hydrate: the positions of m1 and m2, B: 1WL hydrate: the position of m3 along the [001] projection. Please note that non-occupied m3 sites host water molecules coordinated to Na⁺ that are in contact with the upper tetrahedral sheet.

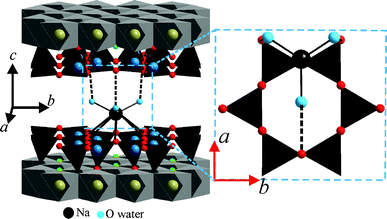
Beyer and von Reichenbach³¹ had to propose this ordering pattern in order to match octahedral coordination of Na⁺ interlayer cations with a H₂O/Na molar ratio of only 4. While this motif is wide-spread for μ-hydroxy-bridges, we are not aware of other examples of μ-aqua-bridges of Na⁺ in the literature. Moreover, we determined a H₂O/Na molar ratio of close to six allowing us to propose isolated [Na(H₂O)₆]⁺. We therefore suggest that the electron density seen in the X-ray experiment is interpreted in an alternative way: for any individual interlayer space, either purely m1 or purely m2 sites are occupied, and m1 and m2 interlayers are stacked randomly with equal probability.

The packing pattern of [Na(H₂O)₆]⁺ complex cations is shown in Fig. 4A. Each Na⁺ in the interlayer is coordinated by six oxygens of water (O_w) (the average of Na–O_w bond length is 2.45 Å). The coordinating oxygen atoms are located in two slightly corrugated planes above and below the plane of Na⁺ (Fig. 2). As pointed out by Beyer and von Reichenbach,³¹ with x = 1.0 pf.u., two densely packed planes of interlayer water result (see Fig. S6, ESI†). However, with x = 0.7 p.f.u., some Na⁺ sites are not occupied and the then non-coordinated water molecules are expected to relax. This might explain why Ferrage et al.¹⁵ had to apply a Gaussian-shaped distribution in their one-dimensional Fourier synthesis. Similarly, Argüelles et al.²⁵ introduced interstitial, non-coordinated water sites.

The stacking order of adjacent 2:1 layers is assured by well-defined hydrogen bonding motifs between the interlayer [Na(H₂O)₆]⁺ and the silicate layers. Each coordinated water molecule is able to connect to one basal oxygen atom of the tetrahedral sheet via hydrogen bonding (Fig. 5). The distance between the two oxygen atoms connected by hydrogen bonding was 2.90–3.03 Å.

Fig. 5 Hydrogen bonding between interlayer [Na(H₂O)₆]⁺ and tetrahedral sheets fixing the stacking order in 2WL Na-hect.

The stacking order puts the basal oxygen atoms of the two tetrahedral sheets encompassing the interlayer space on top of each other. In order to allow for concomitant connection of the octahedral interlayer species to both sides of the interlayer space, the two triangles of oxygen atoms forming [Na(H₂O)₆]⁺ need to be rotated relative to the triangle of the basal oxygens of the tetrahedral sheets. As was already obvious from the PXRD trace, 1WL suffers more severely from stacking faults as compared to 2WL. This is in line with observations for vermiculite where the 1WL material has been labelled as disordered.³⁹ Consequently, the knowledge of interlayer structures is much more limited as compared to 2WL.

However, as shown in the inset of Fig. 1, some comparatively sharp symmetric reflections are superimposed on the asymmetric λ-shaped 11/02-band, indicating that the bulk material also contains well-ordered crystals. Applying these maxima, a unit cell could be indexed and refined even for the 1WL (a = 5.2430 Å, b = 9.0851 Å, c = 12.2150 Å, β = 94.24°). By screening a large number of crystals, we were able to identify relatively well-ordered individuals that allowed a single crystal structure refinement. The unit cell found for this single crystal is in close agreement with the one refined from PXRD. As was already obvious from the metric of the unit cell, the stacking order found for Na-hect differed significantly from what has been reported for the 1WL of vermiculite.³⁹ While these authors reported a monoclinic angle of 90°, we get β = 93.92(3)°, clearly indicating that the relative position of tetrahedral sheets encompassing the interlayer space was different (Fig. 3B). The hexagonal cavities are not arranged opposite to each other but are shifted by 2.62 Å relative to each other, corresponding to an interlayer displacement of a/2. Na⁺ occupies m3 positions (Fig. 4B). As will be explained next, this shifting is required for the coordination of the interlayer cation by basal oxygen atoms of the two tetrahedral sheets encompassing the interlayer space.

In total 4 Na⁺ sites, all partially occupied (≈0.35), are located in the unit cell. Clearly some of the distances to water sites are too short to be occupied concomitantly in the same interlayer space. It would not be expected that the ordering of interlayer species in a particular interlayer space influences the ordering in adjacent interlayer spaces. However, the X-ray beam averages within the coherence length over all possible positions and the electron density is artificially superimposed into an average interlayer space. A tentative assignment of superimposed electron densities into an ordering pattern that makes sense chemically is attempted in the following (Fig. 6): the coordination observed for Na⁺ is unusual and it involves both basal oxygen atoms of the tetrahedral sheet and interlayer water. In the direction of the displacement of the interlayer cation towards the tetrahedral sheet, Na⁺ resides above the hexagonal cavity and is coordinated by six basal oxygens with distances ranging between 3.22 Å and 3.24 Å. On the opposite side of the interlayer region, a single siloxane bridge is located at a rather long distance of 3.52 Å, which was therefore not regarded to be part of the coordination sphere. The coordination of Na⁺ is rather completed by water molecules residing at the central plane resulting in a nine-fold coordination ([Na(O_b)₆(H₂O)₃]⁺). In Fig. 6 we choose the three closest water (2.45–2.55 Å) positions to be coordinated. These three water oxygen atoms are involved in hydrogen bonding to basal oxygens. The range of coordinated water molecules to different basal oxygens is 2.72–3.60 Å. While this interaction pattern explains why the interlayer space is bridged in a well-defined mode resulting in the interlayer displacement of a/2, some arbitrariness remains in the assignment due to the many alternative oxygen positions generated by the four alternative Na⁺ sites clearly visible in the Fo-map of 1WL (see Fig. S3, ESI†). Also, it was not clear whether indeed adjacent upper and lower Na⁺ sites are occupied concomitantly in the same interlayer or whether these alternate sites are rather segregated into different interlayer spaces.

Fig. 6 Tentative coordination of interlayer Na⁺ and connecting mode of adjacent silicate layers for 1WL of Na-hect.

Disorder mode of 1WL Na-hect

As has been pointed out in the literature, stacking faults may significantly alter properties and in consequence applications of clays.^40,41 Therefore, we briefly focus on the diffuse scattering containing the information on such disorder modes. As pointed out before, the 2WL structure is only slightly affected by disorder, and only a little diffuse scattering is apparent in the reciprocal lattice (see Fig. S1 and S2, ESI†). In agreement with the shape of the PXRD traces (Fig. 1), the reciprocal lattice of 1WL diffuse scattering is much more prominent as compared to the 2WL. Moreover, only some hk-rods are affected by the disorder, while others only show sharp Bragg reflections, suggesting that the disorder patterns are commensurate with the lattice (for comparison see Fig. 1 in Slade and Stone⁴²). Clearly, 1WL represents a semi-ordered structure. The most prominent semi-ordered stacking is observed for micas where ±b/3 shifts occur frequently and reflections with k = 3n remain sharp. Please note that tetrahedral rotation for the synthetic Na-hect is close to zero, generating an ideal hexagonal pseudo-symmetry for interlayer species. Therefore, disorder modes will be available that are not feasible for vermiculites.^24,25

In 1WL a different disorder mode was realized, as clearly indicated by the distribution of diffuse scattering in the reciprocal lattice space: 02l, 42l, 24l, 06l, and 46l are diffuse, while 22l, 62l, 04l, 44l, and 26l are sharp. As shown in Fig. 7, translations of the upper layer by combinations of ±a/4 and ±b/4 create the same environment for the interlayer cations, suggesting that random shifts of that type will generate energetically degenerate modes of stacking. This degeneracy in turn is responsible for the stacking disorder observed.

Fig. 7 Illustration of energetically degenerate stacking modes for semi-ordered 1WL explaining the observed diffuse scattering. The translation of the upper tetrahedral sheet (grey) relative to the lower tetrahedral sheet (black) with [(+a/4) + (+b/4)] or [(−a/4) + (+b/4)] provides a similar environment for interlayer species.

Conclusions

By melt synthesis, swelling Na-hect could be synthesized that, upon hydration, converts to semi-ordered (1WL) and ordered (2WL) hydrates. The significant reduction of stacking faults in these synthetic hydrates allowed for the first time solving of the structure of the one-layer hydrate. The interlayer cations reside off the central plane in a nine-fold coordination of six basal oxygen atoms and three water molecules. The stacking order is determined by hydrogen bonding of the latter to the second tetrahedral sheet. The two-layer hydrate structures proposed for vermiculites in the literature were in large confirmed. However, modifications in details like ordering of alternative sites for [Na(H₂O)₆]⁺ were suggested.

Acknowledgements

The authors thank the Bayerisches Geoinstitut, Bayreuth, Germany, for the WDX measurement. This work was supported financially by the graduate school ‘Structure, Reactivity and Properties of Oxide Materials’ within the Elitenetzwerk Bayern, the Deutsche Forschungsgemeinschaft (SFB 840), and the University of Aleppo.

References

1. R. T. Martin, S. W. Bailey, D. D. Eberl, D. S. Fanning, S. Guggenheim, H. Kodama, D. R. Pevear, J. Srodon and F. J. Wicks, Clays Clay Miner., 1991, 39, 333–335.
2. D. D. Eisenhour and R. K. Brown, Elements, 2009, 5, 83–88.
3. A. Baumgartner, K. Sattler, J. Thun and J. Breu, Angew. Chem., Int. Ed., 2008, 47, 1640–1644.
4. M. Stöcker, W. Seidl, L. Seyfarth, J. Senker and J. Breu, Chem. Commun., 2008, 629–631.
5. M. W. Möller, T. Lunkenbein, H. Kalo, M. Schieder, D. A. Kunz and J. Breu, Adv. Mater., 2010, 22, 5245–5249.
6. M. R. Schütz, H. Kalo, T. Lunkenbein, A. H. Groschel, A. H. E. Muller, C. A. Wilkie and J. Breu, J. Mater. Chem., 2011, 21, 12110–12116.
7. M. W. Möller, D. Hirsemann, F. Haarmann, J. Senker and J. Breu, Chem. Mater., 2010, 22, 186–196.
8. J. F. Alcover and L. Gatineau, Clay Miner., 1980, 15, 193–203.
9. J. F. Alcover and L. Gatineau, Clay Miner., 1980, 15, 25–35.
10. H. Suquet and H. Pezerat, Clays Clay Miner., 1987, 35, 353–362.
11. C. de la Calle, H. Suquet and C. H. Pons, Clays Clay Miner., 1988, 36, 481–490.
12. N. Malikova, E. Dubois, V. Marry, B. Rotenberg and P. Turq, Z. Phys. Chem., 2010, 224, 153–181.
13. M. W. Möller, U. A. Handge, D. A. Kunz, T. Lunkenbein, V. Altstadt and J. Breu, ACS Nano, 2010, 4, 717–724.
14. T. J. Tambach, P. G. Bolhuis, E. J. M. Hensen and B. Smit, Langmuir, 2006, 22, 1223–1234.
15. E. Ferrage, B. Lanson, N. Malikova, A. Plancon, B. A. Sakharov and V. A. Drits, Chem. Mater., 2005, 17, 3499–3512.
16. H. Kalo, M. W. Möller, M. Ziadeh, D. Dolej and J. Breu, Appl. Clay Sci., 2010, 48, 39–45.
17. V. Marry, E. Dubois, N. Malikova, S. Durand-Vidal, S. Longeville and J. Breu, Environ. Sci. Technol., 2011, 45, 2850–2855.
18. S. Guggenheim, J. M. Adams, F. Bergaya, M. F. Brigatti, V. A. Drits, M. L. L. Formoso, E. Galan, T. Kogure, H. Stanjek and J. W. Stucki, Clays Clay Miner., 2009, 57, 134–135.
19. N. T. Skipper, K. Refson and J. D. C. Mcconnell, J. Chem. Phys., 1991, 94, 7434–7445.
20. F. R. C. Chang, N. T. Skipper and G. Sposito, Langmuir, 1995, 11, 2734–2741.
21. E. S. Boek, P. V. Coveney and N. T. Skipper, J. Am. Chem. Soc., 1995, 117, 12608–12617.
22. N. T. Skipper, F. R. C. Chang and G. Sposito, Clays Clay Miner., 1995, 43, 285–293.
23. P. G. Slade, P. A. Stone and E. W. Radoslovich, Clays Clay Miner., 1985, 33, 51–61.
24. H. Shirozu and S. W. Bailey, Am. Mineral., 1966, 51, 1124–1143.
25. A. Argüelles, M. Leoni, J. A. Blanco and C. Marcos, Am. Mineral., 2010, 95, 126–134.
26. K. Kitajima, F. Koyama and N. Takusagawa, Bull. Chem. Soc. Jpn., 1985, 58, 1325–1326.
27. M. Stöcker, L. Seyfarth, D. Hirsemann, J. Senker and J. Breu, Appl. Clay Sci., 2010, 48, 146–153.
28. J. Breu, W. Seidl, A. J. Stoll, K. G. Lange and T. U. Probst, Chem. Mater., 2001, 13, 4213–4220.
29. S. W. Bailey, Am. Mineral., 1982, 67, 394–398.
30. J. Breu, W. Seidl and A. Stoll, Z. Anorg. Allg. Chem., 2003, 629, 503–515.
31. J. Beyer and H. G. von Reichenbach, Clay Miner., 2002, 37, 157–168.
32. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
33. C. de la Calle and H. Suquet, Rev. Mineral., 1988, 19, 455–496.
34. C. de la Calle, A. Plancon, C. H. Pons, J. Dubernat, H. Suquet and H. Pezerat, Clay Miner., 1984, 19, 563–578.
35. A. Berghout, D. Tunega and A. Zaoui, Clays Clay Miner., 2010, 58, 174–187.
36. N. T. Skipper, A. K. Soper and J. D. C. Mcconnell, J. Chem. Phys., 1991, 94, 5751–5760.
37. R. P. Tenorio, M. Engelsberg, J. O. Fossum and G. J. da Silva, Langmuir, 2010, 26, 9703–9709.
38. E. Ferrage, B. A. Sakharov, L. J. Michot, A. Delville, A. Bauer, B. Lanson, S. Grangeon, G. Frapper, M. Jimenez-Ruiz and G. J. Cuello, J. Phys. Chem. C, 2011, 115, 1867–1881.
39. C. de la Calle, H. Suquet and H. Pezerat, Clay Miner., 1985, 20, 221–230.
40. A. Plancon, Clay Miner., 2001, 36, 1–14.
41. T. Kogure, J. Elzea-Kogel, C. T. Johnston and D. L. Bish, Clays Clay Miner., 2010, 58, 62–71.
42. P. G. Slade and P. A. Stone, Clays Clay Miner., 1984, 32, 223–226.

---

Footnote

† Electronic supplementary information (ESI) available: CIF files of 1WL and 2WL, Reciprocal lattice space images of 1WL and 2WL, Fo-map of 1WL and 2WL of Na-hect projected along a, Fo-map of the ab-plane of 2WL, CPK representation of densely packed arrangement of interlayer water. CCDC reference numbers 869127, 869128. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c2ra20457f

---