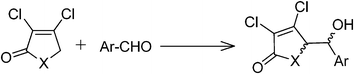Origins of reversing diastereoselectivity of α,β-dichloro-γ-butenolides and γ-butyrolactams in direct vinylogous aldol addition: a computational study†
Md Abdul Shafeeuulla
Khan
a,
Ji
Zhang
b,
Koushik Das
Sarma
*c and
Bishwajit
Ganguly
*a
aAnalytical Discipline and Centralized Instrument Facility, Central Salt & Marine Chemicals Research Institute (Council of Scientific and Industrial Research), Bhavnagar, Gujarat 364 002, India. E-mail: ganguly@csmcri.org; Fax: (+91)-120-2586776
bKing Kai-Ray Pharma, Mail Box 3016, Princeton, NJ-08540, USA
cJubilant Chemsys Ltd., B-34, Sector-58, Noida, UP 201301, India. E-mail: kdsarma@gmail.com; Fax: (+91)-278-2567562
First published on 17th July 2012
Abstract
Oxygenated five-membered ring compounds are more widespread in nature than the corresponding aza-analogues due to their more interesting biological activity. In our earlier studies, we have reported a simple methodology to synthesize novel synthons like 5-(1′-hydroxy)-γ-butenolide and 5-(1′-hydroxy)-γ-butyrolactam through the direct vinylogous aldol addition reaction. The observed diastereoselectivities for γ-butyrolactones and γ-butyrolactams were not understood in that report. We have reported herein a detailed computational study to understand the observed diastereoselectivity of α,β-dichloro-γ-butenolides and α,β-dichloro-γ-butyrolactams. The transition state calculations performed with B3LYP/cc-pVDZ level of theory to examine the diastereoselectivity of α,β-dichloro-γ-butenolides and α,β-dichloro-γ-butyrolactams have been found to be in good agreement with the observed experimental results. The origin of selectivity is examined by an activation strain model and molecular electrostatic potential (MESP) surfaces. The distortion energies calculated using the activation strain model revealed the origin of diastereoselectivities for butenolides and butyrolactams. The reversal in stereochemical outcome of α,β-dichloro-γ-butenolides and α,β-dichloro-γ-butyrolactams is due to the presence of a large substituent at the nitrogen center of the γ-butyrolactams. We have further revealed the enhanced diastereoselectivity of these butenolides while reacting with the aromatic aldehydes bearing ortho substituents. The generated molecular electrostatic potential (MESP) surfaces have shown an additional Vmin of value = −115.0 kcal mol−1 responsible for enhanced diastereoselectivity with ortho-substituted benzaldehydes as compared to unsubstituted benzaldehyde. The difference in transition state distortion energies of syn and anti aldol products are found to correlate with their corresponding differences in activation energies.
Introduction
Studies of γ-butenolide and γ-butyrolactam ring systems have received a considerable attention as these ubiquitous structural motifs have been found in numerous natural products as well as in a number of synthetic drug candidates with diverse biological activities and therefore, become a valuable architectural platform for the development of new asymmetric methodologies.1–6 Especially, 5-(1′-hydroxy)-γ-butenolide/5-(1′-hydroxy)-γ-butyrolactam subunits have been employed as useful intermediates in organic synthesis with medicinal importance.7–11 Owing to the growing interest in these substances, much effort has been directed towards exploiting the efficient methodology for its synthesis and transformation.12–19One of our recent efforts explored a simple and facile method to synthesize novel synthons like 5-(1′-hydroxy)-γ-butenolide and 5-(1′-hydroxy)-γ-butyrolactam from a direct vinylogous aldol addition reaction between α,β-dichloro-γ-butenolide/α,β-dichloro-γ-butyrolactam and aromatic aldehydes.19 Diastereoselectivity has been observed and the effects of substitution on the benzaldehyde on diastereomeric ratio have also been ascertained. From 1H NMR spectra analysis, it has been observed that the syn/anti ratio of aldol product with unsubstituted benzaldehyde is 2/1 (Table 1). It has also been observed that the syn/anti ratio of aldol product with para- and meta-substituted benzaldehydes is same as observed in the case of unsubstituted benzaldehyde, whereas, the syn/anti ratio was enhanced to 5/1 with ortho-substituted benzaldehyde (Table 1).19 We have speculated the role of steric effect between the aromatic aldehydes and chlorine atoms of α,β-unsaturated γ-butenolide or α,β-unsaturated γ-butyrolactam in their transition state geometries to rationalize the observed diastereoselectivity (Scheme 1).19 Interestingly, α,β-unsaturated γ-butyrolactams have shown opposite diastereoselectivity with respect to α,β-unsaturated γ-butenolides (Table 1) under the same reaction conditions. These observations were intriguing and warrant further investigations. In the present article, we have undertaken a computational study to understand the experimentally observed diastereoselectivity for the formation of 5-(1′-hydroxy)-γ-butenolide and 5-(1′-hydroxy)-γ-butyrolactam derivatives by employing DFT calculations. The energetic data of transition state geometries predicted with B3LYP/cc-pVDZ showed a good agreement with the syn/anti diastereomeric ratios determined experimentally. The origin of diastereoselectivity for 5-(1′-hydroxy)-γ-butenolide/5-(1′-hydroxy)-γ-butyrolactam derivatives has been rationalized on the basis of a distortion/interaction energy model20 and steric effects. Molecular Electrostatic Potential (MESP) analysis performed on the transition state geometries revealed the enhanced selectivity of α,β-unsaturated γ-butenolide with ortho-substituted benzaldehyde.
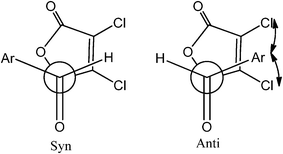 | ||
| Scheme 1 The Newman projections of possible transition state conformers for syn and anti products.19 | ||
X = O or N–R
| Entry | Ar-CHO | Product | syn/anti |
|---|---|---|---|
| 1 |

|

|
2/1 |
| 2 |

|

|
2/1 |
| 3 |

|

|
2/1 |
| 4 |

|

|
5/1 |
| 5 |

|

|
1/5 |
| 6 |

|

|
1/5 |
Results and discussion
Density functional calculations have been performed to obtain transition states for the direct vinylogous aldol addition involving α,β-dichloro-γ-butenolides and aromatic aldehydes. To examine the diastereoselectivity, we have considered four aromatic aldehydes (Scheme 2) viz.1 (unsubstituted benzaldehyde), 2 (para-substituted benzaldehyde), 3 (meta-substituted benzaldehyde) and 4 (ortho-substituted benzaldehyde) with α,β-dichloro-γ-butenolide (deprotonated form, X) to furnish the aldol product.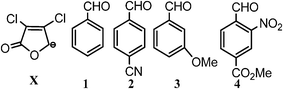 | ||
| Scheme 2 α,β-Dichloro-γ-butenolide, benzaldehyde and its derivatives 1–4. | ||
For simplicity, we have adopted the following notations; 1S is the transition state formed between 1 and X; 2S for 2 and X; 3S for 3 and X; 4S for 4 and X; here S stands for syn orientation. Similarly, 1A, 2A, 3A and 4A are considered for the corresponding anti transition state geometries. All optimized transition state geometries (1S–4S and 1A–4A) are shown in Fig. 1 along with the corresponding solvated Gibbs free energy differences. The carbanion of X moves toward the carbonyl carbon center of 1 at a distance of 1.911 Å in syn orientation to form a transition state (1S). The single imaginary frequency of 1S is 237.1i cm−1, with the normal vibrational mode characterizing the –C⋯C– bond formation. The corresponding bond distance and single imaginary frequency for the anti oriented transition state (1A) are 1.900 Å and 228.3i cm−1, respectively. The B3LPY/cc-pVDZ calculated free energies show that the syn transition state (1S) is energetically more stable by 2.9 kJ mol−1 compared to the corresponding anti transition state (1A) (Fig. 1). The cyano substitution at the para position of benzaldehyde (2) with α,β-dichloro-γ-butenolide (X) also predicted the syn transition state 2S is energetically preferred by 2.1 kJ mol−1 than the anti transition state 2A. The transition states calculated with the meta methoxybenzaldehyde 3 and X showed the preference for the formation of syn transition state (Fig. 1). The enhancement in the formation of syn transition state was observed with 4 and X, where the nitro group is substituted at the ortho position. The syn transition state 4S was found to be 13.0 kJ mol−1 energetically more stable than the corresponding anti transition state 4A. The influence of ortho substitution was further exemplified with ortho-methoxybenzaldehyde. The calculated results suggest that the formation of syn product is preferred by 10.0 kJ mol−1 compared to the formation of anti product in terms of Gibb's free energy as observed in the case of ortho-nitrobenzaldehyde (ESI, Fig. S1†).
![B3LYP/cc-pVDZ optimized transition state geometries of syn (left column) and anti (right column) aldol products of γ-butenolides in methanol along with the corresponding Gibb's free energies () and electronic energies with ZPVE correction [] (grey = carbon, red = oxygen, blue = nitrogen, white = hydrogen and green = chlorine).](/image/article/2012/RA/c2ra21203j/c2ra21203j-f1.gif) | ||
| Fig. 1 B3LYP/cc-pVDZ optimized transition state geometries of syn (left column) and anti (right column) aldol products of γ-butenolides in methanol along with the corresponding Gibb's free energies () and electronic energies with ZPVE correction [] (grey = carbon, red = oxygen, blue = nitrogen, white = hydrogen and green = chlorine). | ||
The role of the methoxy(oxo)methanide group at the para position in 4 was also investigated towards the diastereoselectivity of X. We replaced the methoxy(oxo)methanide group by a hydrogen atom and determined the syn and anti transition states (ESI, Fig. S2†). The calculated free energy difference showed the larger preference for the syn-aldol product over anti-aldol product (ESI, Fig. S2†). Such preference for the formation of syn-aldol over anti-aldol is in good agreement with the observed diastereoselectivity for the aldol reaction between substituted benzaldehydes and α,β-dichloro-γ-butenolide (Table 1). Further, the enhanced syn/anti product ratio for 4 with X compared to 1–3 was also predicted by the transition state calculations (Fig. 1).
Turning to the diastereoselectivity exhibited by α,β-unsaturated γ-butyrolactams, we have considered 5 and 6 to partake in a vinylogous aldol addition reaction with 4-NO2-benzaldehyde (Y) as suggested in our previous19 experimental study (Scheme 3). The optimized syn and anti transition state geometries of (5S, 5A, 6S and 6A) are shown in Fig. 2 along with corresponding free energy differences. Here, 5S is the transition state formed between 5 and Y; 6S is the transition state formed between 6 and Y; again S stands for syn orientation. Similarly, 5A and 6A are considered for the transition state geometries in anti orientation. The carbanion of 5 moves toward the carbonyl group carbon center of Y at a distance of 1.877 Å in syn orientation to form a transition state 5S. The single imaginary frequency of 5S is 187.3i cm−1, with the normal vibrational mode characterizing the –C⋯C– bond formation. The corresponding bond distance and single imaginary frequency for the anti oriented transition state (1A) are 1.887 Å and 192.7i cm−1, respectively. Similarly, the bond distances of 6S and 6A are 1.875 Å and 1.892 Å and the imaginary frequencies are 186i cm−1 and 196.3i cm−1, respectively. The free energy differences calculated with B3LYP/cc-pVDZ level for the syn and anti transition states for 5 and 6 with Y showed that the anti forms are more stable by 5.5 kJ mol−1 and 7.6 kJ mol−1, respectively, than their corresponding syn forms (Fig. 2). This opposite trend in diastereoselectivity of α,β-unsaturated γ-butyrolactams compared to diastereoselectivity of α,β-unsaturated γ-butenolides is in well agreement with the experimentally observed diastereoselectivity of these compounds (Table 1).
![B3LYP/cc-pVDZ optimized transition state geometries of syn (left column) and anti (right column) aldol products of γ-butyrolactams in methanol along with the corresponding Gibb's free energies () and electronic energies with ZPVE correction [] (grey = carbon, red = oxygen, blue = nitrogen, white = hydrogen and green = chlorine).](/image/article/2012/RA/c2ra21203j/c2ra21203j-f2.gif) | ||
| Fig. 2 B3LYP/cc-pVDZ optimized transition state geometries of syn (left column) and anti (right column) aldol products of γ-butyrolactams in methanol along with the corresponding Gibb's free energies () and electronic energies with ZPVE correction [] (grey = carbon, red = oxygen, blue = nitrogen, white = hydrogen and green = chlorine). | ||
 | ||
| Scheme 3 α,β-unsaturated γ-Butyrolactams (deprotonated forms) 5, 6, 7 and the para-nitrobenzaldehyde Y chosen for the study. | ||
The reversal of the diastereoselectivity in the case of α,β-unsaturated γ-butyrolactams (5 and 6) may be due to the presence of large group attached to the nitrogen atom of the five membered ring which is absent in the α,β-unsaturated γ-butenolides. We have replaced the large group on the nitrogen atom in both syn and anti transition state geometries with a hydrogen atom. These model transition state geometries 7S and 7A were optimized at the same level of theory (Fig. 2). Interestingly, the computed free energies show that the syn transition state (7S) is energetically stable by 0.5 kJ mol−1 compared to the anti transition state (7A) geometry of α,β-unsaturated γ-butyrolactams as we have seen in the case of α,β-unsaturated γ-butenolides. Therefore, it is now clear that the stabilization of the anti transition state over the syn transition state is due to the presence of large groups on the nitrogen atoms of the five membered rings of α,β-unsaturated γ-butyrolactams, which causes a larger steric repulsive interaction for the syn orientation over the corresponding anti orientation (Fig. 2). To further examine the effect of ortho-substituted benzaldehyde on the diastereoselectivity of α,β-unsaturated γ-butyrolactams, we have also computed the transition states formed during the reaction of ortho-nitrobenzaldehyde with N-substituted α,β-unsaturated γ-butyrolactam (5) and N-unsubstituted α,β-unsaturated γ-butyrolactam (7). The difference in activation Gibb's free energy data shows that the syn transition state formed between 7 and ortho-nitrobenzaldehyde is 13.0 kJ mol−1 more stable than the corresponding anti transition state as observed in the case of α,β-unsaturated γ-butenolides (ESI, Fig. S3†). However, N-substituted α,β-unsaturated γ-butyrolactam 5 also shows that the syn transition state is 9.6 kJ mol−1 more stable than the anti form in contrast to the reaction with Y (para-substituted benzaldehyde) (ESI, Fig. S3†). Due to the steric effect of ortho-substitution of benzaldehyde, the syn preference is enhanced with the N-unsubstituted α,β-unsaturated γ-butyrolactam 7, whereas, the selectivity is reversed with the N-substituted α,β-unsaturated γ-butyrolactam 5 as compared to the case of para-substituted benzaldehyde. That means, the steric effect of the ortho-substituent outweighs the steric effect of the larger substituent at the N-atom of α,β-unsaturated γ-butyrolactam. Therefore, it appears that the positional isomers of benzaldehydes can drive the diastereoselectivity of α,β-unsaturated γ-butyrolactams.
The origin of diastereoselectivity for the aldol reactions of α,β-unsaturated γ-butenolides/α,β-unsaturated γ-butyrolactams with benzaldehyde derivatives was examined with distortion energy model calculations. The distortion/interaction energy or activation strain model has been applied for many reactions in literature viz. aldol addition, Diels–Alder reactions of cyclo additions and reactions involving chiral dienes and achiral dienophiles, Evans chiral auxiliary-based asymmetric aldol reactions and 1, 3-dipolar cycloadditions by considering transition state distortion energy or interaction energy as a controlling factor towards reactivity.20–25 For syn and anti transition states obtained between the α,β-unsaturated γ-butenolides or α,β-unsaturated γ-butyrolactams and benzaldehyde derivatives, activation strain model was employed to segregate the distortion and interaction energies for the respective systems. The activation strain model calculations suggest that the distortion energies for the syn transition states of the aldol reaction between α,β-unsaturated γ-butenolides and benzaldehyde derivatives are lower than the corresponding anti transition states (ESI, Table S1†). Similarly, the distortion energies calculated for the α,β-unsaturated γ-butyrolactams and benzaldehyde derivatives showed that anti-transition states are energetically less distorted than the syn ones (ESI, Table S1†). A linear correlation is found between the difference of activation energies and the corresponding distortion energies for all the studied reactions with R2 = 0.941 (Fig. 3). Analysis of the transition states employing the activation strain model indicates that the diastereoselectivity of these aldol reactions is mainly governed by the geometric distortions of reactant molecules to achieve corresponding transition state geometries.
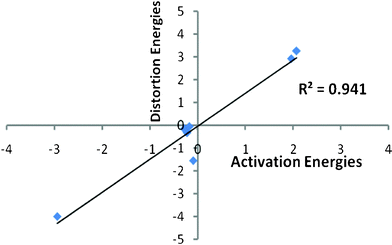 | ||
| Fig. 3 Plot of linear fit computed at B3LYP/cc-pVDZ for the difference of distortion energies between syn and anti transition states (1–7) versus the difference of activation energies between syn and anti transition states (1–7) with energies given in kJ mol−1. | ||
The transition state calculations and activation strain model shed light on the origin of diastereoselectivity for α,β-unsaturated γ-butenolides and α,β-unsaturated γ-butyrolactams with benzaldehyde derivatives. However, the reason for the enhanced syn/anti selectivity in the case of 4 with X is yet to be answered. To address this point, we have generated the MESP surfaces of syn and anti transition states of 1 and 4 with X. MESP is an important and widely used topographical quantity for understanding molecular reactivity, intermolecular interactions, molecular recognition, electrophilic reactions, substituent effects etc.26–37 MESP studies have also been used as tool for measuring electrostatic interactions (repulsions or attractions) due to the π-electron cloud of aromatic rings.38–40 MESP analysis gives the most negative valued point (Vmin) in electron rich regions obtained through topography calculations in any system. The MESP calculations show that in the case of 4A, there is an additional Vmin near to ortho-nitro group and chloro-substituents of the α,β-dichloro-γ-butenolide moiety (Fig. 4). Such large Vmin values can cause severe repulsion to the neighboring partner and hence would destabilize the anti aldol product more compared to 1A. The calculated free energy differences corroborate the MESP results.
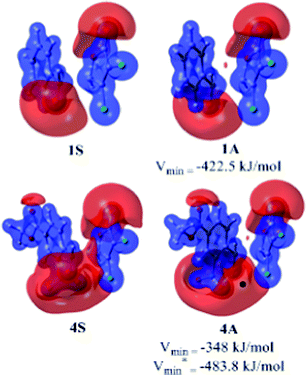 | ||
| Fig. 4 The B3LYP/cc-pVDZ generated MESP surfaces in methanol for 1S and 1A at an isosurface value of −410.0 kJ mol−1, and 4S and 4A at an isosurface value of −340.0 kJ mol−1. Red spots represent location of Vmin at the π-electron cloud of benzene and the black dot represents location of Vmin at the oxygen of the nitro group at the ortho-position. | ||
Conclusions
We have performed DFT calculations with B3LYP/cc-pVDZ level to compute the transition states for the deprotonated α,β-dichloro γ-butenolides and α,β-dichloro γ-butyrolactams with aromatic aldehydes to examine the diastereoselectivity of direct vinylogous aldol addition reactions. The effect of substituent position of benzaldehyde has been investigated through transition state, activation strain model and MESP calculations. The transition state calculations predicted the diastereoselectivity correctly in each case for the aldol reactions between α,β-dichloro-γ-butenolides/α,β-dichloro-γ-butyrolactams with aromatic aldehydes. The activation strain model rationalized the formation of syn aldol products for α,β-dichloro-γ-butenolides with benzaldehyde derivatives and anti aldol products for α,β-dichloro-γ-butyrolactams with aromatic aldehydes. The ease of formation of anti aldol products in the case α,β-unsaturated γ-butyrolactams was explained by model calculations where the larger groups attached to the nitrogen atom of the five membered ring was substituted with a hydrogen atom. However, it has been shown that positional isomers of benzaldehydes can drive the diastereoselectivity of α,β-unsaturated γ-butyrolactams. The enhanced diastereoselectivity of α,β-dichloro-γ-butenolides with ortho-substituted benzaldehyde 4 compared to the unsubstituted benzaldehyde was rationalized with MESP calculations. The present cumulative study of transition state calculations, activation strain model and MESP analysis, clearly explains the experimentally observed diverse and conflicting diastereoselectivity of α,β-unsaturated γ-butenolides and α,β-unsaturated γ-butyrolactams. Such analysis will be helpful in future studies to resolve the stereoselectivities in similar reactions.Computational methodology
All geometries were fully optimized by employing the popular Becke three-parameter exchange functional and the nonlocal correlation functional of Lee, Yang, and Parr (B3LYP) method41,42 in conjunction with Thom Dunning's correlation-consistent, polarized valence double zeta (cc-pVDZ) basis set (which was designed to converge smoothly toward the complete basis set limit using correlated wave functions).43,44 Harmonic frequency calculations at the same level of theory were used to characterize the stationary points as saddle point and to provide thermal and zero point corrections. Methanol is used as the implicit solvent with the polarizable continuum model (PCM).45 Intrinsic reaction coordinate (IRC) calculations were performed to connect all the transition states with their corresponding minima.46-48 Single-point calculations were performed at the B3LYP/cc-pvdz level to generate Molecular Electrostatic Potential (MESP) surfaces in solvent phase. All quantum chemical calculations were performed using Gaussian 09, Revision B.01 program.48 MESP surfaces have been generated with Gauss View 4.1.2 program suit. The MESP was calculated using eqn 1 where ZA was the charge on nucleus A, situated at a distance RA and ρ(r') is the electron density.49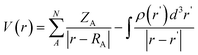 | (1) |
The activation strain or distortion energy model is used to analyze the energy barriers. This method is a fragment-based approach used to understand chemical reactions and their associated barriers.20 The distortion energy depends on the ability of the reactants to reorganize into their deformed structures in the transition state, which is devoid of any interaction between the reactants.21 The distortion energy (ΔEd‡) or interaction energy (ΔEi‡) model is a powerful tool to explain the reactivity in bimolecular reactions.22 By definition, activation energy is ΔE‡ = ΔEd‡ + ΔEi‡. The starting point is the two separate reactants, which approach from infinity and begin to interact and deform each other. The distortion energy computed by this method is associated with the strain caused by deforming the individual reactants. Throughout this article, energies and distances are given in kJ mol−1 and angstroms, respectively.
Acknowledgements
Authors thank DAE BRNS, Mumbai, India; DST, New Delhi, India and CSIR (MSM, SIP), New Delhi, India for financial support of this work. One of the authors MASK is thankful to CSIR (NWP 0010 and CSIR SRF), New Delhi, India for fellowship. KDS thanks Dr Sudhir Singh for support. We thank the reviewers for their comments and suggestions, which have helped us to improve the paper.References
- N. W. Fadnavis, S. K. Vadivel and M. Sharfuddin, Tetrahedron: Asymmetry, 1999, 10, 3675 CrossRef CAS.
- M. W. Saiah, M. Bessodes and K. Antonakis, Tetrahedron Lett., 1993, 34, 1597 CrossRef CAS.
- A. W. Evidente, L. Sparapano, O. Fierro and G. Bruno, J. Nat. Prod., 1999, 62, 253 CrossRef CAS.
- F. W. Alali, X.-X. Liu and J. L. McLaughlin, J. Nat. Prod., 1999, 62, 504 CrossRef.
- J. R. Hanson, Nat. Prod. Rep., 2002, 19, 381 RSC and references cited therein.
- A. D. Rodriguez, Tetrahedron, 1995, 51, 4571 CrossRef CAS.
- G. Rassu, F. Zanardi, L. Battistini and G. Casiraghi, Synlett, 1999, 1333 CAS.
- S. Hanessian, S. Giroux and M. Buffat, Org. Lett., 2005, 7, 3989 Search PubMed.
- H. Konno, N. Hiura, H. Makabe, M. Abe and H. Miyoshi, Bioorg. Med. Chem. Lett., 2004, 14, 629 CrossRef CAS.
- A. K. Ghosh and G. Gong, J. Am. Chem. Soc., 2004, 126, 3704 CrossRef CAS.
- G. Casiraghi, G. Rassu, L. Auzzas, P. Burreddu, E. Gaetani, L. Battistini, F. Zanardi, C. Curti, G. Nicastro, L. Belvisi, I. Motto, M. Castorina, G. Giannini and C. Pisano, J. Med. Chem., 2005, 48, 7675 CrossRef CAS.
- Y. S. Rao, Chem. Rev., 1964, 64, 353 CrossRef CAS.
- Y. S. Rao, Chem. Rev., 1976, 76, 625 CrossRef CAS.
- A. A. Avetisyan and M. T. Dangyan, Russ. Chem. Rev., 1977, 46, 643 Search PubMed.
- D. W. Knight, Contemp. Org. Synth., 1994, 1, 287 RSC.
- E. Negishi and M. Kotora, Tetrahedron, 1997, 53, 6707 CrossRef CAS.
- R. Bruckner, Curr. Org. Chem., 2001, 5, 679 CrossRef CAS.
- T. Montagnon, M. Tofi and G. Vassilikogiannakis, Acc. Chem. Res., 2008, 41, 1001 CrossRef CAS.
- K. D. Sarma, J. Zhang and T. T. Curran, J. Org. Chem., 2007, 72, 3311 CrossRef CAS.
- (a) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114 CrossRef CAS; (b) G. T. de Jong and F. M. Bickelhaupt, ChemPhysChem, 2007, 8, 1170 CrossRef CAS; (c) W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118 RSC.
- C. B. Shinisha and R. B. Sunoj, J. Am. Chem. Soc., 2010, 132, 12319 CrossRef CAS.
- Y. Lan and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 17921 CrossRef CAS and references therein..
- R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366 CrossRef CAS.
- S. Agopcan, N. Çelebi-Ölçüm, M. N. Üçışık, A. Sanyal and V. Aviyente, Org. Biomol. Chem., 2011, 9, 8079 RSC.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646 CrossRef CAS.
- G. Dive and D. Dehareng, Int. J. Quantum Chem., 1993, 46, 127 Search PubMed.
- P. Politzer and J. S. Murray, J. Phys. Chem. A, 1998, 102, 1018 Search PubMed.
- J. S. Murray, F. Abu-awwad and P. Politzer, J. Phys. Chem. A, 1999, 103, 1853 Search PubMed.
- K. D. Sen and P. Politzer, J. Chem. Phys., 1989, 90, 4370 CrossRef CAS.
- G. Naray-Szabo and G. Ferenczy, Chem. Rev., 1995, 95, 829 CrossRef CAS.
- B. Pullman, Int. J. Quantum Chem., 1990, 17, 81 Search PubMed.
- S. R. Gadre and I. H. Shrivastava, J. Chem. Phys., 1991, 94, 4384 CrossRef CAS.
- R. N. Shirsat, S. V. Bapat and S. R. Gadre, Chem. Phys. Lett., 1992, 200, 373 CrossRef.
- R. Bonaccorsi, E. Scrocco and J. Tomasi, J. Chem. Phys., 1970, 52, 5270 CrossRef CAS.
- R. Bonaccorsi, E. Scrocco and J. Tomasi, Theor. Chim. Acta, 1971, 21, 17 CrossRef CAS.
- H. Berthold and A. Pullman, Chem. Phys. Lett., 1975, 32, 233 Search PubMed.
- C. Giessner-Prettre and A. Pullman, Theor. Chim. Acta, 1975, 37, 335 Search PubMed.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 878 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- E. R. Davidson, Chem. Phys. Lett., 1996, 220, 514 CrossRef.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027 CrossRef CAS.
- C. González and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- C. González and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- P. Politzer and J. S. Murray in Reviews in Computational Chemistry, ed. K. B. Lipkowitz, D. B. Boyd, VCH Publishers, New York, 1991, ch 7, vol. 2, pp. 273 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: B3LYP/cc-pVDZ optimized Cartesian coordinates of all stationary points, including all the thermodynamic data generated from frequency calculation and imaginary frequencies of all the transition state geometries. See DOI: 10.1039/c2ra21203j |
| This journal is © The Royal Society of Chemistry 2012 |