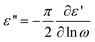Brownian dynamics determine universality of charge transport in ionic liquids
J. R.
Sangoro
ac,
M.
Mierzwa
b,
C.
Iacob
a,
M.
Paluch
b and
F.
Kremer
a
aInstitute of Experimental Physics I, University of Leipzig, Linnéstr. 5, 04103, Leipzig, Germany. E-mail: sangorojr@ornl.gov; sangoro@physik.uni-leipzig.de
bSilesian University, Katowice, Poland
cChemical Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA
First published on 2nd May 2012
Abstract
Broadband dielectric spectroscopy is employed to investigate charge transport in a variety of glass-forming ionic liquids over wide frequency, temperature and pressure ranges. Using a combination of Einstein, Einstein-Smoluchowski, and Langevin relations, the observed universal scaling of charge transport in ionic liquids is traced back to the dominant role of Brownian dynamics.
Charge transport and molecular dynamics in disordered ion-conducting materials continue to be active topics of research with immediate fundamental and technological importance.1 Significant experimental and theoretical progress in the understanding of the interplay between ion dynamics and morphology in different classes of materials including alkali-glasses,2 polymers,3,4 ionomers,5 zwitterionomers,6 and ionic liquids7 has been realized. One of the ubiquitous features of ionic liquids is the universal scaling of charge transport, implied by the coincidence of plots of dc conductivity (σ0) against the characteristic diffusion rate (ωc) at which the real part of the complex conductivity begins to increase with frequency from the σ0 value. This is experimentally observed for a broad class of ionic liquids, from those consisting of small ions like Na+ to those made up of large organic ions like imidazolium-based ionic liquids.6,8,9 Whereas the proportionality between σ0 and ωc can be rationalized based on the Einstein and Einstein-Smoluchowski relations as discussed in our previous manuscripts,9,10 the physical origin of the coinciding plots obtained for remarkably different categories of materials is not yet understood. To date, temperature is the main thermodynamic parameter that has been varied in these studies. Both thermal energy and molecular packing density are altered upon changing the temperature.11 However, to study the relative roles of thermal and density fluctuations as well as their impact on the observed universality of charge transport in disordered ion-conducting materials, measurements at different pressures are also necessary.
In this Communication, we experimentally show for the first time using temperature- and pressure-dependent dielectric data that the universal scaling of charge transport in ionic liquids is traced back to the dominant role of Brownian dynamics.
The ionic liquids investigated in this study (1-hexyl-3-methylimidazolium chloride—[HMIM][Cl] and 1-(2-hydroxyethyl)-3-methylimidazolium tetrafluoroborate—[HEMIM] [BF4] were purchased from Solvent Innovation GmbH (an affiliate of Merck KGaA) and Iolitec GmbH respectively. The ILs were dried in vacuum (10−6 to 10−7 mbar) at 330 K for 12 h prior to measurements.
The dielectric measurements were performed between 0.1 Hz and 1.8 GHz using a high resolution alpha dielectric analyzer (for measurements from 0.1 Hz up to 10 MHz) and a HP impedance analyzer (for high frequency investigations). Quatro temperature controllers, using pure nitrogen as heating agent and maintaining temperature stability better than 0.1 K, were employed. For high-pressure studies, the samples in a parallel-plate configuration were placed in the high-pressure chamber and compressed using silicone fluid through a piston in contact with a hydraulic press (SITEC). A Nova Swiss tensometric meter with a resolution better than 0.1 MPa was used to measure the pressure.12
Due to its ability to probe molecular fluctuations and charge transport over broad timescales spanning a range from picoseconds to several days,6 Broadband Dielectric Spectroscopy (BDS) turns out to be a versatile experimental tool for investigating charge transport in ionic liquids. The technique is based on the interaction of matter with an electromagnetic field and measures the complex dielectric function, ε*, which is equivalent to the complex conductivity function, σ*. This is expressed as σ*(ω,T,p) = iε0ωε*(ω,T,p), implying that σ′ = ε0ωε′′ and σ′′ = ε0ωε′ (where ε0, ω, T, and p denote the vacuum permittivity, radial frequency, temperature, and pressure, respectively). For ion-conducting disordered materials, the dielectric spectra are also often presented in terms of the complex modulus, M*(= 1/ε* = iωε0/σ*), with the real and imaginary parts of the complex modulus given by M′ = ε0ωσ′′/((σ′)2 + (σ′′)2) and M′′ = ε0ωσ′/((σ′)2 + (σ′′)2), respectively. Although related, the different formalisms emphasize certain unique aspects of the underlying processes.
The real part of the complex conductivity function σ′ in ionic liquids is characterised on the intermediate frequency range by a plateau (the value of which gives the dc conductivity, σ0) as well as the characteristic frequency, fc, at which dispersion sets in and turns into a power law at higher frequencies. The value of fc can be determined by calculating the turning point from the second derivative of σ′ with respect to frequency. At lower frequencies, σ′ decreases from σ0 and this is due to electrode polarization, which shows up much earlier in the imaginary part of the complex conductivity, σ′′.13,14 For ionic liquids, it has been observed that fc approximately coincides with the frequency corresponding to the peak in the imaginary part of the electrical modulus, fM.15 Whereas the data of σ0 are easily obtained from the plateau values σ′, several approaches can be used to extract ωc(= 2πfc) from the measured conductivity spectra of ionic liquids. These include, among others, (i) using basic calculus to determine the onset of dispersion of σ′ from the σ0, (ii) the peak frequency obtained after applying the derivative technique16,17
![The complex conductivity σ*(= σ′ + iσ′′) as well as the imaginary part of the complex electrical modulus M′′ of [HMIM][Cl] ionic liquid as functions of frequency at 0.1 MPa for the different temperatures as indicated. The fits are made using the analytical approximation of the random barrier model proposed by Dyre (σ* = ωτeσ0/ln(1 + iωτe)). The fit parameters are: for 290 K: (σ0 =7.8 × 10−6 S cm−1, τe = 1.2 × 10−7 s), 260 K: (σ0 = 5.5 × 10−8 S cm−1, τe = 1.1 × 10−5 s), 240 K: (σ0 = 2.1 × 10−10 S cm−1, τe = 2.6 × 10−3 s), 230 K: (σ0 = 3.6 × 10−12 S cm−1, τe = 1.2 × 10−1 s). Inset: Scaling with respect to the characteristic frequency, fc, and dc conductivity, σ0, for the different temperatures. Lines denote scaled spectra of M′′. The error bars are comparable to the size of the symbols, if not indicated otherwise. The logarithm is to base 10.](/image/article/2012/RA/c2ra20560b/c2ra20560b-f1.gif) | ||
| Fig. 1 The complex conductivity σ*(= σ′ + iσ′′) as well as the imaginary part of the complex electrical modulus M′′ of [HMIM][Cl] ionic liquid as functions of frequency at 0.1 MPa for the different temperatures as indicated. The fits are made using the analytical approximation of the random barrier model proposed by Dyre (σ* = ωτeσ0/ln(1 + iωτe)). The fit parameters are: for 290 K: (σ0 =7.8 × 10−6 S cm−1, τe = 1.2 × 10−7 s), 260 K: (σ0 = 5.5 × 10−8 S cm−1, τe = 1.1 × 10−5 s), 240 K: (σ0 = 2.1 × 10−10 S cm−1, τe = 2.6 × 10−3 s), 230 K: (σ0 = 3.6 × 10−12 S cm−1, τe = 1.2 × 10−1 s). Inset: Scaling with respect to the characteristic frequency, fc, and dc conductivity, σ0, for the different temperatures. Lines denote scaled spectra of M′′. The error bars are comparable to the size of the symbols, if not indicated otherwise. The logarithm is to base 10. | ||
When an electric field, E, is applied to an amorphous electrically conducting material, the charge carriers ultimately attain a mean velocity, υ, determined by the mobility, μ, according to υ = μE. The resulting current density is given by j = nqυ, with n and q denoting the effective number density and the elementary charge for the case of monovalent ions, respectively. Based on Ohm's law, the direct current (dc) conductivity, σ0 can thus be expressed as σ0 = qμn. This is one of the well-established molecular quantities characterizing electrical transport in ion conductors. The physical meaning of ωc will now be described. From combined BDS and dynamic-mechanical spectroscopic studies of a series of ionic liquids, it has been found that ωc coincides with the mechanically obtained structural α-relaxation rates.9,10 The latter is a measure of rotational diffusion. In addition, recent independent computational studies have confirmed that the characteristic times corresponding to translational and rotational diffusion in ionic liquids are identical.18 Experiments by dynamic light scattering and BDS methods have also indicated no remarkable decoupling between rotational and translational diffusion in ionic liquids.19 Therefore, ωc can be interpreted as the characteristic diffusion (both translational and rotational) rate. Thus, based on model-free analyses of the dielectric spectra of ionic liquids, the key quantities characterizing charge transport in ionic liquids namely, σ0 and ωc, are obtained.
One of the theoretical approaches of describing charge transport in disordered ion-conducting materials is the random barrier model proposed by Dyre.20 Within the framework of this model, hopping conduction is the main underlying mechanism of electrical transport in these systems. Charge carriers move in a random spatially varying energy landscape. The transport process is governed by the ability of the charge carriers to overcome the randomly distributed barriers. The highest barrier that must be overcome to achieve infinite cluster of hopping sites determines the dc conductivity, σ0.21 The attempt rate to surmount this barrier is denoted by ωe. Solved within the continuous time random walk approximation,22 an analytical expression of the complex conductivity is obtained of the form: σ*(ω) = σ0[iωτe/ln(1 + iωτe)], where τe = (1/ωe). We have previously demonstrated for numerous ionic liquids that ωe ≅ ωc ≅ ωM,15 thus enabling the interpretation of ωc within the random barrier model. Typical fits of σ′ data using the random barrier model are shown in Fig. 1. One of the severe assumptions of the random barrier model—embodied in the treatment of charge carriers as non-interacting particles—makes its applicability, especially to highly concentrated systems such as ionic liquids, debatable. However, the fact that it quantitatively fits the dielectric/conductivity spectra of ionic liquids may be an indication that it captures the essential underlying physics, that is, the dominant role of Brownian dynamics on the ion conduction as described later in the current article. Indeed, more detailed models explicitly incorporating the contributions of ion-ion interactions to the conductivity spectra yield similar results as the random barrier model.23,24 It should be noted that the results presented herein as well as the interpretation offered do not depend on the afore-mentioned model.
Upon variation of temperature at constant pressure, both the thermal energy and molecular packing of the ions are altered thereby influencing the transport quantities such as σ0, ωc, diffusion coefficients, structural α-relaxation rates and viscosity. However, it is not possible to evaluate the relative impact of thermal fluctuations and density effects in such measurements. For this, hydrostatic pressure—a key thermodynamic variable in controlling inter-molecular distances—is additionally required. As demonstrated in Fig. 2, ωc follows a Vogel-Fulcher-Tammann (VFT) type of thermal activation. This can be described by: ωc(T) = ωHTexp[−B/T − T0], where ωHT, B, and T0 denote the characteristic rate in the high frequency limit, a constant, and Vogel temperature, respectively. For isothermal measurements at different pressures (see Fig. 2), ωc also follows a corresponding VFT-type dependence given as: ωc(p) = ωLPexp[−Cp/p0 −p], where ωLP refer to ωc at ambient pressure, and C, and P0 are constants.25 The VFT nature observed for ωc is obtained upon variation of pressure and temperature.
![The characteristic rate of charge transport ωc for the [HMIM][Cl] ionic liquid as determined from isothermal and isobaric dielectric measurements as indicated. Inset: The apparent activation volume corresponding to ωc as a function of pressure. The lines denote fits by the Vogel-Fulcher-Tammann equation for temperature and pressure described in the article.](/image/article/2012/RA/c2ra20560b/c2ra20560b-f2.gif) | ||
| Fig. 2 The characteristic rate of charge transport ωc for the [HMIM][Cl] ionic liquid as determined from isothermal and isobaric dielectric measurements as indicated. Inset: The apparent activation volume corresponding to ωc as a function of pressure. The lines denote fits by the Vogel-Fulcher-Tammann equation for temperature and pressure described in the article. | ||
Charge transport in ionic liquids is a rate process determined by successful jumps over the rate-limiting energy barriers. Eyring's transition state theory quantifies the rate ωc in the form ωc = (kT/h)exp[−ΔG*/RT], where k, h, ΔG*, and R refer to Boltzmann constant, Planck's constant, activation free energy, and gas constant, respectively.26 ΔG* can be expressed as ΔG* = ΔH* = pΔVc* with ΔH*(ΔV*c) being the enthalpy (volume) changes with respect to the activated state. The apparent activation volume ΔV*c is defined as a function of pressure for isothermally obtained ωc as ΔV*c = RT(dlnτc/dp)T, where τc = (1/ωc). It gives the difference between the volumes occupied by a molecule in activated (transition) and non-activated (in potential minimum) states.25 As shown in the inset of Fig. 2, ΔV*c of mobile ions in [HMIM] [Cl] increases with pressure non-monotonically indicating enhancement of the intermolecular interactions. The experimental link between the apparent activation energies and the mean ion jump lengths λh in the timescale of ωc for a series of ionic liquids was recently reported.27 The average volumes corresponding to these jump lengths can be estimated, assuming spherical geometries with λh as radii. At ambient pressure, the apparent activation volume of 30 cm3 mol−1 would imply a value of 0.23 nm for λh. This is in accord with the range of values of λh obtained experimentally for numerous ionic liquids (typically between about 0.2 nm and 0.3 nm) from combined BDS and pulsed field gradient NMR studies.27 This is a further confirmation of the physical relevance of the apparent activation volumes presented in the current work.
The dc conductivity, σ0, is a product of the mobility and the effective number density, n, of the charge carriers. Using Einstein and Einstein-Smoluchowski relations, σ0 for monovalent ionic liquids becomes: σ0 = nq2λ2hωc/6kT, where q denotes the elementary charge. A successful ion jump over the distance λh can be viewed as a virtual dipole.2 In this sense, the theory of dielectric relaxation proposed by Debye can be applied. The corresponding dielectric relaxation strength in this case is given by Δε = n(qλh)2/3ε0kT. In terms of the dc conductivity, this yields: 2σ0 = ε0Δεωc. This is a form of the empirical Barton-Nakajima-Namikawa (BNN) relation observed for a broad class of ion- and electron-conducting disordered materials.6,8,23 Whereas the fact that σ0∼ωc can be readily justified based on combined Einstein and Einstein-Smoluchowski approaches, a microscopic explanation of the origin of the observed identical thermal activation of the Δε for the different categories of amorphous materials has remained elusive for more than half a century. In Fig. 3, we present the BNN plot for a combination of isothermal and isobaric measurements. Upon increasing pressure to 600 MPa, the characteristic rate ωc decreases by 6 orders of magnitude at lower temperatures (see inset of Fig. 3). The BNN relation still holds in full accord with the data obtained for a wide variety of ionic liquids measured at 0.1 MPa. The coinciding BNN plots obtained by varying pressure and temperature are a proof of the universal scaling of charge transport in disordered materials. The physical origin of this striking result—embodied in the negligible temperature and pressure dependence of the term nλ2/T—is discussed below.
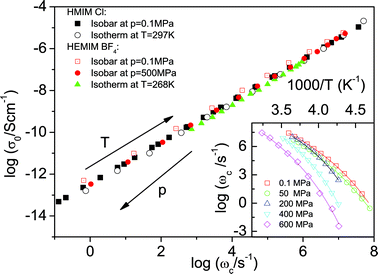 | ||
| Fig. 3 The dc conductivity, σ0, versus the characteristic rate, ωc, for two ionic liquids obtained from isobaric and isothermal dielectric measurements. Inset: The temperature dependence of ωc at different pressures as indicated. | ||
While investigating Brownian fluctuations, Langevin employed Newton's second law and the equipartition theorem to demonstrate that the mean-square displacement, 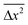 = RTτ/3πnηa, where n, τ, η, and a denote the number density of the particles, the characteristic time, viscosity, and the hydrodynamic radius, respectively.28,29 Using Maxwell's equation linking the viscosity, structural relaxation time, τα, and the instantaneous shear modulus, G∞, one obtains
= RTτ/3πnηa, where n, τ, η, and a denote the number density of the particles, the characteristic time, viscosity, and the hydrodynamic radius, respectively.28,29 Using Maxwell's equation linking the viscosity, structural relaxation time, τα, and the instantaneous shear modulus, G∞, one obtains 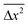 = RTτ/3πnG∞ταa.30 For ionic liquids, it is well established from experimental and theoretical studies that ωc = 1/τα. Therefore, Langevin's equation takes the form nλ2h/T = (R/3πG∞a) in the timescale of ωc. It is immediately evident why this term exhibits negligible temperature dependence. At the dynamic glass transition, G∞ for molecular glass-forming liquids is typically 109 Pa.27,30,31 This quantity is known to exhibit weak temperature dependence, only varying by a factor of 4 in the entire accessible temperature range of the dynamic glass transition. For [BMIM] [BF4] ionic liquid (molecular weight = 226; density = 1.17 g cm−3 at 298 K7), one obtains a value of (R/3πG∞a) ≅ 2 × 104m−1 K−1, assuming a hydrodynamic radius of 0.2 nm.9 This is comparable to the experimentally determined value of 3.98 × 104m−1 K−1. Thus, the universal scaling of charge transport in ionic liquids observed upon variation of composition, temperature, and hydrostatic pressure is traced back to Brownian dynamics persisting as long as the constituent ions possess thermal energy and the equipartition theorem remains valid. It is indeed astonishing that the universality of charge transport in ion-conducting amorphous materials—an empirical finding that has remained a mystery for over three decades since the pioneering studies of Barton, Nakajima and Namikawa8—is explained within the simple framework of Brownian motion for the case of glass-forming ionic liquids.
= RTτ/3πnG∞ταa.30 For ionic liquids, it is well established from experimental and theoretical studies that ωc = 1/τα. Therefore, Langevin's equation takes the form nλ2h/T = (R/3πG∞a) in the timescale of ωc. It is immediately evident why this term exhibits negligible temperature dependence. At the dynamic glass transition, G∞ for molecular glass-forming liquids is typically 109 Pa.27,30,31 This quantity is known to exhibit weak temperature dependence, only varying by a factor of 4 in the entire accessible temperature range of the dynamic glass transition. For [BMIM] [BF4] ionic liquid (molecular weight = 226; density = 1.17 g cm−3 at 298 K7), one obtains a value of (R/3πG∞a) ≅ 2 × 104m−1 K−1, assuming a hydrodynamic radius of 0.2 nm.9 This is comparable to the experimentally determined value of 3.98 × 104m−1 K−1. Thus, the universal scaling of charge transport in ionic liquids observed upon variation of composition, temperature, and hydrostatic pressure is traced back to Brownian dynamics persisting as long as the constituent ions possess thermal energy and the equipartition theorem remains valid. It is indeed astonishing that the universality of charge transport in ion-conducting amorphous materials—an empirical finding that has remained a mystery for over three decades since the pioneering studies of Barton, Nakajima and Namikawa8—is explained within the simple framework of Brownian motion for the case of glass-forming ionic liquids.
In conclusion, charge transport in glass-forming ionic liquids is investigated in wide frequency, temperature, and pressure ranges by means of Broadband Dielectric Spectroscopy. The dielectric spectra are dominated—on the low frequency side—by electrode polarization effects, while, for higher frequencies, charge transport in a disordered energy landscape is the underlying physical mechanism. It is demonstrated that the key quantities describing charge transport, namely—the dc conductivity and the characteristic diffusion rates—exhibit Vogel-Fulcher-Tammann type of temperature and pressure dependence. Using Einstein, Einstein-Smoluchowski, Maxwell and Langevin equations, the universality of charge transport in ionic liquids is traced back to the dominant role of Brownian dynamics in these systems. It would be interesting to check the extent to which the current description could be applicable to other classes of amorphous ion-conducting materials.
Acknowledgements
Financial support from the Deutsche Forschungsgemeinschaft under the DFG SPP 1191 Priority Program on Ionic Liquids and Polish State of Committee for Scientific Research (grant no. N N202 023440) are gratefully acknowledged.References
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- D. L. Sidebottom, Rev. Mod. Phys., 2009, 81, 999 CrossRef.
- J. R. Sangoro, G. Turky, M. Abdel Rehim, C. Iacob, S. Naumov, A. Ghoneim, J. Kaerger and F. Kremer, Macromolecules, 2009, 42, 1648–1651 CrossRef CAS.
- Y. Wang, A. L. Agapov, F. Fan, K. Hong, X. Yu, J. Mays and A. P. Sokolov, Phys. Rev. Lett., 2012, 108, 088303 CrossRef.
- G. J. Tudryn, W. Liu, S.-W. Wang and R. H. Colby, Macromolecules, 2011, 44, 3572–3582 CrossRef CAS.
- F. Kremer and A. Schoenhals, Broadband Dielectric Spectroscopy, Springer, Berlin, 2003 Search PubMed.
- J. Sangoro, C. Iacob, A. Serghei, S. Naumov, P. Galvosas, J. Kärger, C. Wespe, F. Bordusa, A. Stoppa, J. Hunger, R. Buchner and F. Kremer, J. Chem. Phys., 2008, 128, 214509 CrossRef CAS.
- H. Namikawa, J. Non-Cryst. Solids, 1975, 18, 173–195 CrossRef CAS.
- J. R. Sangoro, C. Iacob, A. Serghei, C. Friedrich and F. Kremer, Phys. Chem. Chem. Phys., 2009, 11, 913–916 RSC.
- J. R. Sangoro and F. Kremer, Acc Chem Res, 2012, 45, 525–532 CrossRef CAS.
- M. Paluch, R. Casalini and C. M. Roland, Phys. Rev. B: Condens. Matter, 2002, 66, 092202 CrossRef.
- C. M. Roland, Rep. Prog. Phys., 2005, 68, 1405 CrossRef CAS.
- J. R. Sangoro, A. Serghei, S. Naumov, P. Galvosas, J. Karger, C. Wespe, F. Bordusa and F. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051202 CrossRef CAS.
- A. Serghei, M. Tress, J. R. Sangoro and F. Kremer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184301–184305 CrossRef.
- C. Krause, J. R. Sangoro, C. Iacob and F. Kremer, J. Phys. Chem. B, 2010, 114, 382–386 CrossRef CAS.
- C. J. F. Böttcher, O. C. Belle, P. Bordewijk and A. Rip, Theory of electric polarization, Elsevier Academic Press, Amsterdam, 1973 Search PubMed.
- M. L. Jimenez, F. J. Arroyo, J. van Turnhout and A. V. Delgado, J. Colloid Interface Sci., 2002, 249, 327–335 CrossRef CAS.
- C. Schröder, J. Chem. Phys., 2011, 135, 024502 CrossRef.
- P. Griffin, A. L. Agapov, A. Kisliuk, X. G. Sun, S. Dai, V. N. Novikov and A. P. Sokolov, J. Chem. Phys., 2011, 135, 114509 CrossRef.
- J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468 CrossRef.
- H. Boettger and V. V. Bryksin, Hopping conduction in solids, Akademie-Verlag, Berlin, 1985 Search PubMed.
- H. Scher and M. Lax, Phys. Rev. B: Solid State, 1973, 7, 4491–4502 CrossRef CAS.
- J. C. Dyre and T. B. Schroder, Rev. Mod. Phys., 2000, 72, 873–892 CrossRef.
- W. F. Pasveer, P. A. Bobbert and M. A. J. Michels, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165209–165207 CrossRef.
- G. Floudas, M. Paluch, A. Grzybowski and K. L. Ngai, Molecular dynamics of glass-forming systems: Effects of pressure, Springer-Verlag, Berlin, 2011 Search PubMed.
- J. O. M. Bockris and A. K. N. Reddy, Modern Electrochemistry 1: Ionics, Plenum Press, New York, 1998 Search PubMed.
- J. R. Sangoro, C. Iacob, S. Naumov, R. Valiullin, H. Rexhausen, J. Hunger, R. Buchner, V. Strehmel, J. Karger and F. Kremer, Soft Matter, 2011, 7, 1678–1681 RSC.
- P. Langevin, C. R. Acad. Sci. (Paris), 1908, 146, 530–533 CAS.
- D. Lemons, Am. J. Phys., 1997, 65, 1079 CrossRef.
- J. C. Dyre, Reviews of Modern Physics, 2006, 78, 953–972 CrossRef CAS.
- J. R. Sangoro, C. Iacob, W. K. Kipnusu, M. Jasiurkowska, R. Valiullin, C. Friedrich, J. Karger and F. Kremer, Soft Matter, 2011, 7, 10565–10568 RSC.
| This journal is © The Royal Society of Chemistry 2012 |