Four-level levodopa adsorption on C60 fullerene for transdermal and oral administration: a computational study†
Nilton F.
Frazão
a,
Eudenilson L.
Albuquerque
b,
Umberto L.
Fulco
b,
David L.
Azevedo
c,
Glaydson L. F.
Mendonça
d,
Pedro
Lima-Neto
d,
Ewerton W. S.
Caetano
*e,
Josias V.
Santana
f and
Valder N.
Freire
f
aDepartamento de Física Teórica e Experimental, Universidade Federal do Rio Grande do Norte, 59072-970 Natal, Brazil
bDepartamento de Biofísica e Farmacologia, Universidade Federal do Rio Grande do Norte, 59072-970 Natal, Brazil
cDepartamento de Física, Centro de Ciências Exatas e Tecnologia, Universidade Federal do Maranhão, 65085-580 São Luís, Brazil
dDepartamento de Química Analítica e Físico-Química, Universidade Federal do Ceará, Campus do Pici, 60455-900 Fortaleza, Brazil
eInstituto Federal de Educação, Ciência e Tecnologia do Ceará, 60040-531, Fortaleza, Brazil. Fax: +55-85-33073711; Tel: +55-85-33073666E-mail: ewcaetano@gmail.com
fDepartamento de Física Universidade Federal do Ceará Centro de Ciências, Caixa Postal 6030 Campus do Pici, 60455-760 Fortaleza, Brazil
First published on 7th August 2012
Abstract
After more than fifty years, the administration of levodopa (LDOPA), a prodrug that crosses the blood-brain barrier and is metabolized to dopamine in the central nervous system, remains the most effective treatment for Parkinson’s disease, despite the manifestation of significant side effects. The development of carrier systems to increase the rate of LDOPA crossing the blood-brain barrier, to achieve stable therapeutic plasma levels and minimize side effects, has been a challenge. Innovative nanosystems for delivering LDOPA are being tested for improved Parkinson's disease therapy. In particular, buckminsterfullerene C60 is promising, due to its ability to penetrate through the skin and the gastrointestinal tract, as well as its biomedical applications to enhance drug delivery. Aiming to give theoretical support to attempts in developing levodopa preparations for transdermal and oral administration that may provide more continuous dopamine stimulation and fewer side effects, we present a computational study of levodopa adsorption on C60 fullerene in the 2–8 pH range. The LDOPA state with COO− and NH3+ protonated (LDOPAc) is investigated, with classical molecular dynamics (CMD) and density functional theory (DFT) simulations being undertaken to describe the LDOPAc adsorption onto C60 fullerene, LDOPAc@C60. Annealing calculations were performed to explore the space of molecular configurations of LDOPAc@C60 to obtain optimal geometries. From the DFT simulations, we found a four-level adsorption pattern, which is in agreement with the shell distribution of LDOPAc around C60 that we have obtained from our CMD simulations. Four van der Waals-like interaction potentials, characteristic of the LDOPAc@C60 adsorption levels were estimated, each one related to an –OH group, with energy minima varying from −0.35 eV to −0.73 eV, and centroid–centroid distances in the 6.5–8.8 Å range. Infrared absorption and Raman scattering spectra of the four adsorption configurations were evaluated, allowing us to determine vibrational signatures, which can be very useful in probing the existence of the four adsorption levels.
1 Introduction
Parkinson's disease (PD) is a progressive and chronic neurodegenerative disorder characterized by the loss of nigrostriatal dopaminergic neurons, which worsens over time.1 It is normally caused by insufficient formation and action of the neurotransmitter dopamine, C8H11NO2, but secondary causes may include toxicity, head trauma and medical disorders. The cardinal motor features of PD (tremor, rigidity, and bradykinesia) emerge when a significant proportion of substantia nigra dopamine neurons has been lost and striatal dopamine has been reduced by 60 to 80%.1–4 Since dopamine cannot cross the blood–brain barrier (BBB), the most effective treatment for PD remains the administration of the oral dopamine precursor levodopa (LDOPA, L-3,4-dihydroxyphenylalanine, C9H11NO4) since its introduction in the late 1960s. Levodopa is capable of BBB crossing and is converted into dopamine by the enzyme DOPA decarboxylase.In the current PD standard treatment, levodopa is administered combined with DOPA decarboxylase (such as cardidopa or benserazide) and catechol-O-methyltransferase (COMT) (such as entacapone and tolcapone) inhibitors.1,5 DOPA decarboxylase inhibitors prevent the breakdown of levodopa in the bloodstream, and also delay the conversion of levodopa into dopamine until it reaches the brain, reducing adverse side effects. The peripheral levodopa conversion to dopamine by the enzyme DOPA decarboxylase is responsible for the typical gastrointestinal (nausea, emesis) and cardiovascular (arrhythmia, hypotension) side effects. On the other hand, the inhibition of COMT leads to both an increase in the amount of levodopa in the central nervous system (CNS) and reduced formation of the peripheral metabolite 3-O-methyldopa, which is a competitive inhibitor of the active transport of levodopa through the intestinal mucosa and across the BBB. In multiple clinical trials, the addition of the COMT inhibitors entacapone and tolcapone to levodopa in fluctuating patients has been shown to improve clinical outcomes. As a matter of fact, a recent double-blind clinical trial in early PD patients found that carbidopa-25–levodopa-100–entacapone-200 improved PD signs and symptoms significantly more than carbidopa-25–levodopa-100 without an increase in the development of motor complications.1,5 Consequently, the development of a nanomedicine strategy to improve PD treatment should be based on an enhanced delivery of levodopa, DOPA decarboxylase (like cardidopa or benserazide) and catechol-O-methyltransferase–COMT (like entacapone and tolcapone) inhibitors.
In the case of fullerene C60-based nanomedicine, it is opportune to also consider joint delivery with vitamin C (ascorbic acid).6–8 As a matter of fact, the fullerene C60-ascorbic acid (AsA) complex protects cultured chromaffin cells against levodopa toxicity, thus suggesting the beneficial use of AsA-C60 in association with levodopa as an efficient treatment for Parkinson's disease.6 It is also believed that AsA-C60 should be more effective in preventing oxidative damage than C60 alone, both being potent antioxidants.7 Consequently, focus on a detailed picture of the AsA bonding to C60 is of fundamental importance for biological applications of AsA-functionalized C60. AsA adsorption on C60 was investigated using classical molecular mechanics and density functional theory (DFT).8 The results demonstrated the feasibility of noncovalent functionalization of C60 with AsA and provide minimal adsorption energy values (−0.10 to −0.54 eV) for the several different configurations investigated, which are related to the four –OH groups plus the two oxygen atoms in the AsA ring. It was suggested that the beneficial effects of administering AsA-C60 together with levodopa could be helpful against the neurotoxicity generated by isolated levodopa, allowing for new strategies to treat Parkinson's disease.8 Consequently, it is very opportune to study the adsorption of levodopa, carbidopa (or benserazide) and entacapone (or tolcapone) on C60 fullerene as well.
Levodopa has a short half-life (about 60 min), due to its rapid and extensive decarboxylation to dopamine and methylation to 3-O-methyldopa by dopa decarboxylase and catechol-O-methyltransferase;1 only about 1% of an orally administered levodopa dose enters the brain because of extensive first-pass metabolism and rapid plasma clearance.9 Unfortunately, after several years of levodopa treatment, its efficacy is diminished as a consequence of clinical response modifications, resulting from a complex interaction between the long-term effects of the drug and the disease itself.10 Several new levodopa formulations that may provide more continuous dopamine stimulation are being investigated. These include oral long-acting, once-daily pills, transdermal formulations, and continuous infusion.1,9 An innovative delivery strategy for Parkinson treatment is a skin patch, or transdermal therapeutic system, which offers considerable advantages over parenteral or oral administration of anti-Parkinson therapy.9 The patch could enhance plasma concentration, reduce gastrointestinal variations and avoid first-pass metabolism, simplifying the daily dosing schedule and ensuring a short plasma elimination half-life of the drug after patch removal. Furthermore, there are indications that patient compliance may be increased with a transdermal therapeutic system treatment.9 A large number of nanosystems (nanoparticles, carbon nanotubes, fullerenes, etc) can be potentially used as carriers for transdermal delivery because of their versatile properties, including good biocompatibility, selective targeted delivery and controlled release of carried drugs.11,12 The ability of fullerenes to penetrate through skin13 is widening their applications in cellular drug and gene delivery.14–18
Pursuing the reduction of levodopa side effects through C60 fullerene-based transdermal and gastrointestinal delivery, a theoretical investigation of levodopa adsorption on pristine C60 fullerene is addressed in this work. This procedure can be very helpful in designing an optimized levodopa formulation for transdermal and oral administration, minimizing side effects, enhancing central nervous system bioavailability, and achieving stable therapeutic plasma levels using C60 as a transporter enhancer due to its ability to penetrate through skin and the gastrointestinal tract.11–13,17 When focusing on transdermal and oral administration, it is necessary to take into account the fact that the levodopa-C60 fullerene (LDOPA@C60) adsorbate will be put in an environment with pH varying in the 2.0–8.0 range, which means that the levopoda molecule has its carboxyl and amine groups charged, COO− and NH3+, respectively. Here, we use molecular dynamics to find preliminary optimal geometrical configurations for the protonated LDOPA adsorption on C60. Afterwards, a second geometry optimization is performed within the DFT scope using the local density approximation (LDA) to obtain the interaction energy of the LDOPA@C60 adsorbate as a function of the distance between the centroids of protonated LDOPA and C60. Charge population analysis is employed to study the electron transfer between the protonated LDOPA and C60 molecules, assessing the noncovalent character of their interaction. Finally, the infrared and Raman spectra of the four smallest energy protonated LDOPA-C60 configurations were calculated to check for the existence of vibrational signatures of the non-covalent interactions, which can be valuable for comparison with experiment.
2 Computational details
In order to achieve transdermal or oral delivery of levodopa, it is important to understand the molecular state of levodopa in the skin, gastrointestinal tract, and blood. Measurements of pH changes in the gastrointestinal tract were carried out,19 showing that gastric pH was highly acidic (range 1.0–2.5). The average pH in the proximal small intestine was 6.6, while the mean pH in the terminal ileum was 7.5, rising progressively from the right to the left colon, reaching a final average value of 7.0. On the other hand, normal skin surface pH stays between 4 and 6.5 in healthy people, though it varies in different places.20 Finally, blood pH is regulated to stay within the narrow range 7.35–7.45, making blood slightly alkaline.21 Thus, to describe levodopa delivery through skin and the gastrointestinal tract, it is necessary to consider a pH variation in the 2–8 range. The levodopa protonated states in the 0–14 pH range at 300 K were predicted in this work using the MarvinSketch 5.4 software, and are depicted in Fig. 1.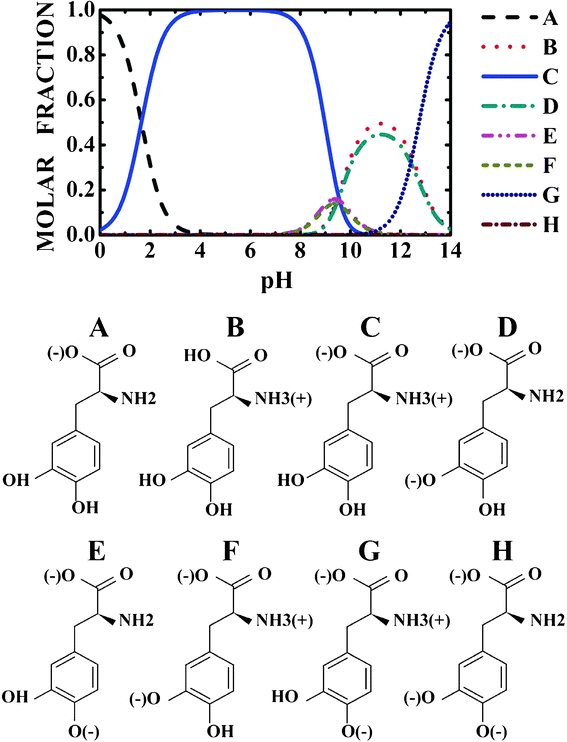 | ||
| Fig. 1 pH dependent population of the levodopa protonated states. | ||
Focusing the NH3+, COO− C-protonated LDOPA (LDOPAc from now on) adsorption on C60, we started by performing a geometry optimization using the Gaussian09 code,22 employing the hybrid B3LYP exchange–correlation functional (which mixes Hartree–Fock and DFT exchange energy terms) together with a 6-31G(d,p) basis set to expand the electronic states for isolated molecules of LDOPAc and C60. Convergence thresholds for geometry optimization were: maximum force smaller than 7.7 × 10−4 eV Å−1, self-consistent field energy variation smaller than 2.7 × 10−5 Å, and maximum atomic displacement smaller than 3.2 × 10−5 Å. The converged C60 and LDOPAc structures were used for the calculation of their infrared and Raman vibrational properties, which are discussed later in this work. A detailed account on how the infrared and Raman spectra are calculated within the DFT framework can be found in ref. 23.
To study the LDOPAc adsorption on C60, a set of about one hundred initial configurations was algorithmically generated from the previously converged structures for the isolated molecules. These configurations were obtained by randomly varying the LDOPAc orientation and its distance to the C60, and afterwards performing a classical annealing simulation using the Forcite Plus code. The Universal Force Field (UFF) was selected to perform about a hundred annealing cycles for each initial geometry. We have adopted the following control parameters for each annealing cycle: mid cycle temperature of 200 K, 50 heating ramps per cycle and 100 dynamic steps per ramp. After each cycle, the smallest energy configuration was optimized classically. The NVE ensemble and the Nosé thermostat were chosen to carry out the molecular dynamics with a time step of 1 fs.
The classically optimized geometries obtained from the annealing process were then optimized at the DFT level using the local density approximation (LDA) as implemented in the DMOL3 code.24,25 It is true that in systems with strong charge-transfer effects, the introduction of contributions from electron density derivatives in the exchange–correlation functional improves the accuracy,8 but this is not the case for the system we investigate here. It is a well known fact that pure DFT methods are unable to provide a good description of systems where noncovalent bonding, such as van der Waals forces, is involved.26–29 Besides, hydrogen bonds are not well characterized by the LDA approximation. Nevertheless, some reports using DFT calculations to investigate layered crystals such as graphite, anhydrous DNA bases and guanine hydrated crystals show that the local density approximation (LDA) is adequate to obtain intermolecular distances.30–33 Kee et al.,34 studying aromatic interactions in the binding of ligands in the active site of an enzyme, showed that the LDA functional agrees well with the more sophisticated MP2 method in comparison with generalized-gradient approximation (GGA) and hybrid functionals. After these results, and due to the relatively cheap computational cost of LDA simulations, we have chosen this functional instead of more advanced (and computationally expensive) levels of theory, to obtain the interaction energies and geometries of LDOPAc adsorbed on C60, following the LDA parametrization of Perdew and Wang.35 To study the interaction between LDOPAc and C60, we let the geometry of the isolated LDOPAc molecule relax to a total energy global minimum. Only the atoms of the LDOPAc molecule were allowed to move during the calculations, the atomic positions of C60 being held fixed. Also, in our DFT-LDA simulations, effective DFT semi-core pseudopotentials (DSPP) were used to describe the core electrons,36 and a double numerical plus polarization basis set (DNP) was adopted to expand the Kohn–Sham electronic eigenstates with an orbital cutoff radius of 3.7 Å.
We define the adsorption energy Eads of LDOPAc on C60 as
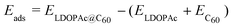 | (1) |
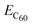 is the calculated total energy of the isolated buckminsterfullerene C60, ELDOPAc is the total energy of the isolated LDOPAc molecule, and
is the calculated total energy of the isolated buckminsterfullerene C60, ELDOPAc is the total energy of the isolated LDOPAc molecule, and 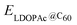 is the total energy of the LDOPAc@C60 complex.
is the total energy of the LDOPAc@C60 complex.
The adsorption energy as a function of the distance d between the C60 and ELDOPAc centroids was evaluated for each optimized LDOPAc@C60 configuration by rigidly moving the LDOPAc molecule along the axis formed by joining the LDOPAc and C60 centroids. Both classical UFF (Forcite plus Universal Force Field) and DFT-LDA (DMol3) calculated geometries were used to obtain Eads(d) for variations in d in the 6.0–11 Å range. However, for reasons of computational economy, the LDA adsorption energies of LDOPAc@C60 were calculated only when necessary.
A classical molecular dynamics simulation of a single C60 molecule interacting with 120 LDOPAc molecules inside a cubic box of side l = 44.386 Å with periodic boundary conditions was also carried out using the GROMACS 4 package37 at room temperature (300 K) and using the NVT ensemble. The OPLS-AA (all-atom) force field was used to calculate the total energy of this system.38 The initial geometry for this simulation was obtained after an equilibration time of 1000 ps using a time step of 0.0005 ps. The total energy of the system was minimized using a combination of steepest descent and conjugate gradient techniques. The production time was 1.0 ns and the non-bond pair-list was updated every 5 steps with both temperature and pressure being controlled using the V-rescale thermostat method.39 Long-range interactions were dealt with using the particle mesh Ewald (PME) with a cutoff distance of 1.2 nm. The summation technique was implemented to describe electrostatic interactions more accurately. A cutoff distance of 1.2 nm was used to take into account the van der Waals and non-bonding interactions.
To investigate the charge distribution of the adsorbate systems, Mulliken population analysis (MPA),40 Hirshfeld population analysis (HPA),41 and an electrostatic fitting of electric charges (ESP)42 were carried out. MPA is limited due to the arbitrary division of the overlap electron population. If the charge transfer is very small, Fukui function indices estimated through MPA are sometimes unpredictable.43 On the other hand, HPA tends to be more accurate, producing more realistic Fukui function indices,44,45 and with good prediction of reactivity trends within a molecule in comparison to MPA,40 natural bond orbital (NBO) analysis,46 and methods that use the molecular electrostatic potential.47 Lastly, HPA tries to minimize the loss of information due to the joining of atoms to form a molecule.48,49 For this reason, the discussion presented here will pay more attention to the charges obtained from the HPA approach, followed by MPA and ESP.
3 Results and discussion
3.1 Adsorption energies and structural changes
Looking at Fig. 1, one can observe that near to pH = 2.0, the protonated NH3+ and NH3+, COO− levodopa populations (see B and C states in Fig. 1) are about 30 and 70%, respectively. The population of the protonated levodopa state C increases remarkably when the pH is changed from 2 to 4, reaching 100% in the 4–8 pH range and decreasing sharply for pH >9. The LDOPAc optimized geometry is depicted in Fig. 2(a), which also shows the atomic labels adopted from now on. N5 and O2, O4 are the positively and negatively charged atoms, respectively, for the 2–8 pH range considered. Bond lengths, angles between bonds and torsion angles of the isolated LDOPAc are shown in Table 1–3. Fig. 2(b) shows the projection of the calculated electron density of LDOPAc onto an electrostatic potential isosurface. From it, one can see that the most negatively charged atoms are O2 and O4, followed by O1 and O3; the most positively charged atoms are the nitrogen N5 and the hydrogen atoms H18, H19 and H16; the ring and remaining carbon atoms are slightly positively charged. By the way, the C60 cage has negative charge, being distributed mainly along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, as can be observed in Fig. 2(c). The mean values for the single and double bond lengths between carbons for the converged C60 cage are 1.42157 Å and 1.42152 Å respectively, which are in good agreement with experimental values, since the weighted average of the two measured bond lengths and the difference between them are 1.439(2) Å and 0.057(6) Å respectively.50
C bonds, as can be observed in Fig. 2(c). The mean values for the single and double bond lengths between carbons for the converged C60 cage are 1.42157 Å and 1.42152 Å respectively, which are in good agreement with experimental values, since the weighted average of the two measured bond lengths and the difference between them are 1.439(2) Å and 0.057(6) Å respectively.50
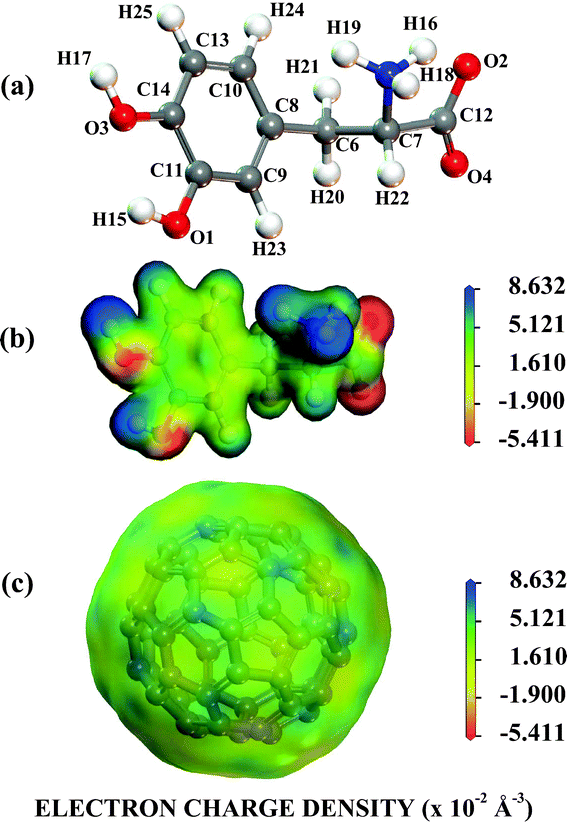 | ||
| Fig. 2 The NH3+,COO− protonated LDOPAc. (a) Its most stable isolated converged structure; (b) the electron density of its most stable isolated converged structure projected onto an electrostatic potential isosurface; (c) the electron density of the C60 most stable isolated converged structure projected onto an electrostatic potential isosurface. | ||
| BL | I | A | B | C | D |
|---|---|---|---|---|---|
| O1–C11 | 1.343 | 1.332 | 1.363 | 1.340 | 1.349 |
| O1–H15 | 0.982 | 0.990 | 0.995 | 0.981 | 0.983 |
| O2–C12 | 1.273 | 1.259 | 1.268 | 1.233 | 1.270 |
| O3–C14 | 1.361 | 1.361 | 1.339 | 1.354 | 1.364 |
| O3–H17 | 0.974 | 0.998 | 0.990 | 0.975 | 0.975 |
| O4–C12 | 1.226 | 1.234 | 1.235 | 1.260 | 1.235 |
| N5–C7 | 1.484 | 1.473 | 1.483 | 1.476 | 1.483 |
| N5–H16 | 1.048 | 1.048 | 1.049 | 1.049 | 1.046 |
| N5–H18 | 1.048 | 1.048 | 1.048 | 1.048 | 1.048 |
| N5–H19 | 1.046 | 1.046 | 1.047 | 1.046 | 1.048 |
| C6–C7 | 1.515 | 1.516 | 1.516 | 1.502 | 1.513 |
| C6–C8 | 1.488 | 1.486 | 1.486 | 1.483 | 1.493 |
| C6–H20 | 1.101 | 1.101 | 1.104 | 1.105 | 1.104 |
| C6–H21 | 1.105 | 1.105 | 1.106 | 1.117 | 1.104 |
| C7–C12 | 1.558 | 1.557 | 1.552 | 1.557 | 1.556 |
| C7–H22 | 1.099 | 1.101 | 1.099 | 1.105 | 1.103 |
| C8–C9 | 1.393 | 1.391 | 1.394 | 1.386 | 1.397 |
| C8–C10 | 1.393 | 1.393 | 1.398 | 1.399 | 1.393 |
| C9–C11 | 1.380 | 1.384 | 1.378 | 1.380 | 1.386 |
| C9–H23 | 1.095 | 1.094 | 1.096 | 1.092 | 1.096 |
| C10–C13 | 1.394 | 1.393 | 1.389 | 1.381 | 1.388 |
| C10–H24 | 1.096 | 1.096 | 1.098 | 1.095 | 1.096 |
| C11–C14 | 1.401 | 1.403 | 1.403 | 1.402 | 1.394 |
| C13–C14 | 1.376 | 1.380 | 1.385 | 1.381 | 1.380 |
| C13–H25 | 1.095 | 1.093 | 1.093 | 1.095 | 1.096 |
| Angles | I | A | B | C | D |
|---|---|---|---|---|---|
| O1–C11–C9 | 121.179 | 121.814 | 124.168 | 121.194 | 121.238 |
| O1–C11–C14 | 119.074 | 118.243 | 114.904 | 119.241 | 119.402 |
| O2–C12–O4 | 132.174 | 131.521 | 131.511 | 131.777 | 131.201 |
| O2–C12–C7 | 111.025 | 112.746 | 112.212 | 115.560 | 111.992 |
| O3–C14–C11 | 113.896 | 114.828 | 118.376 | 114.176 | 114.204 |
| O3–C14–C13 | 125.693 | 124.876 | 122.048 | 125.255 | 125.375 |
| O4–C12–C7 | 116.746 | 115.637 | 116.226 | 112.648 | 116.800 |
| N5–C7–C6 | 110.063 | 110.861 | 110.256 | 112.503 | 113.196 |
| N5–C7–C12 | 103.423 | 103.418 | 103.053 | 103.599 | 101.927 |
| C6–C7–C12 | 109.931 | 108.201 | 109.710 | 111.257 | 112.784 |
| C6–C8–C9 | 120.736 | 120.034 | 120.941 | 120.564 | 120.206 |
| C6–C8–C10 | 120.059 | 120.352 | 120.477 | 119.855 | 120.580 |
| C7–C6–C8 | 111.831 | 112.833 | 112.173 | 112.918 | 111.907 |
| C8–C9–C11 | 120.552 | 120.045 | 120.116 | 120.338 | 120.699 |
| C8–C10–C13 | 120.782 | 120.652 | 121.711 | 120.648 | 120.205 |
| C9–C8–C10 | 118.996 | 119.576 | 118.489 | 119.495 | 119.158 |
| C9–C11–C14 | 119.781 | 119.940 | 120.918 | 119.565 | 119.353 |
| C10–C13–C14 | 119.447 | 119.463 | 119.157 | 119.383 | 120.145 |
| C11–C14–C13 | 120.436 | 120.280 | 119.519 | 120.569 | 120.421 |
| TANG | I | A | B | C | D |
|---|---|---|---|---|---|
| H15–O1–C11–C9 | −54.0428 | −59.87644 | −54.5181 | −172.17287 | 45.60817 |
| H16–O3–C14–C11 | −76.88765 | −85.44804 | −84.28261 | −126.09012 | −101.72035 |
| C6–C7–N5–H19 | −8.61134 | −13.44439 | −9.86245 | 177.9497 | 10.23416 |
| N5–C7–C6–C8 | 175.75 | 179.80728 | 178.38873 | −177.09884 | 178.7859 |
| C7–C6–C8–C9 | −175.52757 | −178.10566 | −175.75967 | 177.16404 | −178.7166 |
| N5–C7–C12–O2 | 179.22864 | 178.14857 | 175.30374 | −179.81239 | 178.51554 |
| C6–C8–C9–C11 | 0.14981 | −0.965 | −1.77518 | −0.25938 | 0.39255 |
| C6–C8–C10–C13 | 0.15907 | −0.87557 | 0.86271 | −0.03188 | 0.20923 |
| C8–C9–C11–O1 | −179.77116 | −177.83328 | −177.04432 | −179.92145 | −179.16274 |
The variation of the adsorption energy with the distance between the centroids of LDOPAc and C60 after the annealing calculations for about a hundred random initial geometries is depicted in Fig. 3(a). One can identify four clusters of adsorption configurations: the first one for d in the 7.0–7.7 Å range; the second one for d in the 7.7–8.3 Å range; the third one for d in the 8.3–9.0 Å range; and the fourth cluster for d in the 9.0–10.5 Å range. These clusters can be associated with four different sets of similar conformations of the LDOPAc adsorption on C60, corresponding to four possible adsorption levels of this system. LDOPAc molecules can take advantage of the C60 spherical symmetry originating different adsorption “orbits” for LDOPAc@C60.
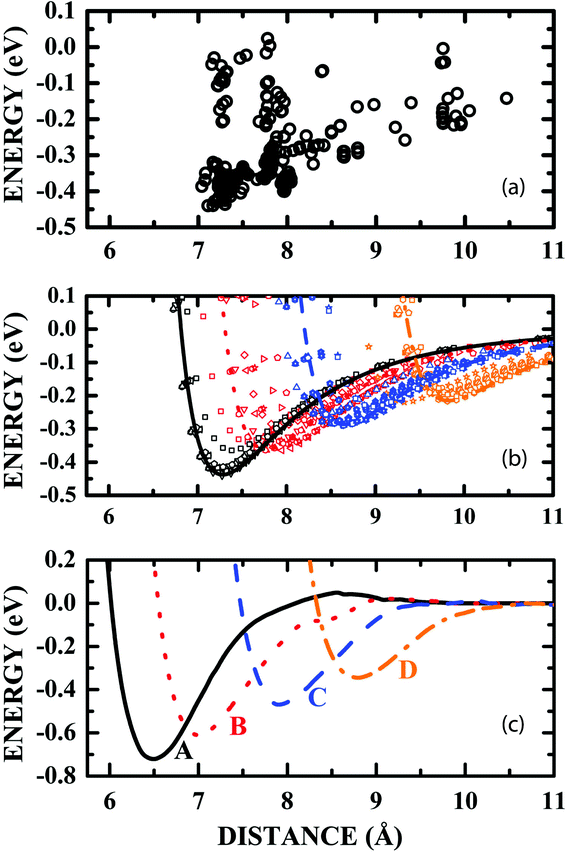 | ||
| Fig. 3 (a) Classical adsorption energies as a function of the distance between the LDOPAc and C60 centroids obtained after the annealing of a hundred initial LDOPAc@C60 spatial configurations; (b) van der Waals-like adsorption potentials obtained classically after the annealing of some of the initial LDOPAc@C60 spatial configurations, i.e. those with smaller adsorption energies at each level; (c) DFT-LDA calculated van der Waals-like adsorption potentials for the A–D configurations of the LDOPAc adsorbed on @C60. They were calculated using as inputs the configurations with the smallest energy at each level obtained classically after the annealing of some of the initial LDOPAc@C60 spatial configurations. | ||
A more detailed description of the adsorption energy as a function of d for some annealed LDOPAc@C60 geometries is shown in Fig. 3(b). In it, the LDOPAc configurations with the smallest adsorption energy for each cluster were selected and displaced rigidly along the centroid–centroid line. The adsorption energy profiles obtained in this way look like classical van der Waals potential energy curves, and are represented by symbols and lines, the latter being associated with the smallest calculated adsorption energies at each adsorption cluster and whose minima can be interpreted as revealing the distance between the centroids corresponding to the respective “adsorption orbit” radius. The classically calculated energies of the four LDOPAc@C60 adsorption orbits are −0.44 eV, −0.37 eV, −0.29 eV and −0.22 eV; the classical radii of the orbits are 7.3 Å, 7.8 Å, 8.7 Å and 9.8 Å, respectively.
An improved description of the four LDOPAc@C60 adsorption configurations is obtained using the quantum DFT-LDA description. Using DFT-LDA, we observe that the adsorption energies increase in comparison with the classical values, and the adsorption energy minimum is shifted to smaller centroid–centroid distances (see Fig. 3(c)). As a matter of fact, the DFT-LDA calculated energies of the four distinct optimized LDOPAc@C60 adsorbates are −0.72 eV, −0.60 eV, −0.46 eV and −0.34 eV; the DFT-LDA calculated centroid–centroid distances corresponding to these geometries are 6.6 Å, 7.0 Å, 7.9 Å and 8.8 Å, in that order. To simplify the description of the results, we will label these four LDOPAc@C60 adsorption geometries as A, B, C and D, in decreasing order of binding energy (defined here as the negative of the adsorption energy), as shown in Fig. 3(c).
We can compare the results for LDOPAc with similar data for the absorption of ascorbic acid (AsA) and ibuprofen on C60, the latter also exhibiting distinct adsorption configurations with adsorption energies in the range −0.65–−0.29 eV and centroid–centroid distances in the 6.3–9.0 Å range.18 For AsA@C60, the optimal adsorption geometry corresponds to an adsorption energy of −0.54 eV and a centroid–centroid distance of about 6.7 Å.8 For a temperature of 300 K, kBT ≈ 26 meV, suggesting that even at room temperature, the lowest energy adsorption configurations of AsA@C60, ibuprofen@C60 and LDOPAc@C60 would be stable. On the other hand, one could consider the possibility of LDOPA to compete with the adsorption of other molecules (proteins, for example) at the C60 surface, displacing LDOPA and weakening or even annulling its adsorption. This possibility is very plausible, and indeed it can be applied to all delivery systems based on molecular adsorption. In the case of other drugs, LDOPA will be definitively displaced if its interaction energy with C60 is equal to or higher than 0.7 eV, which means a covalent or very strong ionic interaction. In the case of proteins, by supposing that:
(a) the binding pocket energy of a general ligand–protein system must be at least of the order of kBT at ambient conditions (e.g. 0.0256 eV),
(b) the adsorption energy of a ligand on the surface of a general protein is smaller than its interaction in the binding pocket,
one can estimate that the quantum adsorption energies for the LDOPA@C60 are about ten times stronger (the weakest C configuration adsorption energy minimum is −0.35 eV). These values strongly suggest that the possibility of LDOPA being displaced from C60 by proteins is very small, which assures us that the four-level levodopa adsorption on C60 fullerene for transdermal and oral administration is a real possibility.
The DFT-LDA calculated A–D configurations of the LDOPAc adsorbed on C60 are displayed in Fig. 4. For the A and B configurations, which are the most stable, one can note that the carbon rings are practically parallel to the C60 surface, showing the important role played by π-stacking interactions in the adsorption mechanism. The most striking difference between the A and B configurations is the positioning of the NH3+ group, which faces the C60 surface in A but not in B. It seems that the charged NH3+ group interacts electrostatically with the C60 surface, improving the binding strength of A LDOPAc@C60 in comparison with the B configuration. DFT-LDA calculated adsorption energies were −0.72 eV and −0.60 eV for A and B, respectively. In the case of the adsorption geometries C and D, with weaker binding, the carbon rings are not parallel to the C60 surface. For the D geometry, one can see that the carbon ring is far away from the fullerene, with the NH3+, COO− groups closer to the C60, while the C adsorption configuration shows both the NH3+ and the carbon ring closer to the C60 and the COO− group moved away. As a matter of fact, the larger distance of the COO− group from the fullerene surface, together with the proximity of the carbon ring, explains why the binding of the C configuration of LDOPAc@C60 is stronger than for the D configuration, with DFT-LDA calculated adsorption energies of −0.46 eV and −0.34 eV for C and D, respectively.
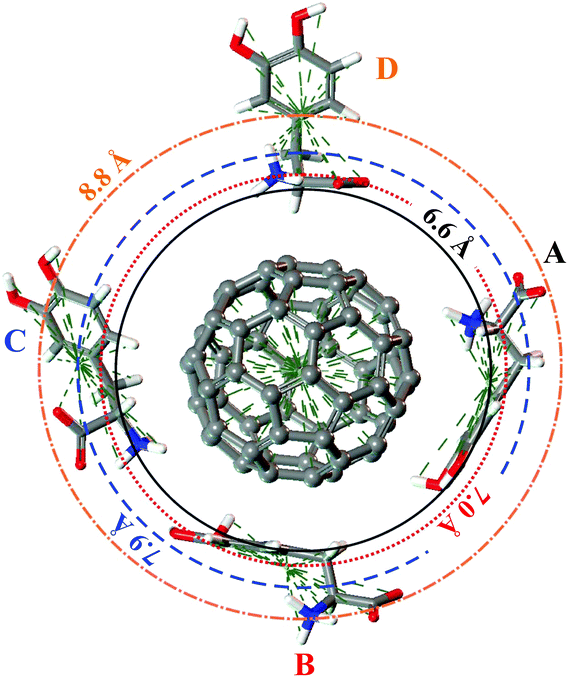 | ||
| Fig. 4 A, B, C and D configurations of the four levels adsorption of LDOPAc on C60. The DFT-LDA calculated “orbits” are represented by circles of radii 6.6 Å (solid), 7.0 Å (dotted), 7.9 Å (dashed) and 8.8 Å (dotted dashed). | ||
Information about the effect of the interaction with the C60 on the LDOPAc molecular structure is obtained by comparing the bond lengths, angles between bonds, and torsion angles of isolated and A–D LDOPAc@C60. While differences in bond length are in general small for most bonds when comparing the adsorbed species of LDOPAc and the LDOPAc in a vacuum, statistical analysis shows that the adsorption process tends to increase the bond lengths of A, B, and D LDOPAc@C60 by about 0.06%, 0.16%, and 0.08%, respectively, while the C geometry exhibits bond lengths smaller by about 0.07% in comparison with the isolated molecule. One can see in Table 1 that the most pronounced decrease in bond length occurs for the O2–C12 bond (about 3.1% for the C adsorbate), while the largest bond length increase is observed for the O3–H17 bond length, about 2.5% for the A adsorption geometry.
On the other hand, statistical analysis of Table 2, which shows the angles between bonds in LDOPAc@C60, reveals that the A and B adsorption geometries do not change significantly in comparison with the isolated LDOPAc molecule, with bond–bond angles smaller by 0.03 degrees on average for the A configuration and larger by 0.01 degrees for the B case (standard deviations of 0.85 degrees and 1.9 degrees, respectively). For the C and D geometries, in contrast, the average bond–bond angle is 0.25 degrees and 0.26 degrees larger, in comparison with the isolated LDOPAc structure, with standard deviations of 1.6 degrees and 1.1 degrees, respectively. The C adsorbate has the largest variation, an increase of about 4.5 degrees, for the O2–C12–C7 angle, being followed closely by the O3–C14–C11 angle for the B adsorption case. The most pronounced bond–bond angle decrease occurs for the B adsorbate involving the O1–C11–C14 chain, of about 4.2 degrees.
Finally, Table 3 reveals the torsion angles involving groups of three adjacent bonds. The A and B adsorption geometries display a small average decrease in the torsion angle, of about 2.1 degrees for A and 1.0 degrees for the B case. The C adsorbate, in comparison, is much more distorted, with large torsion angle variations for practically all torsion angles, except for C6–C8–C10–C13 and C8–C9–C11–O1, which involve three atoms of the carbon ring. For the D adsorbate, the torsion angle variation is larger for the H15–O1–C11–C9 (100 degrees), C6–C7–N5–H19 (19 degrees), and H17–O3–C14–C11 (−25 degrees) torsion angles.
3.2 Charge population analysis
Table 4 presents the calculated electric charges of selected regions of the LDOPAc molecule when isolated and adsorbed on C60. In order to perform the charge population analysis, we divided the LDOPAc molecule into six regions: the COO− group; the NH3+ group; the propionic region (PP), C6–H2–C7H; the first hydroxyl group (HD1), connected to the C11 carbon, O1–H15; the second hydroxyl group (HD2), connected to the C14 carbon, O3–H17; and the phenyl ring (PH). For the isolated LDOPAc, the COO− group has an HPA charge of −0.5, while the MPA and ESP charges are slightly more negative, close to −0.6. The NH3+ group, on the other hand, has an HPA charge of +0.353 and MPA charge of +0.478, with the ESP charge between the HPA and MPA values, at about +0.42. The propionic region has a small negative charge of about −0.051 (HPA), while the HD1 group has a negative charge of −0.017 (HPA) (−0.08 for the MPA and ESP, approximately). The second hydroxyl group, on the other hand, has a positive HPA charge of +0.026, but the MPA and ESP values are negative (−0.187 and −0.133, respectively). Finally, the phenyl ring is positively charged with an HPA charge of +0.043 and MPA and ESP charges of 0.373 and 0.302, in this order. All in all, the ESP and MPA values have a better correlation in comparison with the HPA-ESP and HPA-MPA combinations in the case of isolated LDOPAc.| Group | I | A | B | C | D |
|---|---|---|---|---|---|
| HPA COO− | −0.521 | −0.444 | −0.473 | −0.429 | −0.468 |
| MPA COO− | −0.572 | −0.493 | −0.520 | −0.476 | −0.521 |
| ESP COO− | −0.585 | −0.491 | −0.577 | −0.526 | −0.678 |
| HPA NH3+ | 0.353 | 0.285 | 0.372 | 0.318 | 0.334 |
| MPA NH3+ | 0.478 | 0.486 | 0.496 | 0.489 | 0.492 |
| ESP NH3+ | 0.419 | 0.278 | 0.414 | 0.288 | 0.365 |
| HPA PP | −0.051 | −0.039 | 0.004 | −0.004 | −0.067 |
| MPA PP | −0.068 | 0.024 | 0.009 | 0.004 | 0.008 |
| ESP PP | −0.086 | −0.274 | 0.141 | −0.102 | −0.283 |
| HPA HD1 | −0.017 | −0.027 | −0.025 | −0.010 | −0.022 |
| MPA HD1 | −0.082 | −0.112 | −0.185 | −0.082 | −0.089 |
| ESP HD1 | −0.082 | −0.112 | −0.185 | −0.082 | −0.089 |
| HPA HD2 | 0.026 | −0.039 | −0.024 | 0.030 | 0.024 |
| MPA HD2 | −0.187 | −0.194 | −0.116 | −0.181 | −0.187 |
| ESP HD2 | −0.133 | −0.234 | −0.114 | −0.121 | −0.129 |
| HPA PH | 0.043 | 0.070 | 0.046 | 0.064 | 0.048 |
| MPA PH | 0.373 | 0.429 | 0.387 | 0.488 | 0.376 |
| ESP PH | 0.302 | 0.400 | −0.036 | 0.126 | 0.268 |
When the LDOPAc assumes the A adsorption geometry interacting with C60, the COO− and NH3+ groups become less charged than for the isolated LDOPAc. The HPA charge for COO− changes to −0.444 and the NH3+ charge decreases to +0.285. HPA charges for the PP, HD1, HD2, and PH regions change by a very small amount, with the largest variation observed for the HD2 group, from +0.026 in the isolated LDOPAc case, down to −0.039. For the B adsorbate, the COO− HPA charge is −0.473 and the NH3+ HPA charge is +0.372. So the B LDOPAc charge distribution is closer to the values calculated for isolated LDOPAc in comparison with the A adsorption configuration. It is interesting to note, however, that the ESP charge for the PH region is very different between the isolated and B cases, with the B geometry having a PH ESP charge of −0.036, while the isolated LDOPAc has a PH ESP charge of +0.302. This difference does not occur with the A geometry, where the ESP charge of the PH region is +0.4.
Looking now to the C adsorbate, the COO− and NH3+ HPA charges are −0.429 and +0.318, so these groups are less electrically charged than the isolated LDOPAc. The other regions have HPA charges very close to the isolated molecule values, the largest difference occurring for the ESP charge of the phenyl ring, +0.126 for the C LDOPAc@C60 and +0.302 for LDOPAc. Finally, D LDOPAc@C60, which very much resembles LDOPAc, has very similar values for all HPA charges, except for the COO− region (−0.468, in comparison with −0.585 for LDOPAc). For the ESP charges, the most significant change in contrast with LDOPAc occurs at the PP region (−0.283 versus −0.086 in LDOPAc). All in all, there is a good correlation between the charge trends observed for all the population analysis methods we have employed. For the HPA population analysis, the most striking differences between the four adsorption geometries studied occur for the B adsorbate at regions HD1 and HD2, and for the C adsorbate at the phenyl ring and the COO− group. The charge of the NH3+ region is less affected by adsorption onto C60. The largest positive net charge change due to the interaction with C60 occurs for the C adsorbate (charge increase of +0.136, probably related to the positioning of its oxygen atoms, all moved away from the C60 surface), being followed by B (+0.067), and D (+0.016). A LDOPAc@C60, on the other hand, becomes more negative (by −0.027) in comparison with LDOPAc (and has its oxygen atoms nearer to the C60, especially those belonging to the OH groups, when compared with B, C, and D). Fig. 5 shows equivalent electrostatic potential isosurfaces for each adsorbate with the electron density projected onto them. For the A and B adsorbates, the LDOPAc potential isosurface merges with the C60 corresponding isosurface through the HD2 region, indicating that HD2 is the main binding site of LDOPAc to C60 for both configurations.
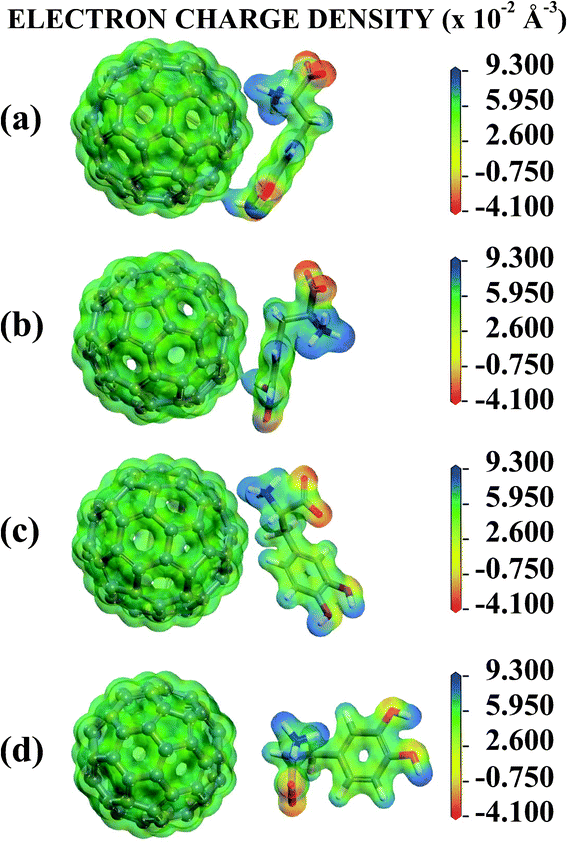 | ||
| Fig. 5 Electronic potential isosurface with projected electron charge density surfaces for the (a) A, (b) B, (c) C and (d) D configurations of the four levels of adsorption of LDOPAc on C60. | ||
3.3 Classical molecular dynamics
Fig. 6 shows the pair correlation function g(r) of LDOPAc in the case of a single C60 fullerene embedded in a unit cell with 100 LDOPAc molecules, obtained from classical molecular dynamics simulations at 300 K, as described in the computational details section. From it, we can see the formation of at least three LDOPAc solvation shells, the first at about 6 Å, the second at about 11 Å and the last shell near 15 Å. Fig. 6 also indicates, through colored arrows, the distances corresponding to the total energy minima of the A (black), B (red), C (blue), and D (orange) adsorption levels found in our computations. The A adsorbate is at the first solvation shell, while B is in the inner part and C is in the outer part of the second shell. The D configuration, on the other hand, can be found in the inner part of the third solvation layer. Looking to Fig. 7, which reveals a snapshot of the molecular dynamics, one can see some LDOPAc molecules, and it is easy to note that many molecules assume geometries very similar to the four optimized adsorption levels we have found, reinforcing that the information we have gathered through classical and quantum simulations can be useful to understand the LDOPAc@C60 system even under more realistic circumstances, where many molecules and thermal motion are present.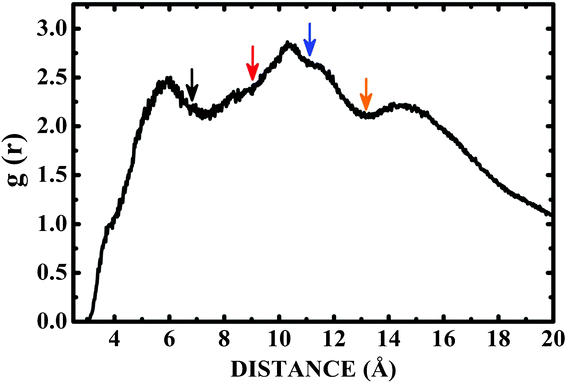 | ||
| Fig. 6 Pair correlation function g(r) for C60 immersed in a box with one hundred LDOPAc molecules obtained through molecular dynamics simulation at room temperature. The colored arrows point to the distances corresponding to the total energy minima of the A (black), B (red), C (blue), and D (orange) adsorption levels found in our computations. | ||
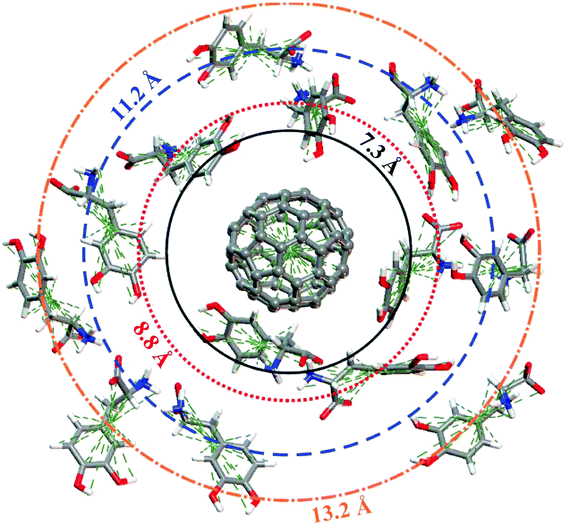 | ||
| Fig. 7 Snapshot of the molecular dynamics simulation at room temperature showing a single C60 surrounded by several LDOPAc molecules. The “orbit” radius corresponds to the structures indicated by arrows in Fig. 6. | ||
3.4 Infrared spectra
To the knowledge of the authors, there are no reports in the literature describing the results of DFT simulations to obtain the infrared and Raman spectra of isolated levodopa molecules. In Fig. 8 and 9 we present the calculated infrared and Raman spectra for the isolated (I) LDOPAc and for the four types of adsorption geometry (A, B, C, and D) of LDOPAc on C60. Isolated levodopa has 69 normal modes, while the adsorbates have 249 normal modes (see ESI†). Looking at the top of Fig. 8, one can see the infrared spectra of these systems in the wavenumber range 0–1000 cm−1. For I LDOPAc, the most important features and assignments of the infrared absorption spectra are presented in the first and second columns of Table 5. For the A and C adsorbates, the infrared absorption peak at 275 cm−1 is shifted to lower frequencies, to 249 cm−1 (−26 cm−1 in comparison with I LDOPAc) and 252 cm−1 (−23 cm−1 relative to I LDOPAc), while for the B and D configurations, the corresponding frequencies are much closer to that observed for the I case. The I peak at 341 cm−1 is shifted for the B adsorbate to 367 cm−1 (+26 cm−1), and to 359 (+18 cm−1) and 353 cm−1 (+12 cm−1) for the C and D configurations, while the I peak at 499 cm−1 changes by −22 cm−1 and −19 cm−1 for the C and A adsorbates, respectively. Finally, the peaks between 780–1000 cm−1 for the isolated LDOPAc structure are well preserved in the infrared absorption spectra of the A and D adsorbates, but change significantly for the B and C adsorption geometries, with the 874 cm−1 peak of I LDOPAc being shifted by 24 (C) and 31 (D) cm−1. The infrared absorption peaks related to the C60 (corresponding frequencies indicated by dashed vertical lines), on the other hand, do not exhibit remarkable changes, with the C60T1u modes at 539 cm−1 and 589 cm−1 (theoretical values, calculated using the same exchange–correlation functional and basis set adopted for the LDOPAc adsorbates) giving rise to absorption bands shifted up and down, respectively, by about 2–7 cm−1 and 5–15 cm−1.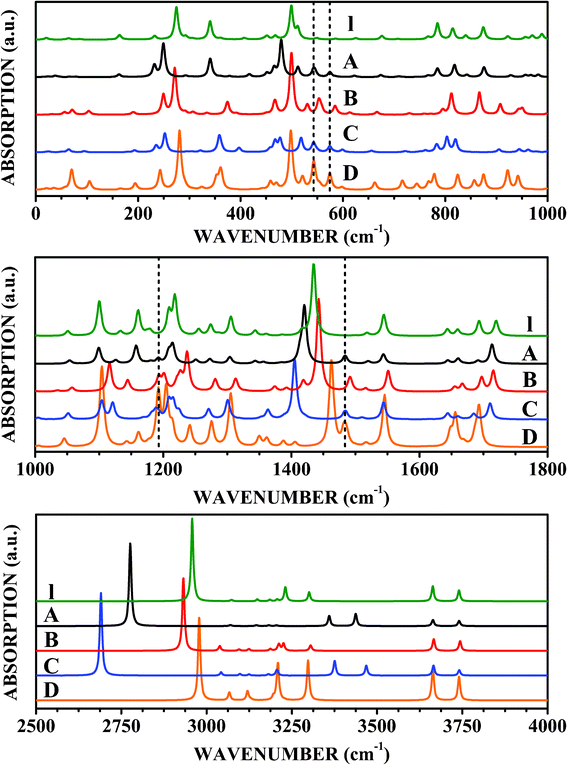 | ||
| Fig. 8 Infrared spectra of LDOPAc I, LDOPAc@C60 A, LDOPAc@C60 B, LDOPAc@C60 C, and LDOPAc@C60 D. | ||
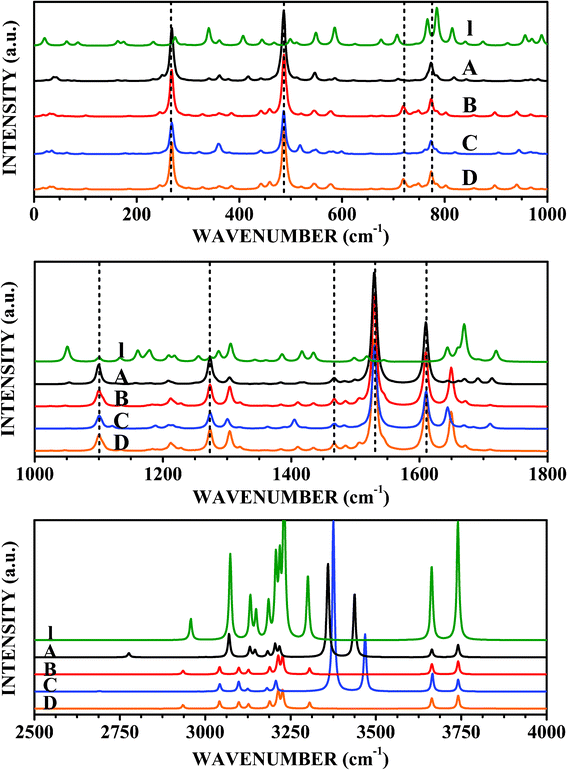 | ||
| Fig. 9 Raman spectra of LDOPAc I, LDOPAc@C60 A, LDOPAc@C60 B, LDOPAc@C60 C, and LDOPAc@C60 D. | ||
| Assignment | I | C60 | A | B | C | D |
|---|---|---|---|---|---|---|
| O3–H17 bending | 275 | 249 | 266 | 252 | 281 | |
| N–C7–C12 deformation | 341 | 341 | 367 | 359 | 353 | |
| O1–H15 bending | 499 | 480 | 491 | 477 | 498 | |
| Phenyl ring in-plane deformation | 512 | 512 | 521 | 518 | 521 | |
| C60T1u | 539 | 542–546 | 542–546 | 541–546 | 542–546 | |
| C60T1u | 589 | 574–575 | 580–584 | 580–584 | 574–575 | |
| Phenyl ring in-plane deformation, COO− scissors, C14–O3 stretching | 785 | 785 | 785 | 783 | 779 | |
| CH phenyl out-of-plane bending, C7–N5 stretching, C6–H2 twisting | 815 | 818 | 802 | 820 | 824 | |
| N5–C7–C12 asymmetric stretching | 874 | 876 | 898 | 905 | 875 | |
| Phenyl in-plane deformation, O3–H17, N5–H3 bending, C6–H2 twisting | 1100 | 1099 | 1106 | 1104 | 1104 | |
| C6–H2 twisting, N5–H3, C7–H22 bending | 1161 | 1158 | 1135 | 1121 | 1161 | |
| O1–H15, C9–H23, C10–H24 bending | 1209 | 1208 | 1209 | 1207 | 1205 | |
| C60T1u | 1215 | 1192–1193 | 1192–1193 | 1192–1193 | 1192–1193 | |
| C7–C12–O2 asymmetric stretching | 1218 | 1215 | 1228 | 1209 | 1205 | |
| C14–O3, C11–O1, C6–C8 stretching, C13–H25 bending | 1306 | 1304 | 1304 | 1301 | 1305 | |
| N5–H3 bending, C12–O4 stretching | 1435 | 1420 | 1435 | 1405 | 1462 | |
| C60T1u | 1460 | 1483–1485 | 1483–1485 | 1482–1486 | 1481–1487 | |
| O3–C14–C11–O1, C6–C8 stretching, C13–H25, C9–H23, C10–H24 bending | 1544 | 1544 | 1545 | 1544 | 1546 | |
| N5–H3 asymmetric bending, COO− asymmetric stretching | 1693 | 1691 | 1692 | 1685 | 1687 | |
| N5–H3 asymmetric bending, COO− asymmetric stretching | 1720 | 1713 | 1711 | 1710 | 1693 | |
| N5–H16 stretching | 2958 | 2776 | 2935 | 2690 | 2978 | |
| H18–N5–H19 symmetric stretching, H18–N5–H16 asymmetric stretching | 3231 | 3360 | 3227 | 3376 | 3209 | |
| H18–N5–H19 asymmetric stretching | 3301 | 3437 | 3306 | 3468 | 3298 | |
| O1–H15 stretching | 3663 | 3664 | 3664 | 3665 | 3664 | |
| O3–H17 stretching | 3740 | 3741 | 3741 | 3741 | 3740 |
Infrared absorption in the 1000–1800 cm−1 wavenumber range is displayed in the middle part of Fig. 8. The A adsorbate has an infrared absorption spectrum very similar to the I LDOPAc, except that the I peak at 1435 cm−1 is shifted down to 1420 cm−1. Small infrared absorption bands in the 1192–1193 cm−1 and 1483–1485 cm−1 ranges are reminiscent of the isolated C60T1u normal modes at 1215 cm−1 and 1460 cm−1, with wavenumber shifts of about −22 cm−1 and +23 cm−1, respectively. In comparison, the main differences between the B and isolated LDOPAc configurations occur for the I normal modes at 1161 cm−1 (B: 1135 cm−1), and 1218 cm−1 (B: 1228 cm−1). The C60 infrared absorption band between 1192 and 1193 cm−1 is more intense than that observed for the A adsorption geometry. For the C adsorbate, on the other hand, the most striking differences with respect to the isolated molecule of LDOPAc and the other adsorption geometries are shifts of −40, −30, and −10 cm−1 of the I peaks at 1161, 1435, and 1720 cm−1. Finally, the D LDOPAc@C60 has infrared vibrational signatures at 1205, 1462, and 1693 cm−1 (−13, +27, and −27 cm−1 relative to the equivalent modes for I LDOPAc).
Looking now at the infrared spectrum between 2500 and 4000 cm−1 (bottom part of Fig. 8), we identify a set of five remarkable absorption peaks for I LDOPAc at 2958, 3231, 3301, 3663, and 3740 cm−1. While the last two infrared absorption peaks do not change significantly for the LDOPAc adsorbed on C60, the first three peaks are significantly shifted for most adsorption geometries (see more on these large shifts in the discussion of the Raman spectra). The 2958 cm−1 I absorption band decreases its wavenumber to 2776 cm−1 (−182 cm−1) for the A adsorbate, while the I LDOPAc absorption bands at 3231 and 3301 cm−1 are shifted to 3360 cm−1 (+129 cm−1) and 3437 cm−1 (+136 cm−1) for the A LDOPAc@C60 configuration, respectively. These large wavenumber shifts can be used as molecular signatures in experimental data suggestive of the presence of the A adsorbate geometry. The B configuration, on the other hand, does not show a very noticeable variation with respect to the isolated form of LDOPAc, having its largest wavenumber shift with respect to the I LDOPAc peak at 2958 cm−1, which decreases to 2935 cm−1 (−23 cm−1), a smaller difference in comparison with A, but still experimentally observable. The C LDOPAc@C60 case, on the other hand, shows a very large wavenumber shift for the I peaks at 3231 and 3301 cm−1, very close to the A shift values, and the largest wavenumber variation for the I peak at 2958 cm−1, which decreases to 2690 cm−1 (−268 cm−1 wavenumber shift). Finally, the D adsorbate shows the largest wavenumber variations in comparison with the isolated LDOPAc molecule for the absorption peaks at 2978 cm−1 (I: 2958 cm−1) and 3209 cm−1 (I: 3231 cm−1). The other absorption peaks, by the way, occur at wavenumbers very close to the corresponding I values. Taking into account these results, we believe that the calculated wavenumber shifts associated with each adsorption geometry in comparison with the isolated molecule provide specific molecular signatures, which can be very helpful in explaining experimental measurements of the infrared spectra produced by LDOPA-C60 systems.
3.5 Raman spectra
The Raman scattering spectra shown in Fig. 9, with the main peak assignments and respective wavenumbers shown in Table 6, give additional ways to detect the four distinct adsorption geometries obtained from our DFT calculations. Looking at the top of Fig. 9, we see the Raman bands in the wavenumber range up to 1000 cm−1. The A LDOPAc adsorption geometry leads to a Raman spectrum which is dominated by the C60 in the 0–1000 cm−1 wavenumber range, with very intense scattering bands at 268–269 cm−1 (corresponding to the 266 cm−1 C60Hg mode), 486 cm−1 (C60: 497 cm−1Ag), and 773–774 cm−1 (C60: 788 cm−1Hg). There is also a weak Raman activity band near 720 cm−1 (C60: 721 cm−1Hg mode). With respect to the isolated LDOPAc, the largest difference occurs for the 815 cm−1 normal mode, which is shifted up by only +3 cm−1. The B adsorbate, on the other hand, has the C60-associated Raman scattering peaks at the same wavenumbers we found for the A configuration (indeed, the same is true for the C and D adsorption geometries). In comparison with I LDOPAc, the most noticeable difference not visible in the infrared spectrum occurs for the 586 cm−1 normal mode, which is shifted down to 579 cm−1 (−7 cm−1). For the C adsorbate, the peak of isolated LDOPAc at 586 cm−1 is now located at 599 cm−1, while the peak at 766 cm−1 is shifted to 761 cm−1 (as for B). Finally, D LDOPAc@C60 has the most pronounced wavenumber shifts in comparison with the I LDOPAc Raman spectrum peaks at 766 and 586 cm−1, −24 and −6 cm−1, in that order.| Assignment | I | C60 | A | B | C | D |
|---|---|---|---|---|---|---|
| C60Hg | 266 | 268–269 | 268–269 | 268–269 | 268–269 | |
| N–C7–C12 deformation | 341 | 341 | 367 | 359 | 353 | |
| C60Ag | 497 | 486 | 486 | 486 | 486 | |
| Phenyl deformation, C6–C7–N5(C12) bending | 549 | 547 | 549 | 550 | 545 | |
| Phenyl ring in-plane deformation | 586 | 586 | 579 | 599 | 580 | |
| C6–C8, C7–C12 stretching, phenyl ring in-plane deformation | 766 | 767 | 761 | 761 | 742 | |
| Phenyl ring in-plane deformation, COO− scissors, C14–O3 stretching | 785 | 785 | 785 | 783 | 779 | |
| C60Hg | 788 | 773–774 | 773–774 | 773–774 | 773–774 | |
| CH phenyl out-of-plane bending, C7–N5 stretching, C6–H2 twisting | 815 | 818 | 802 | 820 | 824 | |
| N5–C7–C12 asymmetric stretching | 874 | 876 | 898 | 905 | 875 | |
| C6–C7–N5 asymmetric stretching | 1051 | 1054 | 1047 | 1051 | 1045 | |
| C60Hg | 1127 | 1099–1100 | 1099–1101 | 1099–1101 | 1100–1101 | |
| C6–H2 twisting, N5–H3, C7–H22 bending | 1161 | 1158 | 1135 | 1121 | 1161 | |
| C6–C8 stretching | 1179 | 1208 | 1209 | 1207 | 1205 | |
| C7–C12–O2 asymmetric stretching | 1218 | 1215 | 1228 | 1209 | 1205 | |
| C60Hg | 1277 | 1273–1274 | 1273–1274 | 1273–1275 | 1273–1276 | |
| C6–H2, C7–H22, N5–H3 bending | 1287 | 1283 | 1304 | — | — | |
| C14–O3, C11–O1, C6–C8 stretching, C13–H25 bending | 1306 | 1304 | 1304 | 1301 | 1305 | |
| Phenyl ring asymmetric stretching, C6–C7 stretching | 1417 | 1414 | 1410 | 1389 | 1406 | |
| N5–H3 bending, C12–O4 stretching | 1435 | 1420 | 1435 | 1405 | 1462 | |
| C60Hg | 1455 | 1464–1468 | 1466–1468 | 1465–1468 | 1465–1469 | |
| C60Ag | 1503 | 1529–1532 | 1529–1532 | 1530–1532 | 1530–1532 | |
| C60Hg | 1617 | 1609–1611 | 1610–1611 | 1610–1611 | 1609–1611 | |
| Phenyl ring alternate stretching | 1644 | 1644 | 1650 | 1644 | 1648 | |
| N5–H3 deformation | 1660 | 1660 | 1662 | 1660 | 1656 | |
| Phenyl ring symmetric stretching | 1670 | 1670 | 1672 | 1670 | 1669 | |
| N5–H3 asymmetric bending, COO− asymmetric stretching | 1720 | 1713 | 1711 | 1710 | 1693 | |
| N5–H16 stretching | 2958 | 2776 | 2935 | 2690 | 2978 | |
| C6–H2 symmetric stretching | 3073 | 3070 | 3042 | 3043 | 3067 | |
| C6–H2 asymmetric stretching, C7–H22 stretching | 3132 | 3131 | 3098 | 3098 | 3120 | |
| C6–H2 asymmetric stretching, C7–H22 stretching | 3149 | 3146 | 3127 | 3125 | 3130 | |
| H25–C13–C10–H24 asymmetric CH stretching | 3185 | 3183 | 3189 | 3181 | 3195 | |
| H25–C13–C10–H24 symmetric CH stretching, C9–H23 stretching | 3207 | 3205 | 3211 | 3205 | 3205 | |
| C9–H23 stretching, H25–C13–C10–H24 symmetric CH stretching | 3218 | 3218 | 3214 | 3207 | 3230 | |
| H18–N5–H19 symmetric stretching, H18–N5–H16 asymmetric stretching | 3231 | 3360 | 3227 | 3376 | 3209 | |
| H18–N5–H19 asymmetric stretching | 3301 | 3437 | 3306 | 3468 | 3298 | |
| O1–H15 stretching | 3663 | 3664 | 3664 | 3665 | 3664 | |
| O3–H17 stretching | 3740 | 3741 | 3741 | 3741 | 3740 |
The middle part of Fig. 9 shows the Raman scattering spectra for the LDOPAc systems under study from 1000 cm−1 to 1800 cm−1. The A adsorbate exhibits strong Raman activities for C60 related normal modes, with very strong bands at 1099–1100 cm−1 (isolated C60: 1127 cm−1Hg mode, largest absolute variation, 27 cm−1), 1273–1274 cm−1 (C60: 1277 cm−1Hg), 1464–1468 cm−1 (C60: 1455 cm−1Hg), 1529–1532 cm−1 (C60: 1503 cm−1Ag second largest absolute variation, about 26 cm−1), and 1609–1611 cm−1 (C60: 1617 cm−1Hg). The most noticeable differences of A LDOPAc@C60 in comparison with I LDOPAc (not overlapping with the infrared spectrum) are: 1179 cm−1 (I) changes to 1208 cm−1 A, and 1287 cm−1 (I) changes to 1283 cm−1 (A). The C60-related high activity peaks for the B, C, and D configurations are also very close to the corresponding A wavenumbers. The I peaks at 1179, 1287, and 1417 cm−1 are shifted to 1209, 1304, and 1410 cm−1, respectively, for the B adsorbate, while for the C adsorbate the most important differences with respect to isolated LDOPAc occur for the I peaks at 1179 cm−1, which is shifted up to 1207 cm−1, and 1417 cm−1, shifted down to 1389 cm−1. The D configuration has the I peak at 1179 cm−1 shifted up to 1205 cm−1, while the I peak at 1417 cm−1 is shifted down to 1406 cm−1.
The highest wavenumber domain, between 2500 and 4000 cm−1, does not have any C60 related Raman activity, Raman scattering peaks being due entirely to LDOPAc vibrational normal modes. The 11 isolated LDOPAc normal modes in this range are all Raman active, originating from CH, NH, and OH bond length oscillations, having the following wavenumbers: 2958, 3073, 3132, 3149, 3185, 3207, 3218, 3231, 3301, 3663, and 3740 cm−1. The adsorbate Raman spectra for wavenumbers above 2500 cm−1 have the same remarkable wavenumber shifts (above 100 cm−1 in absolute value) in comparison with I LDOPAc already noted in the infrared spectra. Wavenumber shifts visible only in the Raman data, however, are much smaller (−3 cm−1 at worst, for the A adsorbate). However, some distinct Raman signatures can be seen for the B, C, and D configurations of LDOPAc@C60. For example, the I peaks at 3073, 3132, and 3149 cm−1 are shifted down to 3042, 3098, and 3127 for the B adsorbate, while for the C adsorbate the corresponding wavenumbers are 3043, 3098, and 3125 cm−1. The C adsorbate also has a wavenumber shift of −11 cm−1 for the I LDOPAc normal mode at 3218 cm−1. The D adsorbate, on the other hand, has its most pronounced wavenumber changes for the I peaks at 3132, 3149, 3185, and 3218 cm−1, which are shifted, respectively, to 3120, 3130, 3195, and 3230 cm−1.
The large wavenumber shifts observed in the infrared and Raman spectra for the A adsorbate from 2958 to 2776 cm−1 (−182 cm−1), from 3231 cm−1 to 3360 cm−1 (+129 cm−1), and from 3301 cm−1 to 3437 cm−1 (+136 cm−1), and the corresponding large shifts for the C adsorbate seem to be due to the stretching of N–H bonds at the NH3+ group, which is very close to the fullerene C60 surface in these adsorption geometries. On the other hand, the B adsorption geometry, which has the NH3+ group moved away from the fullerene surface, has smaller wavenumber shifts in this region of the vibrational spectrum. Lastly, the D adsorption geometry has both the NH3+ and COO− near to the C60 molecule, as well as the C7–H22 atoms, which apparently decreases the strong effect of the NH3+ interaction with the C60 fullerene.
4 Conclusions
In summary, we have presented the results of Classical Molecular Dynamics (CMD) and Density Functional Theory (DFT) simulations for levodopa (LDOPA) adsorbed on the C60 fullerene, taking into account the protonation state of LDOPA when the pH is within the 2–8 pH range (LDOPAc, with NH3+ and COO− groups), which corresponds to a pH range encompassing the gastric, skin, and blood environments. We have done so aiming at potential applications for transdermal and oral administration of LDOPA@C60 adsorbates. After carrying out a search for optimal LDOPA@C60 geometries using classical molecular dynamics and classical annealing, we found four adsorption configurations (A, B, C, and D), which minimize the total energy. These four structures were then submitted to a second round of geometry optimization, this time using DFT with the LDA exchange–correlation functional. The interaction energies between LDOPAc and C60 obtained after the DFT-LDA geometry optimization vary from −0.72 eV (A) up to −0.34 eV (D). So even the D adsorbate exhibits a strong binding interaction, much larger than kBT at room temperature, indicating that these adsorbates could be stable in vivo. The charge of the NH3+ group is the least affected after adsorption, while the A adsorbate presents some electron transfer from C60. A molecular dynamics simulation performed for one hundred LDOPAc molecules and a single C60 molecule in a box at room temperature shows that typical molecular configurations of LDOPAc closely follow the geometry of the four adsorption structures we have found.The four adsorption geometries, together with isolated LDOPAc and C60, were also optimized using the B3LYP exchange–correlation functional and a 6-31G(d,p) basis set to calculate their infrared and Raman spectra. In the 2500 to 4000 cm−1 wavenumber range, a comparison between isolated LDOPAc and each one of the four adsorption geometries shows very clear vibrational signatures of all adsorbates. For C LDOPAc@C60, we have obtained a considerable amount of variation in comparison with the isolated LDOPAc peaks, resembling those observed for the A adsorbate, with the most significant wavenumber change occurring for the LDOPAc peak at 2958 cm−1, which is shifted down by −268 cm−1. The Raman spectra of the adsorbates below 2000 cm−1 is dominated by intense activity bands due to C60, while above 2500 cm−1 one can note that each adsorbate has its own characteristic set of Raman activity frequencies. Overall, our results suggest that the combination of both infrared and Raman spectroscopy is able to identify the four levels of adsorption we have found in our calculations, and also point to the feasibility of LDOPA@C60 as a system for oral and transdermal drug delivery for the treatment of Parkinson's disease. Actually, we are developing efforts to prepare LDOPA@C60 and to probe the vibrational signatures of the adsorption, whose results will be submitted for publication as soon as possible.
Acknowledgements
E. L. A. and V. N. F. are senior researchers from the Brazilian National Research Council (CNPq), and would like to acknowledge the financial support received during the development of this work from the Brazilian Research Agencies CAPES-PROCAD and Rede Nanobiotec, CNPq-INCT-Nano(Bio)Simes project 573925/2008-9, and FAPERN-CNPq (Pronex). E. W. S. C. received financial support from CNPq projects 304283/2010-0 and 474734/2011-0. The authors also thank CENAPAD/CE for providing the computational resources to perform the infrared and Raman spectra calculations using the Gaussian09 code.References
- R. A. Hauser, Eur. Neurol., 2009, 62, 1–8 CrossRef CAS.
- A. E. Lang, Neurology, 2007, 68, 948–952 CrossRef.
- O. Hornykiewicz, Neurol., 1998, 51, S2–S9 CrossRef CAS.
- S. J. Kish, K. Shannak and O. Hornykiewicz, N. Engl. J. Med., 1998, 318, 876–880 CrossRef.
- R. A. Hauser, M. Panisset, G. Abbruzzese, L. Mancione, N. Dronamraju and A. Kakarieka, Movement Disord., 2009, 24, 541–550 CrossRef.
- A. A. Corona-Morales, A. Castell, A. Escobar, R. Drucker-Colin and L. M. Zhang, J. Neurosci. Res., 2002, 71, 121–126 CrossRef.
- C. M. Sayes, A. M. Gobin, K. D. Ausman, J. Mendez, J. L. West and V. L. Colvin, Biomaterials, 2005, 26, 7587–7595 CrossRef CAS.
- S. G. Santos, J. V. Santana, F. F. Maia Jr, V. Lemos, F. V. N., E. W. S. Caetano, B. S. Cavada and E. L. Albuquerque, J. Phys. Chem. B, 2008, 112, 14267–14272 CrossRef CAS.
- A. Di Stefano, P. Spzio, A. Iannitelli and L. S. Cerasa, Expert Opin. Drug Delivery, 2009, 6, 390–404 CrossRef.
- U. Adamiak, M. Kaldonska, G. Klodowska-Duda, E. Wyska, K. Safranow, M. Bialecka and B. Gawronska-Szklarz, Clin. Neuropharmacol., 2010, 33, 135–141 CrossRef CAS.
- G. Cevc and U. Vierl, J. Controlled Release, 2010, 141, 277–299 CrossRef CAS.
- R. Bakry, R. M. Vallant, M. Najam-ul Haq, M. Rainer, Z. Szabo, C. W. Huck and G. K. Bonn, Int. J. Nanomedicine, 2007, 2, 639–649 CAS.
- J. G. Rouse, J. Yang, J. P. Ryman-Rasmussen, A. R. Barron and N. A. Monteiro-Riviere, Nano Lett., 2007, 7, 155–160 CrossRef CAS.
- A. Montellano, T. Da Ros, A. Bianco and M. Prato, Nanoscale, 2011, 3, 4035–4041 RSC.
- N. F. Steinmetz, W. Hong, E. D. Spoerke, K. Breitenkamp, M. G. Finn and M. Manchester, J. Am. Chem. Soc., 2009, 131, 17093–17095 CrossRef CAS.
- B. Sutharaman, T. Y. Zakharian, A. Saraf, P. Misra, J. Ascroft, S. Pan, Q. P. Pham, A. G. Mikos, L. J. Wilson and D. A. Engler, Mol. Pharmaceutics, 2008, 5, 567–577 CrossRef.
- R. Partha and J. L. Conyers, Nanomedicine, 2009, 4, 261–275 CrossRef CAS.
- A. Hadad, D. L. Azevedo, E. W. S. Caetano, V. N. Freire, G. L. F. Mendonça, P. DeLima-Neto, E. L. Albuquerque, R. Margis and C. Gottfried, J. Phys. Chem. C, 2011, 115, 24501–24511 CAS.
- D. F. Evans, G. Pye, R. Bramley, A. Clark and T. Dyson and H. J.D., Gut, 1988, 29, 1035–1041 CrossRef CAS.
- G. Yosipovitch and J. Hu, Skin & Aging, 2003, 11, 88–93 Search PubMed.
- A. Waugh and G. Allison, Ross and Wilson Anatomy and Physiology in Health and Illness, Churchill Livingstone, 10th edn, 2007, p 22 Search PubMed.
- M. J. Frisch, G.W. Trucks and H. B. Schlegelet al., Gaussian 09 Revision A.1, Gaussian Inc.Wallingford CT, 2009 Search PubMed.
- D. Porezag and M. R. Pederson, Phys. Rev. B, 1996, 54, 7830–7836 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701–2705 RSC.
- T. van der Wijst, C. F. Guerra, M. Swart and F. M. Bickelhaupt, Chem. Phys. Lett., 2006, 426, 415–421 CrossRef CAS.
- V. R. Cooper, T. Thonhauser and D. C. Langreth, J. Chem. Phys., 2008, 128, 204102 CrossRef.
- P. L. Silvestrelli, J. Phys. Chem. A, 2008, 113, 5224–5234 CrossRef.
- F. Ortmann, K. Hannewald and F. Bechstedt, J. Phys. Chem. B, 2008, 112, 1540–1548 CrossRef CAS.
- F. F. Maia Jr, V. V. Freire, E.W. S. Caetano, D. L. Azevedo, F. A. M. Sales and E. L. Albuquerque, J. Chem. Phys., 2011, 134, 175101–175110 CrossRef CAS.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. Lett., 2005, 95, 186101–186103 CrossRef CAS.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B, 2006, 73, 205101–205103 CrossRef.
- E. A. Kee, M. C. Livengood, E. E. Carter, M. McKenna and M. Cafiero, J. Phys. Chem. B, 2009, 113, 14810–14815 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244–13249 CrossRef.
- B. Delley, Phys. Rev. B: Condens. Matter, 2002, 66, 1–9 CrossRef.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. TiradoRives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- R. K. Roy, K. Hirao, S. Krishnamurty and S. Pal, J. Chem. Phys., 2001, 115, 2901–2907 CrossRef.
- R. K. Roy, S. Pal and K. Hirao, J. Chem. Phys., 1999, 110, 8236–8245 CrossRef CAS.
- R. G. Parr and W. T. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- R. Bonaccorsi, E. Scrocco and J. Tomasi, J. Chem. Phys., 1970, 52, 5270 CrossRef CAS.
- P. W. Ayers, R. C. Morrison and R. K. Roy, J. Chem. Phys., 2002, 116, 8731–8744 CrossRef CAS.
- R. F. Nalewajski and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8879–8882 CrossRef CAS.
- K. Hedberg, L. Hedberg, D. S. Bethune, C. A. Brwon, H. C. Dorn, R. D. Johnson and M. De Vries, Science, 1991, 254, 410–412 CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available: The calculated normal mode wavenumbers of isolated levodopa and all adsorbates. See DOI: 10.1039/c2ra20606d/ |
| This journal is © The Royal Society of Chemistry 2012 |
