DOI:
10.1039/C2RA20743E
(Paper)
RSC Adv., 2012,
2, 8390-8401
Dynamics of liquid droplets in an evaporating drop: liquid droplet “coffee stain” effect†
Received
21st April 2012
, Accepted 5th July 2012
First published on 6th July 2012
Abstract
In this paper, we demonstrate the dynamics of bidispersed oil droplets in an evaporating water sessile drop. This phenomenon is therefore equivalent to a unique liquid droplet based “coffee stain” effect, with the depositing colloidal particles (of a classical “coffee stain” problem) being replaced by the oil droplets partially wetting the substrate. The important difference with respect to the classical “coffee stain” problem, as revealed by our experiments, is that the oil droplets, unlike the colloidal particles, cannot reach the contact line; rather the aversion of the oil droplets to the air ensures that the oil droplets always remain at a finite distance from the contact line. We call this effect an “enclosure” effect, characterized by this distance. We provide a theoretical model to explain this phenomenon, and our theoretical results match well with the experimental observations. The “enclosure” effect depends on the droplet size, thereby allowing an automatic size-based separation of the oil droplets. Additionally, this effect depends on the wettability of the oil droplets and the sessile drop, as well as the relative velocity of the oil droplets with respect to the rate of decrease of the sessile drop contact angle. Our identification of this new phenomenon in a liquid-droplet based “coffee stain” problem will have a huge impact on microscale control and manipulation of liquid droplets in a two phase system.
1 Introduction
An evaporating coffee drop leaves behind its signature “stain”, formed by the accumulation of colloidal coffee particles at the three phase contact line (TPCL). This is a general problem of inhomogeneous particle deposition, more popularly known as the “coffee stain” problem, which has attracted great attention over the past decade and a half,1–11 and its understanding and applications have overwhelming significance across a plethora of disciplines.12–19 The key to understanding the “coffee stain” problem is to identify that the evaporation from the air–liquid interface of the liquid drop, triggered by the diffusion of the liquid vapor to the air,6,9 drives a capillary transport that advects and deposits the coffee particles at the TPCL thereby forming the “stain”. The major non-triviality associated with this problem is that the evaporation flux diverges at the TPCL, resulting in a diverging velocity field inside the drop,2,6,9,10 whose base radius remains constant (i.e., the contact line is pinned) and the contact angle decreases during the evaporation. There has been considerable modeling efforts to correctly account for this divergence, while describing the particle deposition during the evaporation.2,4,6,9,10,20–24 The nature of such deposition and hence the resultant “stain” depends on various factors such as the physical properties, wettability, shape and size of the particles – there have been studies where the depositing particles have been colloids, carbon nanotubes, biomolecules etc.2,3,11,25–29 To the best of our knowledge, however, there has been rarely any study to date that investigates the “coffee stain” effect with liquid droplets as depositing particles.
In this paper, we study the dynamics of partially wetted oil droplets in an evaporating water sessile drop. Two different sized oil droplets, generated by a focused flow droplet generator chip,30 are introduced in a sessile drop, which subsequently evaporates on substrates of different wettabilities, namely glass and polycarbonate. Unlike particles in an evaporating drop, oil droplets remain inherently wetted to the substrate. Therefore, the deposition does not occur during the evaporation-triggered advection; rather the deposition occurs during the initial period when the oil droplets have been introduced inside the sessile drop. Therefore, the evaporation-driven capillary flow field advects the partially wetted oil droplets, and in the process forms the unique liquid-droplet based “coffee stain” effect [see Fig. 1]. This is similar to the behavior of the colloidal particles in an evaporation drop. However, unlike the colloidal particles, the oil droplets cannot reach the TPCL. This is because if the oil droplets had to reach the TPCL, it would necessitate the formation of a finite air–oil interface, which is extremely unfavorable energetically as dictated by the corresponding spreading parameter (which becomes more than unity).31 Therefore, the closest approach of the oil droplets to the TPCL would be up to a position where the air–water interface is at a tangent to the approaching oil droplets [for a detailed pictorial representation of the effect, kindly refer to Fig. 2]. Hence, there is always a finite distance between the oil droplets and the TPCL, and this distance is a function of the size of the droplets and the wettability of the droplets on the surface [see Fig. 2 and the analysis in the ESI† for more details]. We shall henceforth call this effect an “enclosure” effect. In the present paper, we use bidispersed oil droplets – therefore the “enclosure” effect ensures that the different sized oil droplets are enforced to be located at different distances from the contact line, thereby allowing an elegant size-based separation. Such a size-based separation induced by the interaction of depositing moieties with the contact line (during evaporation) has been recently employed to separate biomolecules32–34. These studies32–34 consider a finite retarding effect on the solid particles on account of the capillary interaction with the air–water interface35 – the interaction of the oil droplets with the air–water interface, as studied here, is physically different (illustrated in section 4.3). In addition, during the formation of the “enclosure” effect, as well as after the complete evaporation, oil droplets can form beautiful patterns, whose richness and intricacies are often dictated by the oil droplet size distribution, as well as the spatiotemporal behavior of the droplets. Also the “enclosure” effect is dictated by the velocity of the oil droplets towards the contact line and the speed at which the contact angle decreases. In other words, the oil droplet dynamics preceding and following the “enclosure” effect are largely dictated by the relative variation of the time taken to complete the “enclosure” effect and the time up to which the contact line remains pinned during the evaporation.
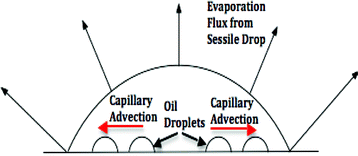 |
| | Fig. 1 A schematic of the evaporating sessile drop and the sliding of the oil droplets from the resulting capillary advection (shown in red arrows). | |
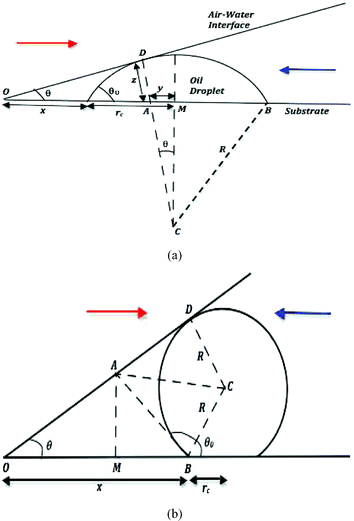 |
| | Fig. 2 A schematic of the “enclosure” effect, quantified by the distance of closest approach x of the droplet to the contact line for the oil droplet having (a) an acute contact angle (e.g., oil droplets on polycarbonate in water medium) and (b) an obtuse contact angle (e.g., oil droplets on glass in water medium). In either of the figures, the arrow (in red) in the left shows the direction of movement of the air–water interface (during pinned contact line evaporation) and the arrow (in blue) in the right shows the direction of movement of the sliding oil droplets (advected by the evaporation-driven capillary transport). | |
There are two important messages of this paper, which presents the first experimental evidence of the liquid droplet-based “coffee stain” effect. First, by employing the size dependent “enclosure” effect we propose a novel method for size based separation of oil droplets. Second, the “enclosure” effect allows for the preferential positioning of the oil droplets, which form self assemblies and interesting patterns under different conditions of surface wettabilities. Therefore in our study we identify a new physical phenomenon (which we term the “enclosure” effect) that utilizes the wettability and the size characteristics of the droplets and paves the way for unique techniques for size based oil droplet separation and pattern formation.
The rest of the paper is organized as follows: in section 2, we discuss the important details of the experimental procedures, in section 3 we provide a detailed theoretical analysis to quantify the reasons and the characteristics of the “enclosure” effect as well the calculation of the droplet dynamics that precede the formation of the “enclosure” effect, in section 4 we discuss the different results from our experiments and their important implications, and finally in section 5 we end with a conclusion.
2 Experimental details
The experimental procedure can be broadly divided into two steps: first is the generation of bidispersed micron sized oil droplets and second is the study of the dynamics of the oil droplets inside an evaporating sessile drop placed on substrates of different wettabilities.
2.1 Droplet generation
In the present work, we generate oil droplets in a water medium using a focused flow droplet generator chip (FC_FFDG.2, Micronit Microfluidics, Enschede, The Netherlands) (kindly see the ESI† for an image of the droplet generator chip and an illustration of the droplet generation). Here, we briefly describe the procedure to generate these droplets (for a more detailed discussion see elsewhere30,36–40). The droplet generation chip, which is made up of glass and consists of channels having width 100 μm, depth 20 μm and nozzle diameter 10 μm, generates droplets by a combination of sheet flow and precise restriction. We use silicon oil (Cargille Laboratories Inc., Cedar Grove, NJ, USA; Density 0.97 − 1.10 × 103 kg m−3 at 23 °C) for the oil droplets and DI water [with 0.1% (by volume) Tween 20 surfactant; surfactant is used to prevent droplet coalescence30 and such a surfactant concentration is above the CMC (Critical Micellar Concentration) value for Tween 20] for the continuous phase. We generate oil droplets of two different diameters by maintaining the flow rates of oil (at 0.05 μL min−1) and water (at 2.5μL min−1) using syringe pump (Pump 11, Harvard Apparatus, MA). Using an oil flow rate of 0.05 μL min−1 and water flow rate of 2.5 μL min−1, we generate oil droplets of two different diameters. Droplets are collected in small bottles at the outlet of the chip for the following evaporation study.
2.2 Dynamics of bi-dispersed oil droplets in an evaporating sessile drop
We consider the evaporation of a 5μL water sessile drop, containing oil droplets of two different sizes (described above), placed on two different substrates, namely glass (with pre-evaporation contact angle θ = 10°) and polycarbonate (with pre-evaporation contact angle θ = 40°). The top and side views of evaporating drop are captured to understand the oil-droplets movements and contact angle/dynamics, simultaneously. A Krüss DSA 100 (Krüss GmbH, Hamburg, Germany) is used to capture the side views and subsequently the corresponding contact angles are measured. Two representative side view images of the sessile drop on the two substrates are shown in Fig. 3(a,b). The top views of the dynamics of the sessile drop are captured by a microscope (60 × magnification, 1.3 Mpixel CMOS image sensor, ViewSolutions GE-5, Howard Electronic Instruments Inc., El Dorado, KS41). We keep a track of the temporal variation of the contact angle and the location of the contact line of the evaporating drop on the two substrates.
 |
| | Fig. 3 Side views of a sessile droplet with micro-oil-drops inside. Images taken when the droplet was put on (a) a glass substrate and (b) a polycarbonate substrate, and the corresponding contact angles are θ = 10° and θ = 40° (both these angles are equilibrium pre-evaporation contact angles). In the inset of each of the figures, we show the side views of the oil droplet on the corresponding substrates in water medium. The oil droplet contact angles are 140° on glass and 45° on the polycarbonate. | |
As the sessile drop evaporates, the resulting capillary flow advects the oil droplets [see Fig. 1 for the schematic]. We study the dynamics of those oil droplets that have attained a partially wetted state (and not floating), as confirmed by magnified side views of the oil droplets on the two substrates [see insets of Fig. 3(a,b)]. For both these substrates, this partial wetting occurs with the oil droplet coming in direct contact with the substrate. There is no possibility of any water film to be present underneath the oil droplet, i.e., in between the oil droplet and the substrate. Had that been the case then the oil droplet would be effectively floating in water, and would be displaced from its position with slight perturbation of the set up – we do perform such a cross check and find no movement of a deposited oil droplet from its partially wetted state confirming that there is no water film underneath. Please note that it takes a finite time for these oil droplets (introduced in the evaporating drop through a syringe) to come to the substrate and attain the partially wetted state. From the measurement, we find that the equilibrium contact angles of the oil droplet are 140° and 45° for the glass and the polycarbonate substrates in water medium. The diameters of the oil droplets on the glass substrate in water medium are ∼20 μm and ∼40 μm. Therefore (using volume conservation) the contact radii of the oil droplets on glass substrate [rc in Fig. 2(b)] are ∼6.4 μm (for smaller droplets) and ∼12.8 μm (for larger droplets) and those on the polycarbonate substrate [rc in Fig. 2(a)] are 47 μm (for smaller droplets) and 94 μm (for larger droplets). The evaporation-driven capillary flow advects the wetted oil droplets towards the TPCL, as observed by studying top views (see above) of the temporal dynamics of the oil droplets inside the evaporating sessile drop. In the presence of the flow, the partially wetted droplets deform, thereby creating unequal advancing (θa) and receding (θr) contact angles.42 For oil droplets on the polycarbonate substrate, we measure θa ≃ 49.5° and θr ≃ 40°. For oil droplets on the glass substrate, however, the contact angle hysteresis is too small (i.e., there is very little difference between θa, θr and the equilibrium angle) – such a behavior is common for drops with large obtuse angle values for the equilibrium contact angles.43 Please note that throughout the experiments, we consider that the oil droplets are in the wetted state. Such a consideration needs to be discussed in the light of the possible alterations in the physical situation that presence of surfactants (above CMC) may trigger. For surfactant concentration above CMC, it is likely that there will be a strong adsorption of the surfactant molecules at the solid substrate.44 Under such a situation, the contact of the oil droplets with the substrate may be affected, particularly if the equilibrium contact angle of the drop is very large (obtuse angle).44 Therefore, although we can safely neglect the effect of adsorbed surfactant for the oil droplet on the polycarbonate substrate (where the equilibrium contact angle of the oil is 45°), for oil droplets on the glass substrate the presence of surfactants may affect the contact of the oil drop in a manner as explicated by Kumar and Biswas.44 However, for the present study, we do not highlight such an effect – however, we do emphasize that the theoretical model (see section 3.3) is mostly valid for the oil drops on the polycarbonate substrate [accordingly, only for the polycarbonate substrate, we provide the comparison between the experimental and theoretical results, see Fig. 7(b)].
Finally, we observe that the dynamics of these deformed advected oil droplets are characterized by the simultaneous occurrence of the oil droplets approaching the contact line, and the air–water interface coming down towards the solid substrate (due to the decrease of the contact angle). These two events finally ensure that the droplets become tangential to the air–water interface, and do not go beyond that point (since the consequent creation of the oil–air interface is energetically unfavorable). This triggers the formation of the “enclosure” effect, characterized by the distance of closest approach of the drop from the TPCL. Time snap shots showing the formation of the “enclosure” effect for both the substrates are provided in Fig. 4, 10. Please note that the captured images are top views of evaporating sessile drops and for better visualization, the original images are processed. The background noise is subtracted from the original images which leads to a distinct representation of the contact lines.
![The dynamics of oil droplets on polycarbonate captured at (a) t = 580 s, (b) t = 745 s and (c) t = 750 s. The enclosure distance measured in (c) ∼50 μm. The sessile drop contact angle measured at t = 750 s ∼ 10°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 53 μm (in this theoretical calculation, we use rc = 47 μm and θd ≈ θ0 ≈ 45°).](/image/article/2012/RA/c2ra20743e/c2ra20743e-f4.gif) |
| | Fig. 4 The dynamics of oil droplets on polycarbonate captured at (a) t = 580 s, (b) t = 745 s and (c) t = 750 s. The enclosure distance measured in (c) ∼50 μm. The sessile drop contact angle measured at t = 750 s ∼ 10°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 53 μm (in this theoretical calculation, we use rc = 47 μm and θd ≈ θ0 ≈ 45°). | |
3 Theory
In this section we shall first discuss the cause of formation, as well as the characteristics of the “enclosure” effect. Following this, we shall present a calculation of the evaporation-triggered fluid flow field and the resulting dynamics of the wetted oil droplets that precede the formation of the “enclosure” effect.
3.1 Formation of the “enclosure” effect
Here, we shall discuss the governing principles and the system parameters that dictate the formation of the “enclosure” effect. Therefore, we implicitly assume that the oil droplets have reached the air–water contact line (the necessary quantifications are provided later).
To analyze the “enclosure” effect, we must address two things: first, the reasons for formation of this “enclosure” effect and second, the role of the system parameters in dictating this effect. Regarding the first question, we need to realize that the formation of the “enclosure” effect implies that a wetted oil droplet has reached a position of closest approach to the TPCL, i.e., it cannot move closer to the TPCL without creating a finite air–oil interface. In other words, it has reached a position where the air–water interface is at a tangent to it. The physical requirements which ensure such a condition is that the spreading parameter S,31 corresponding to the formation of a finite air–oil interface (with the oil being present inside the water), must be positive (this will imply that this finite air–oil interface is energetically unfavorable and will never be formed, or if formed will disappear quickly). Before applying this idea in the present case, let us first discuss the concept of the spreading parameter S in the context of the simplest partially wetting system, i.e., a partially wetting liquid droplet sitting on a solid, with surrounding medium being the vapor of the liquid. For such a case the spreading parameter S is defined by:
where
γsv,
γsl and
γlv are solid–vapor, solid–liquid and liquid–vapor surface tensions. As cos
θeq = (
γsv −
γsl)/
γlv (where
θeq is the equilibrium contact angle made by the drop with the solid), we can easily see that only for
S < 1, we have partially wetted drop formation, or the formation of a finite liquid–solid interface.
For the present case, where we conjecture the formation of a possible air–oil interface, in analogy to the above described case, we can define a spreading parameter S′, where the water droplet is replaced by an oil droplet, the surrounding vapor medium is replaced by a water medium, and the solid substrate is replaced by the air. Therefore, we may write:
where,
γaw,
γao and
γow are air–
water, air–oil and oil–
water surface tensions.
In the present study we operate at a surfactant-concentration level, which is above the CMC (Critical Micelle Concentration). Therefore, we need to consider a reduced value of the air–water and the water–oil surface tensions. Please note that we shall not consider a reduced value of the air–oil surface tension, since the surfactant has been added in bulk water; therefore the effect of the surfactant molecules is only exhibited at an interface whose one component is water. Above the CMC, γaw ≃ 35 mN m−1 (when the surfactant is Tween 20)45 and γow ≃ 7 mN m−1 (when the surfactant is Tween 20 and the oil is silicone oil),46 so that with γao ≃ 20 mN m−1,47 we shall have S′≃ 8 mN m−1 ≫ 0. Therefore the formation of the oil–air interface is energetically extremely unfavorable, leading to the formation of the “enclosure” effect [for the schematic refer to Fig. 2].
The above discussion addresses the fundamental principle that drives the formation of the “enclosure” effect. The second issue is to quantify this “enclosure” effect in terms of the system parameters. As has been seen in the experiments (see section 2), depending on the nature of the substrates, the oil droplets may form acute or obtuse contact angles [acute for polycarbonate and obtuse for glass, see Fig. 2]. For either of these two cases, one can express the “enclosure” distance x as (see the ESI† for detailed derivation):
| | 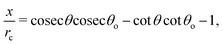 | (3) |
where
rc is the contact radius of the oil droplet,
θ is the contact angle of the sessile drop and
θ0 is the oil droplet contact angle.
Eqn (3) clearly demonstrates that the “enclosure” distance x varies linearly with the size of the droplets rc – therefore the “enclosure” effect ensures a size-based differential positioning of the oil droplets which triggers an extremely efficient size-based separation of the oil droplets. An important assumption involved in the derivation of eqn (3), is that θ0 > θ. For the opposite case of θ0 < θ, the oil droplet will easily reach the TPCL, and there will not be formation of any “enclosure” effect. Also note, here θ is not the equilibrium angle of the sessile drop – rather it is the angle when the oil droplets have approached and touched the air–water contact line (due to evaporation, the contact angle of the sessile droplets reduces from an equilibrium value θeq to θ).
3.2 Evaporation-triggered liquid velocity field
To understand the dynamics of the wetted oil droplets, we need to estimate the evaporation-driven water flow field, which imparts the necessary advective force on the wetted droplets. In this section, we discuss this evaporation-triggered liquid velocity field, under the condition that the evaporation is occurring from the axisymmetric sessile drop with a pinned contact line. We describe the drop in a cylindrical coordinate system, and considering the mass balance across a section (see Fig. 2 in the supplementary information of Ref. 9) within the drop, we can write: | | 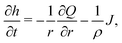 | (4) |
where h = h (r,t) is the instantaneous local value of the drop height, r is the radial coordinate, Q = Q(r,t) is the local volume flow rate, ρ is the liquid density and J is the evaporative flux. The drop is assumed to be a spherical cap (with a contact radius of R),6 and the contact angles are always assumed to be sufficiently small. Therefore, following6,9: | | 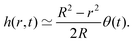 | (5) |
Also for small contact angles, and the case where evaporation is purely driven by diffusion, the evaporation flux J(r) can be expressed as 6,9
| | 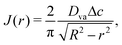 | (6) |
where
Dva is the diffusion coefficient of vapor in air and Δ
c is the vapor concentration difference between the drop surface and the surroundings.
Further, the variation of θ(t) can be obtained as (see9 for derivation):
| | 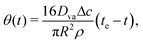 | (7) |
where
te is the total life time of the evaoprating sessile drop.
Therefore, we can obtain Q by integrating eqn (4), in presence of eqn (5,6,7) as well as the condition Q(r = R) = 0 as:
| | 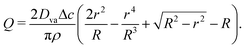 | (8) |
Hence, using ū(r, t) = Q/rh (where ū is the depth-averaged velocity) and eqn (5) to express h, we can obtain:
| | 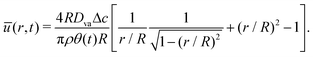 | (9) |
Therefore, we can identify the relevant velocity scale as 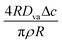 .
.
Please note that the velocity expression provided in eqn (9) gives the depth averaged velocity across the height of the drop. On the other hand, we need the velocity values at the location of the center of mass of the wetted oil droplets, which is at a height hc from the substrate. Employing the analysis prescribed in Marin et al.,9 the transverse (z) variation of the velocity field inside the drop can be expressed as (using the lubrication approximation, under the condition that the drop height is much smaller than the contact radius):
| | 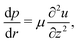 | (10) |
where
p is the pressure,
μ is the dynamic viscosity and
u is the radial velocity. We can integrate
eqn (10) twice in presence of the boundary conditions
u(
r,
z = 0) = 0 and
∂u/
∂z(
r,
z =
h) = 0, to obtain:
| | 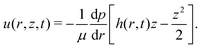 | (11) |
From eqn (11), we can obtain the depth average velocity u(r, t) as:
| | 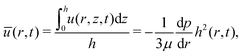 | (12) |
so that, we can express the radial pressure gradient d
p/d
r in terms of
u, thereby modifying
eqn (11) as:
| | 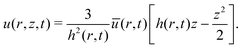 | (13) |
Therefore, we can obtain the velocity at the center of mass of the wetted oil droplets by using eqn (9) to express u(r, t), and replacing z by hc, where,
| | 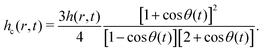 | (14) |
3.3 Sliding motion of the wetted oil droplets
In this subsection, we shall derive the expression for the velocity of the oil droplets. We should like to emphasize here that this expression is mostly valid for the oil droplets on the polycarbonate substrate, i.e., the substrate for which we have a measure of the contact angle hysteresis and can neglect the possible alteration of the solid–oil contact in presence of the adsorbed layer of surfactants. The evaporation-driven water advection velocity, expressed in eqn (13), exerts a drag force on the wetted oil droplets. The oil droplets start to slide, when this drag force becomes equal to the retentive force (which is a function of the wettability of the oil droplets on the solid surface). For the present case, the evaporation-triggered pressure-driven flow (described above) can be assumed to be a slow linear shear-driven flow, so that the drag force FD on the wetted oil droplets can be expressed as42,48,49: | | 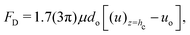 | (15) |
where 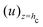 is the flow field evaluated at the center of mass of the wetted oil droplet, do is the effective diameter of the oil droplet and uo is the sliding velocity of the oil droplet. Here, while calculating do, one needs to account for the deformation of the drop during sliding. Therefore, do will be expressed in terms of the deformed volumes V1 and V2 so that following42:
is the flow field evaluated at the center of mass of the wetted oil droplet, do is the effective diameter of the oil droplet and uo is the sliding velocity of the oil droplet. Here, while calculating do, one needs to account for the deformation of the drop during sliding. Therefore, do will be expressed in terms of the deformed volumes V1 and V2 so that following42: | | 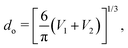 | (16) |
where| | 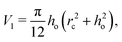 | (17) |
and| | 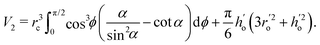 | (18) |
Here ho is the maximum height of the oil droplet, 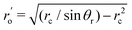 , ho′ = ro′tanθr − ro′/cosθr and α = π − tan−1(−tanθdcosφ) (where θd is the dynamic contact angle expressed as θd = 2φθr/π − (1 − 2φ/π)θa). In these expressions, θa and θr are the advancing and the receding contact angles of the wetted oil droplet and rc is the contact radius of the sessile drop.
, ho′ = ro′tanθr − ro′/cosθr and α = π − tan−1(−tanθdcosφ) (where θd is the dynamic contact angle expressed as θd = 2φθr/π − (1 − 2φ/π)θa). In these expressions, θa and θr are the advancing and the receding contact angles of the wetted oil droplet and rc is the contact radius of the sessile drop.
The retentive force on the sliding oil droplets can be expressed as42,50
| | 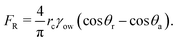 | (19) |
Under the condition of negligible inertia (for sufficiently small sizes of the oil droplets), we can equate eqn (15), (19), to obtain the velocity of the oil droplets as:
| | 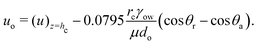 | (20) |
The above calculations, implicitly assume that the oil droplets are always in wetted condition. This will not be true in case the lift force FL due to the evaporation-triggered advection outweighing the adhesion force FA between the wetted oil droplets and the substrate. For the present study, these two forces can be expressed as:
| | 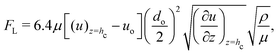 | (21) |
and
| | 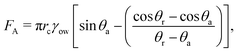 | (22) |
and we shall always need to have
FA >
FL to ensure that the oil droplets are in wetted condition.
Using eqn (20), as well as the condition that 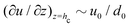 we can obtain:
we can obtain:
| | 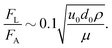 | (23) |
Typically, with d0∼1 mm, u0∼10 μm s−1 we get (in water medium):
| | 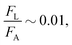 | (24) |
i.e., the lift force is never large enough to disrupt the wetted condition of the droplets.
4 Results and discussion
In this section, we shall discuss the key findings of our study and their overall significance. The most important result of our experiments is the formation of the “enclosure” effect – here we shall discuss the oil droplet dynamics preceding this effect, during this effect and after this effect for each of the two different substrates separately.
4.1 Oil droplet dynamics on polycarbonate substrate
Fig. 4(a,b,c) provide the different time snapshots for the events that lead to the formation of the “enclosure” effect for oil droplets on polycarbonate substrate. The modality of the discussion will be as follows: first we shall characterize the “enclosure” formation and the dynamics intrinsic to it, and secondly we shall elaborate the size-based dynamics of the individual oil droplets, whose collective behavior is manifested as the “enclosure” formation. The key thing to note in Fig. 4(a,b,c) is how the oil droplets change from a random disoriented organization to a more ordered organization, manifesting the triggering of the “enclosure” effect. It can be easily seen that such ordering is most prominent at the location close to the TPCL, i.e., at the location where the “enclosure” effect is formed. In fact, an excellent representation of such ordering can be provided by noting the increase (with time) in number density of the oil droplets (smaller sized) at this region [see Fig. 5]. Also under the condition of the pinned contact-line mode of evaporation, there is a slight increase in the “enclosure” distance. This can be attributed to the lowering of the contact angle of the sessile drop, which brings the air–water interface closer to the substrate, thereby pushing back the oil droplets [see Fig. 6 for the schematic]. The other key information obtained from Fig. 4(a,b,c) is the dependence of the “enclosure” distance on the size of the oil droplets – larger droplets (on an average) are positioned at a much larger distance from the TPCL [also illustrated by eqn (3)].
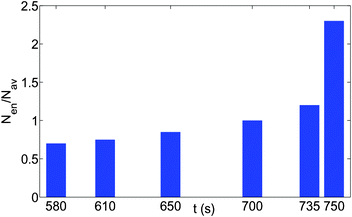 |
| | Fig. 5 The time variation of the number density (total number of oil droplets per unit area) of the smaller oil droplets at the location of the formation of the “enclosure” effect, Nen, made dimensionless with the average number density, Nav. The area of the “enclosure” region is the area of the radial strip which has an extension of 1/9 times the contact radius of the sessile drop. Therefore, we can define 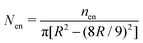 and and 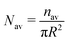 , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop, respectively. , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop, respectively. | |
![A schematic of the increase in the “enclosure” distance [x(t1) < x(t2), with t1 < t2; the part of the schematic shown in black bold lines represents the behavior at time t1, whereas that shown in red dashed lines represents the behavior at time t2] due to the decreasing contact angle during pinned contact line evaporation.](/image/article/2012/RA/c2ra20743e/c2ra20743e-f6.gif) |
| | Fig. 6 A schematic of the increase in the “enclosure” distance [x(t1) < x(t2), with t1 < t2; the part of the schematic shown in black bold lines represents the behavior at time t1, whereas that shown in red dashed lines represents the behavior at time t2] due to the decreasing contact angle during pinned contact line evaporation. | |
The above description of the formation of the “enclosure” effect needs to be discussed in the light of the size-based dynamics of the individual oil droplets, whose collective manifestation is the “enclosure” effect. Fig. 7(a) shows the temporal variation of the radial displacements of the two different sized oil droplets. These oil droplets are randomly chosen and we demonstrate their migration only in that time range in which the sessile-drop undergoes the pinned contact line mode of evaporation. The oil droplet motion can be divided into three distinct regimes. First (over a large time span) there is no movement of the oil droplets. This can be easily understood from eqn (20), where for a relatively large value of the sessile drop contact angle, the retentive force is substantially larger than the advective force. The second regime is characterized by the movement of the oil drops – this becomes possible as, owing to the substantial lowering of the sessile drop contact angle, the advective force on the oil droplets is significantly enhanced and becomes greater than the retentive force. Such a large increase in the advective transport at later stages of the evaporation can be associated to the temporal singularity of the flow velocity, as has been recently observed by Marin et al.9 There is a third regime, where the oil droplets are retarded on account of the interaction with the air–water interface and in the process leads to the formation of the “enclosure” effect. The mathematical model provided in eqn (20) is suitable only for predicting the dynamics in the second regime (and not the third regime), and in Fig. 7(b) we show the comparison of the results obtained from this model with the radial velocity values obtained from the experimental displacement values [for more details kindly see the caption of Fig. 7]. The trend matches pretty well, except for the higher time values where the “enclosure”-induced retardation becomes significant, which our theoretical model does not account for. Also note that only an oil droplet that is sufficiently close to the TPCL can be associated with a large enough initial radius location to cause the evaporation-induced migration – on the contrary, oil droplets that are close to the sessile drop center (barring the diverging situation of r → 0) never encounter such a large advective migration to outweigh the influence of the retentive force, and therefore always remains static.
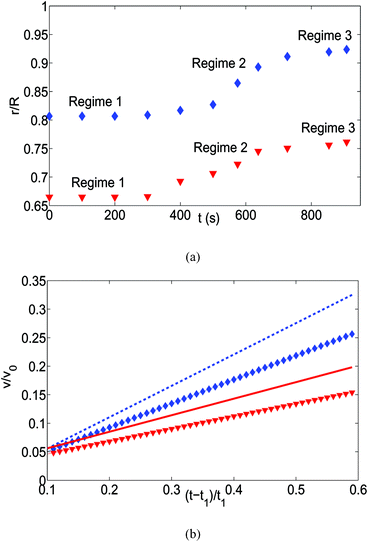 |
| | Fig. 7 (a) The time variation of the radial displacements of the oil droplets of two different sizes (blue diamond markers for smaller oil droplets and red triangle markers for larger oil droplets). The initial positions of the oil droplets are chosen close enough to the TPCL to ensure that the evaporation-triggered migration can overcome the retentive force and induce a finite migration of the oil droplets. (b) The temporal variation of the radial velocities (for regime 2) for the oil droplets of two different sizes. The experimental curves (blue line with diamond markers for smaller oil droplets and red line with triangle markers for larger oil droplets) are obtained by curve-fitting the time variation of the radial displacement (for regime 2) and taking the time derivative. These curve fits have the following equations: 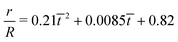 (for smaller oil droplets) and (for smaller oil droplets) and 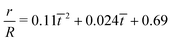 (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 400 s). Therefore v = dr/dt and v0 = R/t1. The theoretical curves (blue dashed line for smaller oil droplets and red bold line for larger oil droplets) use the following parameters: rc = 47 μm (for smaller oil droplets), rc = 94 μm (for larger oil droplets), + θa ≃ 49.5°, θr ≃ 40°, (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 400 s). Therefore v = dr/dt and v0 = R/t1. The theoretical curves (blue dashed line for smaller oil droplets and red bold line for larger oil droplets) use the following parameters: rc = 47 μm (for smaller oil droplets), rc = 94 μm (for larger oil droplets), + θa ≃ 49.5°, θr ≃ 40°, 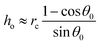 (where θ0 ≃ 45°), μ = 10−3 Pa s, γow ≃ 7 mN m−1, Dva = 24 × 10−6 m2 s−1, Δc = 1.2 × 10−2 kg m−3, R = 3.16 mm and ρ = 998 kg m−3. (where θ0 ≃ 45°), μ = 10−3 Pa s, γow ≃ 7 mN m−1, Dva = 24 × 10−6 m2 s−1, Δc = 1.2 × 10−2 kg m−3, R = 3.16 mm and ρ = 998 kg m−3. | |
The pinned contact line mode of evaporation is followed by the evaporation mode, where the contact line recedes. To discuss the dynamics of the oil droplets during this second mode of evaporation, we assign different hypothetical time values characterizing the different events. For example, let us denote by tc the time up to which the pinned contact line mode of evaporation occurs. Therefore, the description above corresponds to a time t, such that t < tc. Also, suppose te denotes the average time associated with the formation of the “enclosure” effect. Therefore, te refers to the time when oil droplets of different sizes have reached the location of closest approach to the contact line. We can even define tse and tle as the time necessary for the formation of the “enclosure” effect by the smaller and larger oil droplets respectively (with tle > tse). For the oil droplet dynamics on the polycarbonate substrate, we have tse < tc < tle. Therefore, we encounter a situation where the contact line starts to recede, and along with it recedes the smaller oil droplets that have already formed the “enclosure” effect; but the larger oil droplets that have not yet formed the “enclosure” effect migrate radially outwards towards the contact line. Therefore, we encounter a unique situation where there is a bidirectional motion of the oil droplets [see Fig. 8].
 |
| | Fig. 8 The dynamics of oil droplets on a polycarbonate substrate at times t, such that tse < tc < t < tle. The plot in (a) provides the schematic of the dynamics, with the part of the schematic shown in black bold lines representing the behavior at time smaller than that represented in red dashed lines. The plots in (b) and (c) provide experimental results corresponding to t = 943 s and t = 948 s, respectively. In (b) x2(t = 943 s) = 277 μm and in (c) x2(t = 948 s) = 190 μm, therefore clearly demonstrating that the larger oil droplets are moving towards the contact line. Also in (b) x1(t = 943 s) = 58 μm and in (c) x1(t = 948 s) = 59 μm, therefore clearly demonstrating that as the contact line retracts towards the drop center, the enclosure distance of the small oil droplets with the TPCL remains fixed. Consequently we have the bi-directional oil droplet motion. Also note that for this result, we have tse ∼ 820, tc ∼ 900 s and tle ∼ 950 s. In (b), we indicate the larger droplets with arrows. | |
There can be a third scenario, where we are looking at a time t such that t > tc and t > tle. At such a time, we shall have an entire “rigid-body” motion of the contact line and the oil droplets (forming the “enclosure” effect), and the “enclosure” distance remains constant [see Fig. 9]. This process characterizes the end of the life time of the sessile drop, with very little or no water left to be evaporated.
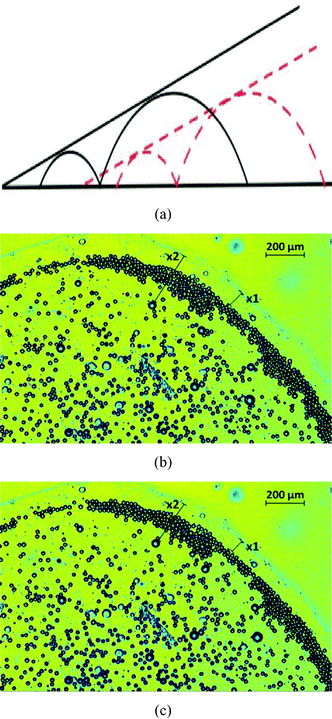 |
| | Fig. 9 The dynamics of oil droplets on a polycarbonate substrate at times t, such that t > tle and t > tc. The plot in (a) provides the schematic of the dynamics, with the part of the schematic shown in black bold lines representing the behavior at time smaller than that represented in red dashed lines. The plots in (b) and (c) provide experimental results corresponding to t = 958 s and t = 963 s respectively. Here there is only a minor change in values of x1 and x2 in figures (b) and (c), thereby clearly establishing a rigid body motion of the contact line and the oil droplets towards the drop center. The values of tc and tle are identical to that in Fig. 8. | |
4.2 Oil droplet dynamics on glass substrate
Fig. 10(a–c) give the time snapshots delineating the formation of the “enclosure” effect on the glass substrate. Similar to the case of the polycarbonate substrate, here too, the “enclosure” effect formation is characterized by a transition from of a disordered state of oil drops to a more ordered state, in particular in the “enclosure” region, as characterized by a temporal increase in the number density of the oil droplets in this region [see Fig. 11]. One thing, however, which is distinctly different from the polycarbonate case, is the time scale of formation of the enclosure effect. For the glass substrate the “enclosure” is formed in just 20–30 s, whereas for the polycarbonate it takes several hundreds of seconds. Two factors can be attributed for this behavior. Firstly, the relatively small initial value of the sessile drop contact angle ensures that the temporal singularity in the flow velocity (caused by the contact angle tending to zero)9 is triggered very quickly. Secondly, the very small contact angle hysteresis of the oil droplets (having large obtuse angle as equilibrium contact angles) ensures a very small value of cosθr − cosθa, so that the retentive force is substantially lowered, ensuring that the advective transport of oil droplets gets initiated much faster [see eqn (20)].
![The dynamics of oil droplets on glass captured at (a) t= 5 s, (b) t = 24 s and (c) t = 34 s. The enclosure distance measured in (c) ∼344 μm. The sessile drop contact angle measured at t = 34 s ∼3°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 329.4 μm (in this theoretical calculation, we use rc = 6.4 μm and θd ≈ θ0 ≈ 140°).](/image/article/2012/RA/c2ra20743e/c2ra20743e-f10.gif) |
| | Fig. 10 The dynamics of oil droplets on glass captured at (a) t= 5 s, (b) t = 24 s and (c) t = 34 s. The enclosure distance measured in (c) ∼344 μm. The sessile drop contact angle measured at t = 34 s ∼3°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 329.4 μm (in this theoretical calculation, we use rc = 6.4 μm and θd ≈ θ0 ≈ 140°). | |
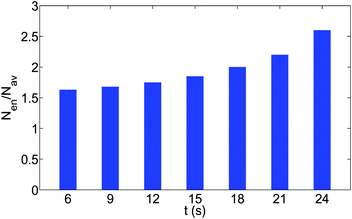 |
| | Fig. 11 The time variation of the number density (total number of oil droplets per unit area) of the smaller oil droplets at the location of the formation of the “enclosure” effect, Nen, made dimensionless with the average number density, Nav. The area of the “enclosure” region is the area of the radial strip which has an extension of 1/9 times the contact radius of the sessile drop. Therefore, we can define 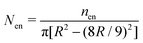 and and 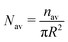 , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop respectively. , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop respectively. | |
Similar to the polycarbonate case, here too, we obtain the temporal variation of size-based displacements of the oil droplets [see Fig. 12]. The three regimes that are visible for the polycarbonate case are equally prevalent in the present case, although the time span for each of the processes is substantially smaller. Also, we do not have a measure of the exact value of the contact angle hysteresis for the oil droplet, neither we can predict the effect of the adsorbed surfactants on the contact of the oil droplet on the glass substrate – therefore we could not make a comparison of the velocity field obtained from the experimental displacement values and the theoretical model [e.g., Fig. 7(b)].
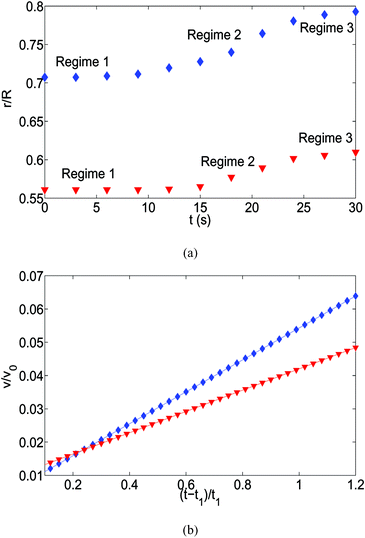 |
| | Fig. 12 (a) The time variation of the radial displacements of the oil droplets of two different sizes (blue diamond markers for smaller oil droplets and red triangle markers for larger oil droplets). The initial positions of the oil droplets are chosen close enough to the TPCL to ensure that the evaporation-triggered migration can overcome the retentive force and induce a finite migration of the oil droplets. (b) Experimental prediction of the temporal variation of the radial velocities (for regime 2) for the oil droplets of two different sizes. The curves (blue line with diamond markers for smaller oil droplets and red line with triangle markers for larger oil droplets) are obtained by curve-fitting the time variation of the radial displacement (for regime 2) and taking the time derivative. These curve fits have the following equations: 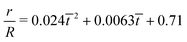 (for smaller oil droplets) and (for smaller oil droplets) and 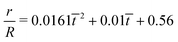 (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 9 s). Therefore v = dr/dt and v0 = R/t1 (here rc ≃ 6.4 μm for smaller oil droplets and rc ≃ 12.4 μm for larger oil droplets). (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 9 s). Therefore v = dr/dt and v0 = R/t1 (here rc ≃ 6.4 μm for smaller oil droplets and rc ≃ 12.4 μm for larger oil droplets). | |
Finally, the different post-“enclosure” behaviors that can be noted for the polycarbonate cannot be seen distinctly in the present case, owing to the exceptionally small time scales associated with these different behaviors.
Overall. we may infer that although the “enclosure” effects occur much faster for the oil droplets on the glass substrate, the different dynamical behaviors associated with the formation of the “enclosure” effect are much richer for the case of the polycarbonate substrate.
4.3 Separation and pattern formation: effects of the “enclosure” phenomenon
From Fig. 4, 10, it is clear that the “enclosure” effect can be associated with the size-based differentiation in the periodic rim formation – this is in accordance with the theoretical calculations [eqn (3)] demonstrating that the “enclosure” distance increases linearly with the contact radius of the oil droplets. Therefore, we get an automatic size-based separation of the oil droplets with the separation parameter varying linearly with the size of the droplets – this can be considered as the main effect of the “enclosure” phenomenon and one of the central results of our investigation. Thus, we demonstrate that in the process of evaporation of a sessile drop, the dispersed oil droplets show a spontaneous size-based separation dictated by their geometry and the physical condition that does not allow them to “see” the air. We have therefore identified a completely new method for size-based separation of liquid droplets. Please note that the evaporation-driven separation of particles/biomolecules, which is apparently very similar to the above effect, is well known.32,34 In fact in a recent study, Wong et al.34 demonstrated an evaporation-induced size-based separation of biomolecules, considering a hypothesis equivalent to this “enclosure” effect to explain the separation – the air–water interface was at a tangent to all the different macromolecules triggering a natural geometric selection [equivalent to Fig. 2]. The key physical idea used in this paper34 was that the capillary forces at the air–water interface exerted a push on the biomolecules opposite in direction to the evaporation-induced migration. In a previous study, Weon and Je35 demonstrated a similar phenomenon where the coffee particles in a “coffee stain” problem are retarded in their radially outward migration by the capillary interaction forces of the air–water interface. The particles are stopped by these air–water capillary interactions only when this retardation force is strong enough to outweigh the evaporation-triggered advective forces. Apparently, in our study the oil droplets are subjected to similar retarding air–water interface capillary interaction forces, making them stop at a certain distance from the TPCL, thereby forming the “enclosure” effect. However, the oil droplets experience an aversion to the air (dictated by the corresponding spreading parameter associated with the formation of the finite air–oil interface), which is physically different from the simple imparting of a retarding force by the air–water interface. In a more simple language, for sufficiently high particle velocities (in the papers of Wong et al.34 and Weon and Je35), the particles can actually overcome the air–water capillary retardation and approach closer to the TPCL; however, for our case such a phenomenon will never be possible owing to the large free energy barrier associated with the corresponding formation of the oil–air interface. Therefore, this “enclosure” effect is a unique characteristic of the liquid droplet based “coffee stain” phenomenon, distinctly different to apparently similar phenomena related to solid particles.34,35
The other phenomenon triggered by the “enclosure” effect is the creation of beautiful patterns of oil droplets [Fig. 4, 10 delineate such pattern formations that occur as the “enclosure” effect develops]. In this paper, we restrict ourselves to the dynamics of droplets of two sizes – therefore the pattern variety is relatively smaller. However, using this size based “enclosure” effect we can easily ensure a much richer pattern variety in the case where we use oil droplets of different possible sizes. Finally, at the end stages of the evaporation, where there is very little liquid left to keep the oil droplets separate, we observe beautiful patterns caused by self assembly of the oil droplets [see Fig. 13(a,b)] – this is the second major consequence of the “enclosure” effect formation.
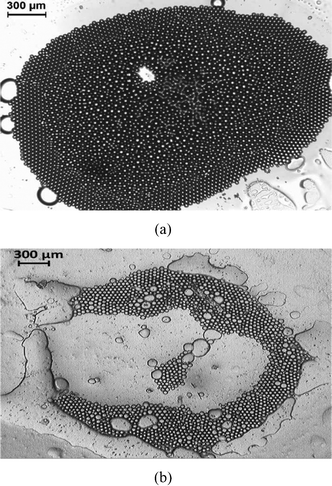 |
| | Fig. 13 Pattern formation by the self assembly of the oil droplets at the end stages of the evaporation (when most of the water has evaporated) for (a) glass substrate (captured at t = 100 s) and (b) polycarbonate substrate (captured at t = 2200 s). | |
5 Conclusions
In this paper, we provide the first investigation on the liquid-droplet based “coffee stain” phenomenon. Similar to the coffee particles in a classical “coffee stain” problem, here, the liquid droplets (which are micron sized bi-dispersed droplets of silicon oil) are advected towards the TPCL by the evaporation-triggered capillary flow inside the evaporating drop. However, in stark contrast to the coffee particle, the oil droplets cannot reach the TPCL, as the creation of the resulting air–oil interface is energetically unfavorable. Therefore, this is the first study on the “coffee stain” problem with appropriate consideration of the free energy penalty associated with the formation of the “coffee stain”. Such a unique situation is characterized by the location of the oil droplets at a given distance from the TPCL, and the physical mechanism responsible for such a scenario is distinctly different from apparently similar previous studies.34,35 We name this distance the “enclosure” distance, and this effect an “enclosure” effect. We provide a detailed theoretical explanation of the phenomenon and the theoretical prediction shows nice agreement with the experimental results. The “enclosure” effect is found to depend strongly on the size of the droplets, wettability of the substrate and the dynamics of the sessile drop evaporation. The net result is a novel size and substrate-property-based separation and pattern formation of the oil droplets, which will be extremely significant in microfluidic handling of oil droplets in soft media.
Acknowledgements
We acknowledge Dr D. S. Nobes, Optical Diagnostics Group, Department of Mechanical Engineering, University of Alberta for providing us with the Micronit droplet generator chip. We also gratefully acknowledge the financial support of ‘Alberta Innovates - Technology Futures’ in the form of scholarships for NSKG and PRW.
References
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827 CrossRef CAS.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 756 CrossRef CAS.
- R. D. Deegan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 475 CrossRef CAS.
- H. Hu and R. G. Larson, Langmuir, 2005, 21, 3963 CrossRef CAS.
- H. Hu and R. G. Larson, Langmuir, 2005, 21, 3972 CrossRef CAS.
- Y. O. Popov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036313 CrossRef.
- H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090 CrossRef CAS.
- W. D. Ristenpart, P. G. Kim, C. Domingues, J. Wan and H. A. Stone, Phys. Rev. Lett., 2007, 99, 234502 CrossRef CAS.
- A. G. Marin, H. Gelderblom, D. Lohse and J. H. Snoeijer, Phys. Rev. Lett., 2011, 107, 085502 CrossRef.
- H. Gelderblom, A. G. Marin, H. Nair, A. van Housselt, L. Lefferts, J. H. Snoeijer and D. Lohse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 026306 CrossRef.
- P. J. Yunker, T. Still, M. A. Lohr and A. G. Yodh, Nature, 2011, 476, 308–311 CrossRef CAS.
- G. McHale, Analyst, 2007, 132, 192–195 RSC.
- R. Blossey and A. Bosio, Langmuir, 2002, 18, 2952–2954 CrossRef CAS.
- Y. Kim, G. B. Hurst, M. J. Doktycz and M. V. Buchanan, Anal. Chem., 2001, 73, 2617–2624 CrossRef CAS.
- S. Choi, S. Stassi, A. P. Pisano and T. I. Zohdi, Langmuir, 2010, 26, 11690–11698 CrossRef CAS.
- M. Layani, M. Gruchko, O. Milo, I. Balberg, D. Azulay and S. Magdassi, ACS Nano, 2009, 3, 3537–3542 CrossRef CAS.
- H. Bodiguel, F. Doumenc and B. Guerrier, Langmuir, 2010, 26, 10758–10763 CrossRef CAS.
- J. X. Huang, A. R. Tao, S. Connor, R. R. He and P. D. Yang, Nano Lett., 2006, 6, 524–529 CrossRef CAS.
- H. B. Eral, D. M. Augustine, M. H. G. Duits and F. Mugele, Soft Matter, 2011, 7, 4954–4958 RSC.
- P. Colinet and A. Rednikov, Eur. Phys. J. Spec. Top., 2011, 197, 89 CrossRef CAS.
- B. J. Fischer, Langmuir, 2002, 18, 60 CrossRef CAS.
- B. J. Masoud and J. D. Felske, Phys. Fluids, 2009, 21, 042102 CrossRef.
- A. J. Petsi and V. N. Burganos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036324 CrossRef CAS.
- C. Poulard, G. Guena, A.-M. Cazabat, A. Boudaoud and M. B. Amar, Langmuir, 2005, 21, 8226 CrossRef CAS.
- S. Maheshwari, L. Zhang, Y. Zhu and H.-C. Chang, Phys. Rev. Lett., 2008, 100, 0044503 CrossRef.
- R. van Hameren, P. Schön, A. M. van Buul, J. Hoogboom, S. V. Lazarenko, J. W. Gerritsen, H. Engelkamp, P. C. M. Christianen, H. A. Heus, J. C. Maan, T. Rasing, S. Speller, A. E. Rowan, J. A. A. W. Elemans and R. J. M. Nolte, Science, 2006, 314, 1433 CrossRef CAS.
- Q. W. Li, Y. T. Zhu, I. A. Kinloch and A. H. Windle, J. Phys. Chem. B, 2006, 110, 13926 CrossRef CAS.
- X. M. Lin, G. M. Wang, C. M. Sorensen and K. J. Klabunde, J. Phys. Chem. B, 1999, 103, 5488 CrossRef CAS.
- D. Brutin, B. Sobac, B. Loquet and J. Sampol, J. Fluid Mech., 2011, 667, 85–95 CrossRef CAS.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- J.-Y. Jung, Y. W. Kim and J. Y. Yoo, Anal. Chem., 2009, 81, 8256–8259 CrossRef CAS.
- V. H. Chhasatia and Y. Sun, Soft Matter, 2011, 7, 10135–10143 RSC.
- T.-S. Wong, T.-H. Chen, X. Shen and C.-M. Ho, Anal. Chem., 2011, 83, 1871–1873 CrossRef CAS.
- B. M. Weon and J. H. Je, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 015305(R) CrossRef.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366 CrossRef CAS.
- C. F. Zhou, P. T. Yue and J. J. Feng, Phys. Fluids, 2006, 18, 092105 CrossRef.
- Y. C. Tan, V. Cristini and A. P. Lee, Sens. Actuators, B, 2006, 114, 350–356 CrossRef.
- A. Woodward, T. Cosgrove, J. Espidel, P. Jenkins and N. Shaw, Soft Matter, 2007, 3, 627–633 RSC.
- L. Yobas, S. Martens, W. L. Ongand and N. Ranganathan, Lab Chip, 2006, 6, 1073–1079 RSC.
- N. S. K. Gunda, B. Bera, N. K. Karadimitriou, S. K. Mitra and S. M. Hassanizadeh, Lab Chip, 2011, 11, 3785–3792 RSC.
- S. Basu, K. Nandakumar and J. H. Masliyah, J. Colloid Interface Sci., 1997, 190, 253–257 CrossRef CAS.
- X. Deng, L. Mammen, H.-J. Butt and D. Vollmer, Science, 2012, 335, 67–70 CrossRef CAS.
- D. Kumar and S. K. Biswas, Colloids Surf., A, 2011, 377, 195–204 CrossRef CAS.
- A. Patist, S. S. Bhagwat, K. W. Penfield, P. Aikens and D. O. Shah, J. Surfactants Deterg., 2000, 3, 53 CrossRef CAS.
- O. Raccurt, J. Berthier, P. Clementz, M. Borella and M. Plissonnier, J. Micromech. Microeng., 2007, 17, 2217 CrossRef CAS.
- W. K. Chan and C. Yang, J. Micromech. Microeng., 2005, 15, 1722–1728 CrossRef CAS.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–660 CrossRef CAS.
- M. E. ONeill, Chem. Eng. Sci., 1968, 23, 1293–1298 CrossRef CAS.
- C. W. Extrand and A. N. Gent, J. Colloid Interface Sci., 1990, 138, 431–442 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ra20743e |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 


![The dynamics of oil droplets on polycarbonate captured at (a) t = 580 s, (b) t = 745 s and (c) t = 750 s. The enclosure distance measured in (c) ∼50 μm. The sessile drop contact angle measured at t = 750 s ∼ 10°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 53 μm (in this theoretical calculation, we use rc = 47 μm and θd ≈ θ0 ≈ 45°).](/image/article/2012/RA/c2ra20743e/c2ra20743e-f4.gif)
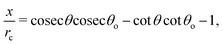
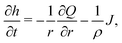
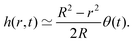
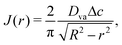
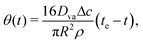
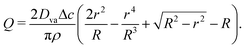
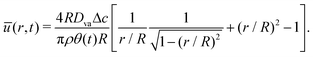
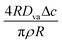 .
.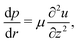
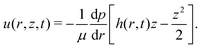
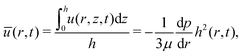
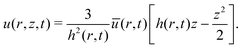
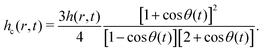
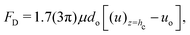
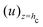 is the flow field evaluated at the center of mass of the wetted oil droplet, do is the effective diameter of the oil droplet and uo is the sliding velocity of the oil droplet. Here, while calculating do, one needs to account for the deformation of the drop during sliding. Therefore, do will be expressed in terms of the deformed volumes V1 and V2 so that following42:
is the flow field evaluated at the center of mass of the wetted oil droplet, do is the effective diameter of the oil droplet and uo is the sliding velocity of the oil droplet. Here, while calculating do, one needs to account for the deformation of the drop during sliding. Therefore, do will be expressed in terms of the deformed volumes V1 and V2 so that following42: 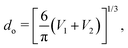
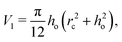
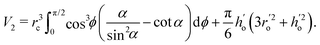
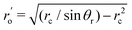 , ho′ = ro′tanθr − ro′/cosθr and α = π − tan−1(−tanθdcosφ) (where θd is the dynamic contact angle expressed as θd = 2φθr/π − (1 − 2φ/π)θa). In these expressions, θa and θr are the advancing and the receding contact angles of the wetted oil droplet and rc is the contact radius of the sessile drop.
, ho′ = ro′tanθr − ro′/cosθr and α = π − tan−1(−tanθdcosφ) (where θd is the dynamic contact angle expressed as θd = 2φθr/π − (1 − 2φ/π)θa). In these expressions, θa and θr are the advancing and the receding contact angles of the wetted oil droplet and rc is the contact radius of the sessile drop.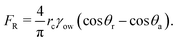
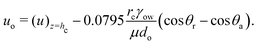
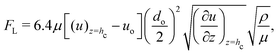
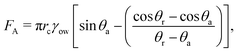
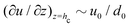 we can obtain:
we can obtain: 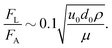
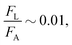

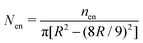 and
and 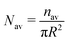 , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop, respectively.
, where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop, respectively.![A schematic of the increase in the “enclosure” distance [x(t1) < x(t2), with t1 < t2; the part of the schematic shown in black bold lines represents the behavior at time t1, whereas that shown in red dashed lines represents the behavior at time t2] due to the decreasing contact angle during pinned contact line evaporation.](/image/article/2012/RA/c2ra20743e/c2ra20743e-f6.gif)

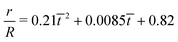 (for smaller oil droplets) and
(for smaller oil droplets) and 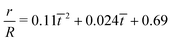 (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 400 s). Therefore v = dr/dt and v0 = R/t1. The theoretical curves (blue dashed line for smaller oil droplets and red bold line for larger oil droplets) use the following parameters: rc = 47 μm (for smaller oil droplets), rc = 94 μm (for larger oil droplets), + θa ≃ 49.5°, θr ≃ 40°,
(for larger oil droplets), where t = (t − t1)/t1 (with t1 = 400 s). Therefore v = dr/dt and v0 = R/t1. The theoretical curves (blue dashed line for smaller oil droplets and red bold line for larger oil droplets) use the following parameters: rc = 47 μm (for smaller oil droplets), rc = 94 μm (for larger oil droplets), + θa ≃ 49.5°, θr ≃ 40°, 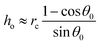 (where θ0 ≃ 45°), μ = 10−3 Pa s, γow ≃ 7 mN m−1, Dva = 24 × 10−6 m2 s−1, Δc = 1.2 × 10−2 kg m−3, R = 3.16 mm and ρ = 998 kg m−3.
(where θ0 ≃ 45°), μ = 10−3 Pa s, γow ≃ 7 mN m−1, Dva = 24 × 10−6 m2 s−1, Δc = 1.2 × 10−2 kg m−3, R = 3.16 mm and ρ = 998 kg m−3.

![The dynamics of oil droplets on glass captured at (a) t= 5 s, (b) t = 24 s and (c) t = 34 s. The enclosure distance measured in (c) ∼344 μm. The sessile drop contact angle measured at t = 34 s ∼3°, so that the theoretical prediction of the “enclosure” effect [following eqn (3)] is 329.4 μm (in this theoretical calculation, we use rc = 6.4 μm and θd ≈ θ0 ≈ 140°).](/image/article/2012/RA/c2ra20743e/c2ra20743e-f10.gif)

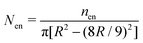 and
and 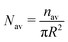 , where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop respectively.
, where nen and nav are the total number of wetted oil droplets in the “enclosure” region and the entire drop respectively.
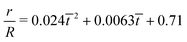 (for smaller oil droplets) and
(for smaller oil droplets) and 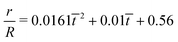 (for larger oil droplets), where t = (t − t1)/t1 (with t1 = 9 s). Therefore v = dr/dt and v0 = R/t1 (here rc ≃ 6.4 μm for smaller oil droplets and rc ≃ 12.4 μm for larger oil droplets).
(for larger oil droplets), where t = (t − t1)/t1 (with t1 = 9 s). Therefore v = dr/dt and v0 = R/t1 (here rc ≃ 6.4 μm for smaller oil droplets and rc ≃ 12.4 μm for larger oil droplets).
