Nylon 6 depolymerization in supercritical alcohols studied by the QM/MC/FEP method
Thanayuth
Kaweetirawatt
ab,
Toru
Yamaguchi
b,
Shota
Hayashiyama
b,
Michinori
Sumimoto
b,
Akio
Kamimura
c and
Kenji
Hori
*b
aUbe Technical Center (Asia) Co., Ltd, 140/8 Moo4, Tambol Tapong, Rayong, Muang Rayong 21000, Thailand
bGraduate School of Science and Engineering, Yamaguchi University, 2-16-1 Tokiwadai, Ube, Yamaguchi, 755-8611, Japan. E-mail: kenji@yamaguchi-u.ac.jp
cGraduate School of Medicine, Yamaguchi University, 2-16-1 Tokiwadai, Ube, Yamaguchi, 755-8611, Japan
First published on 9th August 2012
Abstract
Nylon 6 depolymerization in supercritical (SC) alcohols was theoretically studied using the QM/MC/FEP method. All geometry optimizations and the Gibbs free energy calculation in the gas phase were calculated at the B3LYP/6-31++G(d,p) level of theory. The effect of different types of alcohols, methanol (MeOH) and isopropanol (iPrOH), is the focus on this investigation. There are two candidates for the depolymerization mechanism. One is an intermolecular mechanism (Rxn A), which produces aminocaproic ester as the major product. The other is an intramolecular mechanism (Rxn B), directly giving ε-caprolactam. The activation free energies (ΔG‡rxn) of Rxn A in the two alcohols are lower by 8–9 kcal mol−1 than those of Rxn B. Thus, the calculated rate constants (k) of Rxn A are much larger than those of Rxn B. The cyclization route to the aminocaproic ester is preferable by more than 15.0 kcal mol−1 to the alkylation at the amino group, and aminocaproic ester exclusively produces ε-caprolactam. The further reaction of ε-caprolactam, such as N-alkylation, is able to proceed only in MeOH. The activation free energies of the cyclization of aminocaproic acid are almost the same as those of the aminocaproic ester in the SC alcohols.
Introduction
Supercritical Fluids (SCFs) are recognized as a useful reaction media for processing polymers and many applications have been proposed so far. For example, SCFs have been used to extract low-molecular weight compounds (typically monomers) from polymers.1 The use of supercritical water (SCW) has been widely investigated for the depolymerization of PET,2–5 which was readily converted into its monomers, terephthalic acid (TPA) and ethylene glycol (EG), and the yield of TPA reached almost 100%.6 In addition, extensive studies have been carried out for the degradation of polystyrene (PS) in supercritical acetone7 and materials with a high degree of cross-linking polymers, such as tires and natural rubber, in SCW.8The worldwide production of ε-caprolactam for nylon 6 in the year 2000 was ca. 4.0 million tons.9 The depolymerization of nylon 6 to recycle ε-caprolactam by hydrothermal decomposition10 and SCFs has also been thoroughly investigated. For example, Goto and co-workers11–13 investigated the depolymerization of nylon 6 in SCW. The total yield of monomers was almost 100%. Both ε-caprolactam and aminocaproic acid were detected in the products. The yield of the acid decreased rapidly as the reaction time increased. Therefore, they concluded that the hydrolysis of nylon 6 produced aminocaproic acids first, which underwent subsequent cyclodehydration to afford ε-caprolactam. The subsequent further decomposition of caprolactam gave as the final product a mixture of small molecules. Their results were consistent with the depolymerization of nylon 66 in SCW.14 The reaction started with C–N bond cleavage in the amide group to give adipic acid and hexanediamine at a stage in the reaction. The subsequent cyclization of the initial products produced cyclopentanone and cycloheptylamine.
We have also investigated the depolymerization of nylon 6 in supercritical (SC) alcohols.15 Our results showed that use of secondary and tertiary alcohols resulted in the formation of ε-caprolactam in yields of more than 90%, while primary alcohols were not effective for this purpose. For example, the yield of ε-caprolactam was 91% in SC isopropanol (iPrOH), which was close to 95% in SC tertbutanol (tBuOH), while treatment of nylon 6 with SC methanol (MeOH) only gave ε-caprolactam in a 14% yield. The depolymerization mechanisms in those alcohols were expected to be the same.
There are two possible candidates for the reaction pathways (Fig. 1). The first one is Rxn A, which is similar to the mechanism Goto11–13 and Meng14 reported. In the intermolecular reaction Rxn A, alcohol molecules serve as one of the reactants that randomly attack the carbonyl groups in the polyamide chains to produce aminocaproic esters. The subsequent cyclization produces ε-caprolactam (Rxn C). According to our previous experimental study,16 it is possible to consider another reaction pathway, the intramolecular reaction (Rxn B), in which the cleavage at the amino-terminus leads depolymerization and cyclization to produce ε-caprolactam simultaneously.
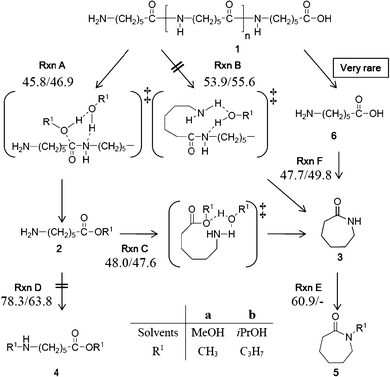 | ||
| Fig. 1 Reaction pathways of nylon 6 depolymerization in this study. | ||
Computer simulation is a very useful tool to not only supply missing experimental data for chemical reactions in solvents, but also obtain information about the solvation structures and their influences on energy barriers to reactions.17,18 The QM/MC/FEP method19–21 is an advanced scheme that calculates the solvent effects on the chemical reaction. The method generates random configurations of the solvent by a Monte Carlo (MC) simulation,22–26 including quantum mechanical (QM) calculations and free energy perturbation (FEP) theory to calculate the free energy of solvation (ΔGsol). It is more attractive than the usual methods because the method needs neither the dielectric constant used for the self-consistent reaction field (SCRF) method27 nor the classical parameters of the solvents needed for molecular dynamics (MD) calculations.28,29 Therefore, QM/MC/FEP calculations are more convenient than QM/MD simulations.30 However the QM/MC/FEP method requires longer CPU times than that of other methods such as QM/MM simulations.31
SCFs possess both a high solubility for organic compounds and a high-degree of dispersion.32–35 It is possible to perform MC simulations under the conditions of high temperature and high pressure used in SCFs. In this study we concentrate on the depolymerization mechanism of nylon 6 in SC alcohols. The mechanistic investigation for the depolymerization reaction was performed using dimeric aminocaproic acid (a dimer of –NH (CH2)5CO–) as a model of the nylon polymer and mechanistic analyses of the reaction were carried out using the two types of alcohol, methanol (MeOH) and isopropanol (iPrOH). The QM/MC/FEP method helped to understand the bulk solvent effects of the alcohols.
In this paper, we attempted to elucidate the mechanisms of the intermolecular (Rxn A) and intramolecular (Rxn B) reactions. In an alcohol solvent, both mechanisms rarely produce aminocaproic acid because only the O-terminus fragment of nylon 6, which ends with the acidic function (COOH), cannot form such an acid. However, the depolymerization under aqueous or wet solvent conditions may give a lot of the acids and their cyclization becomes important under such conditions.36 The cyclization and the N-alkylation of aminocaproic ester (Rxn C and Rxn D, respectively) were compared in order to ascertain that Rxn C is the suitable pathway to proceed and give ε-caprolactam as detected in our experiment.16 We also examined the N-alkylation of ε-caprolactam (Rxn E) to clarify the difference in the reaction course between SC MeOH and SC iPrOH. The cyclization reaction from aminocaproic acid (Rxn F) was also mentioned in the last section.
Methods
Solute calculations
For all the geometry optimizations and activation free energy calculations in the gas phase (ΔG‡gas), the B3LYP/6-31++G(d,p) level of theory in the Gaussian03 program37 was adopted at 643.0 K, 348.4 atm for MeOH and 643.0 K, 218.1 atm for iPrOH.15 These values correspond to the supercritical conditions of those solvents. Intrinsic reaction coordinate (IRC) structures38,39 of the reactions were also obtained for the QM/MC/FEP calculations.QM/MC/FEP calculations
We adopted droplet models for MC simulations in the NPT ensemble.26 Each droplet included a solute molecule in its center and many surrounding solvent molecules. MeOH and iPrOH molecules as the solvents, with the optimized geometry at the B3LYP/6-31++G(d,p) level of theory, were distributed randomly within a spherical droplet with a radius r = 10.0 Å. The solvent density, 0.400 (g cm−3),15 related directly to the number of solvent molecules in the droplet. The volume of the solute and solvent was calculated using van der Waals radii.The 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of MC simulations were used with the Metropolis Sampling Algorithm. The first half of the simulation (20
000 steps of MC simulations were used with the Metropolis Sampling Algorithm. The first half of the simulation (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps) was used to equilibrate the droplet and the second half to perform statistical calculations at 643.0 K. The maximum allowed displacement (α) was 0.06 Å/step and the maximum allowed angle of rotation (β) was 0.12 rad/step. The PM3 Hamiltonian of the MOPAC2000 program was adopted for calculating the bulk effects of solvent.40,41 We previously discussed the quality of the PM3 Hamiltonian.21 The QM/MC/FEP method requires perturbed structures for the FEP calculations. For this purpose, we used structures obtained from the IRC calculations; 100 steps between s = −0.5 to 0.5 amu1/2 Bohr. Moreover, 100 structures were produced by interpolating a tail structure of an IRC calculation and that of reactant or product and used for the FEP calculations.21 For instance, the potential energy profile and geometry transformation of Rxn B along the reaction coordinates are shown in Fig. 2. The geometries of the reactant and product were optimized using the tail structures of the IRC calculations. The activation free energies of the reaction (ΔG‡rxn) were calculated by adding ΔG‡sol to ΔG‡gas.21 The rate constants of the reactions were calculated by using the theory of absolute reaction rates by Eyring.42
000 steps) was used to equilibrate the droplet and the second half to perform statistical calculations at 643.0 K. The maximum allowed displacement (α) was 0.06 Å/step and the maximum allowed angle of rotation (β) was 0.12 rad/step. The PM3 Hamiltonian of the MOPAC2000 program was adopted for calculating the bulk effects of solvent.40,41 We previously discussed the quality of the PM3 Hamiltonian.21 The QM/MC/FEP method requires perturbed structures for the FEP calculations. For this purpose, we used structures obtained from the IRC calculations; 100 steps between s = −0.5 to 0.5 amu1/2 Bohr. Moreover, 100 structures were produced by interpolating a tail structure of an IRC calculation and that of reactant or product and used for the FEP calculations.21 For instance, the potential energy profile and geometry transformation of Rxn B along the reaction coordinates are shown in Fig. 2. The geometries of the reactant and product were optimized using the tail structures of the IRC calculations. The activation free energies of the reaction (ΔG‡rxn) were calculated by adding ΔG‡sol to ΔG‡gas.21 The rate constants of the reactions were calculated by using the theory of absolute reaction rates by Eyring.42
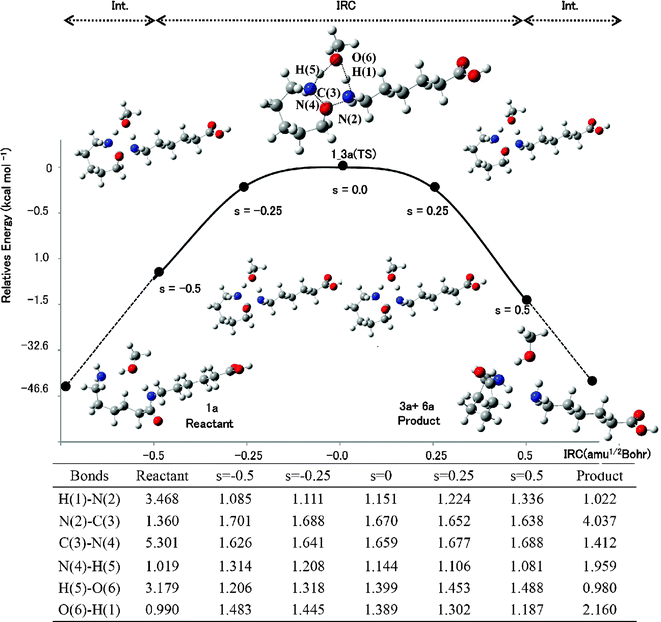 | ||
| Fig. 2 The potential energy profile and geometry transformation along the reaction coordinate of Rxn B in MeOH. The unit of length is Å. | ||
Results and discussion
Depolymerization mechanism
Alcohol molecules such as MeOH and iPrOH are involved in Rxn A and Rxn B and act as one of the reactants. Fig. 3 displays the transition state (TS) structures with MeOH, 1_2a(TS) and 1′_3a(TS) respectively. The dimer with two MeOH molecules in Rxn A is designated 1a and the dimer with one MeOH molecule in Rxn B is 1′a. The bond lengths of the TS structures with MeOH or iPrOH are listed in Table 1.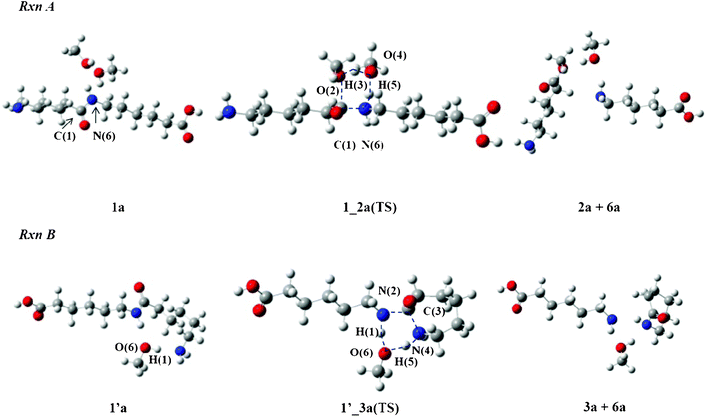 | ||
| Fig. 3 Reaction mechanisms of Rxn A and Rxn B in MeOH. | ||
| Reactions | Solvent | Bond Length | |||||
|---|---|---|---|---|---|---|---|
| a Values in parenthesis are lengths in 1 and 1′. | |||||||
| A | C(1)–O(2) | O(2)–H(3) | H(3)–O(4) | O(4)–H(5) | H(5)–N(6) | C(1)–N(6) | |
| MeOH | 2.039 | 1.219 | 1.188 | 1.451 | 1.122 | 1.567 (1.373)a | |
| iPrOH | 2.115 | 1.237 | 1.177 | 1.477 | 1.110 | 1.563 (1.388)a | |
| B | H(1)–N(2) | N(2)–C(3) | C(3)–N(4) | N(4)–H(5) | H(5)–O(6) | H(1)–O(6) | |
| MeOH | 1.151 | 1.670 | 1.659 | 1.144 | 1.399 | 1.389 (0.990)a | |
| iPrOH | 1.151 | 1.667 | 1.661 | 1.134 | 1.426 | 1.398 (0.989)a | |
Rxn A accompanies proton transfers between the amide group of the dimer and two MeOH molecules. The process causes breaking of the C(1)–N(6) bond and produces aminocaproic ester (2a) and aminocaproic acid (6a) as the products. The O(2) atom in 1_2a(TS) donates its H(3) proton to the O(4) atom of the other MeOH molecule. The lengths of O(2)–H(3) and H(3)–O(4) were calculated to be 1.219 and 1.188 Å, respectively. On the other hand, the O(4) atom donates its H(5) proton to the N(6) atom of the amide group. The O(4)–H(5) and H(5)–N(6) lengths were calculated to be 1.451 and 1.122 Å, respectively. The C(1)–N(6) length is longer by 0.194 Å than that in 1a. The TS structure with iPrOH, 1_2b(TS), is similar to that of 1_2a(TS). The largest difference is seen in the C(1)–O(2) length (2.115 Å), which is longer by 0.076 Å than that of 1_2a(TS).
Rxn B producing ε-caprolactam 3 involves one alcohol molecule in the mechanism. In the 1′_3a(TS) structure, the O(6) atom donates its H(1) proton to the N(2) atom and receives another H(5) proton from the N(4) atom of the amino group. The H(1)–N(2) and H(1)–O(6) lengths were calculated to be 1.151 and 1.389 Å while the N(4)–H(5) and H(5)–O(6) lengths were 1.144 and 1.399 Å, respectively. As the N(2)–C(3) and C(3)–N(4) lengths were found to be 1.670 and 1.659 Å, respectively, it can be deduced that the C(3) atom leaves the N(2) atom for the N(4) atom in order to complete the cyclization process. The geometrical parameters of the related TS structure with an iPrOH molecule are similar to those with a MeOH molecule. For example, the H(1)–N(2) and H(1)–O(6) lengths of 1′_3b(TS) were calculated to be 1.151 and 1.398 Å, respectively, and the N(4)–H(5) and H(5)–O(6) lengths were found to be 1.134 and 1.426 Å, respectively.
The relative differences in the activation free energies are summarized in Table 2. The ΔG‡gas value for 2a is 46.1 kcal mol−1 while that for 3a is 52.8 kcal mol−1. The former is smaller by 6.7 kcal mol−1 than the latter. The ΔG‡gas values for 2b and 3b were computed to be 47.4 and 52.6 kcal mol−1, respectively, and the difference is 5.2 kcal mol−1.
| Solvents | Kinetics | Reactions | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| MeOH | ΔG‡gas | 46.1 | 52.8 | (46.1) 50.9 | 77.9 | 67.8 | (36.8) 49.4 |
| kA/kB = 566.4 | ΔG‡sol | −0.3 | 1.1 | (−1.2) −2.9 | 0.4 | −6.9 | −1.7 |
| kC kD−1 = 1.99 × 1010 | ΔG‡rxn | 45.8 | 53.9 | (44.9) 48.0 | 78.3 | 60.9 | 47.7 |
| k (s−1) | 3.63 × 10−3 | 6.41 × 10−6 | 6.49 × 10−4 | 3.26 × 10−14 | 2.68 × 10−8 | 8.21 × 10−4 | |
| iPrOH | ΔG‡gas | 47.4 | 52.6 | (43.5) 52.6 | 60.2 | — | (39.6) 48.3 |
| kA/kB = 905.9 | ΔG‡sol | −0.5 | 3.0 | (−0.6) −5.6 | 3.6 | — | 1.5 |
| kC kD−1 = 5.13 × 105 | ΔG‡rxn | 46.9 | 55.6 | (42.9) 47.0 | 63.8 | — | 49.8 |
| k (s−1) | 1.54 × 10−3 | 1.69 × 10−6 | 1.42 × 10−3 | 2.77 × 10−9 | — | 1.59 × 10−4 | |
The bulk solvent effects , ΔG‡sol, under supercritical conditions are small and negative with typical values such as −0.3 and −0.5 kcal mol−1 for Rxn A in MeOH and iPrOH, respectively. They result in ΔG‡rxn values of 45.8 kcal mol−1 for MeOH and 46.9 kcal mol−1 for iPrOH. On the other hand, the bulk solvent effects are slightly large and positive for Rxn B, i.e., the values were calculated to be 1.1 and 3.0 kcal mol−1 in MeOH and iPrOH, respectively. Therefore, the ΔG‡rxn values of Rxn B obtained were 53.9 kcal mol−1 and 55.6 kcal mol−1 for MeOH and iPrOH. Inclusion of the alcohol molecules as the reactants is very important to clearly express the enthalpy factor of the solvent effects for the depolymerization reaction. This suggests that there are almost no bulk solvent effects in the SC alcohols.
In summary, the ΔG‡rxn values of Rxn A are smaller than those of Rxn B by 8–9 kcal mol−1. Therefore, the depolymerization of nylon 6 viaRxn A is more favorable than that via the intramolecular process (Rxn B). Consequently, the first major product is 2. The calculations reveal that the difference in the ΔG‡rxn values for Rxn A between the reaction in MeOH and the reaction in iPrOH is only 2.0 kcal mol−1.
Reactions after depolymerization
There are two possible reactions after forming compound 2. One is the formation of ε-caprolactam (Rxn C) and the other is N-alkylation of the terminal amino group (Rxn D). Because the preferred geometries of 2 are different between Rxn C and Rxn D, we show the abbreviation 2 and 2′ to designate its starting geometry for the reactions. The cyclization (Rxn C) is first analyzed. Fig. 4 displays the TS structures in MeOH and iPrOH, 2_3a(TS) and 2_3b(TS). The O(2) atom of the ester group interacts with the H(3) atom of the MeOH molecule and leaves the C(1) atom to form another MeOH molecule. The C(1)–O(2) and O(2)–H(3) distances were calculated to be 2.007 and 1.238 Å, respectively, which are listed in Table 3. While the O(4) atom attracts the H(5) proton of the amino group, the N(6) atom forms a covalent bond with the C(1) atom to produce 3. The O(4)–H(5) and C(1)–N(6) lengths were calculated to be 1.400 and 1.547 Å, respectively. The geometry of 2_3b(TS) is slightly different from that of 2_3a(TS), except for the C(1)–O(2) length. The length of the former differs by 0.067 Å from that of the latter. The IRC calculations confirm that the TS structure connects 2 and 3.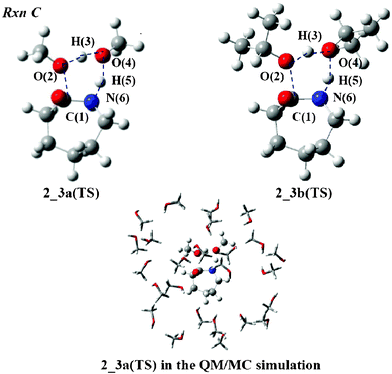 | ||
| Fig. 4 TS structures of Rxn C with MeOH and iPrOH molecules. | ||
| Bond lengths | MeOH | iPrOH |
|---|---|---|
| Reactant geometry | ||
| C | ||
| 2 H(1)–O(2) | 2.746 | 2.965 |
| 2 H(3)–N(4) | 1.916 | 1.930 |
| 2* H(3)–N(4) | 1.905 | 1.929 |
| D | ||
| N(1)–H(7) | 2.530 | — |
| H(2)–O(3) | 2.121 | 2.292 |
| O(3)–H(4) | 0.977 | 1.946 |
| H(4)–O(5) | 1.851 | — |
| E | ||
| N(1)–H(2) | 1.968 | — |
| O(2)–H(5) | 1.858 | — |
| O(6)–H(7) | 2.121 | — |
| MeOH | iPrOH | |
| TS geometry | ||
| Bond lengths | C | |
| C(1)–O(2) | 2.007 | 2.074 |
| O(2)–H(3) | 1.238 | 1.259 |
| H(3)–O(4) | 1.179 | 1.165 |
| O(4)–H(5) | 1.400 | 1.430 |
| H(5)–N(6) | 1.147 | 1.130 |
| C(1)–N(6) | 1.547 | 1.542 |
| D | ||
| N(1)–H(2) | 1.025 | 1.038 |
| H(2)–O(3) | 2.000 | 1.706 |
| O(3)–H(4) | 1.007 | 1.621 |
| H(4)–O(5) | 1.622 | — |
| O(5)–C(6) | 2.072 | — |
| N(1)–C(6) | 2.087 | — |
| O(3)–C(5) | — | 2.496 |
| N(1)–C(5) | — | 2.565 |
| E | ||
| N(1)–C(4) | 1.751 | — |
| N(1)–H(7) | 1.021 | — |
| O(3)–C(4) | 2.228 | — |
| O(3)–H(5) | 1.512 | — |
| H(5)–O(6) | 1.039 | — |
| O(6)–H(7) | 3.655 | — |
Fig. 5 displays the reactant structures optimized from the ends of the IRC calculations using 2_3a(TS) and 2_3b(TS) for Rxn C. Two structures were optimized: one is a bent structure 2 and the other is a linear structure 2*. In both reactions using MeOH and iPrOH, the linear structure 2* is more stable than the bent structure 2, i.e., 2*a is more stable than 2a by 4.8 kcal mol−1 and 2*b is more stable than 2b by 9.1 kcal mol−1, respectively. Therefore, 2* should be taken as the reactant for Rxn C. The ΔG‡gas values of Rxn C were determined to be 50.9 and 52.6 kcal mol−1 for MeOH and iPrOH, respectively.
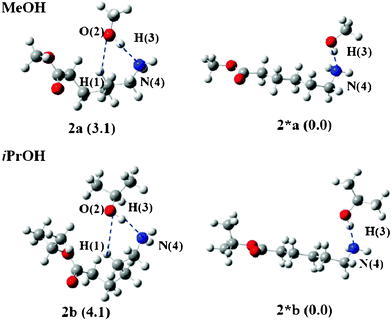 | ||
| Fig. 5 Bent (2) and linear (2*) geometries of the reactant of Rxn C. The values in parenthesis are free energy differences between 2 and 2*. | ||
The ΔG‡rxn(MeOH) value of Rxn C was calculated to be 48.0 kcal mol−1 whereas the ΔG‡rxn(iPrOH) value was found to be 47.0 kcal mol−1. These are smaller than the ΔG‡gas values since the QM/MC/FEP calculations give negative values of ΔG‡sol(MeOH) and ΔG‡sol(iPrOH), such as −2.9 and −5.6 kcal mol−1, respectively. As seen in Fig. 4, the MeOH molecules of the solvent fully surround the solute 2_3a(TS) at the center of the droplet. The density of the solvent under SC conditions is low so that the solute–solvent interaction is expected to be smaller than that under normal conditions. In spite of the fact that the alcohol solvents are different, the ΔG‡rxn values of Rxn C differ by only 1.0 kcal mol−1.
We next examine the N-alkylation process (Rxn D) to the amino group of 2. Two alcohol molecules are also involved in this mechanism. Fig. 6 depicts the TS structures of 2′_4a(TS) and 2′_4b(TS). In 2′_4a(TS), the H(2) atom does not escape from the N(1) atom for the O(3) atom because the length of N(1)–H(2) is 1.025 Å, as listed in Table 3. The O(5)–C(6) bond is cleaved and the N(1)–C(6) bond is formed since the lengths were computed to be 2.072 and 2.087 Å, respectively. 2′a, the reactant from the IRC calculation, consists of a three-hydrogen-bond network connecting the aminocaproic ester to two MeOH molecules.
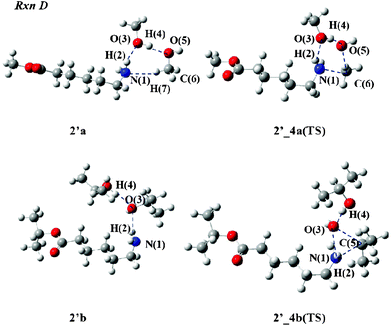 | ||
| Fig. 6 Reactant and TS structures of Rxn D with alcohol molecules. | ||
In the 2′_4b(TS) geometry, the H(2) atom associates with the N(1) atom: the bond lengths of N(1)–H(2) (1.038 Å) and H(2)–O(3) (1.706 Å) are similar to those of 2′_4a(TS). In TS structure, the O(3)–C(5) bond is broken and the C(5) atom forms a covalent bond with the N(1) atom since the O(3)–C(5) and N(1)–C(5) lengths were calculated to be 2.496 and 2.565 Å, respectively. The geometry of 2′b connecting to this TS structure is composed of two hydrogen bonds between aminocaproic ester and two iPrOH molecules. This is significantly different from the 2′a geometry.
The ΔG‡gas values were determined to be 77.9 and 60.2 kcal mol−1 for Rxn D with MeOH and iPrOH, respectively. The ΔG‡gas value for MeOH is higher than that of iPrOH by 17.7 kcal mol−1. The bulk solvent effects have little influence on the activation free energy because ΔG‡sol (MeOH) is only 0.4 kcal mol−1. Thus, the ΔG‡rxn(MeOH) value was found to be 78.3 kcal mol−1. As the ΔG‡sol of iPrOH was 3.6 kcal mol−1, the ΔG‡rxn (iPrOH) value was calculated to be 63.8 kcal mol−1. The activation free energy in iPrOH is lower than that of MeOH by 14.5 kcal mol−1. However, both energies are so high that Rxn D under both conditions has no chance to proceed.
The activation free energies of Rxn C are lower by 30.3 kcal mol−1 in MeOH and 16.8 kcal mol−1 in iPrOH than those of Rxn D. They also result in large differences in the rate constants (k) of those reactions. The ratio of rate constants in MeOH (kC/kD = 1.99 × 1010) shows that the Rxn C is much more favorable and much faster to proceed than the Rxn D. Moreover, the relative difference in the Gibbs free energy in the gas phase (ΔGgas) of Rxn C was calculated to be −3.3 kcal mol−1 in MeOH. After including the bulk solvent effects, the relative difference in the Gibbs free energy of the reaction (ΔGrxn) was obtained to be −6.5 kcal mol−1. It suggests that 3 is more stable than 2. A similar result was obtained for the reaction in iPrOH as the ΔGrxn value was computed to be −8.6 kcal mol−1. Therefore, Rxn C only proceeds to produce 3 and a methylated sub-product seen in the experiment,16 methyl (N,N-dimethylamino) capronate, does not come from 2.
Next, we focus on Rxn E to give N-methylated compound 5. Fig. 7 depicts structures involving in Rxn E in MeOH. In the 3_5a(TS), the C(4) atom leaves the O(3) atom for the N(1) atom since the N(1)–C(4) and O(3)–C(4) lengths are 1.751 and 2.228 Å, respectively. On the other hand, the O(3) atom attracts the H(5) proton to form a water molecule as the lengths of O(3)–H(5) and H(5)–O(6) were calculated to be 1.512 and 1.039 Å, respectively. After the methylation takes place, the H(7) proton leaves the N(1) atom for the O(6) atom because the N(1)–H(7) and O(6)–H(7) lengths become 1.021 and 3.655 Å. The ΔG‡gas value for MeOH was computed to be 67.8 kcal mol−1. The bulk solvent effects give the negative value of −6.9 kcal mol−1. Therefore, the ΔG‡rxn value is 60.9 kcal mol−1.
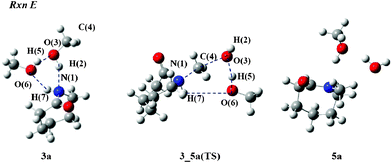 | ||
| Fig. 7 Reactant and TS structures of Rxn E with MeOH molecules. | ||
As exhaustive searches for the TS structure of Rxn E in iPrOH have finished unsuccessfully, the steric effects of the alkyl group should be responsible for this result. The isopropyl group is a secondary alkyl group that has some steric hindrance during the alkylation process toward the amide nitrogen. Note that this is a significant difference between the primary and the secondary alcohols in Rxn E. Therefore, we conclude that the alkylation of the amide nitrogen atom in ε-caprolactam 3 occurs only in the reaction in MeOH. The alkylation reaction does not proceed in SC iPrOH. This is consistent with the experimental results.15
Finally, the cyclization process (Rxn F) is examined. The reaction produces 3, although the reaction is not expected to be a major process during the treatment. The calculations provided a transition state structure 6_3a(TS), which is depicted in Fig. 8. The O(2) atom of the acid group interacts with the H(3) atom and departs from the C(1) atom to generate a water molecule. The C(1)–O(2) and O(2)–H(3) lengths were calculated to be 2.031 and 1.256 Å. The O(4) atom of MeOH interacts with the H(5) proton of the amino group, while the N(6) atom forms a covalent bond with the C(1) atom to produce 3. The O(4)–H(5) and C(1)–N(6) lengths were calculated to be 1.396 and 1.546 Å, respectively. The geometrical parameters of 6_3b(TS) are very similar to those of 6_3a(TS). For example, the C(1)–O(2) length is 2.038 Å. It differs by only 0.007 Å from that of 6_3a(TS).
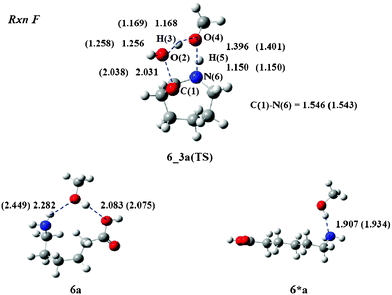 | ||
| Fig. 8 TS structure and reactants of Rxn F with MeOH. The values in parenthesis are bond lengths for the iPrOH system. Unit of length is Å. | ||
Similarly to Rxn C, the reactant geometries of Rxn F adopt 6*a and 6*b instead of 6a and 6b, as shown in Fig. 8. Structure 6*a is more stable than 6a by 12.6 kcal mol−1 and 6*b is more stable than 6b by 8.7 kcal mol−1 in the gas phase. Thus, the ΔG‡gas values increase to 49.4 and 48.3 kcal mol−1 for Rxn F in MeOH and iPrOH, respectively.
The ΔG‡sol values are negative for MeOH and positive for iPrOH by −1.7 and 1.5 kcal mol−1, respectively. The different alcohol solvents cause an absolute difference in the solvation free energies of 3.2 kcal mol−1. Therefore, the ΔG‡rxn values were determined to be 47.7 and 49.8 kcal mol−1. This trend is similar to the results of Rxn C discussed above. The ΔG‡rxn values of Rxn F and Rxn C are similar to within 3.0 kcal mol−1.
Consistency with experiments
Rxn A produces aminocaproic ester 2 and Rxn B directly releases ε-caprolactam 3. According to the present calculations, the primary process of the depolymerization is Rxn A to give aminocaproic ester 2, since the ΔG‡rxn for Rxn A is lower by more than 8 kcal mol−1 than that of Rxn B in both MeOH and iPrOH. These large differences in ΔG‡rxn reflect that the rate constants of Rxn A in the alcohols are 566 and 906 times as large as those of Rxn B. Thus, Rxn B does not proceed. This is consistent with reported experimental results.11–14After the formation of 2, there are two reaction paths, which are the cyclization to give 3 (Rxn C) and the alkylation of the amino group to give 4 (Rxn D). According to our calculations, Rxn C is much more favorable than Rxn D. The difference between ΔG‡rxn(MeOH) and ΔG‡rxn(iPrOH) of the cyclization was calculated to be only by 1.0 kcal mol−1. On the other hand, the N-alkylation is very much solvent dependent. For example, the ΔG‡rxn(MeOH) of Rxn D is 78.3 kcal mol−1, which is larger by 14.5 kcal mol−1 than ΔG‡rxn(iPrOH).
The formation of ε-caprolactam 3 is followed by the N-alkylation (Rxn E). This reaction proceeds only in MeOH and does not take place in iPrOH because no TS structure was obtained after extensive efforts. This is consistent with the experimental results, in which ε-caprolactam was obtained in 91% yield in the reaction under SC iPrOH, while its yield was only 14% and N-methylated caprolactam 5 was observed in the reaction under SC MeOH conditions.
Conclusions
The present calculation study revealed the details of the reaction mechanism of the depolymerization of nylon 6 in SC MeOH and iPrOH. Under the reaction conditions, nylon 6 undergoes C–N bond cleavage through Rxn A to give aminocaproic ester 2, followed by cyclization (Rxn C) to give ε-caprolactam 3. The formation of 3 is very favorable both kinetically and thermodynamically. Direct formation of 3 through the back-bite mechanism (Rxn B) is unlikely because of a higher activation free energy than that of Rxn A. Although there is a possibility of N-alkylation of 2 to produce 4 under these conditions, the calculated results deny the possibility because of the high activation free energy in comparison with that of Rxn C. The reaction in iPrOH gives ε-caprolactam exclusively because there is no possibility for any further reaction; indeed we found no transition state structure for Rxn E with the iPrOH molecules. On the other hand, the transition state structure with MeOH was optimized for Rxn E to give N-methylated caprolactam 5. Our theoretical results clearly explain the difference in the reaction products obtained in experiments. We believe that this information will contribute to the improvement of the reaction procedure in the future.References
- S. Saito, J. Supercrit. Fluids, 1995, 8, 177 CrossRef CAS.
- R. E. N. de Castro, G. J. Vidotti, A. F. Rubira and E. C. Muniz, J. Appl. Polym. Sci., 2006, 101, 2009 CrossRef CAS.
- M. Goto, H. Koyamoto, A. Kodama, T. Hirose and S. Nagaoka, AIChE J., 2002, 48, 136 CrossRef CAS.
- T. Sako, T. Sugeta, K. Otake, N. Nakazawa, M. Sato, K. Mamiki and M. Tsugumi, J. Chem. Eng. Jpn., 1997, 30, 342 CrossRef CAS.
- M. Genta, T. Iwaya, M. Sasaki, M. Goto and T. Hirose, Ind. Eng. Chem. Res., 2005, 44, 3894 CrossRef CAS.
- M. Goto, J. Supercrit. Fluids, 2009, 47, 500 CrossRef CAS.
- S. C. Oh, H. Kwak and S. Bae, J. Chem. Eng. Jpn., 2006, 39, 1004 CrossRef CAS.
- D. T. Chen, C. A. Perman, M. E. Riechert and J. Hoven, J. Hazard. Mater., 1995, 44, 53 CrossRef CAS.
- Y. Ikushima, O. Sato, M. Sato, K. Hatakeda and M. Arai, Chem. Eng. Sci., 2003, 58, 935 CrossRef CAS.
- C. Jinyang, L. Zhi, J. Lujiang, N. Pei, L. Guiyang, H. Haibo, Z. Jianqiu, D. Junping and R. Ruyi, J. Mater. Cycles Waste Manage., 2010, 12, 321 CrossRef.
- M. Goto, M. Umeda, A. Kodama, T. Hirose and S. Nagaoka, Kobunshi Ronbunshu, 2001, 58, 548 CrossRef.
- M. Goto, M. Umeda, A. Kodama, T. Hirose, S. Nagaoka and S. Matsuda, J. Chem. Eng. Jpn., 2004, 37, 353 CrossRef CAS.
- T. Iwaya, M. Sasaki and M. Goto, Polym. Degrad. Stab., 2006, 91, 1989 CrossRef CAS.
- L. Meng, Y. Zhang, Y. Huang, M. Shibata and R. Yosomiya, Polym. Degrad. Stab., 2004, 83, 389 CrossRef CAS.
- A. Kamimura, Y. Oishi, K. Kaiso, T. Sugimoto and K. Kashiwagi, ChemSusChem, 2008, 1, 82 CrossRef CAS.
- A. Kamimura, K. Kaiso, S. Suzuki, Y. Oishi, Y. Ohara, T. Sugimoto, K. Kashiwagi and M. Yoshimoto, Green Chem., 2011, 13, 2055 RSC.
- K. Hori, Y. Hashitani, Y. Kaku and K. Ohkubo, THEOCHEM, 1999, 461, 589 CrossRef.
- K. Hori, Y. Ikenaga, K. Arata, T. Takahashi, K. Kasai, Y. Noguchi, M. Sumimoto and H. Yamamoto, Tetrahedron, 2007, 63, 1264 CrossRef CAS.
- T. Yamaguchi, M. Sumimoto and K. Hori, Chem. Phys. Lett., 2008, 460, 331 CrossRef CAS.
- T. Yamaguchi, M. Sumimoto and K. Hori, J. Comput.-Aided Chem., 2008, 9, 62 CrossRef.
- K. Hori, T. Yamaguchi, K. Uezu and M. Sumimoto, J. Comput. Chem., 2011, 32, 778 CrossRef CAS.
- J. D. Madura and W. L. Jorgensen, J. Am. Chem. Soc., 1986, 108, 2517 CrossRef CAS.
- J. Chandrasekhar, S. F. Smith and W. L. Jorgensen, J. Am. Chem. Soc., 1984, 106, 3049 CrossRef CAS.
- J. Chandrasekhar, S. F. Smith and W. L. Jorgensen, J. Am. Chem. Soc., 1985, 107, 154 CrossRef CAS.
- W. L. Jorgensen, J. F. Blake, D. C. Lim and D. L. Severance, J. Chem. Soc., Faraday Trans., 1994, 90, 1727 RSC.
- Y. Wu, Y. Xue, D. Q. Xie, C. K. Kim and F. S. Yan, J. Phys. Chem. B, 2007, 111, 2357 CrossRef CAS.
- H. Freedman, H. N. Nguyen and T. N. Truong, J. Phys. Chem. B, 2004, 108, 19043 CrossRef CAS.
- H. Freedman and T. N. Truong, J. Phys. Chem. B, 2005, 109, 4726 CrossRef CAS.
- Y. Yamaguchi, N. Yasutake and M. Nagaoka, THEOCHEM, 2003, 639, 137 CrossRef CAS.
- A. J. Page, H. Yamane, Y. Ohta, S. Irle and K. Morokuma, J. Am. Chem. Soc., 2010, 132, 15699 CrossRef CAS.
- L. Tian and R. A. Friesner, J. Chem. Theory Comput., 2009, 5, 1421 CrossRef CAS.
- T. Morita and H. Enomoto, Kagaku Kogaku Ronbunshu, 1999, 25, 940 CrossRef.
- J. Marti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 449 CrossRef CAS.
- T. Adschiri, Shigenkankyoutaisaku, 1998, 34, 1140 CAS.
- L. S. Gen, S. Hong, M. Z. Yue and G. Jie, Geology-geochemistry, 1998, 26, 83 Search PubMed.
- K. Kaiso, T. Sugimoto, K. Kashiwagi and A. Kamimura, Chem. Lett., 2011, 40, 370 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr,T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Qrtiz, Q. Cui, A. G. Baboul, S. Clifford, J. Ciolowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. PopleGaussian 03, Revision C.02, Gaussian Inc.Wallingford CT, 2004.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154 CrossRef CAS.
- T. Kaweetirawatt, T. Yamaguchi, T. Higashiyama, M. Sumimoto and K. Hori, J. Phys. Org. Chem., 2012 DOI:10.1002/poc.2944.
- T. Kaweetirawatt, Y. Kokita, S. Iwai, M. Sumimoto and K. Hori, Chem. Phys. Lett., 2012 DOI:10.1016/j.cplett.2012.06.001.
- “The Theory of Rate Processes” S. Glasstone, K. J. Laidler, H. Eyring, McGraw Hill, New York, 1941.
| This journal is © The Royal Society of Chemistry 2012 |
