The influence of charge ordering on the phase stability of spinel LiNi₂O₄

Abstract

The transition metal ions in spinel LiNi₂O₄ are commonly assumed to be in a single charge state and uniformly distributed throughout the crystal lattice. However, multivalent Ni can exist in a number of different charge states simultaneously within the crystal, whilst still maintaining overall charge neutrality. By carrying out a systematic study of possible charge states of Ni and their distribution in LiNi₂O₄ using first-principles calculations within the framework of density functional theory, we show that two charge-ordered phases are more stable than the charge-disordered spinel phase: (a) an orthorhombic phase containing Ni³⁺ and Ni⁴⁺ ions in a 1 : 1 ratio resulting in Imma symmetry, and (b) a cubic phase with Ni²⁺ and Ni⁴⁺ in a 1 : 3 ratio with P4₃32 symmetry. Our results indicate that charge ordering is an important process in stabilizing the spinel phase of LiNi₂O₄, and should not be ignored in any quantitative study. Our findings are of particular importance for elucidating the relative stabilities of the spinel phase and layered phase of Li_1−xNi₂O₄, a delithiated form of lithium secondary battery cathode material LiNiO₂.

---

Introduction

The Li_xNiO₂ system is being studied intensively in the search for improved cathode materials for Li-ion secondary batteries. The fully lithiated end member LiNiO₂ has an α-NaFeO₂ structure (space group R3̄m)^1–3 composed of alternate layers of Li and NiO₂ in the c direction. In its role as a cathode, Li ions are deintercalated and intercalated between the NiO₂ layers during the charge and discharge processes, respectively. Previous experimental^4–6 and theoretical^7,8 studies have shown that ordering of Li and Li vacancies occurs in the Li layers when x deviates from 1.

One problem afflicting the Li_xNiO₂ system is the low thermal stability of the layered structure. Previous studies have revealed that Li_xNiO₂ decomposes into layer-type LiNiO₂ and spinel-type LiNi₂O₄ at temperatures around 200 °C for Li concentrations of 0.5 < x < 1.^9–11 When x is less than 0.5, Li_xNiO₂ transforms into spinel LiNi₂O₄ and then into a disordered rock-salt structure with the simultaneous release of oxygen gas. The formation of LiNi₂O₄ greatly alters the properties of Li_xNiO₂, degrading its performance as a cathode. In addition, the layer-to-spinel transformation is known to be an exothermic reaction, and such heat generation seriously degrades the durability of batteries.

Spinel-type LiNi₂O₄ was first reported by Thomas et al.¹² almost 20 years ago based on X-ray diffraction patterns of Li_xNiO₂ samples, in which Li ions had been electrochemically extracted at elevated temperatures, but its properties are known only to a limited extent. For example, Li_xNiO₂ with low Li content is known to decompose into a disordered rock-salt type Ni–Li–O solid solution above 300 °C.¹⁰ Because it is difficult to obtain samples of pure spinel LiNi₂O₄ by direct synthesis, however, theoretical calculations offer an attractive alternative means of examining this material. For example, Chazel et al. calculated the local spin density in spinel LiNi₂O₄ using density functional theory (DFT) and analysed the ⁷Li neutron magnetic resonance (NMR) shifts based on their results.¹³ Wang et al. have also systematically computed the thermal stabilities of Li_xMO₂ (M = Ni, Co, Mn) compounds with layer and spinel structures.¹⁴

Given the importance of layer-structured transition metal oxides to lithium ion battery technology and the continuing drive to develop improved cathodes (safer, higher energy and power densities at lower cost), there is a strong need for a better understanding of this material at the electronic and atomic levels. In this article, we investigate the energy states and electronic structure of spinel LiNi₂O₄ using first-principles calculations for the purpose of understanding the layer-to-spinel phase transformation in the Li_xNiO₂ system. Preliminary DFT calculations have revealed that a charge-ordered phase of LiNi₂O₄ is more stable than the ideal spinel phase.¹⁵ We focus on the role of the charge distribution of Ni ions in determining the relative phase stability of spinel LiNi₂O₄.

Computational methodology

First-principles total energy calculations were performed using the projector augmented wave method¹⁶ and the generalized gradient approximation (GGA),¹⁷ as implemented in the VASP code.¹⁸ Plane waves up to 500 eV were used as basis sets. Valence electron configurations of the potentials were taken as 1s² 2s¹ for Li, 3p⁶ 3d⁸ 4s² for Ni, and 2s² 2p⁴ for O. The radial cutoffs of the PAW potentials of Li, Ni and O were 2.05, 2.00 and 1.52 Å, respectively. The strong correlation of Ni 3d electrons was taken into account using the GGA+U method.¹⁹ The value of U was set at 6 eV.¹⁴

The space group of the ideal spinel structure is Fd3̄m. In this structure, all Ni ions are located on 16d sites with octahedral coordination (NiO₆ units) and are symmetrically equivalent. Their nominal valence state is +3.5. If charge separation occurs, however, charge-ordered phases of LiNi₂O₄ are also possible. In this study, two types of model were used to examine charge ordering in LiNi₂O₄. In the first, equal numbers of Ni³⁺ and Ni⁴⁺ ions were distributed over the 16d sites. In the second, Ni ions were separated into 4 Ni²⁺ and 12 Ni⁴⁺ ions per unit cell. We refer to the former and latter models, respectively, as the 1 : 1 and 1 : 3 charge-ordered (CO) phases.

When in octahedral coordination, Ni²⁺ has a spin configuration of t_2g[↑↑↑↓↓↓]e_g[↑↑] (2 Bohr). Assuming a low-spin state, the spin configurations of Ni³⁺ and Ni⁴⁺ are t_2g[↑↑↑↓↓↓]e_g[↑] (1 Bohr) and t_2g[↑↑↑↓↓↓] (0 Bohr), respectively. Thus, Ni²⁺ and Ni³⁺ are magnetic but Ni⁴⁺ is non-magnetic. In charge-ordered LiNi₂O₄ models, initial magnetic moments were set explicitly to these values, as appropriate for each site. The separation of Ni charges over different sites breaks the fcc symmetry of the ideal spinel structure, resulting in a series of different, i.e. symmetrically non-equivalent, configurations that need to be examined individually. In total, the electronic structures and total energies of 114 configurations, 95 for 1 : 1 CO and 19 for 1 : 3 CO models, were calculated; all systems were initially assumed to be in the ferromagnetic state. The size of the simulation cell used was that of the conventional unit cell of spinel (56 atoms). A 3 × 3 × 3 k-point sampling mesh was used in all cases, which provided an energy convergence of less than 2 meV per LiNi₂O₄ formula unit (f.u.). Crystal structures were fully relaxed until residual forces were less than 0.02 eV Å⁻¹. Calculations were also performed with magnetic ions in an antiferromagnetic state for the lowest energy ferromagnetic structures. All crystal structure diagrams and related volumetric 3D data were produced using the visualization program VESTA.²⁰

Results and discussion

Crystal structures and their stability

Examination of the total energies of the 114 different systems reveals that some charge-ordering configurations are more stable than the ideal spinel (Fd3̄m) phase (Fig. 1(a)). Among the ordered phases, the 1 : 1 CO phase in orthorhombic space group Imma and the 1 : 3 CO phases in cubic space groups P4₃32 and P4₁32 are the most stable configurations. The P4₃32 and P4₁32 1 : 3 CO phases are enantiomorphs, and essentially equal in energy. In the remainder we will thus confine ourselves to describing the P4₃32 phase only. Optimized lattice constants for unit cells of Imma and P4₃32 LiNi₂O₄ are listed in Table 1. The calculated lattice constant of the ideal LiNi₂O₄ spinel, 8.157 Å, is about 1.4% larger than the experimentally measured value, 8.041 Å,¹² a typical degree of overestimation by GGA; of the charge-ordered phases, the one with the unit cell most similar in size to that of the conventional spinel cell is P4₃32. The volume of the unit cell of the Imma 1 : 1 CO phase is about half that of the conventional spinel cell. This orthorhombic unit cell can be converted into a pseudo-spinel with volume √2 a_Imma × √2 b_Imma × c_Imma, where a ≅ 7.97, b ≅ 7.97, and c ≅ 8.39 Å.

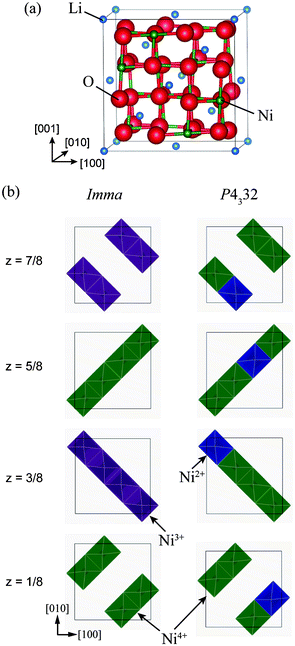Fig. 1 (a) Unit cell of the ideal Fd3m structure of LiNi₂O₄, and (b) schematic representations of Ni charge configurations in 1 : 1 charge-ordered Imma and 1 : 3 charge-ordered P4₃32 phases.

Table 1 Calculated lattice constants and fractional coordinates of ideal and charge-ordered spinel phases of LiNi₂O₄

	Imma		P4332
a/Å	5.641		8.111
b/Å	5.635
c/Å	8.393
Z	4		8
V (Å^3/f.u.)	66.706		66.699
Li	4e	(0, 1/4, 0.362)		(0.246, 0.246, 0.246)
Ni	4d	(1/4, 1/4, 3/4) (3+)	4b	(5/8, 5/8, 5/8) (2+)
	4d	(1/4, 1/4, 3/4) (4+)	12d	12d (1/8, 0.383, 0.867) (4+)
O	8i	(0.279, 0.250, 0.501)	8c	(0.866, 0.866, 0.866)
	8h	(0.000, 0.526, 0.224)	24e	(0.846, 0.356, 0.377)

---

Fig. 1(b) shows schematically the charge-ordered configurations in the Imma and P4₃32 phases, with the Imma phase structure shown in its pseudo-cubic form for ease of comparison with the ideal spinel structure. The Imma 1 : 1 CO phase is isomorphic with LiVCuO₄,²¹ in which Li⁺ ions occupy octahedral sites. LiO₆ octahedra share edges and form a chain structure parallel to (001). Li and Cu layers alternate in the [001] direction. Similarly, the Imma 1 : 1 CO phase of LiNi₂O₄ has alternate layers of Ni³⁺ and Ni⁴⁺ planes in the [001] direction, as seen in Fig. 1(b). The P4₃32 1 : 3 CO phase of LiNi₂O₄ has the same structure as LiNi_0.5Mn_1.5O₄, with Ni and Mn ions occupying octahedral sites in the ratio 1 : 3.²² In LiNi_0.5Mn_1.5O₄, Ni ions are divalent and Mn ions are tetravalent.²³ As with LiNi_0.5Mn_1.5O₄, Ni²⁺ and Ni⁴⁺ ions occupy 4b and 12d sites, respectively, in the P4₃32 unit cell. The total energies of the Imma and P4₃32 CO phases are almost the same, and about 188 meV/f.u. lower than that of the ideal spinel phase.

As mentioned in the previous section, the mean magnetic moment of a Ni ion depends on its valence state. A magnetization density (Δρ_↑↓) map allows the spatial configuration of magnetic Ni³⁺ (or Ni²⁺) and non-magnetic Ni⁴⁺ in charge-ordered LiNi₂O₄ to be distinguished. Here, magnetization density, Δρ_↑↓, is defined as the difference between the densities of up-spin electrons (ρ_↑) and down-spin electrons (ρ_↓), i.e. Δρ_↑↓ = ρ_↑ − ρ_↓. Isosurfaces and contour maps of Δρ_↑↓ for the Fd3̄m, Imma, and P4₃32 phases are shown in Fig. 2. These reveal that Δρ_↑↓ is uniformly distributed over all Ni sites in the ideal spinel phase. This is because all octahedral sites are symmetrically equivalent, and is in agreement with the spin-charge density map reported by Chazel et al.¹³ In contrast, the CO phases show localized magnetization densities on some of the Ni sites. These sites coincide with the positions initially set as Ni³⁺ and Ni²⁺ in the Imma and P4₃32 phases, respectively, shown in Fig. 1(b).

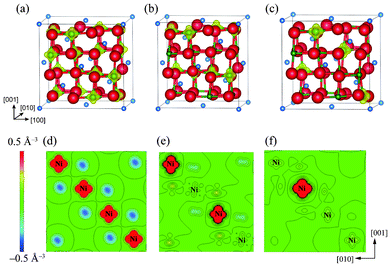Fig. 2 Magnetization density isosurfaces for (a) the ideal Fd3m spinel phase, (b) the Imma 1 : 1 charge-ordered phase, and (c) the P4₃32 1 : 3 charge-ordered phase. Isosurfaces correspond to a charge density of 0.5 Å⁻³. (c), (d) and (e) show contour maps of the magnetization density within (010) NiO₂ planes of the Fd3m, Imma and P4₃32 phases, respectively.

In addition to the ferromagnetic states, we analysed antiferromagnetic states in the Imma and P4₃32 phases. Three antiferromagnetic 1 : 1 CO states in the Imma phase could be identified, an shown in Fig. 3, which we label Types I, II and III. In Types I and II, antiferromagnetic interactions occur in the (001) plane. The difference between these models is the long-range interaction between Ni⁴⁺ planes. Type I consists of a long-range ferromagnetic interaction in the (100) and (010) planes, while in Type II all interactions between Ni³⁺ ions are antiferromagnetic. Type III interactions are the reverse of those in Type I. Interactions in the (001) plane are ferromagnetic, but the interactions within (100) and (010) planes are antiferromagnetic.

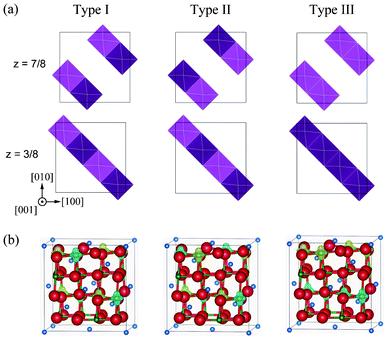Fig. 3 Antiferromagnetic configurations within Ni³⁺ planes in the Imma 1 : 1 charge-ordered phase. Light and dark polyhedra represent the two spin states (up and down, respectively) of Ni³⁺ within NiO₆ octahedra. (b) Magnetization density isosurfaces of 0.5 Å⁻³ for Type I, II and III configurations. Yellow and blue isosurfaces correspond to up and down spin components, respectively.

Fig. 3 shows magnetization density isosurfaces calculated for these models. The patterns of magnetization coincide with the initial antiferromagnetic configurations. Total energies of Type I, II and III configurations are 179, 168 and 173 meV/f.u. lower than the ideal spinel phase, respectively. While the energy difference of 9 meV/f.u. between ferromagnetic Imma and antiferromagnetic Imma is very small, it indicates that the ferromagnetic Imma phase is more stable. This is in accordance with the Goodenough–Kanamori rule that the superexchange interaction of the 90° Ni–O–Ni linkage is weakly ferromagnetic.^24,25 In the case of the P4₃32 CO phase, there is only one non-equivalent antiferromagnetic configuration for four Ni²⁺ ions in the unit cell, with the total energy of the antiferromagnetic phase −189 meV/f.u. lower than the ideal spinel phase. The total energy of the antiferromagnetic P4₃32 phase is only 1 meV/f.u. less than the ferromagnetic Imma and P4₃32 phases. Because this energy difference is quite small, and less than the accuracy of the present calculations, it is reasonable to conclude that the ferromagnetic Imma and ferro- and antiferromagnetic P4₃32 phases are equally stable.

To examine the influence of the magnitude of U on the energies obtained, we performed total energy calculations for various U values. Table 2 lists the total energy differences, ΔE, between the CO phases and ideal spinel phase for different values of U. Here ΔE is defined as ΔE = E_CO − E_spinel, where E_CO is the total energy of the CO phase and E_spinel is the total energy of the ideal spinel phase. A negative ΔE thus means that the CO phase is more stable than the ideal phase. The results in Table 2 confirm that ΔE depends on the value of U. However, the total energy differences for both the Imma CO phase and P4₃32 CO phase are negative and thus these phases are energetically favourable relative to the cubic spinel phase, regardless of the value of U. Similar calculations were carried out for other candidate structures, namely those of LiMn₂O₄ in space groups I4₁/amd²⁶ and Fddd,²⁷ AlV₂O₄ (space group R3̄m),^28–30 and CuIr₂S₄ (space group P1̄).³¹ In these cases, calculations were carried out assuming ferromagnetic states only. Comparison of the total energy differences for all these phases reveals that CO Imma and P4₃32 structures are always more stable than other CO spinel structures for the wide range of U values considered in this study.

Table 2 Total energy differences (ΔE) between the ideal spinel-type and charge-ordered phases per formula unit of LiNi₂O₄ for different U parameters. A negative ΔE means that the charge-ordered phase is more stable than the ideal spinel. Values for hypothetical forms Fddd, I4₁/amd, R3̄m, and P1̄ are also given for comparison

U (eV)	ΔE (meV/f.u.)
	Imma	Imma (AF type I)	P4332	P4332 (AF)	Fddd	I41/amd	R3̄m^a	R3̄m^b	P1̄
a Ref. 28, b Ref. 30.
0	−23	−20	−2	3	−3	−5	−1	1	−14
1	−84	−82	−44	−44	−54	−49	−6	−5	−36
3	−205	−203	−176	−177	−157	−140	−32	−33	−145
5	−242	−238	−239	−239	−194	−181	−63	−60	−179
6	−188	−179	−188	−189	−148	−140	−5	−2	−126
7	−79	−58	−71	−61	−62	−61	133	121	−32

---

Electronic structure

Fig. 4 shows plots of site-projected partial density of states (PDOS) obtained from the ideal spinel and ferromagnetic CO phases of LiNi₂O₄. In the ideal spinel phase, the topmost valence states are partially occupied and exhibit no gap. The electronic structure of the ideal spinel phase is thus metallic. In contrast, Imma and P4₃32 CO phases have a band gap, and are thus semiconductors. Energy states near the valence band top (VBT) and conduction band bottom (CBB) of the Imma phase are mainly composed of Ni³⁺ and O^2– orbitals. In the P4₃32 phase, Ni²⁺ and Ni⁴⁺ orbitals overlap with O^2– orbitals near the VBT and CBB, respectively. Energy states around the band gap are filled by up-spin components in both systems. Fig. 5 shows the band structure and lm-quantum-number-decomposed PDOS of Ni and O ions in the ferromagnetic Imma phase. The band structure was calculated using the primitive cell of the body-centred orthorhombic lattice. The VBT and CBB are located at the Γ point and W point, respectively, showing that the band gap of the Imma phase is indirect. Both band gap edges are filled by up-spin electrons, and the energy gap from the one-electron band energies is 0.36 eV.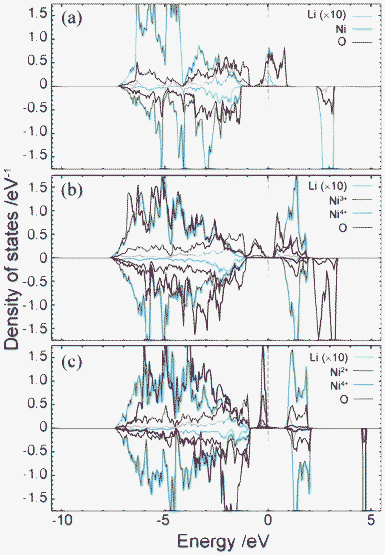

Fig. 4 Total and projected partial density of states for (a) Fd3m spinel, (b) 1 : 1 Imma charge-ordered, and (c) 1 : 3 charge-ordered P4₃32 phases. Positive and negative represent the DOS of up-spin and down-spin, respectively. PDOS of Li are multiplied by 10.

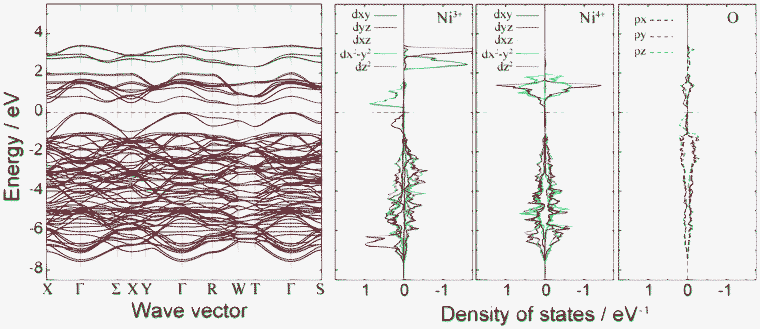Fig. 5 Band structure and lm-decomposed partial density of states for Ni³⁺, Ni⁴⁺, and O²⁻ ions in the 1 : 1 charge-ordered Imma phase.

After determining the locations of the VBT and CBB in terms of their k points, band-decomposed spin densities were obtained from the norms of the corresponding wave functions. Spatial distributions of spin densities within the pseudo-cubic spinel structure are shown in Fig. 6. The lm-decomposed PDOS and band-decomposed spin densities clearly show that the VBT is mainly composed of Ni³⁺ 3d_z² and O 2p_z components. A small contribution is also made from O 2p_x and 2p_y orbitals. Such 3d–2p hybridization has previously been reported for NiO and LiNiO₂ based on first-principles calculations.^32–34 The CBB in the ferromagnetic Imma phase is composed of Ni³⁺ 3d_x²−y², O 2p_x and O 2p_y orbitals. In addition to up-spin, we also investigated the VBT and CBB of down-spin electrons, which we refer to as minor VBT and minor CBB, respectively. The minor VBT is composed almost exclusively from O 2p_z, with little contribution from Ni 3d orbitals. The minor CBB consists of Ni⁴⁺ 3d_z² and O 2p orbitals. It should be noted that the band gap of the Imma phase results from splitting of the Ni³⁺ e_g orbitals into 3d_z² and 3d_x²−y² due to Jahn–Teller (J–T) distortion.

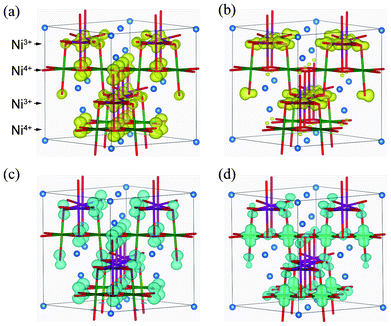Fig. 6 Isosurfaces of band-decomposed charge densities in the 1 : 1 charge-ordered Imma phase: (a) valence band top levels, and (b) conduction band bottom levels, for up-spin electrons; and (c) valence band top levels, and (d) conduction band bottom levels of down-spin electrons. Isosurfaces correspond to 0.01 Å⁻³, with yellow and blue indicating up and down spin components, respectively.

The J–T distortion of the Imma phase can be clearly detected in the coordination environment of Ni ions, as evidenced by the different bond lengths and bond angles of NiO₆ polyhedra in the Imma phase summarized in Table 3. For comparison, local structures of the ideal spinel phase are also listed. In the ideal spinel phase, the Wyckoff position of Ni is 16d, which has site symmetry 3̄m. The NiO₆ polyhedra are slightly distorted, being elongated in the <111> direction, and with non-orthogonal O–Ni–O angles, but with all Ni–O bond lengths equal. In contrast, Ni sites in the 1 : 1 CO Imma phase are of lower symmetry. As shown in Table 3, Ni³⁺–O bond lengths exhibit clear anisotropy, especially for Ni³⁺; Ni³⁺–O bonds in the c direction are 9.9% longer than those in the ab plane. This J–T distortion is a result of the partial occupation of the e_g orbital of Ni³⁺. Elongation of Ni³⁺–O bonds along the c axis reduces repulsive interactions between the electron-occupied e_g orbital and oxide ions in this direction, and thus stabilizes the 3d_z² orbital over the 3d_x²−y² orbital, as seen in the PDOS of Fig. 5. This stabilization of the 3d_z² orbital by J–T distortion results in the Imma CO phase being more stable than the ideal spinel phase. Ni⁴⁺–O bond lengths are shorter than those of Ni^3.5+–O in the ideal spinel and Ni³⁺–O in the Imma phase, consistent with the smaller ionic size of the Ni⁴⁺ ion. Compared to Ni³⁺-containing octahedra, the local distortion around Ni⁴⁺ ions is smaller. All Ni⁴⁺–O bond lengths are almost the same, indicating no J–T distortion. This is because the e_g orbitals of Ni⁴⁺ ions are unoccupied.

Table 3 Bond lengths and angles about octahedrally coordinated Ni ions in the ideal and charge-ordered LiNi₂O₄ phases

	Fd3̄m	Imma		P4332
Ni–O (Å)	1.937 × 6	3+	1.907 × 4 (ab-plane)	2+	2.062 × 6
			2.096 × 2 (c-axis)
		4+	1.882 × 4 (ab-plane)	4+	1.868 × 2
			1.886 × 2 (c-axis)		1.879 × 2
					1.895 × 2

---

O–Ni–O (deg)		3+	83.1 × 2	2+	78.8 × 6
			96.9 × 2		99.4 × 3
			80.1 × 4		103.2 × 3
	83.5 × 6		99.9 × 4
	96.5 × 6	4+	83.0 × 2	4+	82.8 × 2
			97.0 × 2		83.1 × 2
			86.5 × 4		88.6 × 2
			93.5 × 4		94.1 × 2
					94.6 × 2
					95.4
					98.5

---

Fig. 7 shows the band structure and lm-quantum-number-decomposed PDOS of Ni and O ions in the ferromagnetic P4₃32 phase. The VBT and CBB are located at the M point and Γ point, respectively, so that the P4₃32 phase has an indirect band gap, just as with the Imma phase. Both band gap edges comprise up-spin components. The energy gap between one-electron band energies is 0.87 eV, which is larger than that for the Imma phase. Fig. 8 shows the spatial distribution of band-decomposed spin densities originating from the VBT and CBB of up and down spins in the P4₃32 phase. The lm-decomposed PDOS and the spin density isosurfaces clearly show that the VBT is mainly composed of the e_g orbitals, 3d_z² and 3d_x²−y², of Ni²⁺ ions.

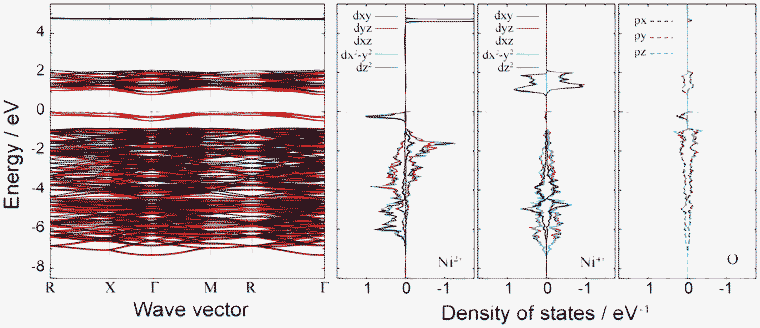Fig. 7 Band structure and lm-decomposed partial density of states of Ni²⁺, Ni⁴⁺, and O²⁻ ions for the 1 : 3 charge-ordered P4₃32 phase.

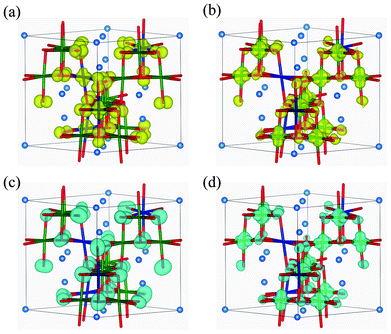Fig. 8 Isosurfaces of band-decomposed charge densities in the 1 : 3 charge-ordered P4₃32 phase: (a) valence band top levels, and (b) conduction band bottom levels, for up-spin electrons; and (c) valence band top levels, and (d) conduction band bottom levels, for down-spin electrons. Isosurfaces correspond to 0.01 Å⁻³, with yellow and blue indicating up and down spin components, respectively.

Hybridization of Ni 3d with O 2p orbitals is also noticeable from the PDOS. This is the same overlapping as occurred in the Imma phase. As seen in Fig. 7 and 8, the VBT bands of the Ni²⁺ e_g orbitals hybridized with O 2p orbitals are strongly localized. The greater stability of the P4₃32 CO phase compared to the ideal spinel phase, which has metallic and delocalized valence states, can be attributed to the localization of Ni 3d electrons. The CBB is composed of Ni⁴⁺ e_g orbitals and O 2p orbitals. Similar to the Imma phase, the minor VBT is principally composed of O 2p orbitals. Ni⁴⁺ e_g and O 2p orbitals constitute the minor CBB.

The coordination environments of Ni ions in the P4₃32 phase are also summarized in Table 3. Ni²⁺O₆ octahedra show no J–T distortion because the e_g orbitals of the up-spin component are fully occupied. All bond lengths of Ni²⁺–O are thus the same. The Ni²⁺–O bond is longer than the Ni³⁺–O and Ni⁴⁺–O bonds because of the larger ionic radius of Ni²⁺. Ni⁴⁺O₆ octahedra are more distorted, but the Ni⁴⁺–O bond lengths and O–Ni⁴⁺–O angles are similar to those of Ni⁴⁺O₆ in the Imma phases, even though the Ni⁴⁺ site (12d), with ..2 site symmetry, has lower symmetry than the Ni⁴⁺ site in the Imma phase (4a with site symmetry 2/m).

The above results suggest that the ground-state structure of spinel-type LiNi₂O₄ is charge ordered with a characteristic electronic structure. Fig. 9 shows schematic diagrams of the bonding states in the ferromagnetic 1 : 1 CO Imma and 1 : 3 CO P4₃32 phases. In both cases, mixing between the 3d orbitals of divalent or trivalent Ni ions and the 2p orbitals of O ions are clearly observed at the VBT. A similar phenomenon is characteristic to NiO.^32–34 In the case of the CBB, in both the Imma and P4₃32 phases it is composed of Ni³⁺ 3d_x²−y² and Ni⁴⁺ e_g orbitals. These Ni 3d orbitals also hybridize with O 2p orbitals. The band gap of CO LiNi₂O₄ is neither a pure Mott–Hubbard type nor a charge-transfer type, and can be regarded as an intermediate type. On the other hand, the minor band gap is of a typical charge-transfer type in both phases. The two characteristic electronic structures thus coexist in ferromagnetic LiNi₂O₄.

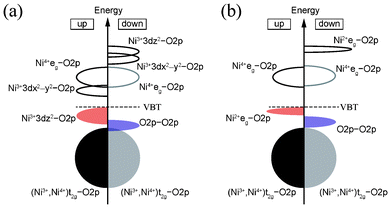Fig. 9 Schematic diagrams of bonding states of ferromagnetic (a) 1 : 1 CO Imma phase, and (b) 1 : 3 CO P4₃32 phase, of LiNi₂O₄.

Heat of transformation for the layered-to-spinel transition

The above calculations indicate that charge ordering needs to be taken into account when determining the stable state of spinel-type LiNi₂O₄. Consequently, quantitative evaluation of the heat of transformation (ΔH) from the layered to the spinel form should be based on a charge-ordered structure for spinel-type LiNi₂O₄. For convenience, in what follows we refer to the layered structure as Li_0.5NiO₂, and to the spinel-type structure as LiNi₂O₄. We calculated ΔH from the total energies of these two phases, using the total energy of the Imma 1 : 1 CO spinel-type phase for LiNi₂O₄, and that of Li_0.5NiO₂ with a monoclinic structure in space group C2/m reported previously.^2,4,5,35 In the latter structure, Li ions are located on 2d sites, with fractional coordinates of (1/2, 0, 1/2) and (0, 1/2, 1/2), and occupancy of 0.5. Because the Li sites are partially occupied, we considered two models for monoclinic Li_0.5NiO₂, one with the Li ion on the (1/2, 0, 1/2) site, and one with the Li ion on the (0, 1/2, 1/2) site. This vacancy ordering leads to a change in space group from C2/m (a base-centred monoclinic lattice) to P2/m (a primitive monoclinic lattice). Geometry optimization of the monoclinic Li_0.5NiO₂ was carried out using the same conditions as for spinel LiNi₂O₄. The value of U used for Ni 3d was 6 eV.

Table 4 shows the optimized lattice constants of monoclinic Li_0.5NiO₂ together with experimental data.⁵ The lattice constants are well reproduced, with errors of less than 1% compared to experiment. The differences in structure and Li positions are negligible. In the same manner as for spinel LiNi₂O₄, Δρ_↑↓ was calculated for layered Li_0.5NiO₂. As shown in Fig. 10, Ni ions within the same (100) plane as Li ions become non-magnetic Ni⁴⁺ ions in both Li_0.5NiO₂ models, indicating that charge ordering also occurs in layered Li_0.5NiO₂. The energy difference between the two monoclinic unit cell models is only about 0.05 meV per Li_0.5NiO₂ formula unit. It can thus be concluded that the choice of occupancy of the Li site hardly affects the energy state of monoclinic Li_0.5NiO₂. Next we constructed a 2 × 2 × 2 supercell of monoclinic Li_0.5NiO₂. This supercell contained 56 atoms, equal to the number of atoms in the spinel-type conventional cell. The total energy of the supercell was calculated using a k-mesh size of 3 × 4 × 3.

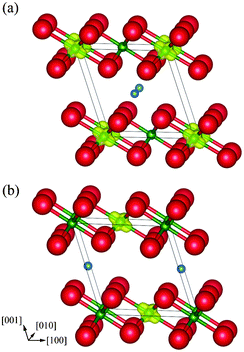Fig. 10 Magnetization density isosurfaces (yellow) of layer-type monoclinic Li_0.5NiO₂ with the Li ion at fractional coordinates (a) (1/2, 0, 1/2), and (b) (0, 1/2, 1/2). Isosurfaces correspond to 0.5 Å⁻³.

Table 4 Calculated lattice constants and fractional coordinates of ideal and charge-ordered spinel phases of LiNi₂O₄

	Calc. (S.G. P2/m)				Exp. (S.G. C2/m)^a
a Ref. 5: Composition of the sample is Li0.49Ni1.01O2.
a (Å)	5.000		5.000		4.9635
b (Å)	2.815		2.815		2.8304
c (Å)	5.122		5.124		5.0769
β (deg.)	108.78		108.76		109.513
V (Å^3/LiNi2O4)	68.33		68.29		67.227
Li	1g	(1/2, 0, 1/2)	1g	(0, 1/2, 1/2)	2d	(0, 1/2, 1/2)
Ni	1a	(0, 0, 0) (3+)	1a	(0, 0, 0) (4+)	2a	(0, 0, 0)
	1e	(1/2, 1/2, 0) (4+)	1e	1e (1/2, 1/2, 0) (3+)
O	2m	(0.294, 0, 0.785)	2m	(0.256, 0, 0.802)	4i	(0.2632, 0, 0.7899)
	2n	(0.756, 1/2, 0.802)	2n	(0.794, 1/2, 0.785)

---

The total energies obtained in this manner produce a heat of transformation, ΔH, of 122 meV per Li_0.5NiO₂ formula unit, equal to 125 J g⁻¹. Lee et al.¹⁰ reported a value of about 100 J g⁻¹ for ΔH from differential scanning calorimetry measurements. The 20% difference between our DFT result and the experimental value may be due to several factors. First, the present calculations are based on general DFT, and temperature effects like lattice vibration are not taken into account. Second, Li and vacancy ordering was limited to the size of the monoclinic unit cell of Li_0.5NiO₂, and it is possible that larger-scale ordering is important. In addition, Li_xNiO₂ systems are known to have a small amount of disorder (cation-antisite or cation-interchange defects) between Li and Ni sites. The effect of such cation disorder is not taken into account in our study. However, it should be noted that the energy level of the error is around 10 meV/f.u. Finally, an experimental error of around 5% is also typical.

Given the above considerations, our result is of the correct order, with reasonable accuracy considering its derivation from first principles. If ΔH is calculated without any charge ordering in the spinel-type LiNi₂O₄ phase, in other words if the total energy of the ideal spinel phase is used, the value of ΔH decreases to only 28 meV/f.u., i.e. 28 J g⁻¹, in which case the discrepancy between experimental and theoretical values is much worse. Our results thus demonstrate that charge ordering is an important factor that cannot be ignored when quantitatively analysing the layer-to-spinel transformation in the Li_xNiO₂ system.

Conclusions

The energy states and electronic structures of charge-ordered and charge-disordered spinel-type LiNi₂O₄ structures were calculated within a DFT+U framework. The results revealed that the Imma 1 : 1 CO phase and P4₃32 1 : 3 CO phase are more stable than the ideal spinel phase with a uniform electronic charge distribution. We also calculated the total energies of LiNi₂O₄ with other hypothetical spinel-type CO compounds, and found that the Imma and P4₃32 phases are energetically more favourable, regardless of the value of the Hubbard U parameter. The Imma and P4₃32 phases are thus the strongest candidates for being the most stable (ground-state) structures of LiNi₂O₄.

Analysis of the electronic structures revealed that hybridization between Ni 3d and O 2p orbitals occurs in LiNi₂O₄, similar to the bonding character in rock-salt NiO. The band gap of ferromagnetic LiNi₂O₄ is found to be of “intermediate” type, i.e., neither a pure Mott–Hubbard nor charge-transfer type. The band gap of the Imma phase is formed between Ni³⁺3d_z²–O2p orbitals constituting the valence band top and Ni³⁺3d_x²−y²–O2p orbitals in the conduction band bottom. Splitting of the e_g orbitals of Ni³⁺ ions resulting from Jahn–Teller distortion was also observed. In the P4₃32 phase, the valence band top comprises Ni²⁺ 3d e_g–O2p orbitals and the conduction band bottom Ni⁴⁺ 3d e_g–O2p.

Our results indicate that charge ordering is an important process in stabilizing the spinel phase of LiNi₂O₄, and needs to be included to calculate reliably the electronic structure and the relative thermal stability of the spinel phase compared with the layered phase. When charge ordering is included, DFT calculations reproduce the heat of transformation from layered to spinel structures with improved accuracy, whereas when charge ordering is ignored the heat of transformation is significantly underestimated.

Acknowledgements

A part of this study was supported by Japan Society for the Promotion of Science (JSPS) through its “Funding Program for World-Leading Innovative R&D on Science and Technology (FIRST Program)”.

References

1. L. D. Dyer, B. S. Borie and G. P. Smith, J. Am. Chem. Soc., 1954, 76, 1499–1503.
2. A. Hirano, R. Kanno, Y. Kawamoto, Y. Takeda, K. Yamaura, M. Takano, K. Ohyama, M. Ohashi and Y. Yamaguchi, Solid State Ionics, 1995, 78, 123–131.
3. K. Mukai, J. Sugiyama and Y. Aoki, J. Solid State Chem., 2010, 183, 1726–1732.
4. H. Arai, S. Okada, H. Ohtsuka, M. Ichimura and J. Yamaki, Solid State Ionics, 1995, 80, 261–269.
5. A. Hirano, R. Kanno, Y. Kawamoto, K. Oikawa, T. Kamiyama and F. Izumi, Solid State Ionics, 1996, 86–88, 791–796.
6. J. P. Peres, F. Weill and C. Delmas, Solid State Ionics, 1999, 116, 19–27.
7. M. E. Arroyo y de Dompablo, A. Van der Ven and G. Ceder, Phys. Rev. B: Condens. Matter, 2002, 66, 064112.
8. M. E. Arroyo y de Dompablo and G. Ceder, Chem. Mater., 2003, 15, 63–67.
9. H. Arai, S. Okada, Y. Sakurai and J. Yamaki, Solid State Ionics, 1998, 109, 295–302.
10. K. K. Lee, W. S. Yoon, K. B. Kim, K. Y. Lee and S. T. Hong, J. Electrochem. Soc., 2001, 148, A716–A722.
11. M. Guilmard, L. Croguennec, D. Denux and C. Delmas, Chem. Mater., 2003, 15, 4476–4483.
12. M. G. S. R. Thomas, W. I. F. David, J. B. Goodenough and P. Groves, Mater. Res. Bull., 1985, 20, 1137–1146.
13. C. Chazel, M. Ménétrier, D. Carlier, L. Croguennec and C. Delmas, Chem. Mater., 2007, 19, 4166–4173.
14. L. Wang, T. Maxisch and G. Ceder, Chem. Mater., 2007, 19, 543–552.
15. A. Kuwabara, C. A. J. Fisher, R. Huang, Y. H. Ikuhara, H. Moriwake, Y. Ikuhara and H. Oki, AMTC Lett., 2010, 2, 200–201.
16. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 59, 1758–1775.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
19. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
20. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
21. M. A. Lafontaine, M. le Blanc and G. Ferey, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45, 1205–1206.
22. K. Ariyoshi, Y. Iwakoshi, N. Nakayama and T. Ohzuku, J. Electrochem. Soc., 2004, 151, A296–A303.
23. G. Q. Liu, L. Wen and Y. M. Liu, J. Solid State Electrochem., 2010, 14, 2191–2202.
24. J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297.
25. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
26. A. S. Wills, N. P. Raju and J. E. Greedan, Chem. Mater., 1999, 11, 1510–1518.
27. J. Rodríguez-Carvajal, G. Rousse; C. Masquelier and M. Hervieu, Phys. Rev. Lett., 1998, 81, 4660–4663.
28. K. Matsuno, T. Katsufuji, S. Mori, Y. Moritomo, A. Machida, E. Nishibori, M. Takata, N. Sakata, M. Yamamoto and H. Takagi, J. Phys. Soc. Jpn., 2001, 70, 1456–1459.
29. K. Matsuno, T. Katsufuji, S. Mori, A. Machida, Y. Moritomo, K. Kato, E. Nishibori, M. Takata, M. Sakata, K. Kitazawa and H. Takagi, Phys. Rev. Lett., 2003, 90, 096404.
30. Y. Horibe, M. Shingu, K. Kurushima, H. Ishibashi, N. Ikeda, K. Kato, Y. Motome, N. Furukawa, S. Mori and T. Katsufuji, Phys. Rev. Lett., 2006, 96, 086406.
31. P. G. Radaelli, Y. Horibe, M. J. Gutmann, H. Ishibashi, C. H. Chen, R. M. Ibberson, Y. Koyama, Y.-S. Hor, V. Kiryukhin and S.-W. Cheong, Nature, 2002, 416, 155–158.
32. A. Fujimori and F. Minami, Phys. Rev. B, 1984, 30, 957–970.
33. J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 55, 418–421.
34. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter, 1991, 44, 943–953.
35. C. Pouillerie, E. Suard and C. Delmas, J. Solid State Chem., 2001, 158, 187–197.

---