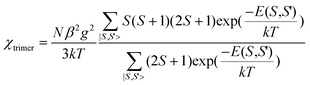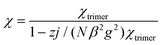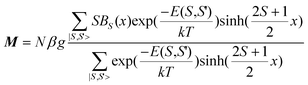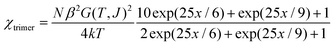DOI:
10.1039/C2RA21173D
(Paper)
RSC Adv., 2012,
2, 10352-10358
Mixed azide and carboxylate bridged trinuclear Mn(II) and Co(II) motifs in coordination ladders: structures and magnetism†
Received
13th June 2012
, Accepted 28th August 2012
First published on 31st August 2012
Abstract
Two isomorphous Mn(II) and Co(II) coordination polymers with an azide and zwitterionic dicarboxylate ligand as coligands were synthesized and structurally characterized, and their magnetic properties were studied. They are formulated as [M3(L)2(N3)6(H2O)2]·2H2O (M = Mn (1), Co (2), L = 1,2-bis(4-carboxylatopyridinium-1-methylene)benzene). The compounds contain anionic linear [Mn3(N3)6(COO)4(H2O)2]4− units built from the simultaneous bridges of a syn–syn carboxylate and two end-on azides. The anionic trinuclear units are linked into ladder-like coordination polymers by the cationic bis(pyridinium) tether of the organic ligand. Analyses of the temperature- and field-dependent magnetic data of the compounds revealed that the mixed [(COO)(EO–N3)2] triple bridges transmit antiferromagnetic and ferromagnetic coupling in 1 and 2, respectively.
1 Introduction
Polynuclear complexes and coordination polymers in which paramagnetic metal ions are bridged by short ligands have attracted great attention in recent years, not only for understanding the fundamental scientific laws underlying the magnetic behaviours of molecular systems, but also for developing new functional molecular magnetic materials with potential applications.1–7 In this context, the azide ion (N3−) is among the most extensively studied bridges for its versatility in both coordination chemistry and magnetism, and a great number of discrete polynuclear and infinite polymeric metal-azido coordination compounds with a diversity of structural motifs and magnetic properties have been reported,8–19 including some long-range ordered materials and a few single-molecule/-chain magnets (SMMs and SCMs).8–11,16–19,20–24
To obtain new compounds with interesting magnetic properties, some systems with simultaneous azide and carboxylate bridges have been prepared.25–45 Recently, we demonstrated that the use of zwitterionic carboxylates as ligands is a good synthetic approach towards mixed azide- and carboxylate-bridged systems.37–44 By this approach, various magnetic systems based on mixed bridging polynuclear clusters,37,38 infinite chains and layers,39,40 and even 3D frameworks have been obtained,41 exhibiting interesting magnetic properties, such as ferromagnetic (FM) coupling,39,40 single-chain magnetism40,43,44 and solvent-modulated magnetism.42,43 As part of our systematic studies on mixed azide and carboxylate systems, here we report the synthesis, structure and magnetic properties of two isomorphous coordination polymers obtained from manganese(II)/cobalt(II), azide and a new zwitterionic dicarboxylate ligand, 1,2-bis(4-carboxylatopyridinium-1-methylene)benzene) (L, Scheme 1). The compounds contain 1D ladders in which anionic Mn3 linear motifs with mixed μ-EO azide and carboxylate bridges serve as rungs and the cationic backbones of the organic ligands as sides. Magnetic studies reveal that the 3-fold mixed bridge propagates antiferromagnetic (AF) coupling in 1, but FM coupling in 2.
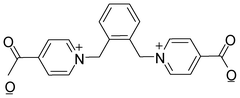 |
| | Scheme 1 The chemical structure of L. | |
2 Experimental
2.1 General procedure
The reagents were obtained from commercial sources and used without further purification. 1,2-bis(4-carboxylatopyridinium-1-methylene)benzene dihydrobromide ([H2L]Br2) was prepared according to the literature.45
Caution: although not encountered in our experiments, azido compounds of metal ions are potentially explosive. Only a small amount of the materials should be prepared, and it should be handled with care.
2.2 Synthesis of [Mn3(L)2(N3)6(H2O)2]·2H2O (1)
[H2L]Br2 (0.051 g, 0.10 mmol) and sodium azide (0.13 g, 2.0 mmol) were dissolved into water (2 ml) and then the solution was added into an ethanol solution (2 ml) of MnCl2·4H2O (0.079 g, 0.40 mmol). The mixture was stirred for a few minutes and was filtered off. Slow evaporation of the filtrate at room temperature afforded orange–yellow crystals of 1 after one day. Yield: 50% based on L. Elemental analysis calcd (%) for Mn3C40N22O12H40: C, 40.52; H, 3.40; N, 25.99%. Found: C, 40. 73; H, 3.27; N, 25.66%. Main IR bands (KBr, cm−1): 2079s [ν(N3)], 2043s [ν(N3)], 1616s [νas(COO)], 1565s, 1451m, 1392s [νs(COO)], 1337w, 765m.
2.3 Synthesis of [Co3(L)2(N3)6(H2O)2]·2H2O (2)
A procedure similar to that for 1 was followed to prepare compound 2. Yield: 45% based on L. Elemental analysis calcd (%) for Co3C40N22O12H40: C, 40.11; H, 3.37; N, 25.73%. Found: C, 40. 31; H, 3.07; N, 25.43%. Main IR bands (KBr, cm−1): 2078s [ν(N3)], 2040s [ν(N3)], 1617s [νas(COO)], 1566s, 1451m, 1391s [νs(COO)], 1332w, 768m.
2.4 Physical measurements
All of the solvents and reagents for synthesis were commercially available and used as received. Infrared spectra were recorded with a NEXUS 670 FTIR spectrometer using KBr pellets. Elemental analysis was carried out with an Elementar Vario EI III elemental analyzer. The powder X-ray diffraction (PXRD) patterns were collected on a Rigaku Ultima IV X-ray diffractometer using Cu-Kα radiation (λ = 1.5405 Å) at 35 kV and 25 mA. Temperature- and field-dependent magnetic measurements were carried out with a Quantum Design SQUID MPMS-XL7 magnetometer. Diamagnetic corrections were made with Pascal's constants.
2.5 Crystal data collection and refinement
Diffraction intensity data of 1 were collected at 293 K on a Bruker APEX II diffractometer equipped with a CCD area detector and graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å). Empirical absorption corrections were applied using the SADABS program.46 The structure was solved by direct methods and refined by the full-matrix least-squares method on F2, with all non-hydrogen atoms refined with anisotropic thermal parameters.47 The hydrogen atoms attached to carbon atoms were placed in calculated positions and refined using the riding model, and the hydrogen atoms of the water molecules were located from the difference maps. Pertinent crystallographic data and structure refinement parameters are summarized in Table 1.
Table 1 Crystal data and structure refinements for compound 1
| Compound |
1
|
| Formula |
C40H40Mn3N22O12 |
|
M
r
|
1185.76 |
|
T/K |
296 |
| Crystal system |
Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
|
a/Å |
8.9045(1) |
|
b/Å |
10.3308(1) |
|
c/Å |
14.0372(2) |
|
α (°) |
106.489(3) |
|
β (°) |
100.946(3) |
|
γ (°) |
90.640(3) |
|
V, Å3 |
1212.8(3) |
|
Z
|
1 |
|
D
C, g cm−3 |
1.624 |
|
μ/mm−1 |
0.855 |
| Reflns collected |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 107 |
| Unique reflns/Rint |
4688/0.0208 |
|
R
1 [I > 2σ(I)] |
0.0289 |
| wR2 (all data) |
0.0815 |
| GOF |
1.050 |
3 Results and discussion
3.1 Crystal structure
The structure of 1 was determined by single crystal X-ray analyses. The structure is shown in Fig. 1 and selected bond distances and angles are given in Table 2. As shown in Fig. 1a, there are two crystallographically independent Mn(II) atoms in 1 (Mn1 and Mn2). Mn1 assumes a distorted mer-octahedral [N3O3] geometry defined by three azide atoms (N1, N4 and N7), two carboxylate oxygen atoms (O2 and O3B), and a water molecules (O5). Mn2 adopts the centrosymmetric trans-octahedral [N4O2] geometry with two equivalent azide nitrogen atoms (N4 and N4A) and two equivalent carboxylate oxygen atoms (O1 and O1A) at the equatorial plane and two other equivalent azide nitrogen atoms (N7 and N7A) at axial positions. The Mn–N/O bond distances for both Mn1 and Mn2 fall in the range of 2.148(1)–2.328(2) Å. Each Mn2 is connected with two Mn1 ions to give a trinuclear [Mn3(N3)6(COO)4(H2O)2] unit, in which the triple bridges consist of two μ-N,N-azides and a syn–syn μ-O,O′-carboxylate. The Mn⋯Mn distances spanned by the triple bridges are 3.32 Å, and the Mn–N–Mn angles are 93.46(6)° and 94.01(6)°. These angles and distances are similar to those observed for previous Mn(II) chains and clusters with (μ-EO-N3)2(μ-COO) bridges.38–40
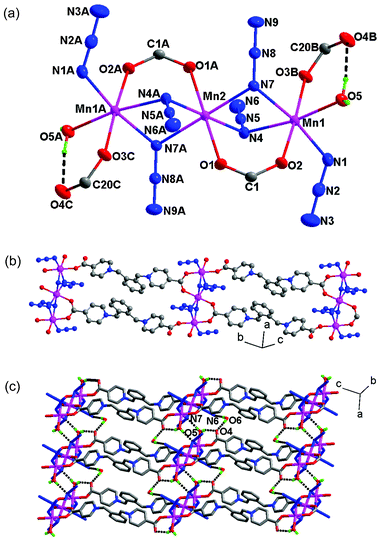 |
| | Fig. 1 (a) A trinuclear cluster in 1 (thermal ellipsoids are drawn at 30% probability). The symmetry codes are A −x, −y, 1 − z; B x, y − 1, 1 + z; C − x, 1 −y, −z. (b) The 1D ladder formed from the trinuclear units. (c) The 2D layer assembled through inter-ladder O–H⋯O and O–H⋯N interactions. | |
Table 2 Selected bond lengths (Å) and angles (°) for compound 1a
|
Symmetry codes: A: −x, −y, 1 −z; B x, y − 1, 1 + z.
|
| Mn1–O2 |
2.154 (1) |
Mn1–O3B |
2.155(1) |
| Mn1–N1 |
2.182 (2) |
Mn1–O5 |
2.200(1) |
| Mn1–N7 |
2.277(1) |
Mn1–N4 |
2.328 (2) |
| Mn2–O1 |
2.148 (1) |
Mn2–N4 |
2.235(1) |
| Mn2–N7 |
2.266 (1) |
Mn2–N4–Mn1 |
93.46(6) |
| Mn2–N7–Mn1 |
94.01(6) |
N11–N10–N9 |
175.0(2) |
| N10–N9–Cu1 |
134.28(1) |
|
|
The L ligand in the structure serves as a μ3 bridge with one carboxylate in the monodentate mode and the other in the syn–syn bridging modes (Fig. 1b), to bind three metal ions from two neighbouring trinuclear units. There are two antiparallel L ligands between neighbouring trinuclear units and hence a 1D ladder-like chain is formed. The Mn⋯Mn distance along the ligand is 19.649(2) Å and 19.486(2) Å.
Within the trinuclear unit, there are two equivalent O–H⋯O hydrogen bonds involving the water molecules (O5) coordinated to Mn1 and the uncoordinated carboxylate oxygen atoms (O4). The coordinated O5 water molecule from one ladder is also hydrogen-bonded to a bridging nitrogen atom (N7) from another ladder. Additionally, the lattice water molecule (O6) serves to link neighbouring ladders by forming hydrogen bonds (O6–H⋯N6 and O6–H⋯O4) with a terminal azide nitrogen from one ladder and a coordinated water from another ladder (Fig. 1c). The relevant data for the hydrogen bonding interactions are given in Table S1.†
We were unable to obtain crystals of 2 suitable for single-crystal X-ray analysis, but the PXRD pattern of the compound is very similar to that of 1 (see ESI, Fig. S1†), suggesting that the two compounds are isomorphous. The unit cell parameters of 2 were refined from the PXRD data using the CELREF program48 with the triclinic cell parameters of 1 as initial values. The final refinement yielded a = 8.9231 Å, b = 10.2869 Å, c = 14.0195 Å, α = 106.25°, β = 100.82°, γ = 90.86° and V = 1210.36 Å3 with good agreement (see ESI, Table S2†).
3.2 Magnetic properties
Compound 1.
The magnetic susceptibility of compound 1 was measured on a crushed sample under 1 kOe in the range of 2–300 K (Fig. 2). The measured χT value at 300 K is about 12.24 emu mol−1 K, slightly lower than the spin-only value (13.13 emu mol−1 K) for three uncoupled Mn(II) ions with g = 2. As the temperature is lowered, the value of χ increases continuously, while the χT value decreases continuously to an approximate platform value of about 4.32 emu mol−1 K below 4.0 K. The data above 44 K follow the Curie–Weiss law with C = 13.12(2) emu mol−1 K and θ = −19.7(3) K, indicating AF coupling interactions between the Mn(II) centres.
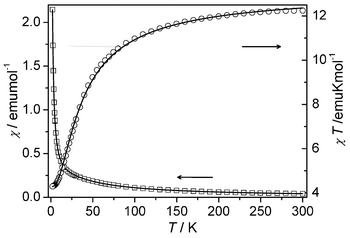 |
| | Fig. 2 Temperature dependence of χ and χT for 1 under 1 kOe. The solid lines represent the best fit to the trinuclear model (see text). | |
Despite the ladder structural feature, the system can magnetically be regarded as an isolated linear trinuclear system, because the magnetic interactions through the long L ligand should be very weak. The Heisenberg Hamiltonian for the trinuclear system can be written as H = −J(Sc·St1 + Sc·St2), where J is the exchange constant between the terminal (spin St1 or St2) and central (Sc) metal ions. The coupling system has a total of 27 spin states denoted by |S, S′ > (S′ is the spin quantum number associated with the vector sum of two terminal spins, S′ = St1 + St2, and S is associated with the total spin S = Sc + S′), and the zero-field energy eigenvalues are
| | | E(S, S′) = −J/2[S(S + 1) − S′(S′ + 1)] | (1) |
By application of van Vleck's equation, an analytical expression of magnetic susceptibility for the trinuclear system can be deduced as2,49
| | 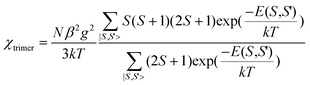 | (2) |
To include any inter-trimer interactions, the magnetic susceptibility can be corrected by applying the molecular-field approximation.2
| | 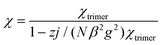 | (3) |
where the
zj parameters represents the effective inter-trimer interaction, with
z = 2 in our case. The best fit parameters are
J = −3.20(2) cm
−1,
j = −0.005(2) cm
−1 and
g = 2.001(2). The agreement factor is
R = Σ[(
χT)
obs − (
χT)
calc]
2/Σ[(
χT)
obs]
2 = 5.0 × 10
−5. We note that the
J value is comparable to those for the previous Mn(
II) chains and clusters with similar (μ-EO-N
3)
2(μ-COO) bridges.
38–40 The very small
j value indicates that the inter-trimer interaction is very weak.
The AF coupling is also supported by the isothermal magnetization measured at 2 K (Fig. 3). The molar magnetization value increases steadily with increased field and reaches a value of 5.08 Nβ at 70 kOe. Note that the magnetization is presented per formula unit, that is, for three Mn(II) ions. In Fig. 3 we have also plotted the theoretical M–H curve for one or three isolated spins according to M = NβgSB5/2(x) or 3NβgSB5/2(x), where x = gβH/(kT) and B5/2(x) is the Brillouin function50 with S = 5/2, g = 2.00 and T = 2 K. As can be seen, the magnetization curve of 1 is far below that expected for three S = 5/2 spins, but shows good agreement with that expected for a single S = 5/2 spin (the deviations at H > 30 kOe will be analyzed in the next paragraphs). The phenomenon clearly indicates that the unit of 1 has a spin sextet ground state, which is the result of intra-trimeric AF coupling (according to eqn (1), the |5/2, 5〉 state has the lowest energy if J < 0). The agreement also indicates that (i) the system is isotropic in magnetic properties, that is, there is no appreciable zero-field splitting (ZFS) effect (otherwise the above equation of M is not followed) and (ii) the magnetic interactions between MnII3 units are very weak, if any.
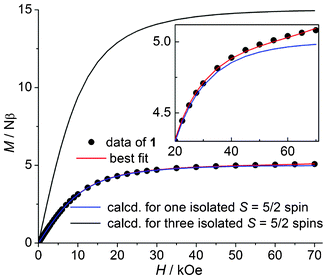 |
| | Fig. 3 Isothermal magnetization curves at 2 K including the data measured for 1, two curves calculated from the Brillouin function and the best-fit to the model outlined in the text. Inset: a blown-up image of the plot. | |
A closer inspection reveals that the magnetization of 1 at high field deviates from the calculated M–H curve for S = 5/2 (Fig. 3, inset). The calculated magnetization increases more and more slowly with field and almost reaches the saturation value (5 Nβ) at 70 kOe, while the experimental magnetization of 1 increases more rapidly than the calculated one and reaches 5.08 Nβ at 70 kOe. More importantly, it seems that the magnetization increase will continue upon further increasing the field, with no indication of saturation. The deviation is not inherent to the sextet ground state of the MnII3 unit and can neither be attributed to ZFS effects or inter-trimeric magnetic interactions. To explain the behavior, we have to consider the magnetization contributions from the low-lying excited states besides the |5/2, 5〉 ground state. In an external magnetic field, each of the 27 |S, S′ > states splits into 2S + 1 Zeeman components |S, S′, Ms〉 (MS = S, S − 1,…,−S) with field-dependent energy EZ(MS) = MSgβH, and there are a total of (2SMn + 1)3 = 216 Zeeman levels with energies E(S, S′, MS) = −J/2[S(S + 1) − S′(S′ + 1)] + MSgβH. According to this expression, the field dependence of the energies for some of the lowest-lying levels is plotted in Fig. 4. As can be seen, when the field increases, the MS = −7/2 (−9/2) level arising from the S = 7/2 (9/2) states is lowered more rapidly than the MS = −5/2 component of the sextet ground state and crossovers between the levels are expected in the high-field region. Thus, at a given temperature, the population of the MS = −7/2 and −9/2 levels increases with the field and thus their contributions to magnetization increase. When the contribution becomes appreciable, the magnetization becomes higher than that expected for the S = 5/2 state and increases with the field. This is just what we have observed for 1. Note that the field needed to observe the phenomenon is dependent on the strength of the intra-trimeric AF coupling. The stronger the AF coupling is, the higher the field.
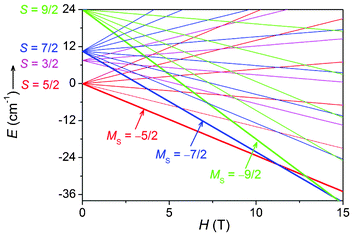 |
| | Fig. 4 Energies of the low-lying states of the MnII3 unit with AF interactions. The zero-field energy of the sextet ground state was set as the zero of energy and the energies were calculated using J = −3.0 cm−1 and g = 2.0. | |
Quantitatively, for a coupling system with zero-field energies E(S,S′) (eqn (1)) and Zeeman energies EZ(MS) = MSgβH, the magnetization can be expressed as51
| | 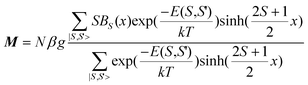 | (4) |
where
BS(
x) represents the Brillouin function associated with the
S spin.
Eqn (4) describes the magnetization as the function of temperature and field with adjustable
g and
J parameters, and thus can be used to fit experimental magnetization data (either temperature- or field-dependent) to evaluate
g and
J. We notice that for
x =
gβH/(
kT) « 1 (
H/T « 0.7
T/K) and by using
χ =
M/
H,
eqn (4) can be easily reduced to
eqn (2), which was derived from van Vleck's equation and has been widely used to fit temperature dependent data. For the field-dependent data at low temperature,
eqn (2) is not valid and we can use
eqn (4). In practice, it may be not necessary to include all of the 27 |
S,
S′> states in the calculations. For
1 at 2 K, we can exclude the states only consider four |
S,
S′> states, |5/2, 5> (ground), |3/2, 4>, |7/2, 5> and |9/2, 5> (see
Fig. 4), which each have at least one appreciably populated Zeeman component in the 0–70 kOe field range. Other states are too far from the ground state to have appreciable population. Thus,
eqn (4) can be reduced to
37with
| P = (5/2)B5/2(x)sinh(3x) + (3/2)B3/2(x)exp(5y/2)sinh(2x) + (7/2)B7/2(x)exp(7y/2)sinh(4x) + (9/2)B9/2(x)exp(8y)sinh(5x) |
and
| Q = sinh(3x) + exp(5y/2)sinh(2x) + exp(7y/2)sinh(4x) + exp(8y)sinh(5x) |
where
y =
J/(
kT). It should be noted that both
eqn (4) and
(5) are not followed if there are appreciable magnetic anisotropy or inter-trimeric interactions. For
1, the experimental magnetization data is fitted to
eqn (5) in good agreement (
Fig. 3, red line), the best-fit parameter being
J = −3.05(2) cm
−1 and
g = 2.006(5) with
R = Σ(
Mobs −
Mcalc)
2/Σ
Mobs2 = 6.9 × 10
−6. We can see that the
J and
g parameters are in excellent agreement with the parameters obtained from the temperature-variable susceptibility data. Magnetic exchange parameters in polynuclear systems are usually obtained by fitting temperature-variable susceptibility to the expressions derived from van Vleck's equation. The evaluation of the parameters from isothermal magnetization data is very rare.
49,52 Kahn
et al. demonstrated that the
J parameter for an acetate-bridged Mn
II3 molecule could be obtained by fitting the magnetization data up to 20 T.
49 In the analysis they took into account all Zeeman components of the |5/2, 5> and |3/2, 4> states, but for the |7/2, 5> and |9/2, 5> states, only the lowest Zeeman components (
MS = −7/2 and
MS = −9/2, respectively) were included. Based on the same consideration, we have recently performed the magnetic analysis with trinuclear Mn(
II) systems.
52 Notably, including all Zeeman components of the four |
S,
S′> states, the expression presented here (
eqn (5)) is more straightforward and has a simpler form. Finally, we would like to note that the fitting procedure illustrated here can be extended to other polynuclear systems in the absence of appreciable magnetic anisotropy and inter-trimeric interactions, provided that the measured magnetizations have appreciable contributions from excited spin states.
Compound 2.
The temperature-dependent magnetic susceptibility for 2 was measured in the temperature range 2–300 K with an applied field of 1000 Oe. As shown in Fig. 5, the χT value per trimer at room temperature is 10.20 emu mol−1 K, which is much larger than the spin-only value for three S = 3/2 centres, but typical of octahedral Co(II) systems with a significant contribution from unquenched orbital momentum. The χ−1versus T plot above 109 K follows the Curie–Weiss law with C = 9.9(1) emu mol−1 K and θ = 10.6(9) K. The positive θ value suggests that a FM interaction between adjacent metal ions is mediated through the three-fold bridges. Upon cooling, after a broad maximum around 119 K, χT decreases slowly to a broad minimum at 40 K, then increases rapidly to a sharp maximum at 3.4 K, and finally drops rapidly. The complex temperature dependence has been observed for other Co(II) systems and is the consequence of the interplay and competition of several effects, including not only the magnetic interactions between Co(II) ions, but also the spin-orbital coupling and symmetry distortion on single Co(II) sites.2,50,53 The overall increase of χT from 300 to 3.4 K is consistent with the occurrence of FM interactions between metal ions, and the decrease from 110 to 40 K is understandable by assuming that the effect of spin-orbital coupling on χT dominates over the effect of FM coupling between metal ions. The final drop below 3.4 K can be due to AF interactions between trinuclear units, ZFS effects and/or saturation effect
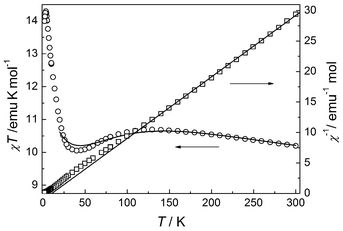 |
| | Fig. 5 Plots of temperature dependence of χT and 1/χ for compound 2. | |
To evaluate the magnetic parameters in 2, we employed the effective-spin approach proposed by Lloret et al.53 In the framework of this approach, each Co(II) ion in the ground Kramer's doublet arising from spin-orbital coupling is considered to have an effective spin Seff = 1/2, which is related to the real spin (S = 3/2) by a factor of 5/3 (eqn (6)) and the magnetic exchange is assumed to occur between the ground doublets. The effective-spin Hamiltonian for a trinuclear Co(II) system can be described by eqn (7).
| | | Ĥ = −(25/9J)(ŜceffŜt1eff + ŜceffŜt2eff) − G(T, J)βH(Ŝceff + Ŝt1eff + Ŝt2eff) | (7) |
Then the expression of the magnetic susceptibility can be derived in the following form (x = J/(kT)),
| | 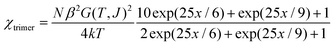 | (8) |
In eqn (7) and (8), the fictitious Landé factor G(T, J) is a temperature function including the contributions from spin-orbital coupling, ligand-field distortion and exchange coupling. An empirical expression of G(T, J) has been derived53 and the variable parameters include λ (spin-orbital coupling parameter), α (orbital reduction factor), Δ (ligand-field distortion factor, assuming an axial distortion) and the magnetic exchange parameter (J). Fitting the data in the whole temperature range to eqn (8) failed to give acceptable agreement and especially the broad maximum and the broad minimum of the χT(T) curve cannot be reproduced. After some trials, we chose the data in the 20–300 K range, which covers the maximum and the minimum. The least-squares fit of the experimental data in the range can reproduce the experimental curve in fair agreement. The best-fit parameter set is J = 9.3(2) cm−1, λ = −110(2) cm−1, α = 1.5(1) and Δ = −623(15) cm−1 with R = Σ[(χT)obs − (χT)calc]2/Σ[(χT)obs]2 = 7.9 × 10−4. The values of the single-ion parameters λ, α and Δ fall within the most common ranges expected for six-coordinated Co(II) complexes.53 The large Δ values suggests significant magnetic anisotropy arising from ligand-field distortion and the J value confirms the intra-trimeric FM interaction through the mixed [(COO)(EO-N3)2] triple bridges. Note that the parameters should be taken as rough estimations for the complexity of the system.
The FM interaction in 2 is also supported by the isothermal magnetization measured at 2 K (Fig. 6). As the field increases, the increase of magnetization is very rapid in the initial region and becomes slower upon further increasing the field. The magnetization at 70 kOe is about 8.30 Nβ (2.77 Nβ per Co(II)), which corresponds to three Co(II) ions (the usual value is 2–3 Nβ per Co(II)). This is in contrast with the case of 1, for which the magnetization per trimer at 70 kOe is close to the saturation value for one Mn(II) ion. Notably, the magnetization of 2 does not reach saturation at 70 kOe, but tends to increase upon further increasing the field. The phenomenon is typical of Co(II) systems with large magnetic anisotropy. A higher field is needed to overcome the anisotropy. Note that the similar magnetization behaviour observed for 1 has been attributed to the increased population of the Zeeman levels of the excited states with higher spins. This explanation is not applicable to 2, because the ground state of the CoII3 unit in 2 has the highest spin due to the FM coupling.
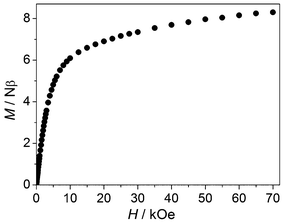 |
| | Fig. 6 The isothermal magnetization curve for 2 at 2 K. | |
Thus, we have demonstrated that in the trinuclear motifs with (μ-COO)(μ-EO-N3)2 bridges, the nature of magnetic coupling changes from AF to FM on going from Mn(II) to Co(II). This can be related to the change in the relative numbers of AF and FM contributions as the ligand-field configuration is changed from t2g3eg2(Mn(II)) to t2g5eg2(Co(II)).39,54 For the octahedral metal centres, it was proposed that the t2g − eg superexchange between the metal ions is AF, while the t2g − t2g and eg − eg combinations are FM. The relative number and magnitude of these contributions determine the nature of the overall coupling. For Co(II) (t2g5eg2), the t2g − eg AF contributions are not strong enough to compensate the t2g − t2g and eg − eg FM exchange. For Mn(II) (t2g3eg2), however, the t2g − eg AF contributions increase much in number and overtake the FM exchange, leading to net AF interactions. This finding in trinuclear motifs is consistent with that in the 1D systems with similar bridges.27,28,39,40
4 Conclusions
We have presented the syntheses, structures, and magnetic properties of Mn(II) and Co(II) compounds with mixed azide and a new zwitterionic dicarboxylate ligand. In the isomorphic compounds, the metal ions are connected into anionic trinuclear units by mixed (μ-COO)(μ-EO-N3)2 bridges, and the anionic units are linked into ladder-like coordination polymers by cationic bis(pyridinium) spacers. It has been shown that the magnetic coupling through the triple bridges is AF in the Mn(II) compound but FM in the Co(II) species, consistent with the change in the ligand-field configurations of the metal ions. This work further demonstrated that the combination of azide and zwitterionic carboxylate ligands can lead to diverse coordination networks with mixed bridges for magnetic coupling.
Acknowledgements
We are thankful for the NSFC (91022017), the Fundamental Research Funds for the Central Universities and the Graduate School of East China Normal University.
References
-
(a) J. S. Miller, Adv. Mater., 2002, 14, 1105 CrossRef CAS;
(b)
Magnetism: Molecules to Materials, ed. J. S. Miller and M. Drillon, Willey-VCH, Weinheim, 2002–2005, vols. I–V Search PubMed.
-
O. Kahn, Molecular Magnetism, Wiley-VCH, Weinheim, 1993 Search PubMed.
-
D. Gatteschi, O. Kahn, J.-S. Miller and F. Palacio, Magnetic Molecular Materials, Kluwer Academic, Dordrecht, The Netherlands, 1991 Search PubMed.
-
E. Coronado, P. Delhaes, D. Gatteschi and J.-S. Miller, Molecular Magnetism: from Molecular Assemblies to Devices, ed. vol. 321, NATO ASI Series 15, Kluwer, Dordrecht, The Netherlands, 1995 Search PubMed.
- J. S. Miller, Adv. Mater., 2002, 14, 1105–1110 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS.
- J. S. Miller and A. J. Epstein, Angew. Chem., Int. Ed. Engl., 1994, 33, 385–415 CrossRef.
- J. Ribas, A. Escuer, M. Monfort, R. Vicente, R. Cortés, L. Lezama and T. Rojo, Coord. Chem. Rev., 1999, 193, 1027–1068 CrossRef.
- A. Escuer and G. Aromí, Eur. J. Inorg. Chem., 2006, 4721–4736 CrossRef CAS.
- X.-Y. Wang, Z.-M. Wang and S. Gao, Chem. Commun., 2008, 281–294 RSC.
- Y.-F. Zeng, X. Hu, F.-C. Liu and X.-H. Bu, Chem. Soc. Rev., 2009, 38, 469–480 RSC.
- P.-P. Liu, A.-L. Cheng, N. Liu, W.-W. Sun and E.-Q. Gao, Chem. Mater., 2007, 19, 2724–2726 CrossRef CAS.
- E.-Q. Gao, Y.-F. Yue, S.-Q. Bai, Z. He and C.-H. Yan, J. Am. Chem. Soc., 2004, 126, 1419–1429 CrossRef CAS.
- M.-M. Yu, Z.-H. Ni, C.-C. Zhao, A.-L. Cui and H.-Z. Kou, Eur. J. Inorg. Chem., 2007, 5670–5676 CrossRef CAS.
- E.-Q. Gao, A.-L. Cheng, Y.-X. Xu, M.-Y. He and C.-H. Yan, Inorg. Chem., 2005, 44, 8822–8835 CrossRef CAS.
- Y.-Z. Zhang, W. Wernsdorfer, F. Pan, Z.-M. Wang and S. Gao, Chem. Commun., 2006, 3302–3304 RSC.
- T. C. Stamatatos, K. A. Abboud, W. Wernsdorfer and G. Christou, Angew. Chem., Int. Ed., 2007, 46, 884–888 CrossRef CAS.
- C. I. Yang, W. Wernsdorfer, G. H. Lee and H. L. Tsai, J. Am. Chem. Soc., 2007, 129, 456–457 CrossRef CAS.
- T. C. Stamatatos, K. A. Abboud, W. Wernsdorfer and G. Christou, Angew. Chem., Int. Ed., 2008, 47, 6694–6698 CrossRef CAS.
- J. H. Yoon, D. W. Ryu, H. C. Kim, S. W. Yoon, B. J. Suh and C. S. Hong, Chem.–Eur. J., 2009, 15, 3661–3665 CrossRef CAS.
- D.-F. Weng, Z.-M. Wang and S. Gao, Chem. Soc. Rev., 2011, 40, 3157–3181 RSC.
- Z.-X. Li, Y.-F. Zeng, H. Ma and X.-H. Bu, Chem. Commun., 2010, 46, 8540–8542 RSC.
- T.-F. Liu, D. Fu, S. Gao, Y.-Z. Zhang, H.-L. Sun, G. Su and Y.-J. Liu, J. Am. Chem. Soc., 2003, 125, 13976–13977 CrossRef CAS.
- D. Visinescu, A. M. Madalan, M. Andruh, C. Duhayon, J. P. Sutter, L. Ungur, W. V. Heuvel and L. F. Chibotaru, Chem.–Eur. J., 2009, 15, 11808 CrossRef CAS.
- L. K. Thompson, S. S. Tandon, F. Lloret, J. Cano and M. Julve, Inorg. Chem., 1997, 36, 3301–3306 CrossRef CAS.
- X.-T. Wang, X.-H. Wang, Z.-M. Wang and S. Gao, Inorg. Chem., 2009, 48, 1301–1308 CrossRef CAS.
- T. Liu, Y.-J. Zhang, Z.-M. Wang and S. Gao, Inorg. Chem., 2006, 45, 2782–2784 CrossRef CAS.
- Z. He, Z.-M. Wang, S. Gao and C.-H. Yan, Inorg. Chem., 2006, 45, 6694–6705 CrossRef CAS.
- H.-J. Chen, Z.-W. Mao, S. Gao and X.-M. Chen, Chem. Commun., 2001, 2320–2321 RSC.
- S. Demeshko, G. Leibeling, W. Maringgele, F. Meyer, C. Mennerich, H.-H. Klauss and H. Pritzkow, Inorg. Chem., 2005, 44, 519–528 CrossRef CAS.
- C. J. Milios, A. Prescimone, J. Sanchez-Benitez, S. Parsons, M. Murrie and E. K. Brechin, Inorg. Chem., 2006, 45, 7053–7055 CrossRef CAS.
- S.-Y. Lin, G.-F. Xu, L. Zhao, Y.-N. Guo, J. K. Tang, Q.-L. Wang and G.-X. Liu, Inorg. Chim. Acta, 2011, 373, 173–178 CrossRef CAS.
- F.-C. Liu, Y.-F. Zeng, J.-R. Li, X.-H. Bu, H.-J. Zhang and J. Ribas, Inorg. Chem., 2005, 44, 7298–7300 CrossRef CAS.
- F.-C. Liu, Y.-F. Zeng, J. Jiao, X.-H. Bu, J. Ribas and S. R. Batten, Inorg. Chem., 2006, 45, 2776–2778 CrossRef CAS.
- Y.-F. Zeng, J.-P. Zhao, B.-W. Hu, X. Hu, F.-C. Liu, J. Ribas, J. R. Arino and X.-H. Bu, Chem.–Eur. J., 2007, 13, 9924–9930 CrossRef CAS.
- Q. Yang, J.-P. Zhao, B.-W. Hu, X.-F. Zhang and X.-H. Bu, Inorg. Chem., 2010, 49, 3746–3751 CrossRef CAS.
- Y. Ma, K. Wang, E.-Q. Gao and Y. Song, Dalton Trans., 2010, 39, 7714–772 RSC.
- Y.-Q. Wang, Q. Sun, Q. Yue, A.-L. Cheng, Y. Song and E.-Q. Gao, Dalton Trans., 2011, 40, 10966–10974 RSC.
- Y. Ma, J.-Y. Zhang, A.-L. Cheng, Q. Sun, E.-Q. Gao and C.-M. Liu, Inorg. Chem., 2009, 48, 6142–6151 CrossRef CAS.
- Q.-X. Jia, H. Tian, J.-Y. Zhang and E.-Q. Gao, Chem.–Eur. J., 2011, 17, 1040–1051 CrossRef CAS.
- Y.-Q. Wang, J.-Y. Zhang, Q.-X. Jia, E.-Q. Gao and C.-M. Liu, Inorg. Chem., 2009, 48, 789–791 CrossRef CAS.
- W.-W. Sun, C.-Y. Tian, X.-H. Jing, Y.-Q. Wang and E.-Q. Gao, Chem. Commun., 2009, 4741–4743 RSC.
- Y.-Q. Wang, W.-W. Sun, Z.-D. Wang, Q.-X. Jia, E.-Q. Gao and Y. Song, Chem. Commun., 2011, 47, 6386–6388 RSC.
- X.-M. Zhang, Y.-Q. Wang, K. Wang, E.-Q. Gao and C.-M. Liu, Chem. Commun., 2011, 47, 1815–1817 RSC.
- F.-K. Zheng, A.-Q. Wu, Y. Li, G.-C. Guo and J.-S. Huang, Chin. J. Struct. Chem., 2005, 24, 940–944 Search PubMed.
-
G. M. Sheldrick, Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Germany, 1996 Search PubMed.
-
G. M. Sheldrick, SHELXTL Version 5.1. Bruker Analytical X-ray Instruments Inc., Madison, Wisconsin, USA, 1998 Search PubMed.
-
J. Laugier and B. Bochu, LMGP, Suite of Programs for the interpretation of X-ray Experiments, ENSP/Laboratoire des Matériaux et de Génie Physique, Saint Martin d'Hères, France, http://www.inpg.fr/LMGP..
- S. Ménage, S. E. Vitols, P. Bergerat, E. Codjovi, O. Kahn, J.-J. Girerd, M. Guillot, X. Solans and T. Calvet, Inorg. Chem., 1991, 30, 2666–2671 CrossRef CAS.
- R. L. Carlin, Magnetochemistry, Springer, Berlin, 1986 Search PubMed.
- O. Waldmann, Phys. Rev. B., 2000, 61, 6138 CrossRef CAS.
- Y.-Q. Wang, K. Wang, Q. Sun, H. Tian, E.-Q. Gao and Y. Song, Dalton Trans., 2009, 9854–9859 RSC.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- C. R. Kmety, Q. Huang, J. W. Lynn, R. W. Erwin, J. L. Manson, S. McCall, J. E. Crow, K. L. Stevenson, J. S. Miller and A. J. Epstein, Phys. Rev., 2000, B62, 5576–5588.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107
107