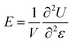DOI:
10.1039/C2RA21228E
(Paper)
RSC Adv., 2012,
2, 9124-9129
Effect of defects on Young's modulus of graphene sheets: a molecular dynamics simulation
Received
20th June 2012
, Accepted 27th July 2012
First published on 30th July 2012
Abstract
The effect of defects including vacancy and Stone–Wales (SW) defects on the Young's modulus of graphene sheets is investigated using molecular dynamic (MD) simulations. The simulations show that the presence of defects reduces the Young's modulus of graphene sheets and Young's modulus decreases with increasing degree of defects. In addition, the vacancy defects bring about a decrease in the Young's modulus, but their reconstruction is an important factor in stabilizing the modulus. Furthermore, we explore the Young's modulus of graphene with defects functionalized by hydrogen atoms and find that the hydrogenation of vacancy defects can increase the Young's modulus of the defective graphene but the hydrogenation of SW defects has the opposite effect.
1. Introduction
Graphene, which consists of a two dimensional sheet of covalently bonded carbon atoms, has been a highlighted material due to its outstanding mechanical, electrical, thermal and optical properties since it was first fabricated using a mechanical cleavage method in 2004.1 The unique structure and particular properties of graphene make it exhibit great promise for applications in various fields such as sensors, batteries, transistors, as well as gas separation membranes.2–5 In particular, graphene is an ideal nanofiller6 to enhance the mechanical properties of polymer based composites because it was reported to be the strongest material with excellent elastic properties and high intrinsic strength.7 Apparently, the key of these features relies on the structural perfection of the hexagonal graphene lattice and strong in-plane sp2 bond between carbon atoms. However, preparation of mass-quantities of perfect graphene sheets may prove challenging and defects are unavoidably present in the graphene materials from various synthesis methods. Previous research has shown that structural defects have a great effect on the chemical, electronic and magnetic properties,8–10 but the influence of various defects on the mechanical properties of graphene has not yet been well investigated and needs to be clarified.
Structural defects, which may appear during growth or processing, can be classified into three main groups: incomplete bonding defects, topological defects and heterogeneous defects. In this work, only vacancy and Stone–Wales (SW) defects which have received much more attention than the others are considered. Vacancy defect, which results from missing carbon atoms in graphene sheets, is the simplest defect. Single vacancy (SV) and double vacancy (DV) in graphene have been experimentally observed by high-resolution transmission electron microscopy (HR-TEM).11 Besides, one of the unique properties of the graphene lattice is its ability to reconstruct by forming non-hexagonal rings. The simplest example is the SW defect,12 which does not involve any removed or added atoms. Four hexagons are transformed into two pentagons and two heptagons by rotating one of the C–C bonds by 90°. On the other hand, Young's modulus is a measure of the stiffness of an elastic material and is therefore one of the most important properties in engineering design. Young's modulus of defect-free and functionalized graphene has been investigated by many experimental and computational researches.7,13,14 Experimentally, the Young's modulus of graphene has been measured by using atomic force microscopy to introduce external strain on graphene and record the force-displacement relation.7 The measured value for Young's modulus of graphene is about 1.0 TPa in this experiment. Theoretically, the Young's modulus of graphene can be studied in a parallel way, Jiang et al.13 used molecular dynamics (MD) to obtain the thermal vibration of graphene and then calculate the Young's modulus from the thermal mean-square vibration amplitude and the theoretical results agreed very well with the experimental ones. Moreover, Zheng et al. investigated the effects of functional groups on the Young's modulus of graphene sheets using MD and molecular mechanics (MM) simulation.14 However, the Young's modulus of defective graphene has not yet been well studied. Based on a large body of experimental and theoretical investigations for carbon nanotubes,15 one can expect that structural defects will have great effects on the Young's modulus of graphene. In order to evaluate the effects of structural defects on Young's modulus of graphene, here we pursue MD simulations for some insights of the underlying mechanisms, which will advise fabrications of graphene materials towards specified mechanical applications.
2. Models and computation methods
In this research, MD simulations were conducted using a commercial software package called Materials Studio. The condensed phase optimization molecular potentials for atomistic simulation studies (COMPASS)16 was used to conduct force field computations and it has been widely employed in simulations for studying the interaction between graphene and carbon nanotubes,17 silicon nanowires18 and polymers.19,20 The force field is expressed as a sum of valence (or bonding), cross-terms, and non-bonding interactions.17,21
In the simulations, non-periodic boundary condition is employed, and the molecular model of a pristine graphene sheet with 1372 carbon atoms was established by using Materials Studio, as known in Fig. 1 (a). The lengths of the graphene in the x and y directions are Lx = 58.232 Å and Ly = 59.04 Å, respectively. Vacancy defects in the graphene structure were formed by removing some carbon atoms from the rings and SW defects were formed by rotating the C–C bonds by 90°. To find the thermal stable morphology and achieve a conformation with minimum potential energy, energy minimization was performed. And these minimum energy conformations were used as initial status in the following MD simulations. Here, MD simulations are performed in the NVT (the volume and the temperature were constant) ensemble and a fixed time step size of 1 fs is used in all cases. The Andersen thermostat method is employed to control the system at a temperature of 1 K to avoid the thermal effect. The cutoff distance for the non-bond interactions is 9.5 Å. The Verlet algorithm is used for the integration of Newton's equations. All the simulations are performed long enough to observe several cycles of thermal vibration.
 |
| | Fig. 1 (a) Schematic of graphene sheet under tensile displacement (b) Strain energy- strain curves for pristine graphene sheet. | |
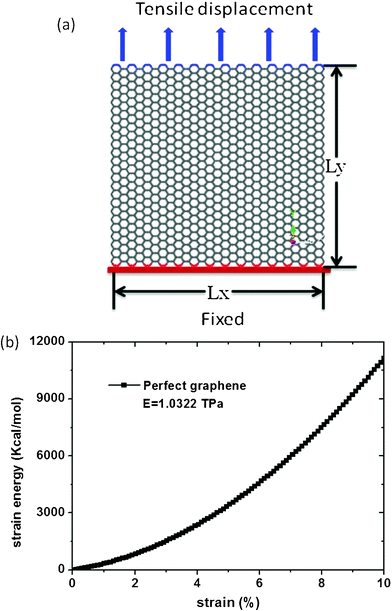
To obtain Young's modulus, the boundary carbon atoms on the bottom edge of graphene are fixed and a positive displacement in the y direction is applied to the boundary carbon atoms on the top edge, as seen in Fig. 1 (a). The system is then relaxed for 30 ps. Young's modulus is given by the following equation:
| | 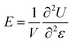 | (1) |
Where E is Young's modulus, V is volume of the graphene, ε is the strain, and U is the strain energy. In the simulations, the strain energy U of the graphene is computed as a function of strain ε by changing the displacement of the carbon atoms on the top side, as seen in Fig. 1 (b). Young's modulus is then determined based on equation (1) by fitting U−ε curves. By fitting the curves, Young's modulus of the graphene sheets is found to be 1.0322 TPa, which is in agreement with nanoindentation measurements22 and ab initio computations,23 confirming the validity of the simulation method used here to characterize the Young's modulus of graphene sheets.
3. Results and discussion
3.1 Effect of defect type and defect degree on Young's modulus of graphene sheets
In our study, the effects of several usual defects, SV or DV defects and SW defects, on the Young's modulus of graphene were investigated. The SV and DV defects were respectively created by removing one carbon atom and two adjacent atoms on the pristine graphene sheet, as shown in Fig. 2 (a) and (b). And the SW defect was formed by rotating a carbon–carbon bond by 90° as shown in Fig. 2 (c).
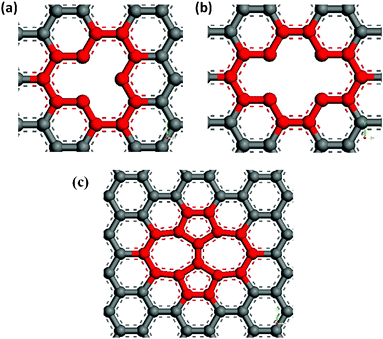 |
| | Fig. 2 Schematic defects in graphene sheets (a) single vacancy defect (b) double vacancy defect (c) Stone–Wales defect SW (55–77). | |
Fig. 3 shows the effect of different types and degree of defects on the Young's modulus of graphene sheets. We define the defect degree of vacancies as the number density of atoms removed from the pristine graphene sheet. For a SW dislocation, defect degree is defined by considering two defected atoms. We found that all the three kinds of defects decrease the Young's modulus of graphene and the detrimental effect increases with the increasing of defects degree, but the degree of the detrimental effects differ with the defect type. As we know, the SW defect contains two heptagons and two pentagons, which preserve interatomic sp2 bonding, thus it has smaller effect on the Young' modulus of graphene than vacancy defects. But for vacancy defects, the missing carbon atoms break the integrity of the pristine graphene sheet that results in dangling bonds near the carbon atoms and a relaxed structure, leading ultimately to a decrease in the elastic modulus. Furthermore, because the graphene with SV defects has more dangling bonds than graphene with DV defects, its Young's modulus is much smaller than graphene with DV defects. Consequently, the elastic property of graphene is deteriorated with defect degree in the sheet and the deterioration is higher with the increasing of defect degree. A higher number of dangling bonds has the potential to cause higher deterioration of elastic properties. The interaction between dangling bonds or chemical instabilities, caused by the missing atoms, could also affect the mechanical behaviour of defective graphene sheets. However, for the same number of missing carbon atoms, the number of dangling bonds plays an important role in the elastic property of graphene.
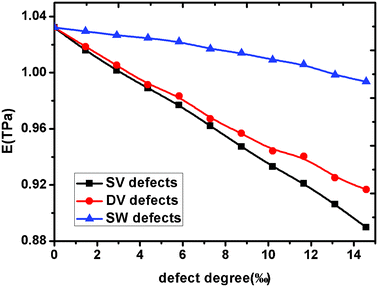 |
| | Fig. 3 The Young's modulus evolution of graphene sheet versus defects degree. | |
To reveal the influence of dangling bonds formed by missing atoms, we setup six types of vacancy defects with the same amount of missing carbon atoms and different amounts of dangling bonds in the graphene sheet. Then the Young's modulus of these defective graphene sheets was calculated, as shown in Fig. 4. For the same missing atoms, the slit-like and hole-like vacancy defects were setup respectively and the slit-like vacancy defects result in many more dangling bonds than the hole-like vacancy defects. By comparing the Young's modulus of these six types defective graphene, we found that the deterioration of the slit-like vacancy defects is much higher than that of the hole-like vacancy defects due to much more dangling bonds near the carbon atoms. The existence of dangling bonds results in the relaxed structure of the graphene sheet, leading to a decrease in the Young's modulus of graphene. In addition, when the length of slit-like vacancy defects is close to the length of the graphene sheet, the detrimental effect of slit-like vacancy defects on the elastic property of graphene is considerable. Besides, the effect of locations of the missing carbon atoms on Young's modulus of graphene sheet is investigated. As shown in Fig. 5, for the same number of missing carbon atoms, the formed SV defects has a more detrimental effect on the Young's modulus than DV defects. Thus, when the missing atoms are dispersive, the effect on the Young's modulus increases to some extent. Therefore, for the same number of missing carbon atoms, the shape and locations of the vacancy defects are also major considerations in their application.
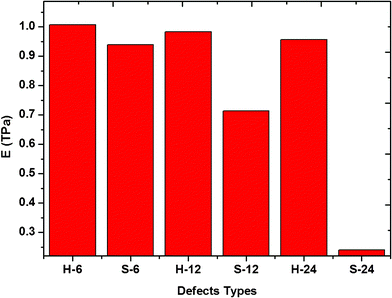 |
| | Fig. 4 The Young's modulus of graphene sheets with slit-like and hole-like vacancy defects. | |
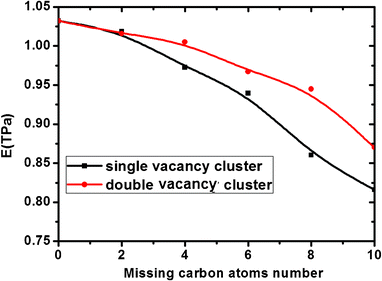 |
| | Fig. 5 Effect of locations of the missing carbon atoms on Young's modulus of graphene sheets. | |
3.2 Effect of vacancy defect reconstruction on Young's modulus of graphene
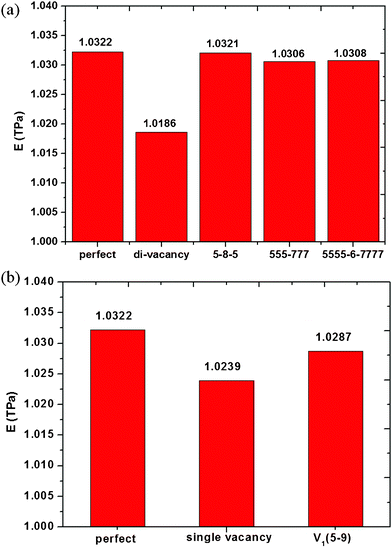
When an atom is removed from its lattice position, the lattice may relax into a lower energy state by changing the bonding geometry around the vacancy. It has been reported that the reconstruction of vacancy defects can be carried out by way of not only temperature but also the defect ratios in single-wall carbon nanotubes (SWNTs) because of the activity of dangling bonds and their space.24 Because graphene has a similar structure with SWNTs, one expects that vacancy defects reconstruction will occur in the graphene sheets. On the other hand, the diffusion and reconstruction of vacancy defects in graphene layers has been investigated by theoretical calculations.25,26 The results show that SV and DV defects have different reconstructions. The SV defect undergoes a Jahn–Teller distortion which leads to the saturation of two of the three dangling bonds toward the missing atom, but one dangling bond always remains owing to geometrical reasons. The reconstruction of SV defects leads to the formation of a five-membered and a nine-membered ring [V1 (5-9) defect], as seen in Fig. 6 (d). As shown in Fig. 6 (a), a fully reconstructed DV has no dangling bond, two pentagons and one octagon [V2 (5-8-5) defect] appear instead of four hexagons in perfect graphene. However, V2 (5-8-5) defect is not the only possible way for a graphene lattice to accommodate two missing atoms and is not the energetically favoured one. The rotation of one of the bonds in the octagon transforms the defect into an arrangement of three pentagons and three heptagons V2 (555-777), as seen in Fig. 6 (b). Furthermore, rotating another bond of V2 (555-777), it would be transformed into a V2 (5555-6-7777) defect, as seen in Fig. 6 (c). The above discussed reconstructed defects have experimentally been observed by high resolution transmission electron microscopy.27 The comparison of Young's modulus of graphene with vacancy defects and reconstructed vacancy defects was shown in Fig. 7, only one defect was made in all the graphene sheets. For graphene with SV defects, the reconstruction increases its Young' modulus, but the Young' modulus of graphene with reconstructed SV defects is still much smaller than that of pristine graphene due to the existence of dangling bonds in the reconstructed structures. However, for graphene with DV defects, the reconstruction increases its Young' modulus and the Young' modulus of graphene with reconstructed DV defects is close to that of pristine graphene because there are no dangling bonds in the graphene sheet. Therefore, we can come to the conclusion that the reconstruction of vacancy defects will be an important factor in stabilizing the Young's modulus. The reconstruction of the defects can further release the potential energy of the system to make the stability of the structure. The general conclusion derived from the study could be used to evaluate the quality of graphene for related applications.
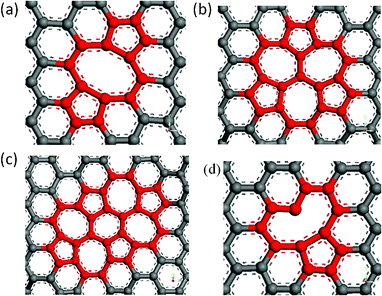 |
| | Fig. 6 Atomic structures of reconstructed single and double vacancy defects in graphene sheets (a) double vacancy V2(5-8-5), (b) V2(555-777), (c) V2(5555-6-7777), (d) single vacancy V1(5-9). | |
 |
| | Fig. 7 Effect of defect reconstruction on Young's modulus of graphene sheets; (a) double vacancy defect reconstruction, (b) single vacancy defect reconstruction. | |
3.3 Effect of hydrogenation of defects on Young's modulus of graphene
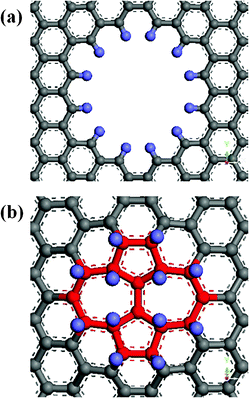
Defects change essentially not only the electronic properties but also the mechanical properties of graphene. Their functionalization is a way to modify the electronic and crystal structure of graphene, which may be important for graphene-based nanoelectronics. Using hydrogen as an example, Boukhvalov and Katsnelson have simulated the chemistry of imperfect graphene for a broad class of defects, such as SW defects, DV defects and nitrogen substitution impurities, by density functional calculations.28 However, the effect of functionalization of defects on the Young's modulus of graphene has not been investigated. Here, we will use hydrogenation as an example of the chemical functionalization of the defects in graphene, multiple vacancy and SW defects were selected to explore the effect of hydrogenation of defects on the Young's modulus of graphene. Optimized geometric structures for the multiple vacancy and SW defects functionalized by twelve hydrogen atoms are shown in Fig. 8. As seen in Fig. 8(a), hydrogen atoms were functionalized on the vacancy and the dangling bonds were saturated. Three types of defective graphene, V6, V12 and V24, which have 6, 12 and 24 missing carbon atoms were selected. There are 6, 12 and 24 dangling bonds existing in the defective graphene, V6, V12 and V24. We calculated the Young's modulus of these three graphene sheets.
 |
| | Fig. 8 Optimized geometric structures for the (a) vacancy defect (b) SW defect functionalized by 12 hydrogen atoms. | |
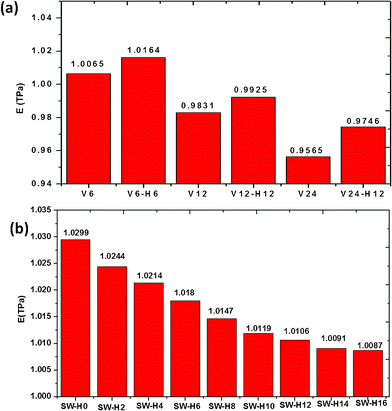
Then these defective graphene sheets were functionalized by hydrogen atoms on the dangling bonds and their Young's modulus were calculated again. The Young's modulus of the six types of graphene were shown in Fig. 9(a), we found that hydrogenation increases the Young's modulus of graphene with multiple vacancy defects, which may result from the saturation of dangling bonds. In addition, hydrogen atoms were functionalized on the SW defects and the bonded graphene atoms are “raised” away from the graphene sheets, as seen in Fig. 8 (b). To obtain more insights into the influence of functionalization of SW defects on the Young's modulus of defective graphene, we respectively modified SW defects with a different number of hydrogen atoms and calculated the Young's modulus of the corresponding graphene. As shown in Fig. 9 (b), Young's modulus decreases with the increase of hydrogen atoms attached on the SW defects. The reduction in Young's modulus is caused by the structural change in the graphene sheets. When the hydrogen atoms were functionalized on the SW defects, the bonded carbon atoms will be pulled away from the original graphene sheet and the length of carbon bonds will become longer. The functionalization on graphene surfaces result in the conversion of carbon bonding from in-plane sp2-hybridization to off-plane sp3-hybridization28 and the decrease of the Young's modulus is due to the local lattice distortion of the graphene sheets. In a word, the hydrogenation of vacancy defects can increase the Young's modulus of defective graphene but hydrogenation of SW defects has the opposite effect. Thus, we should choose appropriate functionalization for different defective graphene in actual applications.
 |
| | Fig. 9 Effect of the functionalized hydrogen atoms number on Young's modulus of graphene sheet (a) vacancy defects (b) SW defects. | |
4. Conclusions
In this paper, the effect of defects including vacancy and SW defects on the Young's modulus of graphene sheets is investigated using MD simulations. The results show that the presence of defects reduces the Young's modulus of graphene sheets and the Young's modulus decreases with increasing degree of defects. In addition, the vacancy defects can decrease the Young's modulus, and the vacancy reconstruction can stabilize the modulus. Furthermore, we explore the Young's modulus of graphene with defects functionalized by hydrogen atoms and find that the hydrogenation of vacancy defects increase the Young's modulus of defective graphene but the hydrogenation of SW defects has the opposite effect. Our results suggest that the effect of defects on the mechanical properties of graphene should be taken into account when analyzing the performance characteristics of nanodevices fabricated from graphene sheets.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (10974258), the Fundamental Research Funds for the Central Universities (11CX05002A, 11CX0460A) and the Natural Science Foundation of Shandong Province (ZR2010AL009, ZR2011AL023).
References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jing, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS.
- E. J. Yoo, J. Kim, E. Hosono, H. S. Zhou, T. Kudo and I. Honma, Nano Lett., 2008, 8, 2277–2282 CrossRef CAS.
- N. Mohanty and V. Berry, Nano Lett., 2008, 8, 4469–4476 CrossRef CAS.
- D. Jiang, V. R. Cooper and S. Dai, Nano Lett., 2009, 9, 4019–4024 CrossRef CAS.
- B. Das, K. E. Prasad, U. Ramamurty and C. N. R. Rao, Nanotechnology, 2009, 20, 125705-1-5 Search PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS.
- D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373–4379 CrossRef CAS.
- G. M. Rutter, J. N. Crain, N. P. Guisinger, T. Li, P. N. First and J. A. Stroscio, Science, 2007, 317, 219–222 CrossRef CAS.
- M. Sepioni, S. Rablen, R. R. Nair, J. Narayanan, F. Tuna, R. Winpenny, A. K. Geim and I. V. Grigorieva, Phys. Rev. Lett., 2010, 105, 207205 CrossRef CAS.
- A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873 CrossRef CAS.
- A. J. Stone and D. J. Wales., Chem. Phys. Lett., 1986, 128, 501–503 CrossRef CAS.
- J. W. Jiang, J. S. Wang and B. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 113405 CrossRef.
- Q. B. Zheng, Y. Geng, S. J. Wang, Z. G. Li and J. K. Kim, Carbon, 2010, 48, 4315–4322 CrossRef CAS.
- E. G. Fefey, R. Mohan and A. Kelkar, Mater. Sci. Eng., B, 2011, 176, 693–700 CrossRef CAS.
- D. Rigby, H. Sun and B. E. Eichinger, Polym. Int., 1997, 44, 311–330 CrossRef CAS.
- D. Xia, Q. Z. Xue, J. Xie, H. J. Chen, C. Lv, F. Besenbacher and M. D. Dong, Small, 2010, 6, 2010–2019 CrossRef CAS.
- L. Y. Chu, Q. Z. Xue, T. Zhang and C. C. Ling, J. Phys. Chem. C, 2011, 115, 15217–15224 CAS.
- C. Lv, Q. Z. Xue, D. Xia, M. Ma, J. Xie and H. J. Chen, J. Phys. Chem. C, 2010, 114, 6588–6594 CAS.
- T. Zhang, Q. Z. Xue, S. Zhang and M. D. Dong, Nano Today, 2012, 7, 180–200 CrossRef CAS.
- M. Grujicic, G. Cao and W. N. Roy, Appl. Surf. Sci., 2004, 227, 349–363 CrossRef CAS.
- Y. Geng, J. Li, S. J. Wang and J. K. Kim, J. Nanosci Nanotechnol, 2008, 8, 6238–6246 CrossRef CAS.
- F. Liu, P. Ming and J. Li, Phys Rev B, 2007, 76, 064120 CrossRef.
- J. H. Yuan and K. M. Liew, Carbon, 2009, 47, 1526–1533 CrossRef CAS.
- A. A. El-Barbary, R. H. Telling, C. P. Ewels, M. I. Heggie and P. R. Briddon, Phys. Rev. B, 2003, 68, 144107 CrossRef.
- G. D. Lee, C. Z. Wang, E. Yoon, N. M. Hwang, D. Y. Kim and K. M. Ho, Phys. Rev. Lett, 2005, 95, 205501 CrossRef.
- J. Kotakoski, J. C. Meyer, S. Kurasch, D. Santos-Cottin, U. Kaiser and A. V. Krasheninnikov, Phys Rev B, 2011, 83, 245420 CrossRef.
- D. W. Boukhvalov and M. I. Katsnelson, Nano Letters, 2008, 8, 4373–4379 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here.