DOI:
10.1039/C2RA21446F
(Paper)
RSC Adv., 2012,
2, 10891-10898
Importance of the CH/π hydrogen bond in the enhancement of CD amplitude of exomethylene steroids†
Received
13th July 2012
, Accepted 7th September 2012
First published on 12th September 2012
Abstract
Introduction of an axial methyl group to a bridgehead carbon has been known to enhance the circular dichroism (CD) amplitude of exomethylene steroids such as 4- and 6-methylene-5α-estrane, at ca. 200 nm (π/π* transition). To investigate the effect of a methyl group on the rotational strength of these steroids, time-dependent density functional theory (DFT) calculations were carried out at the M06-2X/6-311++G(d,p)//MP2/6-31G(d,p) level. It has been shown that the replacement of the bridgehead hydrogen atom at position 10 of these steroids by a methyl group influenced the CD amplitude at the π/π* transition. Analysis of natural bonding orbital (NBO) charges of relevant atoms has provided data consistent with this finding. In view of this, we suggest that the enhancement of the CD amplitude by methyl substitution β to the carbon-carbon double bond originates from the CH/π hydrogen bond occurring between CH groups and the π-system.
Introduction
The origin of abnormal optical rotatory dispersion curves (Cotton effect: CE) of chiral organic molecules, including unsaturated natural compounds such as steroidal ketones, olefins and conjugated dienes, has long been a subject of interest for organic and theoretical chemists.1–4 The above problem, however, has remained unsolved, even though this is one of the central issues in theoretical organic chemistry.5
In 1971, Scott and Wrixon analysed CD spectra of 74 cyclic olefins6 and presented a symmetry rule based on octant diagrams.7 Fetizon and co-workers reported that the CD spectra of these compounds around the π–π* transition region were split into two components of the opposite sign, namely λ1 (ca. 200 nm, πy–πy* transition) and λ2 (ca. 185 nm).8 The nature of the second transition λ2 remained unclear, but was supposed to correspond to the πy–πx* transition. In 1976, Hudec and Kirk examined CD spectra of 228 chiral olefinic compounds and grouped them into four categories (Scheme 1):9 1,1-disubstituted ethylenes (exomethylene, A: 48 compounds, λ1 200 ± 2 nm, λ2 189 ± 1 nm), cis-1,2-disubstituted ethylenes (cycloalkene, B: 31 compounds, λ1 200 ± 2 nm, λ2ca. 185 nm), tri-substituted ethylenes (C: 90 compounds, λ1 203.5 ± 1.5 nm, λ2 192 ± 3 nm) and tetra-substituted ethylenes (D: 59 compounds, λ1ca. 195–210 nm, λ2ca. 185–195 nm).
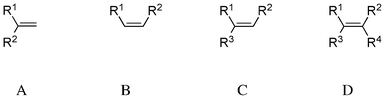 |
| | Scheme 1 Classification of disubstituted ethylene compounds. | |
Table 1 lists the CD data of four exomethylene steroids (type A), which was obtained from a previous paper.10,11 It is remarkable that methyl substitution of the bridgehead hydrogen at C10 of the steroids significantly enhances the CD amplitude at ca. 200 nm (compare 1 with 2, and 3 with 4, Scheme 2). The β-axial methyl group at C10 of 4-methylene and 6-methylene compounds is in the “minus” and “plus” regions of the octant diagram, respectively (Fig. 1).
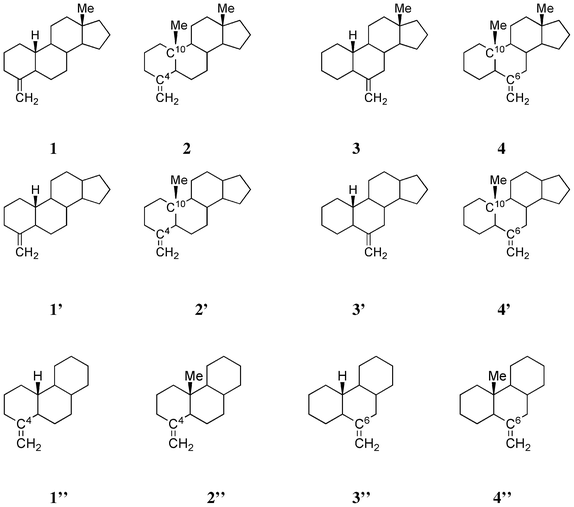 |
| | Scheme 2 Structures of four exomethylene steroids 1, 2, 3 and 4, tetracyclic model compounds 1′, 2′, 3′ and 4′ and tricyclic model compounds 1′′, 2′′, 3′′ and 4′′. | |
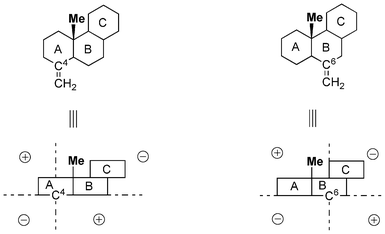 |
| | Fig. 1 Octant diagram showing the position of methyl group in 2 and 4 to the relevant sp2 (C4 or C6) carbon atom. | |
Table 1 CD spectral data of four exomethylene steroids
| Compound |
λ
1/nm |
Δεa |
ΔΔεb |
λ
2/nm |
Δεa |
|
CD amplitude (hexane).
Difference in the CD amplitude between non-methylated (1 or 3) and methylated (2 or 4) steroids.
Lowest wavelength limit and not necessary a maximum in the CD curve.
NR: not reported.
|
| 4-Methylene-5α-estrane 1 |
199 |
−4.1 |
— |
c 185 |
c +6.8 |
| 4-Methylene-5α-androstane 2 |
200 |
−7.2 |
+3.1 |
c 187 |
c +4.8 |
| 4-Methylene-5α-androstane 212 |
200 |
−10.5 |
+6.4 |
NRd |
NR |
| 6-Methylene-5α-estrane 3 |
205 |
−0.3 |
— |
185 |
— |
| 6-Methylene-5α-androstane 4 |
197 |
+4.2 |
−4.5 |
NR |
NR |
In view of the aforementioned evidence, we assumed that the enhancement of CD amplitudes at around 200 nm (λ1) in 2 and 4 is a consequence of the CH/π hydrogen bond,13,14 which may occur between the β-axial methyl group and the relevant carbon-carbon double bond in a through-space manner. The interactions involved in 2 and 4 are quasi-enantiomeric to each other; CH/π hydrogen bonds forming five-membered rings may exist (Fig. 2). Recently we reported on the importance of this type interaction (five- or six-membered CH/π hydrogen bond) in controlling the conformation of organic compounds15 including unsaturated terpenic compounds such as isocarvomenthone,16 α-phellandrene17 and levopimaric acid.18 Herein, we present the computational results obtained by recent versions of the time-dependent density functional theory (TD-DFT).19,20
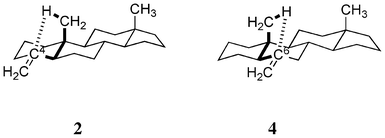 |
| | Fig. 2 Five-membered CH/π hydrogen bond (intensified) may take place in 2 and 4. | |
Computational details
TD-DFT calculations
All calculations were performed with the GAUSSIAN 09 program package. The geometry optimizations were carried out at the MP2/6-31G(d,p) level of theory. The CD spectra of the model compounds have been calculated by using the TD-DFT method. Several functionals and basis sets have been applied to these spectra described in the following sections. The rotational strengths were calculated in the length gauge. Theoretical CD spectra were constructed by convolution of the calculated line spectra using Gaussian functions with a fixed full width at a half maximum (FWHM) of 20.0 nm.
Results and discussion
DFT functional dependence
First, we tested the dependence of the DFT functionals (B3LYP,21 CAMB3LYP,22 M06-2X,23ωB97X-D24) by using model compound 2′′. B3LYP is one of the most popular functionals in computational chemistry. The M06-2X functional is a hybrid functional applicable to relatively weak-bonded systems. CAMB3LYP and ωB97X-D include the long-range corrections to accurately describe the non-Coulomb parts of the exchange functional. The CD spectra calculated by using these functionals, except for B3LYP, gave comparable results (Fig. 3). Presumably, B3LYP cannot describe the dispersion force well, and therefore, it is not suitable for calculations including weak interactions, such as the CH/π hydrogen bond.23,25 However, CAMB3LYP and M06-2X results were in agreement with the experimental data of 2′′.
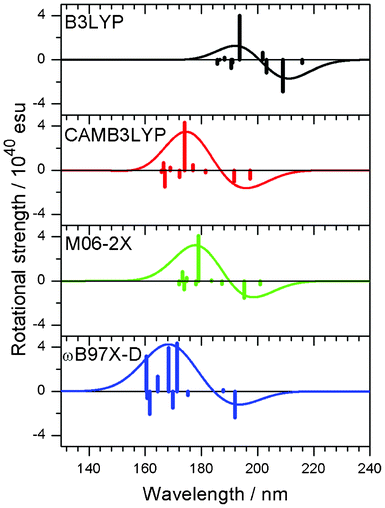 |
| | Fig. 3 CD spectra of a model compound 2′′ obtained with the use of different functionals, B3LYP, CAMB3LYP, M06-2X and ωB97X-D. Vertical lines in each panel correspond to calculated rotational strengths. | |
Basis set dependence
Next, the dependence on the basis set was examined with the use of the M06-2X functional. Fig. 4 shows the CD spectra of 2′′ obtained by different basis sets. The basis sets without diffuse functions showed inaccurate descriptions of the CD spectra, because these basis sets were optimized for the description at the ground state. Therefore, involvement of diffuse functions is essential in obtaining acceptable results.
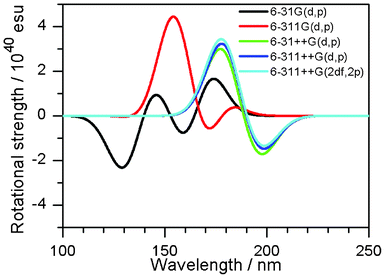 |
| | Fig. 4 CD spectra of 2′′ with different basis sets. The M06-2X functional was applied. | |
Consequently, the rotational strength calculated by using the M06-2X functional with the 6-311++G(d,p) basis set is discussed in the following section.
Assignment of the transitions
In Fig. 3 (line spectra by M06-2X), the vertical lines at ca. 200 and 180 nm included in the first peak were assigned to HOMO–LUMO and HOMO–next LUMO transitions. HOMOs, LUMOs, and next LUMOs of our model compounds are π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), π∗(C
C), π∗(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and σ*(C–H) orbitals, respectively, where σ*(C–H) orbitals are oriented almost perpendicular to the steroidal molecular plane. Therefore, the first well (negative in sign) was assigned as a mixture of π–π* and π–σ* transitions. Fig. 5 shows the HOMOs, the LUMOs and the next LUMOs of 1′′, 2′′, 3′′ and 4′′.
C) and σ*(C–H) orbitals, respectively, where σ*(C–H) orbitals are oriented almost perpendicular to the steroidal molecular plane. Therefore, the first well (negative in sign) was assigned as a mixture of π–π* and π–σ* transitions. Fig. 5 shows the HOMOs, the LUMOs and the next LUMOs of 1′′, 2′′, 3′′ and 4′′.
 |
| | Fig. 5 HOMO (left), LUMO (centre) and next-LUMO (right) of the model compounds: (a) 1′′, (b) 2′′, (c) 3′′ and (d) 4′′. | |
Methane/ethene supramolecular complex
The effect of methyl substitution on the rotational strength of olefins was examined using the methane/ethene supramolecular complex as a simplest model. The intensity of the rotational strength of the first excited state, which was assigned as the π–π* excitation, was monitored.
Fig. 6 shows a contour map depicting the rotational strength of the first excited state in a methane/ethene supramolecular complex. Distance from a hydrogen atom to an olefin plane was fixed at 3.0 Å, which is the typical value for the CH/π hydrogen bond. Fig. 7 shows the dependence of the rotational strength on the CH/π distance for four combinations of horizontal (ΔH) and vertical (ΔV) deviations from the centre of the carbon-carbon double bond of ethene. It has been shown that the relative position of the C–H hydrogen with respect to the carbon-carbon double bond significantly influences the rotational strength of the supramolecular complex. It is therefore expected that the CD spectra are sensitive enough to examine the strength of the CH/π hydrogen bond.
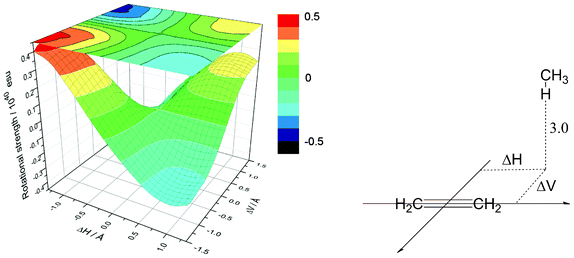 |
| | Fig. 6 Contour map showing the rotational strength in the methane/ethene supramolecular complex. Distance from the hydrogen to the olefin π-plane (R) is kept constant, at 3.0 Å. | |
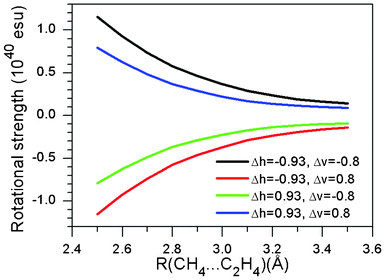 |
| | Fig. 7 Variation of the rotational strength in the methane/ethene supramolecular complex. | |
Calculated CD spectra of model compounds
The rotational strengths of 1′, 2′, 3′ and 4′ were calculated. As could be expected, a change in the sign of CD curves according to the chirality (1′ vs.3′ and 2′ vs.4′) was observed. Furthermore, the introduction of a methyl group β to the carbon-carbon double bond enhanced the CD amplitude at ca. 200 nm (Fig. 8, Table 2). In agreement with this observation, the distances to one of the hydrogen atoms in the methyl group are short in the optimized structures of 2′ [2.602 Å to C4, 2.947 Å to “the exo-carbon” (labeled in bold)] and 4′ (2.697 Å to C6, 3.087 Å to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2).
CH2).
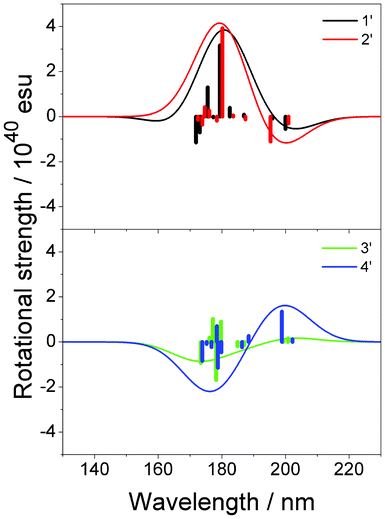 |
| | Fig. 8 Calculated CD spectra of 1′, 2′, 3′ and 4′. Vertical lines in each panel correspond to calculated rotational strengths. | |
Table 2 Calculated rotational strengths of compounds 1′–4′ at the first peak
| Model |
ΔE/eV |
Wavelength/nm |
R/1040esu |
ΔRMe–H/1040esu |
|
1′ (non-methylated) |
6.10 |
203 |
−0.59 |
|
|
2′ (methylated) |
5.90 |
200 |
−1.12 |
−0.53 |
|
3′ (non-methylated) |
6.14 |
202 |
+0.26 |
|
|
4′ (methylated) |
5.90 |
200 |
+1.65 |
+1.39 |
The agreement with the experimental data was fair for 1′, 2′ and 4′. However, the calculated curve of 3′ was considerably different from the expected one. It should be noted that the carbon-carbon double bond in 3′ is a part of the ring B, which is unlike the case in 1′ and 2′ wherein the double bond is in the ring A; this may be a reason for the discrepancy. The CH/π hydrogen bond in 1′ formed a five-membered ring with the following interatomic lengths: 2.819 Å for H6, 3.511 Å for H10 and 3.462 Å for H2 between C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH. In 3′, the CH/π bond lengths of 2.826, 3.499 and 3.445 Å were noted for H4/C, H10/C and H8/C, respectively, though the H–C–C angles were not necessarily good for the CH/π hydrogen bond to form (Scheme 3, Fig. 9).
CH. In 3′, the CH/π bond lengths of 2.826, 3.499 and 3.445 Å were noted for H4/C, H10/C and H8/C, respectively, though the H–C–C angles were not necessarily good for the CH/π hydrogen bond to form (Scheme 3, Fig. 9).
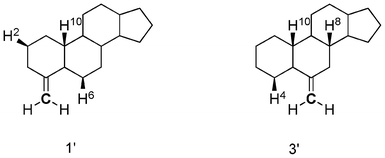 |
| | Scheme 3 Structures of tetracyclic model compounds 1′ and 3′. Hydrogens interacting with a methylene group are shown explicitly. | |
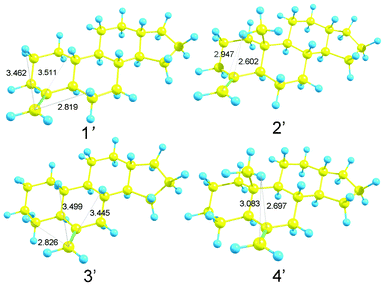 |
| | Fig. 9 Optimized structures of model compounds 1′, 2′, 3′ and 4′. Numbers refer to H/C distances (in Å). | |
To see the effect of alkyl substitution, the CD spectra of C10-alkyl-substituted tricyclic model 1′′ were calculated. Fig. 10 and Table 3 shows the results. Three stable conformers were found for the ethyl and isopropyl-substituted molecules. In these two cases, calculated spectra were generated by the superposition of the spectra of individual conformers by considering the relevant statistical weights. It was demonstrated that the wavelength corresponding to both peaks increases with increasing steric bulk of the functional group R. The reason for this phenomenon remains unclear, however, it is likely that the introduction of a bulky alkyl group at position 10 distorted the conformation of the cyclohexane rings. Unfortunately, to date, the effect of the conformational change on the wavelength of the CD peak is not reported in the literature.
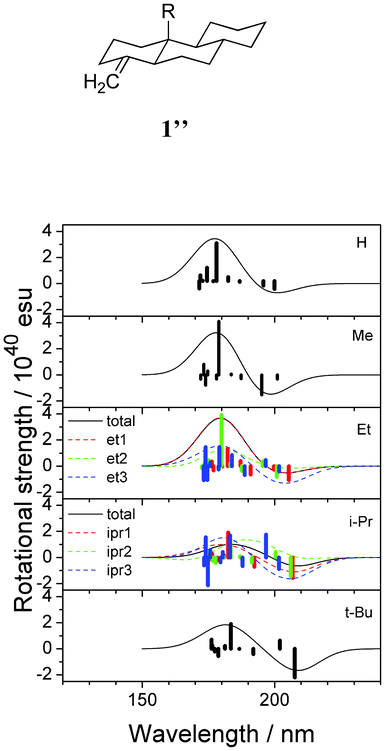 |
| | Fig. 10 Calculated CD spectra of the alkyl-substituted model compounds 1′′ (R = H, Me, Et, i-Pr, t-Bu). Vertical lines in each panel correspond to calculated rotational strengths. | |
Table 3 Calculated rotational strength of alkyl-substituted tricyclic model compounds 1′′ at the first well
|
R
|
ΔE/eV |
Wavelength/nm |
R/1040esu |
| H (=1′) |
6.14 |
202 |
−0.69 |
| Me (=2′) |
6.23 |
199 |
−1.55 |
| Et1 |
6.08 |
204 |
−0.62 |
| Et2 |
6.08 |
204 |
−0.62 |
| Et3 |
6.08 |
204 |
−1.41 |
|
i-Pr1 |
6.02 |
206 |
−1.09 |
|
i-Pr2 |
5.99 |
207 |
0.0 |
|
i-Pr3 |
6.02 |
206 |
−1.72 |
|
t-Bu |
5.93 |
209 |
−1.80 |
Other exomethylene compounds
Exomethylene compounds 2-methylene-5α-androstane 5, deoxy-onocerin 6 and 16-methylene-5α-androstane 7 (Scheme 4) are known to have large CD amplitudes (Table 4);5,9 this may also be a consequence of the introduction of a methyl group at the bridgehead carbon atom. The large CD amplitude is noteworthy in the case of deoxy-onocerin 6, probably due to the dimeric structure of this compound; Fetizon and Hanna have already stated that this type of interaction is additive.12
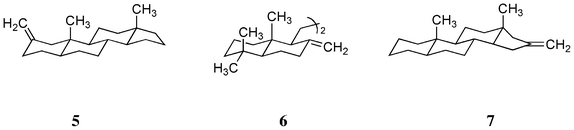 |
| | Scheme 4 Structures of three exomethylene compounds 5, 6 and 7. | |
Table 4 CD spectral data of three exomethylene steroids 5, 6 and 7 at the first peak
| Compound |
λ
1/nm |
Δε |
|
5
|
197 |
+10.5 |
|
6
|
202 |
−14.5 |
|
7
|
193 |
−7.9 |
Therefore, the rotational strength of model compounds, 5′, 6′, 7′ (methylated), 8′, 9′ and 10′ (non-methylated) (Scheme 5) were calculated. Fig. 11 and Table 5 show the results. As expected, changes in the sign of the CD curves according to the chirality of the model compounds was recorded. The data were compatible with our expectation that methyl substitution enhances the CD amplitude. The effect was remarkable in 5′ (vs.8′) and 7′ (vs.10′) but not in 6′ (vs.9′). The result could be explained by the dimeric structure of deoxy-onocerin 6. Accordingly, the enhancement factor should be multiplied by a factor of 2.12 The five-membered ring D of compound 7 is expected to affect the influence of the CH/π hydrogen bond. The minimized structures of model compounds (Fig. 12) in fact show short H/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 (2.681, 2.622, 2.625 Å) and H/C
CH2 (2.681, 2.622, 2.625 Å) and H/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 distances (3.104, 3.021, 3.443 Å), respectively, in 5′, 6′ and 7′). This type interaction is absent in 8′, 9′ and 10′.
CH2 distances (3.104, 3.021, 3.443 Å), respectively, in 5′, 6′ and 7′). This type interaction is absent in 8′, 9′ and 10′.
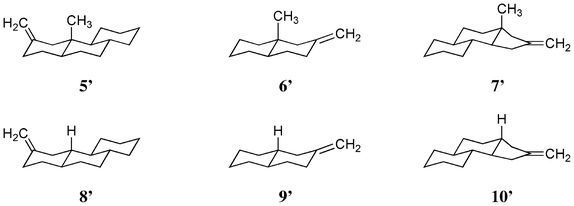 |
| | Scheme 5 Structures of model compounds 5′, 6′ and 7′ (methylated) and 8′, 9′, and 10′ (not-methylated). | |
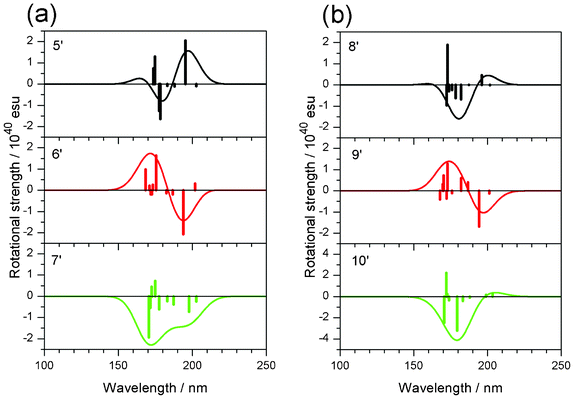 |
| | Fig. 11 Calculated CD spectra of model compounds (a) 5′–7′ (methylated) and (b) 8′–10′ (non-methylated). Vertical lines in each panel correspond to calculated rotational strengths. | |
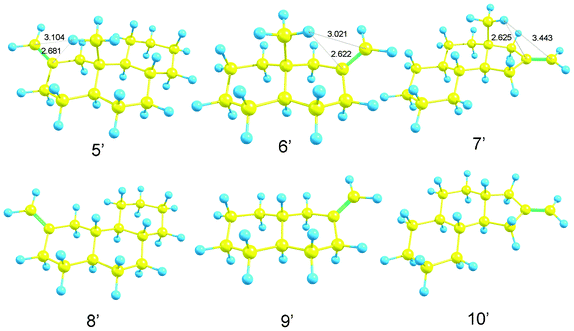 |
| | Fig. 12 Optimized structures of model compound 5′, 6′, 7′, 8′, 9′ and 10′. | |
Table 5 Calculated rotational strength of model compounds 5′–10′ at the first peak
| Model |
ΔE/eV |
Wavelength/nm |
R/1040esu |
ΔRMe–H/1040esua |
|
Difference in the rotational strength between methylated and non-methylated compounds.
|
|
5′ (methylated) |
6.29 |
197 |
1.62 |
1.16 |
|
8′ |
6.20 |
200 |
0.46 |
|
|
6′ (methylated) |
6.36 |
195 |
−1.46 |
–0.45 |
|
9′ |
6.29 |
197 |
−1.01 |
|
|
7′ (methylated) |
6.26 |
198 |
−1.34 |
−1.84 |
|
10′ |
6.08 |
204 |
0.50 |
|
Natural bonding orbital (NBO) charge
It should be noted that the contributions of the Coulombic and charge-transfer interactions to the CH/π hydrogen bond were not negligible, although the stabilization energy of the interaction, for the most part, comes from the dispersion interaction.26,27 In view of the results reported in the foregoing sections, the enhancement of CD amplitude by the methyl substitution could be explained as being a consequence of the CH/π hydrogen bond. To verify this hypothesis, NBO charges of the compounds 1′, 2′, 3′ and 4′ (Scheme 6) were calculated. Table 6 shows that the NBO charges of hydrogens interacting with the sp2-carbon (H1 in 2′ and H1′ in 4′) were more positive as compared to those of H2 and H3 in 2′, and H2′ and H3′ in 4′. The difference between the NBO charges (negative) was not significant for relevant sp2-carbons (C4 and C6); however, the result is in line with our expectations. Furthermore, the above result is in agreement with our previous findings relating to the CH/n hydrogen bond.28 Our studies showed that, in every case, the NBO charge of the interacting hydrogen is more positive than charge of the others, i.e., non-interacting hydrogen atoms. Therefore, the existence of a CH/π hydrogen bond was confirmed by the NBO charge analysis.
 |
| | Scheme 6 Structures of tetracyclic model compounds 1′, 2′, 3′ and 4′. Hydrogens interacting with a methylene group are shown explicitly. | |
Table 6 Natural bonding orbital (NBO) charges estimated for 1′, 2′, 3′ and 4′. The relevant data are underlined
| Model |
H10 |
H1 |
H2 |
H3 |
H1′ |
H2′ |
H3′ |
C4 |
C6 |
|
1′ |
+0.234 |
|
|
|
|
|
|
−0.013 |
|
|
2′ |
|
![[+ with combining low line]](https://www.rsc.org/images/entities/char_002b_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) |
+0.231 |
+0.228 |
|
|
|
−![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif) |
|
|
3′ |
+0.234 |
|
|
|
|
|
|
|
−0.008 |
|
4′ |
|
|
|
|
![[+ with combining low line]](https://www.rsc.org/images/entities/char_002b_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif) ![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif) ![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif) |
+0.230 |
+0.230 |
|
−![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) ![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif) |
Conclusions
The results reported in the previous sections confirm our hypothesis that the CH/π hydrogen bond is responsible for the enhancement of the CD amplitude of steroidal exomethylene compounds. The peculiar chiroptical properties of unsaturated steroidal compounds,29 which are often observed (but remained unexplained) could have originated from the CH/π hydrogen bonds between an alkyl group and a π-system close to it.30,31 The unusual folded conformation reported for terpenic compounds such as isocarvomenthone,16 α-phellandrene17 and levopimaric acid18 has been explained on a similar basis. In the present study, firm evidence for the involvement of CH/π hydrogen bonds in the mechanism of CD spectral amplitude enhancement has not been obtained. However, the importance of CH/π hydrogen bonds is reasonable, because the substitution by an alkyl group at position β to the π-system enhanced the CD amplitude in every case. The precise mechanism of the influence of the CH/π hydrogen bond on the CD spectra remains open for further discussions. Vibrational circular dichroism spectroscopy,32 which is similar to the ECD spectroscopy discussed here, is now becoming a well-developed and popular technique that will stimulate more in-depth computational investigations of the phenomena described in this paper.
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (C) (Contract No. 23540476) of the Ministry of Education, Culture, Sports, Science and Technology, Japan. The authors thank the Information Media Center at Hiroshima University for the use of a grid with high-performance PCs and the Research Center for Computational Science, Okazaki, Japan for the use of Fujitsu PRIMEQUEST. This paper is dedicated to the memory of the late Professor Günther Snatzke, one of the pioneers of this important field of theoretical organic chemistry.
References
-
C. Djerassi, Optical Rotatory Dispersion, McGraw-HillNew York, 1960 Search PubMed.
- G. Snatzke, Angew. Chem., Int. Ed. Engl., 1979, 18, 363–377 CrossRef.
- D. N. Kirk, Tetrahedron, 1986, 42, 777–818 CrossRef CAS.
-
N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy, Wiley & Sons, NY, 2012 Search PubMed.
- M. Nishio and M. Hirota, Tetrahedron, 1989, 45, 7201–7245 CrossRef CAS.
-
(a) A. I. Scott and A. D. Wrixon, Tetrahedron, 1971, 27, 3695–3715 CrossRef;
(b) A. I. Scott and A. D. Wrixon, Tetrahedron, 1971, 27, 4787–4819 CrossRef CAS.
- A. I. Scott and A. D. Wrixon, Chem. Commun., 1969, 1182–1186 RSC.
- M. Fetizon, I. Hanna, A. I. Scott, A. D. Wrixon and T. K. Devon, Chem. Commun., 1971, 545–547 RSC.
- J. Hudec and D. N. Kirk, Tetrahedron, 1976, 32, 2475–2506 CrossRef CAS.
- Ref. 9, Table 2: compounds A2, A3, A22, A23 and A24. CD spectra are not reported in this paper, due probably to the limitation of the measurement (low resolution, overlapping of the bands, instrumental noise, etc.) at that time.
- See also Table of Ref. 8 and Table 16 of Ref. 5.
- M. Fetizon and I. Hanna, Chem. Commun., 1970, 462–463 RSC.
-
M. Nishio, M. Hirota and Y. Umezawa, The CH/π Interaction. Evidence, Nature, and Consequences, Wiley-VCH, New York, 1998 Search PubMed.
- M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900 RSC.
- O. Takahashi, Y. Kohno and M. Nishio, Chem. Rev., 2010, 110, 6049–6076. CrossRef CAS See also Ref. 5.
- O. Takahashi, K. Yamasaki, Y. Kohno, K. Ueda, H. Suezawa and M. Nishio, Tetrahedron, 2008, 64, 2433–2440 CrossRef CAS.
- O. Takahashi, K. Yamasaki, Y. Kohno, K. Ueda, H. Suezawa and M. Nishio, Tetrahedron, 2008, 64, 5773–5778 CrossRef CAS.
- O. Takahashi, K. Yamasaki, Y. Kohno, K. Ueda, H. Suezawa and M. Nishio, Tetrahedron, 2009, 65, 3525–3528 CrossRef CAS.
-
(a) K. Yabana and G. F. Bertsch, Phys. Rev. A, 1998, 58, 2604–2607 CrossRef CAS;
(b) T. Otobe, M. Yamagiwa, J.-I. Iwata, K. Yabana, T. Nakatsukasa and G. F. Bertsch, Phys. Rev. B, 2008, 77, 165104 CrossRef.
-
(a) J. Autschbach, T. Ziegler, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef CAS;
(b) D. M. McCann and P. J. Stephens, J. Org. Chem., 2006, 71, 6074–6098 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- K. S. Thanthiriwatte, E. G. Hohenstein, L. A. Burns and C. D. Sherrill, J. Chem. Theory Comput., 2011, 7, 88–96 CrossRef CAS.
-
M. Nishio, M. Hirota and Y. Umezawa, The CH/π Interaction. Evidence, Nature, and Consequences, Wiley-VCH, New York, 1998, Chapter 3 Search PubMed.
-
(a) M. Nishio, J. Mol. Struct., 2012, 1018, 2–7 CrossRef CAS;
(b)
M. Nishio, Y. Umezawa, H. Suezawa and S. Tsuboyama, The CH/π Hydrogen Bond: Implication in Crystal Engineering. Chapter 1 in The Importance of Pi-Interactions in Crystal Engineering: Frontiers in Crystal Engineering, ed. E. R. T. Tiekink and J. Zukerman-Schpector, John Wiley & Sons, New York, 2012 Search PubMed.
-
(a) O. Takahashi, K. Yamasaki, Y. Kohno, R. Otaki, K. Ueda, H. Suezawa, Y. Umezawa and M. Nishio, Carbohydr. Res., 2007, 342, 1202–1209 CrossRef CAS;
(b) O. Takahashi, K. Yamasaki, Y. Kohno, K. Ueda, H. Suezawa and M. Nishio, Chem. Phys. Lett., 2007, 440, 64–69 CrossRef CAS.
- A. W. Burgstahler, L. O. Weigel and J. K. Gawronski, J. Am. Chem. Soc., 1976, 98, 3015–3016 CrossRef CAS.
-
(a) S. Zushi, Y. Kodama, Y. Fukuda, K. Nishihata, M. Nishio, M. Hirota and J. Uzawa, Bull. Chem. Soc. Jpn., 1981, 54, 2113–2119 CrossRef CAS;
(b) S. Araki, T. Seki, K. Sakakibara, M. Hirota, Y. Kodama and M. Nishio, Tetrahedron: Asymmetry, 1993, 4, 555–574 CrossRef CAS.
- A. W. Burgstahler, G. Wahl, N. Dang, M. E. Sanders and A. Nemirovsky, J. Am. Chem. Soc., 1982, 104, 6873–6874 CrossRef CAS.
-
(a) V. P. Nicu, J. Autschbach and E. J. Baerends, Phys. Chem. Chem. Phys., 2009, 11, 1526–1538 RSC;
(b) V. P. Nicu, M. Heshmat and E. J. Baerends, Phys. Chem. Chem. Phys., 2011, 13, 8811–8825 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ra21446f |
|
| This journal is © The Royal Society of Chemistry 2012 |
Click here to see how this site uses Cookies. View our privacy policy here. 





![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), π∗(C
C), π∗(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and σ*(C–H) orbitals, respectively, where σ*(C–H) orbitals are oriented almost perpendicular to the steroidal molecular plane. Therefore, the first well (negative in sign) was assigned as a mixture of π–π* and π–σ* transitions. Fig. 5 shows the HOMOs, the LUMOs and the next LUMOs of 1′′, 2′′, 3′′ and 4′′.
C) and σ*(C–H) orbitals, respectively, where σ*(C–H) orbitals are oriented almost perpendicular to the steroidal molecular plane. Therefore, the first well (negative in sign) was assigned as a mixture of π–π* and π–σ* transitions. Fig. 5 shows the HOMOs, the LUMOs and the next LUMOs of 1′′, 2′′, 3′′ and 4′′.



![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2).
CH2).

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH. In 3′, the CH/π bond lengths of 2.826, 3.499 and 3.445 Å were noted for H4/C, H10/C and H8/C, respectively, though the H–C–C angles were not necessarily good for the CH/π hydrogen bond to form (Scheme 3, Fig. 9).
CH. In 3′, the CH/π bond lengths of 2.826, 3.499 and 3.445 Å were noted for H4/C, H10/C and H8/C, respectively, though the H–C–C angles were not necessarily good for the CH/π hydrogen bond to form (Scheme 3, Fig. 9).



![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 (2.681, 2.622, 2.625 Å) and H/C
CH2 (2.681, 2.622, 2.625 Å) and H/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 distances (3.104, 3.021, 3.443 Å), respectively, in 5′, 6′ and 7′). This type interaction is absent in 8′, 9′ and 10′.
CH2 distances (3.104, 3.021, 3.443 Å), respectively, in 5′, 6′ and 7′). This type interaction is absent in 8′, 9′ and 10′.



![[+ with combining low line]](https://www.rsc.org/images/entities/char_002b_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[4 with combining low line]](https://www.rsc.org/images/entities/char_0034_0332.gif)
![[+ with combining low line]](https://www.rsc.org/images/entities/char_002b_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif)
![[2 with combining low line]](https://www.rsc.org/images/entities/char_0032_0332.gif)
![[3 with combining low line]](https://www.rsc.org/images/entities/char_0033_0332.gif)
![[7 with combining low line]](https://www.rsc.org/images/entities/char_0037_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[. with combining low line]](https://www.rsc.org/images/entities/char_002e_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif)
![[0 with combining low line]](https://www.rsc.org/images/entities/char_0030_0332.gif)
