Can ionization induce an enhancement of hydrogen storage in Ti₂–C₂H₄ complexes?

Abstract

We predicted here gravimetric hydrogen storage capacity of Ti₂–C₂H₄ and Ti₂–C₂H₄⁺ complexes using density functional theory (DFT) method. The number of adsorbed H₂ on Ti₂–C₂H₄ is limited to ten. It has been seen that controlling the charge-state of this complex enhances its gravimetric hydrogen uptake and the metal bond strength. The resulting cationized complex then adsorbs two additional H₂ molecules than the neutral complex. In addition, we elucidated the effect of exchange and correlation functionals in DFT on H₂ adsorption energy of these complexes. Molecular dynamics simulations were also carried out to confirm whether the complex adsorbs H₂ molecules at a finite temperature. The H₂ uptake capacity of a complex from simulations is the same as that from the geometry optimization only if the H₂ adsorption was energetically favourable i.e. with the positive Gibbs free corrected H₂ adsorption energy.

---

Introduction

Hydrogen storage is one of the important issues for the advancement of hydrogen and fuel cell power technologies in transportation, stationary, and portable applications. There are different ways of storing hydrogen such as physisorption in carbon nanotubes, storage in metal hydrides, storage in high pressure cylinders, storage as liquid hydrogen etc; each with positive and negative sides. Various ways are being adopted to discover novel materials, satisfying all the US Department of Energy (DOE) targets.¹ The suggestion and study of theoretical models which predict the maximum hydrogen capacity, is one of over-arching research and development for all advanced materials. An increase in computational power in recent years has opened up new possibilities for theoretical studies of hydrogen storage.

Carbon nanostructures such as carbon nanotubes^2–5 and buckyballs^6–9 are among the most widely investigated materials for hydrogen storage. Binding energies of hydrogen molecules to naked carbon structures are lower, and lie in the physisorption range. These theoretical binding energies have to be increased. The usual approach to overcome this problem is doping nanomaterials with metals, making sure the selection of metal gives a light weight material and captures as much hydrogen as possible. The interaction between the hydrogen molecules and metal atoms deposited on a surface of substrate can be electrostatic, chemisorption or of Kubas type.^10–13 Recently, it has been seen that there is an excellent agreement between experiments and theoretical calculations for hydrogen storage and other properties for this type of metal decorated organic compounds.^14–16

It is desirable that adsorption and desorption of H₂ molecules should occur at or somewhat above room temperature. As H₂ is the simplest light weight diatomic molecule, careful calculations of H₂ containing systems is required. Thermochemistry calculations can help us to judge the accurate evaluation of Gibbs corrected H₂ adsorption energy of such systems containing H₂ molecules, as there is a considerable energy contribution due to translational and rotational motion of H₂ in gas phase.

In this paper, we explain the hydrogen storage enhancement capability of a Ti₂–C₂H₄ material by means of controlling its charge-state. Gibbs corrected adsorption energy helps to determine whether a complex is energetically favourable or not over a selected temperature range. We have performed ab initio molecular dynamics simulations to verify hydrogen uptake capacity of neutral as well as charged Ti₂–C₂H₄ organometallic material at different temperatures from geometry optimizationm.

Computational details

The geometry optimization of hydrogen adsorbed Ti₂–C₂H₄ and its cation complex is carried out with the Gaussian 03 suite of programs.¹⁷ The valence double-ζ and polarization functions (6–31G(d,p)) is used as a basis set of Ti, C, and H atoms. The thermostatic ab initio molecular dynamic (MD) simulations are carried out using atom-centred density matrix propagation (ADMP)^18–22 starting with optimized geometry using exchange and correlation functionals viz. Perdew–Burke–Ernzerhof (PBEPBE).²³ The time step of ADMP-MD is set at 0.2 fs. The desired temperature of a (neutral as well as charged) molecule is obtained by repeated scaling of nuclear velocities during entire MD simulations time of 1 ps. Maximum allowed deviation from nuclear velocities is of 1 K from desired temperature during MD simulations.

Results and discussion

In the first step, we optimized geometry of a Ti₂–C₂H₄ complex and found that a maximum of ten hydrogen molecules (five on each Ti atom site) can be adsorbed on it (Fig. 1(a)), giving it a hydrogen uptake of ∼14 wt% using PBEPBE level of theory. We then considered H₂ adsorption on Ti₂–C₂H₄⁺ complex. In an induced ionization process, the number of electrons gets reduced in a complex. The vacant d-orbital of Ti in Ti₂–C₂H₄⁺ complex is responsible for the adsorption of an additional two H₂ molecules (a H₂ molecule on each Ti). Thus, a maximum of twelve hydrogen molecules can be bound to Ti₂–C₂H₄⁺ complex by means of controlling its charged-state as shown in Fig. 1(b). This indicates that the ionic process enhances its hydrogen uptake capacity by about 2 wt%. The dynamic stability of these geometries is confirmed by frequency calculations, and it was found that there is no imaginary frequency. We also performed calculations at higher spin-state (triplet for neutral and quartet for charged) for these complexes, and found that geometries have imaginary frequencies. This means that optimized geometries at higher spin-state were not the local minimum of the potential energy surface.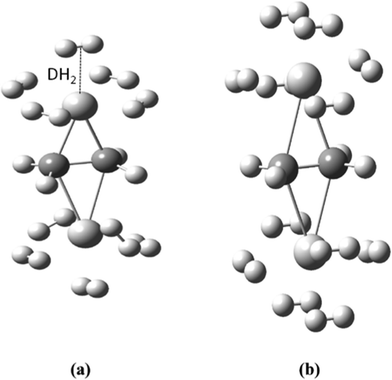

Fig. 1 Optimized geometries of (a) Ti₂–C₂H₄–10H₂ and (b) Ti₂–C₂H₄⁺–12H₂ complexes using PBEPBE/6-31G(d,p) level of theory.

We first investigated the H₂ adsorption energy for H₂ adsorbed Ti₂–C₂H₄ and Ti₂–C₂H₄⁺ complexes. The averaged adsorption energy (ΔE_a) for maximum ‘n’ number of H₂ adsorbed Ti₂–C₂H₄ complexes is calculated as,

ΔE_a = {E[X] + nE[H₂] − E[X(H₂)_n]}/n

and with Gibbs free energy correction (ΔG_a) is calculated as,

ΔG_a = {G[X] + nG[H₂] − G[X(H₂)_n]}/n

Here, E[X] is the total energy of a complex X, G[X] stands for the total energy of a complex X with Gibbs free energy correction. The G[X] and Gibbs free energy correction G_corr[X] are given as,

G[X] = E[X] + G_corr[X]

, and

G_corr[X] = E_zpe[X] + E_thm[X] +k_BT − TS[X]

Here, E_zpe[X] is the zero-point energy, E_thm[X] is the energy due to sum of translational, rotational and vibrational motion of X, k_B is the Boltzmann's constant, and S[X] is the sum of entropy for translational, rotational and vibrational motion of X. Similarly, ΔE_a⁺ and ΔG_a⁺ can be calculated for Ti₂–C₂H₄⁺ complex. The averaged H₂ adsorption energy without (with) Gibbs free energy correction at room temperature is 0.64 (0.20) and 0.46 (−0.01) eV/H₂ in Ti₂–C₂H₄–10H₂ and Ti₂–C₂H₄⁺–12H₂ complex, respectively, at PBEPBE/6–31G(d,p) level of theory. The negative and positive values of ΔG and ΔH, respectively, indicate that the adsorption process is spontaneous and endothermic in nature. We calculated H₂ adsorption energy at different temperatures which provides the temperature range for which H₂ adsorption on a complex is energetically favourable, and is shown in Fig. 2.

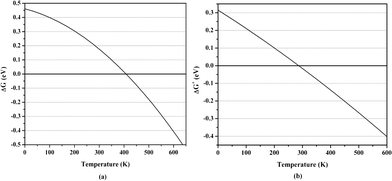Fig. 2 Calculated averaged H₂ adsorption energy for (a) Ti₂–C₂H₄–10H₂ and (b) Ti₂–C₂H₄⁺–12H₂ complex including Gibbs free energy correction at PBEPBE/6–31G(d,p) level as a function of temperature at pressure = 1 bar.

We also carried out calculations using different methods in addition to PBEPBE method. Table 1 gives the averaged adsorption energy for Ti₂–C₂H₄–10H₂ and Ti₂–C₂H₄⁺–12H₂ complex, obtained using MP2 and DFT with different exchange and correlation functionals such as Generalized Gradient Approximation (PBEPBE²³ and BLYP^24,25), two hybrid-functionals (B3LYP²⁶ and PBE1PBE²⁷). The BLYP and B3LYP exchange and correlation functionals give energy of a system that includes Hartree-Fock (HF) exchange contribution. Okamato suggested that the more HF contribution, the lower the averaged adsorption energy.²⁸ This is also true in the case of PBEPBE and PBE1PBE. Table 1 shows that averaged adsorption energy depends on the method used. The energy trend for the H₂ adsorption on organometallic complex is in good agreement with that observed earlier.^28–31 It is worthy to note that Van der Waal interaction is included in MP2, and not to be expected in the DFT method. Table 1 indicates that Van der Waal interaction does not play much of a role in the adsorption of H₂ on both Ti₂–C₂H₄ and Ti₂–C₂H₄⁺ complex which is the same when compared to that observed in previous work.²⁸ However, it is quite different from H₂ adsorption on nanocarbon fragment.²⁹

Table 1 Averaged Gibbs corrected H₂ adsorption energy (eV) in Ti₂–C₂H₄–10H₂ (ΔG_a) and Ti₂–C₂H₄⁺–12H₂ (ΔG_a⁺) complexes at room temperature at different level of theory

	PBEPBE	BLYP	PBE1PBE	B3LYP	MP2
a Negative sign of ΔGa/ΔGa^+ and observed positive value of ΔH (not quoted here) indicate that the adsorption process is spontaneous and endothermic in nature.
(at 298.15 K)
ΔGa	0.20	0.03	0.15	0.01	−0.12^a
ΔGa^+	−0.01^a	−0.10^a	−0.09^a	−0.16^a	−0.25^a

---

Next, we performed Mulliken charge analysis and natural population analysis. A plot of Mulliken charge on Ti atom versus averaged Gibbs corrected H₂ adsorption energy is shown in Fig. 3(a) and 3(b) for Ti₂–C₂H₄–10H₂ and Ti₂–C₂H₄⁺–12H₂ complex, respectively, using four different exchange and correlation functionals viz. BLYP, B3LYP, PBEPBE and PBE1PBE in DFT and MP2. There is a linear relation between them as can be seen in Fig. 3(a) and 3(b). The Mulliken charge on Ti atom obtained using PBEPBE and PBE1PBE methods indicates that negative charge is transferred from C atoms to Ti atoms in the Ti₂–C₂H₄⁺–12H₂ complex. Thus, increasing the electron density of Ti atom contributes attractive interactions between H₂ molecules and Ti-atom in a complex. This relationship is in agreement with the earlier results.^28–31 Natural population analysis shows that the total of about one electron is transferred from each Ti atom to the C₂H₄ substrate in Ti₂–C₂H₄ complex whereas total of about two electrons from each Ti atom to C₂H₄⁺ template in Ti₂–C₂H₄⁺ complex, using PBEPBE level of theory. Thus, enhancement in H₂ uptake of Ti₂–C₂H₄ complex upon ionization can be observed due to more valence electron transfer from Ti atoms to charged substrate and increase in the metal bond strength.

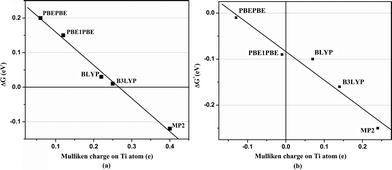Fig. 3 Mulliken atomic charge on Ti atom versus Gibbs corrected averaged H₂ adsorption energy for (a) Ti₂–C₂H₄–10H₂ and (b) Ti₂–C₂H₄⁺–12H₂ complexes.

Furthermore, we performed ADMP-MD simulations to verify the hydrogen uptake capacity of Ti₂–C₂H₄ and Ti₂–C₂H₄⁺ complexes at different temperatures. The distance between the centre of mass of H₂ molecule and Ti atom is denoted by DH₂ as shown in Fig. 1(a). We obtained the DH₂ trajectories with evolution of time, in both Ti₂–C₂H₄–10H₂ and Ti₂–C₂H₄⁺–12H₂ complex. ADMP-MD is carried out using PBEPBE method, since using this method, the H₂ adsorption is energetically favourable for a wider range of temperatures than other methods used for calculations.²⁸ The ADMP-MD simulations are started from the optimized geometry using the same method. Fig. 4 shows time evolution of DH₂ at T = 300 K in Ti₂–C₂H₄–10H₂ complex. It can be seen that all ten H₂ molecules in initial geometry do remain adsorbed on the complex within 1 ps of simulations. The DH₂ of these H₂ molecules oscillate around 1.9 Å. We also performed ADMP-MD simulations at T = 400 K where H₂ adsorption in a complex is energetically unfavourable as per Fig. 2. A snapshot at 0.4 ps (Fig. 5) reveals that out of ten H₂ adsorbed molecules in initial geometry, seven remain adsorbed on the distorted geometry of Ti₂–C₂H₄ complex, some of them adsorbed dissociatively, and remaining desorbed from the complex. This shows the successive desorption of H₂ molecules. Thus, desorption of H₂ molecules can be made by means of the raise in temperature.

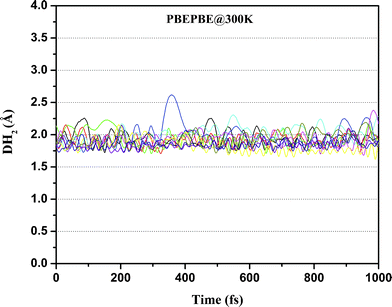Fig. 4 Trajectories of DH₂ in Ti₂–C₂H₄–10H₂ complex at T = 300 K obtained using ADMP-MD simulations with PBEPBE method.

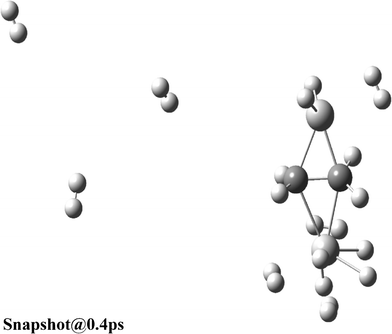Fig. 5 Snapshot of Ti₂–C₂H₄–10H₂ complex at 0.4 ps and T = 400 K obtained using ADMP-MD simulations with PBEPBE method.

We then performed ADMP-MD simulations to confirm whether ionization enhances H₂ uptake capacity of Ti₂–C₂H₄ complex as predicted by geometry optimization. We examined the DH₂ trajectories in Ti₂–C₂H₄⁺–12H₂ complex at T = 300 K with evolution of time. Fig. 2 shows that H₂ adsorption in Ti₂–C₂H₄⁺–12H₂ complex is not energetically favourable at room temperature. Snapshot of Ti₂–C₂H₄⁺–12H₂ complex has been taken at 0.6 ps during simulations, using PBEPBE level of theory as shown in Fig. 6. From Fig. 6, it can be seen that out of twelve H₂ molecules in initial geometry, eight H₂ molecules remain bound to Ti₂–C₂H₄⁺ complex. Fig. 2 shows that H₂ adsorption on Ti₂–C₂H₄⁺ complex is energetically favourable below ∼T = 270 K, using PBEPBE level of theory. To confirm this, we carried out ADMP-MD simulations by lowering temperature where H₂ adsorption on Ti₂–C₂H₄⁺ is energetically favourable. In Fig. 7, ADMP-MD simulations at T = 200 K reveal that all the twelve H₂ molecules remain adsorbed on a complex, and oscillate at distance of around 1.8 Å from Ti atom within 1 ps as can be seen from Fig. 7. Thus, simulations reveal that not a single H₂ molecule desorbed from the metal decorated complex during molecular dynamics simulations of 1 ps.

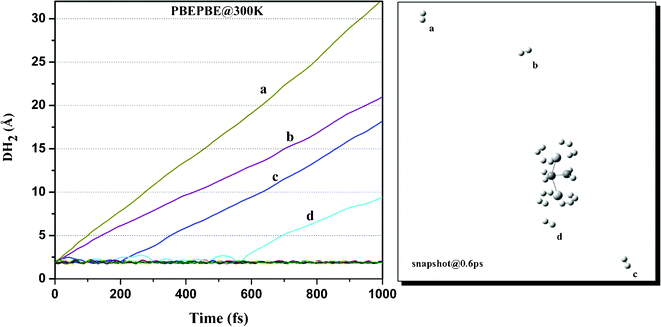Fig. 6 Trajectories of DH₂ in Ti₂–C₂H₄⁺–12H₂ complex at T = 300 K obtained using ADMP-MD simulations with PBEPBE method.

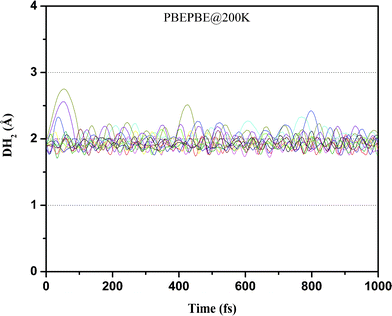Fig. 7 Trajectories of DH₂ in Ti₂–C₂H₄⁺–12H₂ complex at T = 200 K obtained using ADMP-MD simulations with PBEPBE method.

Conclusions

First-principle calculations show that a maximum of ten H₂ molecules can be adsorbed on Ti₂–C₂H₄ complex. H₂ uptake capacity is found to be enhanced by means of controlling its charge-state. We have shown that Ti₂–C₂H₄⁺ can store up to 16 wt% of hydrogen. This enhancement in H₂ uptake of Ti₂–C₂H₄ complex upon ionization is observed due to more valence electron transfer from Ti atom to charged substrate. Adsorption energy is remarkably affected by the exchange and correlation functionals employed in DFT. During ADMP-MD simulations with PBE functional, all the adsorbed H₂ molecules in initial geometry, remain bound to the complex over the temperature range for which H₂ adsorption is found to be energetically favourable, in both Ti₂–C₂H₄–10H₂ and Ti₂–C₂H₄⁺–12H₂ complex. On the other hand, H₂ molecules are found to be desorbed if H₂ adsorption is not energetically favourable. Aspects of controlling charge-state on such systems with complex clustering may lead to findings that its different aggregation behaviour can enhance hydrogen uptake more than the neutral system. It would be interesting to consider the effect of metal atom clustering on hydrogen uptake capacity in such systems. The work towards this direction is in progress in our laboratory.

Acknowledgements

The financial support from CSIR, New Delhi (Grant No. 03(1115)/08/EMR-II) is gratefully acknowledged. We thank C-DAC, Pune, (Maharashtra) India for providing the high performance computing facility. We also thank to Swami Ramanand Teerth Marthwada University, Nanded. Vijayanand Kalamse is supported by University sponsored research fellowship.

References

1. http://www.eere.energy.gov/hydrogenandfuelcells/mypp/ .
2. P. Chen, X. Wu, J. Lin and K. L. Tan, Science, 1999, 285, 91.
3. C. Liu, Y. Y. Fan, M. Liu, H. T. Cong, H. M. Cheng and M. S. Dresselhaus, Science, 1999, 286, 1127.
4. R. Yang, Carbon, 2000, 38, 623.
5. E. Lee, Y. Kim, Y. Jin and K. Chang, Phys. Rev. B, 2002, 66, 73415.
6. Y. H. Kim, Y. Zhao, A. Williamson, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2006, 96, 16102.
7. Q. Sun, P. Jena, Q. Wang and M. Marquez, J. Am. Chem. Soc., 2006, 128, 9741.
8. K. R. S. Chandrakumar and S. K. Ghosh, Nano Lett., 2008, 8, 13.
9. Q. Sun, Q. Wang and P. Jena, Appl. Phys. Lett., 2009, 94, 013111.
10. J. Niu, B. K. Rao and P. Jena, Phys. Rev. Lett., 1992, 68, 2277.
11. L. Gagliardi and P. Pykko, J. Am. Chem. Soc., 2004, 126, 15014.
12. R. C.Lochan and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 1357.
13. E. Durgun, S. Ciraci, W. Zhou and T. Yildirim, Phys. Rev. Lett., 2006, 97, 226102.
14. N. Wadnerkar, V. Kalamse and A. Chaudhari, Theo. Chem. Acc., 2010, 127, 285.
15. N. Wadnerkar, V. Kalamse, A. B. Phillips, B. S. Shivaram and A. Chaudhari, Int. J. Hydrogen Energy, 2011, 36, 9727.
16. C. S. Liu and Z. Zeng, Phys. Rev. B., 2009, 79, 245419.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr.,T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford CT, 2004.
18. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758.
19. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291.
20. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694.
21. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, Israel J. Chem., 2002, 7, 191.
22. S. S. Iyengar and M. J. Frisch, J. Chem. Phys., 2004, 121, 5061.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
24. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
25. C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, B 37, 785.
26. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
28. Y. Okamoto, J. Phys. Chem. C, 2008, 112, 17721.
29. Y. Okamoto and Y. Miyamoto, J. Phys. Chem. B, 2001, 105, 3470.
30. N. Wadnerkar, V. Kalamse and A. Chaudhari, Int. J. Hydrogen Energy, 2011, 36, 664.
31. N. Wadnerkar, V. Kalamse and A. Chaudhari, J. Comp. Chem., 2011, 33, 170.

---