π–π and cation–π interactions in protein–porphyrin complex crystal structures
Blagoje P.
Dimitrijević
a,
Sunčica Z.
Borozan
b and
Srđan Đ.
Stojanović
*c
aClinic for Ruminants and Pigs, Faculty of Veterinary Medicine, University of Belgrade, Serbia
bDepartment of Chemistry, Faculty of Veterinary Medicine, University of Belgrade, Serbia
cICTM - Department of Chemistry, University of Belgrade, Serbia. E-mail: srdjanst@chem.bg.ac.rs; Fax: +381-11-636-061
First published on 25th October 2012
Abstract
In this study we have described the π–π and cation–π interactions between the porphyrin ring and the protein part of porphyrin-containing proteins to better understand their stabilizing role. The number of π–π interactions was higher than that of cation–π interactions in the same set of proteins studied. The pyrrole groups of one porphyrin can be involved in π–π interactions with π systems of another porphyrin in the protein. We have found 5.1% cation–π interactions between porphyrin Fe2+ metal cations and π systems of surrounding amino acids as well as the pyrrole rings of other porphyrins. We observed that most of the π–π interactions have an energy in the range −0.5 to −2.0 kcal mol−1, while the cation–π interactions showed an energy in the range −2 to −4 kcal mol−1. Further, an appreciable number of metal/cation–π interaction pairs have an energy in the range −6 to −13 kcal mol−1. The preferred parallel-stacked orientation is found to be more stable than a T-shaped structure for the full set of π–π interaction pairs. In the case of cation–π interactions, it was found that 44% of the cation–π interactions involved planar stacking, 37% of the interactions belonged to the oblique category, and the remaining 19% of the interactions were of the orthogonal type. The separation distance between the cation group and the aromatic ring decreases as the interplanar angle decreases. Furthermore, in the present study we have found that 10.4% of π residues and 3.9% of cationic residues were found to have one or more stabilization centers. Amino acids deployed in the environment of porphyrin rings are deposited in helices and coils. The results from this study might be used for structure-based porphyrin protein prediction and as scaffolds for future porphyrin-containing protein design.
Introduction
Porphyrins are heterocyclic macrocycles composed of four modified pyrrole subunits interconnected at their α carbon atoms via methine bridges. In addition, porphyrins are aromatic conjugate acids of ligands that bind to metals to form complexes. Some iron-containing porphyrins are called hemes.1,2 Porphyrin-containing proteins are involved in many different processes in living organisms, including oxygen binding, electron transfer, signaling function and catalysis. For example, porphyrin-containing proteins are constituents of photosynthetic reaction centers. A light-harvesting antenna complex is a complex of subunit proteins that may be part of a larger supercomplex of a photosystem, the functional unit in photosynthesis. It is used by plants and photosynthetic bacteria to collect more of the incoming light than could be captured by the photosynthetic reaction center alone using resonance energy transfer.3–8 Understanding porphyrin recognition and its interactions with protein provides insight into how structures are related to porphyrin biological functions.Noncovalent inter- and intramolecular interactions involving aromatic rings are ubiquitous in chemical and biological systems, and span from molecular recognition to self-assembly, and to catalysis and transport.9 Aromatic π–π interactions not only determine biological structures but also modulate the physical properties of residues at enzyme active sites.10 The calculated π–π interaction energies of the parallel, edge–face (T-shaped) and offset stacked are −1.48, −2.46 and −2.48 kcal mol−1, respectively,11 and the major source of attraction is not short-range (such as charge-transfer), but long-range interactions (quadrupole–quadrupole electrostatic and dispersion).12,13 It has been suggested that the perpendicular and parallel-displaced configurations are more common than the sandwich geometry as these, especially the former one, expose three aromatic faces to the outside, offering greater possibility for additional interactions with other groups.14
Cation–π interactions are unique biomolecular binding forces that occur between electron-rich aromatic rings and organic or inorganic (metallic) cations. This type of noncovalent interaction can be very strong, as has been confirmed by solid-state studies of small-molecule crystal structures15,16 and by theoretical and experimental analyses in the gas phase and in aqueous media.9,16 The strength of cation–π interactions ranges between 10 and 150 kcal mol−1,17 which is comparable to the three other major types of molecular interactions: hydrogen bonds, van der Waals interactions, and electrostatic interactions. Cation–π interactions are therefore considered to be an essential force in generating tertiary and quaternary protein structures induced by oligomerization and protein folding.18 While the cation–π interaction is arguably the strongest of the nonbonded interactions, its strength critically depends on the nature of the aromatic system and the charge of the cation.19 Ever since the study of cation–π interactions has gained prominence, the interplay of theory and experiments to see the manifestation of this reasonably strong interaction in chemistry and biology has become inevitable. In a series of pioneering papers Dougherty and co-workers have explored the role, relevance and range of the cation–π interaction between aromatic amino acids and the side chains of arginine, lysine, etc.20 Parallel to this, a series of experimental studies carried out by Rodgers and co-workers to explore the cation–π interaction involving alkali and alkaline metal ions reveal their quantitative strengths.21,22 Computations have played an important role in studying the cation–π interaction in aromatic, heteroaromatic and polycyclic aromatic compounds.23–25 While complexes with a dication have a strength comparable to covalent bonds, monocationic complexes have much smaller binding energies. In contrast, although π–π interactions are much weaker, they have been implicated in a large number of studies where their role has been discussed in eliciting a biological response.26 A strong cooperativity between cation–π interactions involving alkali and alkaline earth metal ions and π–π and hydrogen bonding interactions has also been observed.27,28
Studies of the metal center in heme proteins and model systems have shown that many factors, including noncovalent interactions, may play important roles in the properties of these metalloproteins.29–32 The importance of CH/π interactions of aromatic residues with porphyrin in hemoproteins was shown.33 It was demonstrated that the noncovalent interactions with the propionic groups of porphyrins are very important for the orientations of the imidazoles and that the conformations of the propionic groups have a strong influence on these interactions.34,35 We have previously shown that XH/π interactions are involved in the interactions of every porphyrin ring with surrounding amino acids and that these amino acids are highly conserved, demonstrating that XH/π interactions play important roles in the stability of porphyrin interactions with the protein part.36 Furthermore, we have studied strong hydrogen bonds and hydrophobic interactions,37 and non-canonical interactions38 of porphyrins in porphyrin-containing proteins. In this study, we have extended the analysis of interactions between the porphyrin ring and the protein part of porphyrin-containing proteins on all the π–π and cation–π interactions in order to better understand their stabilizing role. Results from this study might be used for structure-based porphyrin protein prediction and as scaffolds for future porphyrin-containing protein design.
Methodology
Dataset
For this study we used the PDB Select February 2011 list of nonredundant protein chains (25% threshold list, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 protein chains and 741
130 protein chains and 741![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 amino acid residues).39 Chains with a mutual sequence similarity of <25% were included. The following criteria were employed to assemble the set: (1) no theoretical model structures and no NMR structures were accepted, (2) only crystal structures with a resolution of 2.0 Å or better and a crystallographic R-factor of 25.0% or lower were accepted, and (3) crystal structures containing porphyrin were accepted. Using these criteria, we created a dataset of 74 porphyrin-containing protein chains. The PDB IDs are as follows: 1a6mA, 1b0bA, 1c75A, 1cg5B, 1cxyA, 1e29A, 1ecdA, 1ew0A, 1ft5A, 1gq1A, 1gu2B, 1gweA, 1h97B, 1i8oA, 1it2B, 1j0pA, 1jfbA, 1m1qA, 1m70A, 1mj4A, 1ofwB, 1pa2A, 1rwjA, 1v9yA, 1w2lA, 1x3kA, 1x3xB, 1x8qA, 1yccA, 256bB, 2bh4X, 2bk9A, 2bkmB, 2blfB, 2bq4A, 2c1dB, 2c8sA, 2ce0A, 2e74A, 2falA, 2ghcX, 2gkmB, 2h88P, 2hbgA, 2ij2B, 2imqX, 2nw8B, 2o6pB, 2olpA, 2p0bA, 2vebA, 2w72A, 2wtgA, 2wy4A, 2xl6A, 2xtsD, 2z6fA, 2zs0C, 2zxyA, 3a9fA, 3bnjA, 3bxuA, 3cp5A, 3cu4A, 3dr0C, 3egwC, 3fo3A, 3g46A, 3h8tA, 3lb2A, 3lf5B, 3m5qA, 3molA, and 3mvcB.
362 amino acid residues).39 Chains with a mutual sequence similarity of <25% were included. The following criteria were employed to assemble the set: (1) no theoretical model structures and no NMR structures were accepted, (2) only crystal structures with a resolution of 2.0 Å or better and a crystallographic R-factor of 25.0% or lower were accepted, and (3) crystal structures containing porphyrin were accepted. Using these criteria, we created a dataset of 74 porphyrin-containing protein chains. The PDB IDs are as follows: 1a6mA, 1b0bA, 1c75A, 1cg5B, 1cxyA, 1e29A, 1ecdA, 1ew0A, 1ft5A, 1gq1A, 1gu2B, 1gweA, 1h97B, 1i8oA, 1it2B, 1j0pA, 1jfbA, 1m1qA, 1m70A, 1mj4A, 1ofwB, 1pa2A, 1rwjA, 1v9yA, 1w2lA, 1x3kA, 1x3xB, 1x8qA, 1yccA, 256bB, 2bh4X, 2bk9A, 2bkmB, 2blfB, 2bq4A, 2c1dB, 2c8sA, 2ce0A, 2e74A, 2falA, 2ghcX, 2gkmB, 2h88P, 2hbgA, 2ij2B, 2imqX, 2nw8B, 2o6pB, 2olpA, 2p0bA, 2vebA, 2w72A, 2wtgA, 2wy4A, 2xl6A, 2xtsD, 2z6fA, 2zs0C, 2zxyA, 3a9fA, 3bnjA, 3bxuA, 3cp5A, 3cu4A, 3dr0C, 3egwC, 3fo3A, 3g46A, 3h8tA, 3lb2A, 3lf5B, 3m5qA, 3molA, and 3mvcB.
π–π and cation–π interaction analysis
If not already present, all hydrogen atoms were added using the program Discovery Studio Visualizer 3.1.40 The H-atom positions were then refined, keeping the position of the non-H atoms fixed, using the MMFF94 force field.41 When multiple alternative conformations of certain residues were present, as indicated by the altLoc field in the PDB file, only the first conformation was considered.A computer program Discovery Studio Visualizer 3.1 was used for the calculation of various types of π–π and cation–π interactions and their geometrical features with default settings (Fig. 1). π–π interactions are determined following the methodology of McGaughey et al.42 This method finds stacked and staggered π–π interactions by performing the following tests: the distance between the centroid of each pair of π rings is determined to find those which fall within the Center Distance (Rcen) cutoff (default 8 Å). For these, an atom from each ring should be within the Closest Atom Distance (Rclo) cutoff (default 4.5 Å). The angle θ between the normal of one or both rings and the centroid–centroid vector must fall between 0° and ± the Theta Angle cutoff (default 60°), and the angle λ between the normal to each ring must fall between 0° and ± the Lambda Angle cutoff (default 30°). The aromatic rings of the porphyrins and the amino acid side chains of His, Phe, Tyr and Trp are considered to be π systems.
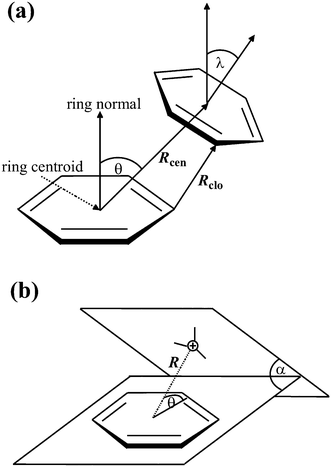 | ||
| Fig. 1 Parameters for π interactions: π–π interactions (a) and cation–π interactions (b). | ||
The following tests are performed to find cation–π interactions:43 cations are found; these are considered to be atoms with a formal charge of >0.5 to allow the inclusion of delocalized cationic species such as lysine and arginine side chains. The distance (R) between each cation and the centroid of each π ring is tested to find those within 1 Å more than the Distance Cutoff (i.e., 7 Å by default). In such cases, the distance between the cation and the mean plane of the ring is determined to find those within the Distance Cutoff (default 6 Å). The angle (θ) between the cation–centroid vector and the ring plane should be more than the Minimum Angle (default 45°). The angle α is the dihedral angle between the two extended planes. The positive charge centers of Arg (NE, CZ, CD, NH1, NH2), Lys (CE, NZ) and the metal atoms from porphyrin are considered to be cations in the present study.
We have computed the energetic contribution of all π–π and cation–π interactions for each protein in the dataset. The total interaction energy (Etotal) has been divided into electrostatic (Ees) and van der Waals (Evdw) energies and were computed using the program NAMD 2.8,44 which has implemented a subset of the OPLS force field to calculate the energies.45
Computation of conservation of amino acid residues
We computed the conservation of amino acid residues in each protein using the ConSurf server.46 This server computes the conservation based on the comparison of the sequence of a PDB chain with the proteins deposited in Swiss-Prot47 and finds the ones that are homologous to the PDB sequence. The number of PSI-BLAST iterations and the E-value cutoff used in all similarity searches were 1 and 0.001, respectively. All the sequences that were evolutionarily related to each one of the proteins in the data set were used in the subsequent multiple alignments. Based on these protein sequence alignments the residues are classified into nine categories from highly variable to highly conserved. Residues with a score of 1 are considered to be highly variable and residues with a score of 9 are considered to be highly conserved.Computation of stabilization centers
Stabilization centers are the clusters of residues that make cooperative, non-covalent and long-range interactions.48 Thus, they are likely to play an important role in maintaining the stability of protein structures. Residues can be considered as parts of stabilization centers if they are involved in medium- or long-range interactions and if two supporting residues can be selected from their C and N terminal flanking tetrapeptides, which together with the central residues form at least seven out of the nine possible contacts. We used an online server, available at http://www.enzim.hu/scide,49 to analyze the stabilization centers of interaction-forming residues. This server defines the stabilization center based on the following criteria: (1) two residues are in contact if there is at least one heavy atom–atom distance smaller than the sum of their van der Waals radii plus 1 Å. (2) A contact is recognized as a “long-range” interaction if the interacting residues are at least ten amino acids apart. (3) Two residues form a stabilization center if they are in a long-range interaction, and if it is possible to select one–one residues from both flanking tetrapeptides of these two residues that make at least seven contacts between these two triplets.49Secondary structure and solvent accessibility studies
The secondary structure and solvent accessibility of the amino acid residues were among the key factors that were essential for understanding the environmental and structure–function relationship of proteins. Hence, a systematic analysis of each interaction forming a residue was performed based on its location in different secondary structures of porphyrin-containing proteins and their solvent accessibility. We used the program DSSP50 to obtain information about secondary structures and solvent accessibility. The secondary structures have been classified into alpha helix, beta turn, beta strand and coil, as suggested by the DSSP output. Solvent accessibility is the ratio between the solvent accessible surface area of a residue in a 3D structure and in an extended tripeptide conformation. Solvent accessibility was divided into three classes: buried, partially buried, and exposed, indicating respectively; the least, moderate and high accessibility of the amino acid residues to the solvent.Fig. 2 and 3 were prepared using the program Discovery Studio Visualizer 3.1.40
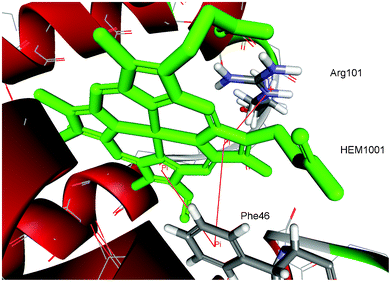 | ||
| Fig. 2 Details of π–π and cation–π interactions for the HEM1001 of hemoglobin from midge larva Propsilocerus akamusi (PDB ID code 1x3k). The interactions are marked with red lines (π–π interactions: HEM1001:C—Phe46, HEM1001:D—Phe46; cation–π interactions: HEM1001:D—Arg101:NE). | ||
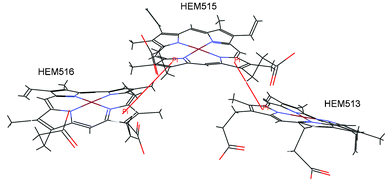 | ||
| Fig. 3 Details of the interactions linking the three porphyrins of the cytochrome c-552 from Wolinella succinogenes (PDB ID code 3bnj). The π–π interactions are marked with red lines (HEM513:D—HEM515:D, HEM515:A—HEM516:A). | ||
Results and discussion
Using the geometrical criteria described in the “Methodology” section, in the nonredundant database of the PDB with 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 protein chains, we found 74 protein chain crystal structures with porphyrin. The analyzed protein set contains 117 porphyrins due to the fact that some of the proteins have more than one porphyrin ring. We have noticed that most of the porphyrins are involved in π–π and cation–π interactions. The quantification of such interactions is of great importance for a rational approach to biological systems including protein structure and function porphyrin binding as well as for the further development of drug design processes.51–53
130 protein chains, we found 74 protein chain crystal structures with porphyrin. The analyzed protein set contains 117 porphyrins due to the fact that some of the proteins have more than one porphyrin ring. We have noticed that most of the porphyrins are involved in π–π and cation–π interactions. The quantification of such interactions is of great importance for a rational approach to biological systems including protein structure and function porphyrin binding as well as for the further development of drug design processes.51–53
Distribution of π–π and cation–π interactions
The distribution of π–π and cation–π interactions is shown in Table 1, based on the data of porphyrin-containing proteins in our dataset. There were a total of 217 interactions. The present dataset contains 117 porphyrins. Thus, on average, every porphyrin forms 1.85 interactions with the protein part. Some of the porphyrins have no interactions (the structures with PBD ID codes 1c75A, 1e29A, 1gu2B, 1jfbA and 1w2lA), while most of the porphyrins have several interactions. Some of the porphyrins have up to 15 interactions (the structures with PBD ID codes 3fo3A and 3molA). The binding pocket for the HEM1001 of hemoglobin from midge larva Propsilocerus akamusi (PDB ID code 1x3k), as an illustrative example for π–π and cation–π interactions, is shown in Fig. 2.| Type of interaction | π–π | Cation–π | ||
|---|---|---|---|---|
| Numbera | %b | Numbera | %b | |
| a The number of times a particular amino acid occurs in an appropriate interaction. b Percent of amino acid occurs in an appropriate interaction. c Pyrrole ring. d Chelate metal ion of porphyrin. | ||||
| Amino acid | ||||
| His | 12 | 5.5 | — | — |
| Phe | 86 | 39.6 | — | — |
| Trp | 4 | 1.8 | — | — |
| Tyr | 24 | 11.1 | — | — |
| Arg | — | — | 34 | 15.6 |
| Lys | — | — | 10 | 4.6 |
| Porphyrinc | 36 | 16.7 | — | — |
| Fe2+d | — | — | 11 | 5.1 |
| Total | 162 | 74.7 | 55 | 25.3 |
The number of π–π interactions was higher than that of cation–π interactions in the same set of proteins studied. Out of the aromatic residues, Phe is the most common amino acid involved in π–π interactions. This might be because, of the aromatic amino acids, Phe occurs most frequently. It is observed that Arg occurs more frequently than Lys among the cationic residues in the set of porphyrin-containing proteins, suggesting its important role in porphyrin recognition and structural stability. Because the sidechain of arginine is larger and less well water-solvated than that of lysine, it likely benefits from better van der Waals interactions with the aromatic ring. This result is consistent with previous studies of globular proteins,20 sugar-binding proteins,54 single chain “all-alpha” proteins,55 and immunoglobulin proteins.56
We have elucidated the structural motifs containing Phe residues, as the most frequently involved, responsible for the π–π interactions using the PDBeMotif web interface.57 We discovered two types of structural motifs significantly over-represented in porphyrin-containing proteins: beta-turn-ir and niche-4r. It has been shown that these small structural motifs could be involved in protein functions such as determining the conformation of enzyme active sites or binding sites.57–59 Our underlying hypothesis was that Phe residues with a high frequency of π–π interactions are probably linked to structural implications.
It is very interesting that in the proteins that contain more than one porphyrin, the pyrrole groups of one porphyrin can be involved in π–π interactions with the π systems of another porphyrin in the protein. We have found 36 (16.7%) of those interactions. It is likely that these interactions contribute significantly to the overall stability of porphyrin rings. Three iron-porphyrins from the binding pocket of the cytochrome c-552 from Wolinella succinogenes (PDB ID code 3bnj) are shown in Fig. 3. There are two π–π interactions between the porphyrins (HEM513:D—HEM515:D, HEM515:A—HEM516:A).
We have found 11 (5.1%) cation–π interactions between porphyrin Fe2+ metal cations and the π systems of surrounding amino acids as well as the pyrrole rings of other porphyrins. The interactions involve Phe, Tyr, and His amino acid residues as the π systems. Three of them include pyrrole rings. Cation–π interactions between metal cations and π systems recently emerged as one of the fundamental bonding motifs of key importance in molecular recognition.60–64
In our analysis, we have investigated multiple π interactions, an illustrative example is shown in Fig. 2. The analysis shows that about 58% of the total π interactions in the dataset are involved in the formation of multiple π interactions. This conveys that furcation is an inherent characteristic of macromolecular crystal structures.38 The furcation level of π–π interactions is much higher than that of cation–π interactions in porphyrin-containing proteins. The majority of furcated interactions exhibit longer distances than the simple non-furcated interactions as expected (Fig. 5).
We used the ConSurf server to compute the conservation score of residues involved in π–π and cation–π interactions in porphyrin-containing proteins. Among the cationic residues 37.8% of them had a conservation score of ≥6, the cutoff value used to identify the stabilizing residues. None of the cationic residues had the highest score of 9. 8.6% of the aromatic residues had the highest score of 9 and 39.7% of the residues had a conservation score of ≥6 and <9. Analysis of the conservation patterns of π–π and cation–π interactions have shown that the multiple interactions have been conserved more than the single interactions, and it is considered that structurally conserved residues are important in protein stability and folding.65
Energetic contribution of π–π and cation–π interactions
The number of π–π and cation–π interaction pairs at different intervals of energy is plotted in Fig. 4. We observed that most of the π–π interactions have an energy in the range −0.5 to −2.0 kcal mol−1. In our database it was found that cation–π interactions showed an energy less than −6 kcal mol−1, and most of them have energy in the range −2 to −4 kcal mol−1. Further, an appreciable number of metal/cation–π interaction pairs have energy in the range −6 to −13 kcal mol−1. These results are consistent with a previous study of globular proteins.20 It has been reported that in globular proteins, roughly one quarter and in membrane proteins 65% of the cation–π interactions have an energy less than −4 kcal mol−1.20,66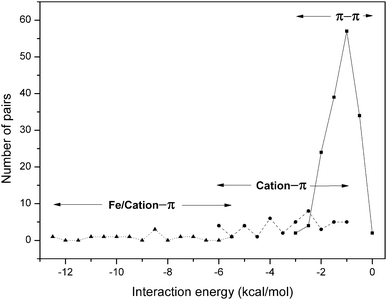 | ||
| Fig. 4 Occurrence of residue pairs at different ranges of π–π ( ) and cation–π ( ; ) interaction energy. | ||
We have calculated the average interaction energy for all possible pairs of porphyrins and aromatic residues and the results are presented in Table 2.
| Interacting pair | N (kcal mol−1) | E es (kcal mol−1) | E vdw (kcal mol−1) | E total (kcal mol−1) |
|---|---|---|---|---|
| a Number of interactions. b Electrostatic energy. c Van der Waals energy. d Total interaction energy. e Pyrrole ring. f Chelate metal ion of porphyrin. The standard deviations are given in parenthesis. | ||||
| π–π | ||||
| Porphyrin–Hise | 12 | 0.14 (0.4) | −1.05 (0.5) | −0.91 (0.4) |
| Porphyrin–Phe | 86 | −0.27 (0.2) | −1.05 (0.4) | −1.32 (0.5) |
| Porphyrin–Trp | 4 | −0.35 (1.1) | −1.53 (0.2) | −1.88 (1.2) |
| Porphyrin–Tyr | 24 | −0.09 (0.3) | −0.96 (0.4) | −1.05 (0.5) |
| Porphyrin–Porphyrin | 36 | 0.03 (0.1) | −0.77 (0.3) | −0.74 (0.3) |
| Cation–π | ||||
| Porphyrin–Arg | 34 | −2.15 (1.1) | −0.72 (0.5) | −2.87 (1.6) |
| Porphyrin–Lys | 10 | −2.09 (0.8) | −0.24 (0.1) | −2.33 (0.9) |
| Fe2+–Hisf | 1 | −9.28 | −0.01 | −9.29 |
| Fe2+–Phe | 5 | −10.32 (1.4) | −0.01 (0.0) | −10.33 (1.4) |
| Fe2+–Tyr | 2 | −6.82 (1.9) | −0.01 (0.0) | −6.83 (1.9) |
| Fe2+–Porphyrin | 3 | −7.25 (0.8) | −0.08 (0.0) | −7.33 (0.9) |
The pairwise π–π interaction energy between the porphyrin ring and aromatic residues shows that the porphyrin–Trp (−1.88 kcal mol−1) energy is the strongest and porphyrin–His (−0.91 kcal mol−1) is the lowest among the all possible pairs as shown in Table 2. However, the energy associated with each porphyrin–porphyrin interaction, which is observed in very few proteins, is found to be the least among the pairs (−0.74 kcal mol−1). π–π interactions have a van der Waals energy that is more than five times stronger than the electrostatic energy for the interacting pairs containing porphyrin and aromatic residues. Regardless of the angle, the aromatic side chains orient in a fashion to minimize Rclo between the two rings and thus maximize the van der Waals attraction. The geometrical parameters of porphyrin–porphyrin interactions are not as good, and this might be due to steric reasons.
The average cation–π interaction energy of Arg and Lys is −2.87 and −2.33 kcal mol−1, respectively. The average energy in other globular proteins is −2.9 and −3.3, respectively, for Arg and Lys. In transmembrane helical and strand proteins, the interaction energy for Arg is stronger than Lys.66 The composition of cation–π interaction energy into electrostatic and van der Waals energy terms showed that in our dataset there is a stronger electrostatic energy than van der Waals energy.
The pair-wise cation–π interaction energy between the cationic and aromatic residues shows that the energetic contribution due to pairs including a metal (Fe2+–His and Fe2+–Phe) was the strongest among all possible pairs in porphyrin-containing proteins. From this observation, we are able to infer that the contributions of pairs including a metal are highly significant to the energetic contribution due to cation–π interactions in the dataset studied. The energies associated with cation–π interactions may be important contributors to the overall protein stability.
Interaction geometry
The frequency distribution of the distance and angle parameters of π–π and cation–π interaction pairs are analyzed (Fig. 5 and 6). The distribution of Rcen, the centroid–centroid distance, for π–π interactions was found to be bimodal with a prominent minimum between 5.5 and 6.5 Å (Fig. 5a). Outside the minimum, there are two distinct maxima with a narrow range of linearity, corresponding to parallel-stacked and T-shaped orientation of the rings, respectively.42 This is because of parallel orientations having a shorter Rcen than T-shaped orientations. The preferred parallel-stacked orientation (Fig. 3) is found to be more stable than a T-shaped structure by 0.7 kcal mol−1 for the full set of interaction pairs. In the parallel-stacked case, the van der Waals contribution is the dominating effect and the electrostatics contribution is actually repulsive, although small (<1 kcal mol−1). On the other hand, the van der Waals contribution in the T-shaped case is not overwhelming, and it is the attractive electrostatics contribution that results in the overall binding of ∼2.0 kcal mol−1. At separation distances below 4.0 and above 6.5 Å, aromatic pairs are rarely observed, a result of obvious physical constraints. The plot of distance distribution derived from cation–π interaction pairs (Fig. 5b), between the cation group and aromatic ring of porphyrin, shows two prominent peaks centered at 4.5 and 5.5 Å.The native structure is the compromise of a large number of noncovalent interactions that exist in proteins and the geometrical features relating two residue-types are expected to be rather broad. However, based on the distribution of interplanar angles it was suggested that there is non-randomness in the packing of side chains.67 Using two angular parameters to define the relative orientations, each pair of planar residues is indeed found to exhibit a preference for one or two geometries, and similarly avoidance for some.
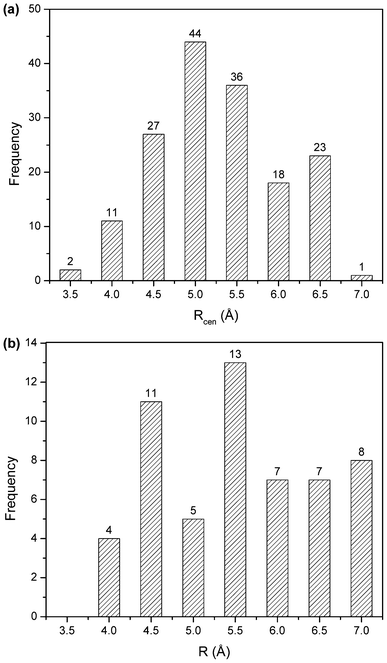 | ||
| Fig. 5 Distance distribution of π–π interactions (a), and cation–π interactions (b). | ||
The angle distributions for the inter-ring orientational angles θ and λ shown in Fig. 6 were generated considering only π interacting pairs between the porphyrin ring and surrounding amino acid side chains. If there was no intrinsic angular energetic preference, the profiles in Fig. 6 would appear flat; instead the θ distribution (Fig. 6a) has a peak near 45° and the λ distributions (Fig. 6b) have peaks around 16 and 26°.
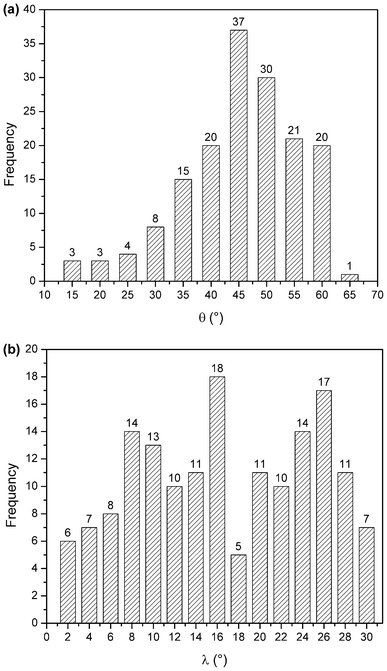 | ||
| Fig. 6 θ angle distribution of π–π interactions (a), and λ angle distribution of π–π interactions (b). | ||
The interaction geometries of cation–π interactions were analyzed. In a previous study of interplanar residue contacts, Brocchieri and Karlin18 found it convenient to partition the interplanar angle (α) into three categories, planar (0° < α < 30°), oblique (30° < α < 60°) and orthogonal (60° < α < 90°). When a similar analysis was applied in the present study, it was found that 44% of the cation–π interactions involved planar stacking between the Lys (CE, NZ atoms) and Arg (NE, CZ, CD, NH1, NH2 atoms) and the aromatic ring of porphyrin. Planar interactions had an average α of 19°. Thirty-seven percent (37%) of the interactions belonged to the oblique category with an average α = 41°. The remaining 19% of the interactions were of the orthogonal type with an average α = 75°. In general, the separation distance between the cation group and the aromatic ring decreases as the interplanar angle decreases. This can be expected since coplanar stacking leads to maximal (shortest distance) contact between the interacting groups.
The geometries that are observed in abundance are not necessarily the ones that have the highest interaction energy between the two moieties in a pair, but the ones that can provide the maximum overall stability to the protein structure by the optimum use of all π interactions.
Stabilization center residues (SC)
Stabilization centers are composed of certain clusters of residues, involved in the cooperative long range interaction of proteins that regulate flexibility, rigidity and stability of protein structures. Stabilization centers are important in regulating the turnover of certain proteins by preventing their decay with cooperative long range interactions. The most frequent stabilization center residues are usually found at buried positions and have a hydrophobic or aromatic side-chain, but some polar or charged residues also play an important role in stabilization. The stabilization centers show a significant difference in the composition and in the type of linked secondary structural elements, when compared with the rest of the residues. The performed structural and sequential conservation analysis showed a higher conservation of stabilization centers over protein families.48,68We have computed the stabilization centers for all π–π and cation–π interaction-forming residues in porphyrin-containing proteins. Table 3 shows the percentage contribution of the individual amino acid residue which is part of the stabilizing center involved in π–π and cation–π interactions with porphyrin rings.
Considering the whole data set of 553 stabilizing residues, 44 (8.0%) are involved in building π–π and cation–π interactions with the porphyrin ring. These data suggest that the amino acids that are part of stabilization centers are not involved in the building of interactions with the porphyrin ring, but they are involved in the stabilization of the surrounding structure and overall structure of the protein. We have found that 10.4% of π residues and 3.9% of cationic residues were found to have one or more stabilization centers. Aromatic residues were found to have more stabilization centers than cationic residues in porphyrin-containing proteins. It may be observed that the highest contribution comes from Phe, His, Tyr among aromatic and from Arg among charged amino acids. Interestingly, Trp and Lys were the least abundant amino acids which are stabilizing centers of the whole data set. This could be explained by the fact that these amino acids are involved in various strong and weak hydrogen bonds with the porphyrin ring and is located in the environment.38 From this we infer that these residues might contribute additional stability to the porphyrin-containing proteins in addition to their participation in π–π and cation–π interactions.
Secondary structure preferences and solvent accessibility of amino acids
The propensity of the amino acid residues to favor a particular conformation is well described. Such a conformational preference is not only dependent on the amino acid alone, but also on the local amino acid sequence.69 In order to obtain the preference and pattern of each π–π and cation–π interaction-forming residue in porphyrin-containing proteins, we conducted a systematic analysis based on their location in different secondary structures and their solvent accessibility.Thus, we have analyzed amino acid secondary structure preferences for the whole data set of 74 proteins. In all analyzed proteins, only two types of secondary structures were present: helices and coils. We have observed a significant number of cation–π interactions between the residues in α-helical segments, which is consistent with previous reports that the residues in α-helices have the tendency to form cation–π interactions.20,70 It was found that, among the cationic residues Lys preferred to be coiled and Arg favored coil and helix conformation. From this observation, we infer that Arg residues might stabilize coils and helices by bonding to porphyrin-containing proteins. The π residues (Phe, Tyr, Trp, His) preferred to be in a helix. This analysis indicates that the π–π and cation–π interactions do not occur at random but have a residue-specific preference for a particular secondary structure.
An interesting question concerns the location of cation–π interactions within protein structures. Cationic residues generally prefer to be on the surface of proteins whereas aromatic amino acids prefer to remain in the hydrophobic core. Because a cation–π interaction contains both a cation and an aromatic, it is not clear whether the interacting pairs should prefer to be located on the surfaces of proteins or in the cores. Traditional methods for determining residue surface accessibility rely on calculating the water-exposed surface area for a given amino acid. Because cation–π partners are necessarily in contact with one another, their water-accessible surface is diminished, even though the interacting pair as a unit may be well solvated. We observed that Arg and Lys preferred to be in an exposed region. Among the aromatic residues, it was observed that Phe and Tyr preferred to be in the partially buried region, while Trp preferred to be in the fully buried regions. This observation is quite reasonable in the sense that the aromatic residues are in principle, non polar residues, and tend to be buried. Since Arg and Lys are polar in nature they tend be exposed to the solvent surface. The polar residues might contribute significantly to the stability of the porphyrin-containing proteins as the contribution of the global energy is much greater in solvation.
Conclusions
The presented study expands on our previous work on the XH/π and non-canonical interactions of porphyrins in protein–porphyrin complex crystal structures by analyzing the same protein group with respect to π–π and cation–π interactions in order to better understand their stabilizing role. Further, the characteristic features of residues involved in π–π and cation–π interactions have been evaluated in terms of the distribution of π–π and cation–π interactions, conservation score, structural motifs, energetic contribution, interaction geometry, stabilizing centers, secondary structure, and solvent accessibility.We observed that the number of π–π interactions was higher than that of cation–π interactions in the same set of proteins studied. Out of the aromatic residues, Phe is the most common amino acid involved in π–π interactions. It is observed that Arg exhibits higher occurrences than Lys among the cationic residues. It is very interesting that in the proteins that contain more than one porphyrin, the pyrrole groups of one porphyrin can be involved in π–π interactions with the π systems of another porphyrin in the protein. We have found 11 (5.1%) cation–π interactions between porphyrin Fe2+ metal cations and the π systems of surrounding amino acids as well as the pyrrole rings of other porphyrins. Analysis of conservation patterns of π–π and cation–π interactions have shown that the multiple interactions have been conserved more than the single interactions. We discovered two types of structural motifs significantly over-represented in porphyrin-containing proteins: beta-turn-ir and niche-4r. It has been shown that these small structural motifs could be involved in protein functions such as determining the conformation of enzyme active sites or binding sites. The analysis of the energetic contribution of the protein interacting residues has revealed that most of the π–π interactions have an energy in the range −0.5 to −2.0 kcal mol−1. In our database it was found that cation–π interactions showed an energy less than −6 kcal mol−1, and most of them have energies in the range −2 to −4 kcal mol−1. The pair-wise cation–π interaction energy between the cationic and aromatic residues shows that the energetic contribution due to pairs including a metal (Fe2+–His and Fe2+–Phe) was the strongest among all possible pairs in porphyrin-containing proteins. The preferred parallel-stacked orientation is found to be more stable than a T-shaped structure by 0.7 kcal mol−1 for the full set of π–π interaction pairs. In the case of cation–π interactions, it was found that 44% of the cation–π interactions involved planar stacking, while 37% of the interactions belonged to the oblique category. The remaining 19% of the interactions were of the orthogonal type. The separation distance between the cation group and the aromatic ring decreases as the interplanar angle decreases. Furthermore, aromatic residues were found to have more stabilization centers than cationic residues in porphyrin-containing proteins. It may be observed that the highest contribution comes from Phe, His, Tyr among aromatic and from Arg among charged amino acids. The secondary structure and solvent accessibility of residues in porphyrin-containing proteins reveal that most of the π–π and cation–π interaction-forming residues prefer the secondary structure of alpha helical segments. It is found that in the porphyrin-containing proteins, the positively charged amino acids, Arg and Lys, involved in π–π and cation–π interactions, prefer to be in the solvent exposed surface but the aromatic amino acids (Phe and Tyr) prefer the partially buried regions of the protein, while Trp prefers to be in the fully buried regions.
In conclusion, observations obtained in this study identify π–π and cation–π interactions and structural motifs that contribute to the stabilization of the porphyrin ring by proteins, relevant to the understanding of structure–function relationships in porphyrin-containing proteins, and useful to the efforts made to design proteins able to incorporate this versatile and ubiquitous prosthetic group.
Acknowledgements
This work was supported by the Ministry of Education and Science of the Republic of Serbia (Grants No. 31085, 172001, 173034).References
- P. Rothemund, J. Am. Chem. Soc., 1935, 57, 2010 CrossRef CAS.
- P. Rothemund, J. Am. Chem. Soc., 1936, 58, 625 CrossRef CAS.
- S. Karrasch, P. A. Bullough and R. Ghosh, EMBO J., 1995, 14, 631 CAS.
- G. McDermott, S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell and N. W. Isaacs, Nature, 1995, 374, 517 CrossRef CAS.
- M. Z. Papiz, S. M. Prince, T. Howard, R. J. Cogdell and N. W. Isaacs, J. Mol. Biol., 2003, 326, 1523 CrossRef CAS.
- A. W. Roszak, T. D. Howard, J. Southall, A. T. Gardiner, C. J. Law, N. W. Isaacs and R. J. Cogdell, Science, 2003, 302, 1969 CrossRef CAS.
- S. Bahatyrova, R. N. Frese, C. A. Siebert, J. D. Olsen, K. O. Van Der Werf, G. R. Van, R. A. Niederman, P. A. Bullough, C. Otto and C. N. Hunter, Nature, 2004, 430, 1058 CrossRef CAS.
- S. Hou, M. F. Reynolds, F. T. Horrigan, S. H. Heinemann and T. Hoshi, Acc. Chem. Res., 2006, 39, 918 CrossRef CAS.
- L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808 CrossRef CAS.
- S. Yanagisawa, P. B. Crowley, S. J. Firbank, A. T. Lawler, D. M. Hunter, W. McFarlane, C. Li, T. Kohzuma, M. J. Banfield and C. Dennison, J. Am. Chem. Soc., 2008, 130, 15420 CrossRef CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525 CrossRef CAS.
- A. V. Morozov, K. M. S. Misura, K. Tsemekhman and D. Baker, J. Phys. Chem. B, 2004, 108, 8489 CrossRef CAS.
- C. Chipot, R. Jaffe, B. Maigret, D. A. Pearlman and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 11217 CrossRef CAS.
- R. A. Kumpf and D. A. Dougherty, Science, 1993, 261, 1708 CAS.
- D. Zhu, B. E. Herbert, M. A. Schlautman and E. R. Carraway, J. Environ. Qual., 2004, 33, 276 CrossRef CAS.
- U. D. Priyakumar, M. Punnagai, G. P. Krishna Mohan and G. N. Sastry, Tetrahedron, 2004, 60, 3037 CrossRef CAS.
- L. Brocchieri and S. Karlin, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 9297 CrossRef CAS.
- J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303 CrossRef CAS.
- J. P. Gallivan and D. A. Dougherty, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9459 CrossRef CAS.
- H. Huang and M. T. Rodgers, J. Phys. Chem. A, 2002, 106, 4277 CrossRef CAS.
- R. Amunugama and M. T. Rodgers, Int. J. Mass Spectrom., 2003, 222, 431 CrossRef CAS.
- D. Vijay and G. N. Sastry, Phys. Chem. Chem. Phys., 2008, 10, 582 RSC.
- Z. H. Li, J. Liu, M. Qiao and K.-N. Fan, Mol. Phys., 2009, 107, 1271 CrossRef CAS.
- N. J. Singh, S. K. Min, D. Y. Kim and K. S. Kim, J. Chem. Theory Comput., 2009, 5, 515 CrossRef CAS.
- M. M. Flocco and S. L. Mowbray, J. Mol. Biol., 1994, 235, 709 CrossRef CAS.
- A. S. Reddy, D. Vijay, G. M. Sastry and G. N. Sastry, J. Phys. Chem. B, 2006, 110, 2479 CrossRef CAS.
- D. Vijay, H. Zipse and G. N. Sastry, J. Phys. Chem. B, 2008, 112, 8863 CrossRef CAS.
- L. Banci, I. Bertini, G. Cavallaro and C. Luchinat, JBIC, J. Biol. Inorg. Chem., 2002, 7, 416 CrossRef CAS.
- O. Iakovleva, M. Reiner, H. Rau and W. Haehnel, Phys. Chem. Chem. Phys., 2002, 4, 655 RSC.
- M. Fabian, L. Skultety, D. Jancura and G. Palmer, Biochim. Biophys. Acta, Bioenerg., 2004, 1655, 298 CrossRef CAS.
- F. A. Walker, Chem. Rev., 2004, 104, 589 CrossRef CAS.
- D. Liu, D. A. Williamson, M. L. Kennedy, T. D. Williams, M. M. Morton and D. R. Benson, J. Am. Chem. Soc., 1999, 121, 11798 CrossRef CAS.
- S. D. Zarić, D. M. Popović and E. W. Knapp, Biochemistry, 2001, 40, 7914 CrossRef.
- A. S. Galstyan, S. D. Zaric and E. W. Knapp, JBIC, J. Biol. Inorg. Chem., 2005, 10, 343 CrossRef CAS.
- S. Đ. Stojanović, V. B. Medaković, G. Predović, M. Beljanski and S. D. Zarić, JBIC, J. Biol. Inorg. Chem., 2007, 12, 1063 CrossRef.
- S. Đ. Stojanović and S. D. Zarić, Open Struct. Biol. J., 2009, 3, 34 CrossRef.
- S. Đ. Stojanović, E. R. Isenović and B. L. Zarić, Amino Acids, 2012, 43, 1535 CrossRef.
- S. Griep and U. Hobohm, Nucleic Acids Res., 2010, 38, D318–D319 CrossRef CAS.
- Accelrys Discovery Studio Visualizer 3.1, 2011, 10188 Telesis Court, Suite 100, San Diego, CA 92121, USA.
- T. Halgren, J. Comput. Chem., 1996, 17, 490 CrossRef CAS.
- G. B. McGaughey, M. Gagne and A. K. Rappe, J. Biol. Chem., 1998, 273, 15458 CrossRef CAS.
- R. Sathyapriya and S. Vishveshwara, Nucleic Acids Res., 2004, 32, 4109 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- W. L. DeLano, Curr. Opin. Struct. Biol., 2002, 12, 14 CrossRef CAS.
- B. Boeckman, A. Bairoch, R. Apweiler, M. C. Blatter, A. Estreicher and E. Gasteiger, Nucleic Acids Res., 2003, 31, 365 CrossRef.
- Z. Dosztanyi, A. Fiser and I. Simon, J. Mol. Biol., 1997, 272, 597 CrossRef CAS.
- Z. Dosztanyi, C. Magyar, G. Tusnady and I. Simon, Bioinformatics, 2003, 19, 899 CrossRef CAS.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577 CrossRef CAS.
- J. M. Lehn, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4763 CrossRef CAS.
- P. A. Maury, D. N. Reinhoudt and J. Huskens, Curr. Opin. Colloid Interface Sci., 2008, 13, 74 CrossRef CAS.
- T. Li, H. L. Bonkovsky and J. T. Guo, BMC Struct. Biol., 2011, 11, 13 CrossRef CAS.
- P. Elumalai, M. Rajasekaran, H. L. Liu and C. Chen, Protoplasma, 2010, 247, 13 CrossRef CAS.
- R. L. Martis, S. K. Singh, M. M. Gromiha and C. Santhosh, J. Theor. Biol., 2008, 250, 655 CrossRef CAS.
- I. A. Tayubi and R. Sethumadhavan, Biochemistry (Moscow), 2010, 75, 912 CrossRef CAS.
- A. Golovin and K. Henrick, BMC Bioinformatics, 2008, 9, 312 CrossRef.
- J. Watson and E. Milner-White, J. Mol. Biol., 2002, 315, 171 CrossRef CAS.
- E. Milner-White and M. Russell, Origins Life Evol. Biosphere, 2005, 35, 19 CrossRef CAS.
- S. D. Zarić, D. M. Popović and E. W. Knapp, Chem.–Eur. J., 2000, 6, 3935 CrossRef.
- U. C. Chaturvedi and R. Shrivastava, FEMS Immunol. Med. Microbiol., 2005, 43, 105 CrossRef CAS.
- E. Masson and M. Schlosser, Org. Lett., 2005, 7, 1923 CrossRef CAS.
- E. N. Salgado, J. Faraone-Mennella and F. A. Tezcan, J. Am. Chem. Soc., 2007, 129, 13374 CrossRef CAS.
- B. Zhang, C. C. Guan, W. T. Chen, P. Zhang, M. Yan, J. H. Shi, C. L. Qin and Q. Yang, Chin. Med. J. (Engl.), 2007, 120, 1830 CAS.
- W. L. DeLano, Curr. Opin. Struct. Biol., 2002, 12, 14 CrossRef CAS.
- M. M. Gromiha, Biophys. Chem., 2003, 103, 251 CrossRef CAS.
- J. B. Mitchell, R. A. Laskowski and J. M. Thornton, Proteins: Struct., Funct., Genet., 1997, 29, 370 CrossRef CAS.
- C. Magyar, M. M. Gromiha, G. Pujadas, G. E. Tusnady and I. Simon, Nucleic Acids Res., 2005, 33, W303–W305 CrossRef CAS.
- S. Chakkaravarthi, M. M. Babu, M. M. Gromiha, G. Jayaraman and R. Sethumadhavan, Proteins: Struct., Funct., Bioinf., 2006, 65, 75 CrossRef CAS.
- M. M. Gromiha, S. Thomas and C. Santhosh, Prep. Biochem. Biotechnol., 2002, 32, 355 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2012 |