Spin-forbidden hydrogen atom transfer reactions in a cobalt biimidazoline system†
Virginia W.
Manner‡
a,
Alex D.
Lindsay
a,
Elizabeth A.
Mader§
a,
Jeremy N.
Harvey
*b and
James M.
Mayer
*a
aUniversity of Washington, Department of Chemistry, Campus Box 351700, Seattle, WA 98195-1700, USA. E-mail: mayer@chem.washington.edu; Fax: +206 685 8665; Tel: +206 543 2083
bCentre for Computational Chemistry and School of Chemistry, University of Bristol, Cantock's Close, Bristol, UK BS8 1TS. E-mail: jeremy.harvey@bristol.ac.uk; Fax: +44 (0)117 925 1295; Tel: +44 (0)117 954 6991
First published on 16th September 2011
Abstract
Described here are hydrogen atom transfer (HAT) reactions from high-spin cobalt(II) tris(2,2′-bi-2-imidazoline) (CoIIIIH22bim) to the hydrogen atom acceptors, 2,2,6,6-tetramethyl-1-piperidinyl-oxyl (TEMPO), 2,4,6-tri-tert-butylphenoxyl radical (tBu3ArO˙), and benzoquinone (BQ). The cobalt product is the oxidized and deprotonated, low-spin cobalt(III) complex (CoIIIIIIHbim), and the organic products are TEMPOH, tBu3ArOH, or hydroquinone, respectively. These reactions are formally spin forbidden because the spin state of the reactants is different from that of the products. For instance, quartet CoIIIIH22bim plus doublet RO˙ can have a triplet or quintet ground state, while the CoIIIIIIHbim + ROH product state is a singlet. Kinetics measured in the forward and reverse directions and thermochemical measurements provide a detailed picture of the reactions. The reactions are quite slow: the reaction of 10 mM CoIIIIH22bim with excess TEMPO requires roughly a day at ambient temperatures to reach equilibrium. This is 3400 times slower than the related reaction of the iron analogue FeIIIIH22bim, which is 2 kcal mol−1 more uphill. Mechanistic analyses show that the TEMPO reaction occurs by hydrogen atom transfer (HAT), and this is likely for the tBu3ArO˙ and BQ reactions as well. This is an unusually well defined spin-forbidden HAT system, which serves as a model for more complex multi-spin state HAT processes such as those suggested to occur in cytochrome P450 and metal-oxo model systems. In principle, HAT could occur before, after, or concerted with spin change. Computational studies indicate a reaction mechanism involving pre-equilibrium spin state interconversion of quartet 44CoIIIIH22bim to its doublet excited state 22CoIIIIH22bim, followed by spin-allowed HAT to the organic acceptor. This mechanism is consistent with the available kinetic, thermochemical and spectroscopic measurements. It indicates that the slow rates are due to the large change in geometry between CoIIIIH22bim and CoIIIIIIHbim, rather than any inherent difficulty in changing spin state. The implications of these results for other spin-forbidden or ‘two-state’ HAT processes are discussed.
Introduction
The influence of spin changes on the reactivity of transition-metal complexes is a topic of increasing importance and debate.1 Spin issues are more complicated in transition-metal chemistry than in organic reactions because the stronger spin–orbit coupling makes spin a less “good” quantum number. A number of studies have suggested that formal spin changes can have a substantial effect on transition-metal reactions,1 while others indicate the opposite.2 Perhaps the greatest attention has been paid to the role of spin states in hydrogen atom transfer (HAT) reactions of transition-metal oxo species, especially the ferryl (Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) active site in cytochrome P450, other enzymes and model systems.3
O) active site in cytochrome P450, other enzymes and model systems.3
HAT reactions involve the concerted transfer of a proton and an electron from one reagent to another (eqn (1)). HAT is a fundamental chemical reaction step4 that has long been recognized as an important part of organic reactivity such as halogenation and combustion.5 It has more recently been recognized as an important type of transition-metal reactivity,1,3,4,6 including industrial processes, enzymatic reactions and organic transformations.7,8 In metal complexes, net H˙ transfer typically occurs with the redox-active metal accepting/donating the electron and the proton moving to/from a basic site on a ligand (eqn (2)).6 In reactions of cytochrome P450 compound I, the proton adds to the oxo group and the electron primarily reduces the porphyrin radical cation.3 Since these reactions have a formal separation of the e− and H+, they can be viewed as a subset of a larger class of concerted proton-electron transfer (CPET) or proton-coupled electron transfer (PCET) reactions.6,9,10
| A–H + B˙ → A˙ + H–B | (1) |
| LnM–X–H + B˙ → LnM–X + H–B | (2) |
Computational studies by Shaik and co-workers, and others, have led the way in showing that the involvement of multiple spin states can significantly affect transition-metal HAT reactivity.3h For instance, such ‘two-state reactivity’ has been suggested to account for some of the unusual experimental observations in P450 and other systems.3,11 Recent experimental studies from Que and co-workers have indicated that their high-spin (S = 2) iron(IV)-oxo species cleave C–H bonds significantly faster than the related intermediate-spin (S = 1) complexes, providing experimental evidence that the high-spin form is more reactive.12 It has often been suggested that unpaired spins at the abstracting atom are critical to this reactivity.13 However, d0permanganate and chromium(VI) compounds have long been known to be reactive H-atom abstractors.6,14 More recently, Prokop, de Visser and Goldberg have reported an S = 0 manganese(V)-oxo complex that is highly reactive for HAT.15 Simple organic compounds, including alkenes, ketones and quinones, can also abstract H-atoms even though they have no unpaired spins.16 We have argued that spin states are not a primary determinant of HAT reactivity.6 We and others have found that in most cases, HAT rate constants can be quantitatively predicted based on the free energy of H-atom transfer (the driving force) and Marcus-type intrinsic barriers.6,17 Steric effects can also be important.18 Resolving this issue has been complicated because most of the proposed ‘two-state reactivity' systems are complex, with multiple intermediates and spin states.
Described here are, to our knowledge, the first fully characterized examples of spin-forbidden HAT reactions, in which the reactants and products are well-characterized species.19 These reactions are relatively simple models for the more complex processes occurring in heme and non-heme enzymes and model systems. The reactions involve hydrogen atom transfer from cobalt(II) tris(2,2′-bi-2-imidazoline), Co(H2bim)32+, abbreviated CoIIIIH22bim (H2bim = 2,2′-bi-2-imidazoline), forming the oxidized and deprotonated analogue Co(H2bim)2(Hbim)2+ (CoIIIIIIHbim, Scheme 1; ancillary H2bim ligands that do not change protonation state during the reaction are indicated just by N–N). The H-atom is transferred to the stable organic radicals TEMPO (2,2,6,6-tetramethyl-1-piperidinyloxyl), 2,4,6-tri-tert-butylphenoxyl (tBu3ArO˙),20 or benzoquinone (BQ, which accepts two hydrogen atoms to form hydroquinone, H22Q). These reactions are overall spin-forbidden because they interconvert high-spin (HS) Co(II) complexes (4T1g, t2g5eg2 in idealized Oh symmetry, S = 3/2) and low-spin (LS) octahedral Co(III) complexes (1A1g, t2g6, S = 0).21 For instance, in the reaction of CoIIIIH22bim (S = 3/2) with tBu3ArO˙ (S = 1/2) (Scheme 1), the reactant state can be S = 1 or S = 2, but the products CoIIIIIIHbim and tBu3ArOH are all S = 0.
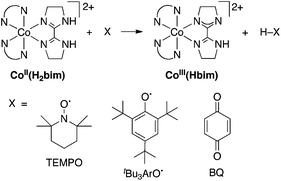 | ||
| Scheme 1 Reactivity of CoIIIIH22bim with hydrogen atom acceptors X. | ||
The cobalt HAT reactions are much slower than similar reactions of the isostructural iron–2,2′-biimidazoline compounds or other related iron and ruthenium complexes.19,22–26 The CoIIIIH22bim/CoIIIIIIHbim HAT self-exchange reaction27 is also much slower than for its Fe and Ru counterparts.22,25a The slowness of the cobalt HAT reactions parallel related electron transfer (ET) reactions that interconvert HS Co(II) and LS Co(III), which are the textbook examples of slow ET.28,29 This report presents experimental and computational studies that probe the detailed mechanism of the reactions, including whether spin-state change precedes the HAT step, follows HAT, or is concerted with HAT. It is concluded that the spin-state change occurs in a rapid pre-equilibrium step prior to HAT, and that the origin of the low reactivity of the cobalt complexes is not due to any inherent difficulty in changing the spin state.
Results
I. Thermochemistry
Cyclic voltammetry of [CoII(H2bim)3][Cl]227,30 in MeCN with 0.1 M [nBu4N][PF6] shows a broad, quasi-reversible wave with E1/2 = −0.60 ± 0.10 V vs. Cp2Fe+/0.19,31 The broadness of the wave is presumably due to slow electrochemical kinetics.27 In order to obtain a more reliable potential, an equilibrium constant was measured for the oxidation of CoIIIIH22bim to CoIIIIIIH22bim by decamethylferrocenium hexafluorophosphate ([Cp2*Fe][PF6]) in MeCN (eqn (3)). Addition of aliquots of CoIIIIH22bim to [Cp2*Fe]+ caused a drop in the optical absorbance of [Cp2*Fe]+ (λmax = 780 nm) and growth of CoIIIIIIH22bim absorbance (Fig. 1). These reactions proceed slowly to equilibrium over about 4000 s. Analyses of the spectra showed good mass balance, with a reasonable isosbestic point at 593 ± 1 nm and yielded K3 = 0.090 ± 0.032 (E3 = −0.062 ± 0.011 V). With E1/2([Cp2*Fe][PF6]) = −0.59 V,32 this gives E1/2(CoIIIIIIH22bim) = −0.53 ± 0.02 V vs. Cp2Fe+/0 in MeCN. | (3) |
![UV-Visible
spectra for the reaction of CoIIIIH22bim + [Cp2*Fe]PF6 (1.32 mM) ⇋ CoIIIIIIH22bim + Cp2*Fe upon reaching equilibrium. Initial [CoIIIIH22bim]: 0 mM, solid red line; 1.12 mM, solid blue line; 1.93 mM, dashed green line; and 3.35 mM, dotted black line.](/image/article/2012/SC/c1sc00387a/c1sc00387a-f1.gif) | ||
Fig. 1
UV-Visible
spectra for the reaction of CoIIIIH22bim + [Cp2*Fe]PF6 (1.32 mM) ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CoIIIIIIH22bim + Cp2*Fe upon reaching equilibrium. Initial [CoIIIIH22bim]: 0 mM, solid red line; 1.12 mM, solid blue line; 1.93 mM, dashed green line; and 3.35 mM, dotted black line. CoIIIIIIH22bim + Cp2*Fe upon reaching equilibrium. Initial [CoIIIIH22bim]: 0 mM, solid red line; 1.12 mM, solid blue line; 1.93 mM, dashed green line; and 3.35 mM, dotted black line. | ||
The pKa of CoIIIIIIH22bim was determined to be 20.3 ± 0.6 in MeCN based on a spectrophotometric titrationvs. the iron complex, FeIIIIIIHbim {pKa(FeIIIIIIH22bim) = 17.5 ± 0.5522} or vs.piperidine (the latter obtained in the presence of 0.1 M [nBu4N][PF6]).19,31 The pKa and E1/2 values together give the bond dissociation free energy (BDFE) of an N–H bond in CoIIIIH22bim of 70 ± 1 kcal mol−1.33–35 This is in agreement with previous equilibrium measurements which give BDFE = 69.5 ± 0.9 kcal mol−1, the bond dissociation enthalpy (BDE) = 62 ± 1 kcal mol−1 and an unusually large negative entropy for H-atom loss, −41 cal mol−1 K−1.19b
II. Reactivity
 | (4) |
| Substrate X | K eq, k | ΔG | ΔH | ΔS |
|---|---|---|---|---|
a Values at 298 K. Units: K4, K5, K5: unitless; K4P, K4S: M−1; k4, k5, k6: M−1 s−1; k–4HAT: s−1; ΔG and ΔH: kcal mol−1; ΔS: cal mol−1 K−1.
b Results from refs. 19b,c. Based on data from 273–313 K for ΔH4‡, ΔS4‡; 278–313 K for ΔH–4HAT‡, ΔS–4HAT‡. k4 = K4Pk4HAT.
c Thermochemical data from ref. 19b. Eyring parameters based on rate constants from 297–341 K.
d Reaction of CoIIIIH22bim + ½![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BQ (benzoquinone) to make CoIIIIIIHbim + ½ BQ (benzoquinone) to make CoIIIIIIHbim + ½![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H22Q (hydroquinone).
e
CoIIIIIIHbim + H22Q → CoIIIIIIHbim|H22Q, See experimental section, ESI and Fig. S1†. H22Q (hydroquinone).
e
CoIIIIIIHbim + H22Q → CoIIIIIIHbim|H22Q, See experimental section, ESI and Fig. S1†.
|
||||
| TEMPO b | K 4 = (5.9 ± 0.8) × 10−3 | ΔG4° = +3.0 ± 0.4 | ΔH4° = −9.3 ± 0.4 | ΔS4° = −41 ± 2 |
| K 4S = 61.3 ± 0.8 | ΔG4S° = −2.44 ± 0.05 | ΔH4S° = −4 ± 2 | ΔS4S° = −9 ± 4 | |
| 0.16 < K4P < 2.6 | ΔG4P° = 0.27 ± 0.83 | |||
| k 4 = (1.8 ± 0.5) × 10−4 | ΔG4‡ = 22.5 ± 0.3 | ΔH4‡ = 9.0 ± 0.8 | ΔS4‡ = −47 ± 3 | |
| k –4HAT = (5.25 ± 0.08) × 10−4 | ΔG–4HAT‡ = 21.9 ± 0.2 | ΔH–4HAT‡ = 23 ± 2 | ΔS–4HAT‡ = 3 ± 6 | |
| t Bu3ArO˙ c | K 5 = 3 × 105 | ΔG5° = −7.5 ± 1.3 | ΔH5° = −21 ± 1.4 | ΔS5° = −45 ± 6 |
| k 5 = 167 ± 22 | ΔG5‡ = 14.4 ± 0.5 | ΔH5‡ = 3.3 ± 0.9 | ΔS5‡ = −37 ± 3 | |
| k 5H/k5D = 1.30 ± 0.06 | ||||
| ½BQ ⇌ ½H22Qd | K 6 = 2.4 ± 0.8 | ΔG6° = −0.52 ± 0.11 | ||
| K 6S = 14 ± 7e | ΔG6S° = −1.6 ± 0.3e | |||
| k −6H/k−6Dca. 1.5 | ||||
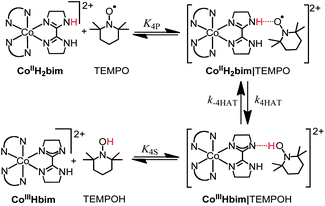
The kinetics of reaction (4) have been monitored in both directions using UV-Visible spectroscopy.19c In the forward direction, the kinetic data are well fit by an opposing second-order approach-to-equilibrium kinetic model over the available range of [TEMPO], with k4 = (1.8 ± 0.5) × 10−4 M−1 s−1 at 298 K. Eyring parameters derived from rate constants from 273–313 K are given in Table 1. In the reverse direction, optical measurements show second-order kinetics at [TEMPOH] < 40 mM, and saturation behaviour above this concentration.19c The kinetics implicate a reversibly formed intermediate, most likely a hydrogen bonded complex on the pathway to HAT, shown as CoIIIIIIHbim|TEMPOH in eqn (4). In the terminology of Marcus Theory, this is the ‘successor complex’, and the observed bimolecular k4 is equal to k4HATK4P. Analysis of the saturation kinetics at 298 K gives K4S = 61.3 ± 0.8 M−1 and the first-order rate constant for the hydrogen atom transfer step k–4HAT = (5.25 ± 0.08) × 10−4 s−1 (Van't Hoff and Eyring parameters in Table 1). No saturation is observed in the forward direction at all experimentally accessible concentrations of TEMPO; K4P was be estimated to be 0.16 < K4P < 2.6 M−1.19c
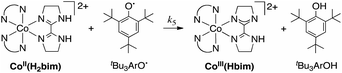 | (5) |
The reaction of CoIIIIH22bim (0.58–1.36 mM) and tBu3ArO˙ (0.65–2.10 mM) has been studied using stopped-flow rapid-scanning UV-visible spectrophotometry under second-order conditions, monitoring the appearance of CoIIIIIIHbim (λmax = 586 nm) and the disappearance of tBu3ArO˙ (λmax = 640 nm) (Fig. 2). Global fitting of the spectra using Specfit™ software36 indicated simple bimolecular kinetics with a rate constant k5 = 167 ± 22 M−1 s−1 (Eyring parameters in Table 1).
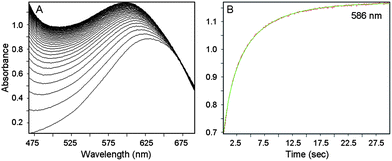 | ||
| Fig. 2 (A) Stack plot showing the UV-Visible spectra of the reaction of 1.36 mM CoIIIIH22bim + 2.10 mM tBu3ArO˙, showing the appearance of CoIIIIIIHbim (and the remaining tBu3ArO˙). (B) Absorbance at 586 nm over 30 s (in red), superimposed with the second-order fit (in green). | ||
The H/D kinetic isotope effect (KIE) for reaction (5) was measured by using 1.6% CD3OD in CH3CN for kinetic studies of CoIIIIH22bim (0.58–0.66 mM) plus tBu3ArO˙ (0.82–4.7 mM). This is at least 600 equivalents of CD3OD per CoIIIIH22bim (or 100 CD3OD per exchangeable H) and thus should achieve high deuterium enrichment of the exchangeable NH protons. Control reactions performed in the presence of CH3OH yielded a rate constant of 156 ± 4 M−1 s−1, within error of k5H, indicating that any solvent effect is negligible. The second-order rate constant k5D = 120 ± 5 M−1 s−1, which gives a small kinetic isotope effect of k5H/k5D = 1.30 ± 0.06 (Fig. 3).
![Plot of second-order rate constants (k5H, red circles; k5D, blue diamonds) measured as a function of [tBu3ArO˙], where the lines show the average rate constant for each reaction.](/image/article/2012/SC/c1sc00387a/c1sc00387a-f3.gif) | ||
| Fig. 3 Plot of second-order rate constants (k5H, red circles; k5D, blue diamonds) measured as a function of [tBu3ArO˙], where the lines show the average rate constant for each reaction. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) Benzoquinone (BQ) ⇄ CoIIIIIIHbim + ½
Benzoquinone (BQ) ⇄ CoIIIIIIHbim + ½![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) Hydroquinone (H22Q).
The reaction between CoIIIIH22bim and benzoquinone (BQ), like the TEMPO reaction above, proceeds to an equilibrium with CoIIIIIIHbim and hydroquinone (H22Q) (eqn (6)). For instance, starting with products for experimental convenience, CoIIIIIIHbim (3.8 mM) reacts with 50.9–105.3 mM 0.5 equivalents of H22Q over approximately one day to form CoIIIIH22bim and 0.5 equiv. BQ. Under similar conditions, the analogous iron reaction is complete in less than a second. 1H NMR spectroscopy shows some decomposition over the timescale of the experiment, with the total Co concentration decreasing by 24 ± 14%. Despite this decay, a reasonable estimate of K6 = 2.4 ± 0.8 could be determined (see Experimental section). This yields ΔG6° = −0.52 ± 0.11 kcal mol−1, which is in excellent agreement with ΔG6° predicted from the BDFEs of CoIIIIH22bim and H22Q (BDFEavg = 70 ± 1 kcal mol−1).35,37
Hydroquinone (H22Q).
The reaction between CoIIIIH22bim and benzoquinone (BQ), like the TEMPO reaction above, proceeds to an equilibrium with CoIIIIIIHbim and hydroquinone (H22Q) (eqn (6)). For instance, starting with products for experimental convenience, CoIIIIIIHbim (3.8 mM) reacts with 50.9–105.3 mM 0.5 equivalents of H22Q over approximately one day to form CoIIIIH22bim and 0.5 equiv. BQ. Under similar conditions, the analogous iron reaction is complete in less than a second. 1H NMR spectroscopy shows some decomposition over the timescale of the experiment, with the total Co concentration decreasing by 24 ± 14%. Despite this decay, a reasonable estimate of K6 = 2.4 ± 0.8 could be determined (see Experimental section). This yields ΔG6° = −0.52 ± 0.11 kcal mol−1, which is in excellent agreement with ΔG6° predicted from the BDFEs of CoIIIIH22bim and H22Q (BDFEavg = 70 ± 1 kcal mol−1).35,37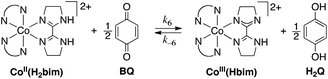 | (6) |
Optical monitoring of the reaction of CoIIIIIIHbim and H22Q showed a rapid decrease in optical absorbance, occurring within the time it takes to mix solutions in a cuvette, followed by slow conversion to CoIIIIH22bim over the course of hours. The initial drop in absorbance is likely due to formation of a hydrogen-bonded complex between CoIIIIIIHbim and H22Q, analogous to the complex formed with TEMPOH (eqn (4)). Analysis of data over a range of concentrations gave K6S = 14 ± 7 M−1 (See Experimental section, ESI and Fig. S1†). Attempts to analyze the subsequent slow spectral changes using single wavelength data, Specfit™ global analysis software, or the method of initial rates were not successful, even using a variety of reasonable kinetic models (see ESI†). In one typical example, 0.64 mM CoIIIIIIHbim + 71.7 mM H22Q, gave an approximate initial rate of d[CoIII]total/dt ≈ 7 × 10−8 M s−1 ([CoIII]total = [CoIIIIIIHbim] + [CoIIIIIIHbim|H22Q]), which could translate to a bimolecular rate constant of k−6 ∼10−3 M−1 s−1, although some data suggested that under some conditions the rates might be second order in [CoIII]total. The difficulties in analyzing the kinetic data likely result from the complexity of the mechanism (as well as the competing decomposition). The reaction likely occurs via formation of the semiquinone radical, CoIIIIIIHbim|H22Q → CoIIIIH22bim + HQ˙, and the HQ˙ likely reacts competitively with another CoIIIIIIHbim to form Q or with CoIIIIH22bim to reform starting materials (both pathways have ΔG° ∼ +8 kcal mol−1).37 This detailed examination of reaction (6) corrects the preliminary estimate of a second-order rate constant reported earlier.19a The reaction of CoIIIIIIDbim + D22Q, with the same concentrations as the example above, showed slower changes in the optical spectra and suggested a small KIE of ca. 1.5.
III. Calculations
Density functional theory calculations were performed on the cobalt-species relevant to HAT (CoIIIIIIHbim and CoIIIIH22bim) in order to gain deeper insight into the factors that govern HAT reactions in this system. Geometry optimizations (using the OPBE functional and a polarized double zeta basis, BSI) were straightforward, showing no unusual features. Several conformers exist for each structure because the protonated non-coordinated nitrogen atoms of the H2bim and Hbim ligands adopt slightly pyramidal structures and the nitrogen lone pairs on each H2bim ligand can be either syn or anti to one another. Test calculations show that different conformers are very close in energy to one another (1 kcal mol−1 or less). The calculated energies, summarized in Table 2, all refer to the ‘same’ overall conformer for each species. The larger basis set BSII is expanded to triple-zeta for the nitrogen atoms.| Method | ΔE/ΔG (4,24,2CoIIIIH22bim) | ΔE/ΔG (1,31,3CoIIIIIIHbim) | ΔE/ΔG (reaction 4) |
|---|---|---|---|
| a In kcal mol−1. For reaction (4), overall energetics are calculated for the transformation 44CoIIIIH22bim + TEMPO → 1CoIIIIIIHbim + TEMPOH. ΔE values are zero-point energy corrected electronic energies, ΔG values are at 298 K and values labelled ‘PCM’ include a correction for acetonitrile solvent effects calculated using PCM at the OPBE/BSI level. | |||
| OPBE/BSI | 9.01/10.83 | −0.66/−3.22 | 26.66/32.00 |
| OPBE/BSII | 8.79/10.62 | −0.21/−2.78 | 27.37/32.71 |
| B3LYP/BSII | 14.44/16.26 | 0.88/−1.68 | 35.88/41.21 |
| B3LYP*/BSII | 10.24/12.07 | 2.63/0.06 | 28.00/33.33 |
| B3LYP**/BSII | 5.83/7.65 | 4.36/1.79 | 19.99/25.32 |
| B3LYP**-D3/BSII | 2.50/4.32 | 7.42/4.85 | 12.82/18.16 |
| OPBE(PCM)/BSI | (−)/7.93 | (−)/4.56 | (−)/17.70 |
| B3LYP**(PCM)/BSII | (−)/4.75 | (−)/9.58 | (−)/11.02 |
| B3LYP**-D3(PCM)/BSII | (−)/1.42 | (−)/12.64 | (−)/3.85 |
| Experiment | (−) | (−) | (−)/3.0 |
The OPBE functional38 was used for geometry optimization partly due to suggestions that it provides accurate relative energies for different spin states of metal complexes.39 Accurate DFT calculation of spin-state splittings is known to be challenging, with results often being very sensitive to small changes in the nature of the functional.40,41 Gas phase calculations at the OPBE/BSI level predict a quartet ground state for CoIIIIH22bim, but surprisingly, the Co(III) species CoIIIIIIHbim is predicted to have a triplet ground state, slightly lower in electronic energy and free energy than the singlet state found experimentally. As can be seen in Table 2, the calculated energies are not very basis-set sensitive, with very small changes in energy resulting from expanding the nitrogen atom basis set to 6-311G* in BSII. The spin-state splittings are however strongly sensitive to the functional used. B3LYP predicts relative spin state energetics for the Co(III) species similar to those found with OPBE, but for Co(II), B3LYP favours the high-spin ground state. Decreasing the proportion of exact exchange (in B3LYP* and B3LYP**) favours the low-spin states in both compounds, as commonly observed.40,41 Including a single-point -D3 correction for dispersion42 at the OPBE structures further favours the slightly more compact low-spin states. Note that the computed splitting for CoIIIIIIHbim may be partly affected by what is likely to be an incorrect description of the triplet state. The latter involves significantly less than two unpaired electrons on Co, with significant spin density on the deprotonated Hbim ligand, corresponding to a mixture of the expected electronic structure with a resonance form with low-spin Co(II) and an Hbim radical. This type of unpaired electron delocalization with ligand oxidation is not supported by the experimental spectroscopy but was noted in a previous computational study of FeIIIIIIHbim complexes,24 and may be due to problems with the electron self-interaction error in DFT. None of the other species show this problem.
To provide some insight into the contribution of solute entropy to the reaction energy, it is interesting also to note the calculated gas-phase entropy changes at 298 K, based on the OPBE/BSI frequency calculations, which are not shown in Table 2. For quartet to doublet excitation of CoIIIIH22bim, and singlet to triplet excitation of CoIIIIIIHbim, these are −8.0 cal mol−1 K−1 and 10.8 cal mol−1 K−1, respectively, consistent with significantly stiffer vibrational behaviour for the low-spin states. This leads to calculated free energies for spin-state exchange (at 298 K) of 10.83 and −3.22 kcal mol−1, respectively.
Inclusion of approximate acetonitrile solvent effects with a polarized continuum model changes the relative energetics significantly, as the low-spin complexes involve tighter metal–ligand binding, hence greater polarization of the ligands, and stronger interactions with solvent.43 The calculated energies in the presence of the continuum solvent model include both enthalpic and entropic effects corresponding to the solute–solvent interaction. This leads to a decreased quartet to doublet excitation free energy for CoIIIIH22bim and an increased singlet to triplet excitation free energy for CoIIIIIIHbim. At the B3LYP**-D3(PCM)/BSII level, these values are 1.42 and 12.64 kcal mol−1, respectively.
The calculated reaction energy for reaction (4), HAT from CoIIIIH22bim to TEMPO, is also shown at various levels of theory in Table 2.44 In the gas phase, this reaction is predicted to be very unfavourable, both in energy and free energy terms. The entropy of reaction (not shown in Table 2) is computed to be −22.6 cal mol−1 K−1, showing that the increase in vibrational frequencies upon oxidation plays a significant role in the reaction thermodynamics. Including the effect of the continuum solvent stabilizes the Co(III) product more strongly than the reactant, leading to a much smaller reaction free energy, with the B3LYP**-D3(PCM) method yielding a value very close to the experimental ΔG4° = +3 kcal mol−1. This is probably in part due to cancellation of errors, but we nevertheless use values based on this method henceforth in the paper.
The solvation calculations do not provide a separate estimate for entropy and enthalpy, but it is reasonable to assume that CoIIIIIIHbim is strongly stabilized in enthalpic terms by solvent, but that this has an entropic cost. This is consistent with the experimental measurement of a highly negative entropy of reaction. Based on the calculations, the negative ΔS° is due partly to the vibrational entropy of the system (calculated gas phase entropy change of −22.6 cal K−1 mol−1) but also to the greater solvent organization around CoIIIIIIHbim.
Many attempts were made to locate an adiabatic transition state for HAT from CoIIIIH22bim to TEMPO, without success.45 This is due to the narrowly avoided nature of the potential energy surface crossing associated with the proton-coupled electron-transfer. Perhaps this indicates that reactions of this type, in which proton and electron transfers are concerted but ‘separate’ in some way, may require different computational approaches such as Hammes–Schiffer's multistate continuum theory.46
Discussion
The cobalt reactions described here are very slow in comparison to similar metal-mediated hydrogen atom transfer (HAT) reactions. HAT from CoIIIIH22bim to TEMPO has k4 = (1.8 ± 0.5) × 10−4 M−1 s−1, while the same reaction with the equivalent iron complex FeIIIIH22bim is 3400 times faster (kFe = 0.62 ± 0.8 M−1 s−1).24 In this comparison, the iron reaction is slightly less favourable, as ΔG4° and ΔGFe° are +3.0 ± 0.4 and +5.0 ± 0.1 kcal mol−1,24 so at the same driving force the iron would likely be another factor of 5 faster.47 The CoIIIIH22bimreduction of benzoquinone takes roughly a day at typical concentrations, while the analogous iron reaction is done in less than a second. In general, the rates of the iron reactions are typical of isoergic or downhill transfers of H˙ between electronegative elements (N or O), while the cobalt examples are unusually slow.48 From another perspective, we have previously estimated H-atom transfer self-exchange rate constants for metal complexes using the Marcus cross relation (an improved version of that analysis is given in ESI†), with the conclusion that the cobalt value is at least a million times smaller than that for iron.27The sections below examine the mechanism of the cobalt reactions at two levels of detail in order to understand both why they are so slow and the role of the spin change. First, we discuss whether the reactions occur by HAT or whether they could occur by stepwise transfer of the electron and the proton. Then, computations are used to examine the TEMPO reaction, which clearly occurs by HAT, to ask whether the H˙ transfer occurs prior to the spin change, after the spin change, or concurrent with spin change. Finally, we discuss how the analysis of this well-characterized system has broader implications for other, more complex spin-forbidden processes.
I. Reaction mechanisms, Part 1: HAT vs. initial PT or ET
Any reaction involving transfer of one electron and one proton can occur by (i) initial proton transfer (PT) followed by electron transfer (ET); (ii) ET followed by PT; or (iii) transfer of e− and H+ in the same kinetic step (HAT/CPET).6,9,35 For the reaction of 44CoIIIIH22bim with 2TEMPO, ΔG° for initial PT to form 44CoIIIIHbim and 2TEMPOH+ is indicated by the pKas of each reactant (the superscripts indicate the spin states; Scheme 2). The pKa of TEMPOH+˙ is ∼ −435 and a lower limit for the pKa of CoIIIIH22bim is given by the known pKa(CoIIIIIIH22bim) = 20.3 ± 0.6.31 Thus ΔpKa > 24 for an initial PT step, and ΔGPT4° > +33 kcal mol−1. Since this is much higher than the observed barrier for the reaction, ΔG4‡ = 22.5 ± 0.3 kcal mol−1, initial PT is not possible. Initial ET from 44CoIIIIH22bim to 2TEMPO forms 11CoIIIIIIH22bim + 1TEMPO−, which is roughly as unfavourable, with ΔE1/2 = −1.42 V (ΔGET4° = +32.7 kcal mol−1), based on E1/2(CoIIIIIIH22bim) = −0.53 ± 0.02 V and E1/2(TEMPO˙/−) = −1.95 V35 (all potentials here vs. Cp2Fe+/0 in MeCN). Thus, the CoIIIIH22bim + TEMPO reaction cannot occur by initial ET or PT; the proton and electron are indicated to transfer in the same kinetic step (HAT).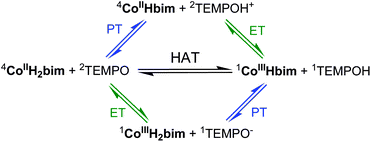 | ||
| Scheme 2 Possible pathways for reaction (4). HAT is thermodynamically favoured over initial PT or ET. | ||
This conclusion is not affected by spin issues. Both in this specific case and in general, forming alternative spin states of the products would be less favourable. For instance, the pKa of CoIIIIH22bim used in the analysis above refers to proton dissociation to give the most stable form of the conjugate base CoIIIIHbim, in this case with the same quartet spin state. Therefore, proton transfer from CoIIIIH22bim to TEMPO to give the doublet CoIIIIHbim would have a more positive ΔG°PT, and therefore is also not a possible mechanism. For electron transfer, the redox potential used in the analysis is for the most thermodynamically favourable spin-forbidden 44CoIIIIH22bim → 11CoIIIIIIH22bim couple (this is why the chemical equilibration in eqn (3) and Fig. 1 requires an hour to go to completion). Electron transfer to form the triplet Co(III) product would only make ΔG°ET more positive. Pre-equilibrium conversion of 44CoIIIIH22bim to 22CoIIIIH22bim would also have no effect on the ΔG°ET. Thus the CoIIIIH22bim + TEMPO reaction cannot occur by initial ET or PT, regardless of spin state.
For the reactions of CoIIIIH22bim with tBu3ArO˙ and CoIIIIIIHbim with H22Q, such thermochemical arguments are not definitive. For CoIIIIH22bim + tBu3ArO˙, PT is ruled out but initial ET is possible (ΔGPT5° > 32 kcal mol−1 is larger than ΔG5‡ = 14.4 ± 0.1 kcal mol−1, but ΔGET5° = 3.9 ± 0.7 kcal mol−1 is smaller).49 A rough estimate of this initial ET rate constant from the Marcus cross relation, kET5 ≤ 1 M−1 s−1, is slower than the observed rate of k5 = 167 ± 22 M−1 s−1, but perhaps within the uncertainty of the cross relation.28,50–52 Another possible pathway could involve initial uphill conversion of 44CoIIIIH22bim to 22CoIIIIH22bim followed by ET to tBu3ArO˙.53 For CoIIIIIIHbim + H22Q, initial ET can be ruled out based on its very high ΔGET° (>36 kcal mol−1), but initial PT is possible based on ΔGPT° = +13 ± 1 kcal mol−1.54 Still, for both the tBu3ArO˙ and BQ/H22Q reactions, other arguments suggest that HAT mechanisms are likely. In both cases, HAT is significantly more favourable than initial ET or PT and primary kinetic isotope effects are observed, k5H/k5D = 1.3 ± 0.1 and k−6H/k−6D = ca. 1.5, indicating that the proton is transferring in the rate determining step.55,56
II. Reaction mechanism, Part 2: The role of the spin-state change
The CoIIIIH22bim + TEMPOH reaction is, to our knowledge, the first spin-forbidden hydrogen atom transfer (HAT) reaction where the reactants and products have all been isolated and characterized. The tBu3ArO˙ and BQ reactions likely also involve spin-forbidden HAT, but we focus on the TEMPOH reaction because its HAT mechanism is better established. The precursor complex containing high-spin (HS) 44CoIIIIH22bim (S = 3/2, 4T1g, t2g5eg2, in octahedral symmetry) and TEMPO (S = 1/2) has a total spin quantum number S = 1 or 2, depending on how the spins couple. The products, however, have S = 0 (no unpaired electrons): low-spin (LS) CoIIIIIIHbim (1A1g, t2g6) and TEMPOH. The reactions are formally spin-forbidden because they start on one spin-state surface and finish on a different one.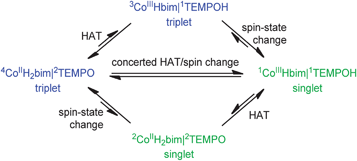 | ||
| Scheme 3 Three possible mechanisms for spin-forbidden HAT. | ||
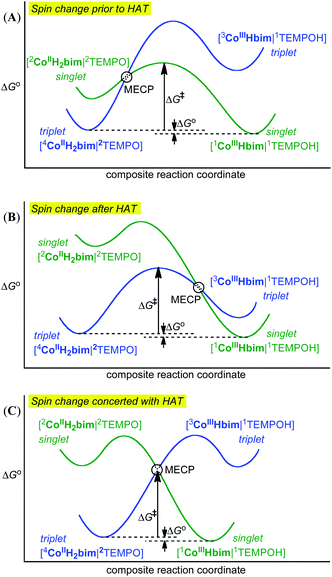 | ||
| Fig. 4 Schematic free energy surfaces for the conversion of the triplet reactant state of 44CoIIIIH22bim|2TEMPO (blue) to the singlet state for 22CoIIIIH22bim|2TEMPO (green) in the three possible cases. (A) Pre-equilibrium spin change prior to HAT; (B) HAT prior to spin change; and (C) HAT concerted with spin change because the minimum energy crossing point (MECP) is below the HAT transition structures on the two surfaces. | ||
The possibility of concerted HAT and spin change (Fig. 4C) has not been probed computationally, both because these calculations are very challenging and because one of the stepwise paths is energetically very reasonable, as described below. This favouring of a stepwise path fits with the suggested general argument1b,66 that except in special circumstances, bimolecular spin-forbidden processes are expected to occur preferentially through stepwise mechanisms, involving a unimolecular spin-state change and a spin-allowed bimolecular step. Since both spin-state changes and bimolecular reactions have unfavourable entropies of activation,1b a spin-forbidden HAT step would be doubly unfavourable for entropic reasons, whereas this is not true for the individual steps of the stepwise mechanism. Some cases where bond-making and breaking occurs concertedly with spin-state change are known.1b This tends to be only in cases where spin-state change in both reactants and products is very unfavourable (e.g., in decomposition of gas phase 3CH3O+ to yield 1HCO+ and H2, the singlet state of the reactant is high in energy, and likewise for the triplet states of products).59 In the present reactions, this is not the case, as the different spin states of the CoIII and especially CoII species are quite close in energy.
One stepwise mechanism involves initial spin-allowed HAT from the quartet state of CoIIIIH22bim to give triplet CoIIIIIIHbim (44CoIIIIH22bim|2TEMPO → 33CoIIIIIIHbim|1TEMPOH), followed by spin relaxation through spin-orbit coupling60 to the experimentally observed singlet state (Fig. 4B). The latter step is assumed to be rapid, for reasons discussed below for the analogous spin-state change of CoIIIIH22bim. The key step here is therefore the first one. Combining the overall calculated reaction energy and the spin-state splitting of Table 1, it can be seen that the initial product in this mechanism, 33CoIIIIIIHbim + TEMPOH, lies much higher in free energy than reactants, by ca. 16 kcal mol−1 according to the B3LYP**-D3 calculations. Though there will inevitably be some error in this calculated value, we note that the different calculations in the Table all tend to give either a large singlet/triplet splitting or a high reaction free energy, so that the total free energy of high-spin products relative to reactants is never lower than 15 kcal mol−1. Hence the large reaction free energy is probably a fairly reliable computational prediction. In addition, octahedral Co(III) complexes are almost always LS. CoIII complexes with nitrogen ligands are far from the spin-crossover point61 (CoF63−,62 and a more recent nitrogen coordinated Co complex63 are some of the rare notable HS CoIII complexes). This indicates that the HS Co(III) state is not likely to be accessible as an intermediate. The transition state for HAT would lie still higher in free energy, due to the unfavourable entropic contribution from bringing two separate molecules together (ca. 10 kcal mol−1) as well as any contribution from the intrinsic barrier to transfer. Indeed, in the related iron reaction,24 the activation free energy for the similar HAT step is 14 kcal mol−1. Hence the free energy of activation of the 44CoIIIIH22bim + TEMPO → 33CoIIIIH22bim + TEMPOH step would probably be well above 25 kcal mol−1. Notwithstanding the computational uncertainties mentioned above, this value is higher than the experimentally observed activation free energy ΔG4‡ = 22.5 kcal mol−1, and therefore initial HAT followed by spin-change is unlikely to be the preferred mechanism.
The second possibility is initial spin crossover of quartet CoIIIIH22bim to its doublet state, followed by spin-allowed HAT to yield singlet CoIIIIIIHbim (Fig. 4A). Experiments64,65 and theory66 both show that spin crossover in transition-metal complexes occurs rapidly when it is thermodynamically favoured, with k > 106 s−1 in almost all cases at room temperature, and often significantly larger. For instance, conversion of LS [CoII(trpy)2]2+ in methanol solution to the HS spin state (ΔH° = +2 kcal mol−1) occurs faster than 2 ns (k > 3 × 108 s−1; trpy = 2-2′;6′,2′′-terpyridine).67,68b For the pathway discussed here, the downhill direction is the reverse process, relaxation of doublet CoIIIIH22bim to quartet. Reaction in the thermodynamically favoured direction is fast especially when the potential energy surfaces of the two states intersect at a point that lies close in energy to the equilibrium structure of the higher-energy spin state. Accordingly, we have optimized the structure of the minimum energy crossing point (MECP) between doublet and quartet potential energy surfaces. These calculations were performed at the OPBE/BSI level of theory in vacuum. As often in such cases, the MECP is indeed found to lie very close in energy to the doublet minimum, just 1.2 kcal mol−1 higher. This value would certainly change somewhat if one included the effect of solvent and switched to a more accurate functional, but it would be expected to remain very low. Hence the process 22CoIIIIH22bim → 44CoIIIIH22bim should be very fast, with a rate constant at least 106 s−1. The calculations therefore support a mechanism of initial spin change followed by HAT (Scheme 4).
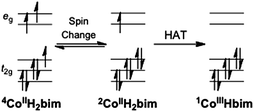 | ||
| Scheme 4 Changes in the occupation of the cobalt d orbitals for the pathway of spin change followed by hydrogen atom transfer. | ||
The free energy at room temperature for the forward spin-state change, 44CoIIIIH22bim → 22CoIIIIH22bim, is calculated to be ∼1.4 kcal mol−1 [B3LYP**-D3/BSII(PCM)] so the predicted spin-crossover equilibrium constant Ksc is ∼0.1. The B3LYP**-D3 level of theory may slightly underestimate the quartet–doublet splitting, but it should be noted that a fairly small splitting is consistent with the spectroscopic analysis in the next section. With this value, and k(2Co → 4Co) > 106 s−1, we estimate that 44CoIIIIH22bim → 22CoIIIIH22bim should have a rate constant of at least 105 s−1. This is nine orders of magnitude faster than the observed rate of reaction, so this step should be in rapid pre-equilibrium. The overall reaction is therefore expected to occur under ‘Curtin–Hammett conditions’, where a rapid pre-equilibrium allows the system to proceed via the more reactive state - in this case via the doublet excited spin state.
A rough estimate of the rate constant for spin-allowed HAT from 22CoIIIIH22bim to TEMPO can be obtained by comparison with the spin-allowed reaction of the iron analogue, iron(II) tris(bis-tetrahydropyrimidine) FeII(H2bip)32+ with TEMPO, which occurs with a rate constant of 2.6 × 102 M−1 s−1 (ΔG‡ = 14 kcal mol−1).24 The reaction of excited-state 22CoIIIIH22bim is a little less favourable in free energy terms than this iron analogue (ca. + 2.4 vs. −0.3 kcal mol−1), which should make the 22CoIIIIH22bim rate constant about a factor of 10 smaller (∼1.3 kcal mol−1 higher barrier). Also, the intrinsic barrier for the cobalt reaction is likely to be higher than the iron case, because the 22CoIIIIH22bim → 11CoIIIIIIH22bim conversion involves significant bond length changes due to the transfer of a σ antibonding (eg) electron (low-spin Co(II) complexes are typically Jahn–Teller distorted68). Thus we estimate an activation free energy for the forward reaction from 22CoIIIIH22bim ≥ 17 kcal mol−1. If one adds the calculated free energy difference between 22CoIIIIH22bim and 44CoIIIIH22bim, this would give an overall activation free energy of ca. ≥ 18 kcal mol−1,69 in reasonable agreement with the experimental value of 22.5 kcal mol−1, especially considering the significant uncertainty in the calculated spin-state splitting. A similar pathway of initial spin crossover has been suggested for electron-transfer self exchange reaction between 4T1g Co(NH3)62+ and 1A1g Co(NH3)63+ on the basis of computations.70
Experimentally, the optical spectrum of CoIIIIH22bim (Fig. 5) provides an estimate of the vertical excitation energy from the 4T1g ground state to the 2Eg excited state (in this analysis we assume idealized octahedral symmetry). Following other analyses of HS Co(II) spectra,68 the two ligand field bands are assigned as [λmax (ε)]: 1035 nm (11 M−1 cm−1), 4T1g(F) → 4T2g, and 485 nm (46 M−1 cm−1): 4T1g(F) → 4T1g(P). Using the d7 Tanabe–Sugano diagram, the ratio of these transition energies (2.13) indicates that Δo ≈ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and B ≈ 690 cm−1 (Δo/B ≈ 15; see ESI†). For comparison, the high-spin [Co(bpy)3]2+ ion in [Co(bpy)3][NaRh(ox)3] has λmax = 870 nm and Δo ≈ 12
000 cm−1 and B ≈ 690 cm−1 (Δo/B ≈ 15; see ESI†). For comparison, the high-spin [Co(bpy)3]2+ ion in [Co(bpy)3][NaRh(ox)3] has λmax = 870 nm and Δo ≈ 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1.68a The parameters for CoIIIIH22bim indicate that the 2Eg state is 4600 cm−1 (13 kcal mol−1) above the ground state at the geometry of the 4T1g ground state.
700 cm−1.68a The parameters for CoIIIIH22bim indicate that the 2Eg state is 4600 cm−1 (13 kcal mol−1) above the ground state at the geometry of the 4T1g ground state.
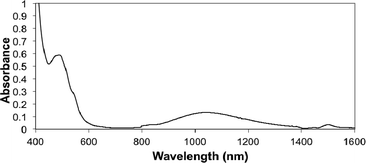 | ||
| Fig. 5 Optical and near-IR spectrum of CoIIIIH22bim in MeCN. | ||
This vertical2Eg − 4T1g excitation energy is of course larger than the energy difference between the minima of the 4T1g and 2Eg states. Computationally, at the OPBE/BSI level, the electronic energy of the doublet at the quartet geometry is 14 kcal mol−1 higher than at the doublet minimum. This deformation energy, plus the best estimate that the doublet minimum is 1.4 kcal mol−1 above the quartet minimum, gives a rough computational estimate of ca. 15 kcal mol−1 for the vertical 2Eg − 4T1g energy. Given the uncertainties in the calculations as well as in the experimental analysis, this is nicely consistent with the spectroscopy. For comparison, the [CoII(trpy)2]2+ ion in solid [Co(trpy)2](PF6)2 has a split transition (λmax = 960 and 1090 nm) close to that of CoIIIIH22bim, and is HS with a small thermal population of the LS state.67 In methanol solution, the order of the spin states is reversed and CoII(trpy)22+ is LS with rapid conversion to the HS spin state. In sum, the experimental and computational results, the spectroscopy, and the literature precedents are all consistent with the conclusion that quartet CoIIIIH22bim has a low-lying doublet-spin state. These data therefore support a mechanism of spin-change prior to HAT, as shown in Fig. 4A and Scheme 4.
Conclusions and implications
TEMPO, tBu3ArO˙ and benzoquinone (BQ) oxidize high-spin (HS, quartet) CoIIIIH22bim to low-spin (LS) CoIIIIIIHbim and TEMPOH, tBu3ArOH and hydroquinone, respectively. The TEMPOH reaction has been shown to proceed by hydrogen atom transfer (concerted transfer of e− and H+) and the tBu3ArO˙ and BQ reactions likely follow the same pathway. The TEMPO reaction has been examined in the most detail, experimentally and computationally. It is, to our knowledge, the first experimentally fully characterized spin-forbidden HAT reaction, converting triplet or quintet 44CoIIIIH22bim + 2TEMPO to singlet products, 11CoIIIIIIHbim + 1TEMPOH.Computational and experimental studies indicate that the 44CoIIIIH22bim + 2TEMPO reaction likely involves a spin change prior to HAT reactivity. Spin-change of the reactant 44CoIIIIH22bim to the excited doublet state is estimated to be about 1.4 kcal mol−1 uphill, after consideration of different functionals and with inclusion of solvent effects. This value is consistent with an estimate of the excitation energy from the optical spectrum. The proposed pathway is illustrated in Fig. 6. The triplet precursor complex [44CoIIIIH22bim|2TEMPO] on the blue surface is in rapid pre-equilibrium with its spin excited state [22CoIIIIH22bim|2TEMPO] on the (green) singlet surface. This singlet precursor complex then undergoes spin-allowed HAT to form the singlet products.
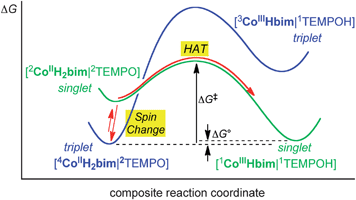 | ||
| Fig. 6 Proposed schematic reaction pathway for the conversion of precursor complex 4CoIIIIIIH22bim|2TEMPO on the blue triplet free-energy surface to the 1CoIIIIIIHbim|1TEMPOH successor complex on the green singlet surface. The suggested reaction pathway is indicated by the red arrows. Initial pre-equilibrium formation of singlet 2CoIIIIH22bim|2TEMPO is calculated to be 1.4 kcal mol−1 uphill, and the experimental values are ΔG‡ = 22 kcal mol−1 and ΔG° = +0.3 kcal mol−1. | ||
The HAT reactions in this study are thus indicated to proceed under ‘Curtin–Hammett conditions’, in which a rapid pre-equilibrium allows access to a spin-allowed HAT step. This mechanism provides an understanding of why the cobalt HAT reactions are so much slower than related reactions. Most examples of roughly isoergic HAT between electronegative atoms occur within seconds at typical concentrations, while the CoIIIIH22bimreduction of benzoquinone requires ca. a day. HAT from CoIIIIH22bim to TEMPO occurs 3400 times slower than the related iron reaction, which is 2 kcal mol−1 less favourable. Under Curtin–Hammett conditions, the overall rate is not affected by the energy of the intermediate, only by the difference between the reactants and the transition state. In other words, the measured rate constant for each reaction takes the form kobs ∼ Ksc*kHAT and the slowness of the reactions has two origins. First of all, the equilibrium constant of the initial spin conversion process, Ksc, is shown from spectroscopy and computations to be <1.71 Secondly, while kHAT is for a spin-allowed process, it is small because of the expected large inner-sphere reorganization on interconversion of LS CoII and LS CoIII, mostly due to the large change in Co–N bond lengths. While experimental structures are not available for LS CoII, the six Co–N bond lengths in high-spin CoIIIIH22bim (∼2.14 Å) are an average of 0.21 Å longer than in low-spin CoIIIIIIH22bim (∼1.92 Å).27 Although the LS CoII complex likely has somewhat shorter distances than the HS form, with only one electron in eg-type σ* orbitals, substantial reorganization is still expected.
This analysis is related to the discussions some time ago of the very slow electron transfer reactions that involve the HS Co(II)/LSCo(III) redox couple.57 These reactions are the classic examples of large inner-sphere reorganization energies λ, due to the large change in cobalt–ligand bond lengths between HS Co(II) and LS Co(III). There have also been proposals that the reactions occur by direct spin-forbidden ET with a small electron coupling, while others have suggested that spin interconversions play a key role.57
These cobalt reactions, complicated as they are, can serve as relatively simple model systems for spin-forbidden HAT processes in heme and non-heme iron-oxo enzymes and related model systems with various metal centres. As noted above, these reactions are of much current interest and have been described as having two-state reactivity.3 This term is increasingly widely used and seems to have taken on a number of meanings. At one level, it simply refers to reactions that involve more than one spin state, and therefore likely involve a formal spin crossing somewhere along the reaction coordinate. The cobalt reactions discussed here clearly fall in this category. ‘Two-state reactivity’ also appears to have been used to indicate that a reaction proceeds concurrently on two different spin states, or that blended spin surfaces are involved.3h,l,o However, the arguments presented above suggest that these solution HAT reactions with multiple accessible spin states will more likely be under Curtin–Hammett conditions, in which rapid initial pre-equilibrium between the spin states allows the reaction to proceed via the lowest energy transition structure (TS) (Fig. 6). This could be the mechanism for many solution and enzymatic HAT reactions, and in fact is one of the pathways discussed for a non-heme iron(IV) oxo system on the basis of DFT calculations.3u Spin interconversion is typically fast, occurring on sub-microsecond timescales for downhill processes.
In summary, the effects of spin-state changes from reactant to product should be pronounced primarily when the excited spin states are high in energy (as in Fig. 4C), or when the reaction chemistry occurs faster than spin conversion. For reactions of first-row transition-metal species with low lying excited spin states, we suggest that the most common mechanism involves rapid spin pre-equilibrium that allows the system to access the lowest energy transition state (Curtin–Hammett conditions). Under these conditions, the spin change should not be a bottleneck for the reaction. The reactions analyzed here are not slow because of any difficulty in changing spin state. They are slow because of their need to convert to a higher energy spin state, and especially because of their large intrinsic barriers resulting from the substantial change in structure between the cobalt(II) and cobalt(III) complexes.
Experimental section
General considerations
All manipulations were carried out under nitrogen using glove-box/vacuum line techniques. 1H NMR spectra were obtained on Bruker Avance spectrometers (Avance-500, DRX-499 and Avance-300), and are reported as (chemical shift δ, assignment, number of protons). All NMR integration errors are estimated as ±10%. UV-visible spectra were obtained with a Hewlett-Packard 8453 diode-array spectrophotometer. Air-sensitive samples were prepared in a glovebox in quartz cuvettes attached to Teflon-stoppered valves and topped with 14/20 ground glass joints. Rapid kinetic measurements were taken using an OLIS RSM-1000 stopped flow instrument which has a rapid scanning monochromator and a UV-Vis detector. More detailed descriptions of the experimental methods are given in ESI†.Materials
Unless otherwise noted, all solvents were purchased from Fisher Scientific or EMD Chemicals. Anhydrous acetonitrile (MeCN; <10 ppm H2O) was purchased from Honeywell Burdick & Jackson, sparged with argon and plumbed from a steel keg directly into a glovebox. Deuterated CD3CN was purchased from Cambridge Isotope Laboratories, dried over CaH2, vacuum transferred to P2O5, then vacuum transferred to fresh CaH2 and finally into an empty vessel. All reagents were purchased by Aldrich and used as received except for H22Q and BQ. H22Q was recrystallized 2–3 times in acetone or ethanol and dried under vacuum. D22Q was prepared by recrystallizing H22Q from D2O–CD3OD. BQ was recrystallized once in ethanol and then sublimed 1–2 times at room temperature under static vacuum. [Cp2*Fe]PF672 and tBu3ArO˙20 were prepared according to literature procedures. Cobalt(II) tris[2,2′-bi-2-imidazoline][perchlorate] ([CoII(H2bim)3][ClO4]2, CoIIIIH22bim) and [CoIII(H2bim)3][ClO4]3 (CoIIIIIIH22bim); and [CoIII(H2bim)2(Hbim)][ClO4]2 (CoIIIIIIHbim) were synthesized and characterized following literature procedures.27CAUTION: perchlorate salts are explosive and should be handled with care and in small quantities. They should not be heated when dry or subjected to friction or shock, such as scratching with a non-Teflon-coated spatula.
K eq measurements
In a typical experiment (reaction of CoIIIIH22bim with [Cp2*Fe]PF6), four Kontes cuvettes were each charged with 2 mL of a 1.32 mM MeCN solution of [Cp2*Fe]PF6 (6.2 mg in 10 mL). CoIIIIH22bim was added as a solid to three of the four cuvettes to form 1.12, 1.93 and 3.35 mM solutions. Spectra of the three reaction cuvettes showed a slow drop in absorbance at 780 nm (λmax for Cp2*Fe+), over ca. 4000 s. Good mass balance was observed, with a reasonable isosbestic point at λ = 593 ± 1 nm. The final, constant absorbance gave the concentration of [Cp2*Fe]PF6 at equilibrium, using ε780 = 600 M−1 cm−1 (no other species absorb at 780 nm). Assuming mass balance, [Cp2*Fe]eq = [Cp2*FePF6]initial − [Cp2*FePF6]eq, [CoIIIIIIH22bim]eq = [Cp2*Fe]eq and [CoIIIIH22bim]eq = [CoIIIIH22bim]initial − [Cp2*Fe]eq. The derived concentrations give the constant K3 = [CoIIIIIIH22bim][Cp2*Fe]/[CoIIIIH22bim][Cp2*Fe+] = 0.090 ± 0.032 and E = (RT/F)ln(K3) = −0.062 ± 0.011 V. Since E1/2([Cp2*Fe]PF6) = −0.59 V vs. Cp2Fe+/0 in MeCN,32E1/2(CoIIIIIIH22bim) = −0.53 ± 0.02 V vs. Cp2Fe+/0 in MeCN. The Keq for CoIIIIIIHbim + H22Q ⇄ CoIIIIIIHbim--H22Q was measured using a similar method.For the reaction of CoIIIIIIHbim+ ½H22Q ⇄ CoIIIIH22bim+ ½BQ, four J. Young NMR tubes were charged with 500 μL of 4 mM CoIIIIIIHbim solution containing HMDS, and solid H22Q was added to four of the five tubes to give 50.9, 74.5 and 105.3 mM solutions. 1H NMR spectra were obtained at intervals from 40 min–44 h, monitoring the integrals of CoIIIIH22bim (δ 21–22 ppm), CoIIIIIIHbim (δ 2.5–5 ppm) and {H22Q + BQ} (δ 6–7 ppm) until the spectra stopped changing (20 h). Mass balance was assumed to obtain estimates of the equilibrium constant K6.
Acknowledgements
We gratefully acknowledge financial support from the U.S. National Institutes of Health (GM50422) and the University of Washington. We thank Dr. J. J. Warren for the preparation of the D2Q and for helpful comments on the manuscript.Notes and references
- (a) cf. R. Poli, Acc. Chem. Res., 1997, 30, 494–501 Search PubMed; (b) J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343 RSC; (c) R. Poli and J. N. Harvey, Chem. Soc. Rev., 2003, 32, 1–8 RSC; (d) P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC; (e) J. W. Turner and F. A. Schultz, Coord. Chem. Rev., 2001, 219–221, 81–97 CrossRef CAS; (f) H. A. Goodwin, Top. Curr. Chem., 2004, 234, 23–47 CAS (in the volume Spin Crossover in Transition Metal Compounds, Vol. II, ed. P. Gütlich, Springer-Verlag, Berlin); (g) P. Gütlich, P. J. van Koningsbruggen and F. Renz, Struct. Bonding, 2004, 107, 27–75; (h) A. B. Gaspar, V. Ksenofontov, M. Seredyuk and P. Gütlich, Coord. Chem. Rev., 2005, 249, 2661–2676 CrossRef CAS; (i) I. Krivokapic, M. Zerara, M. L. Daku, A. Vargas, C. Enachescu, C. Ambrus, P. Tregenna-Piggott, N. Amstutz, E. Krausz and A. Hauser, Coord. Chem. Rev., 2007, 251, 364–378 CrossRef CAS , and references therein; (j) A. S. Veige, L. M. Slaughter, E. B. Lobkovsky, P. T. Wolczanski, N. Matsunaga, S. A. Decker and T. R. Cundari, Inorg. Chem., 2003, 42, 6204–6224 CrossRef CAS; (k) J. L. Detrich, O. M. Reinaud, A. L. Rheingold and K. H. Theopold, J. Am. Chem. Soc., 1995, 117, 11745–11748 CrossRef CAS; (l) C. R. Landis, C. M. Morales and S. S. Stahl, J. Am. Chem. Soc., 2004, 126, 16302–16303 CrossRef CAS.
- One clear example is in ref. 1k. As discussed below, spin-interconversion reactions typically occur very rapidly, on the nanosecond timescale. See ref. 1d,f.
- (a) cf., Cytochrome P450: Structure, Mechanism, and Biochemistry, P. R. Ortiz de Montellano, New York, Kluwer/Plenum, 2005 Search PubMed; (b) J. T. Groves, J. Inorg. Biochem., 2006, 100, 434–447 CrossRef CAS; (c) I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253–2278 CrossRef CAS; (d) S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS; (e) M. T. Green, J. H. Dawson and H. B. Gray, Science, 2004, 304, 1653–1656 CrossRef CAS; (f) K. L. Stone, R. K. Behan and M. T. Green, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12307–12310 CrossRef CAS; (g) J. Rittle and M. T. Green, Science, 2010, 330, 933–937 CrossRef CAS; (h) D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145 CrossRef CAS; (i) B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980 CrossRef CAS; (j) S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS; (k) C. V. Sastri, J. Lee, K. Oh, Y. J. Lee, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin, J. A. Halfen, J. Kim, L. Que Jr, S. Shaik and W. Nam, Proc. Natl. Acad. Sci. USA, 2007, 104, 19181–19186 CrossRef; (l) S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542 CrossRef CAS; (m) D. A. Plattner, Angew. Chem., Int. Ed., 1999, 38, 82–86 CrossRef CAS; (n) J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2003, 238–239, 347–361 CrossRef CAS; (o) H. Hirao, L. Que, Jr, W. Nam and S. Shaik, Chem.–Eur. J., 2008, 14, 1740–1756 CrossRef CAS; (p) P. Comba and G. Rajaraman, Inorg. Chem., 2008, 47, 78–93 CrossRef CAS; (q) D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS; (r) F. Ogliaro, N. Harris, S. Cohen, M. Filatov, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2000, 122, 8977–8989 CrossRef CAS; (s) S. Shaik, M. Filatov, D. Schröder and H. Schwarz, Chem.–Eur. J., 1998, 4, 193–199 CrossRef CAS; (t) S. P. de Visser, J. Am. Chem. Soc., 2006, 128, 15809–15818 CrossRef CAS; (u) H. Hirao, D. Kumar, L. Que, Jr and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590–8606 CrossRef CAS.
- Hydrogen-Transfer Reactions, ed. J. T. Hynes, J. P. Klinman, H.-H. Limbach and R. L. Schowen, Wiley-VCH, Weinheim, 2007 Search PubMed.
- (a) Free Radicals, ed. J. K. Kochi, Wiley, New York, 1973, especially K. U. Ingold, ch. 2, vol. 1, pp. 67ff; G. A. Russell, ch. 7, vol. 1, pp. 275–331; and H. O'Neal and S. W. Benson, ch. 17, vol. 2, pp. 275–359 Search PubMed; (b) J. Fossey, D. Lefort and J. Sorba, Free Radicals in Organic Chemistry, Wiley, New York, 1995 Search PubMed; (c) J. E. Leffler, An Introduction to Free Radicals, Wiley, New York, 1993, ch. 7–8 Search PubMed; (d) B. Halliwell and J. M. C. Gutteridge, Free Radicals in Biology and Medicine, Oxford University Press, New York, 1999 Search PubMed; (e) Oxidative Stress: Oxidants and Antioxidants, ed. H. Sies, Academic, New York, NY, 1991 Search PubMed; (f) Active Oxygen in Chemistry, ed. C. S. Foote, J. S. Valentine, J. Liebman and A. Greenberg, Blackie, Chapman and Hall, Glasgow, 1995 Search PubMed.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS.
- (a) R. A. Sheldon and J. K. Kochi, Metal-Catalyzed Oxidation of Organic Compounds, Academic Press, New York, 1981 Search PubMed; (b) G. W. Parshall and S. D. Ittel, Homogeneous Catalysis: The Applications and Chemistry of Catalysis by Soluble Transition Metal Complexes, Wiley-Interscience, New York, 2nd edn, 1992 Search PubMed; (c) G. W. Parshall and W. A. Nugent, CHEMTECH, 1988, 18, 184–190 CAS; G. W. Parshall and W. A. Nugent, CHEMTECH, 1988, 18, 314–320 CAS; G. W. Parshall and W. A. Nugent, CHEMTECH, 1988, 18, 376–384 CAS; (d) Comprehensive Organic Synthesis Vol. 7 (Oxidation), ed. B. M. Trost, Pergamon, New York, 1991 Search PubMed; (e) Organic Syntheses by Oxidation with Metal Compounds, ed. W. J. Mijs and C. R. H. I. de Jonge, Plenum, New York, 1986 Search PubMed; (f) R. A. Sheldon and H. van Bekkum, Fine Chemicals Through Heterogeneous Catalysis, Wiley-VCH, New York, 2001 Search PubMed; (g) C. Limberg, Angew. Chem., Int. Ed., 2003, 42, 5932–5954 CrossRef CAS; (h) A. A. Gridnev and S. D. Ittel, Chem. Rev., 2001, 101, 3611–3659 CrossRef CAS.
- (a) J. Stubbe and W. A. van der Donk, Chem. Rev., 1998, 98, 705–762 CrossRef CAS; (b) R. P. Pesavento and W. A. van der Donk, Adv. Protein Chem., 2001, 58, 317–385 CAS; (c) E. N. G. Marsh, BioEssays, 1995, 17, 431–441 CrossRef CAS; (d) J. L. Pierre and F. Thomas, C. R. Chim., 2005, 8, 65–74 CrossRef CAS; (e) M. Fontecave and J. L. Pierre, C. R. Acad. Sci. Ser. II C, 2001, 4, 531–538 CrossRef CAS; (f) A. Decker, M. S. Chow, J. N. Kemsley, N. Lehnert and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 4719–4733 CrossRef CAS; (g) S. W. Ragsdale, Chem. Rev., 2006, 106, 3317–3337 CrossRef CAS; (h) M.-H. Baik, M. Newcomb, R. A. Friesner and S. J. Lippard, Chem. Rev., 2003, 103, 2385–2419 CrossRef CAS; (i) B. J. Brazeau, R. N. Austin, C. Tarr, J. T. Groves and J. D. Lipscomb, J. Am. Chem. Soc., 2001, 123, 11831–11837 CrossRef CAS.
- (a) Chem. Rev., 2010, 110, issue 12, 6937–7100 Search PubMed: Introduction: Proton-Coupled Electron Transfer: S. Hammes-Schiffer, Chem. Rev., 2010, 110, 6937–6938 Search PubMed; (b) M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS; (c) C. Costentin, Chem. Rev., 2008, 108, 2145–2179 CrossRef CAS.
- (a) In this report we use the term ‘hydrogen atom transfer’ or HAT only to imply the net transfer of H˙ from one reagent to another, as in eqn (1) and (2). It should be noted, however, that the meaning of this term is being re-examined in light of the formal separation of the e− and H+ that occurs in many transition-metal reactions and some organic processes. See: C. R. Waidmann, X. Zhou, E. A. Tsai, W. Kaminsky, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 4729–4743 Search PubMed; (b) J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS; (c) O. Tishchenko, D. G. Truhlar, A. Ceulemans and M. T. Nguyen, J. Am. Chem. Soc., 2008, 130, 7000–7010 CrossRef CAS; (d) G. A. DiLabio and K. U. Ingold, J. Am. Chem. Soc., 2005, 127, 6693–6699 CrossRef CAS.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2010, 3, 19–27.
- G. Xue, R. De Hont, E. Münck and L. Que, Jr., Nat. Chem., 2010, 2, 400–405 CrossRef CAS.
- cf. D. Balcells, C. Raynaud, R. H. Crabtree and O. Eisenstein, Inorg. Chem., 2008, 47, 10090–10099 Search PubMed.
- (a) Oxidation in Organic Chemistry, ed. K. B. Wiberg, Academic Press, New York, 1965; Part A Search PubMed; (b) R. Stewart, Oxidation Mechanisms, Benjamin, New York, 1964 Search PubMed; (c) J. M. Mayer, Acc. Chem. Res., 1998, 31, 441–450 CrossRef CAS; (d) J. M. Mayer, Annu. Rev. Phys. Chem., 2004, 55, 363–390 CrossRef CAS.
- K. A. Prokop, S. P. de Visser and D. P. Goldberg, Angew. Chem., Int. Ed., 2010, 49, 5091–5095 CAS.
- (a) cf. C. Rüchardt, M. Gerst and J. Ebenhoch, Angew. Chem., Int. Ed. Engl., 1997, 36, 1406–1430 Search PubMed; (b) P. J. Wagner, Y. Zhang and A. E. Puchalski, J. Phys. Chem., 1993, 97, 13368–13374 CrossRef CAS; (c) C. Biondi, R. Galeazzi, G. Littarru and L. Greci, Free Radical Res., 2002, 36, 399–404 CrossRef CAS.
- (a) Correlations of HAT reactivity with driving force have been found in a number of systems, see, for instance, ref. 6,14c,d; (b) A. Gunay and K. H. Theopold, Chem. Rev., 2010, 110, 1060–1081 CrossRef CAS; (c) S. P. de Visser, J. Am. Chem. Soc., 2010, 132, 1087–1097 CrossRef CAS.
- (a) cf., ref. 17b; (b) N. A. Eckert, S. Vaddadi, S. Stoian, R. J. Lachicotte, T. R. Cundari and P. L. Holland, Angew. Chem., Int. Ed., 2009, 48, 3622–3626 CrossRef CAS; (c) J. England, M. Martinho, E. R. Farquhar, J. R. Frisch, E. L. Bominaar, E. Munck and L. QueJr., Angew. Chem., Int. Ed., 2009, 48, 3622–3626 CrossRef CAS; (d) B. Karamzadeh, D. Kumar, G. N. Sastry and S. P. de Visser, J. Phys. Chem. A, 2010, 114, 13234–13243 CrossRef CAS; (e) R. Breslow, X. J. Zhang and Y. Huang, J. Am. Chem. Soc., 1997, 119, 4535–4536 CrossRef CAS; (f) M. S. Chen and M. C. White, Science, 2007, 318, 783–787 CrossRef CAS; (g) S. Das, G. W. Brudvig and R. H. Crabtree, J. Am. Chem. Soc., 2008, 130, 1628–1637 CrossRef CAS , and references therein.
- (a) Some aspects of these reactions have been discussed in other contexts: J. P. Roth, J. C. Yoder, T.-J. Won and J. M. Mayer, Science, 2001, 294, 2524–2526 Search PubMed; (b) E. A. Mader, V. W. Manner, T. F. Markle, A. Wu, J. A. Franz and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 4335–4345 CrossRef CAS; (c) E. A. Mader and J. M. Mayer, Inorg. Chem., 2010, 49, 3685–3687 CrossRef CAS . This report defines reaction (4) in the opposite direction (from CoIIIIIIHbim + TEMPOH) so the thermochemical values are of opposite sign.
- V. W. Manner, T. F. Markle, J. H. Freudenthal, J. P. Roth and J. M. Mayer, Chem. Commun., 2008, 256–258 RSC.
- The spin-states of CoIIIIH22bim and CoIIIIIIHbim have been experimentally determined; see ref. 27.
- J. P. Roth, S. Lovell and J. M. Mayer, J. Am. Chem. Soc., 2000, 122, 5486–5498 CrossRef CAS.
- E. A. Mader, A. S. Larsen and J. M. Mayer, J. Am. Chem. Soc., 2004, 126, 8066–8067 CrossRef CAS.
- E. A. Mader, E. R. Davidson and J. M. Mayer, J. Am. Chem. Soc., 2007, 129, 5153–5166 CrossRef CAS.
- (a) A. Wu and J. M. Mayer, J. Am. Chem. Soc., 2008, 130, 14745–14754 CrossRef CAS; (b) A. Wu, J. Maslan, R. D. Swartz, W. Kaminsky and J. M. Mayer, Inorg. Chem., 2007, 46, 11190–11201 CrossRef CAS.
- (a) J. J. Warren and J. M. Mayer, J. Am. Chem. Soc., 2008, 130, 2774–2776 CrossRef CAS; (b) V. W. Manner, A. G. DiPasquale and J. M. Mayer, J. Am. Chem. Soc., 2008, 130, 7210–7211 CrossRef CAS; (c) S. Miyazaki, T. Kojima, J. M. Mayer and S. Fukuzumi, J. Am. Chem. Soc., 2009, 131, 11615–11624 CrossRef CAS.
- J. C. Yoder, J. P. Roth, E. M. Gussenhoven, A. S. Larson and J. M. Mayer, J. Am. Chem. Soc., 2003, 125, 2629–2640 CrossRef CAS.
- T. J. Meyer and H. Taube, in Electron Transfer Reactions, in Comprehensive Coordination Chemistry, ed. G. Wilkinson, Pergamon, New York, 1987, vol. 1, ch. 7.2 Search PubMed.
- S. Wherland, Coord. Chem. Rev., 1993, 123, 169–199 CrossRef CAS.
- J. C. Wang and J. E. Bauman, Jr, Inorg. Chem., 1965, 4, 1613 CrossRef CAS.
- J. P. Roth, Intrinsic and Thermodynamic Influences on Hydrogen Atom Transfer Reactions Involving Transition Metal Complexes, PhD Thesis, University of Washington, Seattle, WA, 2000, pp. 128–129 Search PubMed.
- N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910 CrossRef CAS.
- BDFE = 23.1E1/2 + 1.37pKa + CG and CG = 54.9 kcal mol−1 in MeCN for potentials referenced to Cp2Fe+/0.19b,34,35.
- M. Tilset, in Electron Transfer in Chemistry, ed. V. Balzani, Wiley-VCH, Weinheim, Germany, 2001, vol. 2, pp.677–713 Search PubMed.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS.
- Specfit™/32, versions v3.0.26 and v3.0.36, Spectrum Software Associates, Marlborough, MA, 2000 Search PubMed.
- (a) The overall reaction has ΔG6° = −0.52 ± 0.11 kcal mol−1. The BDFEs of the two O–H bonds in H22Q are 78 ± 1 and 62 ± 1 kcal mol−1,37b roughly evenly spaced around the BDFE of CoIIIIH22bim (69.5 ± 0.9 kcal mol−1).19b; (b) BDFEs from ref. 35. Alternatively, starting from the gas phase data in: R. M. Borges dos Santos and J. A. Martinho Simoes, J. Phys. Chem. Ref. Data, 1998, 27, 707–739 Search PubMed and converting to MeCN using the method described in ref. 19b gives BDFE(H22Q) = 79 ± 2 kcal mol−1, and therefore BDFE(HQ˙) = 61 ± 3 kcal mol−1, using the average BDFE of both H-atoms in H22Q35; (c) the likely HQ˙ intermediate can react with CoIIIIH22bim to make CoIIIIIIHbim + H22Q; it can react with CoIIIIIIHbim either by HAT to make CoIIIIH22bim + BQ or by PT to make CoIIIIIIH22bim + Q˙−; and it can disproportionate to BQ + H22Q. It is not evident that any of these processes is much slower than the others, making the kinetic treatment complex. It is therefore not surprising that the optical data cannot be well fit to a simple rate law, especially with competing decomposition.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- See e.g. M. Swart, J. Chem. Theory Comput., 2008, 4, 2057–2066 Search PubMed.
- O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729–4737 CrossRef CAS.
- J. N. Harvey, Struct. Bonding, 2004, 112, 151–183 CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. M. Schmiedekamp, M. D. Ryan and R. J. Deeth, Inorg. Chem., 2002, 41, 5733–5743 CrossRef CAS.
- Calculations are performed from the separated reactants to the separated products. It is unlikely that the hydrogen-bonding affects the change in spin state (calculations performed to confirm did not properly converge).
- Test calculations at the B3LYP** level in the presence of continuum solvent were able to locate the pre- and post-reactive complexes 22CoIIIIH22bim|2TEMPO and 11CoIIIIIIHbim|1TEMPOH on the singlet potential energy surface (in the former case, using an unrestricted ansatz). These complexes lie as expected slightly lower in energy than the corresponding separated species, and were used as the starting and ending points in the search for a transition state.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939 CrossRef CAS.
- The iron reactions closely follow the cross relation (with f ≅ 1)19 which implies that rate constants vary with Keq1/2. The 2 kcal mol−1 difference in ΔG° then corresponds to a factor of 5.3 difference in HAT rate constants.
- See ref. 6 and 10a; the vanadium-oxo/hydroxo system presented in ref. 6 is another exception to this generalization.
- (a) ΔGPT5° >32 kcal mol−1 from pKa(tBu3ArOH+˙) = −335 and pKa(CoIIIIH22bim) >20.3 (see above); (b) ΔGET5° = 3.9 ± 0.7 kcal mol−1 from E1/2(CoIIIIIIH22bim) = −0.53 ± 0.02 V and E1/2(tBu3ArO˙/−) = −0.70 V. See ref. 35.
- (a) The Marcus cross relation, kAB = (kAAkBBKABf)½, is applied using ΔGET5° = 3.9 ± 0.7 kcal mol−1, ≤10−6 M−1 s−1 for the CoIIIIH22bim + CoIIIIIIH22bim self-exchange rate constant,27 and <109 M−1 s−1 for the tBu3ArO˙ + tBu3ArO− self exchange (this is the value measured for phenoxyl + 4-methylphenoxide and related electron transfers in water, and is close to the diffusion limit in MeCN); (b) P. Neta and J. Grodowski, J. Phys. Chem. Ref. Data, 2005, 34, 109–199 CrossRef CAS; (c) J. Lind, X. Shen, T. E. Eriksen and G. Merenyi, J. Am. Chem. Soc., 1990, 112, 479–482 CrossRef CAS.
- (a) Some comparisons of measured vs. calculated rate constants using the Marcus Cross Relation: M. Chou, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1977, 99, 5615–5623 Search PubMed; (b) J. Gribble and S. Wherland, Inorg. Chem., 1989, 28, 2859–2863 CrossRef CAS.
- (a) Marcus Theory has also been applied to electron transfer with cobalt complexes in terms of volumes of activation: H. Doine and T. W. Swaddle, Inorg. Chem., 1991, 30, 1858–1862 Search PubMed; (b) M. R. Grace, H. Takagi and T. W. Swaddle, Inorg. Chem., 1994, 33, 1915–1920 CrossRef CAS; (c) R. D. Shalders and T. W. Swaddle, Inorg. Chem., 1995, 34, 4815–4820 CrossRef CAS; (d) ref. 29, and references therein.
- If initial spin-change to the low-spin 22CoIIIIH22bim is uphill by ΔG°4,2Co, then ET from 22CoIIIIH22bim to tBu3ArO˙ is more favorable than ET from by 44CoIIIIH22bim by exactly that amount (by Hess' law). Following Marcus theory, roughly half of that increased driving force should appear in a lower barrier. Thus, all other things being equal, the spin-change-then-ET pathway should be less favorable than direct ET from 44CoIIIIH22bim, by ΔG°4,2Co − ½ΔG°4,2Co = ½ΔG°4,2Co. This could potentially be balanced by a smaller intrinsic barrier for 22CoIIIIH22bim/11CoIIIIIIH22bim, but this is difficult to estimate. 44CoIIIIH22bim has two electrons in the eg antibonding orbitals while 22CoIIIIH22bim has one (t2g6 eg1, low-spin d7) and should be Jahn-Teller distorted. See ref. 68.
- (a) ΔGET° > 36 kcal mol−1 is estimated from E1/2(para-methoxyphenol) = 1.03 ± 0.02 V54c and taking as an upper limit for E1/2(CoIIIIIIHbim) the E1/2 of the protonated CoIIIIIIH22bim, −0.53 V; (b) ΔGPT° = +13 ± 1 kcal mol−1 is determined from pKa(H2Q) = 30 ± 0.354d and the pKa(CoIIIIIIH22bim) given above; (c) T. Osako, K. Ohkubo, M. Taki, Y. Tachi, S. Fukuzumi and S. Itoh, J. Am. Chem. Soc., 2003, 125, 11027–11033 CrossRef CAS; (d) The pKa of H2Q is 19.76 in DMSO,54e which was converted to a value in MeCN following ref. 54f; (e) F. G. Bordwell and J.-P. Cheng, J. Am. Chem. Soc., 1991, 113, 1736–1743 CrossRef CAS; (f) I. M. Kolthoff and M. K. Chantooni, Jr, J. Phys. Chem., 1976, 80, 1306–1310 CrossRef CAS.
- B. K. Carpenter, Determination of Organic Reaction Mechanisms, John Wiley & Sons, Inc., New York, 1984, pp. 97–100 Search PubMed.
- A mechanism of rapid pre-equilibrium ET followed by a rate-limiting PT step is quite unlikely given the slow ET reactions of the cobalt complexes and the quite exoergic PT step that would be involved (ΔG5ET° = 3.9 ± 0.7 kcal mol−1 and the overall ΔG5° of = −7.5 kcal mol−1 imply ΔG5PT° for the second step of an ET/PT path of −11.4 kcal mol−1.
- (a) Ref. 28, 29, 51 and 52 ; (b) M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437 CrossRef CAS; (c) M. D. Newton, J. Phys. Chem., 1991, 95, 30–38 CrossRef CAS; (d) ref. 52c ; (e) J. F. Endicott, B. Durham, M. D. Glick, T. J. Anderson, J. M. Kuszaj, W. G. Schmonsees and K. P. Balakrishnan, J. Am. Chem. Soc., 1981, 103, 1431–1440 CrossRef CAS; (f) E. Buhks, M. Bixon, J. Jortner and G. Navon, Inorg. Chem., 1979, 18, 2014 CrossRef CAS; (g) J. F. Endicott, K. Kumar, T. Ramasami and F. P. Rotzinger, Prog. Inorg. Chem., 1983, 30, 141–187 CAS.
- C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2004, 126, 16834–16840 CrossRef CAS.
- J. N. Harvey and M. Aschi, Phys. Chem. Chem. Phys., 1999, 1, 5555–5563 RSC.
- M. Y. M. Pau, J. D. Lipscomb and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18355–18362 CrossRef CAS.
- A. F. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons, Inc., New York, 6th edn, 1999, pp. 816–824 Search PubMed.
- (a) F. A. Cotton and M. D. Meyers, J. Am. Chem. Soc., 1960, 82, 5023–5026 CrossRef CAS; (b) F. A. Cotton and M. D. Meyers, J. Am. Chem. Soc., 1960, 82, 5027–5030 CrossRef.
- P. Comba, M. Kerscher, G. A. Lawrance, B. Martin, H. Wadepohl and S. Wunderlich, Angew. Chem., Int. Ed., 2008, 47, 4740–4743 CrossRef CAS.
- See e.g. P. Gutlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 Search PubMed.
- M. Besora, J.-L. Carreón-Macedo, A. J. Cowan, M. W. George, J. N. Harvey, P. Portius, K. L. Ronayne, X.-Z. Sun and M. Towrie, J. Am. Chem. Soc., 2009, 131, 3583–3592 CrossRef CAS.
- M. Besora, J.-L. Carreón-Macedo, Á. Cimas and J. N. Harvey, Adv. Inorg. Chem., 2009, 61, 573–623 CrossRef CAS.
- J. K. Beattie, R. A. Binstead, M. T. Kelso, P. Favero, T. G. Dewey and D. H. Turner, Inorg. Chim. Acta, 1995, 235, 245–251 CrossRef CAS.
- (a) I. Krivokapic, M. Zerara, M. L. Dakua, A. Vargas, C. Enachescu, C. Ambrusc, P. Tregenna-Piggott, N. Amstutz, E. Krausz and A. Hauser, Coord. Chem. Rev., 2007, 251, 364–378 CrossRef CAS; (b) J. K. Beattie, Adv. Inorg. Chem., 1988, 32, 1–49 CAS; (c) H. A. Goodwin, Top. Curr. Chem., 2004, 234, 23–47 CAS; (d) ref. 67 .
- This estimate is obtained by adding the increment of 1.3 kcal mol−1 to the spin splitting of 1.4 kcal mol−1, the FeII(H2bip)32+ + TEMPO reaction barrier of 14 kcal mol−1, and an estimated vibrational term of 1.5 kcal mol−1.
- S. Larsson, K. Stahl and M. C. Zerner, Inorg. Chem., 1986, 25, 3033–3037 CrossRef CAS.
- (a) J. I. Seeman, J. Chem. Educ., 1986, 63, 42–48 CrossRef CAS; (b) J. I. Seeman, Chem. Rev., 1983, 83, 83–134 CrossRef CAS , eq. 25.
- D. M. Duggan and D. N. Hendrickson, Inorg. Chem., 1975, 14, 955–970 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford, CT, 2004 Search PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. N. Harvey, A. Aschi, H. Schwarz and K. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Raw data and discussion of rate constants and complications with initial rate data for BQ, Marcus cross relation analysis, estimation of the energy of the 2Eg state for Co(H22bim), detailed experimental methods, and computational details (Cartesian coordinates and energies). See DOI: 10.1039/c1sc00387a |
| ‡ Current address: Explosives Applications and Special Projects, Los Alamos National Laboratory, MS C920, Los Alamos, NM, 87545, USA; vwmanner@lanl.gov. |
| § Current address: Chemical Sciences and Engineering Division, Argonne National Laboratory, 9700 South Cass Ave, CSE/200, Argonne, IL, 60439-4837, USA; mader@anl.gov. |
| This journal is © The Royal Society of Chemistry 2012 |
