Shape resonance in the H + D₂O → D + HOD reaction: a full-dimensional quantum dynamics study

Abstract

We present exact coupled-channel (CC) results of full-dimensional quantum mechanical calculations for the H + D₂O → D + HOD exchange reaction which provide the first evidence for a shape resonance in this reaction, employing the initial state-selected time-dependent wave packet method with both OD bonds in the D₂O reactant treated as reactive bonds. Due to the shallow C_3v minimum along the reaction path, the signature of shape resonance is manifested as the existence of a distinct step-like feature in the CC integral cross sections of the exchange reaction just above the threshold. Our study also shows that the current CC integral cross sections are in very good agreement with the experimental results, and a bit larger than those calculated in the previous quantum dynamics study, where the one reactive bond and centrifugal sudden (CS) approximations were invoked, revealing that the one reactive bond approximation overestimated, while the CS approximation underestimated the integral cross sections.

---

Reactive scattering resonance has been a central topic in the study of chemical reaction dynamics during the past few decades.^1–7 In a typical chemical reaction, the transition state is an energy maximum along the reaction coordinate, and so it does not persist as a discrete structure. However, in certain cases, a reaction complex in the transition-state region could be transiently trapped in vibrationally adiabatic wells along the reaction coordinate. Such a transiently trapped quantum state along the reaction coordinate is normally called a Feshbach resonance, or dynamical resonance.^4–8 Significant efforts have been devoted to investigating the structures and dynamics of Feshbach resonances in chemical reactions, and the F + H₂ reaction has proven to be a truly benchmark system for dynamical resonances. Since the first theoretical prediction of reaction resonances in the F + H₂ reaction in the early 1970s,^9–11 the search for evidence of such resonances in this reaction has attracted much attention from many top research groups in this field.^12–20 Recently, the F + H₂(HD) reaction was studied extensively in an effort to understand the dynamical resonances in this important system,^8,21–23 using the high-resolution crossed molecular beams technique in combination with full quantum scattering calculation based on accurate potential energy surfaces. The advances made in these studies have provided a clear physical picture of dynamical resonances in this benchmark system that has eluded us for decades.

It is precisely the couplings between the reaction coordinate and various degrees of freedom of the system that are perpendicular to the reaction coordinate that are responsible for dynamical (Feshbach) resonances. However, there is another type of reactive scattering resonance, for which the interactions of the various collective modes of the molecule are not taken into account. Merely depending on the depth and width of the well along the reaction path, several quasi-bound quantized states may be transiently trapped in this well. Such quasi-bound quantized states along the reaction coordinate caused by the shape of the interaction potential without couplings between reaction coordinates and other degrees of freedom are normally called shape resonances.^5,24 To the best of our knowledge, shape resonances have been rarely investigated in any chemical reaction dynamics, though small contributions from a shape resonance mechanism in a narrow collision energy range were discovered to produce the forward scattering HF (v′ = 3) channel from the F + H₂ reaction.²³ In this study, we will provide the first evidence for a shape resonance in the tetra-atomic H + D₂O → D + HOD reaction from full-dimensional quantum mechanical calculations.

In the past twenty years, there has been significant progress in quantum mechanical studies of four-atom chemical reactions.^25–46 Starting from reduced dimensionality approaches,^47,48 the development of the wave packet method combined with the tremendous rises in computational power has stimulated theoretical advances in studies of four-atom reactions. Recently, the full-dimensional quantum differential cross sections for the HD + OH → H₂O + D reaction were reported, which is a breakthrough for the quantum scattering methodologies for four-atom reactions, confirming that the problems of most of the four-atom reactions can be finally solved.⁴⁶ H + H₂O and its isotopically substituted reactions have become the prototype for tetra-atomic reactions, in much the same way that the H + H₂ reaction served as the prototype for triatomics. Most of the studies of the OH₃ system were done on the basis that the one of OH bonds in the H₂O reactant is basically a spectator bond that will not be cleaved or highly excited during the reaction. Consequently, one could use a very limited vibrational basis function for the bond, or sometimes just simply freeze it in some approximate studies in order to simplify the calculations.

It has been found in previous studies that one OH bond in the H₂O reactant can be treated very well as a spectator bond for the H + H₂O → H₂ + OH abstraction reaction^40,43,44 and the reverse reaction;^25,30,45,46 however, both OH bonds should be treated as reactive bonds in order to accurately investigate the H′ + H₂O → H′OH + H exchange reaction,⁴⁰ due to the saddle point close to a C_3v geometry. The integral cross section of the H + D₂O → D + HOD reaction was first reported ten years ago,³⁷ in which the reaction probabilities were calculated with one OD bond in the D₂O reactant treated as a spectator bond (only five vibrational bases were used for this OD bond which restricted the bond from being cleaved), and under the centrifugal sudden (CS) approximation for total angular momenta J > 0. It was later presented that the CS approximation was inadequate for the H + H₂O reaction by calculating the reaction probabilities for J = 15 with 2 K-blocks.⁴¹ Thus, the accuracy of the integral cross section presented in ref. 37 is still waiting to be assessed despite the good agreement between theory and experiment there.

In this work, we present the full-dimensional quantum dynamics study of the H + D₂O → D + HOD reaction without any dynamical approximations, with both OD bonds in the D₂O reactant treated as reactive bonds, and without employing the CS approximation. We employed the YZCL2 potential energy surface (PES)⁴⁹ in our calculations, which is a very accurate PES for this system, constructed by the Shepard interpolation method based on high level ab initio calculations.⁵⁰ The same methodology of the initial state-selected wave packet (ISSWP) approach to atom–triatom reactions in full dimension, as has been described before in detail,^28,41 was used in this study. This is the first quantum study from which one can obtain the exact coupled-channel (CC) results for the integral cross sections of the exchange process of the H + H₂O and isotopically substituted reactions. The shape resonance, known as resonance related to the shape of the interaction potential,^5,23,24 appears as a clear step-like feature in the exact CC cross sections of the H + D₂O → D + HOD reaction. There is a shallow C_3v well along the reaction path near the saddle point of the reaction, which is responsible for the presence of the shape resonance structure.

The numerical parameters used for the title reaction are as follows: the interaction region was defined by a rectangular box of [1.0,5.0]a₀ in the r₁ coordinate, [1.0,5.0]a₀ in the r₂ coordinate, and [1.0,5.0]a₀ for the R coordinate. The number of vibrational basis functions used was 32 each for the r₁ and r₂ coordinates. For the R coordinate, we used 30 sine discrete variable representation (DVR) points. The asymptotic region was defined from 5.0 to 12.0a₀ with 52 sine DVR points for the R coordinate and 8 vibrational basis functions for both the r₁ and r₂ coordinates. We used j^max₁ = j^max₂ = 28. Under the CS approximation, we only needed to include the K = 0 rotational basis functions in our calculations, resulting in about 8500 coupled rotational basis functions and a total of about 290 million basis functions. We used up to 8 K blocks to compute accurate reaction probabilities for J up to 30 to get well-converged CC integral cross sections for the reaction. Roughly 119 000 coupled rotational basis functions and a total of 4 billion basis functions were included in the calculation. For lower J, we propagate the wave packets for 10000 a.u. of time to converge the reaction probability in the low energy regime, especially near the resonance peak. Readers can refer to ref. 41 for a more complete description of the basis. Due to the huge number of basis functions included in the calculation, the computation was extremely time and memory consuming.

The total reaction probability for the H + D₂O → D + HOD reaction as a function of the collision energy (E_c) for J = 0, with the D₂O reactant initially in the ground rovibrational state, is presented by the solid curve in Fig. 1. Also shown in the figure by the dashed curve is the same reaction probability obtained by using five vibrational basis functions (VBF) for one OD bond (denoted as OD_b) as done in ref. 37 on the YZCL1 PES,⁴⁹ which restricted the OD_b bond from being cleaved during the collision. First of all, one can see two very different curves in the figure, which clearly shows that the way the OD_b bond is treated is important in studying the exchange process. Furthermore, the total reaction probability obtained with two reactive bonds for the title reaction in full dimension is rather smooth, with one prominent resonance peak just above the threshold, two around E_c = 1.2 eV and 1.4 eV, and some other small resonances here and there. These resonance structures are believed to be associated with the shallow C_3v minimum on the reaction path (about 0.1 eV lower than the saddle point), which have also been found in the H′ + H₂O → HOH′ + H reaction.^40,41

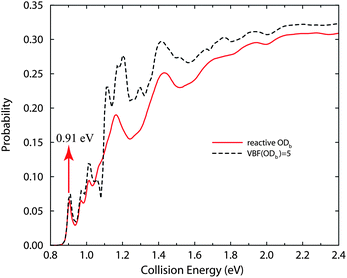Fig. 1 Total reaction probabilities for J = 0 for the H + D₂O → D + HOD reaction as a function of collision energy. The resonance peak at the collision energy of 0.91 eV is shown by the arrow.

The three-dimensional scattering wave function for J = 0 calculated with two reactive bonds, at the collision energy of 0.91 eV for the H + D₂O → D + HOD reaction, is shown in Fig. 2. We plot the wave function as a function of R and r₁ coordinates that were defined in ref. 41, and summed over the remaining degrees of freedom (r₂, θ₁, θ₂, φ). Note that the wave function shown here was calculated after 4500 a.u. of propagation time, when only the resonance wave function was distinctly seen around the shallow C_3v well, but the most part of the wave function had been absorbed. The wave function shows a predominant peak at about R = 2.0 bohr and r₁ = 1.95 bohr, suggesting the resonance state at E_c = 0.91 eV is the ground shape resonance state trapped in the C_3v well along the reaction coordinate.

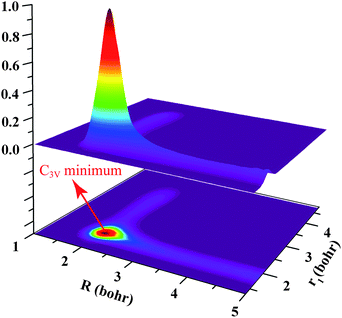Fig. 2 The three dimensional scattering wave function for J = 0 at the collision energy of 0.91 eV, for the H + D₂O → D + HOD reaction, together with a contour map of the upper wave function. The C_3v minimum along the reaction path is also shown by the arrow.

When the OD_b bond is nonreactive, but not frozen vibrationally (VBF(OD_b) = 5), the total exchange probability obtained obviously differs from the exact result, as shown in Fig. 1. The resonance structures are richer and stronger than the exact results, although the positions for these resonance peaks are more or less the same. Overall, the exchange probability calculated using VBF(OD_b) = 5 is considerably larger than the exact result, especially in the medium energy regime. Thus, the one reactive bond approximation used in the calculation of ref. 37 (VBF(OD_b) = 5) has overestimated the total exchange cross section for the H + D₂O → D + HOD reaction by some extent.

Moreover, we also investigated here how the second approximation, the CS approximation, affects the total cross section. To obtain the converged integral cross sections for the title reaction, we calculated the reaction probabilities for a number of total angular momenta J. The energy dependence of the total reaction probabilities for different J for the H + D₂O → D + HOD reaction with the CS approximation and for the exact CC results are presented in Fig. 3(a) and 3(b), respectively. We show here a few J results from the calculated probabilities. With the CS approximation, shown in Fig. 3(a), the J > 0 curves resemble the J = 0 curve, while the probabilities shift toward the high energy regime with increasing J because of the increasingly high centrifugal barriers. The resonance peaks on the J = 0 curve are preserved on the J ≤ 10 curves, though the amplitudes of the resonance peaks become smaller gradually with increasing J. However, for the CC results shown in Fig. 3(b), the overall behaviors of the reaction probabilities for J > 0 are quite different from that of the probability of J = 0. The resonance peaks on the probability curves diminish quickly with the increase of J and disappear from the J = 10 curve. As J increases further, the reaction probabilities behave similarly and increase monotonically with the increase of collision energy, seen from the probabilities for J varying from 10 to 20. The CC reaction probabilities are obviously different from the corresponding CS ones. They show fewer oscillations and slower energy shifts with increasing J than the CS probabilities. Further comparison between the CC and CS reaction probabilities manifests that the CC reaction probabilities are larger than the CS ones in most of the energy regime.

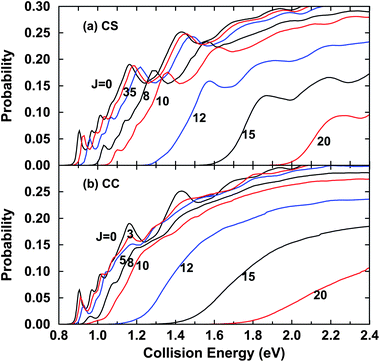Fig. 3 (a) Total reaction probabilities for various J with CS approximation for the H + D₂O → D + HOD reaction as a function of collision energy; (b) same as (a) except for the exact CC results.

The CS and CC integral cross sections calculated for the H + D₂O → D + HOD reaction are shown in Fig. 4(a), up to the collision energy of 2.4 eV. The cross sections, shown in Fig. 4(b), are those in the low energy regime. For the cross sections with the CS approximation, we calculated the reaction probabilities for a total of 25 total angular momenta J from J = 0 to 30 because of the slow diminishing of the resonance peaks. For the CC cross sections, we used up to 8 K blocks for a total of 16 J from J = 0 to 30. Tests show that the total reaction probabilities for J > 0 converge very well with the number of K blocks used, up to the collision energy of 2.4 eV. The cross sections both behave rather smooth and increase steadily as the collision energy increases, as shown in Fig. 4(a). Obviously, the cross sections calculated with the CS approximation underestimate the exact CC results in the entire energy region of [0.9, 2.4] eV. The CC cross sections are roughly 20% larger than the CS ones in most of the energy regime. It is interesting to find from Fig. 4(b) that the CC cross sections show a step-like feature just above the threshold, which predicts the signature of shape resonance in the exchange reaction. This step-like feature is also seen in other isotopically substituted exchange reactions of the OH₃ system, which will be discussed in our following papers.⁵¹ As the resonance peak persists in many partial waves in the CS calculations, the resonance structure can no longer survive the partial-wave summation and is washed out completely in the CS cross section. Depending on the similar step-like feature seen by experiment and quantum dynamics in the excitation function of the F + HD → HF + D reaction, conclusive evidence was presented for the existence of a reactive resonance for the F + HD → HF + D reaction.¹⁷ Hence, some experimental work is also expected to be carried out for the exchange reactions of the OH₃ system, which will further provide the evidence for the resonances in these reactions.

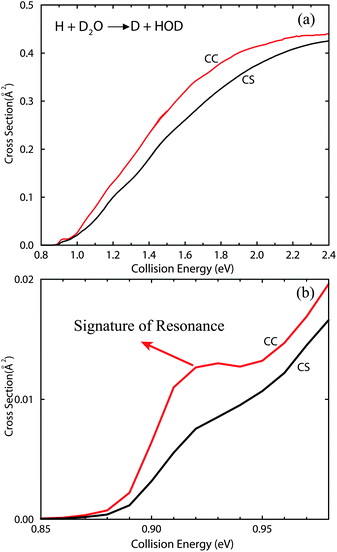Fig. 4 (a) CC and CS integral cross sections for the H + D₂O → D + HOD reaction as a function of collision energy; (b) same as (a) except in the low energy region. A clear step-like feature is shown in the CC cross sections, manifesting the signature of shape resonance in the reaction.

When we plot the current CC cross sections for the title reaction in Fig. 5, together with the theoretical cross sections shown in ref. 37, and the experimental results,^52,53 we are excited to find that the CC cross sections are in very good agreement with the experimental results, and a bit larger than the previous theoretical results calculated under the one reactive bond and CS approximations. It should also be mentioned that two different PESs were employed in the two studies, YZCL2 PES in the current study and YZCL1 PES in the previous study.³⁷ We did not see many differences for the total cross section of the exchange reaction produced from the two PESs. Therefore, the results obtained in this study are quite conclusive that one reactive bond approximation overestimated the cross sections, while the CS approximation underestimated the cross sections. But including these two approximations simultaneously in one study did not introduce substantial errors to the integral cross sections.

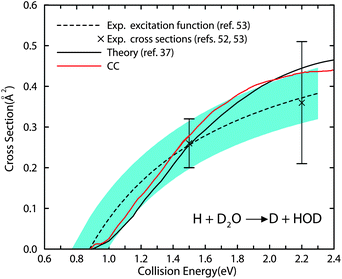Fig. 5 The current CC cross sections, together with the theoretical cross sections reported in ref. 37 invoking two approximations, and the experimental results^52,53 for the H + D₂O → D + HOD reaction. The crosses represent absolute cross sections experimentally at the collision energies of 1.5 and 2.2 eV. The dashed line is the experimental excitation function. The blue shaded area reflects the statistical uncertainty of the global least squares fit procedure used to determine the optimum excitation function (see ref. 53 for details).

In summary, we have carried out a full-dimensional quantum dynamics study for the H + D₂O → D + HOD reaction using the ISSWP approach on the YZCL2 PES, with both OD bonds in the D₂O reactant treated as reactive bonds. This is the first work from which one can obtain CC results with two reactive bonds for four-atom reactions. We calculated the total reaction probabilities up to J = 30 and 8 K-blocks to obtain the converged CC integral cross sections for this reaction up to the collision energy of 2.4 eV. Due to the C_3v minimum along the reaction path, a clear step-like feature is demonstrated in the CC cross sections just above the threshold, presenting the existence of shape resonance in the reaction. The CC cross sections show very good agreement with the experimental results, and are a bit larger than the previous theoretical results, which confirms that the one reactive bond approximation and CS approximation together used in the previous study coincidentally did not lead to substantial errors in the integral cross sections. Our accurate quantum mechanical results can serve as a useful predictive guide in the experimental search for shape resonances in the reaction, and it is expected that the present paper will stimulate such investigations.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 20833007 and 90921014), the Chinese Academy of Sciences, and the Ministry of Science and Technology of China.

Notes and references

1. R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics and Chemical Reactivity, Oxford University Press, New York, 1987.
2. Y. T. Lee, Science, 1987, 236, 793–798.
3. G. C. Schatz, Science, 2000, 288, 1599–1600.
4. K. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139–164.
5. F. Fernández-Alonso and R. N. Zare, Annu. Rev. Phys. Chem., 2002, 53, 67–99.
6. X. Yang, Annu. Rev. Phys. Chem., 2007, 58, 433–459.
7. X. Yang and D. H. Zhang, Acc. Chem. Res., 2008, 41, 981–989.
8. M. Qiu, Z. Ren, L. Che, D. Dai, S. A. Harich, X. Wang, X. Yang, C. Xu, D. Xie, M. Gustafsson, R. T. Skodje, Z. Sun and D. H. Zhang, Science, 2006, 311, 1440–1443.
9. G. C. Schatz, J. M. Bowman and A. Kuppermann, J. Chem. Phys., 1973, 58, 4023–4025.
10. G. C. Schatz, J. M. Bowman and A. Kuppermann, J. Chem. Phys., 1975, 63, 674–684.
11. S.-F. Wu and B. R. Johnson, Mol. Phys., 1973, 25, 839–856.
12. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden and Y. T. Lee, Phys. Rev. Lett., 1984, 53, 226–229.
13. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden and Y. T. Lee, J. Chem. Phys., 1985, 82, 3045–3066.
14. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden, K. Shobatake, R. K. Sparks, T. P. Schafer and Y. T. Lee, J. Chem. Phys., 1985, 82, 3067–3077.
15. J. F. Castillo, D. E. Manolopoulos, K. Stark and H.-J. Werner, J. Chem. Phys., 1996, 104, 6531–6546.
16. F. J. Aoiz, L. Banares, V. J. Herrero, V. S. Rabanos, K. Stark and H.-J. Werner, Chem. Phys. Lett., 1994, 223, 215–226.
17. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, Phys. Rev. Lett., 2000, 85, 1206–1209.
18. S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2002, 116, 7839–7848.
19. F. Dong, S.-H. Lee and K. Liu, J. Chem. Phys., 2000, 113, 3633–3640.
20. T. Takayanagi, Chem. Phys. Lett., 2006, 433, 15–18.
21. Z. Ren, L. Che, M. Qiu, X. Wang, D. Dai, S. A. Harich, X. Wang, X. Yang, C. Xu, D. Xie, Z. Sun and D. H. Zhang, J. Chem. Phys., 2006, 125, 151102-1–4.
22. Z. Ren, L. Che, M. Qiu, X. Wang, W. Dong, D. Dai, X. Wang, X. Yang, Z. Sun, B. Fu, S.-Y. Lee, X. Xu and D. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12662–12666.
23. X. Wang, W. Dong, M. Qiu, Z. Ren, L. Che, D. Dai, X. Wang, X. Yang, Z. Sun, B. Fu, S.-Y. Lee, X. Xu and D. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6227–6231.
24. M. S. Child, Molecular Collision Theory, Academic Press, London and New York, 1974.
25. D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 101, 1146–1156.
26. D. Neuhauser, J. Chem. Phys., 1994, 100, 9272–9275.
27. U. Manthe, T. Seideman and W. H. Miller, J. Chem. Phys., 1993, 99, 10078–10081.
28. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 4544–4553.
29. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 105, 1291–1294.
30. W. Zhu, J. Dai, J. Z. H. Zhang and D. H. Zhang, J. Chem. Phys., 1996, 105, 4881–4884.
31. J. Dai, W. Zhu and J. Z. H. Zhang, J. Phys. Chem., 1996, 100, 13901–13903.
32. S. K. Pogrebnya, J. Echave and D. C. Clary, J. Chem. Phys., 1997, 107, 8975–8984.
33. D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691–697.
34. F. Matzkies and U. Manthe, J. Chem. Phys., 1998, 108, 4828–4836.
35. D. H. Zhang, J. C. Light and S.-Y. Lee, J. Chem. Phys., 1998, 109, 79–86.
36. D. H. Zhang and S.-Y. Lee, J. Chem. Phys., 1999, 110, 4435–4444.
37. D. H. Zhang, M. A. Collins and S.-Y. Lee, Science, 2000, 290, 961–963.
38. D. H. Zhang, M. Yang and S.-Y. Lee, J. Chem. Phys., 2001, 114, 8733–8736.
39. D. H. Zhang, M. Yang and S.-Y. Lee, J. Chem. Phys., 2002, 116, 2388–2394.
40. D. H. Zhang, M. Yang and S.-Y. Lee, Phys. Rev. Lett., 2002, 89, 103201-1–4.
41. D. H. Zhang, M. Yang and S.-Y. Lee, J. Chem. Phys., 2002, 117, 10067–10072.
42. E. M. Goldfield and S. K. Gray, J. Chem. Phys., 2002, 117, 1604–1613.
43. D. H. Zhang, D. Xie, M. Yang and S.-Y. Lee, Phys. Rev. Lett., 2002, 89, 283203-1–4.
44. D. H. Zhang, J. Chem. Phys., 2006, 125, 133102-1–4.
45. M. T. Cvitaš and S. C. Althorpe, J. Chem. Phys., 2011, 134, 024309-1–21.
46. C. Xiao, X. Xu, S. Liu, T. Wang, W. Dong, T. Yang, Z. Sun, D. Dai, X. Xu, D. H. Zhang and X. Yang, Science, 2011, 333, 440–442.
47. D. C. Clary, J. Phys. Chem., 1994, 98, 10678–10688.
48. J. M. Bowman and G. C. Schatz, Annu. Rev. Phys. Chem., 1995, 46, 169–196.
49. M. Yang, D. H. Zhang, M. A. Collins and S.-Y. Lee, J. Chem. Phys., 2001, 115, 174–178.
50. M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324.
51. B. Fu and D. H. Zhang, in preparation.
52. R. A. Brownsword, M. Hillenkamp, T. Laurent, R. K. Vatsa, H.-R. Volpp and J. Wolfrum, Chem. Phys. Lett., 1996, 259, 375–380.
53. R. A. Brownsword, M. Hillenkamp, T. Laurent, H.-R. Volpp, J. Wolfrum, R. K. Vatsa and H.-S. Yoo, J. Phys. Chem. A, 1997, 101, 6448–6454.

---

Footnote

† Present address: Department of Chemistry, Emory University, Atlanta, GA 30322, USA.

---