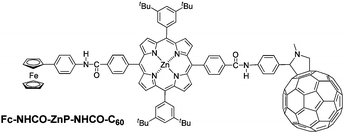
Long-lived long-distance photochemically induced spin-polarized charge separation in β,β′-pyrrolic fused ferrocene-porphyrin-fullerene systems

Abstract

The exceptionally long lived charge separation previously observed in a β,β′-pyrrolic-fused ferrocene-porphyrin-fullerene triad (lifetime 630 μs) and related porphyrin-fullerene dyad (lifetime 260 μs) is attributed to the production of triplet charge-separated states. Such molecular excited-state spin polarization maintained over distances of up to 23 Å is unprecedented and offers many technological applications. Electronic absorption and emission spectra, femtosecond and nanosecond time-resolved transient absorption spectra, and cyclic voltammograms of two triads and four dyads are measured and analyzed to yield rate constants, donor–acceptor couplings, free-energy changes, and reorganization energies for charge-separation and charge-recombination processes. Production of long-lived intramolecular triplet states is confirmed by electron-paramagnetic resonance spectra at 77–223 K, as is retention of spin polarization in π-conjugated ferrocenium ions. The observed rate constants were either first predicted (singlet manifold) or later confirmed (triplet manifold) by a priori semiclassical kinetics calculations for all conceivable photochemical processes, parameterized using density-functional theory and complete-active-space self-consistent-field calculations. Identified are both a ps-timescale process attributed to singlet recombination and a μs-timescale process attributed to triplet recombination.

---

1. Introduction

Mimicry of the natural photosynthetic reaction centre has been a very active research area in recent years as it has potential applications in solar-energy conversion devices and in radiation detectors. Indeed, elucidation of the mechanism of photoinduced electron transfer in photosynthetic reaction centres has led to the development of numerous model systems.^1–14 These artificial reaction centres often emulate the multi-step electron-transfer sequences via intermediate charge-separated states of the natural system, processes that occur with unit quantum yield, with some^9,10 even designed to mimic the spin polarization which is sometimes observed in natural photosystems.^15,16

Porphyrins are commonly employed in artificial reaction centre mimics as they are structurally similar to natural chlorophyllide chromophores. In particular, they contain an extensive conjugated π-system that is suitable for efficient electron transfer,^1–14 and can indeed be used for production of the functional units in an artificial device. Indeed, combinations of porphyrins and other moieties containing stronger electron donating and/or accepting groups provide simple, iconic systems that are readily suited to basic research. Both fullerene acceptor groups and ferrocene donor groups are commonly combined with porphyrins for this purpose, e.g., the ferrocene-(zinc porphyrin)-fullerene triad Fc-NHCO-ZnP-NHCO-C₆₀.^17,18 Fullerenes are remarkable electron acceptors due to their large, symmetrical shape and delocalized π-electron system,^4,17–24 undergoing up to six electrochemical oxidations and reductions, while ferrocene is a stable electron donor used as a reference for electrochemical measurements owing to its simplicity and regularity.^25–27

The electron-transfer process in porphyrin-fullerene dyad systems has been fully investigated in terms of its solvent polarity dependence,¹⁸ its donor–acceptor distance dependence,^28,29 and the role of the spacer.³⁰ These properties also effect the function of related triad systems including ferrocene-porphyrin-fullerenes,^17,18 carotenoid-porphyrin-fullerenes,³¹ and porphyrin-porphyrin-fullerenes.^18,32,33 In general, the primary advantage of triads over dyads is that they increase the separation of the charges and hence slow down the rate of charge recombination. This is an advantageous feature as, if embedded in a more complex practical device, it would allow longer time for some desired process to utilize the captured light energy.

Recently, we showed that the ferrocene-(zinc porphyrin)-fullerene triad Fc-ZnP-C₆₀L, shown in Chart 1, has the longest reported charge-separation lifetime at room temperature for any donor–bridge–acceptor triad (630 μs);³⁴ this molecule is an extension of a previously reported dyad ZnP-C₆₀ that at the time had the longest-reported charge-separation lifetime for a dyad (260 μs).³⁵ These results are astonishing as, in both molecules, the ferrocene and/or fullerene units are connected to the porphyrin macrocycle by imidazole linkers through the β,β′-pyrrolic positions: these linkers establish π conjugation from the ferrocene to the porphyrin and then from the porphyrin to the phenyl group that attaches the fullerene so that significant donor–acceptor interactions are anticipated, interactions that typically lead to very rapid charge recombination. Instead, the observed lifetimes are very long, much longer than say that for the similar but non-conjugated amide-linked triad Fc-NHCO-ZnP-NHCO-C₆₀ reported earlier^17,18 for which the observed lifetime is just 8 μs. Here, the mechanism is determined by which this extraordinary charge separation is established.

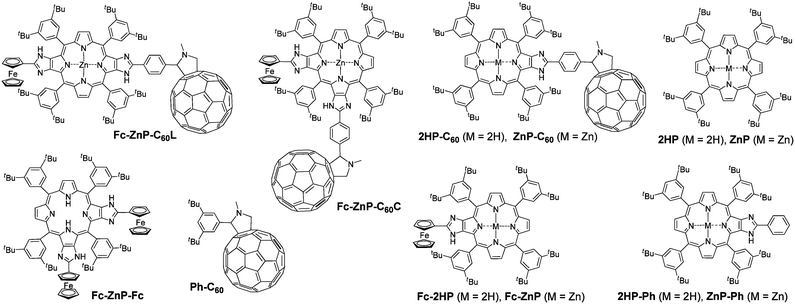Chart 1 Structures of Fc-ZnP-C₆₀L, Fc-ZnP-C₆₀C, 2HP-C₆₀, ZnP-C₆₀, Fc-2HP, Fc-ZnP, 2HP, ZnP, 2HP-Ph, ZnP-Ph, Fc-ZnP-Fc, and Ph-C₆₀

For the ZnP-C₆₀ dyad, the experimental evidence³⁵ leading to the identification of the long lived CS is: (i) fluorescence is quenched after 60 ps, indicating the rate of primary charge separation, (ii) nanosecond absorption spectroscopy verifies that the reaction product is ZnP˙⁺-C₆₀˙⁻ whilst determining the charge-recombination lifetime, and (iii) nanosecond time-resolved absorption spectroscopy on the free-base analogue 2HP-C₆₀, for which the energy of the triplet porphyrin state is lower than that of the charge-separated state, shows only long-lived porphyrin triplet ³2HP^*-C₆₀. Identification of the mechanism through which the long-lived charge separation is maintained, however, requires a comprehensive model of all charge-separation and energy-transfer processes. Detailed time-resolved dynamics of the energy-transfer processes and primary charge-separation processes for the triad Fc-ZnP-C₆₀L has been previously obtained and used to qualitatively indicate the nature of the primary and secondary charge-separation processes,³⁴ but many details of the observed complex spectral history could not be interpreted as the relevant details of processes in simpler molecules were not available. Hence, here we provide a detailed systematic investigation of Fc-ZnP-C₆₀L, ZnP-C₆₀ and 2HP-C₆₀ as well as the other relevant dyads, Fc-ZnP and Fc-2HP. In addition, as delocalization effects involving the porphyrin are implicated in the mechanism, a new molecule Fc-ZnP-C₆₀C featuring an alternate π-conjugation pathway is also synthesized and investigated. Reference compounds synthesized to aid in the analysis include Ph-C₆₀, 2HP, ZnP, 2HP-Ph and ZnP-Ph.

A wide variety of experimental and computational techniques are applied to identify the critical stages of the photochemistry of Fc-ZnP, Fc-2HP, ZnP-C₆₀, 2HP-C₆₀, Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C including: electronic absorption and emission spectroscopy, femtosecond and nanosecond time-resolved transient absorption spectroscopy analyzed through fitting component spectra to the entire data set, nuclear magnetic resonance (NMR) spectroscopy,³⁶ cyclic voltammetry, low-temperature electron-paramagnetic resonance (EPR) studies, fully a priori calculations of charge-separation and charge-recombination rates using density-functional theory (DFT), and a priori calculations of dimerization energies,³⁷ singlet–triplet splitting, and spin–orbit couplings using second-order Mϕller-Plesset perturbation theory (MP2) and complete-active-space self-consistent-field (CASCF) theory. The critical chemical processes are identified and rate constants determined. From these, donor–acceptor coupling matrix elements V and charge-transfer solvent reorganization energies λ_o are deduced using semi-classical rate theory parameterized by all-mode DFT-calculated electron-vibration couplings; these couplings and reorganization energies are found to be in excellent agreement with the a priori calculated values, indicating the key chemical processes are correctly identified.

2. Results and discussion

2.1 Synthesis

Synthesis of the corner ferrocene-(zinc porphyrin)-fullerene triad Fc-ZnP-C₆₀C (Scheme 1) began with the attachment of ferrocene to the porphyrin macrocycle by the imidazole-forming condensation between corner zinc nitroporphyrin-dione³⁸1 and ferrocenecarboxaldehyde following the method developed by Crossley et al.^34,43 The resulting ferrocene-nitroporphyrin 2 was converted into ferrocene-(zinc porphyrin)-dione 3 by the reduction of the nitro group into an amino group utilizing tin(II) chloride dihydrate followed by the photo-oxidation in the presence of rose bengal, and finally a zinc metallation. The resultant dione 3 undergoes another imidazole-forming reaction with terephthaldicarboxaldehyde to give 4 and finally the incorporation of fullerene was achieved by the cycloaddition of the azomethine ylide with sarcosine and C₆₀.^45,46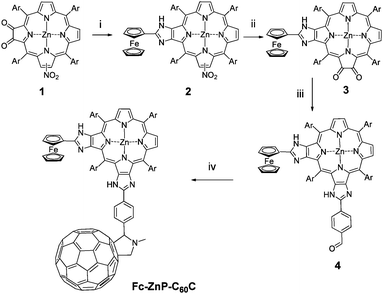

Scheme 1 Synthesis of Fc-ZnP-C₆₀C. Reagents and conditions: i) Ferrocenecarboxaldehyde, NH₄OAc, CHCl₃/AcOH (5 : 1), reflux (76%); ii) 1. SnCl₂·2H₂O, HCl/Et₂O, stir; 2. Rose bengal, CH₂Cl₂, photo-oxidation; 3. HCl(aq)/CH₂Cl₂; Zn(OAc)₂·2H₂O, CH₂Cl₂/MeOH (10 : 1), stir (17%); iii) NH₄OAc, CHCl₃/AcOH (5 : 1),terephthaldicarboxaldehyde, reflux (34%); iv) sarcosine, fullerene, toluene, reflux (78%). Ar = 3,5-di-tert-butylphenyl.

An attempt to form 3 by reacting ferrocenecarboxaldehyde with corner zinc(II) porphyrin-tetraone⁴⁴ (1.2 equiv.) in the presence of ammonium acetate in a refluxing mixture of chloroform and acetic acid gave 2 : 1 adduct Fc-ZnP-Fc (Chart 1). This is in contrast to the corresponding reaction of the linear zinc porphyrin-tetraone (1.2 equiv.) with ferrocenecarboxaldehyde which gave the 1 : 1 adduct linear ferrocene-(zinc porphyrin-dione) in good yield.³⁴ Thus there is a cooperativity in the second ferrocenecarboxaldehyde condensation in the corner case probably as the result of the interleaving 5-aryl group being held more orthogonal to the porphyrin plane after the first condensation thereby opening up access to the second dione unit.

2.2 Steady-state spectroscopy

The observed absorption spectra of the primary dyads and triads and their model compounds are shown in Fig. 1. The spectra of the dyads Fc-2HP, Fc-ZnP2HP-C₆₀, ZnP-C₆₀ are quite similar to those of their respective porphyrin model chromophores 2HP, 2HP-Ph, ZnP, and ZnP-Ph. Broadening of both Soret (450–400 nm) and Q (620–500 nm) band systems is observed, along with 2–3 nm shifts of Q band components. These changes are large enough to indicate that significant intramolecular interactions occur owing to the conjugated linkage between the chromophores, but small enough to indicate that the primary qualitative identity of the chromophores is preserved.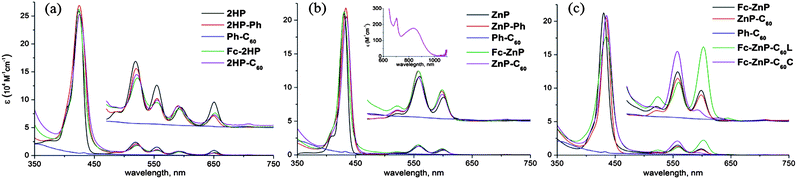

Fig. 1 UV-visible absorption spectra of (a) 2HP, 2HP-Ph, Ph-C₆₀, Fc-2HP and 2HP-C₆₀; (b) ZnP, ZnP-Ph, Ph-C₆₀, Fc-ZnP and ZnP-C₆₀ (inset: CT absorption band measured in PhMe), and (c) Fc-ZnP, ZnP-C₆₀, Ph-C₆₀, Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C in PhCN.

Similarly, comparing the spectra of the dyads Fc-ZnP and ZnP-C₆₀ to those for the triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C indicates that significant perturbations in the Q-band region are observed, owing to the fusing of the second imidazole rings onto the porphyrin macrocycle. However, the qualitative natures of the spectra do not change and so the excited states of the dyads are assumed to be preserved in the triads. Indeed, the intense Soret-band maximum occurs near 440 nm in each molecule while the lowest-energy Q band, the state that dominates luminescence and primary charge separation, is always located near 600 nm. Also shown in Fig. 1 is the absorption spectrum of the functionalized fullerene Ph-C₆₀, showing that it has some weak absorption near 400 nm and hence accounts for ca. 5% of the light absorption of ZnP-C₆₀ at this excitation energy.

The emission spectra observed following excitation at 430 nm in benzonitrile are shown in Fig. 2. Emission from 2HP-Ph, 2HP-C₆₀, Fc-ZnP, ZnP-C₆₀, Fc-ZnP-C₆₀L, or Fc-ZnP-C₆₀C is strongly quenched compared to that from the control compounds 2HP-Ph and ZnP-Ph. This indicates that a new electronic process occurs amongst the excited state of the dyads that is subsequently identified as primary charge separation (CS) forming Fc˙⁺-2HP˙⁻, 2HP˙⁺-C₆₀˙⁻, etc. While in principle these observed fluorescence intensities could be used to estimate fluorescence lifetimes, in practice the fluorescence intensities do not scale linearly with concentration (see ESI Figure S25†) and at best only order-of-magnitude estimates are possible. Weak emission for the fullerene excited singlet state at ca. 710 nm in cyclohexane can also be identified from the concentration dependence of the emission (see ESI Figure S24†), emission that is also quenched in the triad molecules. The fullerene emission peaks at 476 nm and 496 nm in benzonitrile are also quenched (see ESI Figure S28†). These indicate that primary charge separation via hole transfer from the fullerene does occur, but in subsequent time-resolved spectral studies, this photochemical channel is too weak to detect, however.

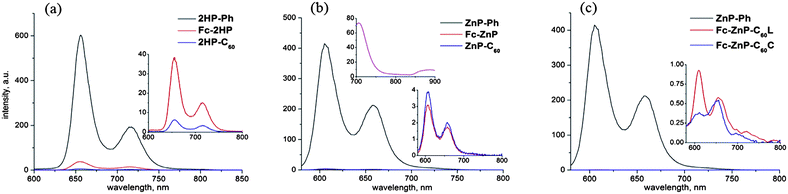Fig. 2 Emission spectra of (a) 2HP-Ph, Fc-2HP and 2HP-C₆₀; and (b) ZnP-Ph, Fc-ZnP and ZnP-C₆₀ and (c) ZnP-Ph, Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C in PhCN following excitation at 430 nm, along with the charge-transfer emission of ZnP-C₆₀ (middle frame, top inset) centred at 890 nm observed in 2.0 × 10⁻⁵ M solution in deaerated toluene following excitation at 560 nm.

The direct intramolecular charge-transfer (CT) absorption and emission bands of ZnP-C₆₀ were observed in deaerated toluene and the results are also shown in Fig. 1 and 2. The absorption is broad and centred at 840 nm, similar to other reports.^46–48 It has a maximum extinction coefficient of 176 M⁻¹cm⁻¹ and a transition moment of 0.043 eÅ. Its absorbance increases linearly with concentration in the range of 10⁻⁵ to 10⁻⁴ M (see ESI Figure S23†) indicating that it is intramolecular in origin. In emission, this band is Stokes-shifted to a centre at 890 nm.

2.3 Electrochemistry

Cyclic voltammetry was carried out in 0.1 M n-Bu₄NPF₆ solution in benzonitrile, the redox potentials of Fc-ZnP-C₆₀L, Fc-ZnP-C₆₀C and the model compounds are summarized in Table 1 while the cyclic voltammograms for the triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C are shown in Fig. 3 and the remainder in ESI Figures S1–S9.† As expected, ferrocene is found to be easier to oxidize than the porphyrin, and the fullerene is also found to be easier to reduce than the porphyrin. The P/P˙⁻ reduction becomes easier by ca. 30 mV when a phenyl group is attached to the imidazole (comparing ZnP with ZnP-Ph and 2HP with 2HP-Ph), indicating that the extension in the conjugation has a significant effect on the unoccupied orbitals. This reduction becomes more difficult by ca. 28 mV on formation of the dyads ZnP-C₆₀ and 2HP-C₆₀ from ZnP-Ph and 2HP-Ph combined with Ph-C₆₀, however, owing to the Coulomb interaction with the nearby fullerene anion. There is also evidence of similar effects of the ferrocene-porphyrin extended conjugation on the P/P˙⁺ couple, with the oxidation of ZnP and 2HP becoming harder by ca. 45 mV following the formation of the dyads Fc-ZnP and Fc-2HP, about twice the change expected based on interaction with the nearby ferrocene cation alone. The porphyrin oxidation becomes ca. 30 mV easier on addition of the second fused imidazole to form the triads Fc-ZnP-C₆₀C and Fc-ZnP-C₆₀L, but Fc-ZnP-C₆₀L becomes easier to reduce by 10 mV whilst Fc-ZnP-C₆₀C becomes harder to reduce by 110 mV.

Table 1 Standard potentials (versus Fc⁺/Fc, in mV)^a of dyads Fc-ZnP, Fc-2HP, ZnP-C₆₀, 2HP-C₆₀, and triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C, and their model compounds ZnP, ZnP-Ph, 2HP, 2HP-Ph and Ph-C₆₀ in deaerated PhCN

	E°/mV in PhCN
	Fc^+/Fc	P˙^+/P	P/P˙^−	C60/C60˙^−	C60˙^−/C60^2^−	C60^2^−/C60^3−
a The standard potentials were determined as E° = 1/2(E°pa + E°pc) by cyclic voltammetry in deaerated PhCN using n-Bu4NPF6 (0.1 M) as supporting electrolyte.
Fc-ZnP-C60L	107	322	−1832	−1045	−1460	−2026
Fc-ZnP-C60C	111	316	−1951	−1044	−1463	−2018
ZnP	—	306	−1849	—	—	—
ZnP-Ph	—	304	−1814	—	—	—
Fc-ZnP	114	349	−1841	—	—	—
ZnP-C60	—	301	−1841	−1034	−1450	−2016
2HP	—	506	−1671	—	—	—
2HP-Ph	—	507	−1639	—	—	—
Fc-2HP	109	550	−1666	—	—	—

---

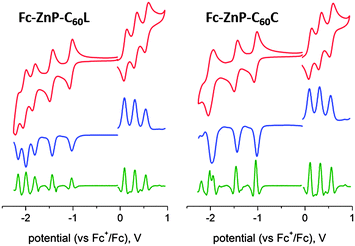Fig. 3 Cyclic voltammograms (top), differential pulse voltammograms (cen.) and their second derivative (bottom) of 1 mM Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C in deaerated PhCN containing 0.1 M n-Bu₄NPF₆ at 298 K.

From the observed redox potentials given in Table 1 it is possible to estimate the free energy changes associated with the various charge separation and charge recombination processes of the triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C as well as the dyads Fc-ZnP, Fc-2HP, ZnP-C₆₀ and 2HP-C₆₀, and the results along with names for the various charge-separation (CS) and charge-recombination (CR) processes in both singlet and triplet excited-state manifolds are given in ESI Table S1.† Only minor differences are found between the energies of reaction of the two triad isomers, but overall the charge recombination free energies vary from −1.12 eV to −2.06 eV and hence the energetic contribution to the observed rate constants is expected to be very profound, making this electrochemical analysis critical to the elucidation of the photochemical mechanisms.

2.4 Transient absorption spectroscopy

Two-dimensional representations of the observed femtosecond-timescale transient absorption spectra for the dyads Fc-ZnP, Fc-2HP, ZnP-C₆₀, and 2HP-C₆₀, as well as that for the triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C, are shown in ESI Figures S12–S17.† These spectra are fitted therein to yield the spectral components and rate constants shown in the upper frames of Fig. 4 for the processes depicted in Scheme 2; the chemical identity of each component is determined based on its observed spectrum and the deduced reaction times (inverse rate constants) are collected in Table 2. These reactions identify only the starting and finishing species and do not include possible intermediates whose concentrations remain too small to detect. Note that different detectors are used above and below 800 nm and the signal to noise ratio becomes poor in the 900–800 nm and 800–750 nm regions. Fig. 4 also contains results (lower frames) for nanosecond-resolved transient absorption spectra and spectral decay profiles at some characteristic wavelengths.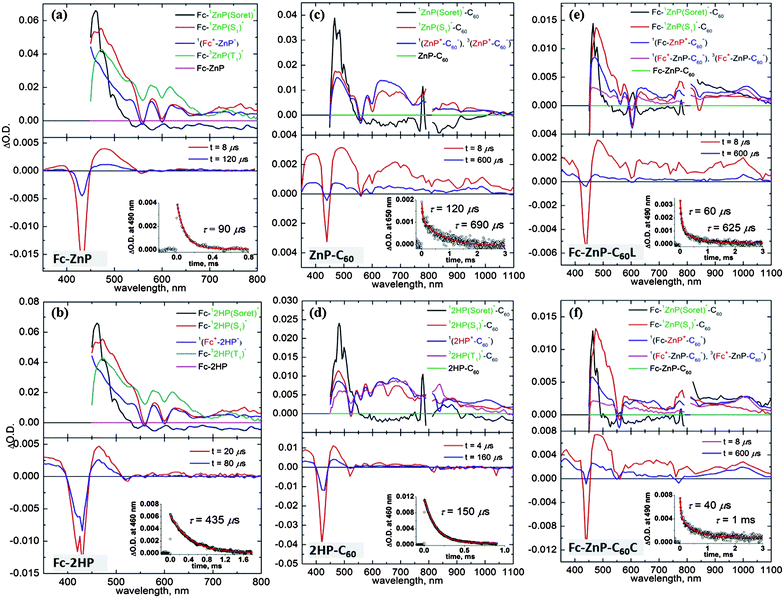

Fig. 4 Transient absorption spectra of (a) Fc-ZnP, (b) Fc-2HP, (c) ZnP-C₆₀, (d) 2HP-C₆₀, (e) Fc-ZnP-C₆₀L, and (f) Fc-ZnP-C₆₀C, following excitation at 430 nm in PhCN at 298 K: (top) component spectra and rise-times fitted to full 2-D femtosecond-timescale data set; (bottom) spectra at various times after nanosecond laser-pulse irradiation, with (inset) time-decay profile of optical density at 490 nm.

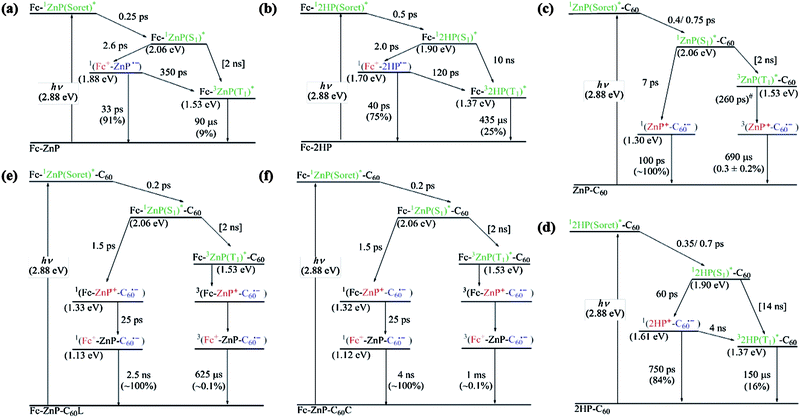Scheme 2 Reaction scheme overviews and energy diagrams of (a) Fc-ZnP, (b) Fc-2HP, (c) ZnP-C₆₀, (d) 2HP-C₆₀, (e) Fc-ZnP-C₆₀L, and (f) Fc-ZnP-C₆₀C in PhCN. #: estimated from electronic coupling and reorganization energy fitted to the other observed rates using eqn (S7) in ESI.†

Table 2 Process lifetimes (inverse rate constants) and yields extracted from the femtosecond and nanosecond transient absorption spectra, Fig. 4

Molecule	^1P(Soret) (ps)^a	^1IC (ps)^b	^1CS primary (ps)^c	^1CS secondary (ps)^c	^1CR final (ps)	^1P → ^3P (ps)^d	^1CS → ^3P (ps)	Triplet yield (%)	^3CR final (μs)	^3P(T1)^* lifetime^g (μs)
a The instrument-limited rise time of the initial excited state. b Internal conversion from the excited Soret states of the porphyrin ^1P(Soret)^* to the lowest-energy Q-state of the porphyrin ^1P(S1)^*. c The available charge separation process options are defined in ESI Table S1,† CS1a and/or CS1b, etc., may in principle be observed. d Calculations indicate that ^1P(S1)^* to ^3P(T1)^* ISC occurs via the ^3P(T2)^* intermediate; The values in parentheses are estimated based on observed lifetimes for the model compounds: ZnP 2500 ps, ZnP-Ph 2000 ps, and 2HP 14000 ps. e ISC time-constant from the fluorescence lifetime of related molecule ZnP-Ph under similar conditions of 0.5 M PhI is 1000 ps, near the diffusion-controlled limit. f Calculations indicate that conversion of the singlet primary charge-separated species to the triplet secondary charge-separated species occurs via the first excited state of the secondary charge-separated species. g Triplet lifetime.
Fc-ZnP	0.06	0.25	2.6	—	33	[2000]	350	9		90
Fc-2HP	0.10	0.5	3.0	—	40	[1000]	120	25		430
ZnP-C60	0.16	0.4, 0.75	7	—	100	2000		0.3 ± 0.2	690
ZnP-C60/PhI	0.12	0.2, 0.45	6	—	150	200^e		3 ± 2
2HP-C60	0.15	0.35, 0.7	60	—	750	[1400]	4000	16		150
Fc-ZnP-C60L	0.18	0.20	CS1a 1.5	CS2a 25	2500	[2000]		∼0.1	630
Fc-ZnP-C60C	0.18	0.20	CS1a 1.5	CS2a 25	4000	[2000]		∼0.1	1000

---

The femtosecond transient absorption spectra are taken following excitation of the porphyrin Soret band at 430 nm, and show instrument-limited rise times of the initial ¹P(Soret)^* excited state of τ = 60–180 fs. This is the first identified component spectrum for all molecules, characterized by a sharp transition from negative to positive differential absorption near 450 nm that decreases to near zero above 500 nm. Internal conversion relaxes this state on the τ = 200–750 fs timescale to the lowest-energy singlet porphyrin Q band ¹P(S₁)^*; this process is sometimes resolved into two separate processes, possibly indicative of intermediate energy flow through the two porphyrin Soret-band states and the two porphyrin Q-band states. These components are characterized by a strong new absorption feature around 500 nm, weak absorption throughout the visible and near-infrared regions, and well resolved negative peaks at 560 nm and 600 nm indicating loss of the standard ground-state Q-band transitions.^{17,18,34,35,49,50} We find that for all molecules the third resolved distinct component is associated with primary charge separation CS₁; the fourth component depicts either primary charge recombination CR₁ or secondary charge separation CS₂, possibly followed by a fifth component depicting secondary charge recombination CR₂.

Specifically, for Fc-ZnP (Scheme 2a, Fig. 4a) subsequent to ¹P(S₁)^* formation a new spectral component appears with a rise time of τ = 2.6 ps and a spectrum matching that expected⁵¹ for ZnP˙⁻. As ferrocene and its cation absorb too weakly to be identified amidst the porphyrin anion spectrum,⁵² this observed spectral component is in fact that expected for the primary charge-separated species Fc˙⁺-ZnP˙⁻. It decays after 35 ps to a final product whose concentration is low (yield 9%) but its extracted, noisy, spectral component does match that observed in the nanosecond transient absorption spectrum of the molecule and is identified as the differential absorption of ³ZnP(T₁)^*.⁵³

Long-lived ³ZnP(T₁)^* products will originate to some extent through intersystem crossing (ISC) from ¹ZnP(S₁)^*. However, the observed lifetimes for this process in the model compounds ZnP and ZnP-Ph are 2500 ps and 2000 ps, respectively, and inclusion of this formation process only in the kinetics modelling results in yields of 0.1%, much less than the observed yield of 9%. To account for the observed yield, charge recombination to the triplet state is included in Scheme 2a, the fitted lifetime of this process being 350 ps. The physical features driving these reactions are discussed in the Section 2.7.

For Fc-2HP (Scheme 2b, Fig. 4b) the scenario is similar but the quantum yield for the production of the triplet porphyrin (³2HP(T₁)^*) increases to 25%. As the observed fluorescence lifetime of 2HP is 14 ns (see ESI Figure S11†), charge recombination to ³2HP(T₁)^* must occur much faster, 120 ps. Also, the observed lifetime of the triplet state is extended from 90 μs for Fc-³ZnP(T₁)^* to 430 μs for Fc-³2HP(T₁)^*.

For ZnP-C₆₀ and 2HP-C₆₀ (Scheme 2c and 2d, Fig. 4c and 4d, respectively), two stages of ¹P(Soret)^* to ¹P(S₁)^* relaxation are observed, followed by primary charge separation (on the 7–60 ps timescale) as revealed by the spectrum of the third distinct observed component. These spectra display strong positive absorption near 500 nm, broad absorption spanning 600–700 nm, and sharp negative features corresponding to the Q-bands of the unexcited porphyrin, and for ZnP-C₆₀ the spectrum in this region matches that³⁵ for electrochemically produced ZnP˙⁺. The observed spectrum of this component in the 950–1050 nm region also matches that expected for C₆₀˙⁻,^{17–19,31–33} unambiguously identifying the product state as ZnP˙⁺-C₆₀˙⁻. Primary charge recombination CR₁ with lifetimes of τ = 100 ps and 750 ps for ZnP-C₆₀ and 2HP-C₆₀, respectively, then occurs (Table 2) leaving behind species in low concentration, determined to be 0.3 ± 0.2% for ZnP-C₆₀ and 16% for 2HP-C₆₀. Again, the long-lived species have similar spectra to those observed by nanosecond transient absorption measurements: for 2HP-C₆₀, the long-lived species is identified as ³2HP(T₁)^*, whilst that for ZnP-C₆₀ is identified as ZnP˙⁺-C₆₀˙⁻. As the quantum yield for this final component is very low, the femtosecond spectra were fitted using the assumption that these spectra are in fact identical.

An extensive series of experiments (described in detail in ESI Section S3.4†) show that the long-lived species does not involve intermolecular interactions between ZnP-C₆₀ molecules. These experiments include transient absorption, NMR, absorption, and emission studies as a function of concentration and excitation power. In particular, the association constant for dimerization of 2HP-C₆₀ is deduced to be 30–300 M⁻¹, similar to that observed⁵⁴ for single porphyrin-fullerene interactions of 100 M⁻¹ while zinc porphyrin-fullerene interactions are weaker in general.⁵⁵ Hence, the only viable possibility is that the long-lived species is the triplet charge-separated state ³(ZnP˙⁺-C₆₀˙⁻) formed from initially prepared ³ZnP(T₁)^*; intermediary ³ZnP(T₁)^* is not directly observable as its lifetime would be short, this subsequently being estimated to be 260 ps based on the coupling and reorganization energy fitted to the observed singlet charge separation rates and the much reduced charge-separation driving force. As indicated in Scheme 2c, the observed low yield of ³(ZnP˙⁺-C₆₀˙⁻) matches that expected for ³ZnP(T₁)^* following ISC from ¹ZnP(T₁)^*. It is also conceivable that ³(ZnP˙⁺-C₆₀˙⁻) is produced by ISC from ¹(ZnP˙⁺-C₆₀˙⁻), but such a process is not feasible as the calculated energy splitting between these two states is much less than kT (see later in Table 4) and so the reverse reaction would proceed equally as quickly and so prevent ³(ZnP˙⁺-C₆₀˙⁻) accumulation. The calculated splitting is much larger than the hyperfine interactions in ZnP˙⁺ and C₆₀˙⁻, inhibiting spin depolarization.

The production of ³ZnP(T₁)^* by ISC is enhanced in the presence of iodobenzene (PhI), with the fluoresce lifetime for model compound ZnP-Ph observed to decrease from 2000 ps to 1000 ps on addition of PhI to 0.5 M concentration in benzonitrile. In ESI Figures S18 and S19,† results of femtosecond transient absorption studies of ZnP-C₆₀ in the presence of PhI are reported, and the results are summarized in Table 2. The yield for the long-lived species increases to 3 ± 2%, apparently considerably more than that expected based on a native yield of 0.3 ± 0.2% and a two-fold enhancement. Nevertheless, these experiments indicate the involvement of triplet states. Furthermore, nanosecond transient absorption spectra of ZnP-C₆₀ in the presence of PhI (not presented) indicate an initial yield of long-lived species of the order expected but the spectra show very poor signal to noise ratios, indicating that PhI also has a profound effect on the charge-recombination process.

Note that the precise nature of the triplet charge-recombination process is not determined experimentally as alternative mechanisms cannot be differentiated. Possibilities include direct recombination of ³(ZnP˙⁺-C₆₀˙⁻) to the ground state via intersystem crossing and spin depolarization leading to uncorrelated biradicals and hence ¹(ZnP˙⁺-C₆₀˙⁻). These and other possibilities are addressed later by a priori calculations.

The spectral components (Fig. 4e–f) and photochemical reactions (Schemes 2e–f) for Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C are similar to each other, with only one internal conversion process observed. The ¹ZnP(S₁)^* states may undergo electron transfer via process CS_1a to form Fc-ZnP˙⁺-C₆₀˙⁻, or hole transfer via process CS_1b to form Fc˙⁺-ZnP˙⁻-C₆₀. However, the observed third spectral components match those found after primary charge separation in the corresponding porphyrin-fullerene dyads, thus indicating that electron transfer dominates primary CS. This result is opposite to that expected based on the observed rates for the corresponding dyad molecules, with the rates of primary charge separation being 2.6 ps and 10 ps for Fc-ZnP and ZnP-C₆₀, respectively, and arises because the CS_1b process is energetically unfavourable in the triads (ΔG = 0.01 eV for Fc-ZnP-C₆₀L and −0.02 eV for Fc-ZnP-C₆₀C) and exothermic in the dyad (ΔG = −0.18 eV for Fc-ZnP), see ESI Table S1.†

Component 4 in Fig. 4e–f is formed from Fc-ZnP˙⁺-C₆₀˙⁻ within 25 ps and is a species in which the fullerene anion signal at 950–1050 nm is maintained while the porphyrin cation signal is significantly diminished. This indicates secondary charge separation CS_2a to produce the final charge-separated state Fc˙⁺-ZnP-C₆₀˙⁻. Decay of this component occurs after 2500–4000 ps to reveal final components with very low yields of ca. 0.1%. (Note that an alternate local-minima to the fits of the experimental data with lifetimes of 800 ps and long-lived yields of 2–5% are possible but the quality of the fits are not as high). The final component spectra are very similar to those observed in the nanosecond experiments and to that observed at earlier times attributed to Fc˙⁺-ZnP-C₆₀˙⁻; to facilitate extraction of the quantum yield, the spectral fitting is performed assuming that the spectra of the final components are indeed identical to those for Fc˙⁺-ZnP-C₆₀˙⁻. By analogy to the conclusions drawn for Fc-ZnP, the major component is identified as ¹(Fc˙⁺-ZnP-C₆₀˙⁻) while the long-lived species is identified as ³(Fc˙⁺-ZnP-C₆₀˙⁻). From the observed nanosecond transient spectra, the lifetimes of the ³(Fc˙⁺-ZnP-C₆₀˙⁻) species are determined to be 630–1000 μs, close to that found for the ZnP-C₆₀ dyad of 690 μs.

The observed spectra for the secondary charge-separated species are unexpected in that significant signal arising for the porphyrin cations is observed, not just the weak spectra of the ferrocenium cation and fullerene anion. The ratio of the intensities of the porphyrin-cation to fullerene-anion signals decrease by a factor of 3 on secondary charge separation, however, and this ratio even for the primary charge-separated species is itself much lower than that observed for ZnP-C₆₀. These results verify that significant delocalization between the ferrocene and porphyrin orbitals occurs under these experimental conditions, as predicted computationally³⁴ and evidenced spectroscopically (Sect. 2.2) and electrochemically (Sect. 2.3).

2.5 Electron Paramagnetic Resonance (EPR) studies

The ferrocenium cation has a notoriously weak EPR spectrum that is only observable at cryogenic temperatures,^56,57 an effect associated in part with fast spin relaxation. This spin relaxation occurs as this species has ²E symmetry and hence experiences significant spin–orbit interaction; a Jahn–Teller distortion is also active.⁵⁸ Hence it is essential to understand how conjugation of the porphyrin macrocycle to the ferrocene modulates this spin relaxation that would cause the equilibration of ¹(Fc˙⁺-ZnP-C₆₀˙⁻) and ³(Fc˙⁺-ZnP-C₆₀˙⁻) to provide a pathway for rapid charge recombination of triplet species. Two sets of experiments were performed to understand this effect.

First, EPR spectra were obtained for the anions of Fc-ZnP, ZnP and Fc obtained by chemical oxidation in benzonitrile using iodine followed by quenching the sample to form a glass at 150 K; the results are shown in ESI Figure S35.† As expected, no signal is observed for the ferrocenium cation under these conditions.^56,57 A large signal at g = 2.0027 is observed for ZnP˙⁺, however, and a very similar but much weaker spectrum is observed for Fc˙⁺-ZnP. The appearance of a porphyrin-cation signal in this dyad could arise from either delocalization of the radical from the ferrocene to the porphyrin, a process well known in other systems,^42,59 or else from chemical equilibrium between these two species. In either case, the results demonstrate that spin polarization in Fc˙⁺-ZnP is maintained on the EPR timescale, in stark contrast to the results found for Fc˙⁺. Only the charge delocalization mechanism explains this qualitative difference, however. The implied degree of delocalization is ca. 10%, much less than the values of 20–30% implied by the spectroscopic measurements, especially that deduced from the observed porphyrin spectral character in the transient-absorption spectra of Fc˙⁺-ZnP-C₆₀˙⁻. Such a reduction can be understood in terms of changing energy levels as a function of temperature.

In the second set of measurements, solutions of ZnP-C₆₀ and Fc-ZnP-C₆₀L were irradiated at 263 K inside an EPR cavity, rapidly quenched to 77–223 K, and their EPR spectra measured in the dark; the results obtained at 77 K are shown in Fig. 5. For ZnP-C₆₀, the spectra at ca. g = 2 reveal charge separated ZnP˙⁺ and C₆₀˙⁻ radical ions whilst that for Fc-ZnP-C₆₀L reveals only C₆₀˙⁻. Based on the observed spectra for Fc-ZnP˙⁺ at 150 K, some porphyrin-cation character would also be expected to be observed in the spectrum of Fc-ZnP-C₆₀L, but such a component is likely to be too weak to detect in this time-resolved experiment. Most significantly, both molecules show in addition a signal near g = 4, clearly indicating triplet-coupled spins.⁶⁰ The emission lifetimes of the triplet excited states of ³ZnP(T₁)^* (44 μs for ZnP)³³ and ³C₆₀(T₁)^* (25 μs for Ph-C₆₀)³³ are all far too short to permit these species to remain on the time scale of the experiment. Hence these experiments unambiguously verify the production of long-lived triplet charge-separated states.

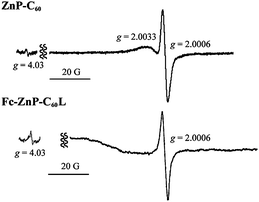Fig. 5 Electron-paramagnetic-resonance spectra of irradiated then cooled ZnP-C₆₀ and Fc-ZnP-C₆₀L in 3.0 × 10⁻⁴ M benzonitrile solutions in the dark at 77 K, revealing the presence of ZnP˙⁺ (at g = 2.0033) and C₆₀˙⁻ (at g = 2.0006) as well as triplet-coupled spins (at g = 4.03).

In ESI Figure S36† is shown the time-decay profile of the CS state of ZnP-C₆₀. EPR signal from illuminated and quenched ZnP-C₆₀ measured at 223 K in benzonitrile glass obtained using different concentrations of the CS state. These concentrations were generated by either varying the molecular concentration or by varying the photoirradiation time. All samples yielded single-exponential kinetics with the same lifetime of 360 s, indicating that long-lived charge recombination in PhCN glass is an intramolecular process. An Eyring plot of the charge-recombination rate constant as a function of temperature is shown in Figure S37† and indicates that the reaction probability is extremely low but occurs over a barrier of just 2.0 kcal mol⁻¹. Extrapolation of this data to 77 K gives an expected lifetime of 1400 h, but alternate decay mechanisms, including phosphorescence from the charge-separated state, are expected to become dominant on this time scale (Section 2.7). More significantly, extrapolation of this data to 300 K gives an expected lifetime of 100 s. This lifetime is much longer than the observed lifetime in solution of 690 μs, indicating that the relaxation processes operating in the glass are quite different to those in solution. Nevertheless, the observation of long-lived triplet-polarized intramolecular charge-separated states confirms critical aspects of the reaction mechanisms determined from the transient absorption spectroscopic data.

2.6 Extraction of solvent reorganization energies and electronic couplings from the observed lifetimes

From the observed free-energy differences listed in ESI Table S1† and the observed rate constants listed in Table 2 it is possible to estimate values of the coupling parameters V and solvent reorganization energies λ_o using the semiclassical rate law,⁶¹ (ESI Eq. S7†), and the results are given in Table 3. This rate law fully incorporates the effects of electron tunnelling, and the Franck–Condon factors depicting this are evaluated from DFT frequency calculations of the vibrational modes of the molecular fragments in their various states of ionization; the vibrational parameters so deduced are given in full in ESI Table S4.†

Table 3 Energies fitted to the rate constants obtained^a from the femtosecond and nanosecond transient absorption spectra are compared to calculated^b values: λ_o- solvent reorganization energy, ¹V and ³V - singlet and triplet manifold respective coupling strengths

Molecule	Process	Observed			Calculated
		λ o (eV)	^1 V (cm^−1)	^3 V (cm^−1)	λ o (eV)	^1 V (cm^−1)	^3 V (cm^−1)
a using the common assumption that the reorganization energies and coupling for charge-separation and charge-recombination are equal. b from TD-DFT calculations of transition moments on the singlet manifold, otherwise from CASSCF calculated spin–orbit couplings. c from the intensity of the charge-transfer absorption band (Fig. 1) this is 32 cm^−1. d using the observed CS2a lifetime and yield as an underestimate of the lifetime for CR1a. e assuming this process occurs via direct recombination to the GS, see Table 4 for other possibilities.
Fc-ZnP	CS1	0.81	940			300^a
	CR1	0.81	940		0.73	1600
	^1CS → ^3P*	[0.81]		25			1.4
Fc-2HP	CS1	0.73	500			470^a
	CR1	0.73	500		0.70	690
	^1CS → ^3P*	[0.73]		34			1.0
ZnP-C60	CS1	0.62	31			50
	CR1	0.62	31^c	0.012	0.51	50	0.052
2HP-C60	CS1	0.66	39			39
	CR1	0.66	39		0.53	11
	^1CS → ^3P*	[0.66]		7.5			0.3
Fc-ZnP-C60L	CS1a	<0.57^d	>66^d			36
	CR1a	<0.57^d	>66^d
	CS2a	0.94–1.06	[500–900]			200
	CR2	[0.7–1.0]	1.7–2.0	0.0033–0.0040	0.77	31	0.039^e
Fc-ZnP-C60C	CS1a	<0.55^d	>69^d			70
	CR1a	<0.55^d	>69^d
	CS2a	0.94–1.06	[500–930]			500
	CR2	[0.7–1.0]	1.3–1.6	0.0027–0.0032	0.78	43	0.030^e

---

Deduction of the coupling and solvent reorganization energy for the dyads is usually made assuming that the reorganization energy and coupling for charge separation are the same as those for charge recombination, making use of the independently observed rates for these processes. While the reorganization energies are indeed likely to be very similar, the coupling of the local excited state and the ground state to the charge-separated state could differ markedly. We assume too that the reorganization energies for processes on the triplet manifold are the same as those for the singlet manifold. This allows a spin–orbit charge-recombination coupling ³V to be calculated on the assumption that charge recombination proceeds via ISC directly to the ground state.

The deduced solvent reorganization energies λ_o for the porphyrin-fullerene dyads from Table 3 are 0.62 to 0.66 eV, slightly less than those for the ferrocene-porphyrin dyads, 0.73 to 0.81 eV. The singlet-state couplings ¹V between the porphyrin and the fullerene of 31–39 cm⁻¹ are very much less than those between the ferrocene and the porphyrin of 500–940 cm⁻¹, however, owing to the break in conjugation between the fullerene and its connecting phenyl ring. The extremely fast charge-separation and charge-recombination processes observed for the ferrocene-porphyrin dyads originate from these very large ferrocene-porphyrin couplings and are anticipated from previous computational studies of model compounds.³⁴

Similar analyses for the triad molecules are restricted as rate constants for the paired processes (CS_1a and CR_1a, CS_2a and its hypothetical reverse, and CR₂ and its associated single-step charge separation) are not all observed. However, it is clear that CR_1a > CS_2a and hence bounds for the reorganization energy of < 0.57 eV and coupling of > 66 cm⁻¹ may be deduced for the primary charge separation process. Low values of the reorganization energy have been previously predicted³⁴ based on partial delocalization of the charge between the ferrocene and porphyrin units, but the deduced increase in the coupling of over a factor of two compared to the porphyrin-fullerene dyads appears anomalous. For CR₂, the known free-energy changes and intramolecular reorganization energies suggest that the rate is near the top of the Marcus parabola and is hence insensitive to the value of λ_o. This reorganization energy must be less than the value observed^17,18 for Fc-NHCO-ZnP-NHCO-C₆₀ and also must be related to the values observed herein for the four dyads. Hence we anticipate 0.7 eV < λ_i < 1.0 eV; using this range, the values deduced for the charge-recombination coupling are 1.3–2.0 cm⁻¹ for recombination on the singlet manifold and 0.0027–0.0040 cm⁻¹ for direct triplet to ground-state recombination.

Charge recombination to form local-porphyrin triplet states is observed for Fc-ZnP, Fc-2HP, and 2HP-C₆₀ and the effective coupling driving this process can be extracted assuming that its reorganization energy is the same as that for primary charge separation from the related local-porphyrin singlet state. This yields coupling of 25 cm⁻¹, 34 cm⁻¹, and 7.5 cm⁻¹, respectively, quite large values for spin–orbit interactions; the likely origin of such large couplings are discussed in the next subsection.

2.7 A priori prediction of the solvent reorganization energies, electronic couplings, and reaction rates

Predictions of the electronic couplings and solvent reorganization energies controlling the photochemical processes on the singlet manifold were made before the experiments were performed and the results are compared with the subsequently obtained experimental values in Table 3. The calculated reorganization energies are evaluated using DFT calculations for the initial and final electronic states using equilibrium and non-equilibrium solvation provided by a dielectric continuum model, as detailed in ESI Section S1.5.† For the porphyrin-fullerene dyads, the calculated values are ca. 0.12 eV less than the observed ones, this difference reducing to 0.03–0.09 eV for the ferrocene-porphyrin dyads. While this underestimation is largely associated with the technical requirement of using the solvent-accessible surface in the calculations (see ESI Section S1.5†), given the complexity of the molecules, the small basis set (3-21G) used, and the questionable assumption used in the experimental analysis that the charge-separation and charge-recombination couplings are equal, the agreement between experiment and calculation is quite acceptable. Indeed, couplings obtained from interpretation of calculated TDDFT transition moments calculated independently for the charge-separation and charge-recombination processes (Table 3) do show significant differences but are of the order of those deduced experimentally. For example, for Fc-ZnP the calculated couplings are ¹V = 300 cm⁻¹ for charge separation and 1600 cm⁻¹ for charge recombination, compared to 940 cm⁻¹ deduced experimentally on the assumption that the couplings are the same for both processes. Such large couplings are the direct manifestation of the π conjugation between the ferrocene and porphyrin. For ZnP-C₆₀, the calculated couplings are equal at ¹V = 50 cm⁻¹ for both processes, however, but these are larger that deduced experimentally from the kinetic data, 31 cm⁻¹. The coupling for primary charge recombination can also be deduced experimentally using the (reliable) assumption that it is equal to that observed for direct excitation of the ground-state to the charge-transfer state. From the band intensity reported in Fig. 1, this gives ¹V = 32 cm⁻¹.

For the triads, the calculations predict couplings for the charge-separation processes of the order of those deduced experimentally. The most significant differences found between calculation and experiment in Table 3 are for the couplings ¹V for the triad secondary charge-recombination process CR₂, however, with the calculated values of 31–43 cm⁻¹ being much larger than the observed ones, 1.3–2.0 cm⁻¹. Most likely the calculations overestimate charge delocalization within the ferrocene-porphyrin cation: while the observation of porphyrin-cation absorption for the supposedly ferrocene-only cation (Fig. 4e–f), clearly indicate significant delocalization, the computational results predict almost complete delocalization.³⁴

Table 4 details calculated properties for processes involving singlet–triplet interconversion including energy splittings Δ between singlet and triplet states as well as the spin–orbit couplings V that mix them. Also included are spin–orbit couplings pertaining to the local triplet excited state, ISC between porphyrin Q bands, charge recombination processes, and processes that loose spin polarization. The calculations indicate that ISC from ¹P(S₁)^* to ³P(T₁)^* occurs via³P(T₂)^* intermediates as the spin–orbit couplings for this path are much larger than those for the direct path. This is expected as the lowest singlet and triplet states are each doubly degenerate in pure metalloporphyrins, enabling large spin–orbit coupling between the components of the degenerate states. Most significantly, the calculations reproduce the observed qualitative feature that the couplings are larger in zinc porphyrins than in free-base porphyrins, and they predict that chemical substitution does not dramatically change ISC rates, as assumed in Scheme 2. Similarly, the calculated spin–orbit couplings depicting porphyrin phosphorescence qualitatively reproduce the observed properties for zinc and free-base porphyrins whilst supporting the assumptions used in the kinetics analysis that local-porphyrin phosphorescence lifetimes are chemical-substitution insensitive.

Table 4 Calculated energy splittings Δ and spin–orbit couplings V for processes involving triplet states, along with the associated final triplet charge-separated state lifetimes τ determined from them for various possible recombination mechanisms

Property^a	ZnP-Ph	Fc-ZnP	Fc-2HP	ZnP-C60	2HP-C60	Fc-ZnP-C60L	Fc-ZnP-C60C
a Δ are energy splittings in cm^−1, V are spin–orbit splittings in cm^−1, τ are process lifetimes. b TDDFT calculations. c fCASSCF calculations (CASSCF with frozen SCF orbitals), possibly including modified Fe d-orbital energies. d from observed V and λo for the singlet process (Table 4) and ΔG (ESI Table S1†) assuming a triplet lifetime of ^3P(T1)^* of 90 μs. e derived from ^1CS emission lifetime of 44 μs (obtained from the observed absorption intensity) scaled by ratio of the fCASSCF calculated (Δ/V)^2 for the interaction of ^1CS and ^3CS. f the observed lifetime of the singlet state scaled by squared ratio of the calculated singlet to triplet couplings. g the observed lifetime of the singlet state scaled by ratio of the fCASSCF calculated (Δ/V)^2 for the interaction of ^1CS and ^3CS. h strong interactions between the TDDFT excitations inhibit determination but large values are implied. i CASSCF with full orbital relaxation yields 2.1 cm^−1. j CASSCF with full orbital relaxation yields 0.0006 cm^−1. k this is very sensitive to the ferrocenium lowest-local-excitation vertical excitation energy ΔE^*, taken here as 0.5 eV, assuming also intramolecular and solvent reorganization energies in the range 0.05–0.1 eV, see text.
Δ final ^1CS to ^3CS^b	—	^h	^h	5.2	0.64	4.8	3.5
Δ primary ^1CS to ^3CS^c	—	170	300	0.86^i	0.51	0.19	0.26
Δ secondary ^1CS to ^3CS^c	—	—	—	—	—	0.56	0.28
V primary ^1CS to ^3CS^c	—	1.0	1.5	0.00014^j	0.00032	0.0063	0.0044
V secondary ^1CS to ^3CS^c	—	—	—	—	—	0.00044	0.00024
V ^3P(T1)^* to GS^c	—	0.53	0.08	0.52	0.21	0.14	0.77
V primary ^3CS to GS^c	—	2.8	1.8	0.052	0.038	0.0039	0.076
V secondary ^3CS to GS^c	—	—	—	—	—	0.039	0.030
V ^1P(S1)^* to ^3P(T1)*^c	0.23	0.29	0.07	0.77	0.07	0.37	0.85
V ^1P(S1)^* to ^3P(T2)*^c	2.0	2.9	1.5	2.8	1.5	3.1	2.7
V ^1(Fc-ZnP˙^+-C60˙^−) to ^1(Fc˙^+*-ZnP-C60˙^−)	—	—	—	—	—		85
V ^1(Fc-ZnP˙^+-C60˙^−) to ^3(Fc˙^+-ZnP-C60˙^−)	—	—	—	—	—	2.4	12
V ^1(Fc˙^+*-ZnP-C60˙^−) to ^1(Fc˙^+-ZnP-C60˙^−)	—	—	—	—	—		70
V ^1(Fc˙^+*-ZnP-C60˙^−) to ^3(Fc˙^+-ZnP-C60˙^−)	—	—	—	—	—	85	105
τ via ^3P(T1)*^d	—			3.5 s
τ via primary ^3CS ISC to GS	—	—	—	—	—	13 ms	76 μs
τ via primary ^3CS spin depolarization	—	—	—	—	—	> 100 μs	> 400 μs
τ via excited ferrocenium cation states	—	—	—	—	—		20 μs-20 ms^k
τ by triplet excited state^e	—			1700 s
τ by ISC to GS^f	—			35 μs		6 μs	9 μs
τ by spin depolarization^g	—			3.8 ms		3.2 ms	4.1 ms

---

Table 4 also gives estimated lifetimes of triplet charge-separated states calculated for four possible types of recombination mechanisms: direct recombination to the ground state via spin–orbit coupling, loss of spin-polarization leading to conversion to the singlet charge-separated state and hence extremely rapid recombination, thermal reactions via higher-energy excited states, and phosphorescence from the charge-separated state. For ³(ZnP˙⁺-C₆₀˙⁻), direct recombination is predicted to have the shortest lifetime, 35 μs, shorter than the observed lifetime of 690 μs but close enough given the likely accuracy of the calculations. Spin depolarization is calculated to require 3.8 ms, of the order of the observed lifetime, whilst reaction via the available higher-energy excited state ³P(T₁)^* is predicted to take 3.5 s and the phosphorescence lifetime of the charge-separated state is estimated to be 1700 s. For the triads, recombination is also possible via thermal excitation of the secondary charge-separated states to the corresponding primary charge-separated states. These primary charge-separated states may decay through direct conversion to the ground state or via spin depolarization, with the calculated rates ranging from 76 μs to > 400 μs, all slower than calculated direct-recombination rate.

As previously discussed, the ²E nature of the ferrocenium cation indicates that low-lying excited states exist for all related species. These excited states are not shown in Scheme 2 as there is no direct evidence, but loss of spin polarization and hence charge recombination could occur through their thermal excitation. Most critical is the parameter ΔE^* describing the adiabatic energy difference between the cationic ground states ^1,3(Fc-ZnP˙⁺-C₆₀˙⁻) and the associated first excited states ^1,3(Fc˙^+*-ZnP-C₆₀˙⁻); this is zero for pure ferrocenium ions and facilitates rapid spin depolarization through the large spin–orbit interaction between the degenerate states. Conjugation of the porphyrin to the ferrocene breaks the symmetry, increasing ΔE^* and thus inhibiting spin relaxation. Most of the electronic couplings V controlling the kinetics of reactions involving the six states ^1,3(Fc-ZnP˙⁺-C₆₀˙⁻), ^1,3(Fc˙⁺-ZnP-C₆₀˙⁻), and ^1,3(Fc˙^+*-ZnP-C₆₀˙⁻) may be calculated using the TD-DFT and CASSCF methods, and the results are given in Table 4; the associated free-energy changes and reorganization energies necessary to evaluate these rates using ESI Eq. S7† are taken from the observed data. Three quantities are not readily calculated, however: the critical energy spacing ΔE^* itself, and the intramolecular and solvent reorganization energies associated with Fc˙⁺ → Fc˙^+*. As only minor charge redistributions and geometry changes are associated with this reaction, both reorganization energies are expected to be small. Evaluation of ΔE^* requires careful treatment of the nearby conical intersection. Density-functional theory is formally inapplicable to ²E states, and while a range of sensible results are obtained from its naïve application, different methods yield vertical excitation energies (the sum of ΔE^* and the intramolecular reorganization energy) of 0.2–0.6 eV. CASPT2 is in principle the simplest computational method that includes all basic qualitative features of the conical intersection, and this method predicts a vertical excitation energy of 0.52 eV.

Assuming a vertical excitation energy of ΔE^* = 0.5 eV and intramolecular and solvent reorganization energies in the range of 0.05–0.1 eV, solution of the six-state kinetics equations predicts charge-recombination lifetimes in the range 20 μs to 20 ms, of the order required to ensure retention of spin polarization. While these calculations are indicative only and are very sensitive to ΔE^* as well as the (large) calculated value of 105 cm⁻¹ (Table 4) for the spin–orbit coupling between ¹(Fc˙^+*-ZnP-C₆₀˙⁻) and ³(Fc˙⁺-ZnP-C₆₀˙⁻), they depict that a feasible qualitative scenario exists in which spin depolarization through spin–orbit coupling within ferrocenium cations is inhibited. Note that these calculations also predict that triplet product ³(Fc˙⁺-ZnP-C₆₀˙⁻) can be produced from the singlet primary charge-separated species ¹(Fc-ZnP˙⁺-C₆₀˙⁻) but the yields are extremely small, justifying the neglect of this process in Scheme 2e–f.

Of interest are also the observed EPR signals at low temperature, revealing, e.g., 1200 s charge-separation lifetimes at 183 K in benzonitrile glass for ZnP-C₆₀. Glass formation effects free-energy changes and reorganization energies in non-trivial ways, and it is not useful; to simply re-evaluate the above solution processes using just a lower temperature in ESI Eq. S7.† For example, the recombination rate of ZnP-C₆₀ glasses extrapolated to room temperature is 100 s, compared to the actual observed value in the liquid, 690 μs. The only recombination process of the charge-separated state not subject to such effects is radiative emission (phosphorescence), for which the calculated lifetime is 1700 s for ZnP-C₆₀ (Table 2).

As all calculated rate constants are at best order-of-magnitude estimates, it is not possible to make an authoritative prediction as to the actual mechanism for triplet charge recombination. The mechanism calculated to give the fastest recombination is the direct recombination mechanism. It is of note that the molecular properties associated with this mechanism are consistent with the well-known case of long-lived spin-polarized charge separation in photosynthesis for which the spin–orbit couplings are similar to those calculated here whilst the weak intermolecular coupling between the chlorophylls is 3 orders of magnitude smaller than for the highly conjugated porphyrin system, enhancing the spin depolarization times by 6 orders of magnitude.¹⁶

3. Conclusions

For the triads Fc-ZnP-C₆₀L and Fc-ZnP-C₆₀C and associated dyads Fc-ZnP and Fc-2HP, ZnP-C₆₀ and 2HP-C₆₀, ps-timescale charge separation and charge recombination processes are observed as well as photochemical species that survive on the μs timescale. The long-lived species are identified as being either local-porphyrin triplet states or else spin-polarized triplet charge-separated states depending on the relative energies of these two competing processes. The quantum yields for the production of long-lived charge-separated states are very small (order 0.1%) and can be accounted for purely from ISC within the porphyrin units, while the yields of porphyrin triplet states are much larger (10–25%) and result from charge recombination. Extensive concentration-dependent studies show that the long-lived species involve intramolecular excitations. Low-temperature EPR studies verify the chemical nature of the long-lived species and the presence of triplet states, demonstrating that the mechanism for rapid loss of spin polarization in Fc˙⁺ is inhibited in Fc˙⁺-ZnP. A priori calculations verify the magnitudes and trends deduced experimentally in the couplings and reorganization energies that control all of the observed photochemical processes. In addition, seven independent mechanisms for loss of spin polarization of triplet charge-separated states were considered and all shown to be consistent with the observed charge-recombination rates. The preferred process for charge recombination from triplet states was calculated to be intersystem crossing directly to the ground state, but reliable rates for the complex pathways involving loss of spin polarization through ferrocenium-cation excited states were particularly difficult to obtain. Nevertheless, the calculations indicate that delocalization of the cation in Fc˙⁺-ZnP and associated triads inhibits ferrocenium spin depolarization.

In general, long-distance charge-separated states rapidly loose spin polarization, and as a result recombination to either the singlet ground-state or local triplet states of lower energy than the charge-separated state typically occurs independent of whether singlet or triplet charge-separated states are initially prepared.^13,39 Conservation of spin polarization in charge-separated states has only been observed previously in small molecules with strong connections between the donor and acceptor, connections sufficient to maintain a large energy gap between the singlet and triplet charge-separated states.^39,42 Very recently spin conservation was observed in a porphyrin-fullerene dyad in which primary charge separation from the triplet state of the fullerene was observed at low temperature,⁴¹ but this system involves an intramolecular complex between the chromophores that provides the energy splitting and keeps the charge separation minimal. In the rigid imidazole-fused β,β′-pyrrolic-linked ferrocene-porphyrin-fullerene triads, spin polarization is maintained in a charge-separated state in which the charges are 23 Å apart through utilization of chromophore π conjugation and delocalization; this is unprecedented.⁴⁰ In materials of technological relevance, connectors must be placed at the ends of molecular functional units that can utilize say long-lived charge or spin separation. Having large molecules available that maintain spin polarization on the millisecond timescale may thus prove considerably useful.

Acknowledgements

This work was supported by a Discovery Research Grant (DP0208776) to M.J.C. and J.R.R. from the Australian Research Council. This work was supported by a Grant-in-Aids (Nos. 20108010 to S.F. and 23750014 to K.O.) from the Ministry of Education, Culture, Sports, Science and Technology, Japan and KOSEF/MEST through WCU project (R31-2008-000-10010-0). S.H.L. thanks The Global COE program “Global Education and Research Centre for Bio-Environmental Chemistry” of Osaka University for his stay in Japan. We thank National Computing Infrastructure (NCI) and the Australian Centre for Advanced Computing and Communications (AC3) for computer resources.

Notes and references

1. G. Steinberg-Yfrach, J.-L. Rigaud, E. N. Durantini, D. G. A. L. Moore and T. A. Moore, Nature, 1997, 385, 239; G. Steinberg-Yfrach, J.-L. Rigaud, E. N. Durantini, D. G. A. L. Moore and T. A. Moore, Nature, 1998, 392, 479.
2. D. Gust and T. A. Moore, in The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guilard, Academic Press, San Diego, CA, 2000, vol. 8, p. 153; D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2001, 34, 40; D. Gust, T. A. Moore and A. L. Moore, in Electron Transfer in Chemistry, ed. V. Balzani, Wiley-VCH, Weinheim, 2001, vol. 3, p. 272; D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890.
3. S. Fukuzumi, in The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guilard, Academic Press, San Diego, CA, 2000, vol. 8, p. 115; S. Fukuzumi and D. M. Guldi, in Electron Transfer in Chemistry, ed. V. Balzani, Wiley-VCH, Weinheim, 2001, vol. 2, p. 270; S. Fukuzumi, Org. Biomol. Chem., 2003, 1, 609; S. Fukuzumi, Bull. Chem. Soc. Jpn., 2006, 79, 177; S. Fukuzumi, Phys. Chem. Chem. Phys., 2008, 10, 2283.
4. K. Ohkubo and S. Fukuzumi, J. Porphyrins Phthalocyanines, 2008, 12, 993; K. Ohkubo and S. Fukuzumi, Bull. Chem. Soc. Jpn., 2009, 82, 303.
5. N. V. Tkachenko, L. Rantala, A. Y. Tauber, J. Helaja, P. H. Hynninen and H. Lemmetyinen, J. Am. Chem. Soc., 1999, 121, 9378; M. Isosomppi, N. V. Tkachenko, A. Efimov and H. Lemmetyinen, J. Phys. Chem. A, 2005, 109, 4881; S. A. Vail, D. I. Schuster, D. M. Guldi, M. Isosomppi, N. Tkachenko, H. Lemmetyinen, A. Palkar, L. Echegoyen, X. Chen and J. Z. H. Zhang, J. Phys. Chem. B, 2006, 110, 14155; D. I. Schuster, K. Li, D. M. Guldi, A. Palkar, L. Echegoyen, C. Stanisky, R. J. Cross, M. Niemi, N. V. Tkachenko and H. Lemmetyinen, J. Am. Chem. Soc., 2007, 129, 15973.
6. J. L. Sessler, B. Wang, S. L. Springs and C. T. Brown, in Comprehensive Supramolecular Chemistry, ed. J. L. Atwood, J. E. D. Davies, D. D. MacNicol and F. Vögtle, Elsevier Science Ltd., Oxford, 1999, vol. 4, p. 311.
7. R. A. Haycock, A. Yartsev, U. Michelsen, V. Sundström and Christopher A. Hunter, Angew. Chem., Int. Ed., 2000, 39, 3616.
8. A. Osuka, N. Mataga and T. Okada, Pure Appl. Chem., 1997, 69, 797.
9. M. R. Wasielewski, Chem. Rev., 1992, 92, 435.
10. M. R. Wasielewski, J. Org. Chem., 2006, 71, 5051.
11. K. D. Jordan and M. N. Paddon-Row, Chem. Rev., 1992, 92, 395; M. N. Paddon-Row, Acc. Chem. Res., 1994, 27, 18.
12. M. E. El-Khouly, L. M. Rogers, M. E. Zandler, G. Suresh, M. Fujitsuka, O. Ito and F. D'Souza, ChemPhysChem, 2003, 4, 474; F. D'Souza and O. Ito, Coord. Chem. Rev., 2005, 249, 1410; F. D'Souza, R. Chitta, S. Gadde, M. E. Zandler, A. L. McCarty, A. S. D. Sandanayaka, Y. Araki and O. Ito, J. Phys. Chem. A, 2006, 110, 4338; F. D'Souza, M. R. El-Khouly, S. Gadde, M. E. Zandler, A. L. McCarty, Y. Araki and O. Ito, Tetrahedron, 2006, 62, 1967; A. S. D. Sandanayaka, Y. Araki, O. Ito, R. Chitta, S. Gadde and F. D'Souza, Chem. Commun., 2006, 2006, 4327.
13. M. Di Valentin, A. Bisol, G. Agostini, M. Fuhs, P. A. Liddell, A. L. Moore, T. A. Moore, D. Gust and D. Carbonera, J. Am. Chem. Soc., 2004, 126, 17074.
14. M. J. Crossley, P. J. Sintic, R. Walton and J. R. Reimers, Org. Biomol. Chem., 2003, 1, 2777; M. J. Crossley, P. J. Sintic, J. A. Hutchison and K. P. Ghiggino, Org. Biomol. Chem., 2005, 3, 852; J. A. Hutchison, P. J. Sintic, P. R. Brotherhood, C. Scholes, I. M. Blake, K. P. Ghiggino and M. J. Crossley, J. Phys. Chem. C, 2009, 113, 11796; J. A. Hutchison, P. J. Sintic, M. J. Crossley, T. Nagamura and K. P. Ghiggino, Phys. Chem. Chem. Phys., 2009, 11, 3478.
15. L. P. Dutton, J. S. Leigh and M. Seibert, Biochem. Biophys. Res. Commun., 1972, 46, 406; M. C. Thurnauer, J. J. Katz and J. R. Norris, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3270.
16. A. J. Hoff, Q. Rev. Biophys., 1984, 17, 153.
17. S. Fukuzumi, Res. Chem. Intermed., 1997, 23, 519; M. Fujitsuka, O. Ito, H. Imahori, K. Yamada, H. Yamada and Y. Sakata, Chem. Lett., 1999, 28, 721; S. Fukuzumi and H. Imahori, in Electron Transfer in Chemistry, ed. V. Balzani, Wiley-VCH, Weinheim, 2001, vol. 2, p. 927.
18. H. Imahori, K. Tamaki, D. M. Guldi, C. Luo, M. Fujitsuka, O. Ito, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 2607; D. M. Guldi, Chem. Soc. Rev., 2002, 31, 22.
19. D. M. Guldi and S. Fukuzumi, in Fullerenes: From Synthesis to Optoelectronic Properties, ed. D. M. Guldi and N. Martin, Kluwer, Dordrecht, 2003, p. 237; D. M. Guldi, Phys. Chem. Chem. Phys., 2007, 9, 1400.
20. L. Echegoyen and L. E. Echegoyen, Acc. Chem. Res., 1998, 31, 593.
21. M. Opallo, Pol. J. Chem., 1993, 67, 2093.
22. T. M. Figueira-Duarte, A. Gégout and J.-F. Nierengarten, Chem. Commun., 2007, 109.
23. H. Imahori and Y. Sakata, Adv. Mater., 1997, 9, 537; H. Imahori and Y. Sakata, Eur. J. Org. Chem., 1999, 2445.
24. Y. Kobori, S. Yamauchi, K. Akiyama, S. Tero-Kubota, H. Imahori, S. Fukuzumi and J. R. NorrisJr, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10017.
25. S. Barlowa and S. R. Marderb, Chem. Commun., 2000, 1555.
26. S. Lu, V. V. Strelets, M. F. Ryan, W. J. Pietro and A. B. P. Lever, Inorg. Chem., 1996, 35, 1013.
27. G. Gritzner and J. Kuta, Pure Appl. Chem., 1984, 56, 461.
28. N. V. Tkachenko, H. Lemmetyinen, J. Sonoda, K. Ohkubo, T. Sato, H. Imahori and S. Fukuzumi, J. Phys. Chem. A, 2003, 107, 8834.
29. G.d. l. Torre, F. Giacalone, J. L. Segura, N. Martín and D. M. Guldi, Chem.–Eur. J., 2005, 11, 1267.
30. H. Imahori, K. Tamaki, Y. Araki, T. Hasobe, O. Ito, A. Shimomura, S. Kundu, T. Okada, Y. Sakata and S. Fukuzumi, J. Phys. Chem. A, 2002, 106, 2803; H. Imahori, H. Yamada, D. M. Guldi, Y. Endo, A. Shimomura, S. Kundu, K. Yamada, T. Okada, Y. Sakata and S. Fukuzumi, Angew. Chem., Int. Ed., 2002, 41, 2344.
31. D. Gust, T. A. Moore, A. L. Moore, F. Gao, D. Luttrull, J. M. DeGraziano, X. C. Ma, L. R. Makings, S. J. Lee, T. T. Trier, E. Bittersmann, G. R. Seely, S. Woodward, R. V. Bensasson, M. Rougée, F. C. De Schryver and M. Van der Auweraer, J. Am. Chem. Soc., 1991, 113, 3638; P. A. Liddell, D. Kuciauskas, J. P. Sumida, B. Nash, D. Nguyen, A. L. Moore, T. A. Moore and D. Gust, J. Am. Chem. Soc., 1997, 119, 1400; D. Kuciauskas, P. A. Liddell, S. Lin, S. G. Stone, A. L. Moore, T. A. Moore and D. Gust, J. Phys. Chem. B, 2000, 104, 4307.
32. S. I. Yang, R. K. Lammi, J. Seth, J. A. Riggs, T. Arai, D. Kim, D. F. Bocian, D. Holten and J. S. Lindsey, J. Phys. Chem. B, 1998, 102, 9426; K. Tamaki, H. Imahori, Y. Sakata, Y. Nishimura and I. Yamazaki, Chem. Commun., 1999, 625; K. Kilsa, J. Kajanus, J. Martensson and B. Albinsson, J. Phys. Chem. B, 1999, 103, 7329.
33. C. Luo, D. M. Guldi, H. Imahori, K. Tamaki and Y. Sakata, J. Am. Chem. Soc., 2000, 122, 6535.
34. D. Curiel, K. Ohkubo, J. R. Reimers, S. Fukuzumi and M. J. Crossley, Phys. Chem. Chem. Phys., 2007, 9, 5260.
35. Y. Kashiwagi, K. Ohkubo, J. A. McDonald, I. M. Blake, M. J. Crossley, Y. Araki, O. Ito, H. Imahori and S. Fukuzumi, Org. Lett., 2003, 5, 2719.
36. M. Gardner, A. J. Guerin, C. A. Hunter, U. Michelsen and C. Rotger, New J. Chem., 1999, 23, 309.
37. Y. Jung and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 2831.
38. M. J. Crossley, C. S. Sheehan, T. Khoury, J. R. Reimers and P. J. Sintic, New J. Chem., 2008, 32, 340.
39. M. R. Roest, A. M. Oliver, M. N. Paddon-Row and J. W. Verhoeven, J. Phys. Chem. A, 1997, 101, 4867; M. N. Paddon-Row, Aust. J. Chem., 2003, 56, 729; L. Hviid, A. M. Brouwer, M. N. Paddon-Row and J. W. Verhoeven, ChemPhysChem, 2001, 2, 232; L. Hviid, W. G. Bouwman, M. N. Paddon-Row, H. J. van Ramesdonk, J. W. Verhoeven and A. M. Brouwer, Photochem. Photobiol. Sci., 2003, 2, 995.
40. T. Da Ros, M. Prato, D. M. Guldi, M. Ruzzi and L. Pasimeni, Chem.–Eur. J., 2001, 7, 816.
41. Y. Kobori, Y. Shibano, T. Endo, H. Tsuji, H. Murai and K. Tamao, J. Am. Chem. Soc., 2009, 131, 1624.
42. F. Gerson, T. Wellauer, A. M. Oliver and M. N. Paddon-Row, Helv. Chim. Acta, 1990, 73, 1586.
43. M. J. Crossley and J. A. McDonald, J. Chem. Soc., Perkin Trans. 1, 1999, 2429.
44. M. J. Crossley, L. J. Govenlock and J. K. Prashar, J. Chem. Soc., Chem. Commun., 1995, 2379; W. E. K. M. Kadish, R. Zhan, T. Khoury, L. J. Govenlock, J. K. Prashar, P. J. Sintic, K. Ohkubo, S. Fukuzumi and M. J. Crossley, J. Am. Chem. Soc., 2007, 129, 6576.
45. M. Maggini, G. Scorrano and M. Prato, J. Am. Chem. Soc., 1993, 115, 9798.
46. T. Drovetskaya, C. A. Reed and P. Boyd, Tetrahedron Lett., 1995, 36, 7971.
47. D. M. Guldi, A. Hirsch, M. Scheloske, E. Dietel, A. Troisi, F. Zerbetto and M. Prato, Chem.–Eur. J., 2003, 9, 4968.
48. A. Hosseini, S. Taylor, G. Accorsi, N. Armaroli, C. A. Reed and P. D. W. Boyd, J. Am. Chem. Soc., 2006, 128, 15903.
49. H. Chosrowjan, S. Tanigichi, T. Okada, S. Takagi, T. Arai and K. Tokumam, Chem. Phys. Lett., 1995, 242, 644.
50. N. Mataga, Y. Shibata, H. Chosrowjan, N. Yoshida and A. Osuka, J. Phys. Chem. B, 2000, 104, 4001.
51. M. Kubo, Y. Mori, M. Otani, M. Murakami, Y. Ishibashi, M. Yasuda, K. Hosomizu, H. Miyasaka, H. Imahori and S. Nakashima, J. Phys. Chem. A, 2007, 111, 5136.
52. S. Fukuzumi, K. Okamoto, C. P. Gros and R. Guilard, J. Am. Chem. Soc., 2004, 126, 10441.
53. J. Fortage, J. Boixel, E. Blart, L. Hammarström, H. C. Becker and F. Odobel, Chem.–Eur. J., 2008, 14, 3467.
54. S. Bhattacharya, S. K. Nayak, S. Chattopadhyay and M. Banerjee, Spectrochim. Acta, Part A, 2007, 66, 243.
55. P. D. W. Boyd and C. A. Reed, Acc. Chem. Res., 2005, 38, 235.
56. R. Prins, Mol. Phys., 1970, 19, 603.
57. H. Imahori, D. M. Guldi, K. Tamaki, Y. Yoshida, C. Luo, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 6617.
58. R. Rai, Can. J. Phys., 1982, 60, 329.
59. W. E, K. M. Kadish, P. J. Sintic, T. Khoury, L. J. Govenlock, Z. Ou, J. Shao, K. Ohkubo, J. R. Reimers, S. Fukuzumi and M. J. Crossley, J. Phys. Chem. A, 2008, 112, 556.
60. H. Hayashi, S. Nagakura and S. Iwata, Mol. Phys., 1967, 13, 489.
61. A. Warshel, J. Phys. Chem., 1982, 86, 2218.
62. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
63. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
64. T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555.
65. W. J. Hehre, L. Radom, P.v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
66. M. E. Zandler and F. D'Souza, C. R. Chim., 2006, 9, 960.
67. M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., GAUSSIAN 03 Rev. B2, Gaussian Inc., Pittsburgh PA, 2003.
68. F. Eckert and A. Klamt, AIChE J., 2002, 48, 369.
69. P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, et al., MOLPRO, version 2010.1, a package of ab initio programs; University of Birmingham: Birmingham, 2010.
70. N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391.
71. J. R. Reimers and N. S. Hush, J. Phys. Chem., 1991, 95, 9773.
72. Z.-F. Xu, Y. Xie, W.-L. Feng and H. F. Schaefer, J. Phys. Chem. A, 2003, 107, 2716; H. P. Lüthi, P. E. M. Siegbahn, J. Almlöf, K. FægriJr and A. Heiberg, Chem. Phys. Lett., 1984, 111, 1.
73. R. A. Marcus, J. Chem. Phys., 1956, 24, 966.
74. J. R. Reimers, J. Chem. Phys., 2001, 115, 9103.
75. H. Imahori, S. Ozawa, K. Ushida, M. Takahashi, T. Azuma, A. Ajavakom, T. Akiyama, M. Hasegawa, S. Taniguchi, T. Okada and Y. Sakata, Bull. Chem. Soc. Jpn., 1999, 72, 485.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis and molecular characterisation, data fitting and computational modelling equations,^62–75 cyclic voltammograms in PhCN of related model compounds, time-resolved fluorescence studies of ZnP and 2HP, femtosecond transient absorption spectra in PhCN, studies on bimolecular charge-transfer of dyads, and low-temperature EPR studies. See DOI: 10.1039/c1sc00614b

---