Shape matters: the diffusion rates of TMV rods and CPMV icosahedrons in a spheroid model of extracellular matrix are distinct†
Karin L. Lee‡a, Logan C. Hubbard‡a, Stephen Herna, Ibrahim Yildiza, Miklos Gratzl*a and Nicole F. Steinmetz*abc
aDepartment of Biomedical Engineering, Case Western Reserve University, Schools of Medicine and Engineering, 10900 Euclid Avenue, Cleveland, OH 44106, USA. E-mail: miklos.gratzl@case.edu; nicole.steinmetz@case.edu
bDepartment of Radiology, Case Western Reserve University, Schools of Medicine and Engineering, 10900 Euclid Avenue, Cleveland, OH 44106, USA
cDepartment of Materials Science and Engineering, Case Western Reserve University, Schools of Medicine and Engineering, 10900 Euclid Avenue, Cleveland, OH 44106, USA
First published on 25th April 2013
Abstract
Nanomaterial-based carrier systems hold great promise to deliver therapies with increased efficacy and reduced side effects. While the state-of-the-art carrier system is a sphere, recent data indicate that elongated rods and filaments have advantageous flow and margination properties, resulting in enhanced vascular targeting and tumor homing. Here, we report on the distinct diffusion rates of two bio-inspired carrier systems: 30 nm-sized spherical cowpea mosaic virus (CPMV) and 300 × 18 nm-sized tobacco mosaic virus (TMV) with a tubular structure, using a spheroid model of the tumor microenvironment and fluorescent imaging.
Shape matters
Nanoparticle-based carrier systems show great promise for applications in tissue-specific imaging and drug delivery, especially for detection and treatment of systemic diseases such as metastatic cancer or cardiovascular disease. The state-of-the-art carrier system is spherical, however, a growing body of data indicates that this may not be optimal. Size and shape (as well as surface chemistry) of nanoparticle carriers determine their cellular and in vivo fate. Distinct advantages of elongated, rod-shaped or filamentous materials over their spherical counterparts have been observed: data indicate that non-spherical materials, such as rods and filaments, have enhanced tumor homing properties.1,2 This is explained by the distinct flow properties of rods/filaments versus spheres.3–7 Based on fluid dynamics elongated, non-spherical materials marginate better toward the vessel wall, thus have a higher probability to recognize and bind to diseased areas.3,8,9 Further, it is indicated that the elongated materials show enhanced transport across membranes and tissues: nanorods and nanospheres with the same effective hydrodynamic radius and diffusive transport in water show increased penetration rates of rods compared to spheres in gels and tumor tissues.10 Combined, enhanced margination and transport phenomena contribute to enhanced tumor retention and accumulation of non-spherical materials in tumor tissue.Still, to date most research is focused on spherical and low-aspect-ratio materials. Physically and chemically tailoring materials at the nanoscale to create high aspect ratio materials remains technically challenging using synthetic materials. A few examples include polymeric filomicelles (mimicking filamentous viruses) and silica nanorods.4–6,11,12 To overcome this synthetic challenge, we turned toward nature's materials, specifically our research is focused on the study of viral nanoparticles (VNPs) formed by plant viruses. Some VNPs naturally assemble into high aspect ratio structures, examples include tobacco mosaic virus (TMV) measuring 300 × 18 nm (aspect ratio: 17), potato virus X (PVX) measuring 515 × 13 nm (aspect ratio: 40) and grapevine virus A (GVA) measuring 800 × 12 nm (aspect ratio: 67).
Viral nanoparticles (VNPs)
The development and application of VNP-derived materials in the medical field is becoming a growing area of interest and impact. There are many novel types of VNPs in development, with bacteriophages and plant viruses favored because they are considered safer in humans than mammalian viruses.13 Viruses can be regarded as nature's carrier systems; they perform the tasks we seek to mimic in nanomedicine, i.e. tissue-specific delivery of cargos. VNPs are genetically encoded and self-assemble into discrete and monodisperse structures of precise shape and size; their structures are known to atomic resolution. This level of quality control cannot yet be achieved with synthetic nanoparticles.Although nature provides VNPs in a variety of shapes and sizes, to date most research is focused on the study and development of icosahedral (sphere-like) VNPs. Based on the emerging data that elongated rods and filaments may provide distinct advantages for drug delivery and imaging, we turned toward a side-by-side evaluation of the tissue penetration properties of VNP rods versus icosahedrons, specifically tobacco mosaic virus (TMV) versus cowpea mosaic virus (CPMV).
In a recent study, we started the evaluation of different shaped VNPs in preclinical tumor models. Data indicate that VNP filaments and icosahedra show differential tumor homing and penetration. Using human tumor xenografts (fibrosarcoma, squamous sarcoma, and colon cancer), it was determined that PEGylated filamentous potato virus X (PVX, 515 by 13 nm) exhibits higher tumor uptake compared to spherical cowpea mosaic virus (CPMV, 30 nm-sized icosahedron), particularly in the core of the tumor. Intravital and ex vivo imaging data were further supported by immunohistochemical analysis of tumor sections, which indicated greater penetration and accumulation of PVX within the tumor tissues.14 Besides shape-derived advantages of PVX, surface charge-derived differences also play a role. PVX has a positive, CPMV a negative zeta potential. The collagen-rich extracellular matrix (which is negatively charged) is a major determinant of interstitial transport.15 Previous studies indicate that charged materials of opposite charges show different tumor homing and penetration properties.16–20 Therefore it is important to separate charge from geometry to elucidate how transport phenomena are impacted by shape. To do this, we turned toward two VNP systems of varying shapes by similar surface charge: TMV and CPMV.
TMV and CPMV properties
TMV and CPMV particles were propagated in Nicotiana benthamiana and Vigna unguiculata plants and purified at yields of 1–2 mg pure VNPs per gram of infected leaf material. TMV particles form a hollow rod-like structure measuring 300 × 18 nm (aspect ratio: 17) with a 4 nm-wide interior channel. CPMV is a 30 nm-sized sphere with icosahedral symmetry. Bioconjugate chemistries on both platforms are well established. TMV is comprised of 2130 identical copies of a coat protein, and each coat protein displays reactive tyrosine side chains on its exterior surface and carboxylic acids on its interior solvent-exposed surface, each of which can be labeled with chemical modifiers.21,22 CPMV consists of 60 copies of an asymmetric unit that is formed by a small and large coat protein. CPMV displays 300 reactive solvent-exposed lysine side chains that can be labeled using N-hydroxysuccinimide (NHS) active esters.23–26 Cu(I)-catalyzed azide–alkyne cycloaddition (click chemistry) can also be applied to introduce functionalities to the VNPs.27TMV was labeled at either external tyrosines or internal carboxylic acids using a two-step reaction: first, an alkyne ligation handle was introduced to the phenol ring of tyrosine through an electrophilic substitution with the diazonium salt generated from 3-ethynylaniline; alternatively, carboxylic acids were labeled with propargylamine via carbodiimide coupling, then Oregon Green 488 was introduced using an azide-activated dye and click chemistry. CPMV was labeled at surface lysine side chains using an NHS-active ester of Alexa Fluor 555 (for detailed bioconjugation protocols, see ESI†). The conjugation sites and chemistries were chosen based on reproducibility in tailoring VNPs with comparable biophysical properties and brightness (see discussion below). Resulting TMV-O488 and CPMV-A555 were purified over sucrose gradients and dialyzed using 10 kDa cut-off spin filters to remove excess reagents.
A combination of techniques was used to confirm structural integrity and quantify the number of dyes covalently attached per VNP (Fig. 1). The degree of conjugation was quantified based on the UV/visible spectrum using the concentration ratio of O488 or A555 (Abs at 496, εO488 = 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1, abs at 555, εA555 = 150
000 cm−1 M−1, abs at 555, εA555 = 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1) to TMV and CPMV particles (Abs at 260, εTMV = 3.0 mL mg−1 cm−1, MW of TMV = 39.4 × 106 g mol−1, εCPMV = 8.1 mL mg−1 cm−1, MW of CPMV = 5.6 × 106 g mol−1). TMV was labeled with 530 ± 10% O488 dyes and CPMV was labeled with 80 ± 10% A555 dyes (denoted as TMV-O488 and CPMV-A555). Transmission electron microscopy (TEM) and dynamic light scattering (DLS) confirmed the presence of monodisperse CPMV nanoparticles and TMV rods. Zeta potential measurements confirmed negative surface potential for both formulations: CPMV-A555 was measured having an effective diameter of 28 nm and a zeta potential of ζCPMV = −7.5 mV; the effective diameter of TMV was measured to be 140 nm with a zeta potential of ζTMV = −16.3 mV. (We would like to note that we used agarose, a neutral polymer, as the extracellular matrix model, see details below. We therefore reason that electrostatic interactions of the VNPs with the tissue model can be avoided and that the difference in surface potential of TMV versus CPMV will only minimally impact the results.) Further, size exclusion chromatography using fast protein liquid chromatography and Superose 6 column indicated that the particles were intact and showed the VNP-characteristic elution profiles. Co-elution of the fluorophores indicated that the dyes were indeed covalently attached. The latter was further verified using SDS-PAGE after extensive dialysis; fluorescent appearance of the protein bands under UV light indicated that the labels were covalently attached to the coat proteins (Fig. 1).
000 cm−1 M−1) to TMV and CPMV particles (Abs at 260, εTMV = 3.0 mL mg−1 cm−1, MW of TMV = 39.4 × 106 g mol−1, εCPMV = 8.1 mL mg−1 cm−1, MW of CPMV = 5.6 × 106 g mol−1). TMV was labeled with 530 ± 10% O488 dyes and CPMV was labeled with 80 ± 10% A555 dyes (denoted as TMV-O488 and CPMV-A555). Transmission electron microscopy (TEM) and dynamic light scattering (DLS) confirmed the presence of monodisperse CPMV nanoparticles and TMV rods. Zeta potential measurements confirmed negative surface potential for both formulations: CPMV-A555 was measured having an effective diameter of 28 nm and a zeta potential of ζCPMV = −7.5 mV; the effective diameter of TMV was measured to be 140 nm with a zeta potential of ζTMV = −16.3 mV. (We would like to note that we used agarose, a neutral polymer, as the extracellular matrix model, see details below. We therefore reason that electrostatic interactions of the VNPs with the tissue model can be avoided and that the difference in surface potential of TMV versus CPMV will only minimally impact the results.) Further, size exclusion chromatography using fast protein liquid chromatography and Superose 6 column indicated that the particles were intact and showed the VNP-characteristic elution profiles. Co-elution of the fluorophores indicated that the dyes were indeed covalently attached. The latter was further verified using SDS-PAGE after extensive dialysis; fluorescent appearance of the protein bands under UV light indicated that the labels were covalently attached to the coat proteins (Fig. 1).
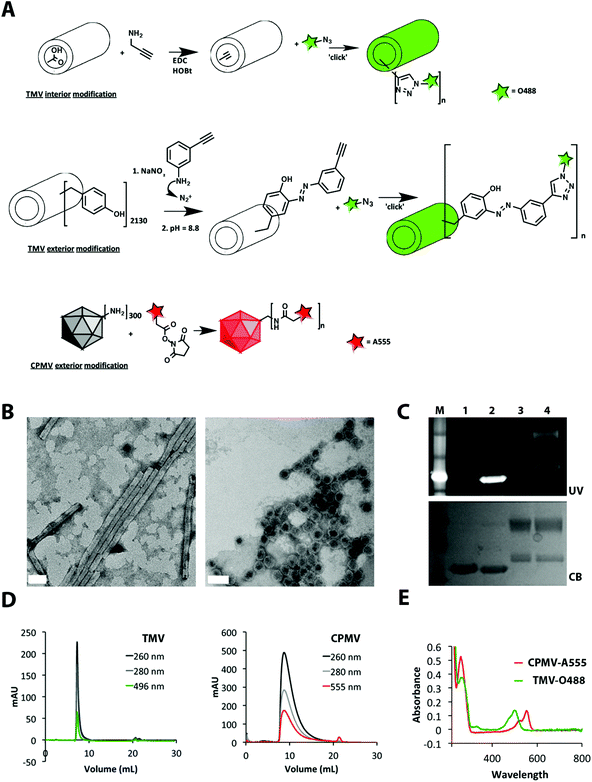 | ||
| Fig. 1 Biochemical characterization of dye-labeled TMV-O488 and CPMV-A555. A: Bioconjugation scheme. B: TEM of UAc negatively-stained TMV-O488 and CPMV-A555, scale bar = 50 nm. C: SDS-PAGE gel under UV light and white light after Coomassie Blue staining, 1 = TMV, 2 = TMV-O488, 3 = CPMV, 4 = CPMV-A555. D: Size exclusion chromatography using FPLC and Superose 6 column of TMV-O488 and CPMV-A555, E: UV/visible spectroscopy of CPMV-A555 and TMV-O488. | ||
The degree of dye conjugation to TMV and CPMV was found to be comparable: for each formulation approximately 25% of the reactive sites were labeled; 530 dyes were attached to TMV's 2130 addressable carboxylic acids and 80 dyes were displayed on CPMV's 300 available lysine side chains. The dye ratio comparing TMV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CPMV equates the molecular weight ratio: TMV has a 7× higher molecular weight compared to CPMV, and TMV has 7× more dyes attached compared to CPMV; the #dye
CPMV equates the molecular weight ratio: TMV has a 7× higher molecular weight compared to CPMV, and TMV has 7× more dyes attached compared to CPMV; the #dye![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MWprotein (MDa) ratio is 13.3 and 13.9 for TMV and CPMV, respectively. Based on the equal chemical labeling with fluorescent dyes, we reasoned that the two formulations would be adequate for the proposed experiments and observed differences could be attributed to differences in shape and size (not the degree of chemical labeling).
MWprotein (MDa) ratio is 13.3 and 13.9 for TMV and CPMV, respectively. Based on the equal chemical labeling with fluorescent dyes, we reasoned that the two formulations would be adequate for the proposed experiments and observed differences could be attributed to differences in shape and size (not the degree of chemical labeling).
Theory: diffusion rates of TMV and CPMV
Diffusion coefficients of spherical materials can be estimated based on the hydrodynamic radius (RH) of the nanocarrier and the Stokes–Einstein relationship:| D0 = kT/6πηRH | (1) |
The Stokes–Einstein relationship does not take the shape of the particle into account. For a more accurate estimation of the diffusion coefficient of elongated TMV-based particles, the diffusion coefficient extrapolated to zero concentration of VNPs (D0) was calculated with the Svedberg equation using the particle weight and sedimentation coefficient extrapolated to zero concentration (s0):
| D0 = s0RT/[M(1 − Vρ)] | (2) |
For elongated, approximately cylindrical nanoparticles, such as TMV, translational diffusion coefficients for axial (D‖t) and transverse (D⊥r) movement are considered, expressed as
| D‖t = (ln(p) + ν‖)kT/2πηL | (3) |
| D⊥r = (ln(p) + ν⊥)kT/4πηL | (4) |
Numerical values for of v‖ and v⊥ are based on the dimensions of the TMV cylinder and have been determined for TMV as:29
| ν‖ = −0.114 − 0.15/ln(2p) − 13.5/(ln 2p)2 + 37/(ln 2p)3 − 22/(ln 2p)4 | (5) |
| ν⊥ = 0.866 − 0.15/ln(2p) − 8.1/(ln 2p)2 + 18/(ln 2p)3 − 9/(ln 2p)4 | (6) |
Further, the macroscopic (or effective translational) diffusion coefficient (Dt) applies to movements in random directions and can be expressed as:28
| Dt = (ln(p) + ν)kT/3πηL | (7) |
Data are summarized in Table 1. In water/aqueous buffer the smaller CPMV sphere has a predicted 3.8× faster diffusion rate compared to the TMV rod (based on the macroscopic diffusion rate of TMV).
| VNP | Diameter or length × width [nm] | RH [nm] (measured by DLS) | Molecular weight [g mol−1] | Sedimentation coefficient s0 [s] (from dbvweb.net database) | Stokes–Einstein diffusion coefficient D0 [cm2 s−1] | Diffusion coefficient D0 based on s0 [cm2 s−1] | Translational axial diffusion coefficient D‖t [cm2 s−1] | Translational trasverse diffusion coefficient D⊥r [cm2 s−1] | Macroscopic diffusion coefficient Dt [cm2 s−1] | Experimental diffusion coefficient DExperimental [cm2 s−1] |
|---|---|---|---|---|---|---|---|---|---|---|
| CPMV | 30 | 14.0 | 5.60 × 106 | 1.08 × 10−11 | 1.57 × 10−7 | 1.98 × 10−7 | NA | NA | NA | Phase I: 6.83×10−8 |
| Phase II: 1.71 ×10−8 | ||||||||||
| TMV | 300 × 18 | 70.0 | 3.94 × 107 | 1.94 × 10−12 | NA | 5.15 × 10−8 | 4.86 × 10−8 | 3.57 × 10−8 | 4.00 × 10−8 | Phase I: 6.91 × 10−8 |
| Phase II: 5.76 ×10−10 |
The spheroid model of the tumor microenvironment
In healthy tissue the movement of molecules is driven by diffusion (concentration gradients) or convection (pressure gradients), often both. Within tumor tissue, leaky vasculature and lack of functional lymphatics lead to elevated interstitial fluid pressure,30 which reduces convective transport from the vessel wall into the interstitial space. Within the tumor microenvironment, tissue diffusion is the primary mode of nanoparticle and drug transport. Therefore, we chose to mimic the tumor microenvironment using an agarose gel that allows diffusion but no convection. In addition, agarose is a neutral polymer, providing for an uncharged environment that minimizes electrostatic interactions between nanoparticles and matrix.31,32 This further allows separation between effects of charge and shape on penetration. The agarose model is cast in the shape of a spheroid: the most commonly used in vitro model of tissue microenvironment.Spheroids are spherical cultures of thousands of cells, typically a few hundred micrometers to 1 mm in diameter. The spheroid is the classical 3D model of the tumor microenvironment that surrounds a blood capillary.33–35 Spheroids replicate, to varying degrees, in vivo behavior such as cell–cell interactions, drug penetration and uptake, and interaction with local acidity, oxygenation, and other experimental factors in tumor tissue. We have studied these phenomena in compact spheroids as well as in spheroids made of low-concentration agarose gel with cells suspended in the matrix. Agarose has pore size distributions similar to the extracellular matrix.36,37 By varying cell volume fraction (CVF) from zero up to compact culture, such agarose constructs can be used to obtain information on drug penetration and uptake as they change with increasing CVF.
The aim of this work was to model the penetration of spherical and rod-shaped VNPs into spheroids made of agarose, with CVF = 0. This is to obtain comparable data for CPMV and TMV based on purely physical interactions and transport within the support matrix and under conditions similar to drug penetration studies conventionally done on spheroids. It should be noted that while the extracellular matrix of a tumor is primarily composed of a network of collagen fibers and other molecules such as glycosaminoglycans (GAGs) which contribute to a negatively-charged environment, our basic, physical model using agarose spheroids offers an electrostatically neutral environment. In the presented study we chose to use a model made of agarose in order to study the effect of one variable alone between the two viruses, i.e. shape, on penetration. Of course, one should keep in mind that future models should consider the more complex biological environment, and must take into account local charges as well as the surface chemistries of the nanocarriers. The long-term goal of this work is to compare penetration and uptake of spherical and rod-shaped VNPs and free drug in spheroids of increasing CVF to compact spheroids so that penetration into tissue can be better understood.
Experimental diffusion rates of TMV and CPMV
To mimic diffusion of the two carrier systems into the tumor environment, we used the well-established spheroid model with one difference: hemispheres were used. It has been problematic to obtain data from different depths of full spherical spheroids during drug penetration. Therefore, in this work, agarose half-spheroids were generated by placing liquid agarose directly onto cover slips. The half-spheroid creates a “window” into the interior of the spheroid from below. This is achieved without altering mass transport, as there would be no net transport perpendicular to the base plane even in the intact spheroid because of radial symmetry of the transport.38 The use of half-spheroids made it possible in this work to obtain snapshots of the distribution of VNPs inside the spheroid during penetration, as they evolve in time.Specifically, 1% (w/v) agarose (type VII) gels were made. Agarose half-spheroids (200–800 μm in diameter) were seeded on a 24-well plate and kept hydrated in PBS solution (see ESI† for detailed description). Confocal imaging was performed at room temperature over a 6 h time frame. In brief, samples (free dye and/or VNP sphere and/or VNP rod) were added to the solution and spheroids imaged. First, the penetration of free dye (O488 or rhodamine red) was analyzed, then CPMV-A555 and TMV-O488. Once the imaging parameters were optimized, competition assays comparing CPMV-A555 versus TMV-O488 were conducted. We also compared the diffusion rates of CPMV-A555 versus free O488 dye and TMV-O488 versus free rhodamine red dye (ESI†).
Based on the much larger molecular weight and size of the VNP-based carrier systems compared to free dye (106–7 g mol−1versus 102 g mol−1), the free dye diffuses much faster and saturates the spheroid within minutes (ESI†).
For the competition diffusion assays, CPMV and TMV were added at comparable concentrations: we performed the imaging keeping the protein concentration (mg mL−1 VNP), and most importantly, the amount of cargo (mM dye delivered) constant rather than the number of particles or molar VNP concentration. The overall goal is to define a carrier system that efficiently delivers a high payload of cargo to tumor tissues (not to deliver a high concentration of carrier). Furthermore, this allowed us to keep the fluorescence intensity of each VNP solution comparable: 0.032 mg mL−1 of CPMV-A555 equates to 15 pmolar dye and 220 fmolar of CPMV nanoparticles, and 0.032 mg mL−1 of TMV-O488 equates to 15 pmolar of dye, but 30 fmolar concentration of nanorods. Data are plotted in fluorescence intensity versus distance and over time (Fig. 2).
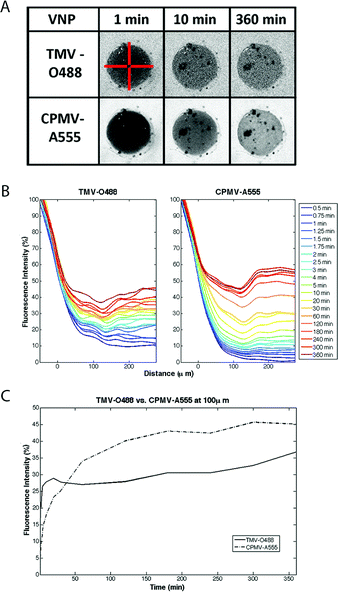 | ||
| Fig. 2 Diffusion rates of VNP rod TMV and sphere CPMV into agarose half-spheroids. A: Snapshots of confocal images showing distinct diffusion of TMV-O488 versus CPMV-A555 (note: the dark spots in the spheroid are microscopic air bubbles). The red bars are 300 microns in size and indicate the 4 slices analyzed and averaged in MatLab (see ESI† for detailed description of MatLab data analysis). B: VNPs were added to the medium and imaging was performed over a 6 hours time frame. Imaging data were analyzed using ImageJ and MatLab software. The fluorescence intensity normalized against reservoir fluorescence intensity is plotted over distance, with 0 μm being the edge of the spheroid structure. Fluorescence intensity versus distance is plotted over time. C: Fluorescence intensity measured at 100 μm distance within the spheroid over time is plotted; data indicate a bi-phasic behavior for TMV and CPMV, with opposite trends of diffusion rates in phase I and II; the diffusion rate in phase I is characterized by Dphase I TMV ≫ CPMV; in phase II this trend is reversed with Dphase II TMV ≪ CPMV. | ||
Overall, we found that TMV rods and CPMV spheres show distinct and bi-phasic diffusion rates, which are characterized by a first, more rapid, loading phase (phase I, ∼10 min) and a second, slower, distribution phase (phase II). Interestingly, the diffusion rate of the TMV rod is faster in phase I compared to the CPMV sphere; in phase II the opposite trend is observed; further phase II is characterized by a much slower diffusion rate for both VNPs.
The diffusion rates of CPMV and TMV in agarose were extracted from the experimental data using diffusion theory.39,40 At short times after the beginning of VNP penetration into the spheroid, and relatively close to the edge of the spheroid, the following equation can be used for the evaluation of diffusion coefficients in the initial period, from the data:39
| CVNP in spheroid(x, t) = CVNP in buffer erfc[x/(√Dt)] | (8) |
In water/aqueous buffer the smaller CPMV sphere has a 3.8× faster diffusion rate compared to the TMV rod as predicted (based on D0, see Table 1). In agarose, at the initial stages of penetration this situation is reversed: at about 5 min and at 50 μm depth the TMV rod has a little higher diffusion rate than the spherical CPMV nanoparticle: the diffusion coefficient of CPMV reduces about 3× in agarose relative to buffer while the diffusion coefficient of TMV slightly increases. However at later times, beyond 30 min, the approximated diffusion coefficient of TMV is about 12-fold less compared to its value at 5 min while that for CPMV reduces relatively little (about 4-fold).
The fast initial loading of TMV rods into the spheroids may be explained by the differences between axial diffusion and transverse diffusion of the high aspect ratio (AR 17) TMV rods. The axial diffusion rate of the TMV rod is 1.36× higher than its transverse rate (see Table 1). For the rod-shaped TMV molecule its spontaneous movement axially is more facilitated than movement transverse to its axis. This is not apparent for a large assembly of molecules in aqueous buffer because all orientations would be equally probable. However, diffusion within the agarose matrix is more complex; the rods diffuse across channels and pores whose dimensions are not much greater than the particles.
The average pore size of the agarose matrix varies with concentration and type of agarose used. Using a similar experimental setup, others reported that 1% (w/v) agarose (2-hydroxyethylagarose type VII, low gelling temperate) gels have a pore size distribution of 100–700 nm with a mean of 400 nm.36,37 The pores are thus expected to be about an order of magnitude larger than CPMV but are on the same size-scale as TMV along its axis. We reason that within the channels the rod-like TMV particles are preferentially oriented with the axis parallel to the channels, supported by neutral uncharged agarose pores. This would promote favored axial diffusion along channels, i.e., more efficient anisotropic diffusion within the agarose model than isotropic diffusion in the buffer. In the same time the spherical CPMV particles would have thermal motion in random directions inside the pores; this is slower than axial diffusion of rods of smaller diameter. The dramatic decrease in TMV diffusion rate after about 20 min is probably because once a TMV rod gets trapped in a pore no other TMV particle can pass by. That CPMV diffusion also slows though gradually and to a much lesser extent is because the smaller pores that TMV cannot even get into can also trap CPMV particles and this reduces the number of available paths for penetration.
Conclusions
The observed faster initial diffusion rates of rod-shaped versus spherical nanoparticles into the tissue is interesting and in agreement with the recent notion that elongated materials show enhanced tumor homing and penetration properties. The enhanced permeability and retention effect observed in some tumors has been utilized to passively target nanomaterials to solid tumors. If the material, however, does not sufficiently fast extravasate and penetrate from the vessel wall into the tissue, washout effects can reduce the effective carrier, and hence drug load, in the tumor tissue. Rapid initial tissue loading of high aspect ratio materials can provide a distinct advantage, allowing the materials to penetrate into the tissue more rapidly thus increasing access while reducing such washout effects. In addition, we propose that similar effects would be beneficial when actively targeting tumors or metastatic disease, rapid tissue penetration is expected to increase the accumulation of the carrier materials at the target disease sites. The movement and diffusion of extravasated drug carrier materials, as modeled and measured here in a tumor microenvironment model, indicate distinct advantages of elongated rod-shaped carrier systems.Acknowledgements
This work was supported by NIH grants NIBIB R00 EB009105 (NFS), NIBIB P30 EB011317 (NFS), and NCI R25 CA148052 Cancer Pharmacology training grant (KLL), Mt. Sinai Foundation (NFS), and grants from Ohio Third Frontier (MG) and Coulter Foundation (MG).Notes and references
- N. Daum, C. Tscheka, A. Neumeyer and M. Schneider, Novel approaches for drug delivery systems in nanomedicine: effects of particle design and shape, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2012, 4, 52–65 CrossRef CAS.
- M. Caldorera-Moore, N. Guimard, L. Shi and K. Roy, Designer nanoparticles: incorporating size, shape and triggered release into nanoscale drug carriers, Expert Opin. Drug Delivery, 2010, 7, 479–495 CrossRef CAS.
- S-.Y. Lee, M. Ferrari and P. Decuzzi, Shaping nano-/micro-particles for enhanced vascular interaction in laminar flows, Nanotechnology, 2009, 20, 495101 CrossRef.
- F. Gentile, C. Chiappini, D. Fine, R. C. Bhavane, M. S. Peluccio and M. M.-C. Cheng, et al., The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows, J. Biomech., 2008, 41, 2312–2318 CrossRef CAS.
- Y. Geng, P. Dalhaimer, S. Cai, R. Tsai, M. Tewari and T. Minko, et al., Shape effects of filaments versus spherical particles in flow and drug delivery, Nat. Nanotechnol., 2007, 2, 249–255 CrossRef CAS.
- D. A. Christian, S. Cai, O. B. Garbuzenko, T. Harada, A. L. Zajac and T. Minko, et al., Flexible filaments for in vivo imaging and delivery: persistent circulation of filomicelles opens the dosage window for sustained tumor shrinkage, Mol. Pharm., 2009, 6, 1343–1352 CrossRef CAS.
- S. Cai, K. Vijayan, D. Cheng, E. M. Lima and D. E. Discher, Micelles of different morphologies—advantages of worm-like filomicelles of PEO-PCL in paclitaxel delivery, Pharm. Res., 2007, 24, 2099–2109 CrossRef CAS.
- P. Decuzzi, B. Godin, T. Tanaka, S-. Y. Lee, C. Chiappini and X. Liu, et al., Size and shape effects in the biodistribution of intravascularly injected particles, J. Controlled Release, 2010, 141, 320–327 CrossRef CAS.
- F. Gentile, C. Chiappini, D. Fine, R. C. Bhavane, M. S. Peluccio and M. M.-C. Cheng, et al., The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows, J. Biomech., 2008, 41, 2312–2318 CrossRef CAS.
- V. P. Chauhan, Z. Popovic, O. Chen, J. Cui, D. Fukumura and M. G. Bawendi, et al., Fluorescent nanorods and nanospheres for real-time in vivo probing of nanoparticle shape-dependent tumor penetration, Angew. Chem., Int. Ed., 2011, 11417–11420 CrossRef CAS.
- P. Decuzzi, R. Pasqualini, W. Arap and M. Ferrari, Intravascular delivery of particulate systems: does geometry really matter?, Pharm. Res., 2009, 26, 235–243 CrossRef CAS.
- P. Decuzzi, B. Godin, T. Tanaka, S-. Y. Lee, C. Chiappini and X. Liu, et al., Size and shape effects in the biodistribution of intravascularly injected particles, J. Controlled Release, 2010, 141, 320–327 CrossRef CAS.
- M. Manchester and P. Singh, Virus-based nanoparticles (VNPs): platform technologies for diagnostic imaging, Adv. Drug Delivery Rev., 2006, 58, 1505–1522 CrossRef CAS.
- S. Shukla, A. Ablack, A. Wen, K. Lee, J. Lewis and N. F. Steinmetz, Increased tumor homing and tissue penetration of the filamentous plant viral nanoparticle Potato virus X, Mol. Pharmaceutics, 2013, 10, 33–42 CrossRef CAS.
- R. K. Jain and T. Stylianopoulos, Delivering nanomedicine to solid tumors, Nat. Rev. Clin. Oncol., 2010, 7, 653–664 CrossRef CAS.
- R. B. Campbell, D. Fukumura, E. B. Brown, L. M. Mazzola, Y. Izumi and R. K. Jain, et al., Cationic charge determines the distribution of liposomes between the vascular and extravascular compartments of tumors, Cancer Res., 2002, 62, 6831–6836 CAS.
- M. Dellian, F. Yuan, V. S. Trubetskoy, V. P. Torchilin and R. K. Jain, Vascular permeability in a human tumour xenograft: molecular charge dependence, Br. J. Cancer, 2000, 82, 1513–1518 CrossRef CAS.
- M. Schmitt-Sody, S. Strieth, S. Krasnici, B. Sauer, B. Schulze and M. Teifel, et al., Neovascular targeting therapy: paclitaxel encapsulated in cationic liposomes improves antitumoral efficacy, Clin. Cancer Res., 2003, 9, 2335–2341 CAS.
- T. Stylianopoulos, B. Diop-Frimpong, L. L. Munn and R. K. Jain, Diffusion anisotropy in collagen gels and tumors: the effect of fiber network orientation, Biophys. J., 2010, 99, 3119–3128 CrossRef CAS.
- T. Stylianopoulos, M. Z. Poh, N. Insin, M. G. Bawendi, D. Fukumura and L. L. Munn, et al., Diffusion of particles in the extracellular matrix: the effect of repulsive electrostatic interactions, Biophys. J., 2010, 99, 1342–1349 CrossRef CAS.
- T. L. Schlick, Z. Ding, E. W. Kovacs and M. B. Francis, Dual-surface modification of the tobacco mosaic virus, J. Am. Chem. Soc., 2005, 127, 3718–3723 CrossRef CAS.
- M. A. Bruckman, G. Kaur, L. A. Lee, F. Xie, J. Sepulveda and R. Breitenkamp, et al., Surface modification of tobacco mosaic virus with “click” chemistry, ChemBioChem, 2008, 9, 519–523 CrossRef CAS.
- N. F. Steinmetz and M. Manchester, PEGylated viral nanoparticles for biomedicine: the impact of PEG chain length on VNP cell interactions in vitro and ex vivo, Biomacromolecules, 2009, 10, 784–792 CrossRef CAS.
- N. F. Steinmetz, A. Ablack, J. L. Hickey, J. Ablack, B. Manocha and J. S. Mymryk, et al., Intravital imaging of human prostate cancer using viral nanoparticles targeted to gastrin-releasing peptide receptors, Small, 2011, 7, 1664–1672 CrossRef CAS.
- A. Chatterji, W. F. Ochoa, M. Paine, B. R. Ratna, J. E. Johnson and T. Lin, New addresses on an addressable virus nanoblock; uniquely reactive Lys residues on cowpea mosaic virus, Chem. Biol., 2004, 11, 855–863 CrossRef CAS.
- E. Basle, N. Joubert and M. Pucheault, Protein chemical modification on endogenous amino acids, Chem. Biol., 2010, 17, 213–227 CrossRef CAS.
- S. Sen Gupta, J. Kuzelka, P. Singh, W. G. Lewis, M. Manchester and M. G. Finn, Accelerated bioorthogonal conjugation: a practical method for the ligation of diverse functional molecules to a polyvalent virus scaffold, Bioconjugate Chem., 2005, 16, 1572–1579 CrossRef CAS.
- M. M. Tirado, C. L. Martinez and J. Garcia de la Torre, J. Chem. Phys., 1984, 81, 2047–2052 CrossRef.
- S. Broersma, J. Chem. Phys., 1981, 74, 6969–6970 CrossRef.
- R. K. Jain, Transport of molecules, particles, and cells in solid tumors, Annu. Rev. Biomed. Eng., 1999, 1, 241–263 CrossRef CAS.
- T. A. Kelly, K. W. Ng, C. C. Wang, G. A. Ateshian and C. T. Hung, Spatial and temporal development of chondrocyte-seeded agarose constructs in free-swelling and dynamically loaded cultures, J. Biomech., 2006, 39, 1489–1497 CrossRef.
- E. Marinho-Soriano, Agar polysaccharides from Gracilaria species (Rhodophyta, Gracilariaceae), J. Biotechnol., 2001, 89, 81–84 CrossRef CAS.
- D. V. Labarbera, B. G. Reid and B. H. Yoo, The multicellular tumor spheroid model for high-throughput cancer drug discovery, Expert Opin. Drug Discovery, 2012, 7, 819–830 CrossRef CAS.
- I. Dufau, C. Frongia, F. Sicard, L. Dedieu, P. Cordelier and F. Ausseil, et al., Multicellular tumor spheroid model to evaluate spatio-temporal dynamics effect of chemotherapeutics: application to the gemcitabine/CHK1 inhibitor combination in pancreatic cancer, BMC Cancer, 2012, 12, 15 CrossRef CAS.
- M. T. Santini and G. Rainaldi, Three-dimensional spheroid model in tumor biology, Pathobiology, 1999, 67, 148–157 CrossRef CAS.
- J. Narayanan, J-. Y. Xiong and X-. Y. Liu, Determination of agarose gel pore size: absorbance measurements vis a vis other techniques, J. Phys., 2006, 28, 83–86 CAS.
- K. W. Ng, C. C. Wang, R. L. Mauck, T. A. Kelly, N. O. Chahine and K. D. Costa, et al., A layered agarose approach to fabricate depth-dependent inhomogeneity in chondrocyte-seeded constructs, J. Orthop. Res., 2005, 23, 134–141 CrossRef.
- Sheth, Multielectrode platform for measuring oxygenation status in multicellular tumor spheroids, PhD thesis, CWRU, 2011 Search PubMed.
- N. F. Steinmetz, C. F. Cho, A. Ablack, J. D. Lewis and M. Manchester, Cowpea mosaic virus nanoparticles target surface vimentin on cancer cells, Nanomedicine, 2011, 6, 351–364 CrossRef CAS.
- J. Crank, The mathematics of diffusion, Oxford University Press, Oxford, 2004 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental methods for propagation, modification, and characterization of CPMV-A555 and TMV-O488, preparation and imaging of spheroids, MatLab data analysis, additional graphs, and analysis of VNPs versus free dye. See DOI: 10.1039/c3bm00191a |
| ‡ Both authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2013 |
