Growth inhibition of calcium oxalate monohydrate crystal by linear aspartic acid enantiomers investigated by in situ atomic force microscopy
Kang R.
Cho
abc,
E. Alan
Salter
d,
James J.
De Yoreo
c,
Andrzej
Wierzbicki
d,
Selim
Elhadj
a,
Yu
Huang
*b and
S. Roger
Qiu
*a
aPhysical and Life Sciences Directorate, Lawrence Livermore National Laboratory, Livermore, CA 94551, USA. E-mail: qiu2@llnl.gov
bDepartment of Materials Science and Engineering, University of California, Los Angeles, CA 90095, USA. E-mail: yhuang@seas.ucla.edu
cMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
dDepartment of Chemistry, University of South Alabama, Mobile, Alabama 36688, USA
First published on 11th September 2012
Abstract
The inhibitory effect of linear enantiomers of L- and D-Asp6 on the growth of calcium oxalate monohydrate crystal has been investigated using in situ atomic force microscopy. The inhibitory magnitude of D-Asp6 on the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face is about 10% larger than that of L-Asp6. While no chiral effect is observed or expected on the growth of the [
00] step on the (010) face is about 10% larger than that of L-Asp6. While no chiral effect is observed or expected on the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face by both enantiomers, their inhibitory effect on this step is much stronger than that on the [
01) face by both enantiomers, their inhibitory effect on this step is much stronger than that on the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face. In both cases, the step morphology indicates that these enantiomers create the impurity pinning along the steps, while the dependence of step speed on supersaturation shows that they also produce a reduction of the step kinetic coefficients. Analysis of the step speed data within the context of an existing model for step pinning and kink blocking shows that the major impact of Asp6 is to block active kink sites. The larger inhibition of the [
00] step on the (010) face. In both cases, the step morphology indicates that these enantiomers create the impurity pinning along the steps, while the dependence of step speed on supersaturation shows that they also produce a reduction of the step kinetic coefficients. Analysis of the step speed data within the context of an existing model for step pinning and kink blocking shows that the major impact of Asp6 is to block active kink sites. The larger inhibition of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step growth by D-Asp6 over L-Asp6 and the substantially larger inhibition of the [
00] step growth by D-Asp6 over L-Asp6 and the substantially larger inhibition of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step over the [
] step over the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step by both enantiomers both result from larger affinity for adsorption to the (010) face and the (
00] step by both enantiomers both result from larger affinity for adsorption to the (010) face and the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, respectively. This is because the larger adsorption leads to a higher density of blocking kink sites along the steps. The estimated difference in binding energy of L- and D-Asp6 to the respective faces from the kinetics model is consistent with the trend predicted by our molecular modeling of the enantiomer binding to the faces.
01) face, respectively. This is because the larger adsorption leads to a higher density of blocking kink sites along the steps. The estimated difference in binding energy of L- and D-Asp6 to the respective faces from the kinetics model is consistent with the trend predicted by our molecular modeling of the enantiomer binding to the faces.
Introduction
Biomolecules play important roles in regulating the formation of biogenic crystalline materials including teeth,1,2 bones,3,4 and kidney stones5–18 as well as shells.19–22 The acidic parts of proteins such as the aspartic acid rich domains are believed to be responsible for the regulatory controls in the biomineralization process.23–27 Of the many biomineral phases formed in humans, calcium oxalate monohydrate (COM) and regulation of its growth by biomolecules has been the subject of many recent investigations10–13,15,18,28,29 due to its clinical importance as the main inorganic component in the majority of human kidney stones. Although normal urine is often supersaturated with respect to calcium oxalate, the formation of human kidney stones is usually impeded, presumably by urinary inhibitors.5–9,11,14Both clinical and physical studies have shown that small molecules like citrate,6–8,12,15–17 as well as macromolecules such as osteopontin11,12,16 and Tamm–Horsfall protein,8,9 all of which contain acidic functional groups, suppress the formation of COM crystals. For example, previous studies12,15 showed that citrate, a small molecule with three carboxylic acid groups, and osteopontin, with an abundance of carboxylic acid groups, modified the growth of COM crystal by asymmetrically attacking existing faces through step-specific interactions. When COM crystals, for which the typical equilibrium habit expresses three distinct faces, namely the {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01}, {010}, and {120} (see Fig. 1A, the assignment of these faces was adopted from the Deganello notation),30 were grown in the presence of citrate, growth on the (
01}, {010}, and {120} (see Fig. 1A, the assignment of these faces was adopted from the Deganello notation),30 were grown in the presence of citrate, growth on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face was strongly inhibited while growth on the (010) face was hardly affected. In contrast, under osteopontin, growth on the (010) face was strongly inhibited while growth on the (
01) face was strongly inhibited while growth on the (010) face was hardly affected. In contrast, under osteopontin, growth on the (010) face was strongly inhibited while growth on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face was hardly affected.
01) face was hardly affected.
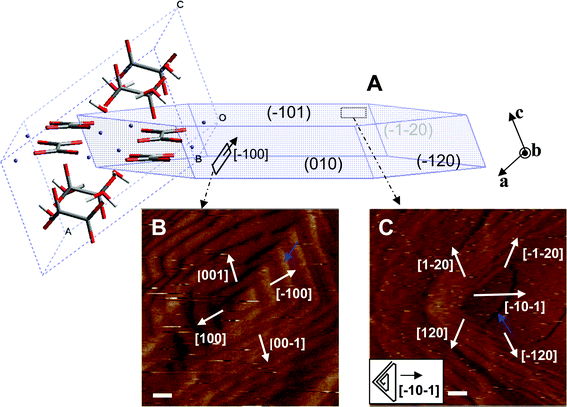 | ||
Fig. 1 (A) Schematic 3D sketch of a typical equilibrium habit of a calcium oxalate monohydrate (COM) crystal showing the commonly expressed planes {![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01}, {010}, and {120} and with an embedded unit cell showing the orientation of oxalate molecules with respect to crystal faces. (B, C) In situ AFM images showing the shape of dislocation hillocks and step directions on the (010) (B) and ( 01}, {010}, and {120} and with an embedded unit cell showing the orientation of oxalate molecules with respect to crystal faces. (B, C) In situ AFM images showing the shape of dislocation hillocks and step directions on the (010) (B) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces (C) of a COM crystal. Scale bars are 100 nm for (B) and 200 nm for (C). 01) faces (C) of a COM crystal. Scale bars are 100 nm for (B) and 200 nm for (C). | ||
A recent study18 utilizing linear 27-residue synthetic peptides designed to mimic the acidic domain of osteopontin found that these long chain peptides exhibited diverse functionalities in regulating COM crystal growth. Depending on the reaction conditions and local environments, they acted like a set of “switches, throttles and brakes” by interacting with specific steps on existing crystal faces to turn growth on and off, accelerate its speed, or slow it down. Other crystal model systems, such as calcite, with short acidic peptides, have also shown similar step-specific interactions.31 Studies of COM crystal growth with synthetic poly-aspartic acids are thus likely to provide insights into the role of aspartic acid rich domains of the biomolecules that regulate the growth of COM.
In this study, we investigate the growth of COM under the influence of 6-residue linear aspartic acid (Asp6) peptides whose molecular size and weight lie between those of citrate and the 27-mers. By performing studies with both L-Asp6 and D-Asp6, we also explored the effects of their chirality on regulating the growth of COM.
Similar to our previous studies, we investigated the effects of L-Asp6 and D-Asp6 on the growth of COM crystal using in situ atomic force microscopy (AFM). We found that Asp6 enantiomers affected growth of steps on both the (010) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces. While the effects on the (
01) faces. While the effects on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face were inhibitory, the effects on the (010) face depended on the step direction, leading to inhibition of the <100> step and slight acceleration of the <001> step.
01) face were inhibitory, the effects on the (010) face depended on the step direction, leading to inhibition of the <100> step and slight acceleration of the <001> step.
To understand the source of the inhibition exerted by L-Asp6 and D-Asp6, we applied a step kinetic model recently developed by Weaver et al.17 to the step speed data. This model was previously used to successfully explain the inhibitory effects of citrate on the growth of COM. Here we show that the growth kinetics of COM in the presence of L-Asp6 and D-Asp6 is also successfully described by this model. From the values of model parameters obtained by fitting the model to the step speed data, we estimate the differences in binding energies of the Asp6 enantiomers to the faces and steps, and compare the values of the binding energies to those predicted on the basis of molecular modeling as described in detail in the Experimental Methods section.
Results
Growth of COM in pure, L-Asp6- and D-Asp6-containing solutions
In the supersaturation range (σ ≤ 0.93) used in this study, COM crystals grew on dislocation (growth) hillocks on existing faces. Representative AFM images of the growth hillocks on (010) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces collected during growth in pure solution at σ = 0.93 are shown in Fig. 1B and C, respectively.
01) faces collected during growth in pure solution at σ = 0.93 are shown in Fig. 1B and C, respectively.
Growth of [![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 00] step on the (010) face
00] step on the (010) face
The growth hillocks on the (010) face (Fig. 1B) are similar to those previously reported12,15 which consisted of two pairs of parallel steps, typically generated at complex, multiple screw dislocations,12,15,18 mostly of the Frank–Reed type.32 The hillocks are bounded by the (120), (02![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (
), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20), and (021) faces.12 The step with the (120) riser plane propagates along the [100] direction, thus is labeled as the [100] step. By the same convention, the other three steps are labeled as [00
20), and (021) faces.12 The step with the (120) riser plane propagates along the [100] direction, thus is labeled as the [100] step. By the same convention, the other three steps are labeled as [00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], [
], [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00], and [001], respectively. When the steps were first born, they came out as single elementary steps. For the first couple of turns, the steps from different sources further merged to form multiple unit-height steps, including double and triple steps. Starting after the first couple of turns, quadruple-height steps with a total height of 1.5 nm were formed. The measured height corresponds well with the unit cell dimension of 1.4588 nm along the b axis.30 This quadrupling of steps is caused by so called “step interlacing”.33,34 A detailed description of their formation is given in ref. 15. One of the quadruple unit-height steps along the [
00], and [001], respectively. When the steps were first born, they came out as single elementary steps. For the first couple of turns, the steps from different sources further merged to form multiple unit-height steps, including double and triple steps. Starting after the first couple of turns, quadruple-height steps with a total height of 1.5 nm were formed. The measured height corresponds well with the unit cell dimension of 1.4588 nm along the b axis.30 This quadrupling of steps is caused by so called “step interlacing”.33,34 A detailed description of their formation is given in ref. 15. One of the quadruple unit-height steps along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction is indicated by a blue arrow in Fig. 1B.
00] direction is indicated by a blue arrow in Fig. 1B.
The Asp6 enantiomers played dual roles in modulating step growth on the (010) face. While slightly accelerating growth of the <001> steps, they produced modest inhibition of growth on the <100> steps. Here we focus upon the inhibitory effects at the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step, which is crystallographically equivalent to the [100] step. Fig. 2A shows the step speed of the [
00] step, which is crystallographically equivalent to the [100] step. Fig. 2A shows the step speed of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step in pure, 2 μM L-Asp6 and 2 μM D-Asp6 solutions over a range of calcium activities (
00] quadruple unit-height step in pure, 2 μM L-Asp6 and 2 μM D-Asp6 solutions over a range of calcium activities (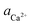 ). Based on the activity at which the [
). Based on the activity at which the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step speed crosses zero in the pure and Asp6-containing systems, we conclude that the addition of 2 μM of either enantiomer has negligible effects on the equilibrium calcium concentration, which was 0.095 ± 0.005 mM for all three systems. From this data, we obtained the equilibrium calcium activity (
00] step speed crosses zero in the pure and Asp6-containing systems, we conclude that the addition of 2 μM of either enantiomer has negligible effects on the equilibrium calcium concentration, which was 0.095 ± 0.005 mM for all three systems. From this data, we obtained the equilibrium calcium activity (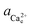 ), 0.042 mM and the equilibrium solubility, Ksp = 1.76 × 10−9 M2 by using Visual Minteq as described in the Experimental Methods section on Activity of ions and supersaturation of solutions. The obtained Ksp for the pure system is very close to the reported values of 1.56 × 10−9 M2 by Weaver et al.17 and 1.66 × 10−9 M2 by Tomazic et al.35
), 0.042 mM and the equilibrium solubility, Ksp = 1.76 × 10−9 M2 by using Visual Minteq as described in the Experimental Methods section on Activity of ions and supersaturation of solutions. The obtained Ksp for the pure system is very close to the reported values of 1.56 × 10−9 M2 by Weaver et al.17 and 1.66 × 10−9 M2 by Tomazic et al.35
![Dependence of step velocities on Ca2+ activities in pure, l-Asp6-, and d-Asp6-containing solutions. (A) [1̄00] quadruple unit-height step on (010) face in pure, 2 μM l-Asp6-, and 2 μM d-Asp6-containing systems and (B) [1̄01̄] double unit-height step on (1̄01) face in pure, 0.3 μM l-Asp6-, and 0.3 μM d-Asp6-containing systems.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f2.gif) | ||
Fig. 2 Dependence of step velocities on Ca2+ activities in pure, L-Asp6-, and D-Asp6-containing solutions. (A) [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step on (010) face in pure, 2 μM L-Asp6-, and 2 μM D-Asp6-containing systems and (B) [ 00] quadruple unit-height step on (010) face in pure, 2 μM L-Asp6-, and 2 μM D-Asp6-containing systems and (B) [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] double unit-height step on ( ] double unit-height step on (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face in pure, 0.3 μM L-Asp6-, and 0.3 μM D-Asp6-containing systems. 01) face in pure, 0.3 μM L-Asp6-, and 0.3 μM D-Asp6-containing systems. | ||
As shown in the step speed plots (Fig. 2A), the slopes for both Asp6-containing systems are all smaller than the slope for the pure system, indicating that both enantiomers inhibit growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face. Moreover, for the same peptide concentration in solutions, the addition of D-Asp6 results in about 10% larger step speed reduction than that of L-Asp6 throughout the entire range of calcium activities, demonstrating that D-Asp6 is a slightly stronger inhibitor than L-Asp6.
00] step on the (010) face. Moreover, for the same peptide concentration in solutions, the addition of D-Asp6 results in about 10% larger step speed reduction than that of L-Asp6 throughout the entire range of calcium activities, demonstrating that D-Asp6 is a slightly stronger inhibitor than L-Asp6.
The effect of L-Asp6 concentration on the kinetics and morphology of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step was investigated at σ = 0.93. Fig. 3 shows the step speed in the L-Asp6-bearing solution (Vi) relative to that for the pure solution (V0) as a function of L-Asp6 concentration (see unfilled black circles). As shown in the figure, the relative step speed decreased with increasing peptide concentration, dropping relatively faster at low peptide concentrations and leveling off starting at ∼2 μM L-Asp6. The morphological evolution of the growth hillocks with increasing peptide concentration corresponding to the step speed data is shown in Fig. 4. Under the influence of L-Asp6, the [
00] quadruple unit-height step was investigated at σ = 0.93. Fig. 3 shows the step speed in the L-Asp6-bearing solution (Vi) relative to that for the pure solution (V0) as a function of L-Asp6 concentration (see unfilled black circles). As shown in the figure, the relative step speed decreased with increasing peptide concentration, dropping relatively faster at low peptide concentrations and leveling off starting at ∼2 μM L-Asp6. The morphological evolution of the growth hillocks with increasing peptide concentration corresponding to the step speed data is shown in Fig. 4. Under the influence of L-Asp6, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] steps roughened, developing cusps and a serrated form indicative of step pinning, while the inter-step distance dropped slightly.
00] steps roughened, developing cusps and a serrated form indicative of step pinning, while the inter-step distance dropped slightly.
![Relative step velocity (Vi/V0) as a function of Asp6 concentration (Ci) in COM solution at a fixed supersaturation of σ = 0.93. Unfilled black circle: Vi/V0 of the [1̄00] quadruple unit-height step on (010) face in the presence of l-Asp6, unfilled square: Vi/V0 of [1̄00] quadruple unit-height step on (010) face in the presence of d-Asp6, and filled triangle: Vi/V0 of [1̄01̄] double unit-height step on (1̄01) face in the presence of d-Asp6. The solid lines are fits of eqn (1) to experimental data.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f3.gif) | ||
Fig. 3 Relative step velocity (Vi/V0) as a function of Asp6 concentration (Ci) in COM solution at a fixed supersaturation of σ = 0.93. Unfilled black circle: Vi/V0 of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step on (010) face in the presence of L-Asp6, unfilled square: Vi/V0 of [ 00] quadruple unit-height step on (010) face in the presence of L-Asp6, unfilled square: Vi/V0 of [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step on (010) face in the presence of D-Asp6, and filled triangle: Vi/V0 of [ 00] quadruple unit-height step on (010) face in the presence of D-Asp6, and filled triangle: Vi/V0 of [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] double unit-height step on ( ] double unit-height step on (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face in the presence of D-Asp6. The solid lines are fits of eqn (1) to experimental data. 01) face in the presence of D-Asp6. The solid lines are fits of eqn (1) to experimental data. | ||
![Sequential in situ AFM images showing the effects of the concentration of l-Asp6 on the growth of the [1̄00] step on the (01̄0) face at a fixed supersaturation of σ = 0.93. Note that the (010) face and the (01̄0) face are equivalent by the monoclinic symmetry. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure (0 μM l-Asp6), (B) 0.3 μM l-Asp6 at solution flow time, t = 23 min, (C) 0.5 μM l-Asp6 at t = 21 min, (D) 2 μM l-Asp6 at t = 24 min, (E) 3 μM l-Asp6 at t = 27 min, and (F) 5 μM l-Asp6 at t = 30 min. Scale bars are 100 nm.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f4.gif) | ||
Fig. 4 Sequential in situ AFM images showing the effects of the concentration of L-Asp6 on the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (0 00] step on the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) face at a fixed supersaturation of σ = 0.93. Note that the (010) face and the (0 0) face at a fixed supersaturation of σ = 0.93. Note that the (010) face and the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) face are equivalent by the monoclinic symmetry. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure (0 μM L-Asp6), (B) 0.3 μM L-Asp6 at solution flow time, t = 23 min, (C) 0.5 μM L-Asp6 at t = 21 min, (D) 2 μM L-Asp6 at t = 24 min, (E) 3 μM L-Asp6 at t = 27 min, and (F) 5 μM L-Asp6 at t = 30 min. Scale bars are 100 nm. 0) face are equivalent by the monoclinic symmetry. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure (0 μM L-Asp6), (B) 0.3 μM L-Asp6 at solution flow time, t = 23 min, (C) 0.5 μM L-Asp6 at t = 21 min, (D) 2 μM L-Asp6 at t = 24 min, (E) 3 μM L-Asp6 at t = 27 min, and (F) 5 μM L-Asp6 at t = 30 min. Scale bars are 100 nm. | ||
The effects of D-Asp6 concentration (unfilled square in Fig. 3) on the step speed of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step was also investigated at σ = 0.93 and were similar to those seen using L-Asp6. As Fig. 3 and 5 show, similar dependencies of the relative step speed and morphology on peptide concentration were obtained. However, D-Asp6 was a somewhat better inhibitor than was L-Asp6, with the reduction in step speed being about 10% greater over the entire concentration range (Fig. 3) and the steps being a little rougher and the inter-step distance slightly smaller at equal peptide concentrations. The underlying reasons for the observed differences between the effect of the L- and D-enantiomers are explored in the Discussion section.
00] quadruple unit-height step was also investigated at σ = 0.93 and were similar to those seen using L-Asp6. As Fig. 3 and 5 show, similar dependencies of the relative step speed and morphology on peptide concentration were obtained. However, D-Asp6 was a somewhat better inhibitor than was L-Asp6, with the reduction in step speed being about 10% greater over the entire concentration range (Fig. 3) and the steps being a little rougher and the inter-step distance slightly smaller at equal peptide concentrations. The underlying reasons for the observed differences between the effect of the L- and D-enantiomers are explored in the Discussion section.
![In situ AFM images showing the effects of the concentration of d-Asp6 on the growth of [1̄00] step on the (01̄0) face at a fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.5 μM d-Asp6 at solution flow time, t = 26 min, (C) pure, (D) 2 μM d-Asp6 at t = 25 min, (E) pure, and (F) 5 μM d-Asp6 at t = 20 min. Scale bars are 100 nm.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f5.gif) | ||
Fig. 5
In situ AFM images showing the effects of the concentration of D-Asp6 on the growth of [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (0 00] step on the (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) face at a fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.5 μM D-Asp6 at solution flow time, t = 26 min, (C) pure, (D) 2 μM D-Asp6 at t = 25 min, (E) pure, and (F) 5 μM D-Asp6 at t = 20 min. Scale bars are 100 nm. 0) face at a fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.5 μM D-Asp6 at solution flow time, t = 26 min, (C) pure, (D) 2 μM D-Asp6 at t = 25 min, (E) pure, and (F) 5 μM D-Asp6 at t = 20 min. Scale bars are 100 nm. | ||
Growth of [![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 01) face
01) face
As shown in the inset of Fig. 1C, the growth hillocks on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face are triangular, expressing the two mirror-symmetry related [
01) face are triangular, expressing the two mirror-symmetry related [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] and [
0] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20] steps and the single [
20] steps and the single [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step (again, the step direction is defined to which the step propagates). The hillock shape seen in the AFM image (Fig. 1C) is, however, significantly distorted from its true shape, especially towards the side defined by the [
] step (again, the step direction is defined to which the step propagates). The hillock shape seen in the AFM image (Fig. 1C) is, however, significantly distorted from its true shape, especially towards the side defined by the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step. As explained in the Experimental Methods section on In situ atomic force microscopy, this distortion results from the finite scan speed of the AFM tip during imaging. This effect is particularly pronounced for the [
] step. As explained in the Experimental Methods section on In situ atomic force microscopy, this distortion results from the finite scan speed of the AFM tip during imaging. This effect is particularly pronounced for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, because it grows much faster for a given solution supersaturation than all other steps on either the (
01) face, because it grows much faster for a given solution supersaturation than all other steps on either the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) or the (010) face.
01) or the (010) face.
For some of the hillocks on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, the [
01) face, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step was observed to grow continuously as a single unit-height step of ∼0.4 nm. More typically, however, newly born steps were double unit-height steps with a measured height of 0.57 nm. The double unit-height step could be resulted from the merge of a fast growing single step of 0.2 nm and the unit-height step of ∼0.4 nm. The measured height is consistent with the molecular structure of COM on the (010) face as discussed in ref. 15 which contains two sub-layers of oxalate when viewing along the [010] direction. An example of a double step is indicated by a blue arrow in Fig. 1C.
] step was observed to grow continuously as a single unit-height step of ∼0.4 nm. More typically, however, newly born steps were double unit-height steps with a measured height of 0.57 nm. The double unit-height step could be resulted from the merge of a fast growing single step of 0.2 nm and the unit-height step of ∼0.4 nm. The measured height is consistent with the molecular structure of COM on the (010) face as discussed in ref. 15 which contains two sub-layers of oxalate when viewing along the [010] direction. An example of a double step is indicated by a blue arrow in Fig. 1C.
Fig. 2B shows the velocities of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] double unit-height step in pure, 0.3 μM L-Asp6-, and 0.3 μM D-Asp6-bearing solutions over a range of calcium activities. Examining the plots, we find that, as expected from the results for the [
] double unit-height step in pure, 0.3 μM L-Asp6-, and 0.3 μM D-Asp6-bearing solutions over a range of calcium activities. Examining the plots, we find that, as expected from the results for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face, the data give an equilibrium calcium concentration of 0.095 ± 0.005, which translates to an equilibrium calcium activity of 0.042 mM.
00] step on the (010) face, the data give an equilibrium calcium concentration of 0.095 ± 0.005, which translates to an equilibrium calcium activity of 0.042 mM.
Fig. 2B also shows that, when 0.3 μM L-Asp6 or 0.3 μM D-Asp6 was added to the growth solutions, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step velocity decreased dramatically at all calcium activities above the equilibrium calcium activity. This result is in stark contrast to that obtained for the [
] step velocity decreased dramatically at all calcium activities above the equilibrium calcium activity. This result is in stark contrast to that obtained for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face as shown in Fig. 2A. Moreover, unlike the [
00] step on the (010) face as shown in Fig. 2A. Moreover, unlike the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step where D-Asp6 caused about 10% larger inhibition than L-Asp6, the [
00] step where D-Asp6 caused about 10% larger inhibition than L-Asp6, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step was equally inhibited by L-Asp6 and D-Asp6. This is expected, as there is no symmetry element in the [
] step was equally inhibited by L-Asp6 and D-Asp6. This is expected, as there is no symmetry element in the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step that can produce a chiral effect.36 Moreover, the strong reduction in the step velocity on the [
] step that can produce a chiral effect.36 Moreover, the strong reduction in the step velocity on the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step occurred at a much smaller peptide concentration (0.3 μM) than that on the [
] step occurred at a much smaller peptide concentration (0.3 μM) than that on the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step (2 μM), a nearly 7-fold difference. This further shows that both enantiomers inhibited the [
00] step (2 μM), a nearly 7-fold difference. This further shows that both enantiomers inhibited the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face much more effectively than they did the [
01) face much more effectively than they did the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face. The effects of peptide concentration on growth of the [
00] step on the (010) face. The effects of peptide concentration on growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step and the physical basis for the observed differences between both the morphological and kinetic effects at the [
] step and the physical basis for the observed differences between both the morphological and kinetic effects at the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] and [
] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] steps are discussed below and in the Discussion section.
00] steps are discussed below and in the Discussion section.
Because the D-Asp6 and L-Asp6 enantiomers had the same or very similar effects in modifying the step kinetics (Fig. 2B) and morphology of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on (
] step on (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, we used only D-Asp6 to investigate the peptide concentration effects. As with the experiments on the (010) face, the solution supersaturation was held constant at σ = 0.93. The relative step speed of the [
01) face, we used only D-Asp6 to investigate the peptide concentration effects. As with the experiments on the (010) face, the solution supersaturation was held constant at σ = 0.93. The relative step speed of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] double unit-height step as a function of D-Asp6 concentration is shown in Fig. 3 and the evolution of the [
] double unit-height step as a function of D-Asp6 concentration is shown in Fig. 3 and the evolution of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step morphology is shown in Fig. 6. As discussed above, because the [
] step morphology is shown in Fig. 6. As discussed above, because the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step moved at a speed that was fast relative to that of all other steps (e.g., 27 nm s−1 for the [
] step moved at a speed that was fast relative to that of all other steps (e.g., 27 nm s−1 for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] vs. 1.6 nm s−1 for the [
] vs. 1.6 nm s−1 for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step at σ = 0.93) in pure solution (Fig. 6A), the apparent [
00] step at σ = 0.93) in pure solution (Fig. 6A), the apparent [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step morphology was significantly distorted from its true morphology illustrated by the inset in Fig. 1C. In contrast, because of the steep drop in [
] step morphology was significantly distorted from its true morphology illustrated by the inset in Fig. 1C. In contrast, because of the steep drop in [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step speed upon introduction of peptide-containing solution (e.g., 27 nm s−1 in pure solution vs. 1.5 nm s−1 at 0.3 μM D- or L-Asp6), the images shown in Fig. 6, B–F are very close to their true morphology.
] step speed upon introduction of peptide-containing solution (e.g., 27 nm s−1 in pure solution vs. 1.5 nm s−1 at 0.3 μM D- or L-Asp6), the images shown in Fig. 6, B–F are very close to their true morphology.
![Sequential in situ AFM images showing the effects of the concentration of d-Asp6 on the growth of [1̄01̄] step on (1̄01) face at fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.05 μM d-Asp6 at solution flow time, t = 20 min, (C) 0.1 μM d-Asp6 at t = 20 min, (D) 0.2 μM d-Asp6 at t = 19 min, (E) 0.3 μM d-Asp6 at t = 20 min, and (F) 2 μM d-Asp6 at t = 20 min. Scale bars are 100 nm.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f6.gif) | ||
Fig. 6 Sequential in situ AFM images showing the effects of the concentration of D-Asp6 on the growth of [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on ( ] step on (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face at fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.05 μM D-Asp6 at solution flow time, t = 20 min, (C) 0.1 μM D-Asp6 at t = 20 min, (D) 0.2 μM D-Asp6 at t = 19 min, (E) 0.3 μM D-Asp6 at t = 20 min, and (F) 2 μM D-Asp6 at t = 20 min. Scale bars are 100 nm. 01) face at fixed supersaturation of σ = 0.93. Morphologies of the hillocks observed in the images (A–F) are from solution with: (A) pure, (B) 0.05 μM D-Asp6 at solution flow time, t = 20 min, (C) 0.1 μM D-Asp6 at t = 20 min, (D) 0.2 μM D-Asp6 at t = 19 min, (E) 0.3 μM D-Asp6 at t = 20 min, and (F) 2 μM D-Asp6 at t = 20 min. Scale bars are 100 nm. | ||
In stark contrast to the moderate reduction of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step velocity on the (010) face, D-Asp6 drastically reduced the growth of the [101] step. As shown in Fig. 6B, upon 0.05 μM D-Asp6 addition, the [
00] step velocity on the (010) face, D-Asp6 drastically reduced the growth of the [101] step. As shown in Fig. 6B, upon 0.05 μM D-Asp6 addition, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step already roughened significantly, showing the typical features of step pinning. As the concentration was increased further, this roughening also increased and the steps along all other directions began to express a similar morphology. At peptide concentrations above 0.2 μM (Fig. 6D), the steps lost their lateral stability, having become highly convoluted and exhibiting step bunching. As was the case for the (010) face, on which the peptide effect approached saturation starting at a peptide concentration ∼2 μM, the effect of the peptide on this face approached saturation beyond about 0.3 μM, both in terms of step inhibition and roughening.
] step already roughened significantly, showing the typical features of step pinning. As the concentration was increased further, this roughening also increased and the steps along all other directions began to express a similar morphology. At peptide concentrations above 0.2 μM (Fig. 6D), the steps lost their lateral stability, having become highly convoluted and exhibiting step bunching. As was the case for the (010) face, on which the peptide effect approached saturation starting at a peptide concentration ∼2 μM, the effect of the peptide on this face approached saturation beyond about 0.3 μM, both in terms of step inhibition and roughening.
The resulting growth hillocks were ellipsoidal, with the major axis slanting a few tens of degrees from the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction. A similar morphology was observed under the influence of citrate.12,15 However, in that case, the hillocks were more disk-shaped and the major axis was co-aligned with the [
] direction. A similar morphology was observed under the influence of citrate.12,15 However, in that case, the hillocks were more disk-shaped and the major axis was co-aligned with the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction. The difference can be attributed to the structural disparity between citrate and the D-Asp6 enantiomer. While citrate inhibited both the [
] direction. The difference can be attributed to the structural disparity between citrate and the D-Asp6 enantiomer. While citrate inhibited both the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20] and [
20] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] steps equally, as we will show in a separate paper to be submitted, the D-Asp6 enantiomer showed preferential inhibition of the [
0] steps equally, as we will show in a separate paper to be submitted, the D-Asp6 enantiomer showed preferential inhibition of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 20] over the [
20] over the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] step, while the L-enantiomer produced the inverse effect. As discussed in that paper, this chiral dependence is a result of preferential binding of the enantiomers to steps that are related by mirror symmetry and it causes the off-[
0] step, while the L-enantiomer produced the inverse effect. As discussed in that paper, this chiral dependence is a result of preferential binding of the enantiomers to steps that are related by mirror symmetry and it causes the off-[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] orientation of the ellipsoidal hillock.
] orientation of the ellipsoidal hillock.
Discussion
Model of impurity-induced step pinning
Recently, a mathematical model describing step kinetics in a mineral system in the presence of impurity was developed by Weaver et al.17 This model reformulates the classic Cabrera–Vermilyea model of step pinning37 by introducing Langmuir-type impurity adsorption dynamics, including the effect of impurity-induced reduction of the kinetic coefficient due to kink blocking when the supersaturation is above the dead zone, and utilizing an exact expression for the Gibbs–Thomson effect so that it is correct at all supersaturations. The model predicts that the step velocity of a crystal in the presence of an impurity (Vi) relative to that for the pure solution (V0) is as follows: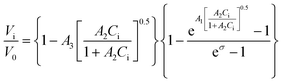 | (1) |
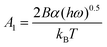 , A2 = kA/kD, and
, A2 = kA/kD, and 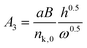 .
.
Here Ci is the impurity concentration in the solution, σ is as defined above, B is the product of three unit-less proportionality constants: 1) the fraction of adsorbed impurities that actually stick to the step and pin it, 2) the geometric factor relating linear impurity spacing to areal density, and 3) the percolation threshold for a step to move through a field of blocking sites derived by Potapenko,38α is step-edge free energy per unit step height, h is step height, ω is molecular volume in the crystal, kB is Boltzmann's constant, T is absolute temperature, kA and kD are the adsorption and desorption rate coefficients, a is the molecular spacing along the step line, and nk,0 is kink density in the absence of impurities.
In eqn (1), Vi/V0 is expressed in terms of three fitting parameters A1, A2, and A3, which are controlled by three fundamental parameters of the system α, kA/kD and nk,0. The term in the first set of curly brackets in eqn (1), determines the active kink density and therefore the kinetic coefficient, while the term in the second curly brackets reflects the Gibbs–Thomson effect and thus the supersaturation below which no growth occurs as a result of the step curvature imposed by impurity pinning. As Fig. 2A and B show, the main impact of the peptides is to reduce the kinetic coefficient, thus A2 and A3 are the most important fitting parameters in controlling the observed inhibition. The lines in Fig. 3 are fits of eqn (1) to our experimental data for Vi/V0 at σ = 0.93. The fitting parameters A1, A2, and A3 are shown in Table 1.
| Impurity | Step and face | A 1 | A 2 (μM−1) | A 3 |
|---|---|---|---|---|
| L-Asp6 | [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00]/(010) 00]/(010) |
0.782 | 0.053 | 8.53 × 10−11 |
| D-Asp6 | [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00]/(010) 00]/(010) |
0.533 | 0.293 | 2.42 × 10−10 |
| D-Asp6 | [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]/( ]/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) 01) |
0.948 | 10.106 | 2.36 × 10−5 |
Factors responsible for differences in the effects of L-Asp6 and D-Asp6: the <100> step
As shown in Fig. 2A and Fig. 3, D-Asp6 inhibited [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step growth more strongly than L-Asp6 over the investigated ranges of calcium activities (
00] quadruple unit-height step growth more strongly than L-Asp6 over the investigated ranges of calcium activities (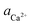 ) and Asp6 concentrations (Ci). Analysis of the fitting parameters provides evidence for the source of this difference. However, it is meaningless to compare the values of A3 for the D-Asp6 and L-Asp6 systems, because even 8-fold variations in their values essentially do not change the quality of the fits. This is because A3 ≪ 1 and the value of (A2Ci/1 + A2Ci)0.5, which gives the fraction (θ) of surface sites occupied by an adsorbed peptide, is less than unity over all investigated Asp6 concentrations for both the L- and D-enantiomers. Thus 1 − A3(A2Ci/1 + A2Ci)0.5 ≈ 1. Unlike A3, the Langmuir constant, A2 (=kA/kD) produces large changes in the quality of fit. For example, when A2 is increased by just a factor of 2 from the current value of 0.053 used in Fig. 3 for the L-Asp6 enantiomer, the resulting r2 value for the fit decreases from 0.94 to 0.64. The best fit of eqn (1) to the data sets for the two enantiomers gives
) and Asp6 concentrations (Ci). Analysis of the fitting parameters provides evidence for the source of this difference. However, it is meaningless to compare the values of A3 for the D-Asp6 and L-Asp6 systems, because even 8-fold variations in their values essentially do not change the quality of the fits. This is because A3 ≪ 1 and the value of (A2Ci/1 + A2Ci)0.5, which gives the fraction (θ) of surface sites occupied by an adsorbed peptide, is less than unity over all investigated Asp6 concentrations for both the L- and D-enantiomers. Thus 1 − A3(A2Ci/1 + A2Ci)0.5 ≈ 1. Unlike A3, the Langmuir constant, A2 (=kA/kD) produces large changes in the quality of fit. For example, when A2 is increased by just a factor of 2 from the current value of 0.053 used in Fig. 3 for the L-Asp6 enantiomer, the resulting r2 value for the fit decreases from 0.94 to 0.64. The best fit of eqn (1) to the data sets for the two enantiomers gives 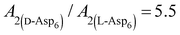 (Table 1). As shown in Fig. 7, converting this ratio to a difference in (010) surface coverage θ gives
(Table 1). As shown in Fig. 7, converting this ratio to a difference in (010) surface coverage θ gives 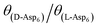 ranging from 5.5 to 3 over the range of peptide concentrations investigated here.
ranging from 5.5 to 3 over the range of peptide concentrations investigated here.
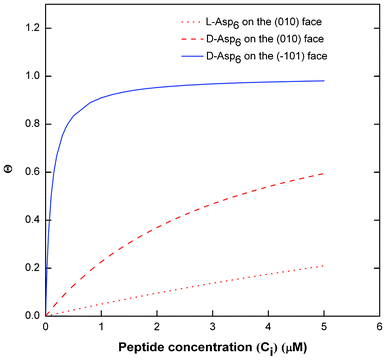 | ||
Fig. 7 Langmuir adsorption curves of surface Asp6 coverage (θ) vs. Asp6 concentration (Ci) in COM solution. The curves are drawn using the values of Langmuir constants (A2) of Asp6 on (010) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) faces obtained from the fitting of eqn (1) to the experimental data of Vi/V0 of COM crystal growth shown in Fig. 3. Solid line corresponds to D-Asp6 on the ( 01) faces obtained from the fitting of eqn (1) to the experimental data of Vi/V0 of COM crystal growth shown in Fig. 3. Solid line corresponds to D-Asp6 on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, the dashed line represents (D-Asp)6 on the (010) face, and the dotted line represents L-Asp6 on the (010) face. 01) face, the dashed line represents (D-Asp)6 on the (010) face, and the dotted line represents L-Asp6 on the (010) face. | ||
While this difference in surface coverage is important, because the number of impurities that actually stick to the moving step plays a critical role in determining the level of inhibition, to further understand the difference in inhibition, we must compare the linear density (Di) of impurities along the step for the two enantiomers. Di is given by:17
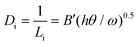 | (2) |
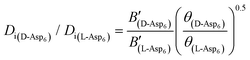 . Of the other two factors that comprise B (see the description after eqn (1)), only the fraction of adsorbed impurities that actually stick to and pin the step can be different for the two enantiomers. As a consequence, we conclude that the difference between the inhibitory effects of the D- and L-enantiomers on the growth of the [
. Of the other two factors that comprise B (see the description after eqn (1)), only the fraction of adsorbed impurities that actually stick to and pin the step can be different for the two enantiomers. As a consequence, we conclude that the difference between the inhibitory effects of the D- and L-enantiomers on the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] quadruple unit-height step is due to the product of the difference in surface coverage of peptides as controlled by kA/kD and the fraction of adsorbed impurities that actually bind to the step.
00] quadruple unit-height step is due to the product of the difference in surface coverage of peptides as controlled by kA/kD and the fraction of adsorbed impurities that actually bind to the step.
To evaluate the difference in Di for the two enantiomers, we note that, because the percolation threshold is simply a geometric term unrelated to the peptide chirality, 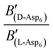 can be replaced by
can be replaced by 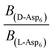 . Moreover, because the similarity of (and small changes in) the inter-step spacing indicate that the values of α are equal or nearly so in the presence of the two enantiomers,
. Moreover, because the similarity of (and small changes in) the inter-step spacing indicate that the values of α are equal or nearly so in the presence of the two enantiomers, 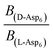 can be replaced by
can be replaced by 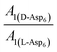 (see formula of A1 in eqn (1)). Thus
(see formula of A1 in eqn (1)). Thus 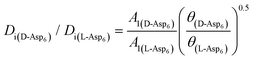 . As shown in Fig. 8 (black solid line), using the values of
. As shown in Fig. 8 (black solid line), using the values of 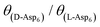 calculated above (and shown in Fig. 7), and the values of A1 for the two enantiomers in Table 1, we find that the density of impurities along the step for D-Asp6 is 1.6–1.2 times larger than for L-Asp6 over the range of investigated peptide concentrations. Of course, in the limit of low peptide concentration, this difference is, in turn, controlled by the differences in binding energy for D-Asp6 and L-Asp6 to the terrace and step through
calculated above (and shown in Fig. 7), and the values of A1 for the two enantiomers in Table 1, we find that the density of impurities along the step for D-Asp6 is 1.6–1.2 times larger than for L-Asp6 over the range of investigated peptide concentrations. Of course, in the limit of low peptide concentration, this difference is, in turn, controlled by the differences in binding energy for D-Asp6 and L-Asp6 to the terrace and step through 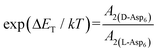 and
and 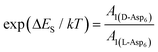 respectively where ΔET and ΔES are the differences between the D-Asp6 and L-Asp6 binding energies at the terrace and step, respectively. From this we estimate ΔET and ΔES to be ∼4 kJ mol−1 and <−1 kJ mol−1, respectively. From this analysis we conclude that the difference in inhibitory effects at the [
respectively where ΔET and ΔES are the differences between the D-Asp6 and L-Asp6 binding energies at the terrace and step, respectively. From this we estimate ΔET and ΔES to be ∼4 kJ mol−1 and <−1 kJ mol−1, respectively. From this analysis we conclude that the difference in inhibitory effects at the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face is primarily due to a difference in the strength of Asp6 binding to the terrace.
00] step on the (010) face is primarily due to a difference in the strength of Asp6 binding to the terrace.
![Solid line represents the ratio of the linear density (Di) of d-Asp6 to that of (l-Asp)6 on [1̄00] step on (010) face as a function of Asp6 concentration (Ci) in COM solution. Dashed line displays the ratio of Di of d-Asp6 on [1̄01̄] step on (1̄01) face to that on [1̄00] step on (010) face as a function of Ci in COM solution.](/image/article/2013/CE/c2ce25936b/c2ce25936b-f8.gif) | ||
Fig. 8 Solid line represents the ratio of the linear density (Di) of D-Asp6 to that of (L-Asp)6 on [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on (010) face as a function of Asp6 concentration (Ci) in COM solution. Dashed line displays the ratio of Di of D-Asp6 on [ 00] step on (010) face as a function of Asp6 concentration (Ci) in COM solution. Dashed line displays the ratio of Di of D-Asp6 on [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on ( ] step on (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face to that on [ 01) face to that on [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on (010) face as a function of Ci in COM solution. 00] step on (010) face as a function of Ci in COM solution. | ||
Factors responsible for differences in the effects of D-Asp6 and L-Asp6: the (010) and (![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 01) faces
01) faces
As shown in Fig. 2B and Fig. 3, the Asp6 enantiomers inhibited the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face far more than they did the growth of the [
01) face far more than they did the growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face. Comparing the values of A1, A2 and A3 from Table 1 for the two faces and step types and performing similar analyses to those detailed above leads to the following conclusions: 1) The surface coverage of adsorbed D-Asp6 peptides is much greater on the (
00] step on the (010) face. Comparing the values of A1, A2 and A3 from Table 1 for the two faces and step types and performing similar analyses to those detailed above leads to the following conclusions: 1) The surface coverage of adsorbed D-Asp6 peptides is much greater on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face than on the (010) face with the difference in surface binding energy estimated to be ∼9 kJ mol−1. 2) The fraction of adsorbed D-Asp6 peptides that stick to the step is several times greater for the [
01) face than on the (010) face with the difference in surface binding energy estimated to be ∼9 kJ mol−1. 2) The fraction of adsorbed D-Asp6 peptides that stick to the step is several times greater for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step (on the (
] step (on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face) than for the [
01) face) than for the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step (on the (010) face), with the difference in step binding energy estimated to be ∼1 kJ mol−1 (see Fig. 8 dashed line, for example, at Ci = 0.3 μM,
00] step (on the (010) face), with the difference in step binding energy estimated to be ∼1 kJ mol−1 (see Fig. 8 dashed line, for example, at Ci = 0.3 μM, 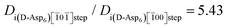 ).
).
These differences in binding energies and the resulting differences in peptide coverage both on the terraces and along the steps provide the underlying reason why the density of pinning sites and step roughening are so much greater for the steps on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face than on the (010) face. The difference in binding affinity can, in turn, be attributed to the stark difference between the arrangements of calcium and oxalate ions on the (
01) face than on the (010) face. The difference in binding affinity can, in turn, be attributed to the stark difference between the arrangements of calcium and oxalate ions on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) and (010) faces and the [
01) and (010) faces and the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] and [
] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step risers, as discussed in our previous reports on the effects of citrate12,15,17 and Asp-rich peptides18 on the growth of COM. The (010) face contains two oxalate sub-lattices, one of which extends beyond the (010) face. As a result, although overall the surface is neutral in charge, an incoming impurity sees the negatively-charged oxalate oxygens. Thus binding by the carboxylate groups of citrate, Asp, or poly-Asp molecules is greatly hindered due to the local electrostatic repulsion. On the other hand, on the (
00] step risers, as discussed in our previous reports on the effects of citrate12,15,17 and Asp-rich peptides18 on the growth of COM. The (010) face contains two oxalate sub-lattices, one of which extends beyond the (010) face. As a result, although overall the surface is neutral in charge, an incoming impurity sees the negatively-charged oxalate oxygens. Thus binding by the carboxylate groups of citrate, Asp, or poly-Asp molecules is greatly hindered due to the local electrostatic repulsion. On the other hand, on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face, the oxalate ions are flat-lying and their negative charge is compensated for by surface-exposed Ca2+ ions. This configuration eliminates the electrostatic repulsion of the carboxylates seen on the (010) face, while the presence of the calcium sites facilitates carboxylate binding. As is also shown in refs. 12 and 15, the arrangement of calcium and oxalate ions in the [
01) face, the oxalate ions are flat-lying and their negative charge is compensated for by surface-exposed Ca2+ ions. This configuration eliminates the electrostatic repulsion of the carboxylates seen on the (010) face, while the presence of the calcium sites facilitates carboxylate binding. As is also shown in refs. 12 and 15, the arrangement of calcium and oxalate ions in the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step riser also differs from that in the [
] step riser also differs from that in the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] riser and, at least in the case of citrate, provides better stereochemical matching to the distribution of carboxylate groups in the adsorbate. Given the structural similarities between poly-Asp and citrate—a linear molecule with multiple carboxylic side groups spaced along its length—we expect similar stereochemical considerations regardless of the chirality to favor Asp6 binding to the [
00] riser and, at least in the case of citrate, provides better stereochemical matching to the distribution of carboxylate groups in the adsorbate. Given the structural similarities between poly-Asp and citrate—a linear molecule with multiple carboxylic side groups spaced along its length—we expect similar stereochemical considerations regardless of the chirality to favor Asp6 binding to the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step over the [
] step over the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step.
00] step.
Computational results
The computational results are summarized in Table 2. As expected, the Asp6 enantiomers favor adsorption onto the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) plane over the (010) plane, regardless of the termination of the (010) surface (A, A′, B, or B′), which has been discussed in detail in ref. 15. The lower binding preference to (010) is expected due to the oxalates, which protrude from its surface. Although the predicted general trend agrees with experimental results, the difference in the calculated binding energies for D-Asp6 to the faces are four to five times larger than the 9 kJ mol−1 estimated from the experiments, with the A and B terminations giving 37 kJ mol−1 and the A′ and B′ terminations—which are likely to be less stable—yielding 40 kJ mol−1.
01) plane over the (010) plane, regardless of the termination of the (010) surface (A, A′, B, or B′), which has been discussed in detail in ref. 15. The lower binding preference to (010) is expected due to the oxalates, which protrude from its surface. Although the predicted general trend agrees with experimental results, the difference in the calculated binding energies for D-Asp6 to the faces are four to five times larger than the 9 kJ mol−1 estimated from the experiments, with the A and B terminations giving 37 kJ mol−1 and the A′ and B′ terminations—which are likely to be less stable—yielding 40 kJ mol−1.
| L-Asp6 | D-Asp6 | ||
|---|---|---|---|
a Equivalent by symmetry to L-Asp6 on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) plane. The ( 01) plane. The (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) surface has a horizontal mirror plane.
b Computed as L-Asp6 on the B′-terminated (0 01) surface has a horizontal mirror plane.
b Computed as L-Asp6 on the B′-terminated (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface.
c Computed as L-Asp6 on the A-terminated (0 0) surface.
c Computed as L-Asp6 on the A-terminated (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface.
d Equivalent by symmetry to the A(A′)-termination results. The B(B′) surface is related to the A(A′) surface by C2 rotation. 0) surface.
d Equivalent by symmetry to the A(A′)-termination results. The B(B′) surface is related to the A(A′) surface by C2 rotation.
|
|||
(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face 01) face |
−193.2 | −193.2a | |
| (010) face | A-termination | −144.5 | −156.7b |
| A′-termination | −151.0 | −153.6c | |
| B-terminationd | −144.5 | −156.7 | |
| B′-terminationd | −151.0 | −153.6 | |
In agreement with experiments, our computational results also predict that chiral recognition should occur on the (010) face, with D-Asp6 binding more strongly than L-Asp6, no matter which termination of the (010) surface is actually expressed. In the case of the A and B terminations, D-Asp6 is preferred by 12 kJ mol−1, while for the A′ and B′ terminations the difference is only 2.6 kJ mol−1, as compared to the value of 4 kJ mol−1 estimated from experiments. Fig. 9 illustrates the favored binding of D-Asp6, as compared to L-Asp6, bound to the A-terminated (010) surface, with its peptide backbone nearly aligned with the c axis of COM. Chiral recognition on (010) is attributed to the geometrical compatibility which permits the D-Asp6 enantiomer to bind along a path between the upright, protruding oxalates along the c axis, while maintaining low internal dihedral strain.
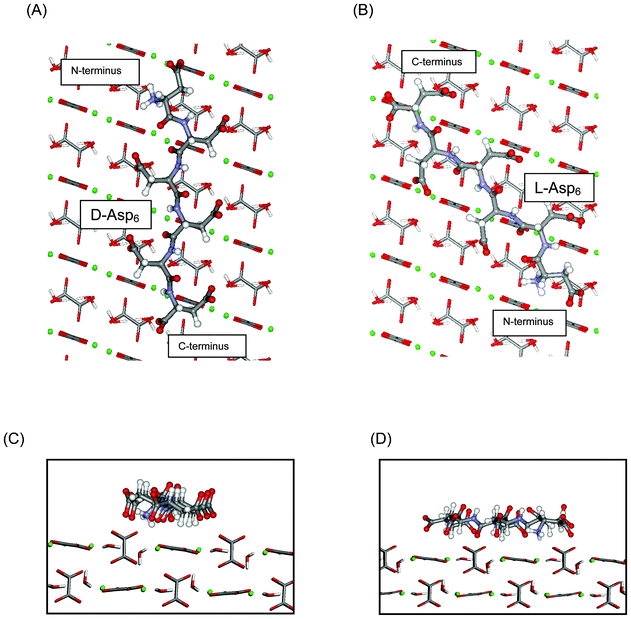 | ||
| Fig. 9 Asp6 enantiomers bound to the flat (010) face of COM: (A) D-Asp6 and (B) L-Asp6. Peptides: ball and stick; COM waters and oxalates: tubes; COM calcium ions: green balls. D-Asp6: The polypeptide backbone is nearly aligned with the c axis of COM and most of the polypeptide follows a path over flat surface oxalates and between two columns of upright, protruding oxalates. The sidechain carboxylates of Asp3 and Asp5 are positioned between protruding oxalates to make favorable interactions with surface calcium ions. The sidechain carboxylate of Asp1, the terminal carboxylate of Asp6, and the carbonyl oxygens of Asp2 and Asp4 are also engaged with calcium ions along a common column, as are the sidechain carboxylates of Asp2, Asp4, and Asp6. L-Asp6: The polypeptide is not aligned with the c axis and instead follows a path passing through a column of protruding oxalates. (C) and (D): Side views along the c axis of the binding shown in (A) and (B), respectively. The A termination of the (010) surface is shown. | ||
Experimental methods
Preparation of COM seed crystals
Seed crystals of COM used for the in situ AFM investigation were grown using a gel method. Details of the method are given in ref. 39.Preparation of 6-residue linear aspartic acid peptides
L-Asp6 and D-Asp6 with purity over 98% (HPLC) were obtained from PEPTIDE 2.0 as a powder and stored at −20 °C before use.Preparation of solutions
Double distilled water was used to make the growth solutions of calcium oxalate monohydrate (CaC2O4·H2O). Supersaturated CaC2O4·H2O solutions with calcium to oxalate ratio of 1 were prepared by mixing CaCl2·2H2O (reagent grade) solution and K2C2O4 (reagent grade) solution in equal volumes. Both the CaCl2·2H2O and K2C2O4 solutions contained the desired amounts of KCl to ensure the growth solution had a fixed ionic strength of 0.05 M.17 The pH of CaC2O4·H2O solutions was adjusted to values between 6.94 and 7.02 by adding small amounts of bases or acids (NaOH, HCl) into the solutions before each experiment. To prepare the Asp6-containing solutions, the desired amount of concentrated Asp6 solution (1 mg per 50 ml) was first introduced into the CaCl2·2H2O solution before it was mixed with the K2C2O4 solution. However, this sequence was not necessary as we found that with the reverse order of mixing, identical results were obtained.Activity of ions and supersaturation of solutions
The activity (a) of an ion in solution is expressed as a = γX where γ is the activity coefficient and X is the concentration of the ion.40 Activities of calcium and oxalate ions in solutions were obtained by using the multi-component speciation program Visual Minteq41 which uses the Davies equation to give the ion activity coefficient. In the concentration range of calcium and oxalate used for the experiments, the activities of calcium and oxalate can be considered to be equal.17 Thus, the supersaturation (σ) defined by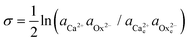 where
where 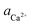 (
(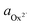 ) and
) and 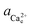 (
(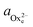 ) are the actual and equilibrium calcium (oxalate) activities in the solution is reduced to
) are the actual and equilibrium calcium (oxalate) activities in the solution is reduced to 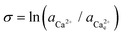 . All solutions were made with equal Ca2+ and Ox2− activities.
. All solutions were made with equal Ca2+ and Ox2− activities.
To determine the equilibrium activities, we first measured the calcium and oxalate concentrations at which steps on COM crystals neither advanced nor retreated. Then 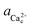 and
and 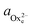 were calculated from these experimentally-obtained equilibrium concentrations (X) and activity coefficients (γ) which were obtained from Visual Minteq by a = γX.
were calculated from these experimentally-obtained equilibrium concentrations (X) and activity coefficients (γ) which were obtained from Visual Minteq by a = γX.
In situ atomic force microscopy
In situ atomic force microscopy (AFM) was performed as described previously.12,15 Briefly, an AFM (Nanoscope III from Digital Instruments, Santa Barbara, CA), commercially available SiN cantilevers (NP-S, Veeco Probes), fluid cell (MTFML, Veeco Probes) and peristaltic pump (Ismatec) were used to perform in situ AFM experiments at room temperature. A seed crystal of COM was glued with inert polyurethane onto a glass cover slip which was already glued to a metallic AFM specimen disc. The mounted seed crystal was then placed inside the O-ring of the fluid cell. In situ images of the surface of the COM seed crystal were obtained in contact mode while solution was flowing through the cell. The solution flow rates were adjusted such that, for a given supersaturation, the step speed did not change with flow rate, i.e., growth was controlled by surface kinetics rather than bulk mass transport. Solution flow rates of about 2 ml min−1 were found to be adequate. No correction was made for distortion of images (hillock shape and step orientation) due to the finite scan rate and non-zero step speed. The step speed was obtained by disabling the slow scanning axis and measuring the difference between the apparent step orientation in images collected during upward and downward scans.42 However, at concentrations close to equilibrium, where steps moved very slowly, step speed was obtained by comparing the positions of steps in images collected sequentially.Computational methods
Modeling surfaces were built from the COM crystallographic unit cell30 (P21/n space group) using Cerius2 crystal builder software (4.8.1 ed.; Accelrys: San Diego, CA 2003). Flat (010) surfaces of unit cell dimension 12 × 8 (a = 75.50 Å, b = 79.81 Å, γ = 107.1°) and four layers deep were constructed with two surface terminations (A and A′). The surface terminations of the (010) surface are as shown in Fig. 1c of ref. 15. Flat (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) surfaces of unit cell dimension 6 × 5 (a = 60.66 Å, b = 72.94 Å, γ = 90°) and two layers deep were built. We have assumed the flat regions of the (
01) surfaces of unit cell dimension 6 × 5 (a = 60.66 Å, b = 72.94 Å, γ = 90°) and two layers deep were built. We have assumed the flat regions of the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) surface to be terminated by layer A, with oxalates lying flat on the surface (Fig. 1d of ref. 15). The L-Asp6 peptide was built with all carboxylates deprotonated and the terminal amine protonated, resulting in a net charge of −6 for the peptide and the system as a whole. The CHARMM22 force-field43 with CMAP dihedral corrections44 was applied to the peptide. For the COM ionic lattice, calcium ions were assigned atomic charges of qCa = +2.0, with nonbonded parameters of ε = −0.1186 kcal mol-1 and Rmin/2 = 1.6508 Å as determined previously for a bulk ionic crystal containing calcium ions;45,46 oxalate carbon and oxygen parameters were taken from the standard CHARMM22 parameters of the carboxylate moiety of aspartate (atom types CC and OC), with atom charges set to qC = +0.52 and qO = −0.76.
01) surface to be terminated by layer A, with oxalates lying flat on the surface (Fig. 1d of ref. 15). The L-Asp6 peptide was built with all carboxylates deprotonated and the terminal amine protonated, resulting in a net charge of −6 for the peptide and the system as a whole. The CHARMM22 force-field43 with CMAP dihedral corrections44 was applied to the peptide. For the COM ionic lattice, calcium ions were assigned atomic charges of qCa = +2.0, with nonbonded parameters of ε = −0.1186 kcal mol-1 and Rmin/2 = 1.6508 Å as determined previously for a bulk ionic crystal containing calcium ions;45,46 oxalate carbon and oxygen parameters were taken from the standard CHARMM22 parameters of the carboxylate moiety of aspartate (atom types CC and OC), with atom charges set to qC = +0.52 and qO = −0.76.
Molecular dynamics and energy minimizations on the COM/ L-Asp6 systems were carried out using NAMD 2.7.47 Starting from the beta-sheet conformation, the peptide was docked in several different initial orientations (20 or more) on flat COM surfaces. 3D periodic boundary conditions were imposed to match the 2D surface dimensions of the COM crystal lattice with a vacuum region above the surface (∼80 Å). An implicit water model (ε = 80) was used, and the atoms of the crystal lattice were held fixed. Optimizations were followed by short NVT dynamics (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, 1 fs step-1) successively at 100, 200, and 298 K, and then followed by a second optimization. The heating phases allowed exploration of more conformations of the peptide at the step and to permit escape from local minima. The energetically most favorable binding orientations were selected for further manual manipulation of the peptide geometry, including shifts of the peptide to similar but nonequivalent locations, followed by new optimizations.
000 steps, 1 fs step-1) successively at 100, 200, and 298 K, and then followed by a second optimization. The heating phases allowed exploration of more conformations of the peptide at the step and to permit escape from local minima. The energetically most favorable binding orientations were selected for further manual manipulation of the peptide geometry, including shifts of the peptide to similar but nonequivalent locations, followed by new optimizations.
The self energy of the fixed crystal is not included in the energy evaluation in our model; thus, a comparison of the final energies of the most stable structures directly indicates the relative binding preferences of L-Asp6 and D-Asp6. We are chiefly interested in the binding preference of say the L-Asp6 enantiomer for a particular step over the mirror-image step, and we assume that the relative free energy of binding is given by ΔΔGb ≈ ΔΔEb = E(L-Asp6/step) − E(L-Asp6/mirror-image step), with near cancellation of entropies and of thermal corrections to the enthalpies. Analogously, we are justified in comparing the energies of the enantiomers at the same step: ΔΔGb ≈ ΔΔEb = E(L-Asp6/step) − E(D-Asp6/step). As the D-Asp6 enantiomer was not explicitly modeled, the energy of D-Asp6 on a particular step was determined by modeling L-Asp6 on the corresponding mirror-image step. Our contention is that the peptide is very flexible and can fairly closely approximate the same coordination with a step or the mirror-image step, but not without introducing the subtle internal strains which are responsible for stereoselective step inhibition. For this analysis, the simple computational model we have chosen is appropriate and preferable to a more complex one involving dynamics in the presence of explicit solvent molecules and perhaps counterions. Such a complex model would greatly obscure the differential internal strains we expect to find and greatly complicate our ability to extract the key information. Moreover, regardless of either the force-field having the ability to account for such subtle strains or not, dynamical modeling will not remedy it.
Conclusions
In this study, some insights into the effects of the aspartic acid rich domains of biomolecules and their chirality on the inhibition of COM crystal growth were obtained by using L-Asp6 and D-Asp6 as surrogate molecules and employing in situ AFM to image the morphological changes and measure the kinetic effects that they induced. On the steps analyzed in this study—the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face and the [
00] step on the (010) face and the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face—the major effect of these peptides was to reduce the kinetic coefficient for step growth. The dependence of growth inhibition on peptide concentration and supersaturation under the influence of both Asp6 enantiomers could be satisfactorily explained using a version of the Cabrera–Vermilyea model37 developed recently by Weaver et al.17 Analysis within this model leads to the conclusion that the major effect of these peptides is to block active kink sites with the imposition of reduced effective supersaturation due to step curvature near pinning sites providing a secondary effect.
01) face—the major effect of these peptides was to reduce the kinetic coefficient for step growth. The dependence of growth inhibition on peptide concentration and supersaturation under the influence of both Asp6 enantiomers could be satisfactorily explained using a version of the Cabrera–Vermilyea model37 developed recently by Weaver et al.17 Analysis within this model leads to the conclusion that the major effect of these peptides is to block active kink sites with the imposition of reduced effective supersaturation due to step curvature near pinning sites providing a secondary effect.
The [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face was inhibited modestly by both enantiomers. However, D-Asp6 had about 10% larger inhibitory effect on growth of the [
00] step on the (010) face was inhibited modestly by both enantiomers. However, D-Asp6 had about 10% larger inhibitory effect on growth of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step than did L-Asp6 at the same Asp6 solution concentration. This difference was due to D-Asp6 having greater probability of adsorption to the crystal surface. In contrast, the data indicate that the binding affinity to the step is nearly identical for the two enantiomers. Analysis of the data gives a difference in the binding energy for D-Asp6 over L-Asp6 to the terrace and step of ∼4 kJ mol−1 and <−1 kJ mol−1, respectively. In comparison, molecular modeling predicts a difference in binding to the terrace of 2.6 or 12 kJ mol−1, depending on the choice of (010) surface termination. Although the inhibitory effects of both enantiomers increased as the Asp6 concentration in solution increased, the effects leveled off at 2 μM Asp6 with the relative step velocity (Vi/V0), being about 0.7 for the addition of D-Asp6 and about 0.8 for the addition of L-Asp6. This saturation of the effect is a reflection of the typical concentration dependence for Langmuir-type adsorption dynamics.
00] step than did L-Asp6 at the same Asp6 solution concentration. This difference was due to D-Asp6 having greater probability of adsorption to the crystal surface. In contrast, the data indicate that the binding affinity to the step is nearly identical for the two enantiomers. Analysis of the data gives a difference in the binding energy for D-Asp6 over L-Asp6 to the terrace and step of ∼4 kJ mol−1 and <−1 kJ mol−1, respectively. In comparison, molecular modeling predicts a difference in binding to the terrace of 2.6 or 12 kJ mol−1, depending on the choice of (010) surface termination. Although the inhibitory effects of both enantiomers increased as the Asp6 concentration in solution increased, the effects leveled off at 2 μM Asp6 with the relative step velocity (Vi/V0), being about 0.7 for the addition of D-Asp6 and about 0.8 for the addition of L-Asp6. This saturation of the effect is a reflection of the typical concentration dependence for Langmuir-type adsorption dynamics.
In contrast to the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] step on the (010) face, the [
00] step on the (010) face, the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step on the (
] step on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face was strongly inhibited by Asp6 with a negligible difference in the magnitude of inhibition for the two enantiomers. Vi/V0 of the [
01) face was strongly inhibited by Asp6 with a negligible difference in the magnitude of inhibition for the two enantiomers. Vi/V0 of the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] step was reduced to 0.065 at a D-Asp6 concentration of only 0.3 μM. Analysis of the data within the modified Cabrera–Vermilyea model leads to the conclusion that this severe level of inhibition is due to a high density of adsorbed Asp6 molecules to both the terrace and the step, with the high binding affinity to the terrace providing the dominant factor. The estimated difference between the binding energy to the (
] step was reduced to 0.065 at a D-Asp6 concentration of only 0.3 μM. Analysis of the data within the modified Cabrera–Vermilyea model leads to the conclusion that this severe level of inhibition is due to a high density of adsorbed Asp6 molecules to both the terrace and the step, with the high binding affinity to the terrace providing the dominant factor. The estimated difference between the binding energy to the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) and (010) face is 9 kJ mol−1. Molecular modeling shows that the reason for the strong difference in binding energy is a result of the strong interaction between the carboxyl groups and the surface Ca2+ ions on the (
01) and (010) face is 9 kJ mol−1. Molecular modeling shows that the reason for the strong difference in binding energy is a result of the strong interaction between the carboxyl groups and the surface Ca2+ ions on the (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) face combined with the repulsive interaction of the carboxyl groups with the negatively charged oxygens of the oxalates on the (010) face.
01) face combined with the repulsive interaction of the carboxyl groups with the negatively charged oxygens of the oxalates on the (010) face.
Acknowledgements
This work was supported by Grant DK61673 from the National Institutes of Health, the Lawrence Scholar Program Student Fellowship from Lawrence Livermore National Laboratory, Office of Science, Office of Basic Energy Sciences of the US Department of Energy under Contract DE-AC52-07NA27344, and Contract DE-AC02-05CH1123. K.R.C. acknowledges initial support for graduate study from Graduate Study Abroad Scholarship by the Korean Science and Engineering Foundation (KOSEF). We thank the Alabama Supercomputing Authority for computational resources. E.A.S. thanks Keith Battle at the University of South Alabama for assistance in carrying out modeling simulations.References
- G. He, T. Dahl, A. Veis and A. George, Nat. Mater., 2003, 2, 552 CrossRef CAS.
- P. H. Tartaix, M. Doulaverakis, A. George, L. W. Fisher, W. T. Butler, C. L. Qin, E. Salih, M. L. Tan, Y. Fujimoto, L. Spevak and A. L. Boskey, J. Biol. Chem., 2004, 279, 18115 CrossRef CAS.
- Q. Q. Hoang, F. Sicheri, A. J. Howard and D. S. C. Yang, Nature, 2003, 425, 977 CrossRef CAS.
- S. R. Qiu and C. A. Orme, Chem. Rev., 2008, 108, 4784–4822 CrossRef CAS.
- H. Shiraga, W. Min, W. J. Vandusen, M. D. Clayman, D. Miner, C. H. Terrell, J. R. Sherbotie, J. W. Foreman, C. Przysiecki, E. G. Neilson and J. R. Hoyer, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 426 CrossRef CAS.
- H. Sidhu, R. Gupta, S. K. Thind and R. Nath, Urol. Res., 1986, 14, 299 CrossRef CAS.
- H. Bekjensen, A. M. Fornander, M. A. Nilsson and H. G. Tiselius, Urol. Res., 1996, 24, 67 CrossRef CAS.
- K. Ganter, D. Bongartz and A. Hesse, Urology, 1999, 53, 492 CrossRef CAS.
- J. A. Gokhale, P. A. Glenton and S. R. Khan, J. Urol., 2001, 166, 1492 CrossRef CAS.
- S. W. Guo, M. D. Ward and J. A. Wesson, Langmuir, 2002, 18, 4284 CrossRef CAS.
- E. Konya, T. Umekawa, M. Iguchi and T. Kurita, Eur. Urol., 2003, 43, 564 CrossRef CAS.
- S. R. Qiu, A. Wierzbicki, C. A. Orme, A. M. Cody, J. R. Hoyer, G. H. Nancollas, S. Zepeda and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1811 CrossRef CAS.
- T. Jung, X. X. Sheng, C. K. Choi, W. S. Kim, J. A. Wesson and M. D. Ward, Langmuir, 2004, 20, 8587 CrossRef CAS.
- J. A. Wesson, V. Ganne, A. M. Beshensky and J. G. Kleinman, Urol. Res., 2005, 33, 206 CrossRef CAS.
- S. R. Qiu, A. Wierzbicki, E. A. Salter, S. Zepeda, C. A. Orme, J. R. Hoyer, G. H. Nancollas, A. M. Cody and J. J. De Yoreo, J. Am. Chem. Soc., 2005, 127, 9036 CrossRef CAS.
- L. J. Wang, W. Zhang, S. R. Qiu, W. J. Zachowicz, X. Y. Guan, R. K. Tang, J. R. Hoyer, J. J. De Yoreo and G. H. Nancollas, J. Cryst. Growth, 2006, 291, 160 CrossRef CAS.
- M. L. Weaver, S. R. Qiu, J. R. Hoyer, W. H. Casey, G. H. Nancollas and J. J. De Yoreo, J. Cryst. Growth, 2007, 306, 135 CrossRef CAS.
- R. W. Friddle, M. L. Weaver, S. R. Qiu, A. Wierzbicki, W. H. Casey and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2009, 107, 11 CrossRef.
- A. M. Belcher, X. H. Wu, R. J. Christensen, P. K. Hansma, G. D. Stucky and D. E. Morse, Nature, 1996, 381, 56 CrossRef CAS.
- A. Berman, L. Addadi and S. Weiner, Nature, 1988, 331, 546 CrossRef CAS.
- G. Fu, S. R. Qiu, C. A. Orme, D. E. Morse and J. J. De Yoreo, Adv. Mater., 2005, 17, 2678 CrossRef CAS.
- G. Fu, S. Valiyaveettil, B. Wopenka and D. E. Morse, Biomacromolecules, 2005, 6, 1289 CrossRef CAS.
- L. Addadi, J. Moradian, E. Shay, N. G. Maroudas and S. Weiner, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 2732 CrossRef CAS.
- B. Akin, M. Oner, Y. Bayram and K. D. Demadis, Cryst. Growth Des., 2008, 8, 1997 CAS.
- S. Mann, Nature, 1988, 332, 119 CrossRef CAS.
- S. Mann, B. R. Heywood, S. Rajam and J. D. Birchall, Nature, 1988, 334, 692 CrossRef CAS.
- Y. Yamamoto, T. Nishimura, A. Sugawara, H. Inoue, H. Nagasawa and T. Kato, Cryst. Growth Des., 2008, 8, 4062 Search PubMed.
- L. J. Wang, J. J. De Yoreo, X. Y. Guan, S. R. Qiu, J. R. Hoyer and G. H. Nancollas, Cryst. Growth Des., 2006, 6, 1769 CAS.
- M. L. Weaver, S. R. Qiu, J. R. Hoyer, W. H. Casey, G. H. Nancollas and J. J. De Yoreo, ChemPhysChem, 2006, 7, 2081 CrossRef CAS.
- S. Deganello and O. E. Piro, Neues Jahrb. Mineral. Monatsh., 1981, 81 Search PubMed.
- S. Elhadj, E. A. Salter, A. Wierzbicki, J. J. De Yoreo, N. Han and P. M. Dove, Cryst. Growth Des., 2006, 6, 197 CAS.
- F. C. Frank and J. H. Vandermerwe, Proc. R. Soc. London, Ser. A, 1949, 198, 205 CrossRef CAS.
- F. C. Frank, Philos. Mag., 1951, 42, 1014 Search PubMed.
- W. J. P. van Enckevort and P. Bennema, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 532 CrossRef CAS.
- B. B. Tomazic and G. H. Nancollas, Invest. Urol., 1979, 16, 329 CAS.
- C. A. Orme, A. Noy, A. Wierzbicki, M. T. McBride, M. Grantham, H. H. Teng, P. M. Dove and J. J. DeYoreo, Nature, 2001, 411, 775 CrossRef CAS.
- Growth and Perfection of Crystals, ed. N. Cabrera and D. A. Vermilyea, Wiley, New York, 1958 Search PubMed.
- S. Y. Potapenko, J. Cryst. Growth, 1993, 133, 141 CrossRef CAS.
- A. M. Cody, H. T. Horner and R. D. Cody, Scanning Electron Microsc., 1982, 1, 13 Search PubMed.
- J. Drever, Geochemistry of Natural Waters, Prentice Hall, 2nd edn, 1998 Search PubMed.
- J. P. Gustaffson, Visual MINTEQ, Department of Land and Water Resources Engineering, Stockholm, Sweden, 2004 Search PubMed.
- T. A. Land, J. J. De Yoreo and J. D. Lee, Surf. Sci., 1997, 384, 136 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586 CrossRef CAS.
- A. D. MacKerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400 CrossRef CAS.
- S. Hauptmann, H. Dufner, J. Brickmann, S. M. Kast and R. S. Berry, Phys. Chem. Chem. Phys., 2003, 5, 635 RSC.
- R. Bhowmik, K. S. Katti and D. Katti, Polymer, 2007, 48, 664 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2013 |
