Effect of bulk pH and supersaturation on the growth behavior of silica biomorphs in alkaline solutions†
Josef
Eiblmeier
a,
Matthias
Kellermeier‡
a,
Doris
Rengstl
a,
Juan Manuel
García-Ruiz
*b and
Werner
Kunz
*a
aInstitute of Physical and Theoretical Chemistry, University of Regensburg, Universitätsstrasse 31, D-93040 Regensburg, Germany. E-mail: werner.kunz@chemie.uni-regensburg.de
bLaboratorio de Estudios Cristalográficos, IACT (CSIC-UGR), Avda. del Conocimiento s/n, P.T. Ciencias de la Salud, E-18100 Armilla, Spain. E-mail: jmgruiz@ugr.es
First published on 4th September 2012
Abstract
Under certain conditions, mineralization of barium carbonate in silica-containing media at high pH results in the formation of complex crystal aggregates called “silica biomorphs”. These self-assembled, purely inorganic materials exhibit hierarchical structure and curved morphologies much reminiscent of certain living forms, thus constituting an interesting model system for the study of the biomineralization processes. In this paper, we report on the influence of the bulk pH on the morphogenesis of silica biomorphs in alkaline solutions. To that end, crystallization experiments were carried out at initial pH values between about 9.8 and 11.9, using atmospheric CO2 as a carbonate source. Formed aggregates were characterized quantitatively by statistical analyses of their morphology, number and size. Corresponding data evidence that well-developed polycrystalline architectures with elaborate shapes occur only when the starting pH is adjusted to values within a rather narrow corridor, ranging roughly from 10.2 to 11.1. Otherwise, merely ill-defined, globular or dumbbell-shaped particles were obtained. In addition, the pH of the mother solutions was monitored continuously during growth and correlated with time-dependent Ba2+ concentration profiles determined by in-situ X-ray fluorescence spectroscopy. By combining the collected data, temporal progressions of the bulk supersaturation were estimated for different conditions and used to re-evaluate the role of pH in the formation of silica biomorphs, particularly with regard to the recently proposed model of the growth mechanism. It is shown that a suitable starting pH is required not only to allow for dynamically coupled co-precipitation of the components, but also to maintain continuous CO2 uptake and hence adequate levels of supersaturation over extended periods of time during growth. Our experiments rationalize previous observations concerning the effect of pH on the formation of silica biomorphs, and disclose fundamental differences between growth in solutions and gels.
1 Introduction
In the past years, the study of biomineral formation has been a central scope of research in the fields of colloidal chemistry and material science, since the strategies learned from nature may lead to potential novel routes for the synthesis of inorganic frameworks with remarkable shapes and structure, typically resulting in outstanding properties. One such concept is to stabilize nanometric crystal building blocks and arrange them in a specific manner, thus constructing higher-order mesoscale patterns.1–3 Concerted self-organization can for example be stimulated by the influence of certain organic polymers, which control the crystallization process in terms of nucleation, growth, as well as the stabilization and coherent alignment of nanocrystal units.4–19 A natural archetype for such materials is the nacreous layer of seashells, which consists of numerous aragonite platelets surrounded by a thin film of biopolymers, resulting in a brick-and-mortar structure of superior hardness.20–22However, the presence of biomolecules or synthetic organic substances is not a mandatory requirement for the production of polycrystalline textures as described above. Indeed, ultrastructures of similar complexity can also be formed from purely inorganic precursors via delicate interactions between the components, as exemplified by the existence of so-called “silica biomorphs”.23,24 These peculiar materials occur when alkaline-earth carbonates and silica are co-precipitated at elevated pH, and self-assemble spontaneously into complex crystal aggregates with non-crystallographic shapes closely resembling certain biogenic forms.23–28 The resulting morphologies are quite diverse and include curved forms such as helicoids as well as coral- and worm-like structures, but also flat sheets.29–38 Detailed analyses of the precipitates revealed that they are composed of a core of uniform rod-like crystallites, which exhibit a slight mutual misalignment and hence describe a long-range orientational field on the mesoscale.32,33 Furthermore, the crystal assembly as a whole happens to be sheathed by a skin of amorphous silica,27,32–34,36,37 and there is also some evidence that individual carbonate crystallites in the core are coated by silica,31,32,39 or adsorb silicate species in their lattice.38
The morphogenetic mechanism underlying the formation of silica biomorphs has for a long time been an enigma. However, recent work revealed crucial aspects of the process and identified both the driving force for co-precipitation on the nano-level and parameters determining the morphological evolution on the micron-scale.40 In essence, a scenario based on two principal stages was proposed. It was shown that morphogenesis is initiated by growth of regular elongated microcrystals, which then undergo self-similar splitting at both ends induced by the poisoning influence of polymeric silicates, to eventually yield heavily branched and more or less closed fractal structures.40 Subsequently, in a second stage, myriads of nanocrystals are nucleated on the surface of these fractal particles, which serve as building blocks for the curved morphologies characteristic of silica biomorphs. The reason for the stabilization of nanosized crystallites and their continuous production at the growing front of an aggregate was proposed to be based on a coupling between the precipitation of silica and carbonate, which relies on their reversed solubility trends with pH.40,41 During growth of carbonate particles in alkaline solutions, CO32−ions are consumed and, as a consequence, nearby HCO3− ions must dissociate to re-establish equilibrium, causing a release of protons and hence a local drop in pH.42 This results in a decrease of the solubility of silica around the just generated crystallites, which therefore become coated by siliceous skins and thus are prevented from further growth. As silica polymerization proceeds in the vicinity of the carbonate particles, ongoing condensation reactions will re-increase the local pH and, ultimately, trigger novel carbonate nucleation. Overall, a feedback cycle is initiated during which the components are alternately mineralized and sinuous polycrystalline aggregates emerge.40,41,43 While their preparation is very simple, growth of silica biomorphs premises certain conditions and the resulting morphologies were shown to depend on various experimental parameters such as species concentrations33,38 or the presence of additives.34,37 However, the most important factor was repeatedly confirmed to be the pH of the medium, from the early works and onwards.24,28,30,31,35 In particular, it was found that when growth is carried out in dilute solutions, typical forms are obtained only when the initial pH was adjusted to values higher than ∼10, while below only cauliflower-like fractal particles occur.28,29 A strong influence of the pH on the growth process appears reasonable when considering that the speciation of both carbonate and silicate varies sensibly with the pH, and that the proposed model assumes pH-dependent changes in their solubility to be responsible for self-organized mineralization. Therefore, we have re-evaluated the role of the pH during the formation of silica biomorphs based on the existing knowledge about the growth mechanism. Indeed, a similar study has recently been carried out by Melero-García et al.,44 but their work was focused exclusively on growth in silica gels. It was found that the formation of shapes with continuous curvature takes place at a pH of less than 9.8, which is significantly lower than what has been argued previously.28,29 In the present work, we have examined the effect of the bulk pH for the case of growth from solution. To that end, dilute silica sols of different pH were prepared and combined with barium chloride solution, covering initial pH values of about 10–12. Crystallization occurred upon prolonged exposure of the mixtures to the atmosphere, due to gradual uptake of CO2. To quantify the influence of the pH, formed precipitates were analyzed statistically with respect to the frequency and size of distinct types of morphologies. In addition, the bulk pH as well as the concentration of Ba2+ in the solutions was monitored in a time-resolved manner, and the acquired data were used to calculate temporal progressions of supersaturation for samples with distinct starting pH. Our results demonstrate that growth of silica biomorphs from solutions occurs at a pH well above 10 and that their morphogenesis is restricted to a certain window of initial pH values.
2 Experimental section
2.1 Crystallization experiments
Growth of silica–witherite biomorphs was performed in stagnant solutions following a procedure described previously.37 As silica source, commercially available water glass (Sigma-Aldrich, sodium silicate solution containing 13.7 wt% NaOH and 26.8 wt% SiO2) was used and diluted with water by a factor of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 (v/v). The resulting silica solution (pH ∼10.6) was then mixed at a ratio of 20
350 (v/v). The resulting silica solution (pH ∼10.6) was then mixed at a ratio of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) with either sodium hydroxide or hydrochloric acid solutions at different concentrations (0.05–0.3 M NaOH and 0–0.1 M HCl), in order to achieve distinct initial pH levels. Eventually, crystallization of barium carbonate was initiated by combining 5 mL of the pH-adjusted silica sol with the same volume of 0.01 M BaCl2 (prepared with BaCl2·2H2O, Sigma-Aldrich, ≥99%). The final concentrations in the reaction mixture thus were 5 mM Ba2+ and 8.4 mM SiO2, with initial pH values ranging from 9.90 to 11.90. Experiments were carried out at 20 ± 1 °C in sterile 6 well microplates (Nunclon, polystyrene, 10 mL total volume, 9.6 cm2 bottom area, 1.7 cm in depth), into which glass coverslips (22 × 22 mm) were placed as growth substrates before filling with solution. After exposure of the samples to the atmosphere over a predefined growth period of 10 h, the substrates were removed with a pair of tweezers and subsequently washed with water and ethanol (Baker, p.a.), followed by drying in air. All solutions were prepared with water taken from a Millipore system and stored in tightly stoppered plastic bottles, to prevent prior uptake of atmospheric CO2 and possible silica contamination from glass walls.
1 (v/v) with either sodium hydroxide or hydrochloric acid solutions at different concentrations (0.05–0.3 M NaOH and 0–0.1 M HCl), in order to achieve distinct initial pH levels. Eventually, crystallization of barium carbonate was initiated by combining 5 mL of the pH-adjusted silica sol with the same volume of 0.01 M BaCl2 (prepared with BaCl2·2H2O, Sigma-Aldrich, ≥99%). The final concentrations in the reaction mixture thus were 5 mM Ba2+ and 8.4 mM SiO2, with initial pH values ranging from 9.90 to 11.90. Experiments were carried out at 20 ± 1 °C in sterile 6 well microplates (Nunclon, polystyrene, 10 mL total volume, 9.6 cm2 bottom area, 1.7 cm in depth), into which glass coverslips (22 × 22 mm) were placed as growth substrates before filling with solution. After exposure of the samples to the atmosphere over a predefined growth period of 10 h, the substrates were removed with a pair of tweezers and subsequently washed with water and ethanol (Baker, p.a.), followed by drying in air. All solutions were prepared with water taken from a Millipore system and stored in tightly stoppered plastic bottles, to prevent prior uptake of atmospheric CO2 and possible silica contamination from glass walls.
2.2 Characterization methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 441 eV) using the Si (311) monochromator setup. Sample fluorescence was monitored with a detector positioned at 90° relative to the incident light path. Data acquisition was started as soon as possible after a single well filled with 2 mL of the BaCl2–silica-mixtures of the desired initial pH (9.90, 10.05, 11.00, 11.15, 11.75, 11.90) had been placed in the center of the beam. Scans from 37
441 eV) using the Si (311) monochromator setup. Sample fluorescence was monitored with a detector positioned at 90° relative to the incident light path. Data acquisition was started as soon as possible after a single well filled with 2 mL of the BaCl2–silica-mixtures of the desired initial pH (9.90, 10.05, 11.00, 11.15, 11.75, 11.90) had been placed in the center of the beam. Scans from 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 to 37
191 to 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 eV were performed continuously for up to 6 h, using a step width of 5 eV in the pre- and post-edge region and 1 eV at the edge jump. The integration time per step was 0.5 s, thus resulting in an overall time resolution of about 7 min. After normalizing the recorded spectra for the incoming beam intensity, the height of the edge jumps was determined by fitting linear equations to the post- and pre-edge region and calculating the step at the inflection point of the curve, as described previously.39 In order to convert the obtained edge jump values to actual Ba2+ concentrations, pure BaCl2 solutions (1–5 mM) without silica were measured with the same routine, giving a straight calibration line with good correlation.
710 eV were performed continuously for up to 6 h, using a step width of 5 eV in the pre- and post-edge region and 1 eV at the edge jump. The integration time per step was 0.5 s, thus resulting in an overall time resolution of about 7 min. After normalizing the recorded spectra for the incoming beam intensity, the height of the edge jumps was determined by fitting linear equations to the post- and pre-edge region and calculating the step at the inflection point of the curve, as described previously.39 In order to convert the obtained edge jump values to actual Ba2+ concentrations, pure BaCl2 solutions (1–5 mM) without silica were measured with the same routine, giving a straight calibration line with good correlation.
| nH+ generated(t) = nHCO3−(t) + 2nCO32− (t) + 2nBaCO3(t) | (1) |
The amount of precipitated barium carbonate can readily be calculated as the difference between the analytical Ba2+ concentration (5 mM in all cases) and the actual value determined at time t by means of XFS measurements, according to:
| nBaCO3(t) = [(5 mM − [Ba2+](t)) × 0.002 L] | (2) |
The mole numbers of dissolved carbonate and bicarbonate ions are in turn accessible considering the law of mass balance and the distribution of carbonate species in solution as a function of pH.39,42 Rearranging eqn (1) in this respect and introducing xCO32− as the fraction of carbonate ions in equilibrium with bicarbonate at a given pH yields the following expression for the amount of dissolved bicarbonate:
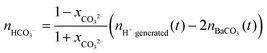 | (3) |
Combining eqn (1)–(3) eventually allows calculating time-dependent variations of the actual carbonate concentration in the mixtures which, together with the XFS data, gives the relative supersaturation S defined as:
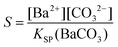 | (4) |
where KSP (BaCO3) is the solubility product of barium carbonate (5.01 × 10−9 mol2 L2).45 However, calculations according to the above-described methodology frequently yielded negative values for S during the first 30 min of growth. These unexpected results likely originate from the fact that a certain amount of carbonate was pre-dissolved in the alkaline silica sol prior to the start of the growth experiments, such that fractional precipitation of BaCO3 occurred immediately after BaCl2 had been added.39 This is evident from the y-axis intercepts of linear fits to the data of the temporal [Ba2+] progression, which were in all cases lower than the analytical barium concentration of 5 mM. Thus, the number of protons generated in the system at t = 0  will not be zero (as assumed in the above calculations), but adopt a positive value that depends on the amount of BaCO3 initially precipitated
will not be zero (as assumed in the above calculations), but adopt a positive value that depends on the amount of BaCO3 initially precipitated 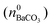 as well as the quantities of carbonate and bicarbonate ions co-existing with the solid phase at this time
as well as the quantities of carbonate and bicarbonate ions co-existing with the solid phase at this time 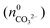 and
and 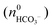 :
:
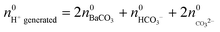 | (5) |
While 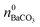 is known from the y-intercept of the [Ba2+]–(t) curve,
is known from the y-intercept of the [Ba2+]–(t) curve, 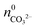 and
and  can be derived from the solubility product of BaCO3, when assuming that the solid phase is in equilibrium with the solution right after mixing of reagents. Finally, the measured amount of generated protons is corrected for initial precipitation according to:
can be derived from the solubility product of BaCO3, when assuming that the solid phase is in equilibrium with the solution right after mixing of reagents. Finally, the measured amount of generated protons is corrected for initial precipitation according to:
 | (6) |
3 Results
3.1 Morphological analysis
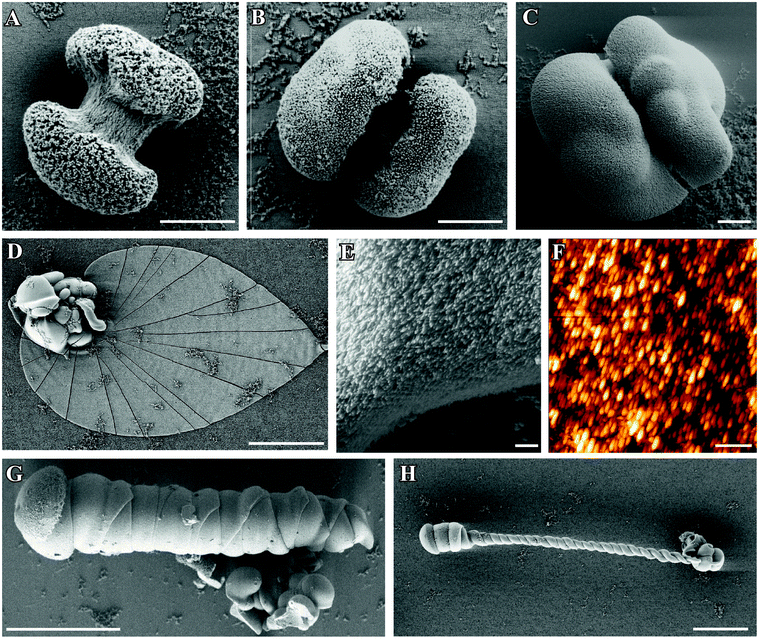 | ||
| Fig. 1 FESEM images of silica–witherite biomorphs grown under “standard” conditions. (A–C): early fractal architectures collected 2.5 h after mixing reagents. (D): extended flat sheet isolated after 10 h, consisting of uniform nanosized crystallites (E). (F) AFM image demonstrating the large degree of co-orientation of individual BaCO3 nanorods. Further morphologies commonly observed for mature crystal aggregates are worm-like braids (G) and helicoidal filaments (H). Scale bars are 2 μm (A–C), 500 nm (E and F), and 50 μm (D, G, H). | ||
Occasionally, polycrystalline assemblies composed of uniform nanosized rods (cf.Fig. 1E and F) sprout from such fractal precursors. This transition, called fibrillation, is accompanied by 3D nucleation of numerous nanoparticles all over the surface of the fractal architecture.40 In accordance with what is usually found in gels,44 extrusion of nanocrystalline aggregates in solution proceeds at first in the form of quasi-2D laminar segments, which may grow in a flat manner to yield extended sheets with dimensions of up to several hundreds of micrometers (Fig. 1D). However, growing sheets also have a certain tendency to curl at some point along their rim and fold back to develop scrolled margins. This singular event, which occurs quite often in solutions, triggers a morphogenetic mechanism that is governed by radial and tangential growth velocities as well as the height and handedness of individual curls,40 resulting in delicate filamentous structures that may loosely be classified into regular helicoids (Fig. 1H) and thicker, more tightly wound worm-like forms (Fig. 1G).
Here, we have quantified the occurrence and size of the three main morphologies displayed by silica biomorphs (i.e. sheets, helicoids, and worms) by means of statistical analysis, and additionally determined the number of fractal precursors formed in the experiments (see Fig. S1 and S2 in the ESI†). For conditions as outlined above, about 55% of the counted fractal globules gave rise to characteristic polycrystalline forms. Among these, worms were found to be the most frequent morphology (ca. 30%), while the percentages of sheets and helicoids are considerably lower and amount to slightly above and below 10%, respectively. These values are in good agreement with the results of a recent study carried out under similar conditions.46
Fig. 2 shows a gallery of optical micrographs granting an overview on precipitates grown from solutions with different initial pH values. It is obvious that flat sheets, easily distinguished by their Maltese-cross extinction pattern between crossed polarizers, are observed predominantly at starting pH values between 10.65 and 11.15 (Fig. 2D–2F). In the same range, fairly large helicoids and worms were obtained (cf. Fig. S2 in the ESI†), with the longest helical filaments (up to 250 μm) and worms (up to 100 μm) being discernible under standard conditions (i.e. pH 11.00). Generally, twisted forms isolated from experiments at initial pH values of 10.65–11.15 looked quite alike in terms of morphological aspects (that is, most of them grew straight and had a roughly constant width), and occurred in approximately equal numbers of right- and left-handed species. The fractal particles formed in this pH regime displayed mainly single-spherical shapes and often agglomerated into rather undefined clusters. The latter feature complicated measurements of the size of individual particles and presumably led to higher apparent mean diameters in the analyses (about 50 μm, cf. Fig. S2 in the ESI†).
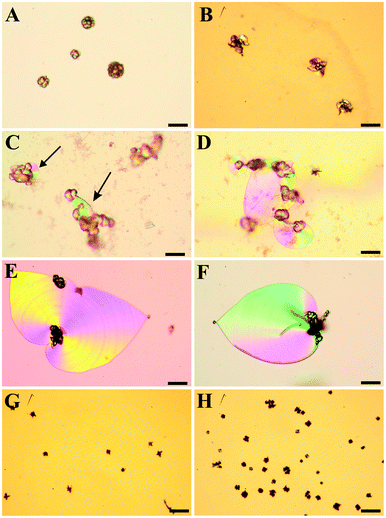 | ||
| Fig. 2 Polarized optical micrographs showing typical morphologies of precipitates isolated after 10 h from solutions at an initial pH value of (A) 9.90, (B) 10.05, (C) 10.20, (D) 10.65, (E) 11.00, (F) 11.15, (G) 11.75, and (H) 11.90. (A,B): at lower pH, globular particles and conglomerates thereof are observed, while characteristic biomorphic forms are absent. (C): at pH 10.20, small sheet-like domains are occasionally seen to emerge from the globular particles (indicated by the arrows). (D–F): between pH 10.65 and 11.15, the formation of non-crystallographic ultrastructures is most pronounced, with spacious sheets and large filaments being typical kinds of morphology. (G,H): at pH values equal to or higher than 11.75, again only fractal particles are found, which now show predominantly dumbbell-like shapes. However, their number is higher and their mean size smaller as compared to counterparts grown at low pH. Scale bars are 50 μm. | ||
When the initial pH of the mother solution was decreased to 10.20 (Fig. 2C), no more worms and helicoids were observed, and the only characteristic morphology of silica biomorphs left were sheets, however their average diameter (ca. 50 μm) was significantly smaller than at starting pH levels of 10.65–11.15 (100–200 μm). Simultaneously, the fraction of fractal particles not associated to any polycrystalline form increased significantly, and their morphology partially changed from closed spherulites to more open, dendritic structures (cf.Fig. 2B and 3B for a close-up view), this indicates that the branching motif is to some degree different at lower pH, in particular with respect to the density of bifurcations in the fractal architectures. These and the above observations are confirmed in a quantitative manner by statistical analyses, as illustrated by Fig. S1 and S2 in the ESI.† At initial pH values of ≤10.05 (Fig. 2A,B), polycrystalline aggregates were fully absent and merely fractal entities were isolated, which mostly had a raspberry-like appearance (see Fig. 2A and 3A). These morphologies presumably result upon further growth (and closure) of the dendritic forms shown in Fig. 2B, and are similar in shape to structures reported previously for growth in solutions at relatively low pH.28 In some cases but very rarely, minute sheets could be distinguished at the border of these fractal particles however, they hardly grew larger than a few microns under these conditions (Fig. 3B inset).
 | ||
| Fig. 3 FESEM and polarized optical images of fractal architectures grown at an initial pH of 9.90 (A), 10.05 (B) and 11.90 (C). Note that particles at low pH are significantly larger and display closed raspberry-like (pH 9.90) or open dendritic (pH 10.05) shapes, whereas those formed at high pH usually show dumbbell-like morphologies. Scale bars are 20 μm (A and B), and 2 μm (C). | ||
When the starting pH was increased to 11.75, morphogenesis of typical polycrystalline forms was largely prevented (Fig. 2G). Indeed, we observed almost exclusively fractal particles and could not find a single worm or helicoid (cf. Fig. S1 in the ESI†). Again, some of the fractal precursors developed laminar domains around their rim, which however rarely grew to sizes beyond a few microns (as at low pH). Interestingly, the fractal architectures obtained at high pH differ from those formed in the intermediate range (pH 10.65–11.15) in that the majority of the particles had a dumbbell-like rather than a closed spherulitic morphology (cf.Fig. 2H and 3C). This suggests that self-similar branching proceeded to a minor degree at elevated pH (rather than there was a change in the mode of branching, as at low pH). In other words, growth of individual particles ended sooner (given that dumbbells are precursors of closed spherulites). This notion is supported by the mean size of these particles, which is markedly smaller than at lower pH (cf.Fig. 3C and Fig. S2 in the ESI†).
The above findings can be summarized in a morphology distribution diagram as given in Fig. 4. It is evident that on both the upper and lower end of the studied pH range (i.e. at initial values of 9.90/10.05 and 11.75/11.90), no characteristic biomorphic forms have been generated after 10 hours of growth and merely fractal architectures (referred to as “globules”) occurred. At intermediate pH levels, the percentage of globules not giving rise to any polycrystalline morphology is in turn decreased and sheets, helicoids and worms are observed.
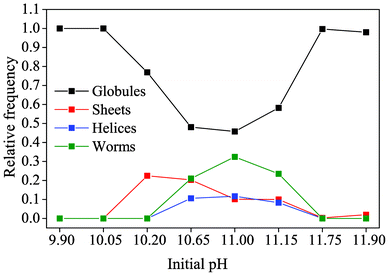 | ||
| Fig. 4 The relative occurrence of the distinct types of morphology displayed by solution-grown silica biomorphs, as depending on the initial pH of the system. Note that the term “globules” signifies those fractal architectures from which none of the characteristic polycrystalline forms developed. | ||
It is worth noting that at the lower limit of pH for which pronounced biomorph formation was verified (i.e. at a starting pH of 10.20), only sheet-like aggregates were obtained, while all three typical morphologies were present in roughly similar ratios between pH 10.65 and 11.15. This indicates that the pH plays a certain role in determining which of the polycrystalline forms is generated. According to the recently proposed formation mechanism of silica biomorphs,40 helicoids and worms can only emerge when an evolving sheet starts to curl and twist. However, in light of the present data, growth of sheets at lower pH is apparently abandoned soon after being initiated, such that curling cannot take place and twisted morphologies are not observed.
To understand the traced growth behavior, it is furthermore interesting to consider the absolute amount of aggregates formed in experiments at a given pH. Corresponding data show that the number of particles on the investigated substrate area is approximately equal for starting pH values of 10.65, 11.00, and 11.15, apart from minor variations (see Fig. S3 in the ESI†). A slight decrease in the number density can be noted at pH 10.20, whereas drastically less particles were counted for initial values of 10.05 and 9.90. In turn, towards higher pH, the total number of precipitates escalates when going from pH 11.10–11.75 and is clearly highest at pH 11.90. This implies that, with increasing bulk pH, a growing number of BaCO3 seeds are nucleated in the samples and subsequently undergo fractal branching. This enhanced nucleation frequency at elevated pH is related to the high supersaturation of the system caused by rapid ingestion of atmospheric CO2, and vice versa. This leads to the formation of a larger number of fractal particles which – since the amount of available Ba2+ is constant – on average grow to smaller dimensions, as reflected by measurements of their size at pH ≤11.75 (cf. Fig. S2 in the ESI†). In turn, at low pH (9.90–10.20), less seed crystals are generated in the solutions and the resulting raspberry-like architectures eventually become larger, again in line with the collected data.
3.2 Evolution of the bulk pH and barium concentration during growth from solution
In order to quantify the above considerations, the time-dependent changes in the concentrations of species relevant for BaCO3 crystallization were traced in situ during growth. For this purpose, two different starting pH values were selected from both the low and high pH regime (where only fractal particles were observed) as well as from the intermediate range, in which well-developed biomorphs formed. While the concentration of dissolved Ba2+ could be directly determined by monitoring its fluorescence upon irradiation with X-rays, information on the amount of carbonate ions present in the system at a given time had to be derived in an indirect manner, that is, by measuring the pH. This was achieved by immersing a microelectrode into the mother solutions during growth. Time-dependent profiles acquired for samples with varying initial pH are displayed in Fig. 5A. In general, the pH was found to decrease with time, reflecting diffusion of atmospheric CO2 into the alkaline mixtures and its conversion to bicarbonate and carbonate ions. The actual ratio of the latter is therefore an intimate function of the actually prevailing pH.32,41,42,44 Once initiated, precipitation of BaCO3 further fuels the absorption of CO2, as carbonate ions are removed from the solution equilibrium.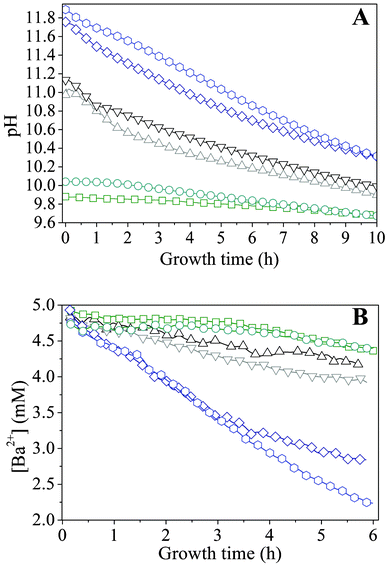 | ||
Fig. 5 Profiles during growth of silica biomorphs from solutions at different initial pH values. -![[hexagon open, flat-side down]](https://www.rsc.org/images/entities/char_e1c0.gif) - pH 11.90, -◇- pH 11.75, -▽- 11.15, -△- 11.00, -○- pH 10.05, and -□- pH 9.90. Note that the decrease in the Ba2+ concentration is linear in time over a period of at least 4 h. - pH 11.90, -◇- pH 11.75, -▽- 11.15, -△- 11.00, -○- pH 10.05, and -□- pH 9.90. Note that the decrease in the Ba2+ concentration is linear in time over a period of at least 4 h. | ||
We note that the traced progressions of pH with time do not show any distinct oscillations, which one might expect in view of the mechanism proposed to underlie the formation of silica biomorphs (i.e. alternating precipitation of carbonate and silica, associated with a slight decrease and subsequent re-increase in pH), at least for those starting pH values where growth of well-developed biomorphs was found to occur (black curves in Fig. 5). However, recent work in stirred systems has suggested that growth takes place only at a local scale within an active region nearby the front of the evolving aggregates, which was estimated to extend merely over some microns into the solution.43 Therefore, subtle variations in pH caused by the growth process of individual aggregates are not reflected in measurements of the bulk pH and should be sensible only in the close vicinity of growing fronts.
Apart from that, the data shown in Fig. 5A evidence that the rate of CO2 uptake is notably affected by the particular starting pH. The higher the value of the starting pH, the steeper the pH declines with time, as is evident from a plot of approximate slopes obtained by linear fits of the experimental data (Fig. 6A). This confirms that uptake of CO2 proceeds faster at higher bulk pH values, likely due to corresponding shifts in the carbonate equilibrium to the side of CO32−. Thus, it can be expected that the concentration of carbonate ions present at a given time will increase with the starting pH and that, during the early stages of growth, the actual supersaturation of barium carbonate should reach higher levels in a shorter period of time under these conditions (as will be discussed in more detail below). The temporal development of the Ba2+ ion concentration is outlined in Fig. 5B for different initial pH values. The data show a nearly linear decrease of the amount of dissolved Ba2+ during the first hours in all cases. This indicates that precipitation of BaCO3 occurs at a constant rate during the formation of silica biomorphs, in good agreement with previous work.39
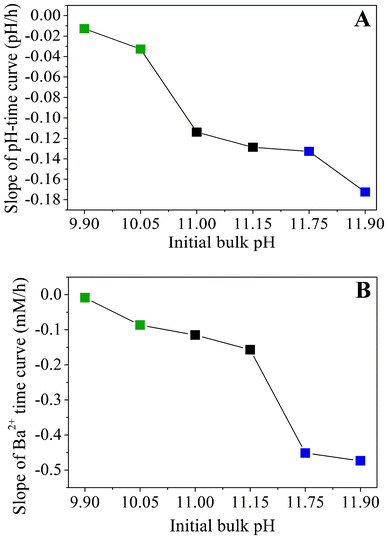 | ||
| Fig. 6 Apparent slopes of (A) the time-dependent pH profiles and (B) the temporal progression of the Ba2+ concentration, both outlined as a function of the initial pH. Values were obtained by approximating the experimental data with linear fits. | ||
Moreover, as the initial pH of the sol is increased, the decay in the Ba2+ concentration becomes steeper, as illustrated by trends in the slopes of linear equations fitted to the data (Fig. 6B). This implies that more barium is consumed at higher pH within the studied period, which is consistent with the results from statistical analyses concerning the absolute number of aggregates produced under the different conditions, and corroborates the notion of an increase in supersaturation towards more alkaline bulk pH. It is worth noting that the slopes of the concentration–time profiles acquired from solutions in the low-pH region (pH 9.90 and 10.05) differ only slightly from those obtained for samples in the intermediate range (pH 11.00 and 11.15), while there is a much more distinct change in the high-pH regime (cf.Fig. 6B). Interestingly, an opposite trend can be discerned in the slopes of the pH–time curves, where the difference between the low- and intermediate-pH region is significantly larger (Fig. 6A). This indicates that insufficient CO2 flux into the solution prevents biomorph formation at low pH, whereas the lack of characteristic morphologies at high pH is due to a too fast decline of the Ba2+ concentration.
4 Discussion
Our results clearly show that when syntheses are carried out in solutions, morphologies characteristic of silica biomorphs can only be obtained when the initial pH is adjusted to values within a rather narrow window which, in view of the statistical analyses carried out in this work, extends roughly from pH 10.2–11.1. Outside this range, predominantly fractal architectures were isolated after 10 h, in the form of either large raspberries (low pH) or smaller dumbbells (high pH). Since these fractal particles result as a consequence of the first stage of the proposed formation mechanism,40 it seems reasonable to assume that at the end of this process, the conditions prevailing in systems at either low or high pH were not appropriate to initiate the second stage of growth, i.e. chemically coupled co-precipitation and the self-assembly of nanoscale crystallites. A crucial prerequisite for chemical coupling to occur is that an appreciable fraction of bicarbonate ions exists in equilibrium with carbonate ions in the solution (given that the envisaged local changes in pH rely on HCO3− dissociation), and that silica is sufficiently, but not too soluble in the bulk medium. In principle, these criteria are met for a pH range of about 9–11, as is evident from Fig. 7, which shows the distribution of carbonate species in solution and the solubility of silica as a function of pH. Above pH 11, the percentage of bicarbonate ions in equilibrium obviously becomes quite small and the solubility of silica very high. Below pH 9, the fraction of carbonate ions is in turn too low to facilitate BaCO3 precipitation. Accordingly, Melero-García et al. found that growth of biomorphs in gels occurs at pH values between 9.3 and 9.8.44 By contrast, the present data prove that the formation of well-developed biomorphs in solutions takes place at significantly higher pH. This is corroborated by time-dependent analyses of the evolving precipitates, which showed that growth of characteristic polycrystalline morphologies starts around 3–4 h after mixing and is essentially terminated after another 6–8 h (cf.Fig. 1). In view of the recorded pH profiles (Fig. 5A), this means that sheets, helicoids and worms form at bulk pH levels well above 10.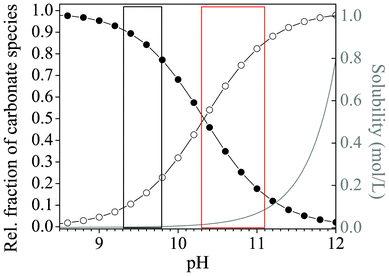 | ||
| Fig. 7 Plot of the relative fractions of carbonate species (-●- HCO3− and -○- CO32−) present in equilibrium as a function of pH, together with the pH-dependent progression of the solubility of silica (grey curve). The red box marks the range of starting pH values for which formation of silica biomorphs was observed in solutions, whereas conditions reported to be suitable for growth in gels are highlighted by the black box.44 Curves were calculated on the basis of the corresponding acid–base equilibria assuming ideal conditions and considering only monomeric silicate species, as described elsewhere.42 | ||
A possible reasoning for these apparent discrepancies is the following. Aside from the principal feasibility of chemical coupling (i.e. that precipitations influence each other via the local pH), another important factor for self-assembly is the actual supersaturation of the system and its variations over time. In gels, this parameter is largely governed by the diffusion of Ba2+ ions from a concentrated solution into the silica matrix already containing a given amount of pre-dissolved CO2.44 To trigger crystallization, enough Ba2+ must be transported to the growth site to establish proper conditions, which is inevitably accompanied by a decrease in pH due to the acidity of the divalent cations. Nevertheless, as long as the pH does thereby not fall below a certain threshold, the second stage of growth can still be initiated. In solutions, supersaturation is in turn regulated by diffusion of CO2 into media with evenly distributed Ba2+ ions. Unlike the situation encountered in gels, this process is not only driven by a concentration gradient, but also depends intimately on the bulk pH, which dictates the rate of CO2 uptake by affecting the H2CO3–HCO3−–CO32− equilibrium. For the emergence of typical biomorphic forms, the pH must still be high after the fractal stage in this case, in order to maintain sufficient CO2 flow into the solution and hence provide adequate levels of supersaturation during self-assembly. In that sense, as already stated in the earlier work,44 there is no universal correlation between the bulk pH and the expected morphologies. Instead, within a distinct window allowing for coupled precipitation (ca. 9–11), particular pH values found to produce regular silica biomorphs mainly reflect the conditions necessary to reach and sustain suitable supersaturation in a given setup. In order to assess these conditions for stagnant solutions as those investigated in the present study, we have used the collected time-dependent data of the pH and Ba2+ concentration to estimate the evolution of the bulk supersaturation during growth. Fig. 8 shows corresponding results for two initial pH values each of the low-, intermediate-, and high-pH regime. On that basis, the growth behavior traced in the present study for different starting pH levels can be explained. At medium pH values of 11.00 and 11.15 (blue curves in Fig. 8), the bulk supersaturation increases gradually over the first 3–4 h, as CO2 is progressively ingested while the Ba2+ concentration is still high. During this period, fractal structures are generated owing to non-crystallographic branching. Subsequently, the curves arrive at a maximum that is followed by a continuous decrease. At this point, the system passes into the second stage of morphogenesis, during which complex crystal aggregates are formed. Importantly, the decay in supersaturation is rather slow up to 10 h, and S remains relatively high until growth of biomorphs is terminated. This suggests that the conditions encountered in this period are those which allow chemical coupling to be excited and, hence, that precipitation of silica biomorphs in solution can occur at bulk supersaturation levels of about 250–450.
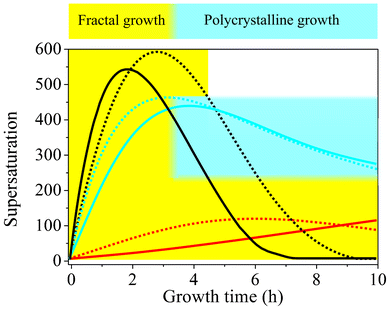 | ||
| Fig. 8 Temporal development of the relative supersaturation of BaCO3 during growth from solutions at different starting pH values. Dashed black line pH 11.90, black line pH 11.75, dashed blue line pH 11.15, blue line pH 11.00, dashed red line pH 10.05, red line pH 9.90. The blue-shaded area indicates the range of bulk supersaturation levels at which the formation of typical biomorphic structures is possible. Fractal growth (yellow-shaded area) in turn occurs over a much broader range of conditions and proceeds as long as the system remains supersaturated. | ||
When growth is carried out at lower starting pH (9.90 and 10.05, red curves in Fig. 8), characteristic crystal aggregates can in turn not be obtained because the bulk supersaturation does not reach values in this range over the entire period investigated. This is most likely due to the depressed flow of CO2 into the system under less alkaline conditions, as evidenced by corresponding pH–time profiles (Fig. 5A). Consequently, the requirements for fibrillation and successive polycrystalline growth to occur are not met (although the bulk pH would as such be suitable for chemical coupling). Therefore, precipitation ceases at the end of the first stage, and any further precipitation of BaCO3 barely leads to an enlargement of fractal structures, which therefore become bigger than at higher pH and adopt their typical raspberry-like appearance.
In turn, when the initial pH is increased to 11.75 and 11.90 (black curves in Fig. 8), the uptake of CO2 is accelerated and significantly higher levels of supersaturation are achieved in a shorter time frame. As a result, nucleation rates are enhanced and a much larger number of BaCO3 crystals are formed in the system (cf. Fig. S3 in the ESI†), which subsequently undergo fractal branching. This becomes clearly manifest in the steep decline of the Ba2+ concentration (cf.Fig. 5B), which causes the supersaturation to run through a maximum after rather short times (2–3 h), despite the relatively high amounts of carbonate ions generated in parallel. Subsequently, S decreases quite rapidly to values that are too low to allow for dynamically coupled co-precipitation, that is, the window of suitable conditions is passed too quickly (<2 h) under these circumstances. In fact, most of the crystals cannot even complete the fractal route and therefore exhibit small dumbbell-like morphologies rather than closed spherulitic shapes at the end of the experiments. This is mainly due to the low amount of Ba2+ available after the fractal stage, owing to previous ample precipitation (as reflected by the slope of the [Ba2+]–time curve, cf.Fig. 5B). Further, even if the Ba2+ concentration would be sufficient to enable polycrystalline growth, the minor fraction of bicarbonate ions existing in equilibrium at pH values close to 12 (cf.Fig. 7) may as such prevent any noticeable interplay between the precipitation of carbonate and silica. On the other hand, it is evident from Fig. 7 that the solubility of silica increases steeply with pH starting from about 11.5. Thus, at pH 11.75 and 11.90, the silica supersaturation is more sensitive to any release of protons around growing carbonate crystals due to bicarbonate dissociation and as a consequence more silica will be incorporated. However growth ceases then after the fractal stage at these pH levels, since the remaining silica supersaturation is not sufficient, rendering stabilization of nanocrystals and coupled growth impossible and hence generally avoiding the formation of biomorphs. In turn, at lower starting pH values, the solubility of silica is reduced and the bulk solution gradually becomes supersaturated as the pH is further decreased over time until, eventually, amorphous silica precipitates independently of the biomorphs. Obviously, this removes reactive silicate species from solution and may be another reason why well-developed crystal aggregates are not observed at low pH. These considerations suggest that, in principle, the supersaturation of both carbonate and silica must be moderate for co-precipitation and the formation of biomorphs to occur.
5 Conclusions
We have studied the crystallization of barium carbonate from alkaline, silica-containing solutions upon diffusion of atmospheric carbon dioxide at various initial pH levels. Our data show that co-precipitation of witherite and silica affords crystal aggregates with complex curved morphologies only if the starting pH of the mother solution is adjusted to values within a certain window, which was found to range roughly from 10.2 to11.1. At both lower and higher initial pH, only fractal architectures, resulting from self-similar branching of the carbonate crystal core, were obtained. This finding is ascribed to inadequate supersaturation levels prevailing in the system at the stage when chemically coupled co-precipitation would actually be initiated (rapid depletion of Ba2+ at high pH, insufficient CO2 flow at low pH). For growth from solutions, the initial bulk pH is a crucial parameter in terms of the speciation of the components, but in particular also with respect to the rate of CO2 uptake and, thus, the temporal evolution of the carbonate concentration. This is a fundamental difference to syntheses conducted in silica gels, where diffusion of Ba2+ ions is the key factor for supersaturation. In both cases, morphogenesis of well-developed biomorphs occurs if, during active growth, the pH of the medium surrounding the aggregates is within a window of approximately between 9 and 11. However, to achieve this and maintain sufficient supersaturation during crystallization, the initial pH of a corresponding solution has to be significantly higher than that of a gel. In the present work, these circumstances have been elucidated in a quantitative manner by in situ measurements of the bulk pH and Ba2+ concentration, yielding time-dependent absolute values for the actual supersaturation of the system at distinct growth stages. Taken together, our experiments have shed new light on the role of the bulk pH in the formation of silica biomorphs from solutions. The quantification of the traced morphological changes with pH, accomplished by statistical analyses of formed precipitates, paints a picture that is widely consistent with previous observations and allows for understanding the effect of the pH on the basis of the recently proposed growth mechanism.Acknowledgements
The authors thank Andreas Picker and Martina Müller for performing parts of the experimental work, Dr. Roman Chernikov (Hasylab/DESY) for valuable advice during the XFS experiments, as well as Prof. Dr. Ralf Witzgall and Dr. Reinhard Rachel (Institute of Microbiology and Archaeal Center, University of Regensburg) for access to their scanning electron microscope and help with the analyses. M. K. is grateful to BASF SE for funding a postdoc position. JMG-R acknowledges support from the Consolider-Ingenio 2010 project “Factoría Española de Cristalización”, the Ministerio de Ciencia y Innovación (MICINN-Project CGL2010-16882).References
- F. C. Meldrum and H. Cölfen, Chem. Rev., 2008, 108, 4332–4432 CrossRef CAS.
- H. Cölfen and S. Mann, Angew. Chem., Int. Ed., 2003, 42, 2350–2365 CrossRef.
- H. Cölfen, M. Antonietti, Mesocrystals and Non-classical Crystallization, Wiley, Chichester, 2008 Search PubMed.
- G. Falini, S. Fermani, M. Gazzano and A. Ripamonti, Chem.–Eur. J., 1997, 3, 1807–1814 CrossRef CAS.
- M. Antonietti, M. Breulmann, C. G. Göltner, H. Cölfen, K. K. W. Wong, D. Walsh and S. Mann, Chem.–Eur. J., 1998, 4, 2493–2500 CrossRef CAS.
- L. B. Gower and D. A. Tirrell, J. Cryst. Growth, 1998, 191, 153–160 CrossRef CAS.
- S. Busch, H. Dolhaine, A. DuChesne, S. Heinz, O. Hochrein, F. Laeri, O. Podebrad, U. Vietze, T. Weiland and R. Kniep, Eur. J. Inorg. Chem., 1999, 1643 CrossRef.
- M. Li, H. Schnablegger and S. Mann, Nature, 1999, 402, 393–395 CrossRef CAS.
- L. Qi, H. Cölfen, M. Antonietti, M. Li, J. D. Hopwood, A. J. Ashley and S. Mann, Chem.–Eur. J., 2001, 7, 3526–3523 CrossRef CAS.
- A. Sugawara, T. Ishii and T. Kato, Angew. Chem., Int. Ed., 2003, 42, 5299–5303 CrossRef CAS.
- T. Wang, H. Cölfen and M. Antonietti, J. Am. Chem. Soc., 2005, 127, 3246–3247 CrossRef CAS.
- Y. Oaki and H. Imai, Langmuir, 2005, 21, 863–869 CrossRef CAS.
- S. H. Yu, H. Cölfen, K. Tauer and M. Antonietti, Nat. Mater., 2004, 4, 51–55 CrossRef.
- N. Nassif, N. Gehrke, N. Pinna, N. Shirshova, K. Tauer, M. Antonietti and H. Cölfen, Angew. Chem., Int. Ed., 2005, 44, 6004–6009 CrossRef CAS.
- M. Balz, H. A. Therese, J. Li, J. S. Gutmann, M. Kappl, L. Nasdala, W. Hofmeister, H. J. Butt and W. Tremel, Adv. Funct. Mater., 2005, 15, 683–688 CrossRef CAS.
- X. H. Guo and S. H. Yu, Cryst. Growth Des., 2007, 7, 354–359 CAS.
- H. Cölfen, Top. Curr. Chem., 2007, 271, 1–77 CrossRef.
- S. Hayashi, K. Ohkawa, Y. Suwa, T. Sugawara, T. Asami and H. Yamamoto, Macromol. Biosci., 2008, 8, 46–59 CrossRef CAS.
- S. Wu, H. Cao, S. Yin, X. Zhang and V. Chernow, Inorg. Chem., 2009, 48, 10326–10329 CrossRef CAS.
- G. Falini, S. Albeck, S. Weiner and L. Addadi, Science, 1996, 271, 67–69 Search PubMed.
- A. G. Checa and A. B. Rodríguez-Navarro, Biomaterials, 2005, 26, 1071–1079 CrossRef CAS.
- L. Addadi, D. Joester, F. Nudelman and S. Weiner, Chem.–Eur. J., 2006, 12, 980–987 CrossRef CAS.
- J. M. García-Ruiz, J. Cryst. Growth, 1985, 73, 251–262 CrossRef.
- J. M. García-Ruiz and J. L. Amorós, J. Cryst. Growth, 1981, 55, 379–383 CrossRef.
- J. M. García-Ruiz, Origins Life Evol. Biosphere, 1994, 24, 451–467 CrossRef.
- J. M. García-Ruiz, A. Carnerup, A. G. Christy, N. J. Welham and S. T. Hyde, Astrobiology, 2002, 2, 353–369 CrossRef.
- J. M. García-Ruiz, S. T. Hyde, A. M. Carnerup, A. G. Christy, M. J. Van Kranendonk and N. J. Welham, Science, 2003, 302, 1194–1197 CrossRef.
- J. M. García-Ruiz, Geology, 1998, 26, 843–846 CrossRef.
- T. Baird, P. S. Braterman, P. Chen, J. M. García-Ruiz, R. D. Peacock and A. Reid, Mater. Res. Bull., 1992, 27, 1031–1040 CrossRef CAS.
- H. Imai, T. Terada, T. Miura and S. Yamabi, J. Cryst. Growth, 2002, 244, 200–205 CrossRef CAS.
- T. Terada, S. Yamabi and H. Imai, J. Cryst. Growth, 2003, 253, 435–444 CrossRef CAS.
- S. T. Hyde and J. M. García-Ruiz, Actual. Chim., 2004, 275, 4–6 Search PubMed.
- S. T. Hyde, A. M. Carnerup, A.-K. Larsson, A. G. Christy and J. M. García-Ruiz, Phys. A, 2004, 339, 24–33 CrossRef CAS.
- A. E. Voinescu, M. Kellermeier, A. M. Carnerup, A. K. Larsson, D. Touraud, S. T. Hyde and W. Kunz, J. Cryst. Growth, 2007, 306, 152–158 CrossRef CAS.
- E. Bittarello and D. Aquilano, Eur. J. Mineral., 2007, 19, 345–351 CrossRef CAS.
- A. E. Voinescu, M. Kellermeier, B. Bartel, A. M. Carnerup, A. K. Larsson, D. Touraud, W. Kunz, L. Kienle, A. Pfitzner and S. T. Hyde, Cryst. Growth Des., 2008, 8, 1515–1521 CAS.
- M. Kellermeier, F. Glaab, A. M. Carnerup, M. Drechsler, B. Gossler, S. T. Hyde and W. Kunz, J. Cryst. Growth, 2009, 311, 2530–2541 CrossRef CAS.
- E. Bittarello, F. R. Massaro and D. Aquilano, J. Cryst. Growth, 2010, 312, 402–412 CrossRef CAS.
- M. Kellermeier, E. Melero-García, F. Glaab, J. Eiblmeier, L. Kienle, R. Rachel, W. Kunz and J. M. García-Ruiz, Chem.–Eur. J., 2012, 18, 2272–2282 CrossRef CAS.
- J. M. García-Ruiz, E. Melero-García and S. T. Hyde, Science, 2009, 323, 362–365 CrossRef.
- W. Kunz and M. Kellermeier, Science, 2009, 323, 344–345 CrossRef CAS.
- M. Kellermeier, E. Melero-García, F. Glaab, R. Klein, M. Drechsler, R. Rachel, J. M. García-Ruiz and W. Kunz, J. Am. Chem. Soc., 2010, 132, 17859–17866 CrossRef CAS.
- M. Kellermeier, E. Melero-García, W. Kunz and J. M. García-Ruiz, J. Colloid Interface Sci., 2012, 380, 1 CrossRef CAS.
- E. Melero-García, R. Santisteban-Bailón and J. M. García-Ruiz, Cryst. Growth Des., 2009, 9, 4730–4734 Search PubMed.
- P. C. Cheng, G. Y. Cheng, M. H. Kou, P. Y. Shia and P. O. Chung, J. Cryst. Growth, 2001, 226, 458–472 CrossRef.
- M. Kellermeier, J. Eiblmeier, E. Melero-García, M. Pretzl, A. Fery and W. Kunz, Cryst. Growth Des., 2012, 12, 3647 CAS.
- H. D. Keith and F. Padden, J. Appl. Phys., 1963, 34, 2409–2421 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ce26132d |
| ‡ Present address: Physical Chemistry, University of Konstanz, Universitätsstrasse 10, D 78457 Konstanz, Germany. |
| This journal is © The Royal Society of Chemistry 2013 |
