Redetermination of crystal structure of Ag(II)SO₄ and its high-pressure behavior up to 30 GPa

Abstract

Here we redetermine the crystal structure of Ag(II)SO₄, an unusual d⁹ system, at 1 atm from powder X-ray data and we report hydrostatic pressure X-ray diffraction experiments on Ag(II)SO₄ inside the diamond anvil cell. AgSO₄ crystallizes in the monoclinic C2/c cell, with a = 12.8476(2) Å, b = 13.6690(4) Å, c = 9.36678(19) Å, β = 47.5653(13)°, and V = 1214.04(5) ų (Z = 16). AgSO₄ exhibits bulk modulus, B⁰, of 36.9 GPa, and undergoes sluggish decomposition at ∼23 GPa yielding a high-pressure phase of Ag₂S₂O₇ (K₂S₂O₇-type), with the substrate and product coexisting at 30 GPa. Theoretical calculations within Density Functional Theory for the C2/c cell nicely reproduce the observed trend for lattice constants as well as the B⁰ values of AgSO₄, and suggest that the rigidity of the infinite [Ag(SO₄)] chains as well as the Jahn–Teller effect for the Ag(II) cation persist even at 30 GPa.

---

Introduction

Although the precise mechanism of high-T_C superconductivity¹ remains a subject of debate,² it is generally believed that the synergistic phonon (BCS-like)-spin mechanisms contribute to the enhancement of the critical superconducting temperature, T_C,^3–5 for oxocuprates. The antiferromagnetic interactions between the spin-½ 3d⁹ Cu(II) cations within [CuO₂] sheets in high-T_C cuprates can be considered as unusually strong with J as large as −129 meV⁶ and ordering temperatures reaching 539 K for CaCuO₂.⁷ The recently discovered iron pnictide superconductors also exhibit 2D antiferromagnetism in their undoped state, with large ordering temperatures up to 559 K for K_0.8Fe_1.6Se₂,⁸ and J up to −50 meV for La(O,F)FeAs.⁹ Searches for antiferromagnetism with similarly large interactions in magnetic insulators with other 3d spin-½ transition metal ions have not been successful to date; it is therefore instructive to more carefully examine materials possessing 4d electrons.¹⁰

Strong antiferromagnetic interactions in 4d systems are exemplified by a high-pressure form of CaRu(IV)O₃¹¹ and by Ag(II)SO₄;¹² both compounds exhibit 1D metal–ligand chains reminiscent of those found for CuO, which host very strong antiferromagnetic interactions. The latter one, black in colour, is of particular interest due to (i) an unusually strong antiferromagnetic superexchange constant of −18.7 meV with superexchange taking place via a two-atomic O⋯O bridge,¹³ (ii) the narrow bandgap at the Fermi level of ca. 1 eV,^11,14 (iii) the pronounced Ag(d)–O(p) mixing in its electronic structure,^11,15 (iv) selective (resonance) enhancement of the Ag–O stretching and O–S–O bending modes in the Raman spectra,¹⁶ and (v) anomalies regarding its thermal decomposition, which takes place via electron transfer between the SO₄²⁻ anion and Ag²⁺ cation and leads to the evolution of O₂.¹⁷ Here, guided by a rule of a thumb that the application of external pressure on low-dimensional networks usually leads to increased structural dimensionality, we report the combined X-ray diffraction study of Ag(II)SO₄ in a diamond anvil cell (DAC) combined with theoretical DFT calculations at pressures up to 30 GPa. To our best knowledge, this is also the first experimental high-pressure study for any compound of divalent silver in a pressure range exceeding 6 GPa.¹⁸

Results and discussion

1. Redetermination of the crystal structure of Ag(II)SO₄

In the original study of Ag(II)SO₄ we reported a small triclinic P1̄ cell derived from powder X-ray study, with a = 4.6923(1) Å, b = 4.7535(1) Å, c = 8.0125(2) Å, α = 103.403(1)°, β = 76.478(1)°, γ = 118.078(1)°, Z = 2 and V = 151.761(6) ų.¹² This cell has helped us to understand the main features of chemical bonding and rationalize the 1D antiferromagnetic ordering observed experimentally for AgSO₄.

Simultaneously with the experimental study¹² the theoretical prediction of the crystal structure of AgSO₄ was published.¹⁹ That was an unprejudiced ab initio screening of various ABX₄ polytypes with the aim to propose the lowest energy structure of AgSO₄. In the outcome of the calculations we have suggested a tetragonal I4₁/a cell with Z = 16, a = 10.56 Å and c = 13.115 Å as the lowest energy polymorph of AgSO₄. Our further study has now shown that a small monoclinic distortion of the tetragonal cell leads to an even lower energy C2/c polymorph and provides a better model for structural refinement in comparison with the previous P1̄ cell.¹² Structure refinement of the monoclinic C2/c cell with Z = 16 using the powder X-ray data (Table 1) yields a more stable and more accurate Rietveld fit than the former triclinic cell, as reflected by the values of R_p = 2.93% and R_wp = 3.84%. The previous refinement for the P1̄ cell yielded R_p = 6.12% and R_wp = 6.26%, and required considerable constraints on S–O bond lengths and O–S–O angles.¹² The DFT-calculated lattice parameters (a = 12.955 Å; b = 13.787 Å; c = 9.480 Å; β = 48.07°; V = 1259.79 ų) and bond lengths for the C2/c cell are in excellent agreement with the experimental values; the errors for lattice vectors do not exceed +1.2%, that on volume is +3.8%, while the β angle is overestimated only slightly, by +1.1%.^20,21

Table 1 Crystal data for Ag(II)SO₄ from powder X-ray data (redetermination, for the previous model cf.ref. 12). FU = formula unit

Empirical formula	AgO4S
M	203.932
T/K	293
λ/Å	1.5418
Crystal system, space group	Monoclinic, C2/c (no. 15)
Unit cell dimensions	a = 12.8476(2) Å; b = 13.6690(4) Å; c = 9.36678(19) Å; β = 47.5653(13)°
V/Å^3	1214.04(5)
Z/FU	16

---

The main difference between the P1̄ and C2/c cells is in the mutual orientation of the sulfate anions. The C2/c cell contains two crystallographically independent SO₄ ions and four different Ag(II) cations as contrasted to one SO₄ and one Ag(II) ion present in the smaller P1̄ cell (Z = 2). This feature of the C2/c cell permits sulfate anions to be arranged in a more diverse fashion than for the former P1̄ cell (Fig. 1).³³ However, the topology of the interatomic connections is similar for both cells: (i) each Ag(II) is coordinated by four oxygen atoms from four distinct sulfate anions (adopting a slightly distorted square planar 2 + 2 coordination), (ii) there are no terminal oxygen atoms in the structure, and (iii) in both cases the infinite 1D [Ag(SO₄)]_∞ chains run along one crystallographic direction (Fig. 1). The presence of these chains allowed us previously to rationalize the 1D antiferromagnetic ordering observed experimentally for AgSO₄.

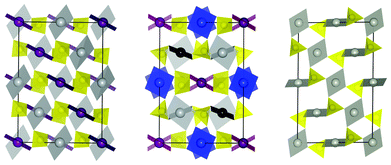Fig. 1 Comparison of AgSO₄C2/c (middle) with AgSO₄P1̄ (left) and high-temperature form of PdSO₄³⁴C2/c (right). Both, AgSO₄ (P1̄) and HT-PdSO₄ were transformed to the AgSO₄ (C2/c) type cell using matrices: (1,-1,1; 3,1,-1; 1,1,1) and (-1,-2,-1; −1,0,1; -1,1,0), respectively, and projected along c for comparison. The square planar coordination of Ag^II (grey, purple, blue, black) and Pd^II (grey) together with SO₄ tetrahedra (yellow) is shown.

Interestingly, all these structural features are characteristic also for high temperature (HT) form of PdSO₄ (Fig. 1).²² AgSO₄ and HT-PdSO₄ have an identical heavy atoms sublattice; the main differences between the two are that: (i) the metal–oxygen distances are by ca. 0.1 Å shorter for Pd(II) than for Ag(II), in accordance with the low-spin d⁸vs. d⁹ electronic configuration of these cations, and (ii) the arrangement of the sulfate anions is less diverse for the latter compound, at a smaller C2/c cell with Z = 4 for PdSO₄ and only one crystallographically independent Pd(II) cation.²² Interestingly, in our theoretical quest for AgSO₄¹⁹ the HT-PdSO₄ polytype was the second lowest energy polymorph of AgSO₄, placed only 3.7 meV per FU above the I4₁/a structure. The previously published P1̄ cell is in fact the PdSO₄-type cell showing a tiny triclinic distortion.

The volume of AgSO₄ (C2/c) equals 75.878(3) ų per one formula unit (FU) and it is slightly smaller than the respective ‘molecular’ volume of the HT-PdSO₄ (79.95 ų).³⁴ However, it is very close to the volume of the low-temperature form of PdSO₄ (75.52 ų, here, atomic positions were not determined).²² The structural polymorphism of AgSO₄ and its relation to that observed for PdSO₄ will be discussed in a separate contribution.

The β angle of the C2/c cell of AgSO₄ is close to 45°, which suggests that this cell is related to some higher-symmetry cell. Indeed, when the C2/c cell is transformed using [(0 1 0) (1 0 -2) (-1 0 0)] matrix, a quasi-tetragonal cell results with a′ = 13.670 Å, b′ = 13.828 Å, c′ = 12.847 Å, α = 90.852°, β = 90.058(1)°, γ = 89.969°, and Z = 32 (Fig. 2). The cell angles are very close to 90° while a ≈ b < c thus revealing the similarity of the transformed cell to that of the NaCl prototype (Fig. 2). Hence AgSO₄ crystallizes in the tetragonally distorted variant of the NaCl-type structure with the infinite [Ag(SO₄)]_∞ chains propagating along the shortest c′ vector.

Fig. 2 Comparison of the crystal structures of AgSO₄ transformed using [(0 1 0) (1 0 -2) (-1 0 0)] matrix in three different projections along a′, b′ and c′ (only Ag and S atoms are showed for clarity) and of the 2 × 2 × 2 supercell of NaCl (in one projection). Ag, Na – gray, S, Cl – yellow balls.

2. High-pressure behaviour and the equation of state of Ag(II)SO₄

Application of external pressure usually leads to increased structural (and often electronic) dimensionality. Therefore, we have examined the evolution of the crystal structure of quasi-1D AgSO₄ in the DAC at pressures up to 30 GPa using the synchrotron X-ray radiation (Fig. 3). The extreme reactivity of the fine powder of AgSO₄ to moisture represents a formidable challenge for high-pressure measurements. Here, only one out of three DAC loadings was successful. In the first two loadings only Ag(I)HSO₄ (i.e. the product of reaction of AgSO₄ with water vapour) was loaded.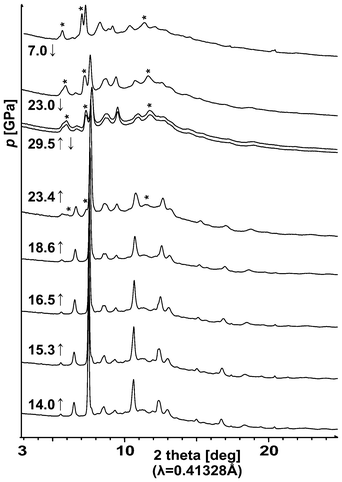

Fig. 3 Evolution of the X-ray powder diffraction patterns for AgSO₄ on compression (↑) up to 29.5 GPa and then on decompression (↓) to 7 GPa. Starlets indicate the most intense reflections from the high-pressure phase of Ag₂S₂O₇, which is quenchable to 7 GPa (cf. Section 4).

We have been able to index all the measured powder diffraction patterns based on the C2/c cell of AgSO₄ and subsequently refine the values of the lattice vectors, while taking into account a preferred orientation of crystallites enclosed within DAC; the obtained values of the unit cell constants for the related NaCl-type unit cell of AgSO₄ are shown in Fig. 4.

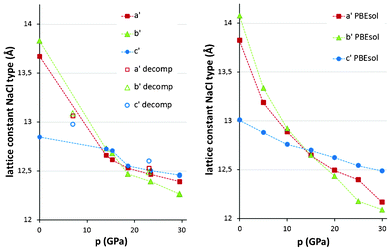Fig. 4 Evolution of the unit cell constants for the NaCl-type unit cell of AgSO₄ as a function of external pressures: experiment (left) and theory (right). Full symbols – compression, open symbols – decompression.

The first point on the compression path is at 14 GPa. The quasi-tetragonal AgSO₄ turns at this pressure to a quasi-cubic NaCl-type with the lattice constants becoming very similar to each other, while the cell angles do not change markedly from 90°. Further compression to 29.5 GPa leads to a rather uniform decrease of all lattice constants with unit cell angles departing from 90° by no more than ±2°. The lattice constants drop to less than 12.5 Å at 29.5 GPa, corresponding to a small reduction of c′ (direction of propagation of the [AgSO₄] infinite chains) from ∼12.85 Å at 1 atm, and a much more pronounced reduction of a′ and b′ from ∼13.67 Å and ∼13.83 Å. This testifies to the rigidity of the 1D [Ag(SO₄)] chains and relative compressibility in directions perpendicular to the chains. DFT calculations very nicely reproduce the pressure trend for all lattice constants (Fig. 4).

Three new reflexes may be detected in the X-ray diffraction pattern measured at 23.4 GPa on compression (Fig. 3) which indicates that AgSO₄ either decomposes or it undergoes a crystallographic phase transition. The nature of this transformation will be discussed in Section 4.²³

It may seem unusual that a soft AgSO₄, which contains a large Ag(II) cation, does not exhibit any crystallographic phase transition prior to decomposition, while its lighter congener, the harder CuSO₄, which contains a smaller Cu(II) cation, shows a structural phase transition at a pressure as low as 5 GPa.²⁴ The reason for that may be that AgSO₄ and CuSO₄ are not isostructural at 1 atm. In this aspect, AgSO₄ also differs from many other metal sulfates, which exhibit a rich spectrum of structural phase transitions (cf. ESI†) at rather low pressures (p < 10 GPa). The high-pressure behaviour thus adds to other peculiarities of AgSO₄ (see Introduction).

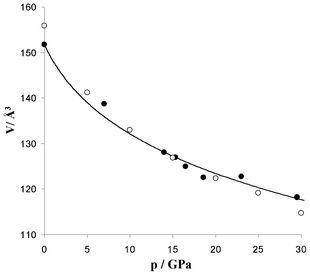Fig. 5 The pressure (p)–volume (V) data for AgSO₄ (experiment – filled, theory – empty circles) and the fit of the experimental data to the Birch–Murnaghan EOS (solid line); data both on compression and decompression. V is given per 2 FUs, to compare with the old P1̄ cell.

The equation of state (EOS) for AgSO₄ (both experimental and theoretical data) and the fit of the Birch–Murnaghan EOS²⁵ to experimental points for the C2/c form is presented in Fig. 4. The volume compressibility of AgSO₄ is similar to that of BaSO₄ as both compounds show comparable, ca. 20%, volume reductions, at ca. 22 GPa.²⁶ The bulk modulus of AgSO₄, B₀, estimated from the 3rd order Birch–Murnaghan EOS equals 36.9 GPa; DFT calculations yield a slightly larger value of B⁰ = 39.5 GPa (B₀′ equals 10.6 GPa and 6.2 GPa for experimental and DFT data, respectively, see ESI†).

3. The crystal structure of AgSO₄ (C2/c) and Jahn–Teller effect for Ag(2+) at high-pressure: DFT view

Since the quality of the X-ray diffraction data was insufficient for determination of the atomic positions for light atoms (S, O) of the C2/c phase, the discussion of this section will be based on theoretical results. For a proper description of the Jahn–Teller effect it was necessary to include a spin polarization to the DFT calculations. Importantly, the inclusion of spin polarization had a negligible effect on unit cell vectors (<1%). Several magnetic models within the C2/c unit cell were built for which a full structure optimization was performed; they all resulted in the same type and magnitude of the Jahn–Teller effect. Here, results for the lowest energy magnetic models are presented: P1̄ and P2₁/c for 0 GPa and 30 GPa, respectively. The magnetic interactions in AgSO₄ are very complex, however, and will be analyzed in detail elsewhere.

At 0 GPa all four crystallographically independent Ag(II) cations exhibit a close to square planar coordination with short Ag–O distances ranging from 2.120 Å to 2.147 Å. When the long apical Ag–O distances are considered, two distinct coordination spheres can be distinguished with half of the Ag(II) cations taking each coordination type (Fig. 6). In one case the Ag(II) cation is axially coordinated with two oxygen atoms (forming a distorted elongated 4 + 2 octahedron with average Ag–O_eq distance equal to 3.135 Å) and in the other case the Ag(II) cation is coordinated with three pairs of oxygen atoms with average Ag–O_eq distances equal to 2.967 Å, 3.164 Å and 3.238 Å, respectively (forming a ten-fold 4 + 6 coordination). The nearly square planar coordination of Ag(2+) is preserved up to 30 GPa except for a small 2 + 2 distortion of the [AgO₄] square (here, Ag is in the extended 10-fold coordination). The four shortest Ag–O distances are not very compressible, with the reduction of 2.5%, from 2.136 Å to 2.083 Å (averaged calculated values for all types of Ag atoms, cf.Fig. 6). Simultaneously, the long apical Ag–O distances experience huge reduction by over 0.7 Å (∼32%), from 3.135 Å to 2.368 Å for the first type of Ag center, and by nearly 0.6 Å (∼23%), from 3.126 Å to 2.536 Å (averaged values) for the second type of the Ag center.

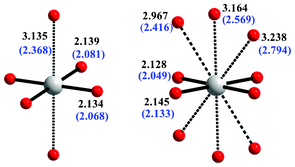Fig. 6 The two distinct Ag(II) coordination spheres present in AgSO₄. The average Ag–O distances calculated for AgSO₄ at 1 atm and at 30 GPa (blue font, in parentheses) are shown.

The ratios of the apical to horizontal Ag–O bond lengths at 30 GPa are close to 1.14 and 1.24 for the octahedral and 10-fold coordination, respectively, which corresponds to a still substantial elongation of the [AgO₆] octahedron.²⁷ This signifies the persistence of the Jahn–Teller effect for the Ag²⁺ cation at this pressure with important consequences for magnetism: the unpaired electron will reside on the local d(x² − y²) orbital of Ag rather than on the d(z²) orbital, just like it is observed for AgSO₄ at 1 atm. The robustness of the Jahn–Teller effect for Ag(II) in compressed AgSO₄ is similar to that of Cu(II) in various compounds at high-pressure.²⁸

4. Pressure-induced decomposition of AgSO₄ yielding Ag₂S₂O₇

As mentioned in Section 2, three new large reflexes and a number of smaller ones appear in the X-ray diffraction pattern measured at 23.4 GPa, which indicates that AgSO₄ either decomposes or undergoes a crystallographic phase transition. The new phase coexists with the C2/c form up to the highest measured pressure of 29.5 GPa, suggesting that the transformation is sluggish. The new phase is seen also on decompression down to 7 GPa with intensities similar to those at 29.5 GPa, hence it is quenchable.

Actually, AgSO₄ is a thermodynamically unstable (metastable) compound at ambient conditions, which thermally decomposes via an exothermic reaction at T > 120 °C yielding Ag₂S₂O₇ (Na₂S₂O₇-type structure).¹⁷ The equilibrium overpressure of O₂ over AgSO₄ at 123.5 °C exceeds 6 × 10¹² atm²⁹ and it is impressive that this compound is metastable for months at room temperature. Thus, we have examined a possibility that AgSO₄ undergoes a pressure-induced decomposition to Ag₂S₂O₇, with ½ O₂ either being liberated in this reaction or oxidizing the surface of the platinum gasket at elevated pressure. We have considered both the ambient-pressure Na₂S₂O₇-type structure as well as a more compact K₂S₂O₇-type.¹⁷

Guided by these considerations, we have performed a two-phase structural refinement with AgSO₄ (C2/c) and the K₂S₂O₇-type Ag₂S₂O₇ (also C2/c, starting at DFT-calculated parameters, cf. ESI†). A nice match between the theoretical and experimental volumes of Ag₂S₂O₇ in the K₂S₂O₇-type was obtained, as illustrated in Fig. 7.

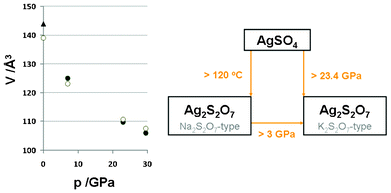Fig. 7 Left: the pressure (p)–volume (V) data points for the high-pressure K₂S₂O₇-type form of Ag₂S₂O₇ (experiment-filled, theory-empty circles); data taken on decompression. V is given per 1 FUs, to compare with the 2 FUs of parent AgSO₄ (Fig. 5). The triangle stands for the 1 atm Na₂S₂O₇-type. Right: the diagram of temperature- and pressure-induced phase transformations of AgSO₄ and of Ag₂S₂O₇. The value of 3 GPa for a supposed pressure of phase transformation of Ag₂S₂O₇ comes from DFT calculations (an extrapolation using common tangent method), and the quenchable character of the HP-form of Ag₂S₂O₇ down to at least 7 GPa has been confirmed by experiment.

The HP phase has a calculated volume per formula unit, V₀, of 138.93 ų at 0 GPa; this is ca. 3.5% smaller than the corresponding volume of the ambient-pressure Na₂S₂O₇-type form, 143.948(5) ų.¹⁷ This is consistent with a better packing of the K₂S₂O₇ polytype as compared to the Na₂S₂O₇ one. Fig. 7 summarizes the observed thermal and pressure-induced instability of AgSO₄, which decomposes to Ag₂S₂O₇ in either the Na₂S₂O₇-type form (>120 °C), or in the K₂S₂O₇-type form (>∼23 GPa).

Concluding this section we should say that experimental evidence suggests that the application of high pressure exceeding ∼23 GPa triggers the decomposition of metastable AgSO₄ and yields the high-pressure form of Ag₂S₂O₇. No phase transitions of AgSO₄ precede decomposition.

Conclusions

We have reinvestigated the crystal structure and got insight into high-pressure behaviour of silver(II) sulfate up to 295 000 atm. Based on theoretical calculations and the X-ray diffraction data we have been able to propose the new C2/c unit cell for AgSO₄ (Z = 16), which more correctly describes this compound at 1 atm than the previously proposed P1̄ cell (Z = 2).¹² The C2/c unit cell may be transformed to the quasi-tetragonal NaCl-type representation with the infinite [Ag(SO₄)] chains running parallel to c′.

AgSO₄ exhibits a rather small bulk modulus, B⁰, of 36.9 GPa. This compound undergoes a pressure-induced decomposition at pressure above ∼23 GPa yielding the high-pressure phase of Ag₂S₂O₇, which is quenchable to 7 GPa. The theoretical DFT calculations confirm the decomposition scenario. AgSO₄ differs from other transition metal sulfates by the fact that they typically require less than 5 GPa for a phase transformation, while AgSO₄ does not show any phase transition preceding its decomposition.

Theoretical calculations within Density Functional Theory nicely reproduce the observed lattice parameters, their pressure evolution, unit cell volume, and the value of bulk modulus for AgSO₄. DFT results suggest that rigidity of the infinite [Ag(SO₄)] chains as well as the Jahn–Teller effect (manifested as elongation of the [AgO₆] octahedra) are preserved at 30 GPa; the unpaired electrons reside mostly within the d(x² − y²) orbitals of Ag.

Experimental procedures and theoretical calculations

All operations with AgSO₄ were performed in an Ar-filled glovebox (MBraun). Synthesis of AgSO₄ was performed according to the published procedure,¹² and the high purity of the specimen was confirmed with X-ray diffraction and Raman spectroscopy.

X-ray diffractometry at 1 atm

Our experimental setup has been described elsewhere.^12,30 Further details of the crystal structure of AgSO₄ at 1 atm may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (Fax: +49 7247-808-666; Email: crysdata@fizkarlsruhe.de) on quoting the ICSD number 424926.

High-pressure experiments

A sample of AgSO₄ (ca. 50 × 20 × 10 μm) was loaded into the DAC with the culet of 300 μm diameter. Loading of DAC with the AgSO₄ powder has been performed using a glovebox. Due to the extreme sensitivity of the material, we decided not to grind the powder manually. Instead, a conglomerate of small grains was picked up with a FEP spatula and loaded as a whole to the high-pressure chamber, the colour of the sample being indicative of its chemical composition (Ag(II)SO₄ is black, while Ag(I) salts are colourless).

One of the seats was WC and the second cBN to get the maximum range in 2θ, and an opening angle of about 40°. Rhenium foil was used as a gasket material, where inside a hole about 100–120 μm diameter the platinum foil was pre-indented; the inner diameter size of the hole was about 60–80 μm. Neon was used as a pressure medium. X-Ray data were collected at Sector 16BM-D beamline of HPCAT, at the Advanced Photon Source, Argonne National Laboratory, using 0.41328 Å radiation and using the MAR345 image plate. After each pressure increase or decrease the pressure was allowed to relax for at least 15 min. Pressure was measured with platinum as an internal standard, usually before the sample has been measured. Reflections from Pt are also visible in some of sample patterns (see ESI†). The sample to detector distance was ∼300 mm; the measurement time was 120 s per image while at very high pressure and at decompression (twice at 29.5 GPa, at 23 GPa at 7 GPa) the recording time was increased to 300 s per image. The sample to detector distance and detector tilt angle was calibrated with the NIST standard CeO₂ powder pattern. The data were integrated azimuthally using FIT2D³¹ and analysed by CheckCell, Eva and TOPAS.³²

The measured XRD patterns do not correspond to a powder sample with a perfectly random orientation of crystallites, but rather to a conglomerate of very small single-crystalline grains. Initial indexing of the diffraction patterns was performed for simplicity using the small P1̄ unit cell (this triclinic cell has identical Ag sublattice as the C2/c cell) with TOPAS, followed by Pawley and eventually structure refinement of the lattice vectors (see ESI† for details). The lattice vectors were then matrix-transformed to those corresponding to the C2/c unit cell and to the NaCl-type representation (ESI†). The preferred orientation was applied and it was found to be crucial for a correct description of the powder patterns.

DFT calculations

The periodic DFT calculations were done using the Vienna ab initio simulation package (VASP)³³ within generalized gradient approximation (GGA),³⁴ PBEsol exchange-correlation functional revised for solids³⁵ and projector-augmented wave method (PAW).³⁶ Parameters for full geometry optimization were: SCF convergence criterion 10⁻⁷ eV, ionic convergence 10⁻⁵ eV, kpoint spacing of 0.3 Å⁻¹ (using the Monkhorst–Pack scheme), valence electrons were described by plane waves with a kinetic energy cutoff of 600 eV. For the spin-polarized calculations GGA(PBEsol) + U method was used with U_(Ag4d) = U_(O2p) = 4 eV, U_(S3p) = 2 eV, and J_{(all atoms)} = 1 eV. The calculations for 12 compact polymorphs¹⁹ of AgSO₄ were performed at 0 GPa, 10 GPa, and their results extrapolated to 25 GPa using a linear tangent method, indicating that any pressure-induced phase transitions should not occur below 30 GPa. We found that taking magnetic interactions into account was important for ranking of structures in enthalpy.

Acknowledgements

The project ‘Quest for superconductivity in crystal-engineered higher fluorides of silver’ is operated within the Foundation for Polish Science ‘TEAM’ Programme co-financed by the EU European Regional Development Fund. WG also acknowledges support from the NCN project AgCENT (2011/01/B/ST5/06673). Portions of this work were performed at HPCAT (Sector 16), Advanced Photon Source (APS), Argonne National Laboratory. HPCAT is supported by CIW, CDAC, UNLV and LLNL through funding from DOE-NNSA, DOE-BES and NSF. APS is supported by DOE-BES, under Contract No. DE-AC02-06CH11357. V. V. S. acknowledges financial support from the Department of Energy under grant # DEFG02-02ER45955. This work was partly supported by the Slovenian Research Agency (ARRS) within the research program P1-0045 Inorganic Chemistry and Technology. DFT calculations were performed at ICM supercomputers within grant G34-10. Kind assistance of beam scientist, Dr. Daijo Ikuta, is gratefully acknowledged.

References

1. G. M. Bednorz and A. K. Müller, Z. Phys. B: Condens. Matter, 1986, 64, 189.
2. (a) P. W. Anderson, P. A. Lee, M. Randeria, T. M. Rice, N. Trivedi and F. C. Zhang, J. Phys.: Condens. Matter, 2004, 16, R755; (b) P. A. Lee, N. Nagaosa and X. G. Wen, Rev. Mod. Phys., 2006, 78, 17; (c) Q. J. Chen, J. Stajic, S. Tan and K. Levin, Phys. Rev., 2005, 412, 1.
3. (a) A. Lanzara, P. V. Bogdanov, X. J. Zhou, S. A. Kellar, D. L. Feng, E. D. Lu, T. Yoshida, H. Eisaki, A. Fujimori, K. Kishio, J. I. Shimoyama, T. Noda, S. Uchida, Z. Hussain and Z. X. Shen, Nature, 2001, 412, 510; (b) J. Lee, K. Fujita, K. McElroy, J. A. Slezak, M. Wang, Y. Aiura, H. Bando, M. Ishikado, T. Masui, J. X. Zhu, A. V. Balatsky, H. Eisaki, S. Uchida and J. C. Davis, Nature, 2006, 442, 546.
4. (a) H. Krakauer, W. E. Pickett and R. E. Cohen, Phys. Rev. B: Condens. Matter, 1993, 47, 1002; (b) B. Batlogg, R. J. Cava, A. Jayaraman, R. B. Vandover, G. A. Kourouklis, S. Sunshine, D. W. Murphy, L. W. Rupp, H. S. Chen, A. White, K. T. Short, A. M. Mujsce and E. A. Rietman, Phys. Rev. Lett., 1987, 58, 2333; (c) X. J. Chen, V. V. Struzhkin, Z. G. Wu, H. Q. Lin, R. J. Hemley and H. K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3732.
5. (a) P. Monthoux, D. Pines and G. G. Lonzarich, Nature, 2007, 450, 1177; (b) N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer and G. G. Lonzarich, Nature, 1998, 394, 39; (c) E. Manousakis, Rev. Mod. Phys., 1991, 63, 1; (d) J. P. Carbotte, E. Schachinger and D. N. Basov, Nature, 1999, 401, 354.
6. (a) D. Vaknin, E. Caignol, P. K. Davies, J. E. Fischer, D. C. Johnston and D. P. Goshorn, Phys. Rev. B, 1989, 39, 9122; (b) Y. Tokura, S. Koshihara, T. Arima, H. Takagi, S. Ishibashi, T. Ido and S. Uchida, Phys. Rev. B: Condens. Matter, 1990, 41, 11657.
7. A. Lombardi, M. Mali, J. Roos, D. Brinkmann and I. Mangelschots, Phys. Rev. B: Condens. Matter, 1996, 54, 93.
8. B. Wei, H. Qing-Zhen, C. Gen-Fu, M. A. Green, W. Du-Ming, H. Jun-Bao and Q. Yi-Ming, Chin. Phys. Lett., 2011, 28, 086104.
9. Z. -Y. Lu, F. Ma and T. Xiang, J. Phys. Chem. Solids, 2011, 72, 319.
10. (a) W. Grochala and R. Hoffmann, Angew. Chem., Int. Ed., 2001, 40, 2742; (b) W. Grochala, J. Mater. Chem., 2009, 19, 6949; (c) W. Grochala, A. Porch and P. P. Edwards, Solid State Commun., 2004, 130, 137.
11. Y. Shirako, H. Satsukawa, X. X. Wang, J. J. Li, Y. F. Guo, M. Arai, K. Yamaura, M. Yoshida, H. Kojitani, T. Katsumata, Y. Inaguma, K. Hiraki, T. Takahashi and M. Akaogi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174411.
12. P. J. Malinowski, M. Derzsi, Z. Mazej, Z. Jagličić, B. Gaweł, W. Łasocha and W. Grochala, Angew. Chem., Int. Ed., 2010, 49, 1683.
13. Note that the value of J divided by 2 was erroneously given in the previous paper (ref. 12). Cf. also: X. Zhang, T. Jia, T. Liu, Z. Zeng and H. Q. Lin, J. Appl. Phys., 2012, 111, 07E136.
14. The value of activation energy for electronic conductivity of Ag(II)SO₄ equals ∼1.0 eV at −50 °C and ∼1.25 eV at +30 °C: R. Jurczakowski, P. J. Malinowski, Z. Mazej and W. Grochala, unpublished impedance spectroscopy data.
15. M. Derzsi, J. Stasiewicz and W. Grochala, J. Mol. Model., 2011, 17, 2259.
16. M. Derzsi, P. J. Malinowski, Z. Mazej and W. Grochala, Vib. Spectrosc., 2011, 57, 334.
17. P. J. Malinowski, M. Derzsi, A. Budzianowski, P. J. Leszczyński, B. Gaweł, Z. Mazej and W. Grochala, Chem.–Eur. J., 2011, 17, 10523.
18. (a) See high-pressure study of AgF₂: B. G. Müller, Nature, 1979, 66, 519; (b) Conclusions from this study severely contradict theoretical calculations unless substantial disorder of fluorine sublattice is considered: J. Romiszewski, W. Grochala and L. Z. Stolarczyk, J. Phys.: Condens. Matter, 2007, 19, 116206; (c) T. Jaroń and W. Grochala, Phys. Status Solidi RRL, 2008, 2, 71.
19. M. Derzsi, K. Dymkowski and W. Grochala, Inorg. Chem., 2010, 49, 2735.
20. Results obtained with the improved PBE functional for solids (PBEsol): J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
21. The former P1̄ cell may be transformed to the new monoclinic cell using the transformation matrix [(1 -1 1) (3 1 -1) (1 1 1)], while preserving the positions of Ag atoms, however, positions of sulfate anions in the transformed cell and in the experimental C2/c cell differ to some extent.
22. High-temperature C2/c form, possibly metastable at ambient conditions, is called M-form in the original paper, while the low-temperature form is denoted as N-form: T. Dahmen, P. Rittner, S. Böger-Seidl and R. Gruehn, J. Alloys Compd., 1994, 216, 11.
23. The analysis based on intensity of reflexes is difficult because of the possibility of (varying) preferred orientation of the small sample enclosed within DAC.
24. C. W. F. T. Pistorius, Z. Kristallogr., 1961, 116, 220.
25. (a) F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244; (b) F. Birch, Phys. Rev., 1947, 71, 809.
26. W. Crichtons, M. Merlini, M. Hanfland and H. Müller, Am. Mineral., 2011, 96, 364.
27. Compare with the typical values for the [AgF₆] octahedra at 1 atm: W. Grochala, Phys. Status Solidi B, 2006, 243, R81.
28. F. Aguado and F. Rodríguez, High Pressure Res., 2006, 26, 319.
29. As calculated from an equilibrium constant of 2.5 × 10⁹, which was derived from the enthalpy of decomposition (−30.7 kJ mol⁻¹ at 1 K min⁻¹) and entropy term of gaseous ½ O_2(g) at 123.5 K (−40.7 kJ mol⁻¹).
30. Z. Mazej, E. Goreshnik, Z. Jagličić, B. Gaweł, W. Łasocha, D. Grzybowska, T. Jaroń, D. Kurzydłowski, P. Malinowski, W. Koźminski, J. Szydłowska, P. Leszczyński and W. Grochala, CrystEngComm, 2009, 11, 1702.
31. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235.
32. DIFFRAC.EVA v.1.2, Software for phase identification and quantitative phase analysis, Bruker AXS, 2011 Karlsruhe, Germany, CheckCell – http://www.inpg.fr/LMGP, TOPAS v 4.2, Total Pattern Analysis Solution Software, Bruker AXS, 2009, Karlsruhe, Germany.
33. (a) G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169; (b) G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15; (c) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
36. P. E. Blöch, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.

---

Footnotes

† This work is dedicated to Prof. Ho–Kwang (Dave) Mao at his 70th birthday and in recognition of his outstanding contribution to high pressure sciences.

‡ Electronic supplementary information (ESI) available: Pressure evolution of X-ray diffraction patterns, refined lattice vectors, database of structural phase transitions for sulfates, and results of DFT calculations. See DOI: 10.1039/c2ce26282g

---