Shape-controlled TiO₂ nanoparticles and TiO₂ P25 interacting with CO and H₂O₂ molecular probes: a synergic approach for surface structure recognition and physico-chemical understanding

Abstract

Integrated studies of CO on truncated bipyramidal TiO₂ anatase nanoparticles mainly exposing smooth (101) surfaces provide the missing link between TiO₂ single crystals and commercial TiO₂ nanopowders with complex morphology. The synergy among high resolution transmission electron microscopy, IR spectroscopy and modeling correlates adsorbed CO stretching frequency to anatase surface types, and reveals how disorder of the adsorbed CO layer affects CO/TiO₂ IR bands. Comparison of the two TiO₂ nanoparticle types highlights the role of low coordination Ti⁴⁺ sites selectively present on TiO₂ P25 in the photocatalytic decomposition of H₂O₂, an important Reactive Oxygen Species (ROS) formed in photocatalytic processes.

---

Introduction

The importance of titania as one of the key materials for sustainable processes ranging from pollutants abatement^1,2 to energy production^3–5 has triggered an intensive quest for its structure–functionality relationships. This target can be addressed by surface-science approaches applied to well-defined systems,⁶ which recently clarified the dependence of photocatalytic activity of anatase and rutile TiO₂ single crystals on some important bulk properties⁷ and established the reactivity in the dark of regular surfaces and derived steps of TiO₂ single crystals.^8,9 Surface properties clearly play a central role in the catalytic and photocatalytic performances of titania^9–11 and spectroscopic methods are very effective tools for unraveling structure and reactivity of surface sites of oxides.^12,13 In particular, the possibility to attain a comparison at a “molecular resolution” level between the surface features of nanoparticles with well shaped or irregular surfaces is offered by the IR spectroscopic studies of adsorbed probe molecules exhibiting vibrational features sensitive to the nature and structure of adsorbing sites. As well known, this is the case of the frequency of the internal stretching mode of adsorbed CO,¹⁴ that can be used to probe a broad variety of systems, from single crystals to finely divided powders.^14,15

Nevertheless, the establishment of a connection between the measured ν_CO and the type of exposed sites only on the basis of experimental data can result in some ambiguity, like for the main band of the spectrum of CO adsorbed on TiO₂ anatase-based powders. Since the seminal work of Busca et al.,¹⁶ the possibility that this signal could be associated with CO on (101) and/or (100) facets has been reported.^17–21 A significant support in elucidating the ν_CO-adsorbing site connection might be provided by theoretical calculations. Comparison between experimental and calculated frequency values is, however, by no means straightforward. Indeed, Mino et al.²² initially proposed on the basis of DFT calculations that the main ν_CO band at 2179 cm⁻¹ on nanoanatase should be due to molecules adsorbed on (100) facets. Nevertheless, in a more recent paper they proposed a reassignment of CO on (101) facets, on the basis of some hypotheses on the surface terminations of TiO₂ P25 particles with complex and heterogeneous morphology.²³ However, possible reasons for the discrepancy between the two assignments have not been considered.

In general, there are also other factors that make band assignment problematic. Most of the available experimental data are obtained, at a finite temperature, on samples exposing different TiO₂ faces, each characterized by a large number and a broad variety of structural defects; nonetheless, because of the very presence of edges and corners on TiO₂ crystals, different types of surface Ti sites are available for CO adsorption, especially on nanostructured TiO₂ samples. Last but not least, the CO distribution on Ti sites is actually disordered even on a perfect TiO₂ surface at monolayer coverage, due to the presence of ¹³CO in natural abundance, thermal effects, and also because many structurally and energetically close adsorption geometries may be possible for an ensemble of CO molecules, thus implying different intermolecular interactions. A theoretical model able to reproduce such a complexity is out of the scope of current resources, and most calculations are normally performed by considering only regular TiO₂ surfaces at 0 K. Such a wide gap between real TiO₂/CO samples and standard computational models might be bridged only by combined efforts of experimental and theoretical researchers aimed at identifying, synthesizing and employing materials and models that could be characterized through a common synergistic strategy. Even though integrated theory–experiment approaches are increasingly relevant in the nanosciences and successful examples of their applications are available,^24–30 the design of new, ad hoc procedures suitable for a given problem is often a necessity. Here, we propose one possible approach to the study of nanostructured TiO₂, involving on one side experimental data for well shaped particles exposing crystallographically defined facets, and on the other side the modeling of adsorbate disorder effects on regular TiO₂ surfaces.

Results obtained with this approach provide important reference data for the recognition of components in the spectra of CO adsorbed on particles with complex/unknown surface structures. Furthermore, whereas a wealth of IR data have been gathered on titania powders, typically featuring a complex and heterogeneous surface morphology,^{16,18–22,31} at the best of our knowledge only one single-crystal study is available in the literature,⁷ dealing with CO adsorbed on the thermodynamically most stable (101) surface of TiO₂ anatase. In this scenario, the use of well-defined TiO₂ nanoparticles could also help bridging the gap between single crystals and powders, which are generally characterized by rough and irregular surfaces like those of commercial TiO₂ nanoparticles. State-of-the-art methods for the preparation of nanoparticles with controlled morphology can provide well-shaped TiO₂ nanocrystals, typically in the form of truncated bipyramids limited by (101) and (001) type facets, with a relative extension dependent on the growth along [001].^11,32–39

On such a basis, well-shaped titania nanoparticles were prepared under selected hydrothermal conditions (hereafter referred to as TiO₂ HT). This material was studied adopting CO as a spectroscopic probe (IR) in comparison with the commercial titania nanopowder Degussa TiO₂ P25, a kind of landmark for photocatalytic applications.⁴⁰ Since hydrogen peroxide is produced on irradiated TiO₂ as O₂ reduction intermediate,⁴¹ and added H₂O₂ can play multiple roles in photocatalytic processes,⁴² the TiO₂ nanoparticles were also tested toward the decomposition of H₂O₂. Hydrogen peroxide is a good ligand for Ti⁴⁺ and the ability of peroxides to adsorb on anatase and rutile surfaces is long known.⁴³ In this light, the photocatalytic transformation of H₂O₂, combined with spectroscopic evidence could probe the nature and distribution of TiO₂ surface sites, as well as give insight into their role in the photocatalytic process, with particular regard to coordinatively defective Ti⁴⁺.

These studies were integrated by HR-TEM and by theoretical modeling of CO adsorption. Such a powerful multi-disciplinary approach uncovered the impact of adsorbate disorder on CO stretching frequencies, allowed us to correlate observed properties with specific structural features of the nanoparticles, and provided a deeper understanding of the interactions of molecules on TiO₂ surfaces, which could be crucial for further development of TiO₂-based nanomaterials and processes.

Experimental and theoretical methods

Materials

The titania nanopowders considered were:

(i) TiO₂ HT (100% anatase). This catalyst was synthesized by forced hydrolysis of an aqueous solution of the Ti(TEOA)₂ complex (TEOA = triethanolamine), with a procedure similar to that developed by Sugimoto, but without the intermediate gelation step.⁴⁴ The following conditions were adopted: complex concentration 40 mM, pH 10 (NaOH), 96 hours of hydrothermal treatment at 453 K. The presence of iron in the Ti(TEOA)₂ solution before hydrothermal treatment was assessed and excluded by the thiocyanate test, after acidification, (Fe(III) < 0.2 mg L⁻¹). At the end of the hydrothermal treatment the sample was calcined at 673 K for 2 hours. The specific surface area, measured by adsorption of N₂ at 77 K and applying the BET model (SSA_BET), of the as synthesized catalyst was of ca. 42 m² g⁻¹, and decreased slightly to ca. 37 m² g⁻¹ after outgassing at 873 K. Water used was prepared by a Millipore MilliQ system (Millipore, Molsheim, France) with a specific resistance >18.2 MΩ cm⁻¹ and TOC < 5 ppb. NaOH pellets (Aldrich, ACS reagent grade) were used as received. Triethanolamine (Aldrich 98%) and titanium isopropoxide (Aldrich, 97%) were vacuum distilled before use.

(ii) TiO₂ P25 by Evonik (formerly Degussa) (∼80% anatase and ∼20% rutile; purity ≥99.50 wt%). The SSA_BET of the as received powder was of ca. 55 m² g⁻¹, and declined to ca. 40 m² g⁻¹ after outgassing at 873 K.

Further characterization data (XRD patterns and IR spectra) are reported in Fig. S1–S3 in the ESI.†

Finally, high purity O₂ and CO (99.999%, Praxair) were used for the thermal treatment and IR measurements, respectively, without further purification except liquid nitrogen trapping.

Methods

High resolution transmission electron microscopy (HR-TEM). HR-TEM images of the materials (powder grains “dry” dispersed on lacey carbon Cu grids) were obtained using a JEOL 3010-UHR microscope with an acceleration potential V = 300 kV.

IR measurements. The powders were pressed in self-supporting pellets, with “optical thickness”, of ca. 10–15 mg cm⁻² (“thin pellets”) or of 20–30 mg cm⁻² (“thick pellets”). The samples were then inserted in a cell equipped with KBr windows, designed to carry out spectroscopic measurements at ca. 100 K, by cooling with liquid nitrogen (see Fig. S4 in the ESI†). The cell was attached to a conventional vacuum line (residual pressure ≤1 × 10⁻⁵ mbar), allowing the thermal treatment and adsorption–desorption experiments to be carried out in situ. Before IR measurements, the samples were outgassed at 873 K for 60 min, and then contacted with O₂ (6 mbar) at the same temperature for 60 min. Then, the pellets were cooled to 473 K in O₂ and further cooled down to room temperature under outgassing. At the end of the procedure, samples were white in color, as expected for stoichiometric (fully oxidized) TiO₂.

Measurements were carried out at a resolution of 2 cm⁻¹ using a Bruker IFS28 spectrometer, equipped with a MCT detector. Spectra of adsorbed CO are reported in Absorbance, after subtraction of the spectra of the samples before CO admission as the background.

Theoretical modeling of CO adsorption. Carbon monoxide adsorption on different anatase facets was simulated with periodic slab models adopting the PBE approximation⁴⁵ for the electronic structure calculations. Electronic states were expanded in planewaves up to a cutoff of 80 Ry (320 Ry for the electronic density) and norm conserving pseudopotentials⁴⁶ were adopted. In the case of Ti, a full core pseudopotential (i.e. a Ti⁴⁺ is considered) was adopted along with the Non Linear Core Correction scheme.⁴⁷ Such a pseudopotential has proved to reproduce structural, vibrational, and electronic features of Ti-containing solid state systems.^48–51 The CPMD code was used for the calculations.⁵² All results presented here refer to calculations at Γ, however validation calculations have been performed (for bulk anatase) by adopting a 2 × 2 × 2 Monkhorst–Pack mesh⁵³ for the Brillouin Zone (BZ) sampling and planewave cutoff up to 120 Ry on a supercell consisting of 3 × 3 × 1 unit cells. Results of such validation tests are reported in Table S1a and b (ESI†). Control calculations were performed on CO adsorbed on (101) anatase with a 2 × 2 mesh for the BZ sampling as well.

Geometry optimizations were carried out at fixed volume, by adopting the cell parameters a = b = 3.785 Å, c = 9.514 Å.⁵⁴

A maximum force of 0.0001 Hartree/Bohr was adopted as a convergence criterion in the optimizations.^55–57 For the slab calculations, the bottom TiO₂ layer was kept fixed in the crystallographic positions during optimizations. A vacuum of 12 Å was considered in order to minimize inter-slab interactions. Relevant structural data are described in Table 1. Binding energies were calculated by the formula—BE = E([TiO₂]_n − mCO) − E([TiO₂]_n) − mE(CO); where E([TiO₂]_n − mCO) is the energy of the optimized slab with m CO adsorbed molecules, E([TiO₂]_n) is the energy of the optimized slab and E(CO) is the energy of an isolated CO molecule.

Table 1 Main structural parameters of the model slabs (Å), along with the concentration of exposed Ti per nm²ρ(Ti), the Ti coordination and the Ti–Ti nearest and next nearest neighbour distances R1 and R2 (Å)

	Slab	TiO2 layers	ρ(Ti)	Ti coordination	R1; R2
(101)	10.239 × 11.355	6[Ti6O12]	5.17	Ti(5)	3.79; 5.46
(100)	11.355 × 9.514	6[Ti6O12]	5.56	Ti(5)	3.10; 3.79
(001)	11.355 × 11.355	6[Ti9O18]	6.98	Ti(5)	3.79; 3.79
(110)	16.058 × 9.514	8[Ti6O12]	3.92	Ti(4)	5.35; 5.46

---

Harmonic frequencies were obtained numerically by finite difference calculations. Since our main target was the CO stretching mode (wavenumbers higher than 2000 cm⁻¹) and TiO₂ modes are below 1000 cm⁻¹, only CO atoms and Ti atoms of top layers were allowed to contribute to the frequency calculations. With such an approximation, ν_CO differs at most by one wavenumber with respect to the value calculated by allowing displacements of all the atoms in the slab.

Regular facets were considered, in particular the (101), (100), (001) and (110) model slabs were taken into account (Fig. S5, ESI†). Moreover, a CO coverage corresponding to θ = 1 was simulated, namely one CO moiety for each exposed Ti.

In addition, a 1 × 4 reconstructed (001) model slab was considered as well (Fig. S5d, ESI†). The reconstruction was as reported by Lazzeri and Selloni.⁵⁸ It is to be noticed that a row of exposed tetracoordinated Ti sites is present in the reconstructed surface. Calculations were performed on perfectly ordered systems and on systems characterized by some degrees of disorder. One kind of disorder was obtained by considering ¹²C → ¹³C substitutions. In these cases, the optimized geometry of the system with 100% ¹²C was retained but harmonic modes were recalculated. A second kind of disorder was thermally induced: by starting from the symmetric optimized structures, Car Parrinello molecular dynamics simulations were carried out for about 1 ps at 100 K. The final “thermally disordered” structures derived from the finite temperature simulations were optimized, and harmonic frequencies were calculated. All discussed structures are characterized by positive frequencies.

H₂O₂ photocatalytic decomposition tests. The hydrogen peroxide photodegradation experiments were carried out using cylindrical pyrex cells (4.0 cm diameter and 2.5 cm height, cut-off at 295 nm)⁵⁹ on 5 ml of aqueous suspension containing the desired amount of the photocatalyst powder (0.5 g dm⁻³) and 1 mM hydrogen peroxide. The suspensions containing TiO₂ were prepared by sonication. The pH was adjusted to 3 ± 0.1 with HClO₄ or with a fluoride buffer (total fluoride concentration 10 mM) for the experiments on pristine and fluorinated catalysts, respectively.

Before use, both photocatalysts were purified from organic and ionic impurities by irradiation of a water suspension under UV light for 2 days, followed by several washings until no chloride ions were detected.

The irradiation was made by TLK 40 W/05 fluorescent lamps (Phillips, Eindhoven, Netherlands) (24 ± 1 W m⁻² in the 290–400 nm range). The lamp spectrum is characterized by an emission band centered at 360 nm with a width at half maximum of 60 nm. The total photon flux in the cell, measured by ferrioxalate actinometry, was 1.82 ± 0.08 × 10⁻⁵ einstein L⁻¹ s⁻¹ in the 295–420 nm range. During irradiation the suspension was magnetically stirred and the cell temperature was 303 ± 3 K. After the irradiation the suspensions were filtered through 0.45 μm cellulose acetate membrane filter (Millipore HA). The H₂O₂ concentration as a function of the irradiation time was monitored spectrophotometrically (Varian Cary 100 Scan UV-Visible Spectrophotometer) by the heptamolybdate catalyzed iodide oxidation method (λ = 350 nm).⁶⁰

H₂O₂ adsorption measurements have been performed equilibrating H₂O₂ solutions in the presence of TiO₂ HT. After filtration on PTFE 0.45 μm filter (Millipore Millex LCR) the amount of hydrogen peroxide in solution has been evaluated by the spectrophotometric heptamolybdate method;⁶⁰ details are in ref. 41.

Results and discussion

HRTEM observations

TEM images representative of TiO₂ HT powder are shown in Fig. 1. Two types of 2D shapes were projected on the image plane, rhombic-like and square-like, both with well defined borders. It is straightforward to associate the rhombic-like shapes, prevalent in number, to images of truncated bipyramidal particles with the main axis (labeled as “c”) oriented almost perpendicular to the electron beam. At high magnification, lattice fringes due to phase contrast appeared, running parallel to one of the main borders (panel B′). Their spacing, 0.352 nm, corresponds to the d₁₀₁ distance for TiO₂ anatase,⁶¹ confirming that the more extended facets are of the (101) type. The sides of the square-like shapes appeared essentially equivalent to the minor axis of the rhombic-like shapes (labeled as “b”). The origin of such shapes was revealed by HR-TEM images exhibiting lattice fringes (panel C), that, on the basis of the measured spacing, appeared again to be due to (101) planes, running parallel to two opposite borders of the particle image. Because of the extremely short wavelength of the electron beam (λ = 0.00197 nm at V = 300 kV) such planes were able to satisfy the diffraction condition being essentially parallel to the impinging beam (Bragg angle: 0.16°). Hence, as shown by a 3D model (Fig. 1), the square-like shape can actually be due to a truncated bipyramid particle with the (101) type facets parallel to the line-of-sight (corresponding to the direction of the impinging electron beam).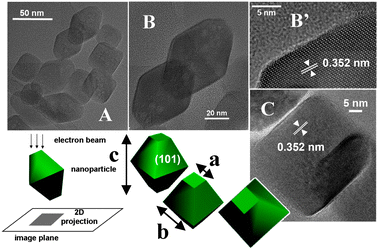

Fig. 1 TEM images representative of an ensemble of particles constituting the TiO₂ HT sample: panels A, B, B′ and C; original magnifications: ×120, ×300, ×800 and ×400 k, respectively.

Turning to TiO₂ P25 (Fig. 2), particles with size ranging from ca. 10 to 50 nm are present, in agreement with data previously reported by Ohno et al.⁶²

Fig. 2 TEM images representative of the TiO₂ P25 sample: panels A and B; original magnifications: ×80, ×500, respectively.

Some of the observed shapes were easily recognized as bidimensional projections of truncated bipyramids with the main axis (almost) parallel to the image plane, as displayed by 3D schemes. In most cases, however, the contours of the projections could be due to more isometric particles. Noticeably, square-like shapes with (101) lattice fringes running parallel to two opposite borders were observed also for TiO₂ P25, but exhibiting some stepping of the profiles (panel B), witnessing for the presence of coordinatively defective surface terminations.

IR spectroscopy of adsorbed CO

The surface of the two materials was then investigated at a molecular level by IR spectroscopy of CO adsorbed on samples pre-outgassed at 873 K. This treatment resulted in the complete desorption of H₂O molecules and in the removal of the overwhelming part of OH groups from surface cations.⁶³ The spectrum collected at high CO coverage for both materials (equilibrium CO pressure: 45 mbar) was dominated by a main peak, narrow and located at 2178 cm⁻¹ for TiO₂ HT, that appeared broader and upshifted at 2179 cm⁻¹ in the case of TiO₂ P25 (Fig. 3, curves a and b, respectively). Higher CO pressure essentially resulted only in an increase in intensity of the component due to CO adsorbed in a liquid-like form (vide infra). This behavior indicated that under this condition no other additional cationic surface sites are available for a specific interaction with probe molecules; hereafter this level of CO coverage will be indicated as θ_CO → 1.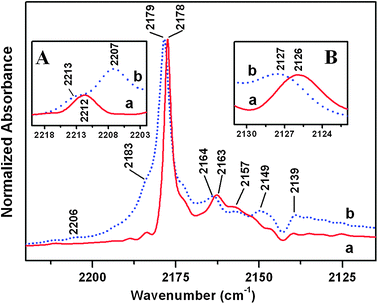

Fig. 3 IR spectra of 45 mbar of CO adsorbed at ca. 100 K on samples outgassed at 873 K: (a) TiO₂ HT; (b) TiO₂ P25. Insets: (A) zoomed view of the 2220–2202 cm⁻¹ range of the IR spectra obtained by using a “thick pellet” (ca. 30 mg cm⁻²) at lower CO coverage than for spectra reported in the main frame; (B) zoomed view of the 2131–2122 cm⁻¹ range of the main frame.

The slight difference in position in the two cases should be due to differences in the interaction among adsorbed CO molecules, and in particular of the static type. Indeed, the same behavior was observed for the very weak band at 2126/2127 cm⁻¹ due to ¹³CO present in natural abundance (Fig. 3, inset B): owing to the high dilution among ¹²CO oscillators,¹⁴ this band is affected only by static coupling. Moreover, the evolution of the main peak under decreasing CO coverage towards singleton adsorbed species (i.e., in the absence of adsorbate–adsorbate interactions) resulted in a nearly identical position, 2189 cm⁻¹, for both materials (Fig. S3 in the ESI†) confirming that the peaks at 2178 and 2179 cm⁻¹ should be due to CO adsorbed on surface sites with a similar local structure. Since the ν_CO shift due to adsorbate–adsorbate interactions¹⁴ [(ν_COθ → 1) − (ν_CO singleton)] depends on the number of coupled oscillators,⁶⁴ its slightly lower value in the case of TiO₂ P25 suggests the presence of some stepping on the facets of these nanoparticles.

On such a basis, and taking into consideration the evidence, provided by HRTEM data, for the overwhelming presence of (101) surfaces in TiO₂ HT, it can be established that: (i) the main component at 2178/2179 cm⁻¹ must be unambiguously assigned to ¹²CO adsorbed on cationic sites exposed on (101) facets (as well as the weak band at 2126/2127 cm⁻¹ related to ¹³CO), (ii) such facets are the most abundant also in TiO₂ P25, confirming and extending the results of TEM observations (Fig. 2). Noticeably, CO adsorbed on the (101) surface of a TiO₂ anatase single crystal was reported to produce an IR signal at 2180 cm⁻¹.⁷

Other features common to the spectra of CO adsorbed on the two types of TiO₂ nanoparticles were a weaker band at 2163/2164 cm⁻¹, a minor component at 2157 cm⁻¹ (likely due to CO adsorbed on residual hydroxy groups; the corresponding perturbation of the ν_OH signals is displayed in Fig. S3 in the ESI†)^18,20 and a pattern below 2149 cm⁻¹ (containing a subband at ∼2139 cm⁻¹ due to CO adsorbed in a liquid-like form).^18,20

Differently, the spectrum of CO on TiO₂ P25 exhibited a shoulder at 2183 cm⁻¹ and two minor absorptions at 2149 and 2207 cm⁻¹, the latter more clearly observed by dosing CO on a thicker pellet (Fig. 3, inset A). The two components at higher frequency (2207, 2183 cm⁻¹) were present also in the spectrum of CO adsorbed on a commercial nanoanatase powder with a rutile content below 2%,²² exhibiting a similar relative intensity with respect to the main peak at 2179 cm⁻¹. This feature indicates that they are mainly due to CO on the anatase phase. This statement is supported by recent data for TiO₂ P25 rutile particles (obtained by etching the pristine material with an HF solution), characterized by an IR spectrum of adsorbed CO exhibiting components with a similar intensity at 2149 and at ca. 2180 cm⁻¹.²³

Moreover, both TiO₂ nanopowders showed a weak feature at 2212/2213 cm⁻¹, likely due to a combination mode among the internal CO stretching mode responsible of the main peak and a low frequency CO-surface external mode.⁶⁵

Theoretical modeling of CO adsorption

The unambiguous assignment of the ν_CO peak at 2178 cm⁻¹ based on the well defined surfaces exposed by TiO₂ HT was one of the main achievements of this work and stimulated to consider disorder effects in the modeling of the adsorption of CO on TiO₂. Indeed, the urgency of a deeper and more realistic theoretical investigation of this system arises also because of the discrepancy of previous studies reported in the literature that, on the basis of the same set of computational data, assigned the main ν_CO band (in such case located at 2179 cm⁻¹) first to probe molecules on (100) facets²² and then, very recently, to CO on (101) facets.²³ Such ambiguities may actually arise by the use of oversimplified models, which could miss some fundamental features of the real system. In such a scenario, the construction of a theoretical model able to capture at least some glimpses of the complexity of a typical CO/TiO₂ laboratory sample would be clearly of fundamental relevance for a molecular-level understanding. Moreover, the effort of unraveling key features of the actual CO–TiO₂ system, that is missing in all the models proposed to date, could help future work in this area to produce/use theoretical data in such a way to avoid possible misinterpretations of experimental data.

Therefore, in order to explore to what extent it might actually be possible to correlate CO stretching frequencies with structural features of a specific TiO₂ surface, different surface types characterized by different densities of Ti sites and Ti coordination were investigated (Table 1). In particular, three surface types exhibiting pentacoordinated Ti (including the most abundant (101) one), and one characterized by four-coordinated Ti sites (i.e., (110)) were considered. As a first step, fully ordered CO arrays were then adsorbed on the above described model surfaces and optimized at 0 K.

Calculated binding energies and relevant geometrical parameters of CO adsorbed on each surface are reported in Table 2, while graphical representations of the calculated minima are shown in Fig. S5 (ESI†). Frequency calculations were performed on these structures and the obtained values were then scaled to facilitate comparison with experimental data.

Table 2 Calculated (optimized) Ti–C, C–O distances (Å), Ti–C–O angles (°), binding energies BE (kcal mol⁻¹) for ordered CO adsorbed on different anatase regular faces at θ = 1

	Ti–C	C–O	Ti–C–O	BE
(101)	1.131	2.342	177	8.0
(100)	1.134	2.352	166	6.0
(001)	1.136	2.274	179	7.7
(110)	1.135	2.293	177	9.8

---

A scaling factor of 1.007 was obtained by rationing the location at 2178 cm⁻¹ of the peak experimentally assigned to ¹²CO on (101) facets to the calculated value for ¹²CO at θ → 1 on the (101) surface (2162.9 cm⁻¹, see Table S2a in ESI†). A significantly different scaling factor, 1.0153, resulted from the ratio between the value pertaining to ¹³CO in natural abundance (2126 cm⁻¹) and the value calculated for one ¹³CO surrounded by ¹²CO on the (101) surface (2093.9 cm⁻¹, see Table S2a in ESI†). Since the vibrational features of isotopically pure arrays of ¹²CO (or ¹³CO) molecules are affected by both dynamic and static adsorbate–adsorbate interactions, whereas for ¹³CO highly diluted in ¹²CO only static interactions occur, the difference between the two scaling factors is related to dynamic coupling. The effect of dynamic coupling, Δν_dyn, can be therefore estimated from the difference between the frequency expected for ¹³CO-only arrays at θ → 1 and the frequency of ¹³CO molecules diluted among the ¹²CO ones. As listed in Table 3, in the case of the experimental data Δν_dyn of 4 cm⁻¹ was found, in good agreement with the literature data of CO adsorbed on TiO₂,¹⁸ whereas it increased to 21 cm⁻¹ for the calculated values. These results indicate that the model system adopted in the calculations overestimates dynamic coupling and is, therefore, more ordered than the experimental adlayer.

Table 3 Evaluation of the contribution of the dynamic adsorbate–adsorbate interactions (Δν_dyn) to the value of the stretching frequency of isotopically pure CO molecules adsorbed on the (101) surface of TiO₂ anatase at θ → 1. B values are derived from the ¹²CO value scaled with respect to the ν_¹³CO/ν_¹²CO ratio, i.e. 0.9778, neglecting the anharmonic contribution

	A	B	C	D
	ν ^12CO/dyn+stat (cm^−1)	ν ^13CO/dyn+stat (A × 0.9778; cm^−1)	ν ^13CO/stat (cm^−1)	Δνdyn (B−C; cm^−1)
ν CO/dyn+stat: frequency of adsorbed CO in the presence of both dynamic and static adsorbate–adsorbate interactions; νCO/stat: frequency of adsorbed CO in the presence of static adsorbate–adsorbate interactions, only.
Exp.	2178	2130	2126	4
Calc.	2162.9	2114.9	2093.9	21.0

---

On such a basis, the modeling conditions (e.g. T = 0 K) were reconsidered, taking into account that experimental data are typically in the 60–100 K temperature range (this work and ref. 7 and 22). The disorder induced by temperature (hereafter “thermal disorder”) can remove the degeneracy of the CO vibrational eigenvalues typical of a perfectly ordered CO arrangement on an ordered surface at 0 K. To show how thermal disorder modulates ν_CO at θ → 1, a thermally disordered array of adsorbed CO was simulated on the most abundant (101) facet. Such a temperature-induced disordered structure, only 1 kcal mol⁻¹ higher in energy than the ordered one, is thermally accessible in the 60–100 K range and should therefore be considered in band assignment. The new calculations on ¹²CO arrays on the (101) surface resulted in multiple values of ν_CO. The scaling factor was obtained by rationing the observed frequency of ¹³CO in natural abundance (2126 cm⁻¹) with respect to the value calculated for thermally disordered ¹³CO surrounded by ¹²CO on (101) (2101.3 cm⁻¹, Table S2a in ESI†). Moreover, as displayed in Fig. 4, the ν_CO degeneracy is removed leading to scaled frequencies in the 2180–2171 cm⁻¹ range, in line with the experimental result. The effect of thermal disorder was considered also for CO on other TiO₂ surfaces that might correspond to less abundant facets exposed by the nanoparticles studied experimentally.

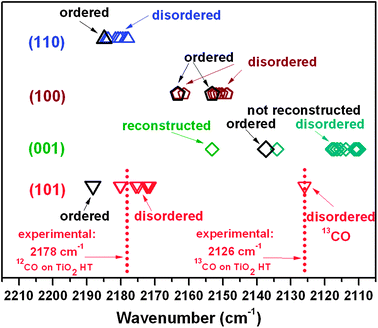Fig. 4 Schematic representation of data reported in Table S2a–d in ESI,† obtained by scaling the calculated frequencies versus thermally disordered ν_¹³CO.

The data (selection in Fig. 4; complete set in Table S2 in ESI†) indicate that the extent of the frequency lowering induced by thermal disorder depends on the surface structure and becomes less significant in the case of long Ti–Ti nearest-neighbor distances (see Table 1). Indeed, the (110) surface, characterized by a low surface density of Ti sites ρ(Ti) and by a large distance between neighboring exposed tetracoordinated (4C) Ti sites (5.4 Å, see Table 1), exhibits the smallest frequency red-shift and spreading (from 2185 cm⁻¹ to the 2184–2178 cm⁻¹ range). One can therefore conclude that ν_CO frequencies calculated for ordered systems represent just an upper bound.

Interestingly, previous experimental studies in the literature generally agreed in assigning the 2163–2164 cm⁻¹ band to the CO/(001) system.^19,20 However, our results suggest that at high CO coverage:

–the regular (001) facets should not contribute to signals characterized by wavenumbers higher than 2134 cm⁻¹ (ESI†Table S2c);

–only CO adsorbed on reconstructed (001) surfaces [the (1 × 4) reconstruction is well known to occur for this type of surface^66,67] might contribute (at the tail) to the 2160–2150 cm⁻¹ region.

–the signal at 2164/2163 cm⁻¹ could also arise from CO on (100) facets.

Furthermore, by properly taking into account disorder, not only the main peak at 2178 cm⁻¹ is unambiguously assigned to CO adsorbed on (101) faces, but also the shoulder at 2183 cm⁻¹, appearing only in the spectrum of TiO₂ P25, matches well with the calculated frequency for CO on tetracoordinated titanium at (110). Facets like the (110) ones (i.e., exposing Ti⁴ sites) are, indeed, essentially absent in the case of TiO₂ HT nanoparticles (Fig. 3).

At present, it is difficult to propose an assignment for the shoulder at ca. 2173 cm⁻¹, common to the spectra of CO adsorbed on both materials. To this aim, and to clarify the assignment of the band at 2163/2164 cm⁻¹, the availability of novel types of well-shaped TiO₂ nanoparticles with dominant faces other than the (101) one might be of great help. Such a challenging aspect could be tackled in a future development of the present work.

Remarkably, CO adsorption on Ti⁴⁺_4C sites is also associated with higher binding energies with respect to Ti⁴⁺_5C ones (see Table 2). Moreover, in the case of ordered adsorbed phases at θ → 1, it is worth noting that whereas CO on Ti⁴⁺_4C sites on (110) oscillates at frequencies higher than CO on Ti⁴⁺_5C on (100) and (001), the highest calculated CO stretching frequency is related to adsorption on the (101) Ti⁴⁺_5C sites (Table S2a–d in ESI†).

As expected, none of the scaled calculated values approached the experimental weak component at 2207 cm⁻¹ (Fig. 3, inset A), that should be due to CO probing highly defective coordinative structures (at steps, edges or corners), usually indicated as α sites,^18,20,31 which should be present in a negligible amount on the well shaped, regular facets exposed by the TiO₂ HT nanoparticles (Fig. 3, inset A).

The presence/absence of the weak band around 2206 cm⁻¹ (depending on CO coverage) and of the shoulder at 2183 cm⁻¹ for TiO₂ P25/TiO₂ HT raised a particular attention, because it monitors the possible presence of surface cationic sites in low coordination that, when hydrated, are able to dissociate water molecules, forming hydroxy groups.⁶³

H₂O₂ photocatalytic decomposition tests

The possible role of the differences in the surface structures of the two types of TiO₂ nanoparticles commented above in their photocatalytic behaviour was then investigated by testing the materials as heterogeneous photocatalysts towards the decomposition of H₂O₂. Under working conditions in the aqueous medium hydroxylation and hydration of surface sites should occur. The new ligands provided by such processes (hydroxy groups or H₂O molecules, in dependence on the dissociative or molecular character of water adsorption) will complete the coordination sphere of surface cationic centres, but the ratio between their number and the pristine ligands constituted by the oxygen anions of the surface should depend on the original surface structure and level of coordinative unsaturation of surface sites with respect to the bulk structure.

Fig. 5 shows the evolution of H₂O₂ concentration in irradiated suspensions of the two TiO₂ nanopowders as a function of time, which was found to follow a pseudo first order kinetic during at least two half lives.

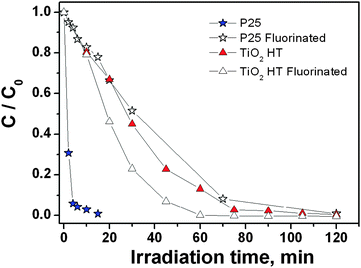Fig. 5 Photocatalytic degradation of 1 mM hydrogen peroxide at pH 3 on TiO₂ P25 and TiO₂ HT pristine and fluorinated (total fluoride concentration 10 mM) in aerated suspensions. TiO₂ concentration 0.5 g dm⁻³.

The initial transformation rates, obtained through the fitting of experimental data to an exponential decay, are 0.61 ± 0.03 and 0.026 ± 0.002 mM min⁻¹, on TiO₂ P25 and TiO₂ HT, respectively, then with a ratio greater than 23. The addition of fluoride ions has a significant impact on the photocatalytic performances of TiO₂ P25,^68,69 leading to a decrease in the initial rate of H₂O₂ consumption down to 0.023 ± 0.002 mM min⁻¹, whereas a slight increase to 0.045 ± 0.005 mM min⁻¹ occurs for TiO₂ HT. Thus, the ratio between the initial rates drops to 0.5. Nonetheless the effect of surface fluorination on the two catalysts is very different. On TiO₂ P25 the adsorption of H₂O₂ is strongly affected by the presence of fluoride ions, dropping from 0.55 ± 0.07 molecules nm⁻² (pH 3, [H₂O₂]_free = 1 mM) to <0.05 molecules nm⁻² (total fluoride: 10 mM).⁴¹ Similar measurements of H₂O₂ adsorption on TiO₂ HT in the pristine and fluorinated (presence of 10 mM total fluoride) forms, resulted in a H₂O₂ surface density of 0.21 ± 0.05 and 0.19 ± 0.05 molecules nm⁻², respectively. Hence, the amount of adsorbed H₂O₂ is ca. one third of the value measured for TiO₂ P25, and is essentially unaffected by fluorination. This evidence suggests the involvement of different H₂O₂ adsorption sites for the two TiO₂ materials.

As for the species resulting from the H₂O₂ interaction with the surface, previous studies indicated the possible formation of –OOH groups.⁷⁰

As for TiO₂ P25, that is a mixture of anatase and rutile (80/20 by weight),⁶² an involvement of the rutile phase could not be ruled out a priori. However, it must be considered that:

–as reported in ref. 23, the rutile phase present in TiO₂ P25 exhibits a specific surface area of 22 m² g⁻¹. By taking into consideration that rutile contributes for ca. 20 wt% to TiO₂ P25, this phase accounts for ca. 4 m² g⁻¹ of the overall 55 m² g⁻¹ measured as SSA_BET for this type of titania. Thus, if only rutile should be responsible for the interaction of H₂O₂ with TiO₂ P25, the density of adsorbed H₂O₂ would be quite high (ca. 7 molecules nm⁻²).

–Rutile particles isolated from TiO₂ P25 exhibited a photoactivity towards a variety of substrates, including electron scavengers,⁴⁰ equivalent or lower (down to one order of magnitude) than pristine TiO₂ P25.

–The contribution of the components due to CO adsorbed on rutile to the ν_CO pattern obtained for TiO₂ P25 (see Fig. 3 and related comments) is significantly smaller than the differences between the spectra of CO adsorbed on the two types of TiO₂ considered.

Hence, it is proposed that the rutile phase should not play a significant role in the different behaviors towards the photocatalytic decomposition of H₂O₂ exhibited by the two types of TiO₂.

Taking into account that: (i) the TiO₂ P25 surface exhibits a population of hydroxylated Ti⁴⁺ sites under low coordination conditions (α sites and sites on (110) facets), readily masked by fluoride ions by ligand exchange between the original hydroxy groups and F⁻ ions,⁶⁵ (ii) the reported adsorption competition between fluoride and H₂O₂ on TiO₂ P25 surface,⁴¹ (iii) the absence of α sites and (110) facets on TiO₂ HT (Fig. 3) as well as the absence of competition between fluoride and H₂O₂ on its surface, the high photoactivity of TiO₂ P25 toward the photocatalytic transformation of hydrogen peroxide can be related to a relevant amount of surface sites with a high level of coordinative unsaturation with respect to the bulk structure. These surface sites could play a pivotal role in the H₂O₂ transformation via an efficient direct transfer of photogenerated e⁻_CB to the hydroperoxy complexes at the surface, as witnessed by the high catalytic activity of TS-1 Ti⁴⁺ tetrahedral centers in H₂O₂ promoted oxidations.^{48,49,51,71–73} The opposite behavior of TiO₂ HT upon fluorination, with a limited increase in the H₂O₂ disappearance rate, substantiates the hypothesis of a different transformation mechanism related to a different surface location of H₂O₂. The increased rate on fluorinated TiO₂ HT can be due to an increase in the production of ˙OH like oxidizing species observed over fluorinated anatase.

Conclusions

TiO₂ anatase nanoparticles with truncated bipyramidal shapes and predominant smooth surfaces can be usefully employed as a model system for the investigation of the IR spectra of adsorbed CO at 100 K. This approach resulted in an unambiguous assignment of the band due to CO adsorbed on (101) facets. At the best of our knowledge, for the first time theoretical calculations highlighted the role of thermal and chemical disorders in determining the ν_CO of adsorbed probe molecules, and made allowance for assigning components due to CO on other, less abundant facets. More remarkably, besides the interpretation of CO/TiO₂ spectroscopic features, such a newly proposed approach appears to provide a more realistic picture of the physical–chemical properties of such systems.

The combined spectroscopic/reactivity study by using morphology controlled TiO₂ nanoparticles reveals that significant aspects of the photocatalytic activity of TiO₂ nanoparticles can be associated with the presence of a population of Ti⁴⁺ sites in low coordination at steps and/or edges, that under certain conditions could improve surface electron/hole transfer through an inner sphere mechanism involving a substrate surface complex. The unexpected finding that shifts in ν_CO frequency and Ti under-coordination are not strictly correlated could contribute to shed new light on structure–reactivity relationships in TiO₂ nanoparticles and will be the subject of future work.

Acknowledgements

The research was funded by Regione Piemonte (Misura I.1.3 “Poli di Innovazione” – II Programma, Polo: Energie Rinnovabili e Biocombustibili; project: FLEXMAT, cod. 186-192C). Cineca (ISCRA project HP10BH8BRA COnTi) is gratefully acknowledged for supercomputing facilities. Authors wish to thank Prof. Salvatore Coluccia and Prof. Claudio Minero (University of Torino) for fruitful discussions.

Notes and references

1. M. R. Hoffmann, S. T. Martin, W. Y. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96.
2. M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–297.
3. M. Bowker, Green Chem., 2011, 13, 2235–2246.
4. A. Fujishima, X. T. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
5. M. Matsuoka, M. Kitano, M. Takeuchi, K. Tsujimaru, M. Anpo and J. M. Thomas, Catal. Today, 2007, 122, 51–61.
6. G. Ertl and H. J. Freund, Phys. Today, 1999, 52, 32–38.
7. M. C. Xu, Y. K. Gao, E. M. Moreno, M. Kunst, M. Muhler, Y. M. Wang, H. Idriss and C. Woll, Phys. Rev. Lett., 2011, 106, 138302.
8. X. Q. Gong, A. Selloni, M. Batzill and U. Diebold, Nat. Mater., 2006, 5, 665–670.
9. X. Q. Gong and A. Selloni, J. Catal., 2007, 249, 134–139.
10. V. Augugliaro, S. Coluccia, E. Garcia-Lopez, V. Loddo, G. Marci, G. Martra, L. Palmisano and M. Schiavello, Top. Catal., 2005, 35, 237–244.
11. M. D'Arienzo, J. Carbajo, A. Bahamonde, M. Crippa, S. Polizzi, R. Scotti, L. Wahba and F. Morazzoni, J. Am. Chem. Soc., 2011, 133, 17652–17661.
12. S. D. Jackson and J. S. J. Hargreaves, Metal Oxide Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2009.
13. Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knözinger and J. Weitkamp, Wiley-VCH Verlag, 2008.
14. K. I. Hadjiivanov and G. N. Vayssilov, Adv. Catal., 2002, 47, 307–511.
15. G. Spoto, E. Gribov, A. Damin, G. Ricchiardi and A. Zecchina, Surf. Sci., 2003, 540, L605–L610 , and references therein.
16. G. Busca, H. Saussey, O. Saur, J. C. Lavalley and V. Lorenzelli, Appl. Catal., 1985, 14, 245–260 , and references therein.
17. K. I. Hadjiivanov, A. A. Davydov and D. G. Klissurski, Kinet. Katal., 1988, 29, 161–167.
18. G. Spoto, C. Morterra, L. Marchese, L. Orio and A. Zecchina, Vacuum, 1990, 41, 37–39.
19. K. I. Hadjiivanov and D. G. Klissurski, Chem. Soc. Rev., 1996, 25, 61–69.
20. K. Hadjiivanov, J. Lamotte and J. C. Lavalley, Langmuir, 1997, 13, 3374–3381.
21. G. Martra, Appl. Catal., A, 2000, 200, 275–285.
22. L. Mino, A. M. Ferrari, V. Lacivita, G. Spoto, S. Bordiga and A. Zecchina, J. Phys. Chem. C, 2011, 115, 7694–7700.
23. L. Mino, G. Spoto, S. Bordiga and A. Zecchina, J. Phys. Chem. C, 2012, 116, 17008–17018.
24. E. Fois, A. Gamba, G. Tabacchi, S. Quartieri and G. Vezzalini, J. Phys. Chem. B, 2001, 105, 3012–3016.
25. E. Fois, A. Gamba, G. Tabacchi, S. Quartieri and G. Vezzalini, Phys. Chem. Chem. Phys., 2001, 3, 4158–4163.
26. E. Fois, A. Gamba, G. Tabacchi, S. Coluccia and G. Martra, J. Phys. Chem. B, 2003, 107, 10767–10772.
27. E. Fois, A. Gamba, G. Tabacchi, R. Arletti, S. Quartieri and G. Vezzalini, Am. Mineral., 2005, 90, 28–35.
28. E. Fois, G. Tabacchi, D. Barreca, A. Gasparotto and E. Tondello, Angew. Chem., Int. Ed., 2010, 49, 1944–1948.
29. D. Barreca, G. Carraro, A. Devi, E. Fois, A. Gasparotto, R. Seraglia, C. Maccato, C. Sada, G. Tabacchi, E. Tondello, A. Venzo and M. Winter, Dalton Trans., 2012, 41, 149–155.
30. E. Fois, G. Tabacchi and G. Calzaferri, J. Phys. Chem. C, 2012, 116, 16784–16799.
31. C. Morterra, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 1617–1637 , and references therein.
32. H. G. Yang, C. H. Sun, S. Z. Qiao, J. Zou, G. Liu, S. C. Smith, H. M. Cheng and G. Q. Lu, Nature, 2008, 453, 638–641.
33. J. H. Wu, S. C. Hao, J. M. Lin, M. L. Huang, Y. F. Huang, Z. Lan and P. J. Li, Cryst. Growth Des., 2008, 8, 247–252.
34. Y. Alivov and Z. Y. Fan, J. Phys. Chem. C, 2009, 113, 12954–12957.
35. Y. Q. Dai, C. M. Cobley, J. Zeng, Y. M. Sun and Y. N. Xia, Nano Lett., 2009, 9, 2455–2459.
36. K. L. Ding, Z. J. Miao, B. J. Hu, G. M. An, Z. Y. Sun, B. X. Han and Z. M. Liu, Langmuir, 2010, 26, 5129–5134.
37. Z. Y. Wang, K. L. Lv, G. H. Wang, K. J. Deng and D. G. Tang, Appl. Catal., B, 2010, 100, 378–385.
38. C. Chen, R. Hu, K. Mai, Z. Ren, H. Wang, G. Qian and Z. Wang, Cryst. Growth Des., 2011, 11, 5221–5226.
39. J. G. Yu, J. J. Fan and K. L. Lv, Nanoscale, 2010, 2, 2144–2149.
40. J. Ryu and W. Choi, Environ. Sci. Technol., 2008, 42, 294–300.
41. V. Maurino, C. Minero, G. Mariella and E. Pelizzetti, Chem. Commun., 2005, 2627–2629.
42. T. Hirakawa and Y. Nosaka, Langmuir, 2002, 18, 3247–3254.
43. H. Boonstra and C. A. H. A. Mutsaers, J. Phys. Chem. A, 1975, 79, 1940–1943.
44. T. Sugimoto, X. P. Zhou and A. Muramatsu, J. Colloid Interface Sci., 2003, 259, 43–52.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
47. S. G. Louie, S. Froyen and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 1738–1742.
48. E. Fois, A. Gamba and E. Spanò, J. Phys. Chem. B, 2004, 108, 154–159.
49. E. Spanò, G. Tabacchi, A. Gamba and E. Fois, J. Phys. Chem. B, 2006, 110, 21651–21661.
50. G. Tabacchi, E. Gianotti, E. Fois, G. Martra, L. Marchese, S. Coluccia and A. Gamba, J. Phys. Chem. C, 2007, 111, 4946–4955.
51. E. Fois, A. Gamba and G. Tabacchi, ChemPhysChem, 2008, 9, 538–543.
52. www.cpmd.org; copyright 2000–2012 by IBM Corp and MPI für Festkörperforschung Stuttgart.
53. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
54. C. J. Howard, T. M. Sabine and F. Dickson, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 462–468.
55. G. Bandoli, D. Barreca, A. Gasparotto, R. Seraglia, E. Tondello, A. Devi, R. A. Fischer, M. Winter, E. Fois, A. Gamba and G. Tabacchi, Phys. Chem. Chem. Phys., 2009, 11, 5998–6007.
56. E. Fois, G. Tabacchi and G. Calzaferri, J. Phys. Chem. C, 2010, 114, 10572–10579.
57. D. Barreca, E. Fois, A. Gasparotto, R. Seraglia, E. Tondello and G. Tabacchi, Chem.–Eur. J., 2011, 17, 10864–10870.
58. M. Lazzeri and A. Selloni, Phys. Rev. Lett., 2001, 87, 266105.
59. E. Pelizzetti, V. Maurino, C. Minero, V. Carlin, E. Pramauro, O. Zerbinati and M. L. Tosato, Environ. Sci. Technol., 1990, 24, 1559–1565.
60. J. E. Frew, P. Jones and G. Scholes, Anal. Chim. Acta, 1983, 155, 139–150.
61. Powder Diffraction File JCPDS 21-1272.
62. T. Ohno, K. Sarukawa, K. Tokieda and M. Matsumura, J. Catal., 2001, 203, 82–86.
63. C. Deiana, E. Fois, S. Coluccia and G. Martra, J. Phys. Chem. C, 2010, 114, 21531–21538 , and references therein.
64. R. Disselkamp, H. C. Chang and G. E. Ewing, Surf. Sci., 1990, 240, 193–210.
65. M. Minella, M. G. Faga, V. Maurino, C. Minero, E. Pelizzetti, S. Coluccia and G. Martra, Langmuir, 2010, 26, 2521–2527.
66. G. S. Herman, M. R. Sievers and Y. Gao, Phys. Rev. Lett., 2000, 84, 3354–3357.
67. Y. Liang, S. P. Gan, S. A. Chambers and E. I. Altman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 235402.
68. C. Minero, G. Mariella, V. Maurino and E. Pelizzetti, Langmuir, 2000, 16, 2632–2641.
69. D. Monllor-Satoca and R. Gómez, J. Phys. Chem. C, 2008, 112, 139–147.
70. D. Klissurski, K. Hadjiivanov, M. Kantcheva and L. Gyurova, J. Chem. Soc., Faraday Trans., 1990, 86, 385–388.
71. F. Bonino, A. Damin, G. Ricchiardi, M. Ricci, G. Spanò, R. D'Aloisio, A. Zecchina, C. Lamberti, C. Prestipino and S. Bordiga, J. Phys. Chem. B, 2004, 108, 3573–3583.
72. A. Gamba, G. Tabacchi and E. Fois, J. Phys. Chem. A, 2009, 113, 15006–15015.
73. E. Fois, A. Gamba and G. Tabacchi, ChemPhysChem, 2005, 6, 1237–1239.

---

Footnote

† Electronic supplementary information (ESI) available: (Fig. S1) XRD patterns. (Fig. S2) IR spectra of TiO₂ HT and TiO₂ P25 samples treated at 873 K. (Fig. S3) IR spectra of CO adsorbed at 100 K on TiO₂ HT and TiO₂ P25. (Fig. S4) Schematic representation of the IR cells. (Table S1) Cutoff dependence of the two inequivalent Ti–O distances in anatase. (Fig. S5) Graphical representations of CO adsorbed on different surfaces. (Table S2) Calculated CO stretching frequencies for CO adsorbed on different TiO₂ anatase surfaces. See DOI: 10.1039/c2cp42381b

---