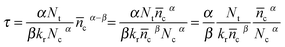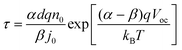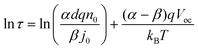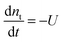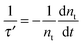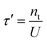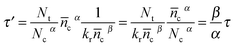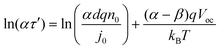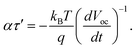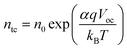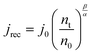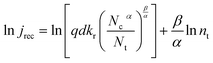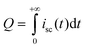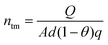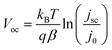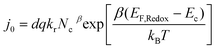Coupled analysis of steady-state and dynamic characteristics of dye-sensitized solar cells for determination of conduction band movement and recombination parameters†
Received
1st July 2012
, Accepted 27th September 2012
First published on 28th September 2012
Abstract
A new research strategy for determining the conduction band movement of TiO2 films and charge recombination between electrons in the TiO2 film and electron acceptors in the electrolyte was proposed. Steady-state short-circuit current density versus open-circuit voltage was employed to attain the exchange current density and recombination reaction order. Transient photovoltage decay and open-circuit voltage decay measurements were carried out to obtain the energetic distribution of trapped electrons. Reduced voltage-dependent trapped electron concentration and trapped electron concentration-dependent recombination current density were used to analyze influence factors of open-circuit voltage, including contributions from conduction band movement and charge recombination. The simulated and measured electron concentration were in agreement and confirmed the validity of this method for extracting conduction band movement and recombination parameters. This new approach provides a physical insight which could help us to more conveniently and efficiently understand the operation of DSCs.
1. Introduction
Dye-sensitized solar cells (DSCs) are currently receiving extensive attention because of a potentially low cost and high energy conversion efficiency.1 Recently, a cell with high open-circuit voltage has achieved an efficiency of over 12% by using co-sensitization of porphyrin dye (YD2-o-C8) with another organic dye (Y123) based on a cobalt redox shuttle.2 The improvement of the open-circuit voltage is mainly attributed to inhibition of recombination. It is justified that the control of recombination plays an important role in improving cell performance and is also a very difficult and complex procedure, which involves optimization of the electronic state of the TiO2 film,3,4 dye molecular structure,5–7 redox shuttle6,8 and so on. So minimizing the recombination losses is a key challenge to further enhance the open-circuit voltage of the cell, and isolation and quantification of the interrelated processes in the cell need to be studied.
Till now, time and frequency domain photoelectrochemical methods have been developed to estimate parameters like electron lifetime,9 recombination resistance or chemical capacitance, and also to understand the recombination process, including electrochemical impedance spectroscopy (EIS),10–13 intensity-modulated photovoltage spectroscopy (IMVS),14–16 transient photovoltage decay (TPV)17 and open-circuit voltage decay (OCVD).18,19 In these measurements, electron lifetime as function of voltage is often used as an indicator for clarifying the recombination kinetics16,18,20 and explaining the open-circuit voltage.21 The electron lifetime as a function of electron concentration22 is useful for understanding the recombination mechanism23 and improving open-circuit voltage. Not long ago, the charge extraction method has been used to extrapolate recombination kinetics of light and dark conditions under the same electron concentration.24 In order to avoid the fast sampling rate of the charge extraction method and complex data analysis of electrochemical impedance spectroscopy, we developed a new and convenient coupled analysis method to research the conduction band movement and charge recombination in DSCs.
In this work, with the aid of a combined model description of the steady-state and dynamics characteristics of cells, focusing on the appraisal of the conduction band movement and charge recombination, critical parameters have been obtained and validated for determining the internal features of the cell, including the exchange current density and charge transfer coefficient, electron lifetime and distribution of electronic state, and electron concentration as function of voltage. Furthermore, the application of this method is tested using cells with different electrolyte compositions. With such a new coupled analysis method, which is only concerning the measurements of steady-state short-circuit current density versus open-circuit voltage and transient photovoltage decay, DSCs' essential characteristics such as conduction band movement and charge recombination could be evaluated.
2. Model
2.1. Analysis of steady state characteristics
Herein, the model of short-circuit current (jsc) versus open-circuit voltage (Voc) is used to obtain recombination information. Consider the non-linear recombination model20 with the recombination reaction order β. The recombination rate U could be described byin which kr is the recombination reaction rate constant and nc is the conduction band electron concentration, which is related to the open-circuit voltage of the cell by| | 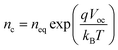 | (2) |
where q is the elementary charge, kB is the Boltzmann constant, T is the absolute temperature, and neq is the conduction band electron concentration under equilibrium state in the dark. If eqn (2) is substituted into eqn (1), the recombination current density (jrec) from TiO2 electron at the open-circuit state is| | 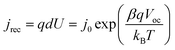 | (3) |
in which d is the film thickness and j0 is the exchange current density (that is reverse saturation current density in the diode model of DSCs), which is expressed byFor DSCs, the electrons come from the photoelectric conversion. At the open-circuit state, the photoinjected electrons are fully consumed by the electron acceptor through the recombination reaction, and under the short-circuit state, the photoinjected electrons are fully collected by the substrate electrode. According to the research,25 the injection efficiency is weakly dependent upon the potential of the TiO2 electrode. So the short-circuit current density could be used to evaluate the photoinjection current density (jinj), and then the relationship of short-circuit current and open-circuit voltage is| | 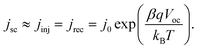 | (5) |
A plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) jscvs. Voc under a series of illumination and yields has an intercept of ln
jscvs. Voc under a series of illumination and yields has an intercept of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j0 and a slope of βq/(kBT). This gives a base to explore the short-circuit current, the open-circuit voltage and the recombination at open-circuit, thus the measurements of steady state jscversus Voc at series of illumination level allow us to obtain the exchange current density and recombination reaction order, providing the initial information about interface recombination reaction.
j0 and a slope of βq/(kBT). This gives a base to explore the short-circuit current, the open-circuit voltage and the recombination at open-circuit, thus the measurements of steady state jscversus Voc at series of illumination level allow us to obtain the exchange current density and recombination reaction order, providing the initial information about interface recombination reaction.
2.2. Dynamic behaviors analysis
2.2.1. Transient photovoltage decay.
The lifetime of an electron in the TiO2 film is an important characteristic parameter to relate the interface recombination and electron concentration in the TiO2 film. The transient photovoltage decay is used to evaluate this parameter. In these measurements, a weak optical step perturbation is imposed first on the cell, which is held at near open-circuit state under continuous steady background illumination. The resultant photovoltage decay from the cell is recorded following the withdrawal of the weak optical step perturbation and responds to the change of electron concentration in TiO2 due to recombination. Herein, the model of the open-circuit voltage dependent lifetime is found to provide information about the energetic distribution of electron state at recombination-control state by the analysis of the transient photovoltage decay data. The relationship of open-circuit voltage and the conduction band electron concentration is also described by| | 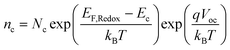 | (6) |
where Nc is the total density of the electronic state of TiO2 at the conduction band energy Ec and EF,Redox is the redox potential of electrolyte. According to eqn (6), from the steady-states before and after a weak optical step perturbation, the change of voltage (Ṽ) and change of electron concentration (ñc) are related by| | 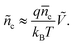 | (7) |
So the change of electron concentration can be obtained from the change of voltage. For the analysis of time-dependent dynamic behaviors, the one-dimensional model is usually used to simulate the conduction band electron concentration profile nc(x,t) where x is the distance from the electron extracting electrode and t is the time, using the continuity equation| | 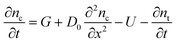 | (8) |
where G is the electron generation rate, D0 is the diffusion coefficient of conduction band electron, U is the recombination rate of conduction band electron and nt is the electron concentration in trapped states. Experimentally nt shows an exponential dependence on open-circuit voltage. So nt can be defined by| | 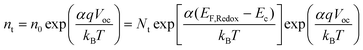 | (9) |
in which α is the distribution coefficient of trapped states, and n0 is electron concentration in trapped states at equilibrium, Nt is the total concentration of trapped states below Ec. For the final state of the decay process is steady-state, the electron concentrations from conduction band (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c) and trapped states (
c) and trapped states (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) t) can be evaluated as steady-state condition. According to eqn (8), this system at final steady-state could be described by
t) can be evaluated as steady-state condition. According to eqn (8), this system at final steady-state could be described by| | 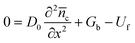 | (10) |
where Gb and Uf are the electron generation rate caused by the background light and recombination rate at the final state of the decay process, respectively. The time-dependent electron concentration during the photovoltage decay process is written as| | 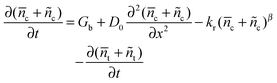 | (11) |
in which ñc and ñt are the change of electron concentrations in conduction band and trapped state after step-light withdrawal, respectively. Considering ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c and
c and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) t as final steady-state conditions for the electrons cumulated at TiO2, which are only dissipated by recombination, eqn (11) can be rearranged to
t as final steady-state conditions for the electrons cumulated at TiO2, which are only dissipated by recombination, eqn (11) can be rearranged to| | 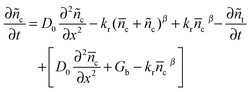 | (12) |
eqn (10) can be substituted into eqn (12) to give the following rearranged equation.| | 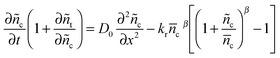 | (13) |
According to the quasi-static approximation,26 (the trap and detrap processes are faster than the process of transport and recombination), the trapped electron concentration can be related to the conduction band electron concentration using eqn (6) and (9).| | 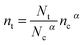 | (14) |
The relationship between change of trapped electron concentration and change of conduction band electron concentration could be written as| | 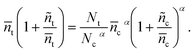 | (15) |
For small values of x (ñc ≪ ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c for the small perturbation), the exponential (1 + x)y − 1 can be approximated as yx with Taylor series approximation, where y = α or β. Eqn (13) and (15) could then be written as
c for the small perturbation), the exponential (1 + x)y − 1 can be approximated as yx with Taylor series approximation, where y = α or β. Eqn (13) and (15) could then be written as| | 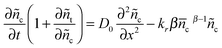 | (16) |
and| | 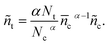 | (17) |
The differentiation of eqn (17) with respect to ñc is | | 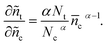 | (18) |
Under the open-circuit state, the electron diffusion term can be neglected. Incorporating eqn (16) and (18) affords eqn (19)| | 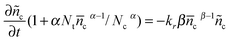 | (19) |
which is solved with the initialization condition: ñc (t = 0) = ñcmaxwhere ñcmax is the perturbation amplitude of conduction band electron concentration referred to final steady-state ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c, τ is the electron lifetime. For 0.1 < α < 0.5 in typical DSCs,
c, τ is the electron lifetime. For 0.1 < α < 0.5 in typical DSCs, 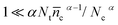 , τ could be expressed as
, τ could be expressed as| | 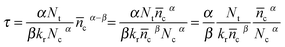 | (21) |
The electron lifetime is affected by the recombination kinetics parameters (kr, β) in addition to the thermodynamic factors (Nt, α). However, the conduction band electron concentration is not easily measured by experiment. Therefore, for obtaining the kinetic and thermodynamic parameters, the relationship of electron lifetime and the steady-state final voltage is needed. With the aid of eqn (4), (6) and (9), eqn (21) can be rewritten as eqn (22)| | 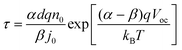 | (22) |
or| | 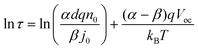 | (23) |
Considering that the change of voltage is caused by the change of electron concentration during the transient photovoltage decay (eqn (7)) then the photovoltage decay in eqn (20) also can be described mathematically aswhere, Ṽmax is the photovoltage perturbation amplitude, and the electron lifetime τ is same as eqn (20). This equation means the single exponential decay curve of photovoltage should be observed from experiments and allows us to find the electron lifetime defined by recombination, and further to obtain parameters α and n0.
2.2.2. Open-circuit voltage decay analysis.
Besides electron lifetime (τ) from small amplitude transient photovoltage decay relaxation, another way to measure the electron lifetime (τ′) in DSCs is the large amplitude open-circuit voltage decay measurement. In this experiment, the cell is held at open-circuit state under a certain steady illumination. The illumination is interrupted and the voltage decay is recorded in the dark. Considering that nt ≫ nc (the majority of electrons in the cell are trapped at open-circuit state)24 and neglecting electron diffusion term under open-circuit conditions, then eqn (8) could be approximated to describe this voltage decay process| | 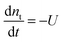 | (25) |
Intuitively, the electron lifetime (τ′) can be defined as18,27| | 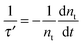 | (26) |
Combining eqn (25) and (26), we found| | 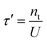 | (27) |
According to eqn (1), (14) and (27), τ′ could be expressed theoretically by| | 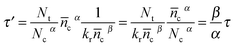 | (28) |
Obviously, the product of electron lifetime τ′ from OCVD and distribution coefficient of trapped states is equal to that of electron lifetime τ from TPV and recombination reaction order. So with OCVD, the important thermodynamic factors (α and then n0) can also be derived. The fitted equation is shown in eqn (29).
| | 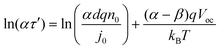 | (29) |
In a plot of ln(ατ′) vs. Voc, the slope is affected by distribution coefficient of trapped states and recombination reaction order of conduction electrons, the intercept of the beeline is controlled by distribution coefficient of trapped states, exchange current density, and electron concentration of trapped states at equilibrium. Using eqn (9) and (26), we can derive the lifetime by
| | 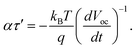 | (30) |
So
ατ′ could be obtained experimentally by differential open-circuit voltage with respect to time.
2.2.3. Simulation of energetic distribution of trapped electrons and recombination rate.
In order to investigate the shift of the conduction band, the equilibrium tapped electron concentration and distribution coefficient of tapped states derived from transient photovoltage decay measurements or open-circuit photovoltage decay measurements are used to calculate the voltage-dependent trapped electron concentration (ntc) with eqn (9).| | 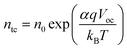 | (31) |
The recombination current density is simulated with the following equation obtained by combining eqn (3) and (9).| | 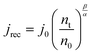 | (32) |
With the aid of eqn (4), (6), and (9), eqn (32) can be rearranged into eqn (33).| | 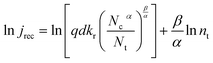 | (33) |
At the same trapped electron concentration, the recombination is mainly affected by the energetic components (Nc, Nt, and α) and kinetic components (kr and β). This allows us to estimate the correlation between trapped electron concentration and the recombination kinetics, outside the complex influence of potentials of conduction band and redox.
2.2.4. Charge extraction.
To evaluate the validity of the new method, the electron concentration calculated needs to be compared with the experimental measured value by charge extraction. In experiments, the cell is switched from its open-circuit state to short-circuit state, while simultaneously turning the light off. The resulting photocurrent decay in eqn (34) is integrated to obtain the charge (Q) in the cells.24| | 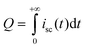 | (34) |
The electron concentration (ntm) in TiO2 can be found by| | 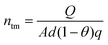 | (35) |
where A and θ in eqn (35) are the area and porosity of the TiO2 film, respectively.
3. Experimental
3.1. Cell fabrication
The mesoporous TiO2 electrodes comprised of a 7 μm transparent layer of 20 nm-sized titania particles and a second 5 μm layer of scattering titania particles were prepared on the fluorine-doped SnO2 (FTO, Nippon Sheet Glass, Solar, 4 mm thick) conducting glass substrates. A benchtop Ambios XP-1 stylus profilometer was used to measure the film thickness. The detailed preparation procedures of titania nanocrystals, pastes for screenprinting, and nanostructured titania films have been reported in a previous paper.28 Acycloidal titania electrode (∼0.28 cm2) was stained by immersing it into a dye solution composed of 150 μM 2-cyano-3-{6-{4-[N,N-bis(4-hexyloxyphenyl)amino]phenyl}-4,4-dihexyl-4H-cyclopenta[2,1-b:3,4-b′]dithiophene-2-yl}acrylic acid (C218)29 and 300 μM cheno in chlorobenzene (CB) for 5 h. After being rinsed with CB and drying by air flow, the electrodes were assembled with a thermally platinized FTO (TEC 15 Ω/□, Libbey–Owens–Ford Industries, 2.2 mm thick) electrode. A 30 μm-thick Bynel (DuPont) hot-melt gasket was used to separate and heating sealed up the electrodes. A liquid electrolyte was introduced to the internal space through a small hole on the counter electrode glass substrate made with a sand-blasting drill. It was sealed with a Bynel sheet and a thin glass cover by heating. Two kinds of electrolytes were used: E1: 1.0 M DMII, 50 mM LiTFSI, 30 mM I2, and 1 M GNCS in acetonitrile; E2: 1.0 M DMII, 30 mM I2 1 M TBP, and 1 M GNCS in acetonitrile.
3.2. Photovoltaic measurements
A model LS1000-4S-AM1.5G-1000W solar simulator (Solar Light Company, USA) in combination with a metal mesh was employed to give an irradiance of 100 mW cm−2. A PMA2144 pyranometer and a calibrated PMA 2100 dose control system were used to test the light intensity. In current-voltage (J–V) experiments, a Keithley 2602 source meter was used to apply a bias potential to a testing cell and measure photocurrent under the full computer control. The measurements were fully automated using Labview 8.0. During all measurements, a metal mask was covered on a testing cell to give an aperture area of 0.28 cm2 for accepting incidence light. An anti-reflection film (λ < 380 nm, ARKTOP, ASAHI Glass) is adhered to the DSC photoanode during J–V measurements.
3.3. Transient measurements
Transient photovoltage decay measurement (TPV) was first applied in dye sensitized solar cells to attain electron lifetime as described by O'Regan et al.17 In experiment, the cell was held at open-circuit conditions under continuous steady illumination. A weak perturbation light to this background illumination level was incident on the TiO2 side of the cell for about 5 s. After the cell was up to steady state, the perturbation light was turned off by a fast solid-state switch. The resulting photovoltage decay was simultaneously monitored. The background illumination and perturbation light were generated by an array of white 1 W LEDs and a ring of red 1 W LEDs, respectively. The background illumination was adjusted to obtain the necessary open-circuit voltage. The perturbation intensity was controlled to keep the ΔV due to the perturbation below 10 mV to satisfy the small perturbation conditions. The perturbation light had a fall time of below 100 ns. The response of the potentiostat was smaller than 1 μs, thus, we could measure the transient processes with time constants above 10 μs accurately. In all cases, photovoltage decays were found to be monoexponential, so the time constant was extracted by fitting the decay curves.
In open-circuit voltage decay measurements,28 the cell was exposed to illumination for obtaining the steady open-circuit voltage. The illumination was turned off and the resulting open-circuit voltage decay was recorded to find the electron lifetime.
Charge extraction24 was at Voc measured by applying a constant background illumination to the cell, while also applying a constant voltage using a voltage source. The voltage source was set to apply exactly the same voltage that the background illumination would generate at the open-circuit conditions for 5 s. After the cell was up to a steady state, the background illumination was turned off and the cell was simultaneously shorted and the resultant discharging current transient was measured. The charge in the cell was found by integrating the current decay curve. The background illumination had a fall time of below 100 ns. The time response of the galvanostat was smaller than 1 μs. This assumed that the recombination loss during charge extraction was not significant relative to the charge extracted.
4. Results and discussion
Current densities versus applied potential measurements were performed for cells exposed to AM1.5G simulated sunlight and the detailed photovoltaic parameters are given in Table 1. The open-circuit voltage difference of 60 mV between the two cells was a remarkable characteristic of the system, which was used to justify this method of conduction band movement and charge recombination research. From eqn (5), we obtain the open-circuit voltage shown in eqn (36).| | 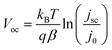 | (36) |
This equation stressed the effect of the three primary parameters jsc, β, and j0 on the final Voc. In a previous study,30j0 and m (m = 1/β)20 were attained by fitting current density-voltage curve with the diode model. Herein, jsc and Voc at series of illumination conditions were measured by setting V = 0 with potentiostat mode and I = 0 with galvanostat mode, respectively, to obtain the β and j0.
Table 1 Photovoltaic parameters of cells under the simulated AM1.5G sunlight: short-circuit current density (jsc), open-circuit voltage (Voc), fill factor (FF), and power conversion efficiency (ηe)
| |
j
sc/mA cm−2 |
V
oc/V |
FF |
η
e/% |
| E1 |
14.59 |
0.776 |
0.710 |
8.0 |
| E2 |
13.46 |
0.836 |
0.690 |
7.8 |
The previous study25 indicated that the efficiencies of electron injection and dye regeneration were almost independent of the potential of the TiO2 electrode in this range. So the short-circuit current density was used to approximate the recombination current density at open-circuit conditions. Fig. 1 showed the short-circuit current densities or recombination current densities plotted as function of open-circuit voltage, which had the most obvious feature that ln(jsc) increases linearly with Voc in all cases, which was consistent with eqn (5) and is the same as that discovered in our previous research.31 The exchange current density and recombination reaction order can be found by fitting the jscversus Voc curves with eqn (5) and the results are shown in Table 2. Although the cell with Li+ electrolyte had the small β, it had the low open-circuit voltage with respect to cell with TBP electrolyte. This was because the j0 played a key important role in determining the open-circuit voltage in this case. With eqn (4) and (6), j0 can be expressed in eqn (37).
| | 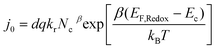 | (37) |
The critical factors (
kr,
EF,Redox −
Ec) governing
j0 needed to be distinguished for a deeper understanding of the recombination mechanism. In DSCs, because the absolute value of
EF,Redox −
Ec was difficult to achieve in experiment, the shift of the conduction band was evaluated previously from the capacitance by
impedance spectra32,33 or from the electron concentration by charge
extraction.
34 Avoiding complex
impedance spectra and charge
extraction methods, the steady state and dynamic characteristics of the cells based on step modulation photovoltage decay technique were researched here to obtain the electron concentration, and thus the shift of the conduction band edge.
Table 2 Parameters derived from open-circuit voltage-dependent short-circuit current density (Fig. 1) and electron lifetime (Fig. 2C): exchange current density (j0), recombination reaction order (β), electron density of trapped state (n0) under the equilibrium in the dark, and distribution coefficient of trapped state (α)
| |
j
0/mA cm−2 |
β
|
n
0/cm−3 |
α
|
| E1 |
2.3 × 10−9 |
0.75 |
3.6 × 1014 |
0.29 |
| E2 |
2.2 × 10−14 |
1.05 |
2.8 × 1014 |
0.28 |
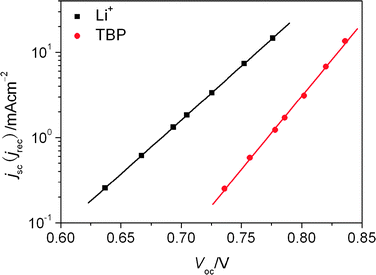 |
| | Fig. 1 The plots of short-circuit current density versus open-circuit voltage: the square point for cell with E1; the circle point for cells with E2; the solid line was the fitting line with eqn (5). | |
The transient photovoltage decay measurements were carried out under open-circuit conditions with a series of background irradiations to obtain the recombination information by analyzing the dynamic behaviors of cells. With the small perturbation employed, the typical TPV transients shown in Fig. 2A and B gave monoexponential decay features, which were consistent with the description of eqn (24). The TPV transients were also plotted on semilog and log-log coordinates for data validating (shown in Fig. S1, ESI†). So by fitting this small amplitude voltage decay, the electron lifetime at each illumination could be obtained, and its relation with voltage is shown in Fig. 2C. This linear relation relationship followed eqn (23). Therefore, the distribution coefficient of trapped states α could be first derived from the slope with knowing the β parameter, then the electron concentration in trapped states n0 could be attained from intercept with knowing j0. As shown in eqn (9), n0 determined by thermodynamic factors (Nt, α, and EF,Redox − Ec) is used to estimated the approximate value of EF,Redox − Ec. In practice, similar values of α allow the shift of conduction band to be estimated by the displacement of electron concentration. Compared to the cell with TBP, the cell with Li+ has a larger n0 value with similar α (Table 2) indicating that the lower conduction band is caused by Li+ absorbed on the surface of TiO2.31,35,36
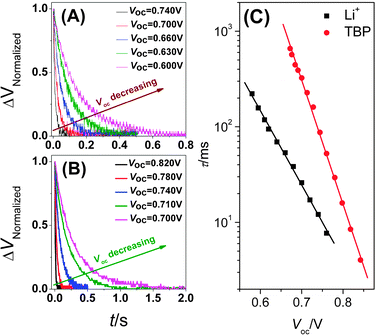 |
| | Fig. 2 The normalized transient photovoltage decay curves of two cells under different open-circuit voltage by changing series of light intensity: (A) for E1; (B) for E2. (C) The plots of electron lifetime versus open-circuit voltage. The experimental points were derived from Fig. 2A and B by eqn (24), the square point for E1, the circle point for E2. The solid line was fitted using eqn (23). | |
Besides the small amplitude TPV technique, the large amplitude open-circuit voltage decay measurements can be used also to obtain the electron lifetime (τ′) as an alternate choice. Fig. 3A shows the typical open-circuit voltage decays of the two cells. The voltage-dependent ατ′ was calculated by analyzing this open-circuit voltage decay with eqn (30) and then was compared to βτ from TPV in Fig. 3B. The equivalent relationship of ατ′ and βτ is consistent with the theoretical expression shown in eqn (28). These results revealed clearly that the same n0 and α can also be obtained by OCVD, when the difference of recombination and that of trap–detrap mechanism can be neglected in large amplitude open-circuit voltage decay and voltage decay relaxation by small perturbation.
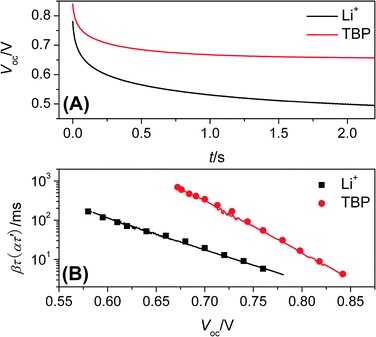 |
| | Fig. 3 (A) Open-circuit voltage decay curves: the black curve for E1, the red curve for E2; (B) comparison of electron lifetimes from TPV (the big solid point) and OCVD (the line). | |
After n0 and α are obtained, the trapped electron concentration as function of voltage was deduced through eqn (31) and shown in Fig. 4A (the solid line). The good similarity between this electron concentration profile and the one determined experimentally by the charge extraction method (the square and circle points in Fig. 4A) strongly support the validity of new method. The shift of the conduction band edge was 60 mV obtained from the voltage difference under the same trapped electron concentration. The recombination current density as function of nt from eqn (32) was used to compare the recombination dynamics shown in Fig. 4B. Although the cell with Li+ electrolyte had a high recombination current density under the same trapped electron concentration, the smaller β of the cell with Li+ electrolyte resulted in the differences of recombination from these two cells becoming smaller with the increase of background light intensity. When the background light was up to the simulated AM1.5G sunlight, the improvement of 60 mV open-circuit voltage (in Table 1) is mainly attributed to the negative shift of conduction band of the cell with TBP with respect to the cell with Li+.
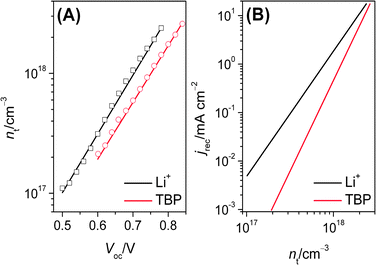 |
| | Fig. 4 (A) Comparison of trapping electron concentration measured (the black square for E1; the red circle for E2) from charge extraction method and simulated (the solid line) with eqn (31). (B) Plot of simulated recombination current density versus trapping electron concentration: the black line for E1; the red line for E2. | |
Beginning with steady-state short-circuit current density and open-circuit voltage at a series of illumination conditions, recombination reaction order β and exchange current density j0 were obtained, then combined with TPV or OCVD experiments the distribution coefficient of trapped states α and the electron concentration in trapped states n0 were gained. Subsequently, the electron lifetime τ and the recombination current density jrec were analysed, which were useful for obtaining valuable information about conduction band movement and recombination kinetics.
5. Conclusions
A new method based on combined analysis of the steady-state and dynamic behaviors of cells was developed to research the conduction band movement and charge recombination. The important recombination parameters (exchange current density and recombination reaction order) were derived from the relation of short-circuits current density vs. open-circuit voltage. The theoretical relation of electron lifetimes from transient photovoltage decay relaxation and large amplitude open-circuit voltage decay was established and approved by experiments. This allowed the fast measurement of electron lifetime, also electron concentration for trapped states at equilibrium and the distribution coefficient of trapped states could be attained by either method. The electron concentration from the steady-state and dynamic experiments and the directly measured experimental electron concentration from charge extraction were in agreement, which also provides clear evidence for the validity of this new method. Our investigation afforded a faster and more concise method for appraising conduction band movement and charge recombination than the charge extraction and EIS method.
Acknowledgements
The National 973 Program (No. 2011CBA00702), the National Science Foundation of China (Nos. 51125015, 50973105 and 51103146) and National 863 Program (No. 2011AA050521) have supported this work. We are grateful to Dyesol for supplying the WERO-2 scattering paste and to DuPont Packaging and Industrial Polymers for supplying the Bynel film.
Notes and references
- M. Gratzel, Nature, 2001, 414, 338–344 CrossRef CAS.
- A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Gratzel, Science, 2011, 334, 629–634 CrossRef CAS.
- E. M. Barea, V. Gonzalez-Pedro, T. Ripolles-Sanchis, H.-P. Wu, L.-L. Li, C.-Y. Yeh, E. W.-G. Diau and J. Bisquert, J. Phys. Chem. C, 2011, 115, 10898–10902 CAS.
- Y. Geng, Y. Shi, L. Wang, B. Ma, R. Gao, Y. Zhu, H. Dong and Y. Qiu, Phys. Chem. Chem. Phys., 2011, 13, 2417–2421 RSC.
- J. R. Jennings, Y. Liu, Q. Wang, S. M. Zakeeruddin and M. Graetzel, Phys. Chem. Chem. Phys., 2011, 13, 6637–6648 RSC.
- M. Ohta, N. Koumura, K. Hara and S. Mori, Electrochem. Commun., 2011, 13, 778–780 CrossRef CAS.
- M. Tuikka, P. Hirva, K. Rissanen, J. Korppi-Tommola and M. Haukka, Chem. Commun., 2011, 47, 4499–4501 RSC.
- M. J. DeVries, M. J. Pellin and J. T. Hupp, Langmuir, 2011, 27, 5166–5166 CrossRef CAS.
- A. Y. Anderson, P. R. F. Barnes, J. R. Durrant and B. C. O'Regan, J. Phys. Chem. C, 2011, 115, 2439–2447 CAS.
- J. Bisquert, J. Phys. Chem. B, 2002, 106, 325–333 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago, N. S. Ferriols, P. Bogdanoff and E. C. Pereira, J. Phys. Chem. B, 2000, 104, 2287–2298 CrossRef CAS.
- F. Fabregat-Santiago, J. Bisquert, G. Garcia-Belmonte, G. Boschloo and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2005, 87, 117–131 CrossRef CAS.
- F. Fabregat-Santiago, J. Bisquert, E. Palomares, L. Otero, D. B. Kuang, S. M. Zakeeruddin and M. Gratzel, J. Phys. Chem. C, 2007, 111, 6550–6560 CAS.
- W. Q. Liu, L. H. Hu, Z. P. Huo and S. Y. Dai, Prog. Chem., 2009, 21, 1085–1093 CAS.
- J. Kruger, R. Plass, M. Gratzel, P. J. Cameron and L. M. Peter, J. Phys. Chem. B, 2003, 107, 7536–7539 CrossRef.
- G. Schlichthorl, S. Y. Huang, J. Sprague and A. J. Frank, J. Phys. Chem. B, 1997, 101, 8141–8155 CrossRef.
- A. B. Walker, L. M. Peter, K. Lobato and P. J. Cameron, J. Phys. Chem. B, 2006, 110, 25504–25507 CrossRef CAS.
- A. Zaban, M. Greenshtein and J. Bisquert, ChemPhysChem, 2003, 4, 859–864 CrossRef CAS.
- J. Bisquert, A. Zaban, M. Greenshtein and I. Mora-Sero, J. Am. Chem. Soc., 2004, 126, 13550–13559 CrossRef CAS.
- J. Bisquert and I. Mora-Sero, J. Phys. Chem. Lett., 2010, 1, 450–456 CrossRef CAS.
- J. Villanueva-Cab, H. Wang, G. Oskam and L. M. Peter, J. Phys. Chem. Lett., 2010, 1, 748–751 CrossRef CAS.
- J. R. Jennings, A. Ghicov, L. M. Peter, P. Schmuki and A. B. Walker, J. Am. Chem. Soc., 2008, 130, 13364–13372 CrossRef CAS.
- P. R. F. Barnes and B. C. O'Regan, J. Phys. Chem. C, 2010, 114, 19134–19140 CAS.
- P. R. F. Barnes, A. Y. Anderson, M. Juozapavicius, L. Liu, X. Li, E. Palomares, A. Forneli and B. C. O'Regan, Phys. Chem. Chem. Phys., 2011, 13, 3547–3558 RSC.
- S. E. Koops, B. C. O'Regan, P. R. F. Barnes and J. R. Durrant, J. Am. Chem. Soc., 2009, 131, 4808–4818 CrossRef CAS.
- J. Bisquert and V. S. Vikhrenko, J. Phys. Chem. B, 2004, 108, 2313–2322 CrossRef CAS.
- M. Ansari-Rad, Y. Abdi and E. Arzi, J. Phys. Chem. C, 2012, 116, 10867–10872 CAS.
- P. Wang, S. M. Zakeeruddin, P. Comte, R. Charvet, R. Humphry-Baker and M. Gratzel, J. Phys. Chem. B, 2003, 107, 14336–14341 CrossRef CAS.
- R. Z. Li, J. Y. Liu, N. Cai, M. Zhang and P. Wang, J. Phys. Chem. B, 2010, 114, 4461–4464 CrossRef CAS.
- W. J. Potscavage, A. Sharma and B. Kippelen, Acc. Chem. Res., 2009, 42, 1758–1767 CrossRef CAS.
- Q. J. Yu, D. F. Zhou, Y. S. Shi, X. Y. Si, Y. H. Wang and P. Wang, Energy Environ. Sci., 2010, 3, 1722–1725 CAS.
- E. M. Barea, C. Zafer, B. Gultekin, B. Aydin, S. Koyuncu, S. Icli, F. F. Santiago and J. Bisquert, J. Phys. Chem. C, 2010, 114, 19840–19848 CAS.
- E. M. Barea, J. Ortiz, F. J. Paya, F. Fernandez-Lazaro, F. Fabregat-Santiago, A. Sastre-Santos and J. Bisquert, Energy Environ. Sci., 2010, 3, 1985–1994 CAS.
- B. C. O'Regan, J. R. Durrant, P. M. Sommeling and N. J. Bakker, J. Phys. Chem. C, 2007, 111, 14001–14010 CAS.
- R. Z. Li, D. X. Liu, D. F. Zhou, Y. S. Shi, Y. H. Wang and P. Wang, Energy Environ. Sci., 2010, 3, 1765–1772 CAS.
- Y. S. Shi, Y. H. Wang, M. Zhang and X. D. Dong, Phys. Chem. Chem. Phys., 2011, 13, 14590–14597 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The transient photovoltage decay data. See DOI: 10.1039/c2cp42216f |
|
| This journal is © the Owner Societies 2013 |
Click here to see how this site uses Cookies. View our privacy policy here. 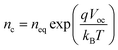
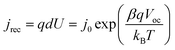
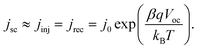
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) jscvs. Voc under a series of illumination and yields has an intercept of ln
jscvs. Voc under a series of illumination and yields has an intercept of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j0 and a slope of βq/(kBT). This gives a base to explore the short-circuit current, the open-circuit voltage and the recombination at open-circuit, thus the measurements of steady state jscversus Voc at series of illumination level allow us to obtain the exchange current density and recombination reaction order, providing the initial information about interface recombination reaction.
j0 and a slope of βq/(kBT). This gives a base to explore the short-circuit current, the open-circuit voltage and the recombination at open-circuit, thus the measurements of steady state jscversus Voc at series of illumination level allow us to obtain the exchange current density and recombination reaction order, providing the initial information about interface recombination reaction.

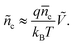
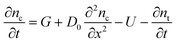
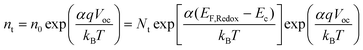
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c) and trapped states (
c) and trapped states (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) t) can be evaluated as steady-state condition. According to eqn (8), this system at final steady-state could be described by
t) can be evaluated as steady-state condition. According to eqn (8), this system at final steady-state could be described by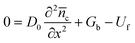
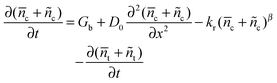
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c and
c and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) t as final steady-state conditions for the electrons cumulated at TiO2, which are only dissipated by recombination, eqn (11) can be rearranged to
t as final steady-state conditions for the electrons cumulated at TiO2, which are only dissipated by recombination, eqn (11) can be rearranged to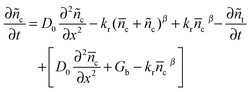
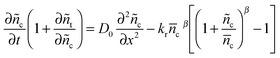
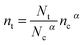
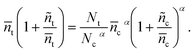
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c for the small perturbation), the exponential (1 + x)y − 1 can be approximated as yx with Taylor series approximation, where y = α or β. Eqn (13) and (15) could then be written as
c for the small perturbation), the exponential (1 + x)y − 1 can be approximated as yx with Taylor series approximation, where y = α or β. Eqn (13) and (15) could then be written as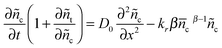
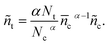
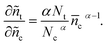
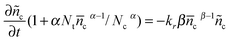
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c, τ is the electron lifetime. For 0.1 < α < 0.5 in typical DSCs,
c, τ is the electron lifetime. For 0.1 < α < 0.5 in typical DSCs, 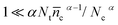 , τ could be expressed as
, τ could be expressed as