 Open Access Article
Open Access ArticleA variable temperature synchrotron X-ray diffraction study of the ferroelastic double perovskite Ba2GdMoO6
Thomas K.
Wallace
,
Ross H.
Colman
and
Abbie C.
Mclaughlin
*
Department of Chemistry, University of Aberdeen, Meston Walk, Aberdeen AB24 3UE, UK. E-mail: a.c.mclaughlin@abdn.ac.uk
First published on 3rd January 2013
Abstract
A study of the magnetic and structural properties of the double perovskite Ba2GdMoO6 has been performed. The crystal structure distorts from the ideal cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure to the tetragonal space group I4/m at 220 K, before undergoing a second distortion to a triclinic system (I
m) structure to the tetragonal space group I4/m at 220 K, before undergoing a second distortion to a triclinic system (I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) at 80 K. The phase transition to triclinic symmetry is also evident in magnetic susceptibility measurements. The variable temperature synchrotron powder X-ray diffraction results reveal that Ba2GdMoO6 is ferroelastic, with the onset of ferroelastic domain formation occurring at the cubic–tetragonal phase transition. A number of Rietveld refinement techniques for modelling diffuse scattering from ferroelastic domain boundaries have been explored.
) at 80 K. The phase transition to triclinic symmetry is also evident in magnetic susceptibility measurements. The variable temperature synchrotron powder X-ray diffraction results reveal that Ba2GdMoO6 is ferroelastic, with the onset of ferroelastic domain formation occurring at the cubic–tetragonal phase transition. A number of Rietveld refinement techniques for modelling diffuse scattering from ferroelastic domain boundaries have been explored.
I. Introduction
Transition metal perovskites (ABX3) have received much attention as a result of their diverse properties. These include colossal magnetoresistance (CMR) as observed in doped manganites such as La1−xSrxMnO3,1 ferroelectricity in BaTiO3,2 superconductivity in Ba1−xKxBiO33 and ferroelasticity in LaCoO3.4 As well as these useful properties, it is the ability to easily adapt the perovskite structure by chemical substitution and produce materials with optimised properties that makes studying the perovskites such an attractive proposition.Double perovskites have the general formula A2BB′X6 and are formed by extension of the basic perovskite structure, where a mixture of cations occupy the octahedrally coordinated B sites.5 Within this B site sub-lattice, cations can be disordered; or ordered in a layered, columnar or rock salt arrangement. As with the basic perovskite structure, double perovskites regularly undergo symmetry lowering distortions such as octahedral tilting,5 B site cation displacements6,7 and orbital ordering leading to Jahn–Teller (JT) distortions.8 Such structural flexibility results in extremely versatile materials that readily undergo distortions away from the ideal cubic symmetry.
Double perovskites also exhibit diverse electronic and magnetic properties. Superconductivity has been evidenced in doped double perovskites such as A2Y(Ru1−xCux)O6 (where A = Ba or Sr),9 Sr2MgMoO6−δ is an oxide ion conductor with potential application in solid oxide fuel cells,10 low field magnetoresistance has been observed in Sr2FeMoO611 and ferroelasticity has been reported for materials such as Ba2GdNbO6.12 More recently, there have been a number of studies of Mo5+ double perovskites with chemical formula Ba2LnMoO613–16 where Ln = lanthanide or Y3+ ion. Ba2LnMoO6 materials are electrically insulating and show antiferromagnetic interactions between Mo5+S = 1/2 spins.13–15 Across this series, a picture of the magnetic and structural behaviour of these materials is beginning to emerge. No evidence for magnetic order has been reported down to 2 K in Ba2LnMoO6 (RE = Gd, Dy–Yb and Y).13,14 However, the substitution of rare earth cations with larger ionic radii induces antiferromagnetic ordering. This ordering is observed at the anomalously high temperatures of TN = 112 K in Ba2EuMoO6 (rEu = 0.947 Å), TN = 130 K in Ba2154SmMoO6 (rSm = 0.958 Å) and at the lower temperature of TN = 15 K, in Ba2NdMoO6 (rNd = 0.983 Å).13,15,17
Detailed variable temperature neutron diffraction studies on Ba2154SmMoO6 and Ba2NdMoO6 have revealed further differences between the two materials.15,18 In both materials, distortions from a higher symmetry tetragonal (space-group I4/m) to a lower symmetry triclinic phase (space-group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) occurs. However, in Ba2154SmMoO6 this tetragonal–triclinic distortion occurs at around 290 K, whereas, in Ba2NdMoO6 it occurs at the lower temperature of 130 K. Furthermore, the evolution of Mo–O bond lengths with temperature highlights a different relationship between magnetism and orbital ordering in these two materials. At 130 K a Jahn–Teller distortion was observed simultaneously with antiferromagnetic order in Ba2154SmMoO6; the single Mo5+ unpaired electron occupies both the dxz and dyz orbitals resulting in an elongation of the apical Mo–O bond length. In Ba2NdMoO6, this same JT distortion evolves over a wider temperature range 130–60 K resulting in a gradual elongation of the apical Mo–O bond well above TN = 15 K.
) occurs. However, in Ba2154SmMoO6 this tetragonal–triclinic distortion occurs at around 290 K, whereas, in Ba2NdMoO6 it occurs at the lower temperature of 130 K. Furthermore, the evolution of Mo–O bond lengths with temperature highlights a different relationship between magnetism and orbital ordering in these two materials. At 130 K a Jahn–Teller distortion was observed simultaneously with antiferromagnetic order in Ba2154SmMoO6; the single Mo5+ unpaired electron occupies both the dxz and dyz orbitals resulting in an elongation of the apical Mo–O bond length. In Ba2NdMoO6, this same JT distortion evolves over a wider temperature range 130–60 K resulting in a gradual elongation of the apical Mo–O bond well above TN = 15 K.
Another member of this series that has generated significant interest is Ba2YMoO6 which is the first reported example of a valence bond glass (VBG).19 This magnetic ground-state has been predicted theoretically,20 and is a consequence of geometric frustration of Mo5+S = 1/2 spins, which are arranged on the corners of a lattice of edge sharing tetrahedra. Consequently, all antiferromagnetic interactions cannot be satisfied simultaneously, leading to a gradual freezing of spins into a disordered pattern of spin singlets upon cooling. A subsequent study carried out on Ba2−xSrxYMoO6 showed that the VBG phase persists despite a lowering of symmetry from cubic to monoclinic (P21/n)21 which demonstrates that the VBG phase is robust to structural distortions.
Given the remarkable behaviour seen in Ba2YMoO6, Ba2154SmMoO6 and Ba2NdMoO6, further studies of the double perovskites Ba2LnMoO6 are required to build a comprehensive understanding of the magnetic and structural properties of these materials. This study focuses on the structural and magnetic properties of the molybdenum double perovskite, Ba2GdMoO6 which exhibits a ferroelastic phase transition below 220 K; a property that has not been reported so far for Mo5+ double perovskites.13–16,18
II. Experimental
Ba2GdMoO6 was prepared by solid state reaction of stoichiometric amounts of MoO3, BaCO3 and Gd2O3 powder of 99% purity or higher. These oxides were mixed by thorough grinding, pelletised and then heated to 800 °C and held for 15 minutes. The temperature was then raised to 1000 °C and held for 15 minutes and then finally to 1200 °C and held for 12 hours. Three further heat treatments at 1200 °C were then carried out with intermediate grinding and pelleting to ensure complete reaction and sample homogeneity. To prevent oxidation of Mo5+, all heat treatments were carried out under flowing 5% H2/N2.Variable temperature synchrotron X-ray diffraction patterns were recorded at a wavelength of λ = 0.3948 Å on the ID31 powder diffraction beamline at ESRF, Grenoble, France. A sample of Ba2GdMoO6 was inserted into a 0.5 mm-diameter borosilicate glass capillary mounted on the axis of the diffractometer and spun at ∼1 Hz to improve the powder averaging of the crystallites. Diffraction patterns were recorded over a range of temperatures from 5 K to 290 K over the angular range 5° < 2θ < 45° and rebinned to a constant step size of 0.002° for each scan.
III. Results/discussion
The variable temperature synchrotron X-ray diffraction data for Ba2GdMoO6 were fitted using the Rietveld refinement technique22 using the Topas software.23Fig. 1 shows Rietveld refinements of synchrotron XRD data at both 290 K and 5 K. At 290 K, a good fit to the data was achieved with the cubic symmetry space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m [a = 8.45509(20) Å]. Upon reducing the temperature, the material undergoes a structural phase transition to the tetragonal space group I4/m [a = 5.97444(20) Å, c = 8.45848(9) Å] at 220 K. This phase transition is confirmed by the observation of peak splitting below 250 K. Fig. 2 shows a selected area of the synchrotron X-ray diffraction pattern evidencing the (400) reflection at 250 K. There is clear evidence of peaks splitting below 220 K with further splitting seen in 180 K data. This transition is driven by the rotations of octahedra about the cubic (001) axis, which can be described using the Glazer tilt system (a0a0c−). A second transition from the tetragonal space group I4/m to the triclinic crystal system space group I
m [a = 8.45509(20) Å]. Upon reducing the temperature, the material undergoes a structural phase transition to the tetragonal space group I4/m [a = 5.97444(20) Å, c = 8.45848(9) Å] at 220 K. This phase transition is confirmed by the observation of peak splitting below 250 K. Fig. 2 shows a selected area of the synchrotron X-ray diffraction pattern evidencing the (400) reflection at 250 K. There is clear evidence of peaks splitting below 220 K with further splitting seen in 180 K data. This transition is driven by the rotations of octahedra about the cubic (001) axis, which can be described using the Glazer tilt system (a0a0c−). A second transition from the tetragonal space group I4/m to the triclinic crystal system space group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) [(a−a−c−) Glazer tilt system, a = 5.97444(20) Å, b = 5.96863(18) Å, c = 8.45848(9) Å] occurs at 80 K, which was confirmed by the observation of further peak splitting and broadening and is corroborated by the differences in the fit statistics between the two models; χ2 = 2.62 and 2.98 and Rwp = 14.96 and 17.03 for the triclinic and tetragonal models respectively at 80 K. The same phase transitions are observed for Ba2NdMoO6 and Ba2SmMoO613,15 upon cooling and are in corroboration with a recent group theoretical analysis of structural distortions of double perovskites.7
[(a−a−c−) Glazer tilt system, a = 5.97444(20) Å, b = 5.96863(18) Å, c = 8.45848(9) Å] occurs at 80 K, which was confirmed by the observation of further peak splitting and broadening and is corroborated by the differences in the fit statistics between the two models; χ2 = 2.62 and 2.98 and Rwp = 14.96 and 17.03 for the triclinic and tetragonal models respectively at 80 K. The same phase transitions are observed for Ba2NdMoO6 and Ba2SmMoO613,15 upon cooling and are in corroboration with a recent group theoretical analysis of structural distortions of double perovskites.7
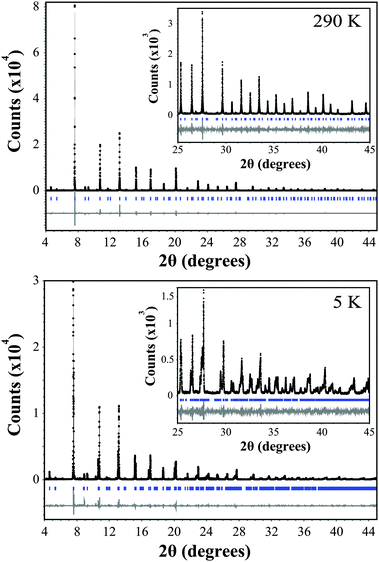 | ||
| Fig. 1 Rietveld refinement of the synchrotron X-ray diffraction data for Ba2GdMoO6. The black line represents the actual data, the black circles represent the calculated pattern and the trace below is the difference between calculated and collected data. A region between 6.65 and 7.45 2θ (degrees) is excluded due to a peak associated with a small amount of unknown impurity. | ||
![A selected area of the synchrotron X-ray diffraction pattern of Ba2GdMoO6 showing the [400] structural peak at 250 K (top). There is clear evidence of peak splitting at the cubic to tetragonal phase transition displayed here for T = 220 K (middle) and 180 K (bottom). This peak splitting increases upon reducing the temperature.](/image/article/2013/CP/c2cp43732e/c2cp43732e-f2.gif) | ||
| Fig. 2 A selected area of the synchrotron X-ray diffraction pattern of Ba2GdMoO6 showing the [400] structural peak at 250 K (top). There is clear evidence of peak splitting at the cubic to tetragonal phase transition displayed here for T = 220 K (middle) and 180 K (bottom). This peak splitting increases upon reducing the temperature. | ||
Upon decreasing the temperature below 220 K the quality of fit to both the tetragonal (100–220 K) and triclinic phases (5–80 K) gets progressively worse with decreasing temperature. There is clear evidence of diffuse scattering between the diffraction peaks below 220 K as shown in Fig. 3(a) which displays a close up of the [004] and [220] reflections (angular range 10.5 < 2θ < 11) at 5 K. The black line represents the actual data whilst the shaded region represents the calculated pattern. Such additional scattering between diffraction peaks is characteristic of a ferroelastic transition. A ferroelastic material exhibits spontaneous strain under an external stress and the transition (Tc) from the paraelastic high temperature phase to the ferroelastic low temperature phase is inherently linked to a change in symmetry of the crystal structure.24 For Ba2GdMoO6 the ferroelastic transition is observed at 220 K when the crystal structure distorts from cubic to tetragonal symmetry. The spontaneous strain in a ferroelastic material is strongly influenced by the microstructure of the crystal and domains/twins are commonly observed below Tc. Scattering associated with the domain boundaries results in asymmetry in the direction of the hypothetical high symmetry peak and a characteristic hkl-dependent line broadening in X-ray and neutron diffraction patterns (as observed in the synchrotron X-ray diffraction data of Ba2GdMoO6 below 220 K). This characteristic scattering presents a challenge when attempting to extract crystallographic information from Rietveld refinement, and a range of approaches have previously been adopted.25 Most commonly an extra phase is introduced to account for the domain wall scattering.
![Magnification of the [004] and [220] reflections at 5 K, different refinement techniques used are shown by shaded regions and correspond to: (a) conventional refinement using a single triclinic phase (b) refinement using two distinct triclinic phases attempting to model ‘bulk’ phase reflections and diffuse scattering separately (c) single phase model combined with anisotropic peak asymmetry, considering contributions from ‘bulk’ and diffuse scattering together.](/image/article/2013/CP/c2cp43732e/c2cp43732e-f3.gif) | ||
| Fig. 3 Magnification of the [004] and [220] reflections at 5 K, different refinement techniques used are shown by shaded regions and correspond to: (a) conventional refinement using a single triclinic phase (b) refinement using two distinct triclinic phases attempting to model ‘bulk’ phase reflections and diffuse scattering separately (c) single phase model combined with anisotropic peak asymmetry, considering contributions from ‘bulk’ and diffuse scattering together. | ||
Fig. 3(a) shows the Rietveld refinement of the 5 K synchrotron X-ray diffraction data, modelled with the I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) triclinic space group. It is clear that the model is not suitable because of the relative intensity mismatch and the unsuccessful modelling of the intensity between the peaks. The poor quality of fit is further illustrated by the goodness of fit statistics; χ2 = 3.664, Rwp = 21.910 and Rp = 17.582. In order to obtain reliable crystallographic information from the Rietveld refinement an appropriate model capable of accounting for the intensity between peaks was sought. Fig. 3(a–c) shows a close up of the [004] and [220] reflections at 5 K, modelled in three different ways. Fig. 3(b) shows the two-phase model where a second crystallographically distinct phase (space group I
triclinic space group. It is clear that the model is not suitable because of the relative intensity mismatch and the unsuccessful modelling of the intensity between the peaks. The poor quality of fit is further illustrated by the goodness of fit statistics; χ2 = 3.664, Rwp = 21.910 and Rp = 17.582. In order to obtain reliable crystallographic information from the Rietveld refinement an appropriate model capable of accounting for the intensity between peaks was sought. Fig. 3(a–c) shows a close up of the [004] and [220] reflections at 5 K, modelled in three different ways. Fig. 3(b) shows the two-phase model where a second crystallographically distinct phase (space group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) is incorporated into the refinement (cell parameters: a = 5.9541(2) Å, b = 5.9452(2) Å, c = 8.4778(2) Å, α = 89.971(3)°, β = 90.194(3)°, γ = 90.150(3)°) to account for the diffuse scattering originating from the domain boundaries. The refinement statistics [χ2 = 2.866, Rwp = 17.139 and Rp = 13.027] show the two-phase model generates an improved fit to the 5 K data. However the introduction of a secondary phase does not fully model the intensity between peaks and only results in a minimal improvement to the fitting of the reflections associated with the primary phase.
) is incorporated into the refinement (cell parameters: a = 5.9541(2) Å, b = 5.9452(2) Å, c = 8.4778(2) Å, α = 89.971(3)°, β = 90.194(3)°, γ = 90.150(3)°) to account for the diffuse scattering originating from the domain boundaries. The refinement statistics [χ2 = 2.866, Rwp = 17.139 and Rp = 13.027] show the two-phase model generates an improved fit to the 5 K data. However the introduction of a secondary phase does not fully model the intensity between peaks and only results in a minimal improvement to the fitting of the reflections associated with the primary phase.
The next approach introduced a single triclinic phase (space group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) to the refinements that incorporated anisotropic peak asymmetry. This was key as the integrated intensity is central to attaining useful structural information. Due to the microstrained domain boundary origin of the asymmetric reflection tails, there is a well defined hkl dependence to the magnitude and direction of asymmetry for each peak so that an additional convolution to the peak profile was needed to adequately model the data. Two different fourth-order spherical harmonic functions were introduced in TOPAS23 to account for both the two-theta and systematic hkl-dependence of the asymmetry. This fitting procedure resulted in extremely good fits across the entire dataset and could be applied successfully at all temperatures. Fig. 3(c) shows the [004] and [220] reflections at 5 K are modelled successfully by this approach. The statistical values of fit quality [χ2 = 2.535, Rwp = 15.060 and Rp = 10.484] reflect the improvement in fit compared to the previous models. Crystallographic information was taken from the refined data using this approach, in the temperature range 5–290 K. The peak shapes were modelled with a pseudo-Voigt function incorporating the asymmetry described above. Refined atomic coordinates, isotropic/anisotropic thermal parameters, cell parameters, statistical measures of fit quality and selected bond lengths and angles are shown in Tables 1 and 2. All of the metal and oxygen occupancies refined to within ±1% of full occupancy and were fixed to 1. There was no evidence for cation anti-site disorder or oxygen non-stoichiometry.
) to the refinements that incorporated anisotropic peak asymmetry. This was key as the integrated intensity is central to attaining useful structural information. Due to the microstrained domain boundary origin of the asymmetric reflection tails, there is a well defined hkl dependence to the magnitude and direction of asymmetry for each peak so that an additional convolution to the peak profile was needed to adequately model the data. Two different fourth-order spherical harmonic functions were introduced in TOPAS23 to account for both the two-theta and systematic hkl-dependence of the asymmetry. This fitting procedure resulted in extremely good fits across the entire dataset and could be applied successfully at all temperatures. Fig. 3(c) shows the [004] and [220] reflections at 5 K are modelled successfully by this approach. The statistical values of fit quality [χ2 = 2.535, Rwp = 15.060 and Rp = 10.484] reflect the improvement in fit compared to the previous models. Crystallographic information was taken from the refined data using this approach, in the temperature range 5–290 K. The peak shapes were modelled with a pseudo-Voigt function incorporating the asymmetry described above. Refined atomic coordinates, isotropic/anisotropic thermal parameters, cell parameters, statistical measures of fit quality and selected bond lengths and angles are shown in Tables 1 and 2. All of the metal and oxygen occupancies refined to within ±1% of full occupancy and were fixed to 1. There was no evidence for cation anti-site disorder or oxygen non-stoichiometry.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group at 290 K are Ba (1/4, 1/4, 1/4), Mo (0, 0, 1/2), Gd (0, 0, 0), O (0, 0, x). Atom positions in tetragonal I4/m space group at 220 K are Ba (0, 1/2, 1/4), Mo (1/2, 1/2, 1/2), Gd (0, 0, 0), O1 (0, 0, z), O2 (x, y, 0). Atom positions in triclinic I
m space group at 290 K are Ba (1/4, 1/4, 1/4), Mo (0, 0, 1/2), Gd (0, 0, 0), O (0, 0, x). Atom positions in tetragonal I4/m space group at 220 K are Ba (0, 1/2, 1/4), Mo (1/2, 1/2, 1/2), Gd (0, 0, 0), O1 (0, 0, z), O2 (x, y, 0). Atom positions in triclinic I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group at 80 K are Ba (x, y, z) Mo (0, 0, 1/2), Gd (0, 0, 0), O1 (x, y, z), O2 (x, y, z), O3 (x, y, z)
space group at 80 K are Ba (x, y, z) Mo (0, 0, 1/2), Gd (0, 0, 0), O1 (x, y, z), O2 (x, y, z), O3 (x, y, z)
| Atom | Temperature (K) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 30 | 50 | 80 | 100 | 120 | 150 | 180 | 220 | 250 | 290 | ||
| Ba | x | −0.0010(8) | −0.0010(8) | 0.0002(8) | −0.0010(9) | 0 | 0 | 0 | 0 | 0 | 1/4 | 1/4 |
| y | 0.4997(6) | 0.4999(6) | 0.4998(6) | 0.5000(9) | 1/2 | 1/2 | 1/2 | 1/2 | 1/2 | 1/4 | 1/4 | |
| z | 0.2507(4) | 0.2508(4) | 0.2507(4) | 0.2497(5) | 1/4 | 1/4 | 1/4 | 1/4 | 1/4 | 1/4 | 1/4 | |
| U iso (Å2) | 0.00253(5) | 0.00233(5) | 0.00253(5) | 0.00299(5) | 0.00305(5) | 0.00331(5) | 0.00385(5) | 0.00440(5) | 0.00520(5) | 0.00714(5) | 0.00811(5) | |
| Gd | U iso (Å2) | 0.00253(5) | 0.00233(5) | 0.00253(5) | 0.00299(5) | 0.00305(5) | 0.00331(5) | 0.00385(5) | 0.00440(5) | 0.00520(5) | 0.00714(5) | 0.00811(5) |
| Mo | U iso (Å2) | 0.00253(5) | 0.00233(5) | 0.00253(5) | 0.00299(5) | 0.00305(5) | 0.00331(5) | 0.00385(5) | 0.00440(5) | 0.00520(5) | 0.00714(5) | 0.00811(5) |
| O1 | x | −0.003(7) | −0.003(7) | −0.002(7) | 0.004(7) | 0 | 0 | 0 | 0 | 0 | 0.2709(4) | 0.2710(4) |
| y | 0.008(4) | 0.008(4) | 0.008(4) | 0.017(3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| z | 0.2662(10) | 0.2670(10) | 0.2671(9) | 0.2661(10) | 0.2724(11) | 0.2723(11) | 0.2724(13) | 0.2723(16) | 0.2714(23) | 0 | 0 | |
| U iso (Å2) | 0.0073(13) | 0.0070(13) | 0.0071(13) | 0.0081(13) | 0.0113(12) | 0.0103(11) | 0.0139(12) | 0.0157(10) | 0.0157(12) | 0.0132(1) | 0.0133(1) | |
| O2 | x | 0.238(3) | 0.236(3) | 0.239(3) | 0.271(3) | 0.290(2) | 0.289(2) | 0.286(2) | 0.275(4) | 0.268(5) | — | — |
| y | 0.317(3) | 0.315(3) | 0.316(3) | 0.255(4) | 0.253(2) | 0.254(2) | 0.258(2) | 0.268(5) | 0.277(5) | — | — | |
| z | 0.003(3) | 0.002(3) | 0.004(3) | 0.001(4) | 0 | 0 | 0 | 0 | 0 | — | — | |
| U iso (Å2) | 0.0073(13) | 0.0070(13) | 0.0071(13) | 0.0081(13) | 0.0113(12) | 0.0103(11) | 0.0139(12) | 0.0157(10) | 0.0157(12) | — | — | |
| O3 | x | 0.724(3) | 0.722(3) | 0.725(3) | 0.744(3) | — | — | — | — | — | — | — |
| y | 0.262(4) | 0.263(4) | 0.264(4) | 0.317(3) | — | — | — | — | — | — | — | |
| z | −0.005(4) | −0.004(4) | −0.005(4) | −0.007(3) | — | — | — | — | — | — | — | |
| U iso (Å2) | 0.0073(13) | 0.0070(13) | 0.0071(13) | 0.0081(13) | — | — | — | — | — | — | — | |
| a (Å) | 5.93893(8) | 5.93934(8) | 5.94043(8) | 5.94639(10) | 5.95213(4) | 5.95612(3) | 5.96055(3) | 5.96470(4) | 5.96990(4) | 8.45150(2) | 8.45509(2) | |
| b (Å) | 5.93990(9) | 5.94046(10) | 5.94190(9) | 5.94701(11) | — | — | — | — | — | — | — | |
| c (Å) | 8.51813(9) | 8.51758(9) | 8.51483(9) | 8.50201(11) | 8.49183(7) | 8.48442(6) | 8.47788(6) | 8.47159(7) | 8.46457(9) | — | — | |
| α (°) | 89.8673(12) | 89.8677(11) | 89.8660(11) | 89.8614(11) | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | |
| β (°) | 89.9493(12) | 89.9495(12) | 89.9511(12) | 89.9587(13) | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | |
| γ (°) | 89.9830(13) | 89.9850(13) | 89.9833(13) | 89.9793(17) | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | 90.0 | |
| χ 2 | 2.530 | 2.528 | 2.627 | 2.614 | 2.635 | 2.510 | 2.463 | 2.432 | 2.505 | 2.344 | 2.290 | |
| R wp (%) | 15.026 | 15.352 | 14.881 | 14.948 | 15.271 | 14.708 | 14.609 | 14.536 | 15.075 | 14.275 | 14.046 | |
| R p (%) | 10.448 | 10.680 | 10.084 | 9.943 | 10.875 | 10.015 | 9.871 | 9.682 | 10.160 | 10.990 | 11.095 | |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to tetragonal (space group I4/m), with a further structural phase transition to triclinic (space group I
m) to tetragonal (space group I4/m), with a further structural phase transition to triclinic (space group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) at 80 K
) at 80 K
| Bond | Temperature (K) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 30 | 50 | 80 | 100 | 120 | 150 | 180 | 220 | 250 | 290 | |
| Mo–O(1) (Å) | 1.990(8) | 1.988(8) | 1.983(8) | 1.979(9) | 1.93(1) | 1.932(9) | 1.930(11) | 1.929(13) | 1.935(20) | 1.936(3) | 1.936(3) |
| Mo–O(2) (Å) | 1.897(16) | 1.912(16) | 1.896(15) | 1.898(18) | 1.931(9) | 1.930(9) | 1.927(12) | 1.929(26) | 1.923(32) | — | — |
| Mo–O(3) (Å) | 1.942(21) | 1.928(21) | 1.940(21) | 1.94(3) | — | — | — | — | — | — | — |
| Gd–O(1) (Å) | 2.270(8) | 2.272(8) | 2.276(8) | 2.274(9) | 2.31(1) | 2.310(9) | 2.309(11) | 2.307(13) | 2.298(20) | 2.290(3) | 2.291(3) |
| Gd–O(2) (Å) | 2.260(21) | 2.274(20) | 2.263(21) | 2.267(26) | 2.290(9) | 2.293(9) | 2.295(12) | 2.289(26) | 2.299(32) | — | — |
| Gd–O(3) (Å) | 2.356(16) | 2.341(16) | 2.356(15) | 2.340(19) | — | — | — | — | — | — | — |
| Mo–O(1)–Gd (°) | 177.2(14) | 177.3(14) | 177.3(14) | 177.2(16) | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 |
| Mo–O(2)–Gd (°) | 176.1(15) | 176.0(14) | 176.4(15) | 177.5(17) | 171.5(5) | 172.9(5) | 173.4(6) | 178.3(14) | 177.8(17) | — | — |
| Mo–O(3)–Gd (°) | 161.8(9) | 161.9(9) | 162.2(8) | 165.6(10) | — | — | — | — | — | — | — |
Fig. 4 shows the evolution of cell parameters in the temperature range 5–290 K. The tetragonal to triclinic transition is manifest in the cell parameters where a slight elongation along c, coinciding with a contraction along a is detected. Fig. 5 shows the evolution of Mo–O bond lengths with temperature down to 5 K. The triclinic structural phase transition is manifest in the Mo–O(1) and Gd–O(1) bond lengths which elongate and contract respectively below 100 K (Fig. 5, Table 2). In contrast Gd–O(2) exhibits a smooth reduction upon cooling. The Mo–O–Gd bond angles are reported in Table 2 and the tetragonal to triclinic phase transition is clearly evident in thermal variation of the Mo–O(2)–Gd bond angles where a reduction in the buckling of Mo–O(2)–Gd is observed below 100 K.
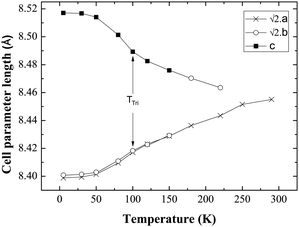 | ||
Fig. 4 Evolution of the cell parameters with temperature evidencing a structural transition to triclinic symmetry below 100 K (TTri); a and b have been multiplied by 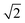 for ease of comparison. for ease of comparison. | ||
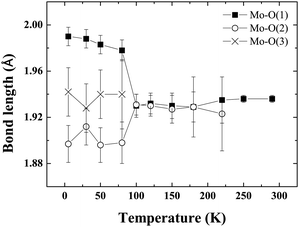 | ||
| Fig. 5 The thermal evolution of the Mo–O bond lengths in Ba2GdMoO6. There is no evidence of the Jahn–Teller distortion previously reported for Ba2LnMoO6 (Ln = Nd, Sm). | ||
There is no evidence of the Jahn–Teller distortion previously reported for Ba2NdMoO613 and Ba2SmMoO6.15 The disappearance of the Jahn–Teller distortion is probably related to the reduced distortion of the MoO6 octahedra in Ba2GdMoO6. Upon replacing Nd with Gd in Ba2LnMoO6 the Goldschmidt tolerance factor26 increases from 0.975 to 0.985. It is known that when t < 1, B–O and B′–O bonds within the structure are compressed, whilst A–O bonds are stretched27 so that octahedral rotations and tilts occur to alleviate stress. If the tolerance factor is very close to 1, then the ideal cubic structure should be observed. The results here suggest that a minimum distortion is required in order to evidence the Jahn–Teller distortion in Mo5+ double perovskites; otherwise the electronic stability conferred by the Jahn–Teller is insufficient to induce a further deformation of the structure. The results also suggest that the Jahn–Teller distortion present in Ba2LnMoO6 (Ln = Nd, Sm) stabilises the tetragonal to triclinic transition; when the Jahn–Teller distortion is no longer apparent Ttri is observed at a much lower temperature (Ttri = 130 K, 290 K and 80 K for Ln = Nd, Sm and Gd respectively). Further variable temperature diffraction studies on other members of the Ba2LnMoO6 series are required in order to understand the complex coupling between structural and Jahn–Teller distortions in Mo5+ double perovskites.
Magnetic susceptibility measurements were also performed on Ba2GdMoO6; Fig. 6 shows the temperature variation of χ−1 and dχ−1/dT. There is no evidence of a magnetic transition down to 2 K. A Curie–Weiss fit to the susceptibility data between 300 K and 100 K yields a Weiss temperature of θ = 2.35 K and a Curie constant, C of 8.18 emu mol−1 K−1, corresponding to an overall effective moment of 8.14 μB, close to the predicted total magnetic moment of 8.13 μB. Below 100 K, the inverse susceptibility deviates from the Curie–Weiss law. Fig. 6 (inset) evidences a subtle peak in the thermal evolution of dχ−1/dT at 100 K, which correlates with the tetragonal to triclinic structural transition temperature reported above.
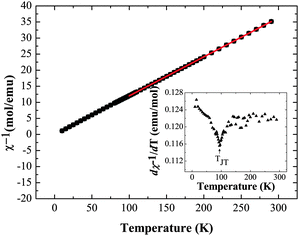 | ||
| Fig. 6 Inverse magnetic susceptibility data χ−1vs. T and dχ−1/dT vs. T (inset) for Ba2GdMoO6, evidencing the structural transition from tetragonal to triclinic symmetry below 100 K. | ||
IV. Conclusions
The results demonstrate that the double perovskite Ba2GdMoO6 is ferroelastic, whereby it exhibits spontaneous strain under an external stress. Such an effect has not been reported previously for Mo5+ double perovskites. This ferroelastic transition is manifest in synchrotron X-ray diffraction patterns as diffuse scattering associated with scattering from domain boundaries is detected below the cubic to tetragonal phase transition at 220 K. In order to model this and gain useful crystallographic information, the peak asymmetry was convoluted with a fourth order spherical harmonic (SH), to model the direction and magnitude of peak asymmetry. Ba2GdMoO6 undergoes a transition from a cubic (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to a tetragonal system (space group I4/m) at 220 K before undergoing a second transition to a triclinic system (space group I
m) to a tetragonal system (space group I4/m) at 220 K before undergoing a second transition to a triclinic system (space group I![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) at 80 K. Magnetic susceptibility data shows a deviation from Curie–Weiss behaviour below 100 K which coincides with the structural transition from tetragonal to cubic symmetry.
) at 80 K. Magnetic susceptibility data shows a deviation from Curie–Weiss behaviour below 100 K which coincides with the structural transition from tetragonal to cubic symmetry.
References
- J. Fontcuberta, B. Martinez, A. Seffar, S. Piñol, J. L. García-Muñoz and X. Obradors, Phys. Rev. Lett., 1996, 76, 1122–1125 CrossRef CAS.
- G. Shirane, H. Danner and R. Pepinsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1957, 105, 856–860 CAS.
- H. Khosroabadi, J. Kobayashi, K. Tanaka, S. Miyasaka, S. Tajima, H. Uchiyama and A. Q. R. Baron, J. Supercond. Novel Magn., 2010, 23, 1385–1389 CrossRef CAS.
- N. Orlovskaya, Y. Gogotsi, M. Reece, B. Cheng and I. Ginson, Acta Mater., 2002, 50, 715–723 CrossRef CAS.
- M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197–233 CrossRef CAS.
- P. M. Woodward, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1997, 53, 32–43 Search PubMed.
- C. J. Howard, B. J. Kennedy and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 463–471 CrossRef.
- J.-W. G. Bos, J. P. Attfield, T.-S. Chan, R.-S. Liu and L.-Y. Jang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014101 CrossRef.
- D. Y. Chen, F. Z. Chien, D. C. Ling, J. L. Tseng, S. R. Sheen, M. J. Wang and M. K. Wu, Physica C, 1997, 282–287, 73–76 CrossRef CAS.
- C. Bernuy-Lopez, M. Allix, C. A. Bridges, J. B. Claridge and M. J. Rosseinsky, Chem. Mater., 2007, 19, 1035–1043 CrossRef CAS.
- K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677 CrossRef CAS.
- H. Boysen, Z. Kristallogr., 2005, 220, 726–734 CrossRef CAS.
- E. J. Cussen, D. R. Lynham and J. Rogers, Chem. Mater., 2006, 18, 2855–2866 CrossRef CAS.
- A. C. McLaughlin, Solid State Commun., 2006, 137, 354–357 CrossRef CAS.
- A. C. Mclaughlin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 132404 CrossRef.
- T. K. Wallace, C. Ritter and A. C. Mclaughlin, J. Solid State Chem., 2012, 196, 379–383 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1976, 32, 751–767 CrossRef.
- E. J. Cussen and W. J. Cameron, J. Mater. Chem., 2010, 20, 1340–1347 RSC.
- A. C. Mclaughlin, M. A. de Vries and J.-W. G. Bos, Phys. Rev. Lett., 2010, 104, 177202 CrossRef.
- M. Tarzia and G. Biroli, EuroPhys. Lett., 2008, 82, 67008 CrossRef.
- A. C. Mclaughlin, M. A. de Vries and J.-W. G. Bos, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094424 CrossRef.
- H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- TOPAS, program available from Bruker AXS GmbH, Ostliche Rheinbrukenstrasse 50, 76187 Karlsruhe, Germany.
- E. K. H. Salje, Phase transitions in ferroelastic and co-elastic crystals, Cambridge University Press, Cambridge, 1991 Search PubMed.
- I. Grinberg, M. R. Suchomel, W. Dmowski, S. E. Mason, H. Wu, P. K. Davies and A. M. Rappe, Phys. Rev. Lett., 2007, 98, 107601 CrossRef.
- V. M. Goldschmidt, Die Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- J. B. Goodenough, Rep. Prog. Phys., 2004, 67, 1915–1993 CrossRef CAS.
| This journal is © the Owner Societies 2013 |
