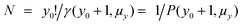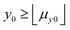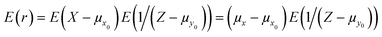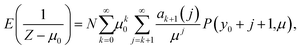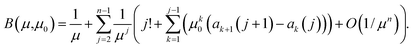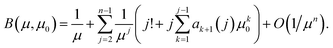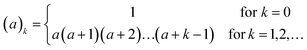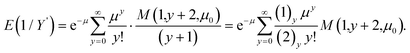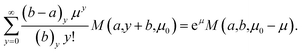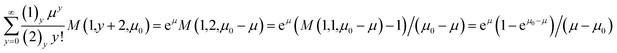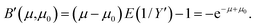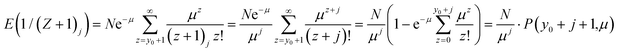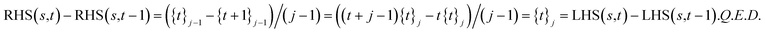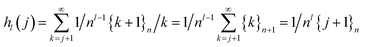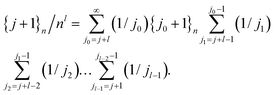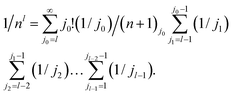Statistical bias in isotope ratios
Christopher D.
Coath
*a,
Robert C. J.
Steele†
a and
W. Fred
Lunnon
b
aUniversity of Bristol, School of Earth Sciences, Wills Memorial Building, Queens Rd., Bristol, UK. E-mail: chris.coath@bristol.ac.uk; Fax: +44 (0)117 925 3385; Tel: +44 (0)117 954 5370
bDepartment of Computer Science, National University of Ireland, Maynooth, co., Kildare, Republic of Ireland
First published on 13th November 2012
Abstract
This paper presents the mathematics of the systematic bias in the expected value of the ratio of two noise-corrected Poisson-distributed variables, such as ion counting measurements. Such bias can lead to the reporting of incorrect ratios and, in some cases, systematic correlations with other measurements which can impact the scientific interpretation. We describe a novel method of treating such measurements which results in a negligible, exponentially small bias. We also re-examine the conventional approach deriving an exact expression for the bias including the noise correction explicitly.
1 Introduction
Analysts measuring a time series of ion beam intensities are faced with choices of how to process the data in order to estimate intensity ratios. Is it preferable, for example, to calculate the mean of the ratios, the ratio of the means or is there a better approach entirely? At the heart of the problem is the fact that the mean value a ratio estimator returns, over the long term, is biased relative to the true ratio being estimated. A simple example serves to illustrate the phenomenon of bias as follows. Suppose we write a 1 and a 3 on the faces of coin A and a 3 and 5 on the faces of coin B. Clearly, the mean value of a coin flip is 2 and 4 for coins A and B respectively. We now flip the two coins and record the ratio, B/A, as indicated by the upturned faces. In such an experiment, there are four equally probable outcomes: 3/1, 3/3, 5/1, and 5/3. Hence, the expectation value of the ratio, E(B/A) = (3 + 1 + 5 + 5/3)/4 or 8/3. The expectation value of B/A is the mean value of B/A over the long term. If we had hoped to estimate the ‘true’ ratio equal to the ratio of the means for each coin, 4/2 = 2, then clearly the estimator B/A is biased. We define the bias as the relative difference between E(B/A) and the true ratio. In this example, therefore, the bias is (8/3–2)/2 = 1/3.The situation with ratios of ion-counting signals in isotope ratio measurements is directly analogous. The number of ions counted is accurately modelled by Poisson statistics which states that the probability of detecting X ions is given by
| Pois(X;μx) = e−μxμXx/X!, | (1) |
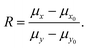 | (2) |
In principal, any function, f(X,Y), may have it's bias relative to R determined by deriving the expectation valve, E(f), given by the double summation over all X and Y of f(X,Y)·Pois(X;μx)·Pois(Y;μy). For example, the commonly used ratio estimator,
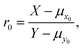 | (3) |
1.1. Previous work
Coakley et al.1 and Ogliore et al.2 have shown that X/Y is a biased estimate of R. Similar approaches by both1,2 yield| E(X/Y) ≈ μx/μy(1 + 1/μy + 2/μ2y) | (4) |
Ogliore et al.2 compare ratio estimators r1 = ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) /ȳ (the ‘ratio of the means’) and
/ȳ (the ‘ratio of the means’) and 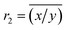 (the ‘mean of the ratios’) where
(the ‘mean of the ratios’) where ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = n−1∑ni=1xi, and ȳ = n−1∑ni=1yi are the means of samples xi and yi, and
= n−1∑ni=1xi, and ȳ = n−1∑ni=1yi are the means of samples xi and yi, and 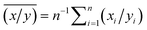 by deriving expressions for E(r1) and E(r2). Note, however, that these reduce to a single problem as follows. Let xi and yi be instances of independent random variables X and Y respectively where X has a Poisson distribution with mean μx, which we shall write X ∼ Pois(μx), and similarly Y ∼ Pois(μy). Since the sum of Poisson variables is itself a Poisson variable, we have n
by deriving expressions for E(r1) and E(r2). Note, however, that these reduce to a single problem as follows. Let xi and yi be instances of independent random variables X and Y respectively where X has a Poisson distribution with mean μx, which we shall write X ∼ Pois(μx), and similarly Y ∼ Pois(μy). Since the sum of Poisson variables is itself a Poisson variable, we have n![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ∼ Pois(nμx) and similarly for nȳ. With this nomenclature, E(r2) = E(X/Y) and is given by approximation 4 above and E(r1) has the same form with μx and μy replaced by nμx and nμy respectively (see Ogliore et al.2eqn (19) and (22)). The biases in r2 and r1 are, therefore, O(μy−1) and O{(nμy)−1} respectively. Note that both r1 and r2 have, to first order, biases proportional to the reciprocal of the mean number of counts in the denominator when the ratio is taken.
∼ Pois(nμx) and similarly for nȳ. With this nomenclature, E(r2) = E(X/Y) and is given by approximation 4 above and E(r1) has the same form with μx and μy replaced by nμx and nμy respectively (see Ogliore et al.2eqn (19) and (22)). The biases in r2 and r1 are, therefore, O(μy−1) and O{(nμy)−1} respectively. Note that both r1 and r2 have, to first order, biases proportional to the reciprocal of the mean number of counts in the denominator when the ratio is taken.
Ogliore et al.2 also consider Beale's ratio estimator, r3, given by
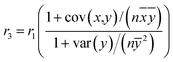 | (5) |
2 The ratio of noise-corrected Poisson variables
We will assume that the distribution of the ion counts, X and Y, obeys Poisson statistics. Furthermore, we will consider only cases where X and Y are independent. This latter restriction is not so severe as it might seem since by far the most important correlated variations in ion counting signals are common mode ‘intensity’ fluctuations, that is, proportional changes in both μx and μy which largely cancel by taking the ratio. Of course, common mode variations will not be completely rejected on account of any intensity dependence of the bias.Let R be defined as given by eqn (2) and let Z be distributed like Y but truncated at y0, that is, the probability distribution function, Pr(Z), is given by
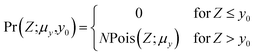 | (6) |
where γ is the incomplete gamma function and P the normalised incomplete gamma function.3 We shall choose y0 to be sufficiently large to ensure Z − μy0 cannot be zero or negative, i.e.
. Note that, in cases of large signal to noise ratio, the probability of Y ≤ μy0 may be so small as to make excluding these events notional in practice. We shall now derive an expression for the expectation value of
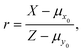 | (7) |
For independent random variables we can separate them thus
The Taylor series expansion of 1/(Z − μ0) about μ0 = 0 is,
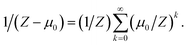 | (8) |
Note that the truncation of the distribution ensures ∣μ0/Z∣ < 1, guaranteeing convergence. To take the expectation value of the right-hand side (RHS) of eqn (8) requires an expression for the expectation value of 1/Zk. This problem is addressed in the appendix and given by eqn (25). Substituting into eqn (8) gives,
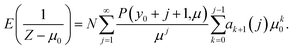 | (9) |
The first few values of ak(j) are,
| j = | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| a1(j) | 1 | 1 | 2 | 6 | 24 |
| a2(j) | 1 | 3 | 11 | 50 | |
| a3(j) | 1 | 6 | 35 | ||
| a4(j) | 1 | 10 |
From the exact form eqn (9), we can derive an asymptotic form in the limit as μ → ∞ and bounded μ0 by replacing the infinite sum with a finite sum, and using P(y0 + j + 1,μ) → 1, which is true so long as y0 and j are also bounded. Hence,
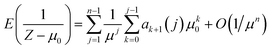 | (10) |
Define the bias, B(μ,μ0), as the relative difference between E(1/(Z − μ0)) and 1/(μ − μ0), i.e.
| B(μ,μ0) = (μ − μ0)E(1/(Z − μ0)) − 1. |
Substituting from eqn (10) and after some cancellation we have
| ak+1(j + 1) − ak(j) = jak+1(j), | (11) |
For example, putting n = 3 we have
| B = 1/μ + (2 + 2μ0)/μ2 + O(1/μ3) | (12) |
3 Quasi-unbiased ratios
Here we present an alternative ratio estimator which reduces the bias to a factor which is exponentially small or quasi-unbiased. Furthermore, the method does not require truncation of the distribution so all the measured data can be used.Let Y be distributed as before. We define a new random variable,
| Y′(Y,μ0) = (Y + 1)/M(1,Y + 2,μ0) | (13) |
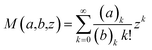 | (14) |
Explicitly,
| E(1/Y′) = (μ − μ0)−1(1 − e−μ + μ0). |
A summation of this form is given by Prudnikov et al.5 which is
Substituting a → 1 and b → 2 gives,
where we have used Gradshteyn and Ryzhik6 equation 9.212 and M(1,1,z) = ez.
Let B′ be the bias of E(1/Y′) relative to (μ − μ0)−1,
Therefore, noise-corrected quasi-unbiased ratios, r′, can be computed from measurements of Poisson events X and Y with,
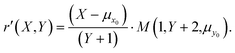 | (15) |
Using eqn (15) a ratio can be calculated at each cycle of data collection and, if required, statistics on these such as the mean and standard deviation. This contrasts using either the ratio of the means, r1, or Beale's estimator, r3, both of which return a single ratio from a set of n measurements.
Fig. 1 compares conventional and quasi-unbiased ratios from 128 cycles of measurements on boron isotopes 10B and 11B. The ion counts have been summed in ‘blocks’ of p cycles, the ratio taken for each block and the mean over all blocks plotted. The value of p, therefore, controls integration period and the total number of blocks, q = 128/p. Let the total counts in each block be xi and yi for the two isotopes, where i = 1,2,…q. We use p = 1,2,4,8 and 16 and plot the means of r′(xi,yi)(ty/tx) (red) and (xi/yi)(ty/tx) (blue) against mean of 1/yi, where tx and ty are the cycle integration times for the two isotopes. The ‘ratio of the means’, equivalent to putting p = 128, is also shown and is indistinguishable from Beale's estimator. The noise is negligible for these data and has been set to zero. Both 11B/10B and its reciprocal are plotted to demonstrate that the effect is independent of which isotope is chosen as the denominator. The plots show that, to first order and, as predicted by theory, the conventionally processed data, shown in blue, plot as a straight line with equal slope and intercept. The y-intercept, which corresponds to counts → ∞, should equal the unbiased ratio. Our novel quasi-unbiased ratio estimator (eqn (15)), shown by the red data have, as expected, no bias regardless of the number of counts.
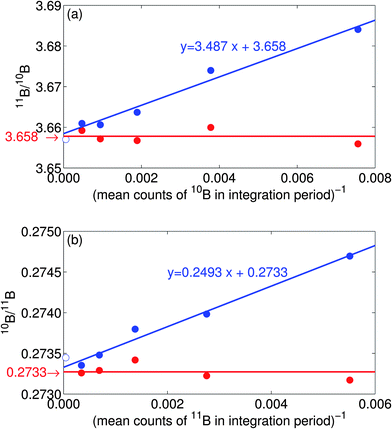 | ||
| Fig. 1 Boron isotope ratios (a) 11B/10B and (b) 10B/11B as a function of the mean number of counts per integration period showing the conventionally computed ratios in blue and the novel quasi-unbiased ratios (eqn (15)) in red. Ratios are calculated for each integration period in the analysis and the mean value plotted. Note that the quasi-unbiased ratios (red) show no trend and give the desired result regardless of the integration period. All plotted points are computed from the same 128 cycles of data by summing the counts in blocks of p adjacent cycles for p = 1,2,4,8, and 16, dividing the analysis into 128/p integration periods. The greatest bias in the blue data corresponds to p = 1 which plots at the far right. The ‘ratio of the means’ is also shown (open blue symbol), which is equivalent to p = 128, close to Beale's estimator (not shown) which lies below the open symbol in both (a) and (b) by 0.0056% and 0.0035% respectively. See main text for further details. Data are raw secondary-ion mass spectrometry (SIMS) data from an analysis of a foraminifera using a CAMECA IMS 1270. | ||
Fig. 2 shows the results of a Monte-Carlo simulation with μx = μy = 20 and noise from 0 to 15. The simulation shows the noise-corrected ratio calculated in four ways: (i) conventionally without data rejection (eqn (3)), (ii) conventionally with rejection when the denominator is zero or negative (eqn (7)), (iii) Beale's estimator, and (iv) quasi-unbiased (eqn (15)) all with μx0 = μy0 = b. The mean of 106 ratio estimations is plotted for each value of the noise, which is incremented in steps of 0.01. The simulated quasi-unbiased ratios are closer to unity (no bias) than either of the conventional ratios or Beale's estimator over the entire range of b, although significant scatter does occur for large b (see caption). Beale's estimator (eqn (5)) on the noise-corrected data requires, for each of the 106 simulated ratio estimations, the variance, covariance and mean intensities to be calculated. We calculate these statistics from a dataset of n simulated data pairs, {xi,yi; i = 1…n}, and to make the comparison with the other estimators fair we draw these from a Poisson distribution with mean value 20/n, from which noise of b/n is subtracted. Beale's estimator is now
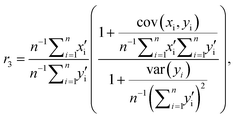 | (16) |
| x′i = xi − b/n | (17) |
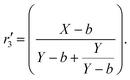 | (18) |
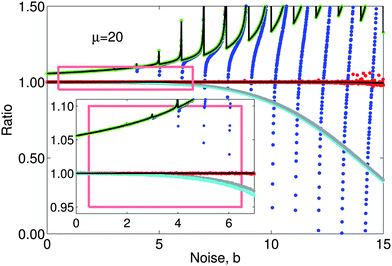 | ||
| Fig. 2 Monte-Carlo simulation of (X − b)/(Y − b) (blue), (X − b)/(Z − b) (green), Beale's estimator (grey, see main text), simplified Beale's estimator r′3 (cyan, eqn (18)) and the novel quasi-unbiased ratio, r′ (red, eqn (15)) with μx0 = μy0 = b, where X and Y are independent Poisson variables with means, μx and μy, equal to 20 and Z = Y for Y > b and rejected otherwise. For each data point the simulation computes the mean over 106 samples. Rare single events where Y is small can significantly shift the mean r′ for large values of b giving rise to the observed scatter in the red data for b ≳ 10. Black lines show the theoretical behaviour in the cases of the green and red data. Much of the blue data are obscured behind the green. The noise, b, is incremented in steps of 0.01. | ||
These substitutions are arrived at by noting that, for independent Poisson distributions, E{cov(X,Y)} = 0 and E{var(Y)} = E(Y). Simulations of both r3 and r′3 are included in Fig. 2. Note that for zero noise, r′3 = X/(Y + 1), i.e. identical to r′ (eqn (15)), and for b > 0 the (absolute) bias of r′3 is marginally greater (more negative) than that of r3.
Fig. 3 compares the variance of r′ (eqn (15)) with that of r (eqn (7)) as a function of mean signal, μx = μy = μ, for three different noise to signal ratios. Over the plotted parameter range the variance of r′ is always the smaller (var(r′)/var(r) < 1) and, therefore, more efficient ratio estimator.
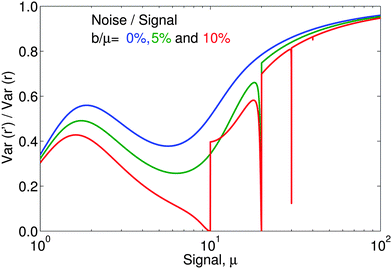 | ||
| Fig. 3 Variance of quasi-unbiased ratio, r′ (eqn (15)), divided by the variance of r = (X − b)/(Z − b) as a function of mean signal, μx = μy = μ, for relative noise, b/μ = 0, 5% and 10% showing that the variance in r′ is always smaller than that of the conventional ratio, r, over this range of parameters. | ||
4 Discussion
Quasi-unbiased ratios offer advantages over conventional methods of calculating noise-corrected ratios of ion-counting measurements, namely, (i) an exponentially small statistical bias, (ii) no need to sacrifice within-analysis information by summing counts over entire analysis before taking the ratio, (iii) insensitivity to common-mode changes in signal intensity, (iv) no mathematical singularities, and (v) good stability even with low signal to noise ratios (≳2).Ratio bias has increasing importance in isotope ratio measurements since the scientific demands lead researchers to strive for ever higher precisions on small quantities of sample. This is particularly the case in secondary-ion mass spectrometry (SIMS) where, because of low blanks, very low count rates are acceptable. In studies on short-lived radionuclides (SLRs) (e.g. see ref. 7–10) the bias is particularly insidious as it can give rise to an apparent linear relationship between measurements of the daughter nuclide and a proxy for the parent nuclide on a so-called ‘isochron’ plot. To illustrate, consider the SLR 60Fe which decays to 60Ni. A suite of measurements are made on phases with a range of Fe/Ni ratios and an isochron plot is made of the daughter, 60Ni, against the parent element, Fe. Both are plotted as ratios using some stable isotope of Ni as the denominator. A straight line with positive slope (the isochron) indicates that 60Fe was present at the time the Fe and Ni were fractionated between the phases. It is sometimes the case that most or all of the variation in Fe/Ni is controlled by the Ni content which, since it appears in the denominator on both axes, will give rise to a linear relationship in the data as a consequence of the bias, adding to the positive slope due to in-growth of 60Ni. Huss et al.11 have recently reported this problem with some of their own published data on the Fe–Ni system concluding that in some, but not all, samples their published estimates of initial 60Fe can no longer be distinguished from zero. They also discuss the likely size of any corrections to other published work on10Be, 26Al and 53Mn concluding that any changes to the published conclusions are small except for one older study on the Mn–Cr system in pallasites.
Note that, where internally normalised ratios are calculated, i.e. where a third isotope is used to correct for mass-bias, the magnitude of the statistical bias can increase or decrease, depending on the relative mass differences, by propagation of the bias of the normalising ratio. For example and assuming a linear mass bias law, in the case of 60Ni/61Ni normalised to 62Ni/61Ni the statistical bias on 60Ni/61Ni increases by a factor of two, whereas using 62Ni as the denominator the statistical bias on 60Ni/62Ni stays the same magnitude but changes sign as it does in the case of 26Mg/24Mg normalised to 25Mg/24Mg. For 53Cr/52Cr normalised to 50Cr/52Cr the statistical bias increases by a factor of 1.5.
Studies where mass-bias correction is made by sample – standard bracketing are potentially susceptible to statistical bias in cases where there are differences in analyte concentration (ion count rate) between sample and standard. Standards are usually chosen to have analyte concentrations high enough that good precision can be achieved in a short time under the same analytical conditions employed on the sample. Where ion counts are higher on standards than samples and ratios are calculated conventionally, the statistical bias will result in systematically high ratios reported on samples corrected by sample-standard bracketing. In short, sample-standard bracketing does not necessarily eliminate the bias.
Huss et al.11 rightly point out that ratio bias is a problem that the community will have to be aware of to avoid this source of systematic error in future work. However, we disagree that the best solution is necessarily to sum the counts over the entire analysis before taking the ratio (with or without using Beale's ratio estimator), or to correct for the bias based upon eqn (4) or (12), for the reasons (i)–(v) given at the beginning of this discussion, but rather to use eqn (15) to compute the ratio r′ at each measurement cycle.
It may seem laborious to have to evaluate the Kummer confluent hypergeometric function for every measurement cycle but this should not be particularly so if (i) a good library of special functions is available to the software developers or (ii) the signal to noise ratio is sufficiently high to be able to truncate the infinite series of eqn (14) to yield an approximate value for M(1,Y + 2,μ0). The truncation error, εn, using an upper summation limit of n − 1 in eqn (14) is given by,
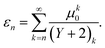 | (19) |
Let α = μ0/(Y + 2) be subject to the constraint 0 ≤ α < 1. This constraint is not severe: it is sufficient only that the signal is at least as large as the mean noise (and both are positive). Since (Y + 2)k ≥ (Y + 2)k we may write,
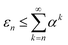 | (20) |
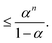 | (21) |
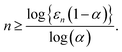 | (22) |
Therefore, if we wish to calculate M(1,Y + 2,μ0) with a truncation error no larger than ν we can use
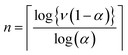 | (23) |
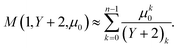 | (24) |
Appendix
A.1 The expectation value of 1/Zl
For Z distributed as a truncated Poisson distribution (eqn (6)) we have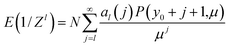 | (25) |
| P(a,z) = γ(a,z)/(a − 1)! a = 1,2,… |
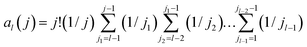 | (26) |
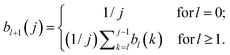 | (27) |
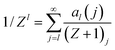 | (28) |
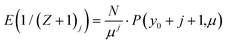 | (29) |
where we have used Arfken12 equation 10.70 in the final step completing the proof.
Eqn (28) yields as follows. Denote
| {p}j = 1/(p)j. |
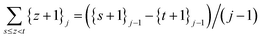 | (30) |
Proof: for s = t, obviously RHS = LHS = 0. For t > s, by induction on t − s using
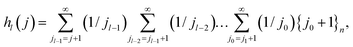 | (31) |
| hl(j) = 1/nl{j + 1}n | (32) |
Proof: by induction on l. From the definition (eqn (31)) follows the recursion
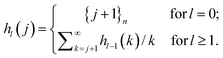 | (33) |
The result is trivial for l = 0; for l > 0, substituting the RHS value for hl−1(k) (eqn (32)) into the recursion (eqn (33)),
Changing the order of summation and combining eqn (31) and (32) gives
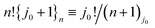 ,
,With n → Z this completes the proof of eqn (28) and, hence, also of eqn (25).
Acknowledgements
The SIMS data in Fig. 1 were collected at the Edinburgh Ion Microprobe NERC Facility on a sample provided by Dr Laura Foster of the University of Bristol. Dr Coath is supported in this work by STFC grant ref. ST/F002734/1.References
- K. Coakley, D. Simons and A. Leifer, Int. J. Mass Spectrom., 2005, 240, 107–120 CrossRef CAS.
- R. C. Ogliore, G. R. Huss and K. Nagashima, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1910–1918 CrossRef.
- Digital Library of Mathematical Functions, National Institute of Standards and Technology, 2010, ch. 8 Search PubMed.
- Digital Library of Mathematical Functions, National Institute of Standards and Technology, 2010, ch. 13 Search PubMed.
- A. Prudnikov, Y. Brychkov and O. Marichev, in More Special Functions, Gordon and Breach, 1986, vol. 3, p. 409 Search PubMed.
- I. Gradshteyn and I. Ryzhik, in Tables of Integrals, Series and Products, Academic Press, 7th edn, 2007, p. 1023 Search PubMed.
- K. McKeegan, M. Chaussidon and F. Robert, Science, 2000, 289, 1334–1337 CrossRef CAS.
- E. Kurahashi, N. T. Kita, H. Nagahara and Y. Morishita, Geochim. Cosmochim. Acta, 2008, 72, 3865–3882 CrossRef CAS.
- P. Hoppe, D. Macdougall and G. W. Lugmair, Meteorit. Planet. Sci., 2007, 42, 1309–1320 CrossRef CAS.
- S. Tachibana and G. Huss, Astrophys. J., 2003, 588, L41–L44 CrossRef CAS.
- G. Huss, R. Ogliore, K. Nagashima, M. Telus and C. Jilly, 42nd Lunar and Planetary Science Conference, #2608, 2011 Search PubMed.
- G. Arfken, in Mathematical Methods for Physicists, Academic Press, Inc., 3rd edn, 1985, p. 566 Search PubMed.
Footnote |
| † Present address: University of California, Los Angeles, Department of Earth and Space Sciences, 595 Charles Young Dr E., Los Angeles, CA 90095-1567, USA. |
| This journal is © The Royal Society of Chemistry 2013 |