Atropisomerization of di-para-substituted propyl-bridged biphenyl cyclophanes

Abstract

The influence of electron donors and electron acceptors of variable strength in the 4 and 4′ position of 2 and 2′ propyl-bridged axial chiral biphenyl cyclophanes on their atropisomerization process was studied. Estimated free energies ΔG^‡(T) of the rotation around the central biphenyl bond which were obtained from ¹H-NMR coalescence measurements were correlated to the Hammett parameters σ_p as a measure for electron donor and acceptor strength. It is demonstrated that the resulting nice linear correlation is mainly based on the influence of the different substituents on the π-system of the biphenyl cyclophanes. By lineshape analysis the rate constants were calculated and by the use of the Eyring equation the enthalpic and entropic contributions were evaluated. Density functional theory calculations show a planar transition state of the isomerization process and the calculated energy barriers based on this reaction mechanism are in good agreement with the experimentally obtained free energies.

---

Introduction

The well-defined spacing of the terminal units in biaryls caused by their rigidity and the ability to provide detectable signals even in poorly communicating conformations because of their compactness make biaryls maybe the simplest compounds to study the communication between two individual π-systems.^1,2 The possibility to adjust this communication by variation of the surrounding of biphenyls^3,4 and bipyridines⁵ leads to unique physical and chemical properties. The success of such structural motifs can be documented by the use of biphenyl and bipyridine structural elements in an amazing amount of compounds in material science like polymers,⁶ OLEDs,⁷ non-linear optics,⁸ molecular motors,⁹ molecular electronics,^1,3,4 light harvesting metal complexes,^10,11 dyes,¹² artificial photosynthesis¹³ and catalysis^14–17 to name just a few possible applications. By variation of the torsion angle Φ between the planes of the two phenyl rings, the degree of π overlap in the two phenyl rings and the resulting extent of delocalization over both π-systems can be fine-tuned. In most cases known in the literature, this tuning was performed by substituting biaryls in the 2 and 2′ position with different sterically demanding groups^18–24 or by interlinking the two positions with chains of different lengths.^3,4,8,25 By substituting biaryls in the 2,2′ position differently from the 6,6′ position not only the torsion angle is adjusted but also axial chirality is introduced which opens up a variety of new potential applications like POLED (based on circular polarized luminescence),²⁶ or new powerful ligands for enantioselective catalytic processes. Although enantioselective syntheses of axial chiral biphenyls are known, the preparation has been to date synthetically challenging, time consuming and mostly limited to 2,2′,6,6′ crowded biphenyl compounds.^27–32 Much easier still is the separation of the two atropisomers which can be achieved by chiral HPLC or GC when the rotation barrier between the two phenyl rings is higher than 93.5 kJ mol⁻¹ at 300 K.²⁹ One of the major problems towards applications using axial chiral di-ortho-substituted biaryls is, among others, their relatively low atropisomerization energies. Low barriers essentially lead to fast racemization when these compounds are incorporated into more complex structures or when used as ligands for metal complexes in catalysis or light harvesting molecules. The configurational stability of axial chiral biaryls is determined by the steric demand of substituents, existence, rigidity and length of bridges and involvement of atropisomerization mechanisms different from a physical rotation, for example by chemically or photochemically induced processes.²⁹ One possibility to enhance the isomerization energies of axial chiral biaryls is therefore to introduce sterically demanding groups in the 6,6′ position different from the ones in the 2,2′ position. Major drawbacks include that coordination sites will be blocked, the torsion angle will be close to 90° lowering the communication between the two aryl rings significantly, or even worse an overall change in the electronic nature of the biaryl.

To design molecules with rotation energies high enough to separate the two enantiomers and to be able to perform chemical reactions with the enantiomerically pure atropisomers, it is necessary to study the inversion mechanism and the influence of substituents on the di-ortho-substituted biaryls in detail. By understanding the inversion mechanism in detail it will then be possible to substitute biaryls in positions where for example the electronic structure is not influenced and/or important binding sites are not blocked. Up to date several investigations on the atropisomerization of biaryls were carried out leading to conflicting outcomes.^33–43 From several available studies on the physical rotation of biaryls, it was concluded that only the push–pull cases show a linear and planar transition state whereas in all other cases an out-of-plane bending is the dominating factor which significantly influences the energy barrier. Furthermore Müllen and co-workers estimated the energy barriers of an amazing collection of 2,2′,6,6′-substituted biphenyls by NMR coalescence studies and derived an inversion mechanism where the interlinking 1 and 1′ carbons stay in plane, whereas the individual phenyls are distorted.³⁷ Besides this, many computational studies displayed a planar transition state^24,44–47 and recent studies of biphenyl based push–pull cyclophanes have shown that the racemization barrier reflects the crowdedness of the transition state.³⁸

In this article, we have investigated the rotation barriers of 4,4′-disubstituted torsion-angle-restricted biphenyl cyclophanes 1a–1l synthesized by our group that were already investigated in single molecular conductance measurements (Fig. 1).^3,4 By correlation of the obtained data with the Hammett parameter we wanted to gain further insight into the influence of π-substituents in the para position to the central biphenyl bond. In this series push–push, push–pull and pull–pull cases were considered. The push–pull compound 1i was included because a charge-transfer between the donor and the acceptor is present causing a double-bond character of the central C–C bond. This forces the system into a planar transition. Thus, if the rotation barrier of compound 1i correlates with the others in a Hammett-correlation a strong hint for a planar transition state can be obtained. By comparison of the measured inversion energy with quantum chemical calculations we also intended to clarify the influence of the propyl bridge as well as of changing the electronic properties of the biphenyl core on the atropisomerization mechanism.

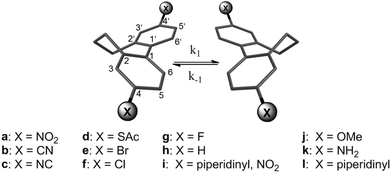Fig. 1 Studied torsion-angle-restricted biphenyl cyclophanes 1a–1l.

Methods and materials

Previous studies of 2,2′ alkyl-bridged push–pull biphenyls showed that the ethyl-bridged derivative isomerized too fast to record the coalescence temperature by ¹H-NMR measurements, whereas for the propyl-bridged derivative 1i the interconversion of the two enantiomers was slow enough to be monitored. The butyl- and the pentyl-bridged push–pull cyclophanes atropisomerized even slower so that only separated diastereotopic protons were observed in the ¹H-NMR.³⁸ Since it was of interest to study the inversion process it was decided to perform the above mentioned studies on the influence of different substituents in the 4,4′ position with a series of propyl-bridged biphenyls 1a–1l to exclude possible already conformational stable atropisomers which potentially can occur in the butyl- or pentyl-bridged derivatives.

Syntheses

Compound 1a was synthesized starting from the already available diamino derivative 1k⁸ by oxidation using a potassium iodide–tert-butyl hydroperoxide catalytic system (see ESI†).⁴⁸ The dipiperidinyl substituted biphenyl cyclophane 1l was obtained by an azacycloalkylation of the diamino biphenyl precursor with 1,5-dibromopentane in an aqueous sodiumdodecylsulfate solution and sodium hydrogencarbonate as a base.⁸ The difluoro biphenyl derivative 1g was obtained from 4,4′-diaminobiphenyl 1k by a Schiemann-type reaction using tetrafluoroboric acid.⁴⁹ Dibromobiphenyl derivative 1e was treated with t-BuLi and afterwards quenched with a saturated aqueous ammonium chloride solution to obtain the unfunctionalized derivative 1h.⁵⁰ All other compounds were previously synthesized in our lab.^3,4,8,51

NMR studies

All samples were prepared in deuterated solvents (>99.8% D, Cambridge Isotope Laboratories, Burgdorf, CH). The NMR experiments were performed on a Bruker Avance III – 600 MHz NMR spectrometer, equipped with a self-shielded z-axis pulsed field gradient dual channel broadband inverse probe-head. Chemical shifts were referenced to residual solvent peaks and the temperature was calibrated using a 4% methanol in a 96% methanol-d4 sample (for detailed information see ESI†).⁵²

To ensure thermal equilibrium, at least 15 min of equilibration time was allowed for each temperature step. The activation energy was calculated from the following form of the Eyring equation (eqn (1)).⁵³

ΔG^‡ = 0.0191 T_c (9.97 + lg(T_c/(Δν))) (1)

ΔG^‡ = Gibbs free activation energy [kJ mol⁻¹], T_c = coalescence temperature [K], Δν = chemical shift difference in slow exchange [Hz].

Kinetic data were obtained from line shape analysis of the propyl-bridge spin system as it is involved in the rotation process. Line shape analysis was performed with the commercially available software d-NMR (Bruker Bio Spin AG®). The confidence interval between simulated and measured spectra was set to 95%. The resulting rate constants were further analyzed by Eyring plots and the thermodynamic data calculated using eqn (2) and (3).^54,55 The coalescence temperatures were determined by line width analysis for each temperature followed by a Lorentzian fitting.

ΔH^‡ = −mR (2)

y(x = 0) = ln(k_B/h) + (ΔS^‡/R) (3)

ΔH^‡ = activation enthalpy [kJ mol⁻¹], m = slope of the Eyring plot, R = universal gas constant = 8.3144 J mol⁻¹ K⁻¹, y(x = 0) = intercept of the Eyring plot, k_B = Boltzmann constant = 1.38 × 10⁻²³ J K⁻¹, h = Planck constant = 6.626 × 10⁻³⁴ J s, ΔS^‡ = activation entropy [J mol⁻¹ K⁻¹].

Computational studies

All calculations in this work were performed with the TURBOMOLE program package.⁵⁶

Equilibrium and transition state structures involved in the atropisomerization process of symmetrically substituted biphenyl cyclophanes were optimized within the framework of density functional theory (DFT). In order to assess the performance of different types of density functionals, we chose the generalized gradient approximation (GGA) functional BP86,^57–59 the meta-GGA functional TPSS,⁶⁰ and the hybrid functional B3LYP.⁶¹ Accurate calculations of the rotation barrier in biphenyl (C₁₂H₁₀) have shown that the B3LYP functional agrees well with both the highest-level extrapolated ab initio results and experiment.⁶² Each functional was used in combination with a def2-TZVP basis set,⁶³ tight convergence criteria (SCF energy: 10⁻⁸E_h, energy gradient: 10⁻⁴E_h/a₀ or less, inclusion of derivatives of quadrature weights), and fine quadrature grids (m5).⁶⁴ For non-hybrid functionals, the efficient resolution of the identity (RI) approximation for two-electron Coulomb integrals was employed. The nature of the obtained stationary points (minimum or first order saddle point) was confirmed through analysis of the force constants and vibrational frequencies.

Gibbs free activation energies were computed for a standard pressure of 0.1 MPa and for the coalescence temperatures T_c as determined in the NMR experiment. For the calculation of the partition functions, the vibrational frequencies were scaled by a factor of 0.9914 (BP86 and TPSS) or 0.9614 (B3LYP).⁶⁵

In the case of X = NH₂, OMe, SAc and piperidinyl, the rotation about the C–X bond as well as rotations within the substituent allowed for several conformational isomers. Here, we considered all energetically low lying equilibrium structures with C₂ symmetry together with their corresponding transition states. The reported values for these substituents were obtained by taking the Boltzmann average of the respective conformers.

Results

The interconversion of the two atropisomers of cyclophanes 1a–1l can be monitored by NMR coalescence experiments if the half lifes of the enantiomers are in the range of microseconds to seconds. For thermodynamic investigations the slow and the fast exchange regime, as well as the coalescence condition have to be reached.. Determination of the coalescence temperature and the chemical shift differences in the slow exchange regime yields the Gibbs free activation energy ΔG^‡(T) using the modified form of the Eyring equation (eqn (1)). Experimental coalescence temperatures Tc were estimated from the measured spectra with an accuracy of 1 K. As shown in Table 1, different ΔG^‡(T) were obtained for the push–push, push–pull and pull–pull systems depending on different substituents. The activation energy is in the range of 44 to 55 kJ mol⁻¹ for all compounds 1a–1l.

Table 1 Coalescence temperatures of the biphenyl cyclophanes 1a–1l (Fig. 1) in chloroform with their characteristic separation Δν and the resulting Gibbs activation energy ΔG^‡(T) with standard deviation

Compound	T c/K	Δν/Hz	ΔG^‡/kJ mol^−1
1a	281.4 ± 1	218.0	54.2 ± 0.5
1b	275.1 ± 1	181.0	53.3 ± 0.5
1c	270.1 ± 1	161.0	52.6 ± 0.5
1d	259.6 ± 1	111.0	51.3 ± 0.5
1e	260.2 ± 1	113.0	51.3 ± 0.5
1f	260.7 ± 1	118.0	51.4 ± 0.5
1g	265.0 ± 1	109.0	52.4 ± 0.5
1h	263.3 ± 1	95.0	52.4 ± 0.5
1i	245.0 ± 1	132.0	47.9 ± 0.5
1j	242.1 ± 1	79.0	48.4 ± 0.5
1k	224.2 ± 1	31.0	46.4 ± 0.5
1l	218.9 ± 1	44.0	44.6 ± 0.5

---

The line shape analysis delivered insight into the kinetics of the rotation.^55,66,67 Rate constants for each temperature and substituent were determined and analyzed using Eyring plots. According to this, enthalpy and entropy parameters were obtained using eqn (2) and (3). A representative comparison of experimental and calculated spectra is shown in Fig. 2 and the corresponding Eyring plot is given in Fig. 3.

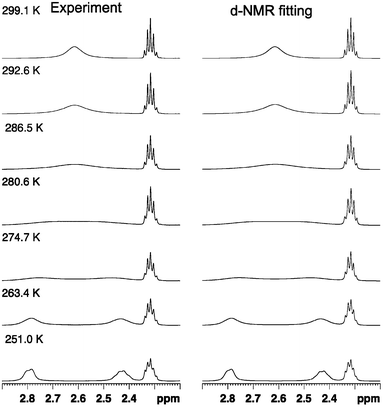Fig. 2 Comparison of experimental and simulated NMR spectra for the dinitro substituted biphenyl 1a at variable temperatures. Line shape analysis was performed for the whole propyl-bridge spin system involved in the rotation process. The simulated spectra have an accuracy of >95%.

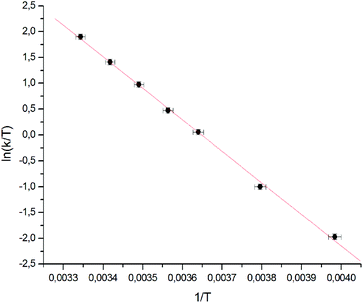Fig. 3 Eyring plot for the dinitro substituted biphenyl 1a correlating the rate of rotation with temperature. Linear regression delivers directly the thermodynamic data.

Activation enthalpy ΔH_Eyring^‡, activation entropy ΔS_Eyring^‡ and the free energy ΔG_Eyring^‡(T) are shown in Table 2. The coalescence temperatures T_c were estimated from experimental spectra whereas the calculated coalescence temperatures T_c-lineshape were obtained after Lorentzian fitting of the line width (see ESI†). The error bar on the Gibbs free energy, the enthalpy and the entropy in Table 2 is equal to one standard deviation. It is obtained by assuming a statistical error in the temperature of 1 K and a statistical error in the rate constant with a standard deviation of 5% (except for 1l, where a standard deviation of 20% was assumed).

Table 2 Overview over thermodynamic data calculated from line shape analysis with d-NMR. The coalescence temperatures were calculated by Lorentzian fitting of the line width. Thermodynamic data were obtained from Eyring plots

Compound	T c-lineshape/K	ΔGEyring^‡/kJ mol^−1	ΔHEyring^‡/kJ mol^−1	ΔSEyring^‡/J(mol^−1 K^−1)
1a	280.4 ± 1.1	54.2 ± 0.1	50.7 ± 1.6	−12.6 ± 5.6
1b	274.1 ± 1.3	53.3 ± 0.1	52.7 ± 2.0	−1.9 ± 7.3
1c	269.1 ± 1.1	52.6 ± 0.1	49.9 ± 1.3	−10.0 ± 4.6
1d	261.6 ± 1.7	52.0 ± 0.1	45.9 ± 1.0	−21.8 ± 3.6
1e	263.2 ± 1.3	51.7 ± 0.1	50.0 ± 2.7	−6.4 ± 10.4
1f	259.7 ± 1.3	51.5 ± 0.1	46.0 ± 1.0	−21.0 ± 3.7
1g	263.0 ± 1.6	52.6 ± 0.1	47.8 ± 1.3	−18.5 ± 4.7
1h	262.3 ± 1.4	52.4 ± 0.1	47.4 ± 1.2	−19.1 ± 4.6
1i	244.0 ± 1.2	47.8 ± 0.1	37.4 ± 0.8	−42.6 ± 3.0
1j	241.1 ± 1.3	48.8 ± 0.1	43.4 ± 1.5	−22.5 ± 6.2
1k	221.6 ± 2.1	46.8 ± 0.1	39.3 ± 1.5	−33.8 ± 6.6
1l	217.9 ± 1.4	45.4 ± 0.2	28.3 ± 1.7	−78.4 ± 7.3

---

In order to validate the two state model used for the interpretation of the experimental data and the determination of the free energy, we compared the results for ΔG^‡(T) obtained from experimental and simulated NMR data (Tables 1 and 2). The error on the Gibbs free activation energy depends mainly on the coalescence temperature estimated from measured NMR spectra. The accuracy of calculated coalescence temperatures is mainly influenced by the number of points measured in fast exchange and slow exchange. Therefore the calculated data for compounds with a low coalescence temperature are less precise compared to the ones with higher coalescence temperatures. Simulation of the spectrum of 1l was troublesome because of the low coalescence temperature. Only two spectra could be measured below T_c because the freezing point of CDCl₃ was reached. The increased viscosity of CDCl₃ at low temperatures resulted in broader NMR signals which lead to rate constants that are larger than they are in reality. Therefore a correction factor for slow exchange rate constants was estimated by measuring a reference sample.

The differences between experimental and simulated ΔG^‡(T) values are small (up to 0.8 kJ mol⁻¹) and for all cases within the statistical errors. It has thus been shown that the two state model approach is valid and that differences in the determined ΔG^‡(T) values of more than 1 kJ mol⁻¹ are statistically significant.

Density functional theory calculations were performed in order to gain further insight into the atropisomerization mechanism of the propyl-bridged biphenyls. In this context it was also of interest to have a closer look at the influence of the different substituents in the para position on the structural parameters as well as on the thermodynamic properties. We considered all aforementioned synthesized compounds except the unsymmetrically substituted push–pull system 1i.

All optimized equilibrium structures exhibit (or in the case of conformational freedom were chosen to exhibit) C₂ symmetry and the torsion angle between the phenyl rings amounts to about 47°. The careful inspection of the rotation about the central phenyl–phenyl bond revealed that the two atropisomers are connected via a single transition state. The relevant structures are shown in Fig. 4 for the unfunctionalized compound 1h. It can be seen that the transition state is accessible from the equilibrium structure via rotation of an ortho CH₂ group, which leads to a geometry with a torsion angle of 0°. The phenyl rings are coplanar but, as they are slightly bent towards the unbridged side, not perfectly linear.

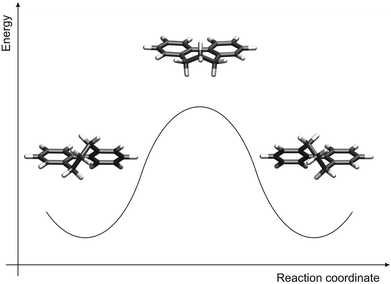Fig. 4 Calculated atropisomerization mechanism: equilibrium structure before the rotation of the phenyl rings (left), transition state structure (middle), and equilibrium structure after the rotation (right).

On the basis of our determined species in the reaction pathway, we computed the Gibbs free energy of activation, ΔG_theo^‡, at the coalescence temperature T_c. The results for the various density functionals and substituents are summarized in Table 3. Similar trends for the dependence on the substituents are observed. The contributions of the enthalpy of activation, ΔH_theo^‡, and the entropy of activation, ΔS_theo^‡, are given in Table 4. We find that all obtained absolute values for ΔS_theo^‡ are smaller than 4 J mol⁻¹ K⁻¹, and thus of about the size of the error we expect for the underlying method.

Table 3 Calculated Gibbs free activation energies ΔG_theo^‡ using different types of density functionals. All values are given in kJ mol⁻¹

Compound	ΔGBP86^‡	ΔGTPSS^‡	ΔGB3LYP^‡
1a	48.4	49.7	52.0
1b	47.6	48.7	51.2
1c	47.2	48.2	50.6
1d	48.0	48.9	52.4
1e	47.0	48.0	50.4
1f	47.0	48.0	50.3
1g	48.4	49.4	51.6
1h	48.4	49.3	51.7
1j	45.7	46.5	48.9
1k	44.0	44.8	47.3
1l	42.5	43.3	46.2

---

Table 4 Enthalpy (ΔH_theo^‡) and entropy (ΔS_theo^‡) contributions to the Gibbs free activation energy as calculated with different types of density functionals. Values for ΔH_theo^‡ are given in kJ mol⁻¹, values for ΔS_theo^‡ are given in J mol⁻¹ K⁻¹

Compound	ΔHBP86^‡	ΔSBP86^‡	ΔHTPSS^‡	ΔSTPSS^‡	ΔHB3LYP^‡	ΔSB3LYP^‡
1a	49.1	2.5	50.1	1.4	52.5	1.8
1b	48.1	1.9	48.8	0.6	51.7	1.6
1c	47.6	1.5	48.3	0.5	50.9	1.2
1d	47.8	−0.9	48.5	−1.5	51.5	−3.7
1e	47.3	0.9	48.0	−0.1	50.6	0.8
1f	47.2	0.8	47.9	−0.2	50.5	0.7
1g	48.6	0.6	49.3	−0.3	51.8	0.5
1h	48.8	1.2	49.4	0.3	52.0	1.2
1j	45.9	0.9	46.5	0.0	49.0	0.8
1k	44.2	0.7	44.8	−0.1	47.5	0.5
1l	43.1	2.8	43.7	1.9	46.7	2.3

---

Discussion

The atropisomerization energies ΔG^‡(T) obtained from the Eyring eqn (1) were found between 44 kJ mol⁻¹ (for the strongest π-donor piperidinyl 1l) and 55 kJ mol⁻¹ (for the nitro-substituted derivative 1a as the strongest π-acceptor). These results demonstrate that the influence of the substituents in the 4,4′ position on the racemization is less pronounced than variation of the length of the alkyl bridge³⁸ or changing the steric demand of substituents in the ortho position to the central biphenyl bond^18–24 as shown previously. For the diacceptor substituted propyl-bridged biphenyl derivatives 1a–1c, significantly higher rotation barriers ΔG^‡(T) were measured than for the compounds substituted with two donors. The free energy of the dimethoxy cyclophane 1j is slightly higher than the one of the push–pull system 1i, which is consistent with the values obtained by Oki.³⁶ As demonstrated there, acceptors increase the rotation energy of such systems whereas donors decrease the free energy. For the only weak π-donating halogen substituted cyclophane derivatives 1e–1g and the unfunctionalized derivative 1h similar atropisomerization energies ΔG^‡(T) of around 52 kJ mol⁻¹ were measured.

Since it was of interest to investigate the influence of donors and acceptors of variable strength, the measured free energies ΔG^‡(T) were plotted against the Hammett parameters σ_p (Fig. 5).^68,69

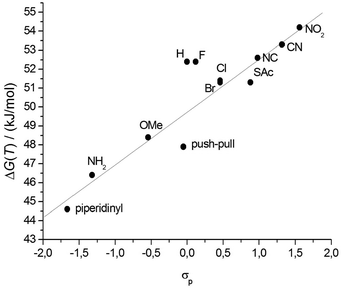Fig. 5 Hammett correlation of the propyl-bridged biphenyl systems 1a–1l (R² = 0.84).

The σ-parameter can be used in this case as a collective measure of the total electronic effects (resonance and inductive effect) and reflects the ability to withdraw or donate electrons from the reaction site, in this particular case the central C–C bond of the biphenyl. To obtain adequate parameters for the two substituents in the 4 and 4′ position, the Hammett parameters for each individual substituent were summed up as demonstrated by Hart⁷⁰ and Wirz.⁷¹ The influence of the propyl chain was disregarded because its influence was constant throughout the whole series. The free energy ΔG^‡(T) is dependent on the logarithm of the rate constant and therefore these Hammett parameters can be directly correlated to ΔG^‡(T).⁶⁸ By performing such a correlation the effect of the substituents on the transition state compared to the initial state can be visualized. Since the reference system, namely the unfunctionalized derivative 1h, is included in the correlation, a normalization was not performed. Inspection of the obtained Hammett plot clearly shows a linear free energy relation, which implies that the atropisomerization process is strongly dependent on the electron density at the central C1–C1′ bond. According to this observation, the rotation barrier is increased when the electron density is reduced at the reaction site and decreased when the electron density is increased. Furthermore the slope of the linear free energy relationship ρ of 2.8 indicates the sensitivity of the atropisomerization process on electronic perturbation. Additionally, the fact that there are only minor deviations from linearity and especially the fact that 1i only marginally deviates from this correlation indicates that all derivatives 1a–1l follow the same atropisomerization mechanism. To gain further insight into the effect of the substituents, the Hammett parameters σ_p were split in accordance with Swain and Lupton into their field effect (F) parts and their resonance (R) parts.⁷² The pronounced correlation of the obtained free energy values to the modified resonance parameter R (R² = 0.85) demonstrates that the substituents in the 4 and 4′ position influence the atropisomerization process by disturbing the π-system of the biphenyl system (Fig. 6). This is further supported by the weaker correlation to the field effect parameter F (R² = 0.40) which is a measure for the polarization of the σ-skeleton of the reaction site.

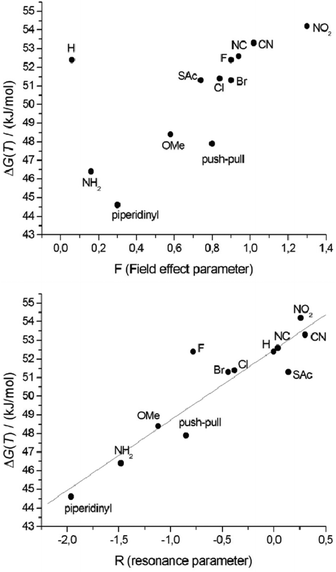Fig. 6 Correlation of ΔG^‡(T) with the field effect parameter F (top), and with the resonance parameter R (bottom).

These observations suggest that an inversion mechanism where the system strives for conjugation of the π-systems (close to planar and linear) is most probable, rather than the one in earlier publications postulating partial rehybridization of the central carbon atoms.³⁵

The linear relationship between ΔG^‡(T) and the resonance parameter R, a measure for the influence of different end-groups on the conjugation in the biphenyl system, indicates that the different substituents in the 4 and 4′ position dictate the energy needed for the isomerization process by distortion of the π-system of the biphenyl core. Therefore, this suggests a planar transition state for the atropisomerization process which is also supported by DFT calculations. The reason why the energy barrier of the difluorobiphenyl 1g is higher than expected according to the correlations against σ_p and R and why this is not the case for the field effect F remains unclear. Probably the Hammett parameter σ_p and the resonance parameter R underestimate the electron withdrawing behavior of the fluoride which is a strong σ-acceptor and only a weak π-donor.

By the above described line shape analyses of the ¹H-NMR coalescence spectra, the rate constants for the interconversion process were estimated at different temperatures and by using the Eyring equation the free energies of rotation ΔG^‡(T) were divided into their enthalpic and entropic parts (Table 2). Thereby it becomes evident that the main contribution to the rotation barrier of the central biphenyl bond is dominated by the enthalpic contribution.

The reaction mechanism for the atropisomerization was further studied using quantum chemical calculations. We find a planar and nearly linear transition state for the inversion of all symmetrically substituted propyl-bridged biphenyls (Fig. 4). The computed Gibbs free activation energies based on this mechanism range from 42 kJ mol⁻¹ to 52 kJ mol⁻¹ (Table 3). For comparison, ΔG_theo^‡ values of less than 10 kJ mol⁻¹ are found for the unsubstituted biphenyl molecule itself. This means that the influence of the substituents in the para position on ΔG^‡ is much smaller than the influence of the propyl bridge. In the course of the reaction, both ortho CH₂ groups rotate and pass by each other in the transition state which seems to be the crucial factor dictating the inversion energy. Thus, the functionalization of the propyl bridge may provide the possibility to further adjust the height of the atropisomerization barrier. In Fig. 7, the calculated free activation energies ΔG_theo^‡ obtained with DFT methods are compared to the experimentally determined values (Table 1).

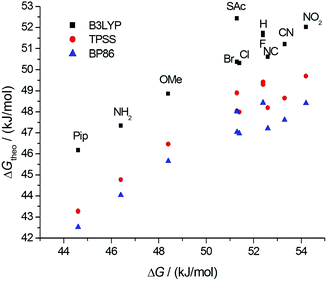Fig. 7 Comparison of the calculated free energies ΔG_theo^‡ to the measured free energies ΔG^‡(T): BP86 (blue), TPSS (red), B3LYP (black).

A linear relationship is observed for all three density functionals, indicating that they are equally well suited to describe the trends in ΔG^‡ as a function of the substituent. The computed differences between the various substituents are, however, somewhat smaller than the measured ones. For a deeper understanding of the influence of both the propyl bridge and the substituents in the para position, we had a closer look at the equilibrium and transition state geometries. We find that the length of the phenyl–phenyl bond (C1–C1′) is affected most by structural variations. In the unsubstituted biphenyl molecule, this bond is elongated by less than 1 pm going from the equilibrium to the transition state. In contrast, for the propyl-bridged biphenyls elongations of 3 pm and more are observed. This increase can be mainly attributed to the space requirements of the propyl bridge. In Fig. 8, the correlation between the bond length change and the computed Gibbs free activation energies is shown. We observe a linear relationship which implies that the elongation of the C1–C1′ bond is directly linked to the barrier height.

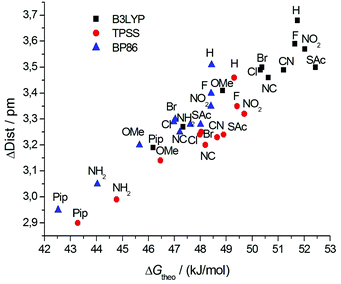Fig. 8 Correlation of the change of the calculated phenyl–phenyl distance in the transition state and the ground state with the calculated free energies ΔG_theo^‡.

The calculated contributions of the enthalpy of activation, ΔH_theo^‡, and the entropy of activation, ΔS_theo^‡, are given in Table 4. As expected for the considered inversion reaction in the gas phase, the calculated entropy does not change between the equilibrium state and the transition state.

Comparison of the calculated enthalpies and entropies (Table 4) with the experimentally obtained ones (Table 2) shows much larger deviations than in the case of the free energies. Especially for the donating substituents, that is for low coalescence temperatures T_c, the values deviate significantly. Two explanations for the observed discrepancies can be thought of.

(1) For the measured values, only statistical errors have been considered. It is possible that the systematic errors are much larger, in particular for the problematic low temperature regime. Even though the error is small for T = T_c, large systematic errors may result for ΔH^‡ and ΔS^‡ (that is, the slope and intercept of the Eyring plot) while ΔG^‡ can be still obtained to high accuracy.

(2) The computed values are for the gas phase reaction and intermolecular interactions – either with a neighboring biphenyl (π–π-stacking) or with the surrounding solvent in the experiment – are not considered. The formation of aggregates was excluded by ¹H-NMR titration with a limited series of concentrations. Preliminary solvent dependent ¹H-NMR coalescence measurements for 1b, 1e and 1j indicated a dependence of the enthalpy and the entropy on the solvent used (MeOD, CDCl₃, toluene), while the free energies remained more or less constant (see ESI†). However comparison of enthalpic and entropic contributions to the free energy in different solvents is troublesome since the method used to calculate these parameters is not very robust towards external changes. Instrument and solvent limit the temperature region that can be used to record the NMR spectra. Therefore small changes in the peak width, coalescence temperature and chemical shift difference can potentially result in large errors if measurements in different solvents are compared.

Conclusion and outlook

In conclusion, we demonstrated that the rotation barriers of di-para-substituted propyl-bridged biphenyls are strongly dependent on the nature of the phenyl–phenyl bond and hence on the nature of substituents in the para position to this bond. Atropisomerization processes were quantified by ¹H-NMR coalescence measurements. Correlation of the obtained free energies ΔG^‡(T) to the Hammett parameter σ_p, the resonance parameter R and the field effect parameter F allowed for identifying the π-electron density as the predominant factor that dictates the rotation barrier. This was further confirmed by DFT calculations, from which a planar and nearly linear transition state was obtained. In the future, it will be of interest to substitute the propyl bridge of the biphenyl cyclophanes 1a–1l to further hinder the atropisomerization without changing the electronic nature of the system or without changing the torsion angle. In addition it will be of interest to investigate the influence of the bridge length for which preliminary results already showed higher rotation barriers when elongated compared to the propyl-bridged systems.³⁸

Acknowledgements

The authors acknowledge financial support from the Swiss National Science Foundation and the National Center of Competence in Research ‘Nanoscale Science’. The authors furthermore acknowledge financial support from the Deutsche Forschungsgemeinschaft through the Center for Functional Nanostructures (CFN) in Karlsruhe (project nos. C3.3 and C3.8).

Notes and references

1. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907.
2. J. Wang, G. Cooper, D. Tulumello and A. P. Hitchcock, J. Phys. Chem. A, 2005, 109, 10886–10896.
3. D. Vonlanthen, A. Mishchenko, M. Elbing, M. Neuburger, T. Wandlowski and M. Mayor, Angew. Chem., Int. Ed., 2009, 48, 8886–8890.
4. D. Vonlanthen, A. Rudnev, A. Mishchenko, A. Käslin, J. Rotzler, M. Neuburger, T. Wandlowski and M. Mayor, Chem.–Eur. J., 2011, 17, 7236–7250.
5. R. P. Thummel, F. Lefoulon and R. Mahadevan, J. Org. Chem., 1985, 50, 3824–3828.
6. N. Berton, F. Lemasson, J. Tittmann, N. Stürzl, F. Hennrich, M. M. Kappes and M. Mayor, Chem. Mater., 2011, 23, 2237–2249.
7. W.-Y. Wong and C.-L. Ho, J. Mater. Chem., 2009, 19, 4457–4482.
8. J. Rotzler, D. Vonlanthen, A. Barsella, A. Boeglin, A. Fort and M. Mayor, Eur. J. Org. Chem., 2010, 1096–1110.
9. C. Tepper and G. Haberhauer, Chem.–Eur. J., 2011, 17, 8060–8065.
10. D. Kuang, S. Ito, B. Wenger, C. Klein, J.-E. Moser, R. Humphry-Baker, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 4146–4154.
11. C. Giansante, P. Ceroni, V. Balzani and F. Vögtle, Angew. Chem., Int. Ed., 2008, 47, 5422–5425.
12. H. Langhals, A. Hofer, S. Bernhard, J. S. Siegel and P. Mayer, J. Am. Chem. Soc., 2011, 76, 990–992.
13. N. Sakai, R. Bhosale, D. Emery, J. Mareda and S. Matile, J. Am. Chem. Soc., 2010, 132, 6923–6925.
14. E. R. Strieter, D. G. Blackmond and S. L. Buchwald, J. Am. Chem. Soc., 2003, 125, 13978–13980.
15. S. Lee, M. Jørgensen and J. F. Hartwig, Org. Lett., 2001, 3, 2729–2732.
16. J. J. Becker, P. S. White and M. R. Gagné, J. Am. Chem. Soc., 2001, 123, 9478–9479.
17. K. Mikami, T. Korenaga, M. Terada, T. Ohkuma, T. Pham and R. Noyori, Angew. Chem., Int. Ed., 1999, 38, 495–497.
18. K. Mislow, M. A. W. Glass, R. E. O'Brien, P. Rutkin, D. H. Steinberg, J. Weiss and C. Djerassi, J. Am. Chem. Soc., 1962, 84, 1455–1478.
19. F. Grein, J. Phys. Chem. A, 2002, 106, 3823–3827.
20. L. Lunazzi, M. Mancinelli, A. Mazzanti, S. Lepri, R. Ruzziconi and M. Schlosser, Org. Biomol. Chem., 2012, 10, 1847–1855.
21. L. Lunazzi, A. Mazzanti, M. Minzoni and J. E. Anderson, Org. Lett., 2005, 7, 1291–1294.
22. A. Mazzanti, L. Lunazzi, M. Minzoni and J. E. Anderson, J. Org. Chem., 2006, 71, 5474–5481.
23. R. Ruzziconi, S. Spizzichino, L. Lunazzi, A. Mazzanti and M. Schlosser, Chem.–Eur. J., 2009, 15, 2645–2652.
24. R. Ruzziconi, S. Spizzichino, A. Mazzanti, L. Lunazzi and M. Schlosser, Org. Biomol. Chem., 2010, 8, 4463–4471.
25. A. Boeglin, A. Barsella, H. Chaumeil, E. Ay, J. Rotzler, M. Mayor and A. Fort, Proc. SPIE Int. Soc. Opt. Eng., 2010, 7774, 777408–777408–10.
26. B. Kiupel, C. Niederalt, M. Nieger, S. Grimme and F. Vögtle, Angew. Chem. Int. Ed., 1998, 37, 3031–3034.
27. J. L. Gustafson, D. Lim and S. J. Miller, Science, 2010, 328, 1251–1255.
28. J. Hassan, M. Sévignon, C. Gozzi, E. Schulz and M. Lemaire, Chem. Rev., 2002, 102, 1359–1470.
29. G. Bringmann, A. J. Price Mortimer, P. A. Keller, M. J. Gresser, J. Garner and M. Breuning, Angew. Chem., Int. Ed., 2005, 44, 5384–5427.
30. G. Bringmann, M. Breuning, R.-M. Pfeifer, W. A. Schenk, K. Kamikawa and M. Uemura, J. Organomet. Chem., 2002, 661, 31–47.
31. K. Kamikawa and M. Uemura, Synlett, 2000, 938–949.
32. P. Lloyd-Williams and E. Giralt, Chem. Soc. Rev., 2001, 30, 145–157.
33. K. Ohkata, R. L. Paquette and L. A. Paquette, J. Am. Chem. Soc., 1979, 101, 6687–6693.
34. R. B. Bates, F. A. Camou, V. Kane, P. K. Mishra, K. Suvannachut and J. J. White, J. Org. Chem., 1989, 54, 311–317.
35. M. Oki, H. Iwamura and G. Yamamoto, Bull. Chem. Soc. Jpn., 1971, 44, 262–265.
36. M. Oki and G. Yamamoto, Bull. Chem. Soc. Jpn., 1971, 44, 266–270.
37. K. Müllen, W. Heinz, F. Klärner, W. R. Roth, I. Kindermann, O. Adamczak, M. Wette and J. Lex, Chem. Ber., 1990, 123, 2349–2371.
38. J. Rotzler, H. Gsellinger, M. Neuburger, D. Vonlanthen, D. Häussinger and M. Mayor, Org. Biomol. Chem., 2011, 9, 86–91.
39. L. Meca, D. Řeha and Z. Havlas, J. Org. Chem., 2003, 68, 5677–5680.
40. C. C. K. Ling and M. M. Harris, J. Chem. Soc., 1964, 1825–1835.
41. A. C. T. Van Duin, B. Hollanders, R. A. Smits, J. M. A. Baas, B. Van de Graaf, M. P. Koopmans, J. S. S. Damste and J. W. De Leeuw, Org. Geochem., 1996, 24, 587–591.
42. G. Bringmann, H. Busse, U. Dauer, S. Güssregen and M. Stahl, Tetrahedron, 1995, 51, 3149–3158.
43. M. Irie, K. Yoshida and K. Hayashi, J. Phys. Chem., 1977, 81, 969–972.
44. J. Pedersen, J. Krane, B. Rietz, A. Haaland and Å. Pilotti, Acta Chem. Scand., 1972, 26, 3181–3195.
45. A. Karpfen, C. H. Choi and M. Kertesz, J. Phys. Chem. A, 1997, 101, 7426–7433.
46. J. Hernández-Trujillo and C. F. Matta, Struct. Chem., 2007, 18, 849–857.
47. F. Ceccacci, L. Giansanti, G. Mancini, P. Mencarelli and A. Sorrenti, New J. Chem., 2007, 31, 86–92.
48. K. R. Reddy, C. U. Maheswari, M. Venkateshwar and M. L. Kantam, Adv. Synth. Catal., 2009, 351, 93–96.
49. B. Dolensky, J. Fluorine Chem., 2001, 107, 147–148.
50. X.-Z. Shu, Y.-F. Yang, X.-F. Xia, K.-G. Ji, X.-Y. Liu and Y.-M. Liang, Org. Biomol. Chem., 2010, 8, 4077–4079.
51. D. Vonlanthen, J. Rotzler, M. Neuburger and M. Mayor, Eur. J. Org. Chem., 2009, 120–133.
52. S. Berger and S. Braun, 200 and More NMR Experiments: A Practical Course; 1. Aufl., Wiley-VCH Verlag GmbH & Co. KGaA, 2004.
53. M. Hesse, H. Meier and B. Zeeh, Spektroskopische Methoden in der Organischen Chemie; 7., überarb. Aufl., Thieme, Stuttgart, 2005.
54. H. Friebolin, Ein- und zweidimensionale NMR-Spektroskopie; 3. Aufl., Wiley-VCH, 1999.
55. M. Oki, Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH Pub, 1985.
56. Program Package for ab initio Electronic Structure Calculations. TURBOMOLE, Version 6.3; a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH 1989–2007, Turbomole GmbH since 2007, http://www.turbomole.com.
57. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
58. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
59. A. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
60. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
61. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
62. M. P. Johansson and J. Olsen, J. Chem. Theor. Comput., 2008, 4, 1460–1471.
63. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
64. O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354.
65. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
66. K. Marjani, Spectrochim. Acta A, 2011, 79, 1798–1802.
67. S. Toyota, Bull. Chem. Soc. Jpn., 2000, 73, 2591–2597.
68. H. H. Jaffé, Chem. Rev., 1953, 53, 191–261.
69. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
70. H. Hart and E. A. Sedor, J. Am. Chem. Soc., 1967, 89, 2342–2347.
71. F. Kita, W. Adam, P. Jordan, W. M. Nau and J. Wirz, J. Am. Chem. Soc., 1999, 121, 9265–9275.
72. C. G. Swain and E. C. Lupton, J. Am. Chem. Soc., 1968, 90, 4328–4337.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ob26243f

‡ All authors contributed equally to this publication.

---