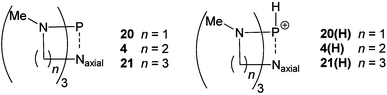The formation of high-purity isocyanurate through proazaphosphatrane-catalysed isocyanate cyclo-trimerisation: computational insights†
Received
6th August 2012
, Accepted 7th November 2012
First published on
8th November 2012
Abstract
Polyurethane foams are widely used materials and control of their physical properties is a significant challenge. Management of cyclo-trimerisation during the polymerisation process is vital when tailoring the mechanical properties of the foam. Proazaphosphatranes are known to efficiently catalyse the cyclo-trimerisation of organic isocyanates, giving high purity isocyanurate with little uretdione by-product. The mechanism of this catalysis was previously unknown, although some zwitterionic intermediates have been identified spectroscopically. We have investigated a nucleophilic-catalysis reaction pathway involving sequential addition of methyl isocyanate to activated zwitterionic intermediates using density functional theory calculations. Evidence for significant transannulation by the proazaphosphatrane nitrogen was found for all intermediates, offering stabilisation of the phosphonium cation. Steric crowding at the proazaphosphatrane nucleophilic phosphorus gives rise to a preference for direct isocyanurate formation rather than via the uretdione, in sharp contrast to the uncatalysed system which has been found to preferentially proceed via the kinetic uretdione product. The investigations suggest the mechanism of proazaphosphatrane catalysed cyclo-oligomerisation does not proceed via the uretdione product, and hence why little of this impurity is observed experimentally.
Introduction
Polyurethane foam is a polymeric foam formed by exploitation of organic isocyanate's reactivity towards alcohol and water, to give the urethane linkage and carbon dioxide, respectively. The carbon dioxide produced by the reaction of isocyanate and water swells the polymer matrix into a strong, porous structure, with a range of foam densities accessible by varying the water content of the reacting mixture. Polyurethane foam formation involves many competing reactions (Fig. 1), with polymerisation occurring as a result of isocyanate and polyol multifunctionality and biuret, allophanate and isocyanurate formation.
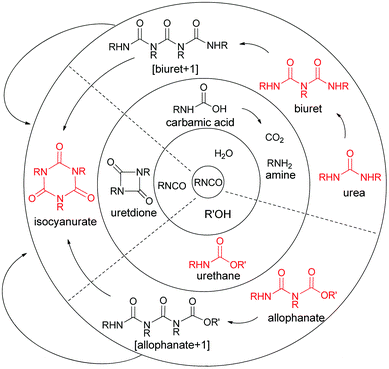 |
| | Fig. 1 Competing reactions in polyurethane foam formation. R and R′ are polyfunctional and so these reactions lead to polyurethane. Sites of branching in the red structures are responsible for the majority of the crosslinks in the polymer.‡ | |
Applications of polyurethane foam include thermal insulation (for low density foams) and as a structural material (for high density foams). As the thermomechanical properties of polyurethane foam are heavily influenced by the relative levels of the reaction products formed, knowledge of their control is integral to the intelligent design of novel foams. The density of covalent crosslinks introduced into the polymer matrix is considered an important parameter linked to the mechanical strength of the foam.1
Dimer (uretdione, UD) and trimer (isocyanurate, ICU) formation from cyclo-oligomerisation of organic isocyanates has been well documented, with the latter used to increase crosslink density in polyurethane foams,2 and in activating and crosslinking polymerisation reactions.3,4 The formation of high purity isocyanurate while avoiding uretdione contamination has become a significant challenge, with uretdione known to significantly hamper the activating ability of isocyanurate in the anionic polymerisation of ε-caprolactam to polyamide.5,6
Cyclo-trimerisation of isocyanate1 to isocyanurate 3 is known to occur spontaneously (Scheme 1), although many catalysts have been developed to catalyse the reaction. Conventional amine bases can catalyse the reaction but often significant levels of uretdione by-products 2 are observed.7–9 The discovery of the strong non-ionic bases proazaphosphatranes (4–7) heralded the possibility of producing isocyanurates in an unprecedentedly high purity.10,11 Although proazaphosphatranes effectively catalyse various reactions,12–14 it is their cyclo-trimerisation of isocyanates that shows them to be remarkably efficient catalysts,15 giving isocyanurate with very low levels of the cyclic dimer uretdione, quickly and at low catalyst loadings (typically 0.1 mol%, see ESI† for catalytic activities).16
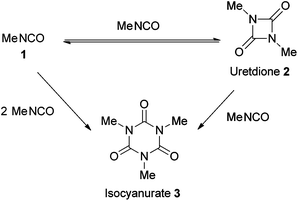 |
| | Scheme 1 Uncatalysed methyl isocyanate cyclo-oligomerisation. | |
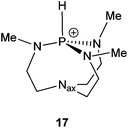
The Lewis basicities of proazaphosphatranes are very high, typically possessing pKa values over 30, due to the stabilisation of the protonated species offered by electron density donation by the phosphorus’ flanking nitrogens and, more dramatically, transannulation of the cationic phosphorus by the basal/axial nitrogen.17 The geometry of this protonated species could foreseeably lead to multiple geometries, varying in the degree of transannulation, including pro-atranes A, quasi-atranes B and atranes C (Fig. 2).14 X-ray derived P–Nax distances have been used to deduce that substituted proazaphosphatrane species invariably occupy B, C or borderline B/C geometries (see ESI†).18–24
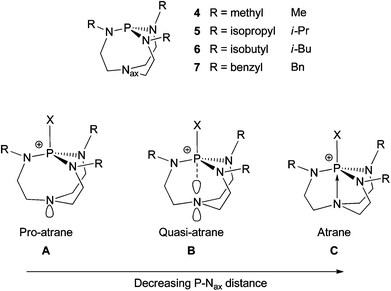 |
| | Fig. 2 Proazaphosphatrane geometry change due to transannulation. | |
The mechanism of proazaphosphatrane catalysed cyclo-trimerisation has been suggested to involve the formation of zwitterionic intermediates (8–10) in a stepwise fashion (Scheme 2),15,25 finally forming the linear activated trimer 10 before ring closing to form the isocyanurate product 3. It is also possible that uretdione 2 acts as an intermediate, reacting with the initial zwitterionic intermediate 8 to form 10. Evidence for an initial intermediate similar to 8 has been obtained from 31P NMR and MS experiments on a phenyl isocyanate system catalysed by proazaphosphatrane 4.15 The initial zwitterionic intermediate of a related, tri-n-butylphosphine catalysed system was also characterised using low temperature 31P NMR,26 lending credence to the zwitterionic mechanism proposed (rather than a metallacyclic mechanism) for palladium(0)-catalysed isocyanate trimerisation.27 A recently proposed reaction pathway for disilazane catalysed isocyanate cyclo-trimerisation also points towards the formation of activated intermediates in a sequential fashion.28 In an effort to understand the selective formation of isocyanurate in proazaphosphatrane catalysed reactions, we decided to undertake a computational study of both the uncatalysed and proposed catalytic mechanisms.
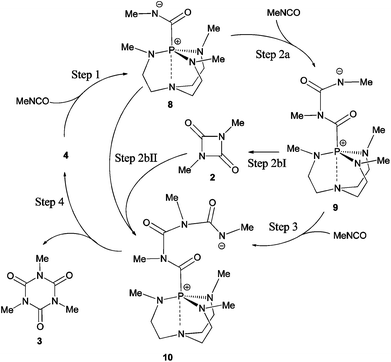 |
| | Scheme 2 Proposed nucleophilic catalysis stepwise mechanisms for cyclo-oligomerisation of methyl isocyanate by proazaphosphatrane 4. | |
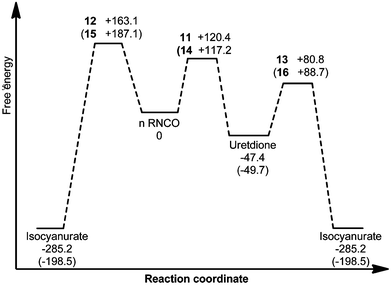 |
| | Fig. 3 Free energy reaction profile (kJ mol−1) for various intermediates and transition states of uncatalysed methyl isocyanate cyclo-oligomerisation. Barriers derived from gas phase geometry Gibbs free energies (B3LYP/6-31G**) corrected with PBF toluene phase (ε = 2.4) energies calculated at the M05-2X/6-31G** level. PhNCO values are given in parentheses. | |
Computational methods
Density functional theory (DFT) calculations were performed using the Jaguar 7.5 computational chemistry package.29 Default convergence criteria, medium grid density and a quick accuracy level were used throughout, employing the 6-31G** basis set,30,31 and the B3LYP hybrid functional,32–34 or the exchange-correlation functional M05-2X.35 The conformational space of each stationary point was thoroughly assessed using Macromodel 9.7 conformational searches.36 All ground and transition states were fully optimised, unconstrained and verified by vibrational frequency analysis. All quoted energies and energy differences were zero point energy (ZPE) corrected (scaled by 0.9).37
Transition structures were confirmed to link the appropriate minima via the quick (QRC),38 or intrinsic reaction coordinate (IRC) method,39 as well as visual assessment of the single imaginary frequency. Single point energy calculations were carried out on stationary point geometries at the M05-2X/6-31G** level, and used to correct the B3LYP derived Gibbs free energy. The effect of toluenesolvent (ε = 2.4) was considered by the implicit Poisson–Boltzmann model,40 using a polarisable continuum dielectric solvent in Jaguar.41,42
Results and discussion
Uncatalysed isocyanate cyclo-oligomerisation
The uncatalysed cyclo-dimerisation and cyclo-trimerisation of methyl isocyanate was investigated by DFT. The split-valence polarised 6-31G** basis set,30,31 and the well established,32,33 B3LYP exchange correlation hybrid functional were used. The mechanisms were also investigated using the highly parameterised empirical exchange-correlation functional M05-2X, to better describe non-covalent interactions.35
Reactant complexes, products and transition structures were found for the concerted cyclo-dimerisation and -trimerisation of methyl isocyanate (MeNCO) using both B3LYP/6-31G** and M05-2X/6-31G** methods (Table 1). The root mean square deviation (RMSD) in transition structure geometries of uretdione and isocyanurate formation calculated using the different methods was found to be 0.182 and 0.840 Å, respectively. Comparison of reaction barriers suggested B3LYP/6-31G** to be sufficient for describing stationary point geometries, and that the using an M05-2X enthalpy correction on the B3LYP Gibbs free energy gave similar results to using M05-2X for exploring geometries, as has been previously noted.43 The method of calculating the M05-2X corrected Gibbs free energy, G“M05-2X” is shown in eqn (1).
| | 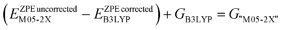 | (1) |
Table 1 Gas phase reaction barriers calculated using different functionals with the 6-31G** basis set. (i) B3LYP (ii) M05-2X (iii) opt. (B3LYP) and M05-2X enthalpy correction)
| |
ΔE‡/kJ mol−1 |
ΔG‡/kJ mol−1 |
| (i) |
(ii) |
(iii) |
(i) |
(ii) |
(iii) |
| 2 MeNCO → UD |
124.7 |
114.3 |
113.2 |
134.5 |
130.8 |
164.0 |
| 3 MeNCO → ICU |
173.7 |
151.1 |
141.1 |
195.6 |
161.5 |
258.5 |
| Δ(ICU-UD) |
49.0 |
36.8 |
27.9 |
62.6 |
30.6 |
94.5 |
The mechanisms of uncatalysed methyl and phenyl isocyanate cyclo-oligomerisation were therefore investigated at the B3LYP/6-31G** level, with subsequent correction of free energies with M05-2X/6-31G** single-point calculations (Fig. 3). Pathways going directly to the isocyanurate and indirectly via the uretdione were considered. No evidence of a stepwise mechanism was found, all geometries discussed here correspond to a concerted mechanism. Calculated transition structures are shown in Fig. 4 and all possess a single imaginary frequency relating to the reaction coordinate (as confirmed by QRC or IRC). Solvent (toluene) effects were considered by using M05-2X/6-31G** solvent phase energy calculations on the gas phase geometries to correct the B3LYP solvent phase Gibbs free energy. Little structural difference between methyl and phenyl isocyanate transition structures was observed (Table 3). Comparison of reaction barriers (Table 2) shows the formation of the thermodynamic cyclic trimer isocyanurate product preferentially occurs via the cyclic dimer uretdione product, which provides an ‘energetic stepping stone’ between stationary points. This energetic preference to proceed via the uretdione product is relatively independent of solvation, the free energy reaction pathways differing by 41.5 and 42.7 kJ mol−1 in the gas and toluene phase (for methyl isocyanate), respectively. This lack of solvation effect can be rationalised by considering the relatively apolar nature of the transition structures.
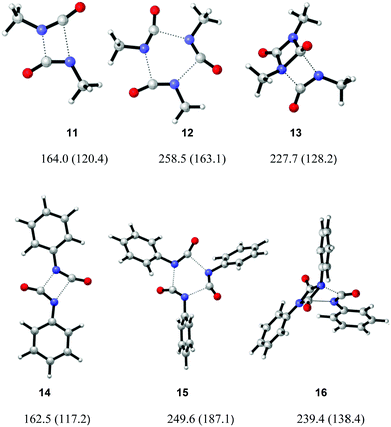 |
| | Fig. 4 Transition structures for the uncatalysed cyclo-oligomerisation of methyl and phenyl isocyanate. Geometries calculated at the B3LYP/6-31G** level, gas phase (toluene phase) free energy barriers (ΔG‡) from M05-2X/6-31G** corrected calculations. | |
Table 2 Reaction barriers for the uncatalysed cyclo-oligomerisation of methyl and phenyl isocyanate (B3LYP/6-31G**). Calculated using (i) B3LYP/6-31G** (ii) B3LYP/6-31G** geometries and solvent phase Gibbs free energy with M05-2X/6-31G** correction. PBF toluene values in parentheses
| R |
Reactants |
TS |
P |
ΔE‡/kJ mol−1 |
ΔG‡/kJ mol−1 |
iFreq/cm−1 |
| (i) |
(ii) |
(i) |
(ii) |
(i) |
| Me |
2 MeNCO |
11
|
2
|
124.7 (120.2) |
113.2 (107.8) |
134.5 (132.9) |
123.0 (120.4) |
i429.2 |
| Me |
3 MeNCO |
12
|
3
|
173.7 (176.1) |
141.1 (143.4) |
197.1 (195.8) |
164.5 (163.1) |
i402.2 |
| Me |
2 + MeNCO |
13
|
3
|
145.8 (139.0) |
118.4 (111.1) |
167.6 (156.2) |
140.2 (128.2) |
i276.3 |
| Ph |
2 PhNCO |
14
|
2(Ph)
|
122.5 (122.7) |
105.0 (105.3) |
133.5 (134.6) |
116.1 (117.2) |
i246.2 |
| Ph |
3 PhNCO |
15
|
3(Ph)
|
210.0 (206.8) |
167.0 (163.2) |
226.8 (230.7) |
180.1 (187.1) |
i430.7 |
| Ph |
2(Ph) + PhNCO |
16
|
3(Ph)
|
164.5 (160.2) |
136.2 (131.7) |
185.5 (166.9) |
152.7 (138.4) |
i305.3 |
Table 3 Geometric comparison of uretdione and isocyanurate forming transition structures. The atoms used to calculate RMSD value are those reacting (isocyanate N, C) and those immediately connected (isocyanate O, methyl or phenyl C)
| |
TS |
NC distance/Å |
RMSD/Å |
Me ESP partial charge |
| Me |
Ph |
Me |
Ph |
N |
C |
| 2RNCO |
11
|
14
|
1.27 |
1.27 |
0.156 |
−0.41 |
0.58 |
| 3RNCO |
12
|
15
|
1.25 |
1.27 |
1.887 |
−0.49 |
0.67 |
|
2 + RNCO |
13
|
16
|
1.30 |
1.30 |
2.224 |
— |
— |
We are aware of only one previous computational study investigating uretdione and isocyanurate formation (although alternative, non-direct, pathways were not investigated).44 Comparison of our transition structures with those of Okumoto and Yamabe suggest similar geometries were found for the direct cyclo-dimerisation and cyclo-trimerisation of methyl isocyanate (Table 4), with our calculations also providing an energetically preferable, though indirect, route via the uretdione.
Table 4 Geometric and energetic comparison of gas phase transition structures obtained via computational methods in this study and that of Okumoto and Yamabe
| |
This work B3LYP/M05-2X |
Okumoto and Yamabe RHF/6-31G*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
| N–C I |
N–C II |
ΔE‡ |
N–C I |
N–C II |
ΔE‡ |
| 2MeNCO → UD |
1.27 |
2.00 |
113.2 |
1.27 |
1.91 |
164.8 |
| 3MeNCO → ICU |
1.25 |
2.13 |
141.1 |
1.26 |
1.98 |
242.3 |
Computational investigation of proazaphosphatrane catalysed systems
The calculation of proazaphosphatrane structures is known to be sensitive to the computational method used, with HF and DFT/B3LYP methods24,45 overestimating P–Nax distances in comparison to X-ray values. It has been shown that the MP2 method gives structures that are geometrically closer to experimental values,24,45 although our DFT/B3LYP and DFT/M05-2X derived structures (entries 1 and 5, respectively) display a reasonable agreement with experimental X-ray P–Nax values (Table 5). LMP2 calculations were found to take a prohibitively long time (see ESI†). A slight over-estimation of P–Nax distance may indeed be more representative of the solvent phase geometries investigated.
Table 5 Structural information of protonated proazaphosphatrane 17 calculated at various levels. No counter anion considered (gas phase)
|
|
| Entry |
Level |
PNax/Å |
PH/Å |
Av. NPN/° |
RMSD/Å |
|
Ref. 20.
BF4− counter anion.
|
| 1 |
B3LYP/6-31G** |
2.091 |
1.406 |
119.3 |
|
| 2 |
B3LYP/6-31G**++ |
2.103 |
1.407 |
119.3 |
0.0246 |
| 3 |
B3LYP/6-311G**++ |
2.097 |
1.407 |
119.3 |
0.0563 |
| 4 |
LMP2/6-31G** |
2.076 |
1.393 |
119.3 |
0.1776 |
| 5 |
M05-2X/6-31G** |
2.066 |
1.406 |
119.3 |
0.0446 |
| 6 |
Cryst. expt.a,b |
1.967 |
|
|
|
As proazaphosphatrane-containing structures are invariably rather large systems, the reaction of 4 with MeNCO was initially characterised at various levels to assess the optimal level to use for further reactions (Table 6). There is significant literature precedent for the use of the 6-31G** basis set in related zwitterionic phosphorus-46,47 and nitrogen-containing systems.48 Due to the significantly polar nature of some species in the reaction (namely the activated isocyanate species 8) the effect of adding diffuse functions was assessed using the 6-31G**+ basis set. The M05-2X functional, which has been shown to be proficient at investigating intramolecular interactions,49 mechanisms50,51 and mechanistic preferences,52 was also investigated.
Table 6 Barriers for the reaction of proazaphosphatrane 4 and MeNCO obtained at different levels
|

|
| Level |
ΔE‡/kJ mol−1 |
ΔG‡/kJ mol−1 |
| B3LYP/6-31G** |
54.03 |
68.79 |
| B3LYP/6-31G**+ |
55.13 |
52.16 |
| M05-2X/6-31G** |
45.37 |
50.29 |
| M05-2X/6-31G** (corr.) |
40.08 |
54.84 |
Results suggest the 6-31G** basis set to be sufficient for describing proazaphosphatrane system geometries, with the diffuse functions making little difference in reaction barriers and only serving to cause convergence difficulties. Literature precedent exists for the use of similar basis sets for investigation of proazaphosphatrane systems.53 Comparison of M05-2X geometries/energies and B3LYP derived geometries with a subsequent M05-2X single-point energy correction, suggest the latter, less computationally intensive method to be sufficient for characterising the reactions in question (Table 6), in a similar fashion to the uncatalysed cyclo-oligomerisation investigated earlier. Furthermore the transition structure calculated using M05-2X was found to have a small (i8 cm−1) imaginary frequency in addition to the larger frequency (i174 cm−1) corresponding to the reaction coordinate. This small imaginary frequency withstood multiple optimisation attempts. Hence all further reactions were characterised using B3LYP/6-31G** geometries with subsequent M05-2X single point energy calculations in the gas and toluene phases to correct the Gibbs free energy.
Bicyclic phosphines other than proazaphosphatrane (20, 21), differing by the number of methylene units in the rings and hence ring size formed upon quasi-atrane or atrane geometry adoption, were investigated. Comparison of optimised neutral and protonated species (Table 7) suggests transannulation to be more pronounced in proazaphosphatranes than in the other bicyclic phosphines, quantified by measurement of the P–Naxial distance. Perhaps unsurprisingly the formation of the four-membered ring in 20(H) was shown to be significantly less favoured than the six-membered ring in 21(H). The relative stability of the protonated bicyclic phosphines also gave an indication of the degree of transannulation, with 4 changing in energy by 97 kJ mol−1 more than 21. The protonated species differ not only in P–Nax distance but also in the geometry of the phosphorus, with the protonated proazaphosphatrane displaying a much more planar arrangement (note the average N–P–N angle). Significant N–P transannulation changes the phosphorus geometry from tetrahedral (20(H) NPN = 107.6°) to trigonal bipyramidal (4(H) NPN = 119.3°).
Table 7 Geometric and energetic comparison of bicyclic phosphines, neutral (N) and protonated (P). Gas phase derived geometries calculated at the B3LYP/6-31G** level, with M05-2X single point energies
|
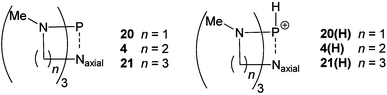
|
| Species |
n
|
P–Naxial/Å |
P–H/Å |
Av. N–P–N/° |
ΔEprotonat/kJ mol−1 |
| N4P |
N4PH |
Diff. |
N4PH |
N4PH |
|
20
|
1 |
2.73 |
2.49 |
0.24 |
1.396 |
107.6 |
−948.6 |
|
4
|
2 |
3.11 |
2.09 |
1.02 |
1.406 |
119.3 |
−1163.4 |
|
21
|
3 |
3.79 |
2.96 |
0.83 |
1.419 |
115.0 |
−1066.4 |
Mechanism of proazaphosphatrane catalysed isocyanate cyclo-oligomerisation
Likely reactant, zwitterionic intermediate and product geometries involved in the reaction of proazaphosphatrane 4 and MeNCO were calculated at the B3LYP/6-31G** level. Transition structures (Fig. 5) corresponding to all steps shown in Scheme 2 were also found. These calculations suggest that uretdione and isocyanurate formation occur via a stepwise mechanism involving initial formation of the corresponding proazaphosphatrane-activated isocyanate dimer and trimer, respectively (Table 8). Gas (and toluene) phase reaction barriers show the formation of isocyanurate proceeds via the activated-trimer 10, which can either be derived from the reaction of 8 + uretdione (27 ΔG‡ = 56.3 (48.9) kJ mol−1) or 9 + MeNCO (24 ΔG‡ = 50.1 (45.6) kJ mol−1).
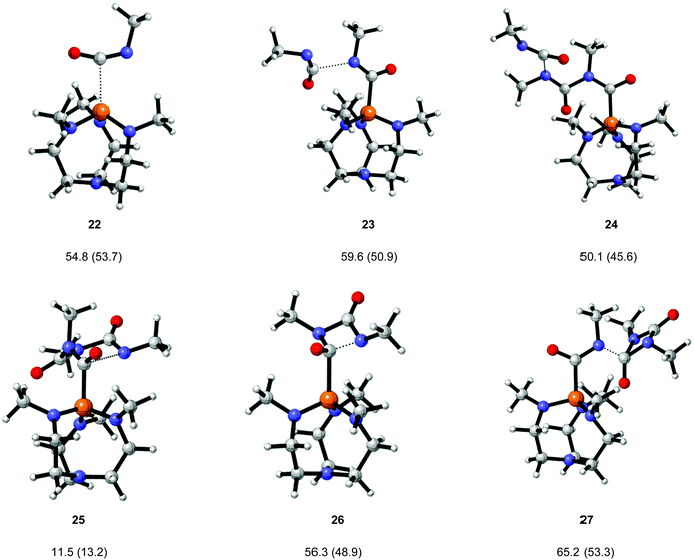 |
| | Fig. 5 Transition structures for the proazaphosphatrane catalysed cyclo-oligomerisation of methyl isocyanate. Geometries calculated at the B3LYP/6-31G** level, gas phase (toluene phase) free energy barriers (ΔG‡) from M05-2X correction. | |
Table 8 Reaction barriers and geometric parameters for methyl isocyanate cyclo-oligomerisation catalysed by proazaphosphatrane 4. All geometries calculated at the (i) B3LYP/6-31G** level (gas phase) (ii) with single-point energy corrections at the M05-2X/6-31G** level. PBF toluene values in parentheses
| Step |
Reactant |
TS |
P |
ΔE‡/kJ mol−1 |
ΔG‡/kJ mol−1 |
iFreq/cm−1 |
r(TS P–Nax)/Å |
| (i) |
(ii) |
(i) |
(ii) |
(i) |
| 1 |
4 + MeNCO |
22
|
8
|
54.0 |
40.1 (39.0) |
68.8 |
54.8 (53.7) |
i160.2 |
3.338 |
| 2a |
8 + MeNCO |
23
|
9
|
63.2 |
46.4 (37.6) |
76.4 |
59.6 (50.9) |
i196.1 |
3.084 |
| 3 |
9 + MeNCO |
24
|
10
|
48.7 |
38.7 (34.2) |
60.1 |
50.1 (45.6) |
i180.3 |
3.057 |
| 4 |
10
|
25
|
3 + 4 |
8.2 |
6.0 (7.7) |
13.6 |
11.5 (13.2) |
i27.3 |
3.072 |
| 2bI |
9
|
26
|
2
|
41.3 |
61.1 (53.8) |
36.5 |
56.3 (48.9) |
i118.0 |
3.258 |
| 2bII |
8 + 2 |
27
|
10
|
85.7 |
37.6 (25.8) |
113.3 |
65.2 (53.3) |
i173.5 |
3.062 |
In stark contrast with the uncatalysed system, the reaction profile (Fig. 6) suggests that the proazaphosphatrane catalysed system proceeds directly via linear activated oligomers (8–10) rather than via the uretdione 2. This mechanistic preference can be rationalised by consideration of the more severe steric congestion around the phosphorus centre in the uretdione transition structure 26 than in that proceeding to the activated linear trimer 24. It is suggested that increasing the size of the substituent on the proazaphosphatrane quasi-equatorial nitrogens (i.e.5 and 6) would lead to an even greater reduction in uretdione impurities, a particularly important factor when the isocyanurate is to be used as an anionic polymerisation activator.
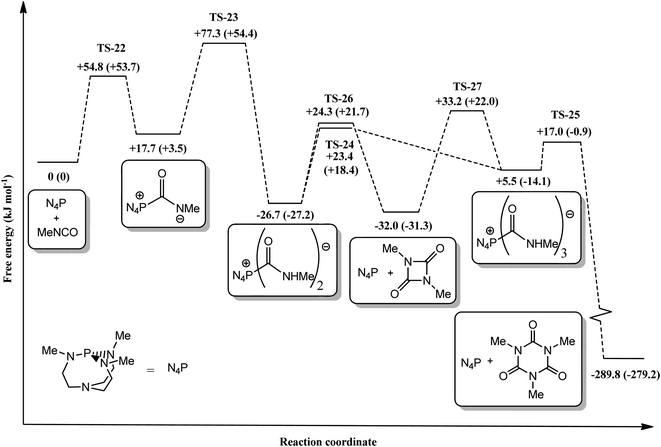 |
| | Fig. 6 Free energy reaction profile (kJ mol−1) depicting the various intermediates and transition states involved in the cyclo-oligomerisation of methyl isocyanate catalysed by proazaphosphatrane 3. All geometries calculated at the B3LYP/6-31G** level (gas phase) with single-point energy corrections at the M05-2X/6-31G** level. PBF toluene values in parentheses. | |
A qualitative assessment of the phosphorus electron density can be found by comparison of transition structure P–Nax distance. In the sequential addition of methyl isocyanate to proazaphosphatrane 4 to form the activated linear oligomers 8–10, assessment of the transition structures 22–24 suggests that the P–Nax distance decreases with increasing system size. This can be rationalised by consideration of the greater charge present on the phosphorus of the larger structures due to the more distant zwitterionic anion (located on the terminal isocyanatenitrogen). All transition structures were found to adopt the quasi-atrane geometry (B, Fig. 2). The activated linear dimer 9 is noted to have a rather high P–Nax distance, indicating transannulation is not occurring to such a degree as in other stationary point geometries. However, the relative energy of the geometry seems not to suffer from this lack of transannulation, mainly due to the stabilising effect brought about by the end isocyanate oxygen (d O–P = 2.06 Å), essentially forming a five membered ring (Fig. 7).
 |
| | Fig. 7 Stabilising interaction observed for the zwitterionic intermediate 9, serving to decrease the degree of transannulation. | |
Conclusions
We have carried out a computational study of the spontaneous and proazaphosphatrane catalysed cyclo-oligomerisation of methyl isocyanate. The uncatalysed cyclo-trimerisation of isocyanate to isocyanurate was found to proceed via the kinetic uretdione product, an energetic stepping stone and impurity. Due to the synchronous and apolar nature of the stationary points involved, solvent effects were shown to be minimal. Investigating the catalysed mechanism proposed by Verkade and co-workers, we predict the reaction proceeds via sequential addition of the isocyanate to the proazaphosphatrane-activated linear oligomer. In contrast to uncatalysed cyclo-oligomerisation, the cyclic dimer uretdione is not the kinetic product, with the reaction instead proceeding directly to the isocyanurate. An investigation of neutral and protonated bicyclic phosphines has suggested that the five-membered atrane ring formed upon Nax–P transannulation is crucial to the high basicity and catalytic potency of the proazaphosphatranes. The use of superbasic proazaphosphatranes as catalysts, therefore, should minimise uretdione formation and lead to polyurethane of high isocyanurate content displaying improved mechanical properties.
Acknowledgements
We gratefully acknowledge the Atomic Weapons Establishment (AWE) for financial support and the continued help of Dr Colin Warriner, Dr Karen Pockett and Dr Kevin Hunt. We also thank Dr David Plant (AWE, Aldermaston) for helpful discussions.
Notes and references
- F. Chambon, Z. S. Petrovic, W. J. MacKnight and H. H. Winter, Macromolecules, 1986, 19, 2146–2149 CrossRef CAS.
- D. W. Duff and G. E. Maciel, Macromolecules, 1991, 24, 651–658 CrossRef CAS.
- C. Han, X. Ran, K. Zhang, Y. Zhuang and L. Dong, J. Appl. Polym. Sci., 2007, 103, 2676–2681 CrossRef CAS.
- A. Matsumoto, Prog. Polym. Sci., 2001, 26, 189–257 CrossRef CAS.
- J. Horsky, U. Kubanek, J. Marick and J. Kralicek, Chem. Prum., 1982, 32, 599–602 CAS.
- Z. Bukac and J. Sebenda, Chem. Prum., 1985, 35, 361–363 CAS.
- H. Ulrich, J. Cell. Plast., 1981, 17, 31–34 CrossRef CAS.
- P. I. Kordomenos and J. E. Kresta, Macromolecules, 1981, 14, 1434–1437 CrossRef CAS.
- D. K. Hoffman, J. Cell. Plast., 1984, 20, 129–137 CrossRef CAS.
- J. Tang, J. Dopke and J. G. Verkade, J. Am. Chem. Soc., 1993, 115, 5015–5020 CrossRef CAS.
- P. B. Kisanga, J. G. Verkade and R. Schwesinger, J. Org. Chem., 2000, 65, 5431–5432 CrossRef CAS.
-
J. Verkade, in New Aspects in Phosphorus Chemistry II, ed. J.-P. Majoral, Springer, Berlin/Heidelberg, 2003, vol. 223, pp. 1–44 Search PubMed.
- J. G. Verkade, Coord. Chem. Rev., 1994, 137, 233–295 CrossRef CAS.
- J. G. Verkade, Acc. Chem. Res., 1993, 26, 483–489 CrossRef CAS.
- J.-S. Tang and J. G. Verkade, Angew. Chem., Int. Ed., 1993, 32, 896–898 CrossRef.
- S. M. Raders and J. G. Verkade, J. Org. Chem., 2010, 75, 5308–5311 CrossRef CAS.
- J. G. Verkade and P. B. Kisanga, Tetrahedron, 2003, 59, 7819–7858 CrossRef CAS.
- V. Galasso, J. Phys. Chem. A, 2004, 108, 4497–4504 CrossRef CAS.
- M. A. H. Laramay and J. G. Verkade, J. Am. Chem. Soc., 1990, 112, 9421–9422 CrossRef CAS.
- C. Lensink, S. K. Xi, L. M. Daniels and J. G. Verkade, J. Am. Chem. Soc., 1989, 111, 3478–3479 CrossRef CAS.
- J. Tang, T. Mohan and J. G. Verkade, J. Org. Chem., 1994, 59, 4931–4938 CrossRef CAS.
- S. K. Xi, H. Schmidt, C. Lensink, S. Kim, D. Wintergrass, L. M. Daniels, R. A. Jacobson and J. G. Verkade, Inorg. Chem., 1990, 29, 2214–2220 CrossRef CAS.
- J. C. Clardy, D. S. Milbrath and J. G. Verkade, Inorg. Chem., 1977, 16, 2135–2137 CrossRef CAS.
- T. Mohan, S. Arumugam, T. Wang, R. A. Jacobson and J. G. Verkade, Heteroat. Chem., 1996, 7, 455–460 CrossRef CAS.
- J. Mizuya, T. Yokozawa and T. Endo, J. Polym. Sci., Part A: Polym. Chem., 1991, 29, 1545–1548 CrossRef CAS.
- Z. Pusztai, G. Vlád, A. Bodor, I. T. Horváth, H. J. Laas, R. Halpaap and F. U. Richter, Angew. Chem., Int. Ed., 2006, 45, 107–110 CrossRef CAS.
- F. Paul, S. Moulin, O. Piechaczyk, P. Le Floch and J. A. Osborn, J. Am. Chem. Soc., 2007, 129, 7294–7304 CrossRef CAS.
- M. Roman, B. Andrioletti, M. Lemaire, J.-M. Bernard, J. Schwartz and P. Barbeau, Tetrahedron, 2011, 67, 1506–1510 CrossRef CAS.
-
Jaguar, version 7.6, Schrödinger, LLC, New York, NY, 2009 Search PubMed.
- P. M. W. Gill, B. G. Johnson, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1992, 197, 499–505 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theor. Comput., 2006, 2, 364–382 CrossRef.
-
MacroModel, version 9.7, Schrödinger, LLC, New York, NY, 2009 Search PubMed.
- R. S. Grev, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1991, 95, 5128–5132 CrossRef CAS.
- J. M. Goodman and M. A. Silva, Tetrahedron Lett., 2003, 44, 8233–8236 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS.
- D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard, J. Am. Chem. Soc., 1994, 116, 11875–11882 CrossRef CAS.
- B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
- L. Simón and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689–700 Search PubMed.
- S. Okumoto and S. Yamabe, J. Comput. Chem., 2001, 22, 316–326 CrossRef CAS.
- J. Kobayashi, K. Goto, T. Kawashima, M. W. Schmidt and S. Nagase, J. Am. Chem. Soc., 2002, 124, 3703–3712 CrossRef CAS.
- N. N. Bhuvan Kumar, M. Chakravarty and K. C. Kumara Swamy, New J. Chem., 2006, 30, 1614–1620 RSC.
- Y. G. Gololobov, M. A. Galkina, O. V. Dovgan, I. Y. Krasnova, P. V. Petrovskii, M. Y. Antipin, I. I. Voronzov, K. A. Lyssenko and R. Schmutzler, Russ. Chem. Bull., 2001, 50, 279–286 CrossRef CAS.
- R. R. Julian, J. L. Beauchamp and W. A. Goddard, J. Phys. Chem. A, 2001, 106, 32–34 CrossRef.
- M. Solimannejad, F. Shahbazi and I. Alkorta, J. Phys. Chem. A, 2010, 114, 9388–9393 CrossRef CAS.
- G. Ghigo, S. Cagnina, A. Maranzana and G. Tonachini, J. Org. Chem., 2010, 75, 3608–3617 CrossRef CAS.
- Y. Li, J.-J. Zou, X. Zhang, L. Wang and Z. Mi, Fuel, 2010, 89, 2522–2527 CrossRef CAS.
- A. Vega-Rodriguez and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2009, 11, 7649–7658 RSC.
- A. K. Phukan and A. K. Guha, Inorg. Chem., 2011, 50, 1361–1367 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates, total energies. See DOI: 10.1039/c2ob26547h |
| ‡ Crossing a solid line signifies reaction with isocyanate. Polymerisation occurs due to the multifunctionality (f ≥ 2) and often branched nature of the isocyanates and polyols used. Matrix crosslinking also arises from allophanate, isocyanurate and biuret formation. |
|
| This journal is © The Royal Society of Chemistry 2013 |
Click here to see how this site uses Cookies. View our privacy policy here. 




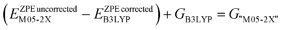

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44
44