Saccharide receptor achieves concentration dependent mannoside selectivity through two distinct cooperative binding pathways†
Stephen
Rieth
,
Matthew R.
Miner
,
Clifford M.
Chang
,
Brisa
Hurlocker
and
Adam B.
Braunschweig‡
*
Department of Chemistry and The Molecular Design Institute, New York University, New York, NY 10003, USA. Fax: +1 212-995-3884; Tel: +1 212-998-8495
First published on 26th September 2012
Abstract
Tetrapodal receptor 1 relies upon structural flexibility to reveal new binding modes for saccharide recognition and to achieve unique pyranoside binding affinity and concentration dependent selectivity. The association constants, Kas, between 1 and eight pyranosides commonly found in cell surface glycans were measured in CDCl3 by 1H NMR titrations, revealing a preference for α- and β-octyl mannopyranosides (α-Man and β-Man). Whereas most of the pyranosides studied – α/β-octyl glucopyranoside (α/β-Glc), α/β-octyl galactopyranoside (α/β-Gal), and α/β-octyl N-acetylglucosaminopyranoside (α/β-GlcNAc) – bind 1 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry at 25 °C, β-Man exclusively forms a 2
1 stoichiometry at 25 °C, β-Man exclusively forms a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor–pyranoside complex. Alternatively, in an excess of pyranoside, 1 binds α- and β-Man in a 1
1 receptor–pyranoside complex. Alternatively, in an excess of pyranoside, 1 binds α- and β-Man in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 receptor
2 receptor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyranoside stoichiometry with a high degree of positive cooperativity (K2/K1 ∼ 13.7 and 7.6 for α- and β-Man respectively) and selectivities as high as 16.8
pyranoside stoichiometry with a high degree of positive cooperativity (K2/K1 ∼ 13.7 and 7.6 for α- and β-Man respectively) and selectivities as high as 16.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 α-Man
1 α-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α-Gal. Moreover, this preference changes as a function of pyranoside concentration, favoring β-Glc at low concentration (<0.1 mM) and favoring mannosides at higher concentrations. The thermodynamic binding parameters (ΔH0 and ΔS0) reveal that the cooperativity in the second binding events drive the formation of 12:β-Man or 1:β-Man2 because of a decrease in unfavorable entropy upon each second binding event compared to the first. The structures of the complexes were determined by 1D and 2D 1H NMR spectroscopy in combination with molecular modeling. The 1:β-Man2 complex exhibits C2 symmetry, where both β-Man equivalents bind identical sites within 1, such that the pyranosides within the complex are symmetrically equivalent. Alternatively, 12:β-Man is a cage-like structure where only three of the aminopyrrolitic arms of the receptor are involved in binding, leaving a fourth available for further functionalization in later generation receptors. Multivalency and cooperativity are ubiquitous in Nature, and 1 utilizes these modes of recognition to achieve selectivity for monosaccharide residues.
α-Gal. Moreover, this preference changes as a function of pyranoside concentration, favoring β-Glc at low concentration (<0.1 mM) and favoring mannosides at higher concentrations. The thermodynamic binding parameters (ΔH0 and ΔS0) reveal that the cooperativity in the second binding events drive the formation of 12:β-Man or 1:β-Man2 because of a decrease in unfavorable entropy upon each second binding event compared to the first. The structures of the complexes were determined by 1D and 2D 1H NMR spectroscopy in combination with molecular modeling. The 1:β-Man2 complex exhibits C2 symmetry, where both β-Man equivalents bind identical sites within 1, such that the pyranosides within the complex are symmetrically equivalent. Alternatively, 12:β-Man is a cage-like structure where only three of the aminopyrrolitic arms of the receptor are involved in binding, leaving a fourth available for further functionalization in later generation receptors. Multivalency and cooperativity are ubiquitous in Nature, and 1 utilizes these modes of recognition to achieve selectivity for monosaccharide residues.
Introduction
Natural saccharide-binding proteins, including lectins and periplasmic substrate-binding proteins, use water desolvation, hydrogen bonding (H-bonding), and C–H⋯π interactions to selectively recognize glycans that may differ only by the orientation of a single hydroxyl group to achieve binding affinities, Kas, as high at 106 M−1.1 Selective carbohydrate recognition with artificial receptors remains a major area of investigation because of the challenge of differentiating between molecules with subtle structural differences, their ability to reveal fundamental aspects of saccharide binding, and their potential applications in disease detection, therapy, or catalysis.2 These receptors employ both covalent and noncovalent interactions to stabilize complexation. For example, the reversible reaction of boronic acids to syn-diols has been employed successfully to selectively bind sugars, such as glucose and ribose, and sugar alcohols, like sorbitol and mannitol,2f,3 but the recognition of monosaccharides possessing axial hydroxyl groups, such as mannose, remains challenging by this approach. Alternatively, by following Cram's principles of electronic complementarity and structural preorganization,4 molecules were created that bind through only noncovalent interactions and do not distort significantly upon binding. In these receptors, recognition groups are rigidly positioned in three dimensional space, like natural lectins,5 to overcome entropy–enthalpy compensation – whereby any favorable enthalpic change that arises from the formation of noncovalent bonds is offset by the entropically unfavorable decrease of the internal motions of host and guest upon binding.6Noteworthy examples of preorganized synthetic saccharide receptors that bind through only noncovalent interactions are the “temple” family of hosts developed by Davis and coworkers and the “tripodal” receptors pioneered by the Roelens7 and Mazik8 groups. The temple receptors position polar amidopyridine groups between apolar aromatic surfaces, and these receptors are highly selective for mono- and disaccharides containing all equatorial hydroxide groups, such as β-glucose (Glc),9 β-N-acetylglucosamine (GlcNAc),10 and β-D-cellobioside11 in water. The tripodal receptors rely upon a 1,3,5-triethylbenzene scaffold to rigidly orient three aminopyrrolitic arms that can form H-bonds with saccharide hydroxyl groups. The preorganization induced by the three ethyl arms adds an estimated 4.5 kcal mol−1 in additional stabilization upon complexation.12 The tripodal receptors bind strongly to glycosides with an affinity of 102 to 105 M−1 in chloroform and acetonitrile, and by changing to a chiral diaminopyrrolic motif, high selectivity for octyl mannosides in acetonitrile has been observed, ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 β-GlcNAc
7 β-GlcNAc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α-Man to 1
α-Man to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 α-Gal
38 α-Gal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β-Man.7c Mannose is a particularly interesting monosaccharide target because it is a biomarker for several cancers,13 and as a consequence developing mannose specific synthetic receptors remains an active area of research.7a,c–e,g,14 However, synthetic carbohydrate receptors with increased binding affinity, expanded substrate scope beyond all-equatorial glycosides, and increased selectivity to levels comparable with their biological counterparts are still needed before these receptors become more widely utilized.
β-Man.7c Mannose is a particularly interesting monosaccharide target because it is a biomarker for several cancers,13 and as a consequence developing mannose specific synthetic receptors remains an active area of research.7a,c–e,g,14 However, synthetic carbohydrate receptors with increased binding affinity, expanded substrate scope beyond all-equatorial glycosides, and increased selectivity to levels comparable with their biological counterparts are still needed before these receptors become more widely utilized.
To address these challenges, we have chosen to pursue an alternate design approach towards synthetic saccharide receptors that involves preparing a flexible host that does not possess rigid preorganization and as a result is capable of binding carbohydrates through pathways that arise from conformational rearrangements and positive homotropic cooperativity. Homotropic cooperativity – whereby an initial association of a target substrate induces conformational restrictions that enhance further binding of the same substrate – has been employed previously in synthetic receptors to increase binding strength towards targets such as diacids and syn-diols.15 However, synthetic receptors that utilize homotropic cooperativity remain rare,16 and few examples exist of hosts that rely upon cooperativity to enhance saccharide binding,16d,q,r despite the fact that cooperativity and multivalency are ubiquitous elements of carbohydrate recognition in biology.1a The advantages that could arise with carbohydrate receptors that employ positive allosteric cooperativity include (1) shorter synthetic sequences because specificity and affinity are the direct result of allostery, (2) increased solubility associated with receptor flexibility, and (3) employing the same binding mechanisms as natural saccharide receptors could provide fundamental insights into the complex carbohydrate recognition motifs that are prevalent in nature. To this end, we have designed receptor 1 that contains the aminopyrrolitic groups pioneered by Roelens,7b,f but they are appended to a flexible scaffold with eight freely rotating methylene groups and a freely rotating biphenyl bond (Fig. 1). Thus, 1 is designed to dynamically explore thermodynamic and conformational space and confirm that increased receptor flexibility can induce specificity for carbohydrate guests through allostery despite a higher entropic penalty experienced in an initial association step. Through the use of 1H NMR titrations, we found that 1 achieves excellent selectivity for octyl mannosides through two allosteric cooperative pathways (Fig. 2) with an overall selectivity as high as 16.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 α-Man
1 α-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α-Gal in chloroform. Moreover, the selectivity is directly dependent on pyranoside concentration, where 1 binds preferentially to β-Glc at low pyranoside concentration (<0.3 mM), then binds α- and β-Man at higher pyranoside concentrations. To the best of our knowledge, 1 is the first synthetic carbohydrate receptor that (1) relies on cooperativity to increase selectivity and (2) whose selectivity switches with saccharide concentration.
α-Gal in chloroform. Moreover, the selectivity is directly dependent on pyranoside concentration, where 1 binds preferentially to β-Glc at low pyranoside concentration (<0.3 mM), then binds α- and β-Man at higher pyranoside concentrations. To the best of our knowledge, 1 is the first synthetic carbohydrate receptor that (1) relies on cooperativity to increase selectivity and (2) whose selectivity switches with saccharide concentration.
 | ||
| Fig. 1 Structures of 1 (blue) and octyl pyranosides (red), with carbon numbering scheme, whose binding with 1 was studied. | ||
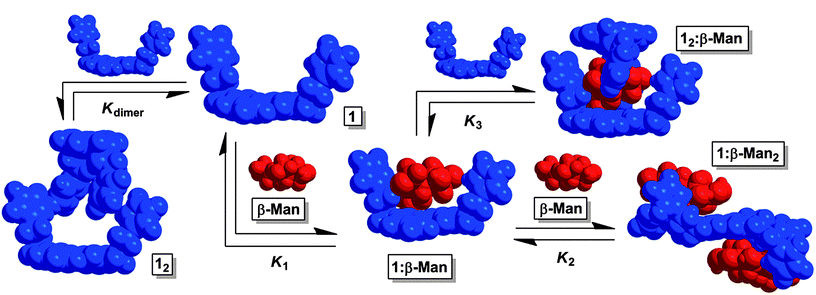 | ||
Fig. 2 The equilibria present in a chloroform mixture of 1 and β-Man at 25 °C. Upon increasing the β-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, K2 determines the dominant species in solution. If instead, β-Man 1 ratio, K2 determines the dominant species in solution. If instead, β-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 decreases, K3 controls the equilibrium mixture. 1 decreases, K3 controls the equilibrium mixture. | ||
Results and discussion
Pyranoside binding
Receptor 1 was prepared in a five step synthetic sequence in a 64% overall yield.17 The binding affinity and selectivity of 1 for eight octyl pyranosides (Fig. 1), which were chosen as guests because they are common terminal residues found on cell surface glycoconjugates and are used as standards for assaying synthetic receptor selectivity,1a,18 were investigated by variable temperature 1H NMR titrations in CDCl3. Chloroform facilitates the binding studies of new carbohydrate receptors2b–d,f because the solvent does not compete for H-bonding between host and guest, thereby enhancing polar noncovalent bonds. These titrations revealed that the selectivity of 1 for octyl mannosides arises through a cooperative, multistep equilibrium (Fig. 2). In solution, 1 exists as a dimer, 12, that comes apart to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with the eight pyranosides with little selectivity. Upon altering the 1
1 complexes with the eight pyranosides with little selectivity. Upon altering the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyranoside ratio from 1
pyranoside ratio from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, two new mannoside-selective binding modes emerge that are both the result of positive cooperativity at 25 °C. When the concentration of mannoside is increased, 1
1, two new mannoside-selective binding modes emerge that are both the result of positive cooperativity at 25 °C. When the concentration of mannoside is increased, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 receptor–pyranoside complexes form only with α-Man (1:α-Man2) and β-Man (1:β-Man2). If instead, the concentration of 1 increases with respect to pyranoside, a 2
2 receptor–pyranoside complexes form only with α-Man (1:α-Man2) and β-Man (1:β-Man2). If instead, the concentration of 1 increases with respect to pyranoside, a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor–monosaccharide complex forms only with β-Man (12:β-Man). To understand the origin of the preferential binding of mannosides by 1, these binding stoichiometries and the structures of 12:β-Man, 1:α-Man2, and 1:β-Man2 were established through a variety of 1D and 2D 1H NMR methods, and all values of K1, K2, K3, ΔH0 and ΔS0 were determined for each of these equilibria.
1 receptor–monosaccharide complex forms only with β-Man (12:β-Man). To understand the origin of the preferential binding of mannosides by 1, these binding stoichiometries and the structures of 12:β-Man, 1:α-Man2, and 1:β-Man2 were established through a variety of 1D and 2D 1H NMR methods, and all values of K1, K2, K3, ΔH0 and ΔS0 were determined for each of these equilibria.
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 Receptor
2 Receptor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) pyranoside binding
pyranoside binding
The binding of pyranosides was first studied under conditions where receptor 1 was maintained at a low concentration (<70 μM) to minimize the contribution of the Kdimer and K3 equilibria (Fig. 2).19 Once the values of K1 and K2 were determined, their values were held invariant in subsequent peak shift fittings, which facilitated the quantification of the other Kas. The incremental addition of a 10–12 mM solution of each of the eight octyl pyranoside to a dilute solution of 1 (58.6 μM) induced changes in the 1H NMR chemical shifts corresponding to the protons of 1, owing to a fast exchange between bound and unbound substrates on the NMR timescale (Fig. 3A). Notably, the change of mannoside proton chemical shifts, Δδ, was significantly greater than the other pyranosides, suggesting that the overall binding free energy, ΔG0, was greater for mannosides than other pyranosides (Fig. 3B). When the observed chemical shifts were plotted against the molar equivalents of pyranoside (Fig. 3C), the observed perturbations for the mannoside protons follow a sigmoidal pattern, indicating that multiple equilibria in addition to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation are occurring in the titration.20 The titration induced peak shifts occurring upon addition of both anomers of glucose (α/β-Glc), galactose (α/β-Gal), and N-acetylglucosamine (α/β-GlcNAc) produced no such sigmoidal curve and instead follow the hyperbolic shape of a 1
1 complexation are occurring in the titration.20 The titration induced peak shifts occurring upon addition of both anomers of glucose (α/β-Glc), galactose (α/β-Gal), and N-acetylglucosamine (α/β-GlcNAc) produced no such sigmoidal curve and instead follow the hyperbolic shape of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding isotherm (Fig. 3B).21 Since the concentration of pyranosides was intentionally kept low to prevent the formation of micelles, the saturation region of the binding isotherm was only reached for the mannosides (Fig. 3C), thus K1 could not be determined for the other pyranosides from these experiments, although we were able to obtain these values by titrating 1 into solutions of pyranoside (presented in the next section).
1 binding isotherm (Fig. 3B).21 Since the concentration of pyranosides was intentionally kept low to prevent the formation of micelles, the saturation region of the binding isotherm was only reached for the mannosides (Fig. 3C), thus K1 could not be determined for the other pyranosides from these experiments, although we were able to obtain these values by titrating 1 into solutions of pyranoside (presented in the next section).
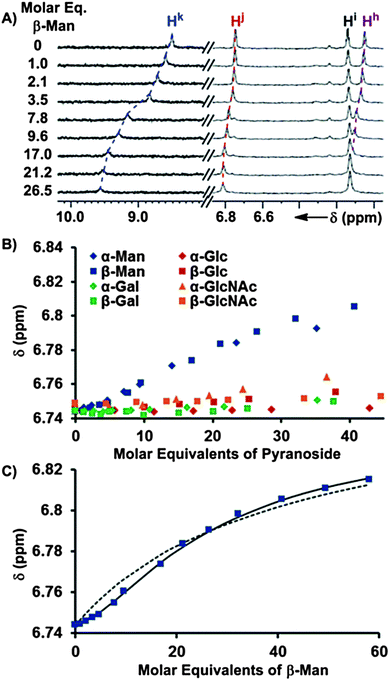 | ||
| Fig. 3 (A) 1H NMR (600 MHz, CDCl3, 25 °C) spectra obtained after the incremental addition of a 10.4 mM solution of β-Man to a 58.6 μM solution of 1, with dashed lines illustrating the induced changes in chemical shifts. (B) The chemical shift dependences of Hj of 1 (58.6 μM) is plotted as a function of molar equivalents of each of the eight added pyranosides from the 1H NMR titrations. (C) The fittings of the Hj chemical shift changes in response to the addition of β-Man to a model containing K1 (dashed line) and K1 + K2 (solid line). | ||
The chemical shift changes that occur because of the interaction of 1 with α- and β-Man were subjected to a global nonlinear fitting analysis with a model incorporating Kdimer, K1, and K2. Satisfactory fits to the Δδs were obtained to provide macroscopic Kas, indicating the presence of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 receptor–mannoside complexes 1:α-Man2 and 1:β-Man2.17 For an allosteric receptor possessing two equivalent binding sites, the experimentally measured Kas must be corrected for the existence of two identical 1
2 receptor–mannoside complexes 1:α-Man2 and 1:β-Man2.17 For an allosteric receptor possessing two equivalent binding sites, the experimentally measured Kas must be corrected for the existence of two identical 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intermediates to obtain microscopic association constants that accurately describe the association of each binding site.22 Since there are two identical pathways by which α/β-Man can associate with 1 to form a 1
1 intermediates to obtain microscopic association constants that accurately describe the association of each binding site.22 Since there are two identical pathways by which α/β-Man can associate with 1 to form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, the macroscopic Ka for the first association process was divided by 2 to obtain microscopic association constant K1. Likewise, as there are two identical pathways for dissociation in 1:Man2, the macroscopic Ka for the second association process was multiplied by 2 to obtain microscopic association constant K2 (Table 1). The interaction parameter, α, is the ratio of a microscopic Ka in the presence of cooperativity over its value in the absence of cooperativity, or reference Ka, and is a quantitative measure of cooperativity.22 Since both binding sites are identical, the reference Ka is equivalent to K1 and thus α = K2/K1. An α value greater than 1 indicates that the first association event enhances the second, i.e. positive cooperativity.22 Likewise, the binding is negatively cooperative if α is less than 1, and the binding is non-cooperative if α is equal to 1. From an analysis of the microscopic Kas, α-Man and β-Man were both found to possess α values of 13.7 and 7.6 respectively with receptor 1, indicating that a high degree of positive cooperativity occurs between 1 and both mannosides (Table 1).
1 complex, the macroscopic Ka for the first association process was divided by 2 to obtain microscopic association constant K1. Likewise, as there are two identical pathways for dissociation in 1:Man2, the macroscopic Ka for the second association process was multiplied by 2 to obtain microscopic association constant K2 (Table 1). The interaction parameter, α, is the ratio of a microscopic Ka in the presence of cooperativity over its value in the absence of cooperativity, or reference Ka, and is a quantitative measure of cooperativity.22 Since both binding sites are identical, the reference Ka is equivalent to K1 and thus α = K2/K1. An α value greater than 1 indicates that the first association event enhances the second, i.e. positive cooperativity.22 Likewise, the binding is negatively cooperative if α is less than 1, and the binding is non-cooperative if α is equal to 1. From an analysis of the microscopic Kas, α-Man and β-Man were both found to possess α values of 13.7 and 7.6 respectively with receptor 1, indicating that a high degree of positive cooperativity occurs between 1 and both mannosides (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (upper value), 1
1 (upper value), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (middle value), and 2
2 (middle value), and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (lower value) 1:pyranoside binding stoichiometries determined by NMR titrations and the intrinsic median binding concentration BC050 calculated from Kdimer, K1, K2, and K3 for each pyranoside interacting with 1 in CDCl3 at 25 °C
1 (lower value) 1:pyranoside binding stoichiometries determined by NMR titrations and the intrinsic median binding concentration BC050 calculated from Kdimer, K1, K2, and K3 for each pyranoside interacting with 1 in CDCl3 at 25 °C
| Glycoside | Log K | ΔH0 (kcal mol−1) | ΔS0 (e.u.) | BC 050 (mM) |
|---|---|---|---|---|
| a No detectable binding. b Estimated by extrapolation of a van't Hoff plot with the assumption ΔCp = 0. c Not determined. | ||||
| α-Glc | 2.75 ± 0.04 | −12.5 ± 0.3 | −29 ± 1 | 1.86 ± 0.16 |
| a | — | — | ||
| a | — | — | ||
| β-Glc | 3.16 ± 0.01 | −16.5 ± 0.1 | −41 ± 1 | 0.70 ± 0.02 |
| a | — | — | ||
| 0.39b | −6.6 ± 0.4 | −21 ± 1 | ||
| α-Man | 2.57 ± 0.19 | c | c | 0.46 ± 0.05 |
| 3.71 ± 0.10 | c | c | ||
| a | — | — | ||
| β-Man | 2.46 ± 0.31 | −20.5 ± 0.8 | −57 ± 3 | 0.73 ± 0.10 |
| 3.34 ± 0.11 | −20.2 ± 1.2 | −52 ± 4 | ||
| 2.45 ± 0.09 | −11.0 ± 0.4 | −26 ± 2 | ||
| α-Gal | 2.18 ± 0.02 | −13.1 ± 0.5 | −34 ± 2 | 7.74 ± 0.31 |
| a | — | — | ||
| a | — | — | ||
| β-Gal | 2.59 ± 0.03 | −15.4 ± 0.8 | −40 ± 3 | 2.74 ± 0.18 |
| a | — | — | ||
| a | — | — | ||
| α-GlcNAc | 2.53 ± 0.02 | −11.4 ± 0.2 | −26 ± 1 | 3.18 ± 0.14 |
| a | — | — | ||
| a | — | — | ||
| β-GlcNAc | 2.65 ± 0.05 | −11.8 ± 0.5 | −27 ± 4 | 2.37 ± 0.26 |
| a | — | — | ||
| a | — | — | ||
The thermodynamic origin of this positive allosteric cooperativity in the formation of 1:β-Man2 was investigated by determining ΔH0 and ΔS0 associated with each binding step. The 1H NMR titrations between 1 and β-Man were repeated at 20, 15, and 10 °C, and K1 and K2 values for each temperature were obtained and subjected to van't Hoff analyses (Fig. S23, ESI†) to provide the thermodynamic parameters associated with each binding event. Notably, the ΔH0s of association for the first and second binding step are identical, −20.5 ± 0.8 and −20.2 ± 1.2 kcal mol−1 respectively, suggesting that both equivalents of β-Man bind 1 with an identical number of noncovalent interactions and that the mannosides do not interact with each other when bound to 1. A comparison of the corresponding ΔS0 values indicates a decrease in the unfavorable ΔS0 occurs in the second binding step compared to the first, −52 ± 4 and −57 ± 3 e.u. respectively.17
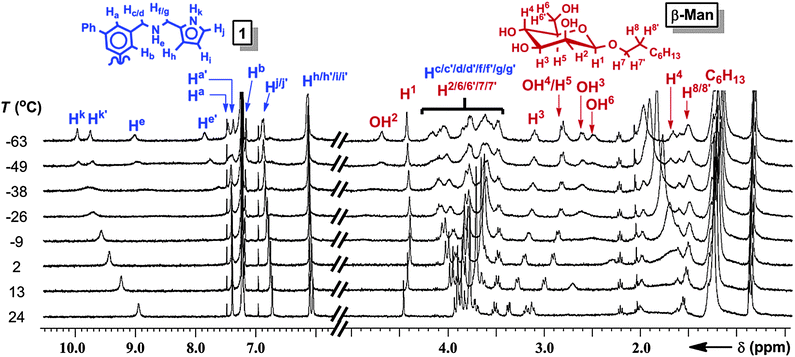
The geometries of 1:β-Man and 1:β-Man2 were determined by 1D and 2D 1H NMR and computational modeling to understand the structural origin of the cooperative binding. The 1H NMR spectrum of a solution of 1 (1 mM) and β-Man (2 mM) in CDCl3 exhibits averaged signals for all protons at 25 °C because of a fast exchange of the signals corresponding to 1, β-Man, 1:β-Man2, and 1:β-Man. Upon cooling, the 1H NMR resonances corresponding to 1, except Hb, decoalesce into two sets of peaks at −40 °C (Fig. 4), indicating a partial desymmetrization occurring with receptor 1. No decoalescence was observed for the resonances corresponding to β-Man upon cooling the solution (Fig. 4), suggesting that both equivalents of β-Man occupy identical chemical environments in the 1:β-Man2 complex. In the absence of β-Man, the signals corresponding to 1 in the 1H NMR spectrum do not decoalesce at low temperature, but rather are broadened.17 Thus, the new signals that arise upon cooling of the mixed sample can be attributed to a complex consisting of 1 and β-Man. A comparison of the 1H NMR spectra at −63 °C with varying ratios of 1:β-Man revealed that the broad signals corresponding to free 1 disappear when more than two molar equivalents of β-Man are present in solution, further confirming the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry of the complex (Fig. S12, ESI†). The two sets of signals observed in the 1H NMR spectrum at −63 °C (Fig. 4) for the receptor and only one for the mannoside, indicate that both pyranosides are bound to two aminopyrrolitic arms of 1 and are symmetrically equivalent, resulting in a 1:β-Man2 complex that exhibits C2 symmetry. A configuration where each mannose binds to two aminopyrrolitic arms on the same aromatic ring would render both Hb protons of receptor 1 symmetrically equivalent, which is consistent with the lack of decoalescence of the Hb peak in 1:β-Man2. The two amine protons, He and He′, shift considerably downfield to 9.1 and 7.9 ppm (Fig. 4), indicating that both protons are involved in H-bonding.23 Likewise, the large complexation-induced shift (CIS) of H4 from 3.7 to 1.2 ppm is consistent with a C–H⋯π interaction between H4 and a phenyl ring of 1. Finally, the 1H–1H ROESY spectrum of the mixture revealed a through-space correlation between the octyl chain (presumably H9) and pyrrole proton Hj′,17 which confirms that the octyl chain of β-Man is within close proximity to one of the aminopyrrolitic arms of 1.
2 stoichiometry of the complex (Fig. S12, ESI†). The two sets of signals observed in the 1H NMR spectrum at −63 °C (Fig. 4) for the receptor and only one for the mannoside, indicate that both pyranosides are bound to two aminopyrrolitic arms of 1 and are symmetrically equivalent, resulting in a 1:β-Man2 complex that exhibits C2 symmetry. A configuration where each mannose binds to two aminopyrrolitic arms on the same aromatic ring would render both Hb protons of receptor 1 symmetrically equivalent, which is consistent with the lack of decoalescence of the Hb peak in 1:β-Man2. The two amine protons, He and He′, shift considerably downfield to 9.1 and 7.9 ppm (Fig. 4), indicating that both protons are involved in H-bonding.23 Likewise, the large complexation-induced shift (CIS) of H4 from 3.7 to 1.2 ppm is consistent with a C–H⋯π interaction between H4 and a phenyl ring of 1. Finally, the 1H–1H ROESY spectrum of the mixture revealed a through-space correlation between the octyl chain (presumably H9) and pyrrole proton Hj′,17 which confirms that the octyl chain of β-Man is within close proximity to one of the aminopyrrolitic arms of 1.
With NMR providing a general understanding of how β-Man sits within 1, a molecular mechanics (AMBER*)24 Monte Carlo conformational search was utilized to model the binding geometry of the 1:β-Man complex. The identical values of ΔH0 that were determined for each binding step and the C2 symmetry observed in the 1H NMR spectrum of the 1:β-Man2 complex indicate that the mannosides occupy identical binding sites on the receptor. Proton H4 was constrained to be within close proximity of the biphenyl ring system in accordance with the experimentally observed C–H⋯π interaction, and the octyl chain was positioned near one arm of 1 with a restricted distance of 2–4 Å between H9 and Hj as dictated by the observed NOE between these two protons. The conformational searches yielded only one minimum energy structure for 1:β-Man, which was further optimized using density functional theory (B3LYP/6-31G+(d)). The resulting calculated structure (Fig. 5A) is in excellent agreement with the experimental 1D 1H NMR data because all polar hydrogens shifted significantly downfield (Hk, Hk′, He, He′, and OH2) in the NMR spectrum participate in H-bonds in the model, and a C–H⋯π interaction is present between H4 and a phenyl ring of 1. Likewise, the protons of the hydroxyl groups bound to the C3, C4, and C6 of β-Man do not participate in H-bonding in the calculated structure, and the corresponding peaks are observed in the 1H NMR region typical for hydroxyl protons not participating in H-bonding (2.4–2.8 ppm).
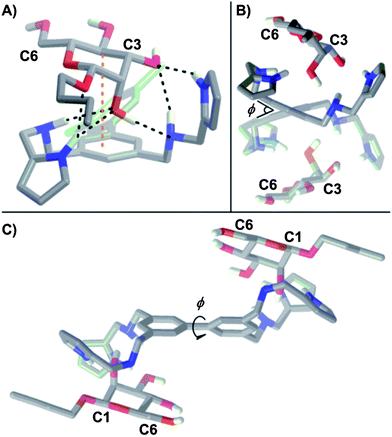 | ||
| Fig. 5 (A) Energy minimized structure (DFT, B3LYP/6-31+(d)) for 1:β-Man from an initial binding geometry obtained by an AMBER* mixed low-mode/torsional Monte Carlo conformation search. Intermolecular H-bonds are denoted by black dashed lines and C–H⋯π interactions are denoted by orange dashed lines. Three H-bonds occur between the hydroxyl group of C2 and both amino He and one pyrrole Hk protons of the receptor. Additionally, a C–H⋯π interaction between the phenyl ring and H4 and two more H-bonds between the hydroxyl group of C3 and an amino He and pyrrole Hk proton of the receptor were observed. Side views (B) parallel and (C) perpendicular to the biphenyl linkage of the energy minimized structure (DFT, B3LYP/6-31+(d)) for C2 symmetrical 1:β-Man2. The biphenyl dihedral is denoted by φ. | ||
The origin of the cooperativity in receptor 1 was examined computationally by varying the dihedral about the biphenyl bond (φ, Fig. 5B and C) as this is the only dynamic element of the receptor that is shared by both binding sites. While desolvation contributes significantly to ΔS0, it is not a source of cooperativity as both binding sites and mannosides are solvated identically. Previously, both restricted bond rotations16a,c,o and induced torsional strain25 have been cited as a source of positive cooperativity in a system where rotation must be halted to bind two equivalents of a substrate. A comparison of the DFT (B3LYP/6-31G+(d)) minimized structures corresponding to 1, 1:β-Man, and 1:β-Man2 revealed φ values of 40.2°, 38.5°, and 39.1° respectively, indicating that the contribution of torsional strain towards the observed cooperativity is negligible because φ in the bound state is close to the preferred φ of unbound 1. More likely, the presence of a bound β-Man restricts the rotation about φ and incurs an entropic penalty that is only paid in the first association.
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 Receptor
1 Receptor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) pyranoside binding
pyranoside binding
The K1 and K3 of the binding of 1 to pyranosides were determined by titrating a solution of 1 (53.0–62.5 mM) into a 1.0 mM CDCl3 solution of each octyl glycoside until a large excess of 1 was reached. Addition of 1 produced considerable changes in the 1H NMR resonances of the receptor and all eight pyranosides (Fig. 6A and ESI†). For each non-mannoside, K1 was determined by subjecting all resolvable resonances from each titration at 25 °C to a global nonlinear fitting analysis with a model combining K1 and Kdimer (13.0 ± 0.5 M−1), which was measured independently by 1H NMR dilution experiments (Table 1).17 Likewise, when the observed upfield chemical shift changes associated with α-Man were fit to a model incorporating Kdimer and the previously determined values of K1 and K2, excellent fits for the peak shifts were obtained (Table 1). However, the peak shifts for the β-Man titration could only be fit accurately when the formation of a complex consisting of two molecules of 1 and one molecule of β-Man (12:β-Man, Fig. 2) was considered (Fig. 6B). The observed Δδs were fit to a model consisting of Kdimer, K1, K2, and K3, with every binding constant except K3 held invariant, to determine K3 for β-Man. The values of log K1 for binding between 1 and all pyranosides range from 2.5 to 3.3 with the highest values associated with α- and β-Man and β-Glc (Table 1). Importantly, little difference exists between the K1s for the eight pyranosides, indicating that little selectivity occurs in the first binding event. In contrast to the modest selectivity found in K1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding is only observed for β-Man at 25 °C (K3 = 282 M−1), although a value of K3 = 3 M−1 for β-Glc can be extrapolated from a van't Hoff plot.17 Interestingly, a second receptor association does not occur with α-Man suggesting that the octyl chain at the anomeric position, which would be orientated away from the biphenyl base of 1 in 1:α-Man (Fig. 5A), interferes with the association of a second receptor.
1 binding is only observed for β-Man at 25 °C (K3 = 282 M−1), although a value of K3 = 3 M−1 for β-Glc can be extrapolated from a van't Hoff plot.17 Interestingly, a second receptor association does not occur with α-Man suggesting that the octyl chain at the anomeric position, which would be orientated away from the biphenyl base of 1 in 1:α-Man (Fig. 5A), interferes with the association of a second receptor.
 | ||
| Fig. 6 (A) 1H NMR (900 MHz, CDCl3, 25 °C) spectra obtained upon the titration of a 62.5 mM solution of 1 to a 0.98 mM solution of β-Man with dashed lines illustrating the induced changes in δ. (B) Chemical shifts, δ, of β-Man as a function of molar equivalents of 1 at 5 °C. The theoretical global fits with a model incorporating Kdimer, K1, and K2 (dashed line) and with Kdimer, K1, K2, and K3 (solid line) are shown. | ||
The cooperativity that facilitates the formation of 12:β-Man can be understood through the interaction parameter, α, which is the ratio between the values of K3 in the presence and in the absence of cooperativity, the latter being the reference Ka.22 Since the two faces of β-Man are inequivalent, the two receptors do not bind to identical sites, thus K1 is not an appropriate reference Ka. Rather, since K3 describes the binding of the β-face26 of β-Man, which contains H1, H3, and H5, in the presence of a receptor bound to the α-face, which contains H4, the reference Ka would describe the receptor binding to the β-face in the absence of a receptor bound to the α-face. From the −63 °C 1H–1H ROESY spectrum of 1:β-Man2, there are no observable NOEs between the pyranoside protons on the β-face and the biphenyl base of receptor 1.17 Likewise, a ROESY spectrum performed at conditions that would produce significant quantities of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1:β-Man complex revealed only a NOE between H4 of the α-face and Ha.17 Under these experimental conditions, a 1
1 1:β-Man complex revealed only a NOE between H4 of the α-face and Ha.17 Under these experimental conditions, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding event between 1 and the β-face does not occur to any appreciable extent, so an approximate baseline value of Ka ≤ 104 M−1 was obtained.27 Thus, an estimated K3 ≥ 282 M−1 is evidence for positive cooperativity in K3 with β-Man, with a corresponding α of at least 2.7.
1 binding event between 1 and the β-face does not occur to any appreciable extent, so an approximate baseline value of Ka ≤ 104 M−1 was obtained.27 Thus, an estimated K3 ≥ 282 M−1 is evidence for positive cooperativity in K3 with β-Man, with a corresponding α of at least 2.7.
To determine why K3 occurs exclusively with β-Man at room temperature, ΔH0 and ΔS0 of association for each binding event between 1 and all pyranosides were obtained by repeating the 1H NMR titrations at 20, 15, 10, and 5 °C and subjecting the resulting Kas to van't Hoff analyses (Table 1 and ESI†).17 All monosaccharides fit satisfactorily to a Kdimer + K1 model at all temperatures, except for β-Man at all temperatures and β-Glc, at 15, 10, and 5 °C, which required inclusion of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor
1 receptor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyranoside equilibrium (K3) to achieve satisfactory fits to the titration data.17 When comparing the thermodynamic parameters for the formation of each 1
pyranoside equilibrium (K3) to achieve satisfactory fits to the titration data.17 When comparing the thermodynamic parameters for the formation of each 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, a decrease in ΔH0 occurs with a decrease in magnitude of ΔS0, which can be rationalized within the context of enthalpy–entropy compensation.6 Notably, the two β-monosaccharides with the highest 1
1 complex, a decrease in ΔH0 occurs with a decrease in magnitude of ΔS0, which can be rationalized within the context of enthalpy–entropy compensation.6 Notably, the two β-monosaccharides with the highest 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding enthalpies, β-Man and β-Glc, are the only pyranosides that participate in K3. The large difference in ΔH0 between 1:β-Man and 1:β-Glc, −20.5 and −16.5 kcal mol−1 respectively, suggests that the high selectivity in K3 for β-Man is the result of 1 forming more noncovalent contacts with β-Man than with β-Glc, resulting in a more preorganized 1
1 binding enthalpies, β-Man and β-Glc, are the only pyranosides that participate in K3. The large difference in ΔH0 between 1:β-Man and 1:β-Glc, −20.5 and −16.5 kcal mol−1 respectively, suggests that the high selectivity in K3 for β-Man is the result of 1 forming more noncovalent contacts with β-Man than with β-Glc, resulting in a more preorganized 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. The ΔH0s for the formation of 12:β-Glc and 12:β-Man, −6.6 and −11.0 kcal mol−1 respectively, suggest that significantly more noncovalent contacts are formed in the latter, indicating that the selectivity for β-Man in the second binding event is enthalpically driven.
1 complex. The ΔH0s for the formation of 12:β-Glc and 12:β-Man, −6.6 and −11.0 kcal mol−1 respectively, suggest that significantly more noncovalent contacts are formed in the latter, indicating that the selectivity for β-Man in the second binding event is enthalpically driven.
The binding geometries of 1:β-Man and 12:β-Man were determined and compared to understand how the preorganization of 1:β-Man facilitates the formation of 12:β-Man. A 1H–1H ROESY experiment that was performed under conditions that favour the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (1:β-Man
1 complex (1:β-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:β-Man2 = 2
1:β-Man2 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5) displayed a NOE between H4 and Ha,17 which is consistent with the previously determined binding geometry for 1:β-Man. Notably, in the 1:β-Man geometry, a significant portion of β-Man is exposed to solvent because one of the arms of 1 is orientated downwards underneath the n-octyl chain of β-Man, which provides a window for a second equivalent of 1 to bind onto the exposed β-face of β-Man. The structure of 12:β-Man was determined by performing a 1H–1H ROESY experiment with a concentrated 2
1.5) displayed a NOE between H4 and Ha,17 which is consistent with the previously determined binding geometry for 1:β-Man. Notably, in the 1:β-Man geometry, a significant portion of β-Man is exposed to solvent because one of the arms of 1 is orientated downwards underneath the n-octyl chain of β-Man, which provides a window for a second equivalent of 1 to bind onto the exposed β-face of β-Man. The structure of 12:β-Man was determined by performing a 1H–1H ROESY experiment with a concentrated 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor
1 receptor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyranoside CDCl3 mixture at −10 °C where 12:β-Man would be the major species in solution. NOEs were observed between protons located on the biphenyl base and pyrroles, suggesting a geometry where one molecule of β-Man is encaged by two molecules of 1, and the two molecules of 1 are in close contact.17 By using a similar AMBER* conformational search that was used to obtain the 1:β-Man structure, a 12:β-Man structure was obtained (Fig. 7) that is consistent with the thermodynamic data and the 1D and 2D 1H NMR spectra. Notably, noncovalent interactions between the second equivalent of 1 and OH4 and OH3 of β-Man are observed in the calculated structure, thereby explaining the high ΔH0 of the second binding event. Also in the calculated 12:β-Man structure, pyrrole protons of one molecule of 1 are within close proximity (<4.0 Å) to biphenyl protons Ha and Hb of the second molecule of 1, which is consistent with the experimentally observed NOEs between these atoms. In contrast, the 1H–1H ROESY of β-Glc and 1 under conditions that favour the 1
pyranoside CDCl3 mixture at −10 °C where 12:β-Man would be the major species in solution. NOEs were observed between protons located on the biphenyl base and pyrroles, suggesting a geometry where one molecule of β-Man is encaged by two molecules of 1, and the two molecules of 1 are in close contact.17 By using a similar AMBER* conformational search that was used to obtain the 1:β-Man structure, a 12:β-Man structure was obtained (Fig. 7) that is consistent with the thermodynamic data and the 1D and 2D 1H NMR spectra. Notably, noncovalent interactions between the second equivalent of 1 and OH4 and OH3 of β-Man are observed in the calculated structure, thereby explaining the high ΔH0 of the second binding event. Also in the calculated 12:β-Man structure, pyrrole protons of one molecule of 1 are within close proximity (<4.0 Å) to biphenyl protons Ha and Hb of the second molecule of 1, which is consistent with the experimentally observed NOEs between these atoms. In contrast, the 1H–1H ROESY of β-Glc and 1 under conditions that favour the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex revealed that the axial protons on both faces of β-Glc have observable NOEs with the biphenyl base of 1,17 indicating that more than one binding geometry exists at equilibrium since 1 cannot interact with both faces of β-Glc simultaneously. Because the entropic penalty for the preorganization of 1:β-Glc has not been paid, we speculate that the ΔS0 associated with a second molecule of 1 binding to the 1
1 complex revealed that the axial protons on both faces of β-Glc have observable NOEs with the biphenyl base of 1,17 indicating that more than one binding geometry exists at equilibrium since 1 cannot interact with both faces of β-Glc simultaneously. Because the entropic penalty for the preorganization of 1:β-Glc has not been paid, we speculate that the ΔS0 associated with a second molecule of 1 binding to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex becomes prohibitively high, preventing the formation of a 2
1 complex becomes prohibitively high, preventing the formation of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. It should be noted that in the calculated structure of 12:β-Man only three arms of each equivalent of 1 participate in binding to β-Man, so the fourth arms can be replaced in future receptors to increase function.
1 complex. It should be noted that in the calculated structure of 12:β-Man only three arms of each equivalent of 1 participate in binding to β-Man, so the fourth arms can be replaced in future receptors to increase function.
 | ||
| Fig. 7 Energy minimized structure (AMBER*) for 12:β-Man obtained by a mixed low-mode/torsional Monte Carlo conformation search. The carbons of 1 that binds the α-face are colored green, and the carbons of 1 bound to the β-face are colored red for clarity, nitrogens are blue, oxygens are red, and intermolecular H-bonds are denoted by dashed lines. Upon the association of the second equivalent of 1, 3 new H-bonds are observed with the β-face. | ||
The structures of 1:β-Man and 12:β-Man and the thermodynamic binding parameters explain the high selectivity of K3 towards β-Man. The preference for β-Man over α-Man arises because the n-octyl chain of α-Man is perpendicular to the pyranoside ring, which interferes with a second association of 1. The preference of the second association event for β-Man over other β-pyranosides occurs because the observed ΔH0 for the formation of 1:β-Man is nearly 4 kcal mol−1 greater than the next highest 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ΔH0 (β-Glc), highlighting the dominant role of enthalpy in selectivity. Notably, the axial C2 hydroxyl group of mannosides is positioned to form two N–H⋯O bonds and one O–H⋯N bond with two secondary amines and one pyrrole of 1. Additional non-covalent interactions – such as a C–H⋯π interaction with H4 and the aromatic ring and three N–H⋯O bonds between receptor 1 and the oxygens at C1 and C3 of β-Man – result in a tightly bound 1:β-Man complex, thus explaining why 1 exhibits cooperativity with mannosides and not its epimers such as galactosides or glucosides. Additionally, in the 1:β-Man geometry, a significant portion of the mannoside is exposed to solvent because one of the arms of 1 is orientated downwards underneath the n-octyl chain of β-Man, which provides a window for a second equivalent of 1 to bind. Because 1 is flexible, each equivalent of 1 that is bound to β-Man adopts a different conformation, so a 2
1 ΔH0 (β-Glc), highlighting the dominant role of enthalpy in selectivity. Notably, the axial C2 hydroxyl group of mannosides is positioned to form two N–H⋯O bonds and one O–H⋯N bond with two secondary amines and one pyrrole of 1. Additional non-covalent interactions – such as a C–H⋯π interaction with H4 and the aromatic ring and three N–H⋯O bonds between receptor 1 and the oxygens at C1 and C3 of β-Man – result in a tightly bound 1:β-Man complex, thus explaining why 1 exhibits cooperativity with mannosides and not its epimers such as galactosides or glucosides. Additionally, in the 1:β-Man geometry, a significant portion of the mannoside is exposed to solvent because one of the arms of 1 is orientated downwards underneath the n-octyl chain of β-Man, which provides a window for a second equivalent of 1 to bind. Because 1 is flexible, each equivalent of 1 that is bound to β-Man adopts a different conformation, so a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor–pyranoside complex is unlikely to form from a highly preorganized receptor.
1 receptor–pyranoside complex is unlikely to form from a highly preorganized receptor.
Implications of competing equilibria on the selectivity of 1
In the presence of β-Man, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, 1:β-Man, can either bind a second molecule of pyranoside, to form 1:β-Man2 (K2), or 1, to form 12:β-Man (K3). The outcome of these two competing processes is dependent on the concentrations of each substrate, with K2 dominating at high concentrations of β-Man relative to 1, whereas K3 is preferred in the presence of excess 1. Thus, the numerous equilibria operating simultaneously in a solution of 1 and pyranoside (Kdimer, K1, K2 and K3) and the concentration dependence of cooperative binding complicate the analysis of the overall selectivity of 1 for the eight pyranosides. To simplify the analysis of saccharide receptors that possess multiple binding pathways, the Roelens group has previously employed the median binding concentration, BC50, to describe binding strength.7f,i The BC50 values of each of the pyranosides – defined as the total concentration of receptor 1 needed to bind 50% of the available pyranosides in solution – were computed over a pyranoside concentration range of 0 to 10.0 mM to probe both the magnitude and concentration dependence of the selectivity of 1 for the eight pyranosides (Fig. 8A). Note that all equilibria present in a receptor–pyranoside mixture contribute toward the calculated BC50 value, and a higher 1/BC50 value is indicative of a higher overall binding strength.
1 complex, 1:β-Man, can either bind a second molecule of pyranoside, to form 1:β-Man2 (K2), or 1, to form 12:β-Man (K3). The outcome of these two competing processes is dependent on the concentrations of each substrate, with K2 dominating at high concentrations of β-Man relative to 1, whereas K3 is preferred in the presence of excess 1. Thus, the numerous equilibria operating simultaneously in a solution of 1 and pyranoside (Kdimer, K1, K2 and K3) and the concentration dependence of cooperative binding complicate the analysis of the overall selectivity of 1 for the eight pyranosides. To simplify the analysis of saccharide receptors that possess multiple binding pathways, the Roelens group has previously employed the median binding concentration, BC50, to describe binding strength.7f,i The BC50 values of each of the pyranosides – defined as the total concentration of receptor 1 needed to bind 50% of the available pyranosides in solution – were computed over a pyranoside concentration range of 0 to 10.0 mM to probe both the magnitude and concentration dependence of the selectivity of 1 for the eight pyranosides (Fig. 8A). Note that all equilibria present in a receptor–pyranoside mixture contribute toward the calculated BC50 value, and a higher 1/BC50 value is indicative of a higher overall binding strength.
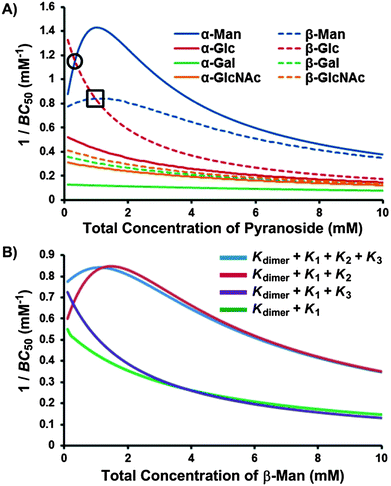 | ||
| Fig. 8 1/BC50 plots describing (A) the pyranoside concentration dependence for the overall binding strength (1/BC50) of receptor 1 toward each pyranoside, where higher values are indicative of stronger binding and crossover points, marked within a circle for β-Glc → α-Man and square for β-Glc → β-Man, denote changes in binding preference with increasing pyranoside concentration; and (B) the influence of each positive cooperative binding equilibria (K2 and K3) on the BC50 value of receptor 1 for β-Man. | ||
The 1/BC50 plots reveal the effects of positive cooperativity on the binding affinity of 1 toward mannosides. Molecules with K2 possess parabolic curves in the 1/BC50 plot. This is particularly evident for α-Man which possesses the highest affinity for 1 compared to all other pyranosides at a 0.8 mM pyranoside concentration. Interestingly, for β-Man, which exhibits cooperativity in both K2 and K3, a broader parabolic shape is observed, and little concentration dependence on the overall binding strength occurs between 0 and 4.0 mM of β-Man. When the calculated 1/BC50 plot is compared to a hypothetical plot in which only K1 and K3 are present, it was found that the presence of K3 induces a substantial increase in selectivity at low concentrations (<1.5 mM) of β-Man (Fig. 8B). Alternatively, when a hypothetical plot is generated with only K1 and K2, K2 enhanced selectivity when [β-Man] is greater than 1.0 mM, thus demonstrating the direct contribution of cooperative, complex equilibria on selectivity in saccharide receptors (Fig. 8B). Moreover, these plots confirm that pyranoside concentration controls which equilibrium, i.e. K2 or K3, prevails. At concentrations below 1.0 mM of β-Man, higher stoichiometry binding is achieved through K3, while at greater β-Man concentrations, K2 dominates.
As each 1/BC50 plot is a measure of affinity between 1 and pyranosides, comparing the plots of two or more pyranosides provides a means of assessing selectivity. Thus, the concentration of α-Man where the maximum 1/BC50 value is obtained (0.8 mM) is also where the maximum selectivity occurs for α-Man relative to the other pyranosides. Beyond this value, the selectivities gradually approach 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mannoside
1 mannoside![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pyranoside, which is a consequence of the differences in binding stoichiometry – receptor 1 can accommodate two molecules of mannosides and only binds 1
pyranoside, which is a consequence of the differences in binding stoichiometry – receptor 1 can accommodate two molecules of mannosides and only binds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the other pyranosides. Importantly, crossover points in the BC50 plots are observed between β-Glc and the mannosides (Fig. 8A), meaning that the selectivity of 1 changes as a function of pyranoside concentration. At low pyranoside concentrations (<0.3 mM), receptor 1 binds β-Glc with the highest affinity owing to its high value of K1, which effectively competes with the cooperative binding of 1 toward mannosides. From 0.3 mM to 1.0 mM, the binding order for 1 is α-Man > β-Glc > β-Man. At higher pyranoside concentrations (>1.0 mM), the binding order for 1 changes to α-Man > β-Man > β-Glc as a result of the 2
1 for the other pyranosides. Importantly, crossover points in the BC50 plots are observed between β-Glc and the mannosides (Fig. 8A), meaning that the selectivity of 1 changes as a function of pyranoside concentration. At low pyranoside concentrations (<0.3 mM), receptor 1 binds β-Glc with the highest affinity owing to its high value of K1, which effectively competes with the cooperative binding of 1 toward mannosides. From 0.3 mM to 1.0 mM, the binding order for 1 is α-Man > β-Glc > β-Man. At higher pyranoside concentrations (>1.0 mM), the binding order for 1 changes to α-Man > β-Man > β-Glc as a result of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding stoichiometry that occurs only with mannosides. Consequently, a new concentration dependence has been discovered that governs the stoichiometry of the resulting complex and the pyranoside preference of the receptor.
1 binding stoichiometry that occurs only with mannosides. Consequently, a new concentration dependence has been discovered that governs the stoichiometry of the resulting complex and the pyranoside preference of the receptor.
While 1/BC50 plots describe the concentration dependent affinity of 1 for different pyranosides, a standardized metric describing the binding ability of receptors exhibiting multiple equilibria, the intrinsic median binding concentration, BC050, has been employed by the Roelens group. BC050 is calculated by the integration of the inverse BC50 function versus the molar fraction of bound receptor, χH:7c
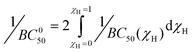 | (1) |
The BC050 values of the pyranosides for receptor 1 were determined using eqn (1). For the mannose-selective synthetic lectins developed by the Roelens group, the reported BC050 values range from 13.5 mM to 83 μM, with the latter corresponding to an outstanding chiral diaminopyrrolitic receptor for β-Man in acetonitrile.7c For receptor 1, the two pyranosides that exhibit positive cooperativity, α-Man and β-Man, have lower BC050 values of 460 and 730 μM respectively, than were observed for the other pyranosides, where BC050 values range from 1860 to 7740 μM, except for β-Glc (BC050 = 700 μM). The ratio of BC050 values has been used to compare the selectivities of carbohydrate receptors for mannosides7c and range from excellent (16.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for α-Man
1 for α-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α-Gal) to modest (1.5
α-Gal) to modest (1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for α-Man
1 for α-Man![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β-Glc) for 1. However, BC050 values do not fully reflect the binding behavior of 1 because they suggest that 1 binds β-Glc preferentially over β-Man rather than describe the subtleties of concentration dependent selectivity.
β-Glc) for 1. However, BC050 values do not fully reflect the binding behavior of 1 because they suggest that 1 binds β-Glc preferentially over β-Man rather than describe the subtleties of concentration dependent selectivity.
Conclusions
Flexible supramolecular host 1 was developed to examine how the ability to rearrange and dynamically sample conformational and thermodynamic space could reveal new modes for carbohydrate recognition. The association between 1 and eight octyl pyranosides was studied by variable temperature 1H NMR titrations to determine Kas, and van't Hoff analyses were performed to derive the thermodynamic parameters for each association event. These studies revealed that 1, which possesses four aminopyrrolitic arms and aromatic rings, forms N–H⋯O, O–H⋯N, and C–H⋯π interactions with pyranoside guests, resulting in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest complexes with similar affinities for all eight pyranosides. Upon altering the host
1 host–guest complexes with similar affinities for all eight pyranosides. Upon altering the host![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) guest ratio beyond 1
guest ratio beyond 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, new equilibria emerge that lead to the formation of 1
1, new equilibria emerge that lead to the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 receptor–pyranoside complexes exclusively with mannosides at 25 °C. The geometries of these complexes were determined by 1D and 2D 1H NMR spectroscopy and molecular modeling to reveal a C2-symmetric structure for 1:β-Man2 and a cage structure for 12:β-Man that were consistent with all data sets. Importantly, the structure of 12:β-Man indicates that only three of the four aminopyrrolitic arms are involved in binding, suggesting that the fourth arm could be replaced to increase the functionality of future receptors and enhance binding in competitive solvents.
1 receptor–pyranoside complexes exclusively with mannosides at 25 °C. The geometries of these complexes were determined by 1D and 2D 1H NMR spectroscopy and molecular modeling to reveal a C2-symmetric structure for 1:β-Man2 and a cage structure for 12:β-Man that were consistent with all data sets. Importantly, the structure of 12:β-Man indicates that only three of the four aminopyrrolitic arms are involved in binding, suggesting that the fourth arm could be replaced to increase the functionality of future receptors and enhance binding in competitive solvents.
Mannosides are important targets because they are both diagnostic and prognostic for several cancers,13 and receptors that target mannosides could be used for detection and delivery, so developing synthetic carbohydrate receptors remains a major area of research. An analysis of the binding constants for the first and second association events for 1:β-Man2 (K1 and K2) and 12:β-Man (K1 and K3) indicates that the binding is cooperative – that the first association event facilitates the second. The selectivity of 1 for mannosides arises as a direct result of the preorganization of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. The flexible receptor 1 achieves selectivity between pyranosides that may differ only by the orientation of a single hydroxyl group, despite the entropic penalty that must be paid to organize the complexes. In fact, the lack of preorganization in the strong 1:β-Glc complex precludes the formation of a stable 12:β-Glc structure, so entropy contributes significantly to selectivity. Although receptor 1 does not achieve the same overall affinity as the best rigidly preorganized mannose-specific receptors, the selectivity is comparable despite the differences in binding mechanisms, thus confirming the hypothesis that increasing the receptor dynamics reveals new binding geometries because of the ability of flexible hosts to dynamically explore conformational space.
1 complex. The flexible receptor 1 achieves selectivity between pyranosides that may differ only by the orientation of a single hydroxyl group, despite the entropic penalty that must be paid to organize the complexes. In fact, the lack of preorganization in the strong 1:β-Glc complex precludes the formation of a stable 12:β-Glc structure, so entropy contributes significantly to selectivity. Although receptor 1 does not achieve the same overall affinity as the best rigidly preorganized mannose-specific receptors, the selectivity is comparable despite the differences in binding mechanisms, thus confirming the hypothesis that increasing the receptor dynamics reveals new binding geometries because of the ability of flexible hosts to dynamically explore conformational space.
Finally, it should be noted that synthetic carbohydrate receptors can provide insight into the subtleties of natural lectin–carbohydrate interactions and reveal how carbohydrate recognition conveys complex information in biological networks. Eukaryotic cell surfaces are coated with a carbohydrate layer, the glycocalyx, where the multivalent presentation of carbohydrates on a cell surface enhances binding affinity, a phenomenon termed the cluster glycoside effect.28 Interestingly, the selectivity of 1 changes with pyranoside concentration, where 1 preferentially binds glucosides at low concentration (<0.3 mM) and mannosides at higher concentrations that are similar to the increased localized concentrations present in mannoside clusters on cell surfaces. While concentration dependent selectivity may be unprecedented with synthetic carbohydrate receptors, multivalency and cooperativity are ubiquitous in biology, so concentration dependent switching may commonly occur with natural lectins and could have implications for hierarchical organization and information transfer in biological networks.
Experimental
1H NMR titrations
1H NMR dilution experiments to determine Kdimer at all temperatures were accomplished through the incremental addition of a 62.5 mM solution of 1 to neat CDCl3. Kdimer values at 25, 20, 15, 10, and 5 °C were determined to be 13.0, 15.3, 16.9, 20.8, and 24.2 ± 0.5 M−1 respectively. The addition of 1 to a CDCl3 pyranoside solution or vice versa resulted in the perturbation of the chemical shifts (δ) corresponding to resonances of both 1 and pyranoside. This is the result of an exchange process involving 1 (H) and pyranoside (G) equilibria products exchanging fast on the NMR timescale, resulting in the averaging of chemical shifts of protons in differing chemical environments. Accordingly, equilibrium constants, Ka, can be quantified by first defining a model that includes the correct set of equilibria,17 calculating the hypothetical concentrations of equilibrium species and the corresponding chemical shifts, and finally fitting the resulting data to the experimental results.19 Theoretical chemical shifts for 1 (H) and pyranoside (G) were calculated with eqn (2) and eqn (3). | (2) |
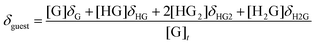 | (3) |
Fittings were conducted in Microsoft Excel 2007 using the Solver feature. All observable H and G peaks were simultaneously fitted by minimizing the total sum of squared residuals (SSR, eqn (4)), where wi are the weights assigned to each resonance, using the binding constants (Kdimer, K1, K2, K3) and the individual chemical shifts (δH, δG, δH2, δHG, δHG2, and δH2G) as fitting parameters.
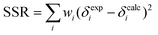 | (4) |
Molecular modeling
Initial structures for receptor 1 with β-Man were determined with distance constraints according to the experimental NMR data using the Maestro software package.29 All minimizations used the AMBER* force field24 with conjugate gradients and a dielectric constant of 4.8 Debyes with extended cutoff to treat remote interactions. A maximum number of 5000 iterations using the PRCG method and a convergence threshold of 0.05 were used. For the conformational searches, a Monte-Carlo mixed torsional/low-mode sampling method30 was used with a maximum number of 3000 steps, 100 steps per rotatable bond, 50.0 kJ mol−1 energy window, and a distance of 3.0–6.0 Å for low-mode movements. The initial results found through such minimizations were used as inputs for further conformational searches. The conformational search protocol yielded only one 1:β-Man conformer, which was further optimized with density functional theory (B3LYP/6-31G+(d)) using Gaussian 09.31Acknowledgements
We thank the Air Force Office of Scientific Research (Young Investigator Award #FA9550-11-1-0032), New York University, and the New York Structural Biology Center (NYSBC). The Bruker Avance 400 and 500 MHz NMR spectrometers were acquired through the support of the National Science Foundation under Award CHE-01162222.Notes and references
- (a) A. Varki, R. Cummings, J. Esko, H. Freeze, G. Hart and J. Marth, Essentials of Glycobiology, Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY, 1999 Search PubMed; (b) B. Ernst, G. W. Hart and P. Sinay, Carbohydrates in Chemistry and Biology Part II: Biology of Saccharides, Wiley-VCH, Weinheim, 2000 Search PubMed; (c) M. Ambrosi, N. R. Cameron and B. G. Davis, Org. Biomol. Chem., 2005, 3, 1593–1608 RSC; (d) E. J. Toone, Curr. Opin. Struct. Biol., 1994, 4, 719–728 CrossRef CAS; (e) R. W. Lemieux, Acc. Chem. Res., 1996, 29, 373–380 CrossRef CAS.
- (a) A. P. Davis, Org. Biomol. Chem., 2009, 7, 3629–3638 RSC; (b) A. P. Davis and R. S. Wareham, Angew. Chem., Int. Ed., 1999, 38, 2978–2996 CrossRef; (c) M. Mazik, RSC Adv., 2012, 2, 2630–2642 RSC; (d) M. Mazik, Chem. Soc. Rev., 2009, 38, 935–956 RSC; (e) S. Kubik, Angew. Chem., Int. Ed., 2009, 48, 1722–1725 CrossRef CAS; (f) S. Jin, Y. Cheng, S. Reid, M. Li and B. Wang, Med. Res. Rev., 2010, 30, 171–257 CAS; (g) D. B. Walker, G. Joshi and A. P. Davis, Cell. Mol. Life Sci., 2009, 66, 3177–3191 CrossRef CAS.
- (a) T. D. James, M. D. Phillips and S. Shinkai, Boronic Acids in Saccharide Recognition, The Royal Society of Chemistry, Cambridge, UK, 2006 Search PubMed; (b) T. D. James, K. R. A. S. Sandanayake and S. Shinkai, Angew. Chem., Int. Ed., 1996, 35, 1910–1922 CrossRef.
- (a) D. J. Cram and J. M. Cram, Container Molecules and Their Guests, The Royal Society of Chemistry, Cambridge, UK, 1997 Search PubMed; (b) S. P. Artz and D. J. Cram, J. Am. Chem. Soc., 1984, 106, 2160–2171 CrossRef CAS; (c) D. J. Cram, G. M. Lein, T. Kaneda, R. C. Helgeson, C. B. Knobler, E. Maverick and K. N. Trueblood, J. Am. Chem. Soc., 1981, 103, 6228–6232 CrossRef CAS; (d) D. J. Cram and J. M. Cram, Acc. Chem. Res., 1978, 11, 8–14 CrossRef CAS.
- W. I. Weis and K. Drickamer, Annu. Rev. Biochem., 1996, 65, 441–473 CrossRef CAS.
- L. Liu and Q.-X. Guo, Chem. Rev., 2001, 101, 673–695 CrossRef CAS.
- (a) A. Arda, F. J. Cañada, C. Nativi, O. Francesconi, G. Gabrielli, A. Ienco, J. Jimenez-Barbero and S. Roelens, Chem.–Eur. J., 2011, 17, 4821–4829 CrossRef CAS; (b) M. Cacciarini, C. Nativi, M. Norcini, S. Staderini, O. Francesconi and S. Roelens, Org. Biomol. Chem., 2011, 9, 1085–1091 RSC; (c) C. Nativi, O. Francesconi, G. Gabrielli, A. Vacca and S. Roelens, Chem.–Eur. J., 2011, 17, 4814–4820 CrossRef CAS; (d) A. Arda, C. Venturi, C. Nativi, O. Francesconi, F. J. Canada, J. Jimenez-Barbero and S. Roelens, Eur. J. Org. Chem., 2010, 64–71 CrossRef CAS; (e) A. Arda, C. Venturi, C. Nativi, O. Francesconi, G. Gabrielli, F. J. Canada, J. Jimenez-Barbero and S. Roelens, Chem.–Eur. J., 2010, 16, 414–418 CrossRef CAS; (f) C. Nativi, M. Cacciarini, O. Francesconi, A. Vacca, G. Moneti, A. Ienco and S. Roelens, J. Am. Chem. Soc., 2007, 129, 4377–4385 CrossRef CAS; (g) C. Nativi, M. Cacciarini, O. Francesconi, G. Moneti and S. Roelens, Org. Lett., 2007, 9, 4685–4688 CrossRef CAS; (h) M. Cacciarini, E. Cordiano, C. Nativi and S. Roelens, J. Org. Chem., 2007, 72, 3933–3936 CrossRef CAS; (i) A. Vacca, C. Nativi, M. Cacciarini, R. Pergoli and S. Roelens, J. Am. Chem. Soc., 2004, 126, 16456–16465 CrossRef CAS.
- (a) M. Mazik and A. C. Buthe, Org. Biomol. Chem., 2008, 6, 1558–1568 RSC; (b) M. Mazik and A. Hartmann, J. Org. Chem., 2008, 73, 7444–7450 CrossRef CAS; (c) M. Mazik, A. Hartmann and P. G. Jones, Chem.–Eur. J., 2009, 15, 9147–9159 CrossRef CAS; (d) M. Mazik and C. Sonnenberg, J. Org. Chem., 2010, 75, 6416–6423 CrossRef CAS; (e) M. Mazik and C. Geffert, Org. Biomol. Chem., 2011, 9, 2319–2326 RSC.
- N. P. Barwell, M. P. Crump and A. P. Davis, Angew. Chem., Int. Ed., 2009, 48, 7673–7676 CrossRef CAS.
- Y. Ferrand, E. Klein, N. P. Barwell, M. P. Crump, J. Jimenez-Barbero, C. Vicent, G.-J. Boons, S. Ingale and A. P. Davis, Angew. Chem., Int. Ed., 2009, 48, 1775–1779 CrossRef CAS.
- (a) B. Sookcharoenpinyo, E. Klein, Y. Ferrand, B. Walker, P. R. Brotherhood, C. Ke, M. P. Crump and A. P. Davis, Angew. Chem., Int. Ed., 2012, 51, 4586–4590 CrossRef CAS; (b) Y. Ferrand, M. P. Crump and A. P. Davis, Science, 2007, 318, 619–622 CrossRef CAS.
- T. D. P. Stack, Z. Hou and K. N. Raymond, J. Am. Chem. Soc., 1993, 115, 6466–6467 CrossRef CAS.
- (a) M. L. A. d. Leoz, L. J. T. Young, H. J. An, S. R. Kronewitter, J. Kim, S. Miyamoto, A. D. Borosky, H. K. Chew and C. B. Lebrilla, Mol. Cell. Proteomics, 2011, 10, M110.002717 CrossRef; (b) H. J. Ann, S. R. Kronewitter, M. L. A. d. Leoz and C. B. Lebrilla, Curr. Opin. Chem. Biol., 2009, 13, 601–607 CrossRef.
- Y. Nakagawa, T. Doi, Y. Masuda, K. Takegoshi, Y. Igarashi and Y. Ito, J. Am. Chem. Soc., 2011, 133, 17485–17493 CrossRef CAS.
- (a) S. Shinkai, M. Ikeda, A. Sugasaki and M. Takeuchi, Acc. Chem. Res., 2001, 34, 494–503 CrossRef CAS; (b) M. Takeuchi, M. Ikeda, A. Sugasaki and S. Shinkai, Acc. Chem. Res., 2001, 34, 865–873 CrossRef CAS; (c) L. Kovbasyuk and R. Kramer, Chem. Rev., 2004, 104, 3161–3187 CrossRef CAS; (d) I. Tabushi, Pure Appl. Chem., 1988, 60, 581–586 CrossRef CAS.
- (a) R. Wakabayashi, T. Ikeda, Y. Kubo, S. Shinkai and M. Takeuchi, Angew. Chem., Int. Ed., 2009, 48, 6667–6670 CrossRef CAS; (b) T. Ikeda, O. Hirata, M. Takeuchi and S. Shinkai, J. Am. Chem. Soc., 2006, 128, 16008–16009 CrossRef CAS; (c) M. Ayabe, A. Ikeda, Y. Kubo, M. Takeuchi and S. Shinkai, Angew. Chem., Int. Ed., 2002, 41, 2790–2792 CrossRef CAS; (d) A. Sugasaki, M. Ikeda, M. Takeuchi and S. Shinkai, Angew. Chem., Int. Ed., 2000, 39, 3839–3842 CrossRef CAS; (e) J.-I. Setsune and K. Watanabe, J. Am. Chem. Soc., 2008, 130, 2404–2405 CrossRef CAS; (f) S.-Y. Chang, M.-C. Um, H. Uh, H.-Y. Jang and K.-S. Jeong, Chem. Commun., 2003, 2026–2027 RSC; (g) S. Goswami, N. K. Das, D. Sen, G. Hazra, J. H. Goh, Y. C. Sing and H.-K. Fun, New J. Chem., 2011, 35, 2811–2819 RSC; (h) P. Lusterberger, R. Welti and F. Diederich, Helv. Chim. Acta, 1998, 81, 2190–2200 CrossRef; (i) F. Embeyer and J. Julius Rebek, Angew. Chem., Int. Ed., 1990, 29, 1148–1150 CrossRef; (j) J. Julius Rebek, T. Costello, L. Marshall, R. Wattley, R. C. Gadwood and K. Onan, J. Am. Chem. Soc., 1985, 107, 7481–7487 CrossRef; (k) C. Schmuck and L. Geiger, J. Am. Chem. Soc., 2005, 127, 10486–10487 CrossRef CAS; (l) H. Kawai, R. Katoono, K. Nishimura, S. Matsuda, K. Fujiwara, T. Tsuji and T. Suzuki, J. Am. Chem. Soc., 2004, 126, 5034–5035 CrossRef CAS; (m) F. Huang, F. R. Fronczek and H. W. Gibson, J. Am. Chem. Soc., 2003, 125, 9272–9273 CrossRef CAS; (n) T. Ishi-i, M. Crego-Calama, P. Timmerman, D. N. Reinhoudt and S. Shinkai, J. Am. Chem. Soc., 2002, 124, 14631–14641 CrossRef CAS; (o) J. Raker and T. E. Glass, J. Org. Chem., 2002, 67, 6113–6116 CrossRef CAS; (p) V. V. Borovkov, J. M. Lintuluoto, H. Sugeta, M. Fujiki, R. Arakawa and Y. Inoue, J. Am. Chem. Soc., 2001, 124, 2993–3006 CrossRef; (q) A. Sugasaki, K. Sugiyasu, M. Ikeda, M. Takeuchi and S. Shinkai, J. Am. Chem. Soc., 2001, 123, 10239–10244 CrossRef CAS; (r) A. Sugasaki, M. Ikeda, M. Takeuchi, K. Koumoto and S. Shinkai, Tetrahedron, 2000, 56, 4717–4723 CrossRef CAS.
- See ESI† for details.
- D. B. Werz, R. Ranzinger, S. Herget, A. Adibekian, C.-W. v. d. Lieth and P. H. Seeberger, ACS Chem. Biol., 2007, 2, 685–691 CrossRef CAS.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- C. S. Wilcox, J. C. Adrian, T. H. Webb and F. J. Zawacki, J. Am. Chem. Soc., 1992, 114, 10189–10197 CrossRef CAS.
- K. A. Connors, Binding Constants: The Measurement of Molecular Complex Stability, John Wiley & Sons, Inc., New York, 1987 Search PubMed.
- (a) K. A. Connors, A. Paulson and D. Toledo-Valasquez, J. Org. Chem., 1988, 53, 2023–2026 CrossRef CAS; (b) C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS; (c) G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762–1768 CrossRef CAS.
- H. Friebolin, Basic One- and Two-Dimensional NMR Spectroscopy: Fourth Completely Revised and Updated Edition, Wiley-VCH, Weiheim, 2005 Search PubMed.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1697 CrossRef CAS.
- G. Ercolani, Org. Lett., 2005, 7, 803–805 CrossRef CAS.
- I. A. Rose, K. R. Hanson, K. D. Wilkinson and M. J. Wimmer, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 2439–3441 CrossRef CAS.
- The detection limit of the NMR instrument used is roughly 10 nmol, which corresponds to a concentration of 0.02 mM. Using the derived equilibrium constants, the concentration of 1:β-Man was determined to be 0.11 mM under the experimental conditions. Since no NOEs are observed on the β-face of β-Man, the concentration of the receptor bound to this face is at or below the detection limit. Under the experimental conditions, a 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex at 0.02 mM would result from an equilibrium constant of 104 M−1.
1 complex at 0.02 mM would result from an equilibrium constant of 104 M−1. - J. J. Lundquist and E. J. Toone, Chem. Rev., 2002, 102, 555–578 CrossRef CAS.
- Maestro, A Powerful, All-Purpose Molecular Modeling Environment, Schrodinger, LLC, 2010, New York, NY Search PubMed.
- I. Kolossvary and W. C. Guida, J. Comput. Chem., 1999, 20, 1671–1684 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, X. L. M. Caricato, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, 2009, Gaussian, Inc., Wallingford, CT Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures, characterization data, 1H NMR titration data, van't Hoff plots, and ROESY experiments. See DOI: 10.1039/c2sc20873c |
| ‡ Current address: Department of Chemistry, University of Miami, Coral Gables, FL 33146 USA; E-mail: E-mail: a.braunschweig@miami.edu |
| This journal is © The Royal Society of Chemistry 2013 |