Origin of the size-dependent fluorescence blueshift in [n]cycloparaphenylenes†
Cristopher
Camacho
a,
Thomas A.
Niehaus
b,
Kenichiro
Itami
a and
Stephan
Irle
*a
aDepartment of Chemistry, Graduate School of Science, Nagoya University, Nagoya 464-8601, Japan. E-mail: sirle@chem.nagoya-u.ac.jp
bDepartment of Physics, University of Regensburg, D-93040 Regensburg, Germany
First published on 22nd October 2012
Abstract
Quantum chemical electronic structure calculations were employed to investigate the nature of the low-lying excited states of [n]cycloparaphenylenes ([n]CPPs) and the role of static and dynamic geometrical distortions in the bright states. The lowest-energy bright states involve single-electron excitations from S0 ground state to S2 and S3 states, which are at the Franck–Condon geometry the two components of a twofold degenerate 1E state. They couple to a twofold degenerate e vibration which induces Jahn–Teller (JT) deformation of the CPP geometry from circular to oval shape. Non-radiative decay from the S2/S3 states to the ground S0 and first excited, dark S1 states is suppressed due to symmetry rules. The emission spectral features in CPPs with large number of phenylene units n can therefore largely be attributed to the E⊗e JT system associated with S2 and S3. However, absorption and emission energies computed at the respective S0 and S2/S3 minimum energy geometries are found to be nearly identical, independent of the molecular size n in the CPP molecules. In contrast, molecular dynamics simulations performed on the excited state potential surfaces are able to explain the experimentally observed fluorescence blueshift of the strongest emission peaks with increasing molecular size. This unusual feature turns out to be a consequence of large vibrational amplitudes in small [n]CPPs, causing greater Stokes shifts, while large [n]CPPs are more rigid and therefore feature smaller Stokes shifts (“dynamic blueshift”). For the same reasons, symmetry rules are violated to a greater extent in small [n]CPPs, and it is expected that in their case a “static blueshift” due to emission from S1 contributes in the fluorescence spectra.
1 Introduction
[n]Cycloparaphenylenes ([n]CPPs) are fascinating molecules due to their high molecular symmetry (Fig. 1), and have only recently been successfully synthesized.1–10 They can be regarded as the smallest possible single-walled carbon nanotube (SWCNT), and have fueled speculations of their use as template to synthesize armchair (n,n) SWCNTs from the bottom up.3,9,11,12 They are also of great interest in their own right for materials sciences due to their photophysical properties, most notably an unusual blueshift of UV/Vis emission wavelength with increasing size n.1,6,13 This phenomenon is in sharp contrast to the size-dependence of UV/Vis emissions in linear oligoparaphenyles (OPPs), which exhibit the usual redshift with increasing number of paraphenylene (PP) rings.6,14 In past discussions of the origin of this blueshift, mostly vague speculations were offered, lacking factual evidence. In the following paragraph, we will briefly review these hypotheses.![Schematic structure of [8] and [10]CPP.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f1.gif) | ||
| Fig. 1 Schematic structure of [8] and [10]CPP. | ||
Iwamoto et al. formulated in ref. 6 the hypothesis that “the larger Stokes shift of the smaller CPPs can be explained by the release of strain energy in the excited state. Because smaller CPPs are more strained, they would undergo a larger structural change in the excited state than would the larger CPPs.” However, the amount of ring strain in the excited state has never before been estimated. A somewhat related hypothesis was given by Bertozzi et al. in the earliest reported work on CPP compounds in 2008:1 “In the smaller nanohoops, enhanced curvature leads to greater sp3 hybridization and increasingly asymmetric p orbitals, with their smaller lobes oriented inside the nanohoops. This factor reduces steric interactions and facilitates a larger decrease in dihedral angle in the excited state for the smaller nanohoop. Thus smaller hoops have the potential for larger structural relaxation and Stokes shifts.” A very recent theoretical study of the geometry relaxations occurring in the lowest excited singlet (S1) electronic state indeed found that the torsional angle between phenylene units increases from 14° for [8]CPP to 25° for [13]CPP.15 However, it was recently reported that emission emission from S1, which corresponds to a LUMO → HOMO transition, is actually symmetry-forbidden,6,13 and that the photophysical properties of this state therefore cannot explain the bright CPP emissions, especially in case of the larger nanohoops. Rather, bright emissions involve HOMO-1 → LUMO and HOMO → LUMO+1 excitations associated with the second- and third-lowest excited singlet states, S2 and S3.13 Moreover, larger [n]CPPs exhibit a pronounced, clear double peak in emission, which is difficult to understand on the basis of emission from S1 alone. An earlier theoretical study by Wong, who had also associated the blueshift with the unusual behavior of HOMO and LUMO levels involved in the S1 → S0 emission in [n]CPPs,16 does therefore also not provide a satisfactory explanation.
We hence conclude this recount of previous explanations by determining that, until now, no clear understanding of the CPP fluorescence has been reached, and that a satisfactory explanation of the unusual blueshift is still lacking. The theoretical study presented here is first to give a detailed account of the Jahn–Teller effect associated with the bright excited states, and to explicitly compute the emission spectra on the basis of excited states molecular dynamics simulations. In doing so, this work solves the mystery of the CPP blueshift by quantification of relaxation (static) and dynamic effects in the excited states. In addition, we address the above-mentioned hypotheses by providing computed data for the quantities that were invoked in these explanations, and show that such data is insufficient to understand the fascinating CPP photophysics. For the sake of clarity, we present in this work only simulations of fluorescence spectra for [8] and [10]CPPs as prototypical examples that have been already synthesized,4,6 even on the gram-scale.10 The two systems clearly exhibit the size effect observed in the CPP fluorescence spectra.
2 Computational methods
Density functional theory (DFT) and time-dependent DFT (TD-DFT) calculations have been carried out using the Coulomb-attenuating CAM-B3LYP exchange-correlation functional,17 which we selected based on extensive benchmark calculations involving a large variety of other functionals and variants of multireference perturbation theory.18–21 All DFT and ab initio calculations have been performed with the GAMESS quantum chemistry package22 in C1 symmetry without applying any constraints. The double-ζ-quality polarized def-SV(P) basis set developed by Ahlrich's et al.23 was employed for economical reasons since benchmark calculations for [8]CPP with larger cc-pVTZ basis set24 show excellent agreement of excitation energies. As initial structure for the geometry optimization in the ground state, we selected the fully alternant global minimum structures of [8]CPP and [10]CPP, reported earlier by Segawa et al.25 Ground and excited state geometries were optimized using tight convergence criteria: The largest component of the gradient was required to be smaller than 10−6 Ha/a0. The solvent field effect of chloroform on excitation energies was investigated for [8]CPP using the PCM approach.26 Harmonic vibrational frequency analyses for the electronic ground state at the global minimum S0 geometries were carried out using the analytical second energy derivatives implemented in TURBOMOLE27 at the B3LYP/def-SV(P) level of theory after re-optimization.For the simulation of fluorescence spectra, we followed both a static and a dynamic approach. In the static approach, we first optimized the geometries of the dark S1 and lowest bright (S2) state based on all conformational isomers reported for the ground state by Segawa et al.25 using CAM-B3LYP. It was found that also in the excited states the global minimum corresponds to a fully alternant conformation of the PP rings in the [8]CPP and [10]CPP compounds. The geometry relaxation in the excited states most notably induces a decrease of the dihedral angles between adjacent PP rings, a quinoid bond length deformation, and in the case of S2 a slight oval deformation of the circular CPP structure. Geometry optimization of the second-lowest bright (S3) state at the TD-DFT level of theory leads to a state-crossing where S3 and S2 switch in energy; it is therefore not possible to locate the minimum on the S3 surface. Our TD-CAM-B3LYP/def-SV(P) optimized geometries of S1 states agree well with the TD-B3LYP/6-31G(d) geometries reported by Fujitsuka et al.,15 indicating that for geometrical parameters the Coulomb-attenuating method (CAM) is not necessarily required. In all excited states calculations, we computed transition energies and oscillator strengths f up to 8 excited singlet states.
In the dynamic approach, we performed direct molecular dynamics (MD) simulations on excited state potential energy surfaces based on the time-dependent self-consistent-charge density-functional tight-binding (TD-DFTB) method.28 The semiempirical method was selected due to the enormous computational cost associated with TD-DFT calculations of CPP compounds. TD-DFTB valence excited state geometries are typically in excellent agreement with higher level methods, while absolute transition energies are negatively affected by the minimum basis set employed in the DFTB method. We therefore resorted to the technique of trajectory sampling, hereafter denoted as TD-CAM-B3LYP/def-SV(P) ← TD-DFTB/MD, where A ← B indicates that single point excitation energies were computed using method A for randomly selected trajectory snapshot geometries from the quantum chemical MD (QM/MD) simulation using the potential of method B. For each CPP in each of the excited states of interest (S1, S2, and S3), the fluorescence spectra were separately simulated using the respective gradients during the MD simulations. Equations of motion for every time step were integrated by means of the Verlet algorithm with a time step of 0.29 fs. Ten trajectories were computed on the most important S2 excited state potential energy surface, whereas only four trajectories were run on the surfaces of S1 and S3 excited states. TD-DFTB optimized excited state geometries were chosen as the starting configurations, except for S3, for which we used the same optimized geometry as for S2, and random initial nuclear velocities were assigned corresponding to 298 K temperature. In order to approach a proper velocity distribution, we first performed a brief isothermal (NVT) simulations for about 43.50 fs using a scaling of velocity thermostat with 20% overall scaling probability. The endpoint geometries and velocities from these short NVT simulations were then used to initialize microcanonical (NVE) production trajectories with a duration of 2.90 ps. This time is long enough to accommodate a full period of the lowest frequency mode vibrations in [8] and [10]CPPs, which are 1.35 ps (24.8 cm−1) and 2.05 ps (16.3 cm−1), respectively, according to the B3LYP/def-SV(P) level of theory. Since the excited state dynamics are ergodic, the effectively calculated simulation time can be obtained by multiplying the individual trajectory simulation time by the number of trajectory replicas, which means we simulated the dynamics for a total of 29 ps on the S2 surface and 11.6 ps dynamics on both S1 and S3 surfaces. The trajectory sampling was then performed from the available NVE trajectories, drawing independently selected sets of 12, 16, 20, and 24 geometries for subsequent TD-CAM-B3LYP single point excitation energy calculations. Details of the samples used for the TD-CAM-B3LYP/def-SV(P) ← TD-DFTB/MD procedure, and resulting simulated spectra, are given in the ESI.† This data suggests that 24 point-sampling produces converged emission spectra. For graphical representation of the emission spectra we used Gaussian envelopes with a finite width at half maximum (FWHM) of 15 nm for the TD-CAM-B3LYP-computed band positions and oscillator strengths.
3 Results and discussion
3.1 Frontier molecular orbitals
The low energy UV/Vis absorption and emission bands of [n]CPPs arise mainly from electronic transitions involving HOMO, LUMO, as well as the doubly degenerate (or nearly degenerate in case of odd n) HOMO-1 and LUMO+1 orbitals.6,13 The nature of these MOs has been discussed before, but to the best of our knowledge, a quantitative explanation of their different behaviors with increasing n has not been given yet. In the following section, we will fill this gap.For the sake of simplicity, we will restrict the following discussion to CPPs with even n, and classify the orbitals by the irreducible representations (irreps) of the lowest applicable molecular symmetry point group that can capture the essential feature of doubly degenerate HOMO-1 and LUMO+1 levels, namely C4 for [8]CPP and C5 for [10]CPP.‡ In the Cn/2 point groups, HOMO-1 and LUMO+1 belong to the doubly degenerate e irrep, whereas HOMO and LUMO both belong to the a irrep. HOMO and LUMO are qualitatively related to the HOMO-1 and LUMO+1 levels, respectively, as these orbitals are linear combinations of the HOMO (aromatic) and LUMO (quinoid) of the individual PP units.
Fig. 2a displays the energies of these frontier MOs computed at the ground state global minimum geometries as a function of [n]CPP size (n = 6,8,10,…,16). The CPP HOMO-LUMO gap ΔEHL = εLUMO − εHOMOincreases with increasing n, and our CAM-B3LYP/def-SV(P) orbital energies follow rather closely the B3LYP/6-31G(d) results reported previously.6,13 As was pointed out in these works, the increase of ΔEHL with increasing system size is an unusual behavior, as usually the opposite is observed. Iwamoto et al. have quoted the smaller aromaticity of the PP units in smaller CPP compounds as the origin of the unusual HOMO–LUMO gap behavior.6 Ground state nucleus independent chemical shift (NICS)29 calculations by Wong16 are indeed consistent with reduced PP aromaticity for smaller n. Yet, on the other hand, the e-type HOMO-1 and LUMO+1 levels of CPP follow the expected patterns, the only difference from HOMO and LUMO being the presence of a nodal plane, thus an explanation of the size-dependence of ΔEHL based on aromatic character does not provide the full picture. We note that, as n → ∞, the HOMO and LUMO levels converge to the highest and lowest energy levels of the π-valence and π-conduction bands, respectively, in the language of band structure theory. These limits are −6.90 and −0.67 eV at the CAM-B3LYP level of theory, obtained from an extrapolation of the HOMO and LUMO energies of linear oligoparaphenylenes (OPPs) shown in Fig. 2b (red curves), and added in Fig. 2a as gray dashed lines.
![Molecular orbital energies for (a) [n]CPPs and for (b) [n]OPPs and [n]cPPs as a function of the number of PP units n.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f2.gif) | ||
| Fig. 2 Molecular orbital energies for (a) [n]CPPs and for (b) [n]OPPs and [n]cPPs as a function of the number of PP units n. | ||
In order to clarify the surprising behavior of CPP HOMOs and LUMOs, we now turn to a discussion of a comparison between CPP frontier MOs and HOMO and LUMO levels of linear (=“open”) [n]OPP, calculated at the ground state global minimum geometries as a function of n. For OPP compounds, the “usual” behavior of the HOMO–LUMO gap is observed, in agreement with the calculations by Iwamoto et al.6 and Segawa et al.13 Note that n for OPPs was chosen as n/2 of the CPPs. To understand how ring strain and non-planarity deformation affects occupied and virtual π-orbital energies in CPPs, we “bent” the linear [n/2]OPPs into half-circular geometries by “cutting” the optimized geometries of [n]CPPs in half (hence the use of the factor 1/2 for n of the OPPs) and mending the broken C–C bonds with hydrogen. The resulting HOMO and LUMO levels of “cut” OPPs (abbreviated as “cPPs”) are shown in Fig. 2b (blue curves). We note significant upward (HOMO) and downward (LUMO) shifts (indicated by green arrows for the cases of n = 6 and n = 12) in orbital energies from linear OPP to bent cPP orbital levels that are nearly quantitatively in agreement with the shifts of the HOMO and LUMO levels of CPP from the n = ∞ limits (corresponding to the green arrows in Fig. 2a, their lengths taken from the cPP/OPP comparison in Fig. 2b). It thus appears that the [n]CPP HOMOs and LUMOs respond to the bending and torsional deformations as if their energies were fixed at their n = ∞ limits. Closer inspection of the CPP HOMO and LUMO levels shows that these π-MOs indeed possess constant MO amplitudes on each PP unit, and that their energies in π-space are therefore independent from the number of PP units. However, bending and torsion promote σ–π mixing, and enhance antibonding orbital contacts in the HOMO while reducing bonding orbital contacts in the LUMO, and these shifts are almost, although not precisely, isoenergetic. Hence, the HOMO and LUMO energies appear nearly symmetric with respect to the Fermi level (defined as εF = εHOMO + ΔEHL/2, which is approximately the same for all [n]CPPs at about εF = −3.74 eV). Thus, the unusual size dependence of ΔEHL in [n]CPP is a result of two factors: (i) εHOMO and εLUMO are constant and independent from n in π-space due to the circular boundary conditions of the MOs and their constant amplitudes on each PP unit, and (ii) bending and torsion cause the observed stabilization of the HOMO and destabilization of the LUMO with increasing system size, hence an increase in ΔEHL. We refer the reader to a more detailed and quantitative discussion of the orbital energy changes due to bending and torsion for a terphenyl model system in the ESI.†
3.2 Jahn–Teller distortion
Symmetry rules predict that the electronic transition between ground state S0 (X1A, g parity) and first excited singlet state S1 (A1A, also g parity), arising from the HOMO → LUMO transition, is not allowed and therefore should not be visible, or at best, weakly visible in the UV/Vis absorption spectra.6,13 Indeed, our computed oscillator strengths f for S0–S1 transitions are practically zero, both in the Franck–Condon (FC) region as well as at S1 optimized geometries. To the contrary, electronic excitation from the ground to the B1E state (HOMO → LUMO+1, strongly mixed with nearly isoenergetic HOMO−1 → LUMO), are symmetry-allowed. In fact, they possess exceptionally large oscillator strengths f that increase as a function of system size, as the associated transition dipole moment matrix elements 〈S2|∑iri|S0〉 and 〈S3|∑iri|S0〉 increase in magnitude.14 In the Cn/2 point groups, these two states are the two energetically degenerate components of the B1E state (u parity), composed of the linear combinations of HOMO → LUMO+1 and HOMO-1 → LUMO transitions. Spatially, they behave as x and y components, with HOMO-1 and LUMO+1 having yz and xz nodal planes, respectively. Fig. 2 displays on the right-hand side the y component of the e-type HOMO-1, a-type HOMO, a-type LUMO, and the y component of the e-type LUMO+1, in order of ascending orbital energy. The x components of the energetically degenerate HOMO-2 and LUMO+2 MOs possess amplitudes that are rotated from those of the y components by an angle of 90°.Fig. 3a and b depict the energies of S0 to S3 electronic states for [8]CPP and [10]CPP at the FC geometry on the center vertical axis, relative to the X1A minimum energy. The energy levels to the left and to the right of each diagram correspond to the state energies at the relaxed geometries of the bright S2 state. We first discuss the vertical excitation energies in the FC region. TD-CAM-B3LYP calculations predict a “static” blueshift of 0.16 eV for S1 ← S0 excitations in going from n = 8 to n = 10. However, the associated oscillator strengths are practically zero, as mentioned above. Experimental observations confirm the absence of such a blueshift in UV/Vis absorption spectra, with the exception of a weak shoulder around 400 nm in the cases smaller CPP compounds with n = 8,9,10.6,13,15 S2 ← S0 and S3 ← S0 excitations are energetically degenerate, and possess identical, large oscillator strengths, which increase with increasing n from 0.90 (n = 6) to 2.87 (n = 12). As discussed above, S2 and S3 bright states are the x and y components of the degenerate B1E state, which are characterized by a linear combination of two one-electron excitations, contributing about 80% to the wave function, according to our TD-DFT calculations. The two leading contributions correspond to HOMO-1 → LUMO and HOMO → LUMO+1 excitations. Because the upward- and downward-shifts of CPP HOMO and LUMO orbitals are nearly of same magnitude, and the HOMO-1 and LUMO+1 levels are practically symmetric around the Fermi level (see Fig. 2), the energies corresponding to B1E ← X1A excitations are nearly independent on the CPP molecular size n, as evident from similar energies for [8] and [10]CPPs around 4.19 eV = 296 nm. Our calculations are in qualitative agreement with experimental absorption spectra in the sense that all [n]CPPs absorb at the same energy of 3.65 eV = 340 nm. TD-CAM-B3LYP is known to predict excitation energies that are generally blueshifted in comparison to experiment,30 but we selected this functional since the CAM correction reasonably eliminates the self-interaction error of DFT, which leads other functionals to the incorrect prediction of redshifted absorption spectra for [n]CPPs with increasing n.13
![Jahn–Teller energy diagram for (a) [8] and (b) [10]CPP at the TD-CAM-B3LYP/def-SV(P) level.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f3.gif) | ||
| Fig. 3 Jahn–Teller energy diagram for (a) [8] and (b) [10]CPP at the TD-CAM-B3LYP/def-SV(P) level. | ||
The B1E bright state undergoes first-order Jahn–Teller (JT) distortions, following the lowest two, e-type frequency modes in [8] and [10]CPPs, shown in Fig. 4 and 5. They both lead to oval deformations that are rotated by 45° along the two modes, namely Qθ with x2 − y2 transformation properties, and Qε with xy transformation properties. These two modes, which are energetically degenerate at a circular geometry, reduce the molecular point group symmetry to C2, as schematically indicated by the oval shapes on the axes of Fig. 3 and 6. Equatorial elongation along the positive direction of Qθ (elongation along the y axis and compression along the x axis) lowers the energy of the state's Ey component (xz nodal plane, a linear combination of HOMO → LUMO+1y and HOMO-1y → LUMO excitations), while elongation along the negative direction of Qθ (elongation along the y axis, compression along the x axis) lowers the energy of the Ex component (yz nodal plane, linear combination of HOMO → LUMO+1x and HOMO-1x → LUMO excitations). This situation had been depicted in Fig. 3. Similar relations hold for the distortions following the Qε mode. Therefore, the electronic B1E excited states of [n]CPPs belong to the famous E⊗e class of JT systems.
![S0 (blue) and S2 (red) optimized geometries for [8]CPP, and degenerate Jahn–Teller-active e vibrational modes (24.77 cm−1) obtained on the electronic ground state.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f4.gif) | ||
| Fig. 4 S0 (blue) and S2 (red) optimized geometries for [8]CPP, and degenerate Jahn–Teller-active e vibrational modes (24.77 cm−1) obtained on the electronic ground state. | ||
![S0 (blue) and S2 (red) optimized geometries for [10]CPP (left), and degenerate Jahn–Teller-active e vibrational modes (16.28 cm−1) obtained on the electronic ground state.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f5.gif) | ||
| Fig. 5 S0 (blue) and S2 (red) optimized geometries for [10]CPP (left), and degenerate Jahn–Teller-active e vibrational modes (16.28 cm−1) obtained on the electronic ground state. | ||
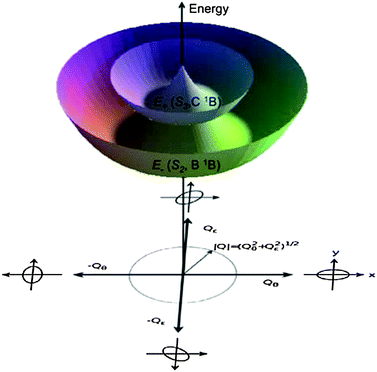 | ||
| Fig. 6 Schematic representation of the Jahn–Teller active, twofold degenerate e-type vibrational modes Qθ and Qε. The Franck–Condon (FC) geometry is in the center of the plot, whereas oval geometries resulting from the deformations are shown on the boundaries. In the limit of linear vibronic coupling, the S2 low- and S3 high-energy adiabatic potential energy surfaces (APES) arising from the two components of the B1E excited state at the FC region take the shape of two stacked Mexican hats,31 with identical energy isovalues at constant values of |Q|, and a conical intersection at |Q| = 0. | ||
In the distorted molecule, the two x and y components of the bright B1E state are mixed by vibronic coupling to yield a low-energy E− (S2, B1B) and a high-energy E+ (S3, C1B) adiabatic branch, according to
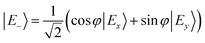 | (1) |
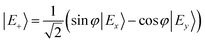 | (2) |
We briefly wish to mention that another, dark 1E excited state exists close to the bright 1E excited state described above. It is composed of negative linear combinations of HOMO → LUMO+1x and HOMO-1x → LUMO excitations in the case of the dark 1Ex state, and analogously for the dark 1Ey state, as opposed to the corresponding positive linear combinations in the bright B1E excited state, that were discussed above. These dark states are sometimes intermingled with the bright states, depending on the DFT functional (in particular, conventional TD-B3LYP predicts these states to be lower in energy for smaller [n]CPPs), while they are always slightly higher in energy with the CAM-B3LYP functional. They do follow the same JT characteristics as the bright B1E states. One can expect emissive contributions from these dark states to increase when the molecular geometries are more perturbed and symmetry rules become increasingly violated. This should be the case in the more flexible, smaller [n]CPPs, as we will explain further below.
In order to understand which CPP excited electronic state contributes to the observed fluorescence spectra, it is important to consider the mechanism of radiationless decay, commonly found in organic molecules, which usually causes emission spectra to be dominated by S1 → S0 transitions. As a matter of fact, Jasti et al.,1 Wong,16 and Fujitsuka et al.15 have based their explanation of the size-dependent fluorescent blueshift on the behavior of this transition, considering its unusual dependence as a function of CPP size. Our calculations confirm that a noticeable blue-shift occurs in the emission from S1 when comparing results for [8] and [10]CPP, consistent with the calculation results reported in ref. 15. However, the exceedingly small oscillator strengths associated with S0 → S1 transitions, and the double-peak feature in the experimental fluorescence spectra, provide evidence that the non-optical decay mechanism is largely suppressed in case of CPPs with large n (n ≥ ∼10). We rationalize this by the fact that the vibronic coupling matrix elements 〈S1∣∂/∂Qθ∣S2〉 and 〈S1∣∂/∂Qθ∣S3〉 as well as the equivalent matrix elements concerning coupling via ∂/∂Qε, which govern radiationless decay from S2 and S31B states to the totally symmetric 1A S1 state, are negligible, since the parity of the oval deformations ∂/∂Qθ and ∂/∂Qε is of g type, while the parities of the two electronic states are u and g, respectively. This fact leads to an overall u⊗g⊗g = u parity of the vibronic coupling matrix elements, and the integral vanishes accordingly, rendering nonradiative decay ineffective due to the symmetrical properties of the CPP skeleton and the electronic state symmetries. Thus, these circular molecules are able to maintain a high population of the high-energy components of the 1E state for an unusually long time after excitation. It is important that the oval shape is effectively maintained due to the peculiarity of the Mexican hat APES. As a consequence, emission from the bright B1E state after geometry relaxation is associated with two different emission energies, giving rise to a double peak in experimental UV/Vis spectra.1,6,13
Nevertheless, the JT distortion and relaxation in the excited state is apparently not responsible for the observed size-dependent fluorescence blueshift of the most intensive peaks. The relative energies of B1B and C1B bright states at relaxed geometries of [8] and [10]CPPs, shown in Fig. 3a and b, are very similar. Since the increase of S0 in this geometry is also nearly identical for both [8] and [10]CPPs, no blueshift is apparent in their emission from the two bright 1B states: The B1B → X1A and C 1B → X1A transitions for [8] and [10]CPPs are practically identical with values of 3.58 and 3.90 eV ([8]CPP) and 3.55 and 3.89 eV ([10]CPP)! This result is not all too surprising, however, since the orbital energies of HOMO-1 and LUMO on the one hand, and HOMO and LUMO+1 on the other, are pretty much parallel over the entire range of n, as shown in Fig. 2a. Recalling that the B1E ← X1A excitation at the Franck–Condon region occurred around 4.2 eV = 300 nm in both systems, we find a predicted constant Stokes shift of about 0.62 eV (52 nm) for both [8] and [10]CPP. Experimentally, this shift is as large as 1.35 eV (200 nm) in [8]CPP. A possible reason for this discrepancy could be the inadequacy of the theoretical method used to compute the emission energy. We have carefully considered this possibility. We found that the use of a larger cc-pVTZ basis set in single-point TD-CAM-B3LYP calculations in case of the [8]CPP compound increases the predicted Stokes shift only by 5.74 nm, not enough to explain the large difference between experimental and theoretical value obtained from relaxed excited state geometries. In addition, we considered the solvent electric field, and performed PCM calculations using the dielectric constant of chloroform. The resulting TD-CAM-B3LYP/def-SV(P) Stokes shift with PCM correction for the [8]CPP compound only increases by 7.50 nm, again, not enough to explain the large gap between experiment and static theoretical approach, even in combination with the correction by the increase in the basis set. Last, we considered the level of accuracy of the TD-CAM-B3LYP method itself for the prediction of the Stokes shift in the CPP compounds. For this purpose, we performed single point generalized multiconfigurational wave function (GMCQDPT) calculations18,19 for the [8]CPP Franck–Condon and relaxed excited state geometries. We considered both single and double excitations with 33 parent configurations spanning an active space including 24 active electrons within 24 active orbitals. The calculations indicated that the nature of the relevant excited states are properly described by single-electron excitations. We are therefore confident that the large discrepancy between experiment and TD-DFT predicted Stokes shifts by the static approach does not stem from contributions of double excited configurations. This assumption is also reasonable in the light of the fact that the difference between dihedral angle relaxation upon excitation to the S2 state between [8] and [10]CPPs is only 1.0°, while the ovality deformations in both systems are nearly indistinguishable. Thus, the relaxed S2 excited state geometries are very similar for different-size CPPs, hence giving rise to similar S2 → S0 emission energies.
3.3 Excited states molecular dynamics
Although our static calculations were able to reproduce absorption spectra with a single optically active transition independent of n, and the appearance of a Stokes-shifted double emission, the blueshift in emission spectra with increasing molecular size n was not observed for emission from S2 and S3. This finding is not surprising since it is in agreement with the size-dependence of the frontier MO energies, yet contradicting experimental observations. We therefore performed MD simulations in the excited states, as the potential energy surfaces of excited and ground state may not be, and are in general, not parallel to each other, causing large variations in optical transition energies. Specifically, we computed microcanonical trajectories on S1 to S3 excited states using the TD-DFTB method, and simulated fluorescence spectra based on TD-CAM-B3LYP transition energies computed for randomly selected snapshot geometries from the respective trajectories, as described in the Computational methods section.The simulated emission spectra of [8] and [10]CPP from S1 (grey), S2 (blue), and S3 (red) are shown in Fig. 7a and b, respectively. According to these simulations, the emission maxima for the [8]CPP system are located at 524.5 nm (2.36 eV, S1), 371.7 nm (3.36 eV, S2), and 348.3 nm (3.56 eV, S3), while those of the [10]CPP are blueshifted with values of 467.8 nm (2.65 eV, S1), 353.2 nm (3.51 eV, S2) and 341.1 nm (3.63 eV, S3). The size-dependent fluorescence blueshift from the bright excited states is relatively small, but clearly visible! The reason for this blueshift now becomes clear: Not static relaxation to the excited state minimum geometry, but dynamic effects play a transcendental role. This happens because the S2/S3 potential energy surfaces of small n CPPs are shallower (have smaller force constants) than those of large [n]CPPs, as shown schematically in Fig. 7c and d for [8] and [10]CPP, respectively. Thermal vibrations can induce larger deformations in the case of small n compounds, inline with the notion that their molecular skeleton is more flexible than that of the large n compounds, as originally suspected, but not proven by Jasti et al.1 We note that, once again, the simulated Stokes shifts are much smaller than experimentally observed. Since we are confident that the method reproduces differences between Stokes shifts of different [n]CPP systems accurately, and since we found that distortions of the JT geometries results in large redshifts, we suspect that distortions induced by collisions with solvent molecules might play a role for the prediction of the changes in the Stokes shift due to system size. From our results, however, it is already evident that smaller CPPs undergo larger dynamic Stokes shifts than larger CPPs.
![(a and b) Fluorescence spectra for [8] and [10]CPPs calculated at the TD-CAM-B3LYP/def-SV(P) ← TD-DFTB/MD, respectively. Grey lines (S1) are hardly visible due to small oscillator strengths. (c and d) Schematic potential energy surface for [8] and [10]CPPs, respectively.](/image/article/2013/SC/c2sc20878d/c2sc20878d-f7.gif) | ||
| Fig. 7 (a and b) Fluorescence spectra for [8] and [10]CPPs calculated at the TD-CAM-B3LYP/def-SV(P) ← TD-DFTB/MD, respectively. Grey lines (S1) are hardly visible due to small oscillator strengths. (c and d) Schematic potential energy surface for [8] and [10]CPPs, respectively. | ||
Regarding the symmetry-forbidden optical transition between S0 and S1, we find that during MD, oscillator strengths are not precisely zero, causing small peaks in the simulated emission spectra (grey curves in Fig. 7a and b). These peaks should be more intensive the more flexible the compounds are, and thus it is not surprising that they appear as a shoulder near 420 nm in experimental absorption spectra, and to an even greater degree in emission spectra, with dramatic Stokes shifts, owing to the unusual behavior of the HOMO–LUMO gap. Since our MD simulations were performed in vacuum, it can be expected that symmetry breaking events are more pronounced in solution, in particular because the initial geometry of the trajectories was the circular fully alternant conformation of the S1 minimum geometry.
In order to analyze the geometrical changes during excited states QM/MD simulations, we evaluated two geometrical parameters, namely the ovality O = a/b (a and b are the equatorial and polar radii, respectively) and the average dihedral angle between all PP units of an [n]CPP, for the 24 snapshot geometries. The left panel of 8 shows the relative energy of S0, S1, and S2 as a function of O, while the right panel presents the transition energies between S0 and S1 and between S0 and S2, also as a function of O. Similarly, 9 shows the relative energy and transition energies of S0, S1, and S2 as a function of the average absolute value of the dihedral angles between PP units. It is immediate from Fig. 8 and Fig. 9 that the data points are more spread out in the horizontal axis for [8] than for [10]CPPs, confirming that smaller CPPs undergo larger geometrical changes in comparison with larger CPPs. This is because the larger CPPs possess greater aromatic character as discussed for the energy dependence of the frontier MOs with ring size n. Therefore, upon single electron excitation from the occupied to virtual (quinoid) MO space, large CPPs retain more of their aromatic character than small CPPs, and will resist planarization and ellipsoidal deformations more.
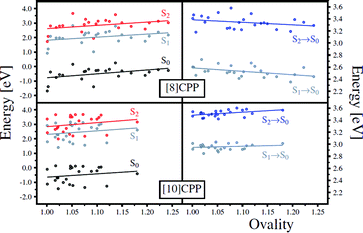 | ||
| Fig. 8 Relative energy with respect to S2 optimized energy (left panel) and transition energy (right panel) as a function of the ovality for 24 sampling geometries. | ||
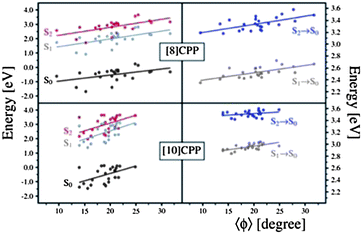 | ||
| Fig. 9 Relative energy with respect to S2 optimized energy (left panel) and transition energy (right panel) as a function of the torsion angle for 24 sampling geometries. | ||
3.4 Examination of ring strain release in the excited states
As already indicated in the introduction to this paper, Iwamoto et al. formulated in ref. 6 the interesting hypothesis that “the larger Stokes shift of the smaller CPPs can be explained by the release of strain energy in the excited state.” In order to verify this statement, we computed the hypothetical reaction| [n]CPP + H2 → [n]OPP + ΔEH + ΔEstr | (3) |
4 Conclusions
Static and dynamic approaches suggest that the double peak observed in the larger [n]CPP fluorescence spectra originates from the doubly-degenerate bright B1E excited state, which splits via a first-order Jahn–Teller (JT) effect involving two degenerate e-type oval deformation modes into two bright S2 and S3 states. These two 1B-type excited states form the adiabatic potential energy surface (APES) of an E⊗e JT system, and we find that the two S2 (low energy, E−) and S3 (high energy, E+) branches of the JT-distorted B1E excited state are close in energy and able to interconvert at the point of the conical intersection with an energy barrier of only 0.33 eV relative to the S2 global minimum. The nonradiative decay of the two bright states to the close-lying, dark 1A-type S1 state in larger CPPs (n ≥ ∼10) is inefficient due to the symmetry of the vibrational deformations and that of the electronic states. We also predict, using the same argumentation, that the nonradiative decay to the electronic 1A-type S0 ground state should be inefficient. Here it is important to stress that the overall fluorescence quantum yield decreases with the increase of emission from the formally symmetry-forbidden S1 excited state with CPPs decreasing in size. Thus, larger CPPs are endowed with an extraordinarily high fluorescence quantum yield, which is in perfect agreement with experimental observerations.13,15Emission spectra computed from fully relaxed geometries of the bright S2 excited state are unable to reproduce the size-dependent fluorescence blueshift in the emission spectra of CPPs. Our calculations have demonstrated that only dynamic effects can explain the blueshift phenomenon of the prominent CPP double peak in emission spectra, indicating that smaller CPPs feature smaller force constants at their minimum energy geometries in comparison to larger CPPs. The steeper potential energy surfaces of larger CPPs are the result of their larger degree of aromatic character (bending) and greater steric hindrance (dihedral angles between adjacent paraphenylene units) in comparison with smaller CPPs. We therefore find that emissions associated with the double emission from S2/S3 JT states, prevalent in large [n]CPPs, are exhibiting a “dynamic blueshift”. Since the smaller [n]CPPs and chiral CPPs32 are less stiff and can be expected to suffer larger and more irregular deformations of their oval molecular shapes, symmetry rules governing both radiative and non-radiative emissions are more relaxed and S1 should become more highly populated via the nonradiative decay from the JT states. This state indeed shows a static blueshift due to its lower energy in smaller CPPs, as discussed by Wong,16 possibly accompanied by a dynamic blueshift of its own. Unfortunately, emission from S1 is difficult to simulate with our methodology, as this would require the use of explicit solvent molecules and surface hopping or Ehrenfest dynamics trajectories allowing transitions from S2/S3 to S1 during excited state dynamics. Nevertheless, we find that all available experimental fluorescence spectra of smaller CPPs are consistent with our data, and can be explained straightforwardly on the basis of our CPP emission model.6 We therefore conclude that larger CPPs emit from S2/S3 JT states, whereas smaller CPPs undergo easily radiationless decay and emit dominantly (and inefficiently) from S1. This emission model is also consistent with recently measured experimental relaxation times.15
In conclusion, we expect that any π-conjugated, circular macrocyclic compound with constant-amplitude/constant energy HOMO and LUMO levels should show the described dynamic and static emission blueshifts, and that these blueshifts should exhibit a significant temperature effect due to their dynamic origin.
Acknowledgements
This work was supported by a CREST (Core Research for Evolutional Science and Technology) grant from the Deutsche Forschungsgemeinschaft (GRK 1570), and by a EU 7th Framework Marie Curie Actions IRSES project (grant no: 295172). We thank Profs. Yasutomo Segawa and Aiko Fukazawa (both Nagoya University) for discussions, Prof. Henryk Witek at NCTU for technical help to prepare Fig. 6, Dr Hai-Bei Li at Kyoto University to prepare Fig. 1, and an anonymous reviewer for helpful comments on the manuscript.References
- R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647 CrossRef CAS.
- H. Takaba, H. Omachi, Y. Yamamoto, J. Bouffard and K. Itami, Angew. Chem., Int. Ed., 2009, 48, 6112–6116 CrossRef CAS.
- H. Omachi, S. Matsuura, Y. Segawa and K. Itami, Angew. Chem., Int. Ed., 2010, 49, 10202–10205 CrossRef CAS.
- S. Yamago, Y. Watanabe and T. Iwamoto, Angew. Chem., Int. Ed., 2010, 49, 757–759 CrossRef CAS.
- R. Jasti and C. R. Bertozzi, Chem. Phys. Lett., 2010, 494, 1–7 CrossRef CAS.
- T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361 CrossRef CAS.
- Y. Segawa, S. Miyamoto, H. Omachi, S. Matsuura, P. Šenel, T. Sasamori, N. Tokitoh and K. Itami, Angew. Chem., Int. Ed., 2011, 50, 3244–3248 CrossRef CAS.
- T. J. Sisto, M. R. Golder, E. S. Hirst and R. Jasti, J. Am. Chem. Soc., 2011, 133, 15800–15802 CrossRef CAS.
- J. Xia, J. W. Bacon and R. Jasti, Chem. Sci., 2012, 3, 3018–3021 RSC.
- J. Xia and R. Jasti, Angew. Chem., Int. Ed., 2012, 51, 2474–2476 CrossRef CAS.
- E. H. Fort and L. T. Scott, J. Mater. Chem., 2011, 21, 1373–1381 RSC.
- H.-B. Li, A. J. Page, S. Irle and K. Morokuma, ChemPhysChem, 2012, 13, 1479–1485 CrossRef CAS , in press.
- Y. Segawa, A. Fukazawa, S. Matsuura, H. Omachi, S. Yamaguchi, S. Irle and K. Itami, Org. Biomol. Chem., 2012, 10, 5979–5984 CAS.
- Molecular Photonics, ed. K. Horie, H. Ushiki and F. M. Winnik, Kodansha, Tokyo and John Wiley & Sons, Weinheim and Chichester, 2000, p. 48 Search PubMed.
- M. Fujitsuka, D. W. Cho, T. Iwamoto, S. Yamago and T. Majima, Phys. Chem. Chem. Phys., 2012, 14, 14585–14588 RSC.
- B. M. Wong, J. Phys. Chem. C, 2009, 113, 21921–21927 CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Ebisuzaki, Y. Watanabe and H. Nakano, Chem. Phys. Lett., 2007, 442, 164–169 CrossRef CAS.
- H. Nakano, R. Uchiyama and K. Hirao, J. Comput. Chem., 2002, 23, 1166–1175 CrossRef CAS.
- K. Andersson, P. Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis, J. John and A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- T. H. Dunning, Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- Y. Segawa, H. Omachi and K. Itami, Org. Lett., 2010, 12, 2262–2265 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- TURBOMOLE V6.3 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, http://www.turbomole.com.
- T. A. Niehaus, J. Mol. Struct., 2009, 914, 38–49 CrossRef CAS.
- P. Schleyer, M. Manoharan, Z.-X. Wang, B. Kiran, H. Jiao, R. Puchta and N. van Eikema Hommes, Org. Lett., 2001, 3, 2465–2468 CrossRef CAS.
- D. Jacquemin, E. Brémond, A. Planchat, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2011, 7, 1882–1892 CrossRef CAS.
- The Jahn–Teller Effect, ed. I. B. Bersuker, Cambridge University Press, New York, 2006 Search PubMed.
- B. M. Wong and J. W. Lee, J. Phys. Chem. Lett., 2011, 2, 2702–2706 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sc20878d |
| ‡ Highest possible molecular point groups of the ground state global minima are D(n/2)d for even n and C2 for odd n. |
| This journal is © The Royal Society of Chemistry 2013 |
