Towards predictable transmembrane transport: QSAR analysis of anion binding and transport

Abstract

The transport of anions across biological membranes by small molecules is a growing research field due to the potential therapeutic benefits of these compounds. However, little is known about the exact mechanism by which these drug-like molecules work and which molecular features make a good transporter. An extended series of 1-hexyl-3-phenylthioureas were synthesized, fully characterized (NMR, mass spectrometry, IR and single crystal diffraction) and their anion binding and anion transport properties were assessed using ¹H NMR titration techniques and a variety of vesicle-based experiments. Quantitative structure–activity relationship (QSAR) analysis revealed that the anion binding abilities of the mono-thioureas are dominated by the (hydrogen bond) acidity of the thiourea NH function. Furthermore, mathematical models show that the experimental transmembrane anion transport ability is mainly dependent on the lipophilicity of the transporter (partitioning into the membrane), but smaller contributions of molecular size (diffusion) and hydrogen bond acidity (anion binding) were also present. Finally, we provide the first step towards predictable anion transport by employing the QSAR equations to estimate the transmembrane transport ability of four new compounds.

---

Introduction

The development of new transport systems for anionic species is attracting significant attention.^1–5 The synthesis of new compounds capable of mediating the lipid bilayer transport of anions has generated compounds that can form membrane spanning channels,^6–8 relay systems that can ‘hand’ anions across a membrane,⁹ and anionophores that coordinate anions and encapsulate them in a lipophilic coat that allows the complex to diffuse through the hydrophobic interior of the bilayer.^10–13 There are potential future applications of these compounds in treating diseases caused by malfunctioning anion transport proteins in cell membranes (such as cystic fibrosis),¹⁴ or in perturbing pH gradients within cancer cells leading to apoptosis.^15–18 Our interest in this latter approach led us to develop anion transporters that initially contained multiple hydrogen bond donors that were based on some of the most effective anion receptor motifs known, such as tris(2-aminoethyl)amine (tren).^19,20 However, in order for these species to be eventually applied in vivo we decided to move away from the types of compound traditionally used as receptors and instead develop simpler transporters that have lower molecular masses, lower numbers of hydrogen bond donors and acceptors and lower log P values (octanol–water partitioning coefficient) in order to optimize the chances that these compounds possess acceptable ADME properties (absorption, diffusion, metabolism and excretion), i.e. are more ‘drug-like’.²¹ By doing this we discovered that very simple small molecules such as thioureas,^22,23 cyanoguanidines²⁴ and squaramides²⁵ are capable of effective transmembrane transport of chloride and bicarbonate.

In this paper we report the effect of varying a single functional group in 1-hexyl-3-phenylthiourea on the transport properties of a series of compounds (1–22). Previous studies by Davis and co-workers have shown the effect of varying functional groups on cholic acid-based transmembrane anion transporters,²⁶ while Quesada and co-workers have studied the effect of lipophilicity by increasing the length of an alkyl chain.²⁷ However, these previous reports link the anion transport ability to molecular properties such as anion binding in a non-quantitative manner. Since the ultimate goal of the development of transmembrane anion transporters lies in their medicinal use, we decided to apply the techniques frequently used in the optimization of pharmacologically active compounds to the study of supramolecular transmembrane transport of anions. By employing various types of QSAR (quantitative structure–activity relationship) we have tried to elucidate the parameters that are key for efficient transport in this series of molecules and have successfully used this analysis to predict the transport properties of related compounds. Furthermore, the anion binding properties of this series of compounds could be rationalized and predicted using standard QSAR techniques.

Results and discussion

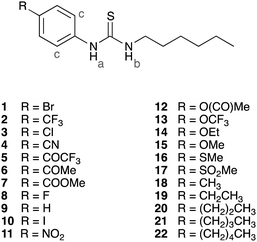
Selection of compounds

A total of 22 1-hexyl-3-phenylthioureas with various substituents in the para-position of the phenyl ring were synthesized in one or two steps from commercially available products using standard procedures (ESI,† compounds 2,²³9²⁴ and 11²⁸ have been previously reported). The majority of the compounds were crystalline solids and crystal structures were obtained using single crystal X-ray diffraction (ESI†).^29,30 Out of these 22 compounds, four receptors (1, 6, 14 and 20) were randomly selected, whilst ensuring they cover the range of observed transport abilities, and were not used to build the QSAR models, but rather were used as a test set to validate the models (predictions). The remaining 18 compounds formed the training set and are discussed in detail in the following sections.

QSAR analysis of anion binding

The ability of the receptors to bind anions in solution was investigated using ¹H NMR titration techniques in DMSO-d₆ containing 0.5% water (with the anions added either as tetrabutylammonium (TBA) or tetraethylammonium (TEA) salts). The binding studies were performed for anions relevant in biological systems (TBA nitrate, TBA chloride, TBA dihydrogen phosphate and TEA bicarbonate). Where possible, the change in chemical shift of the thiourea NH signals or the ortho CH signal was fitted to a 1 : 1 binding model using the WinEQNMR2 computer program³¹ and the results are summarized in Table 1. The association of 1-hexyl-3-phenylthioureas with anions decreases in the following order: HCO₃⁻ ≈ H₂PO₄⁻ > Cl⁻ > NO₃⁻. No interaction could be observed with nitrate, while weak interactions were obtained for chloride and stronger associations were detected in the case of dihydrogen phosphate and bicarbonate (Table 1). More interestingly, the association constants in Table 1 also show a clear influence of the substituents on anion binding, with the highest association constants obtained for the most electron withdrawing substituents such as –NO₂ and –SO₂Me.

Table 1 Overview of anion binding data: association constants (log K_a) for the training set with various anions in DMSO-d₆/0.5% water at 298 K (error <15%), along with the Hammett constant for the substituent in the para-position (σ_p), and overview of anion transport data: log P, initial rate of chloride release (k_ini), EC₅₀ and n (the transport results are an average of at least 3 independent repeats and standard deviations are given between brackets)

Compound	Anion binding data, log Ka				Anion transport data
	σ p	Cl^−^b	H2PO4^−^b	HCO3^−^c	log P^d	k ini	EC50^f	n
a Values taken from ref. 32. b Anion added as TBA salt, data for the alkyl thiourea NHb is given. c Anion added as TEA salt, data for the ortho CH is given due to peak broadening of the thiourea NHs. d Clog P values calculated using Daylight version 4.73. e Values calculated by fitting the plot of relative chloride release (y) versus time (x) for 2 mol% transporter to lipid to an asymptotic function y = a − bc^x. The initial rate of chloride release (kini in % s^−1) is given by −bln(c). f EC50 (in mol% transporter to lipid) is the concentration of transporter needed to obtain 50% chloride efflux in 270 s. Values obtained by means of Hill plot. g Hill coefficient n value obtained by means of Hill plot. h Association constant could not be obtained due to decomposition of the compound. i Peak broadening/overlap and deprotonation of the compound make the obtained binding constant unreliable.
2 (CF3)	0.54	1.42	2.93	2.97	4.938	2.3 (±0.4)	0.44 (±0.04)	1.65 (±0.08)
3 (Cl)	0.23	1.30	2.63	2.63	4.541	0.60 (±0.15)	1.0 (±0.2)	1.57 (±0.19)
4 (CN)	0.66	1.50	3.04	3.19	3.661	1.4 (±0.5)	0.8 (±0.2)	2.11 (±0.13)
5 (COCF3)	0.80	1.62	—^h	—^h	4.075	3.8 (±1.0)	0.9 (±0.1)	1.93 (±0.13)
7 (COOMe)	0.45	1.41	2.85	2.77	4.046	0.19 (±0.05)	2.3 (±0.4)	1.76 (±0.19)
8 (F)	0.06	1.19	2.43	2.48	3.971	0.22 (±0.07)	2.0 (±0.4)	1.67 (±0.15)
9 (H)	0.00	1.13	2.32	2.35	3.526	0.17 (±0.03)	2.7 (±0.5)	0.91 (±0.11)
10 (I)	0.18	1.30	2.65	2.75	4.951	0.69 (±0.16)	1.0 (±0.1)	1.87 (±0.31)
11 (NO2)	0.78	1.63	2.92	(2.54)^i	3.917	2.8 (±0.6)	0.45 (±0.05)	2.05 (±0.08)
12 (OCOMe)	0.31	1.24	2.44	2.42	3.059	0.025 (±0.004)	12 (±2)	1.94 (±0.14)
13 (OCF3)	0.35	1.39	2.63	2.64	4.738	1.8 (±0.4)	0.42 (±0.09)	1.41 (±0.15)
15 (OMe)	−0.27	1.03	2.12	2.16	3.629	0.076 (±0.007)	5.5 (±0.9)	1.29 (±0.03)
16 (SMe)	0.00	1.17	2.45	2.50	4.085	0.17 (±0.04)	2.6 (±0.7)	1.60 (±0.44)
17 (SO2Me)	0.72	1.58	2.97	2.85	2.641	0.041 (±0.007)	10.6 (±0.6)	2.48 (±0.19)
18 (Me)	−0.17	1.04	2.21	2.17	4.025	0.32 (±0.12)	1.3 (±0.5)	0.88 (±0.19)
19 (Et)	−0.15	1.13	2.23	2.18	4.554	0.55 (±0.12)	0.3 (±0.1)	0.63 (±0.04)
21 (Bu)	−0.16	1.10	2.21	2.34	5.612	1.10 (±0.13)	0.12 (±0.04)	0.77 (±0.15)
22 (Pe)	−0.15	1.11	2.34	2.26	6.141	1.4 (±0.2)	0.08 (±0.01)	0.86 (±0.17)

---

A good descriptor to quantify the electron withdrawing effect of a particular substituent can be found in the Hammett constant,³² which is well tabulated for most substituents and has been extensively used in QSAR analyses³³ and has previously been linked to hydrogen bond based anion recognition.^34–40 A plot of the log K_a values versus the Hammett constants of substituents in the para-position (σ_p) can be found in Fig. 1. Linear fits through these plots resulted in eqn (1)–(3) that possess acceptable R² values (0.96 for the association with Cl⁻, 0.92 for H₂PO₄⁻ and 0.84 for HCO₃⁻), indicating that the electronic effect of the substituent is the main factor that influences the interaction towards the anion. Single crystal X-ray analysis of the free receptors indicated that hydrogen bonding interactions between the thiourea NH and the substituent is possible in the solid state for substituents containing hydrogen bond acceptors (ESI†). However, these substituent interactions do not seem to affect the association of the receptor with anions in solution, as the Hammett constant alone is sufficient to describe anion binding. It is also evident that the best fit is obtained for the interaction with chloride, with lower R² values for dihydrogen phosphate and bicarbonate (eqn (1)–(3), N is the number of data points, RMSE is root mean square error and F is the F-test value).

log K_a(Cl⁻) = 0.55(±0.03)σ_p + 1.17(±0.01), N = 18, R² = 0.96, R_adj² = 0.96, RMSE = 0.04, F = 424 (1)

log K_a(H₂PO₄⁻) = 0.85(±0.06)σ_p + 2.38(±0.02), N = 17, R² = 0.92, R_adj² = 0.91, RMSE = 0.09, F = 167 (2)

log K_a(HCO₃⁻) = 0.88(±0.10)σ_p + 2.40(±0.04), N = 16, R² = 0.84, R_adj² = 0.83, RMSE = 0.13, F = 73 (3)

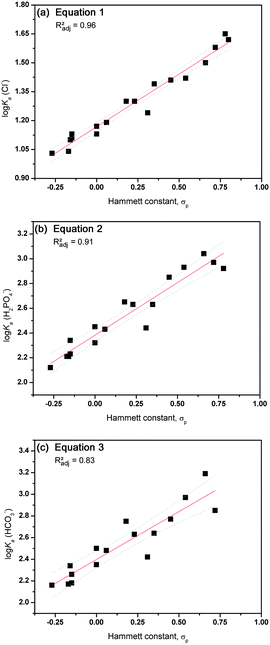Fig. 1 Graphical representation of the correlation between anion binding (log K_a) and the Hammett constant σ_p for compounds 1–22 (excluding 1, 6, 14 and 20). Linear fits are represented by a red line with 95% confidence levels shown as dotted grey lines. (a) Interaction with Cl⁻vs. Hammett constant; (b) interaction with H₂PO₄⁻vs. Hammett constant; (c) interaction with HCO₃⁻vs. Hammett constant.

The lower R² values for dihydrogen phosphate and bicarbonate are most likely due to competing deprotonation of the receptor by the anion, an event that is more significant in the case of more acidic receptors (i.e. stronger electron withdrawing substituent) and more basic anions such as dihydrogen phosphate and especially bicarbonate.^41,42 In the case of the most electron withdrawing substituent of the series (COCF₃), the addition of HCO₃⁻ and H₂PO₄⁻ results in decomposition of the receptor, presumably due to deprotonation. Also compound 11, containing the strongly electron withdrawing –NO₂ group, appeared to be unstable in the presence of bicarbonate. Similarly, attempts were made to synthesize a 1-hexyl-3-phenylthiourea with the even more electron withdrawing –SO₂CF₃ group (σ_p = 0.96), but the compound proved to be unstable and degraded in a few hours. In brief, it appears that the anion binding properties of simple thioureas follow a normal Hammett correlation where the highest binding is observed for the receptor containing the most electron withdrawing substituent, but deprotonation of the thiourea functionality can compete with anion binding in the case of basic anions and extremely electron withdrawing substituents.⁴³

In order to investigate this effect in more detail, we also examined the influence of the Hammett constant of substituents in the meta-position (σ_m) and the pK_a of both thiourea NHs (calculated using ACD iLabs 2.0, algorithm version v12.1.0.50374).⁴⁴ No correlation was found between log K_a and σ_m, or between log K_a and the pK_a of NH_b. However, a good correlation does exist between log K_a and the pK_a of NH_a (for correlation with log K_a(Cl⁻) R² = 0.93), which is unsurprising as the Hammett constants were originally derived from pK_a values (see ESI†).⁴⁵ These results imply that the influence of the substituents on the anion binding affinity of 1–22 is due to their influence on the pK_a (and therefore hydrogen bond donating ability) of NH_a, and not due to increased participation of aromatic CH_c in the binding event (which should result in correlation with σ_m), as previously observed for another set of anion receptors.⁴⁶

Another parameter that can be used to model the electronic factors in anion binding is given by the electrostatic potential surface maxima points, V_S,max, which is an easy to calculate parameter that has previously been shown to correlate well with hydrogen bonding capacity^47,48 and acidity.⁴⁹V_S,max values were computed for all receptors at B3LYP/6-311++G** level, using the optimized structures of their chloride complexes with the same basis set after removing the anion, according to the method described by Politzer et al. (see ESI† for computational details).⁵⁰ For all of the receptors the most positive region of the molecule is the N–H binding area, as exemplified for receptor 4 in Fig. 2, with the electrostatic potential mapped on the molecular electron density (left) and showing the maximum, drawn as a pink dot (right), located at the binding pocket. In the case of compounds 1–22 the calculated V_S,max values correlate well with the Hammett constants (σ_p, R² = 0.97) and as a consequence also with the anion binding constants (for correlation with log K_a(Cl⁻) R² = 0.91) (see ESI† for details).

Fig. 2 Electrostatic potential mapped on the molecular electron density surface (0.001 electrons per Bohr³) for receptor 4. The colour scale ranges from blue (+0.11 a.u.) to red (−0.07 a.u.). The pink dot corresponds to the location of the V_S,max.

For this set of compounds, the V_S,max parameter might therefore not be relevant as the anion binding properties are easily correlated to the Hammett parameters. However, V_S,max, which is a quantum parameter, has the advantage that it can be calculated for any type of receptor while the Hammett constant, an empirical parameter, is specific for one substituent only. We therefore believe that V_S,max calculations can be useful in the future when analysing or modelling the anion binding ability of more complicated receptors containing more than one substituent and several (convergent) anion binding sites.

Anion transport mechanism

The transmembrane anion transport abilities of 1–22 were assessed using standard methods.^51,52 Initially, we prepared a series of unilamellar 1-palmitoyl-2-oleoylphospatidylcholine (POPC) vesicles of defined size (200 nm in diameter). The vesicles were loaded with a buffered sodium chloride solution (489 mM in 5 mM phosphate buffer at pH 7.2) and suspended in an isotonic sodium nitrate solution. A thiourea was then added as a solution in a small amount of DMSO (2 mol% thiourea to lipid) and the resultant transport of chloride out of the vesicles was monitored using an ion selective electrode (ISE). At the end of the experiment, the vesicles were lysed by addition of detergent and the final reading was used to calibrate the ISE to 100% chloride release. From this data it is possible to calculate the initial rate of chloride release (k_ini), as shown in Table 1. A graphical representation of the results can be found in Fig. 3 for a selection of compounds and clearly indicates a strong influence of the nature of the substituent on the chloride transport rate. Some compounds, such as 22 (–pentyl) and 11 (–NO₂), are able to transport nearly all chloride ions out of the vesicles in 2 minutes, while other compounds (e.g.17 (–SO₂Me)) can only transport 10% chloride in 5 minutes. A detailed analysis that can clarify the nature of this substituent effect therefore seems justified (see next section).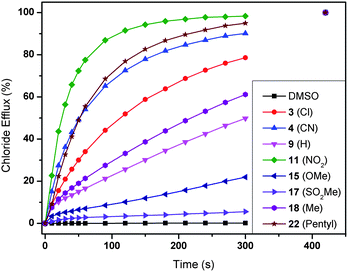

Fig. 3 Chloride efflux promoted by a selection of compounds 1–22 (2 mol% thiourea to lipid) from unilamellar POPC vesicles loaded with 489 mM NaCl buffered to pH 7.2 with 5 mM sodium phosphate salts. The vesicles were dispersed in 489 mM NaNO₃ buffered to pH 7.2 with 5 mM sodium phosphate salts. At the end of the experiment, detergent was added to lyse the vesicles and calibrate the ISE to 100% chloride efflux. Each point represents the average of at least 9 trials. DMSO was used as a control.

According to the results in Fig. 3, the 1-hexyl-3-phenylthioureas 1–22 can transport chloride via either an antiport mechanism (charge balance through transport of NO₃⁻) or a symport mechanism (charge balance through transport of Na⁺ or H⁺). The experiments were therefore repeated with CsCl encapsulated within the vesicles in order to determine the role of the cation in the transport process. Under these conditions no significant change was observed in chloride transport rate, evidence that leads us to suggest that a chloride/nitrate exchange process is occurring in these experiments. Further support for an antiport mechanism was obtained when the experiments were repeated with the vesicles suspended in sodium sulfate solution (162 mM Na₂SO₄ in 20 mM phosphate buffer at pH 7.2). Sulfate is highly hydrophilic and hence it can normally be assumed that sulfate will not be transported by small molecule anion carriers.⁵³ Under these conditions no significant chloride transport was observed (ESI†). After 120 seconds a pulse of NaHCO₃ was added to this extravesicular sulfate solution (to make the external solution 40 mM NaHCO₃). This allowed the thioureas to transport chloride via a chloride/bicarbonate antiport process and chloride efflux was observed (ESI†).

The anion transport ability of 1–22 can be due to ion channel formation or to a mobile carrier mechanism. Even though ion channel formation by small thioureas seems unlikely, U-tube experiments using nitrobenzene as an organic phase separating two aqueous phases, one containing the anion salt and one receiving phase, were carried out and indicated that these receptors can operate via a mobile carrier mechanism (ESI†). Hill analyses were conducted on all of the transporters for chloride/nitrate exchange by measuring the chloride efflux mediated by various concentrations of transporter.⁵⁴ Each Hill plot was repeated a minimum of 3 times to ensure adequate repeatability. These studies elucidated n values <2.5 for these experiments consistent with a mobile carrier mechanism (Table 1).⁵⁵ The Hill analyses also provide a quantitative measure for anion transport activity in the form of EC₅₀ values, i.e. the concentration of transporter required to achieve 50% chloride efflux in 270 s. The obtained values are given in Table 1 and again show a profound effect of the substituent on anion transport ability, with the best transporter (22, –pentyl, EC₅₀ = 0.08) being 150 times more active than the least active transporter (12, –OCOMe, EC₅₀ = 12).

QSAR analysis of anion transport

The previous discussion has shown that various substituents can significantly alter the anion transport behaviour of thioureas. It is our aim to identify the exact nature of this substituent effect so that it can be used in the design of future anion transporters. However, anion transport is a more complex process than anion binding and there are many equilibria and side reactions possible during transmembrane anion transport, as shown in Fig. 4. For example, the transport of anions across a lipid bilayer depends on the partitioning of the free receptor and the anion complex into the membrane, diffusion of the receptor and the complex through the aqueous phase and through the bilayer, binding of a specific anion on one side of the membrane and release of the anion at the other side of the membrane, interference/competition with other ions (including buffer), interactions with the phospholipids of the membrane (and subsequent flippase activity, i.e. the phospholipid is transported from the inner to the outer membrane leaflet and vice versa),^56,57 and many other environmental factors (Fig. 4). A given substituent can have an influence on all of these events and hence it can be challenging to pinpoint the exact nature of the substituent effect and to extrapolate the physical properties that are required to obtain a highly active anion transporter. Quantitative structure–activity relationship (QSAR) is a technique that is often used in medicinal chemistry to optimize a potential drug and to elucidate the mechanism by which this drug operates.⁵⁸ QSAR analysis often consists of the modelling of biological activity (often log(1/IC₅₀)) as a linear combination of molecular properties.^58–60 Most drugs require diffusion/distribution throughout the biological system, crossing of cellular membranes and interactions with the target protein (binding), and the analogy with anion transport is clear. We therefore postulate that the same QSAR techniques can be employed in the study of anion transport specifically and supramolecular chemistry in general.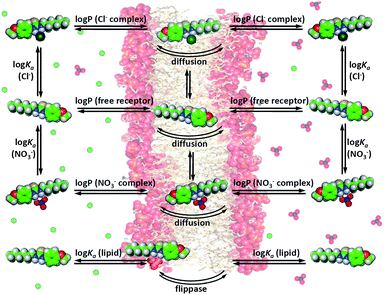

Fig. 4 Graphical depiction of the most important equilibria present during transmembrane anion transport.

The first question to be asked is which measurement of anion transport activity is suitable for QSAR analysis. Table 1 represents two different measurements of anion transport ability, namely the initial rate of chloride efflux mediated by 2 mol% transporter (k_ini) and the EC₅₀ values, and it appears that they do not show the same trend in activity. The receptor that transports chloride faster at 2 mol% loading (5, –COCF₃), for example, does not correspond to the receptor with the lowest EC₅₀ value (22, –pentyl). However, the compounds with the lowest EC₅₀ values also display the lowest Hill coefficients n. This implies that their transport activity is less concentration dependent and hence that the receptors are able to transport chloride out of the vesicles at very low loadings (low EC₅₀ values), even if the chloride transport never becomes very fast (low k_ini). It is possible to correlate the experimental values of k_ini, n and EC₅₀ to each other according to eqn (4). Due to the fact that EC₅₀ and k_ini are interchangeable, both measurements should be suitable for QSAR analysis. However, the k_ini values have an upper limit depending on the response time of the ion-selective electrode, which can cause problems during analysis. Furthermore, the EC₅₀ values as defined in anion transport (concentration of transporter needed to obtain 50% chloride efflux in 270 s) are similar to the EC₅₀ (effective concentration) or IC₅₀ (inhibitory concentration) values often used in medicinal chemistry QSAR modelling and it is reasonable to assume that the anion transport EC₅₀ values can be treated in an analogous fashion. In the following discussion the EC₅₀ values are converted to log(1/EC₅₀) prior to analysis, as is customary in QSAR analysis.

log(1/EC₅₀) = −0.68(±0.06)n − 1.25(±0.08)log(1/k_ini)/n + 1.3(±0.1), N = 18, R² = 0.95, R_adj² = 0.94, RMSE = 0.14, F = 145 (4)

Previous reports on the effect of substituents on the anion transport ability of a receptor have focused on the electronic influence of the substituent and hence on the link between anion binding and anion transport.^27,40 However, it is often overlooked that strongly electron withdrawing substituents also have an effect on the geometry, solubility and partitioning of the molecule. Furthermore, there have been recent studies regarding the importance of lipophilicity on anion transport ability,^20,61 including a systematic study of various alkyl chain derivatives of tambjamines.²⁷ In this paper, we therefore want to quantitatively prove whether the effect of a large variety of substituents (alkyl, electron donating or withdrawing) is mainly due to their influence on anion binding, lipophilicity or a combination of both.

Octanol–water partitioning coefficients (log P values) are often used as a quantitative measure for lipophilicity and there are many computational tools available to calculate these values.^44,62–66 Unfortunately, they do not all yield the same results or trends. In order to obtain reliable calculated log P values for this series of compounds, we measured experimental retention times on reversed-phase HPLC.⁶⁷ The results show that log P values calculated using Daylight v4.73 (Clog P)⁶⁴ give the highest correlation with the HPLC retention times (see ESI†). In the following discussion, log P will always refer to the values calculated using this method and are shown in Table 1. In principle, both the retention times (RT) and the log P values can be used to build a QSAR model. Whereas the retention times are experimental values and will result in better models that give more insight into the mechanism of transport, log P values can be calculated without the need to synthesize the molecule and are therefore more useful to predict the anion transport activity of unknown receptors.

The correlation between the anion transport activity and lipophilicity was calculated by standard least-squares linear regression using the JMP 9.0.0 software package⁶⁸ and resulted in eqn (5) (retention time) and (6) (log P). The strong correlations shown in eqn (5) and (6) (R² = 0.84 and 0.79 respectively) firmly establish the importance of lipophilicity as a factor in anion transport, where an increase in the log P value of a receptor results in an increase in anion transport activity. Previous reports have noted an optimum log P value after which a decrease in transport ability is observed upon a further increase of log P (due to low solubility or the inability to move towards the aqueous phase to pick up a suitable ion).^20,27,61 This could be modelled by the addition of a squared term (RT² or (log P)²), but this did not significantly improve the model in this case (see ESI†). It seems that for this set of compounds the lipophilicity has not yet reached its optimum value.

log(1/EC₅₀) = 0.75(±0.08)RT − 9.5(±1.0), N = 18, R² = 0.84, R_adj² = 0.83, RMSE = 0.24, F = 87 (5)

log(1/EC₅₀) = 0.62(±0.08)log P − 2.6(±0.3), N = 18, R² = 0.79, R_adj² = 0.77, RMSE = 0.28, F = 60 (6)

Even though the statistics of eqn (5) and (6) are good, lipophilicity alone cannot explain all events during anion transport. Anion binding also plays an important role, as is evident from the fact that only anions are transported and not cations (antiport mechanism). Furthermore, compounds 2 (–CF₃) and 11 (–NO₂) have similar EC₅₀ values (0.44(±0.04) mol% and 0.45(±0.05) mol% respectively) but display a large difference in log P (4.938 and 3.917 respectively). Inversely, compounds 5 (–COCF₃) and 16 (–SMe) are equally lipophilic (log P 4.07 and 4.08 respectively), but displayed a significant difference in anion transport activity (EC₅₀ 0.9(±0.1) mol% and 2.5(±0.7) mol% respectively). Presumably, these discrepancies are due to the influence of the substituents on molecular properties other than lipophilicity, such as binding ability, size, shape, polarizability and others. With a dataset of 18 compounds we can in theory build statistically reliable models containing up to 3 descriptors. In order to find which molecular properties best explain the remaining variation in anion transport, we calculated a total of 286 molecular descriptors using ChemDraw Ultra 12.0,⁶⁹ e-Dragon,^62,63 ACD iLabs 2.0,⁴⁴ Chemicalize⁷⁰ and DFT calculations (see ESI†). Stepwise multiple linear regression was performed using the JMP 9.0.0 software package⁶⁸ to select a suitable QSAR model. It was observed that the best two parameter models contained one term describing lipophilicity and one describing molecular size/shape, whereas the best three parameter models contained a lipophilicity term (e.g. RT), an electronic term (e.g. σ_p) and a molecular size term (e.g. SPAN) (see ESI†). Eqn (7) and (8) were selected as good models for anion transport by 1-hexyl-3-phenylthioureas. The increase in both R² and R_adj² compared to eqn (5) and (6), combined with a pass for Student's t-test for all parameters, indicates that eqn (7) and (8) are indeed statistically relevant models and that all descriptors contribute significantly to the model (see ESI†).

log(1/EC₅₀) = 0.94(±0.07)RT + 0.48(±0.14)σ_p − 0.31(±0.07)SPAN − 9.0(±0.8), N = 18, R² = 0.93, R_adj² = 0.92, RMSE = 0.17, F = 68 (7)

log(1/EC₅₀) = 0.81(±0.08)log P + 0.65(±0.19)σ_p − 0.29(±0.09)SPAN − 0.73(±0.79), N = 18, R² = 0.89, R_adj² = 0.87, RMSE = 0.21, F = 39 (8)

The physical meaning of eqn (7) and (8) is immediately apparent. The first term describes lipophilicity (retention time (RT) or log P) and has a positive coefficient assigned to it, which implies that an increase in lipophilicity causes an increase in anion transport ability. This can be explained by increased partitioning of the transporter (and anion complex) into the lipid bilayer and an enhanced ability to screen the inherently lipophobic anions from the apolar inner membrane. The second term is the Hammett coefficient for substituents in the para-position, σ_p, and is therefore a term for anion binding (vide supra). The positive sign related to this term implies that the greater the anion binding ability of a given thiourea, the greater its anion transport ability. Similar to anion binding, equally valid models can be obtained when the Hammett coefficient in eqn (7) and (8) is replaced with the pK_a of NH_a or with V_S,max (see ESI†). The third term, SPAN, is defined as the radius of the smallest sphere centred on the centre of mass completely enclosing all atoms of the molecule and is therefore a descriptor for molecular size.^71,72 The negative sign of the coefficient leads to a decrease in transport ability for larger molecules. This is most likely due to the slower diffusion of larger molecules through the aqueous layer and the membrane and is further proof that 1-hexyl-3-phenylthioureas function as mobile carriers rather than ion channels (which do not depend on diffusion of the transporter inside the membrane). The coefficients in eqn (7) and (8) were obtained using absolute values for RT, log P, σ_p and SPAN, and cannot be compared to each other to judge which term is most important. Scaled estimates of the coefficients were therefore calculated using JMP 9.0.0 and are shown in Fig. 5.⁷³Fig. 5 clearly shows that the variation in anion transport ability of compounds 1–22 is dominated by lipophilicity (log P or retention time) with smaller, yet significant, contributions from anion binding (σ_p) and diffusion (SPAN).

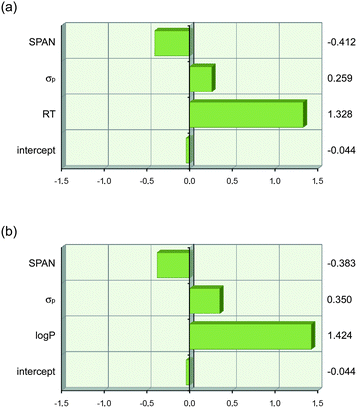Fig. 5 Graphical depiction of the values of the coefficients in eqn (7) and (8) when the descriptor values are scaled to have a mean of zero and a range of two using JMP 9.0.0. This shows that lipophilicity (RT or log P) has the strongest effect on anion transport. The values of the scaled coefficients for each descriptor are shown on the right hand side. (a) eqn (7) and (b) eqn (8).

Another consequence of using absolute, unscaled descriptor values during QSAR analysis is that the intercept becomes ill-defined (e.g.eqn (8)). This can be overcome by using relative descriptor values. The Hammett constant is a substituent descriptor and is defined relative to an unsubstituted compound. Hansch defined a substituent lipophilicity descriptor, π, which is also defined relative to an unsubstituted parent molecule and can be obtained by log P(x) − log P(unsubstituted).⁵⁹ By analogy, we can define Δ_SPAN as the substituent size descriptor relative to unsubstituted parent compound 9. When all parameters in eqn (8) are replaced by these relative descriptors, eqn (9) is obtained. The intercept in eqn (9) (−0.38(±0.11)) should now correspond to the experimental log(1/EC₅₀) value of parent compound 9 (−0.43(±0.10)), when π = σ_p = Δ_SPAN = 0. We can reduce the amount of optimized parameters to three by restraining the intercept to the experimental log(1/EC₅₀) value of 9 to obtain final eqn (10).

log(1/EC₅₀) = 0.81(±0.08)π + 0.65(±0.19)σ_p − 0.29(±0.09)Δ_SPAN − 0.38(±0.11), N = 18, R² = 0.89, R_adj² = 0.87, RMSE = 0.21, F = 39 (9)

log(1/EC₅₀) = 0.82(±0.08)π + 0.66(±0.18)σ_p − 0.26(±0.07)Δ_SPAN − 0.43, N = 18, R² = 0.89, R_adj² = 0.87, RMSE = 0.21, F = 42 (10)

In summary, eqn (4)–(10) represent statistically relevant QSAR models for the anion transport ability of simple mono-thioureas. They highlight the importance of lipophilicity and can be useful to predict the anion transport ability of other thioureas, although the anion binding properties and size of the substituents also need to be taken into account.

Predicting anion binding and transport

The most interesting aspect of QSAR models is their ability to estimate the activity of new, unknown compounds. This can be employed to predict which analogue will have improved activity compared to the original training set and will be the most useful to synthesize and study. In order to test the predictability of models 1–10, four receptors (1, 6, 14 and 20) were initially excluded from the training set and were not used to build models 1–10. The ability of this test set to bind to chloride, phosphate and bicarbonate (log K_a) was predicted using eqn (1), (2) and (3) respectively and their anion transport abilities were predicted according to eqn (5)–(10). The results are given in Table 2. The calculated values were compared with experimentally observed anion association constants and log(1/EC₅₀) values (Table 2). An easy way to judge predictability is by studying the actual versus predicted plot, which is given in Fig. 6 for both the training and test set for a selection of models. Fig. 6 shows that eqn (1) is excellent in predicting the association constant of a given 1-hexyl-3-phenylthiourea with TBA chloride. It is also clear that both eqn (6) and (10) possess a good degree of predictability, with eqn (10) still outperforming eqn (6). This is another confirmation that the transport activity of a mono-thiourea can be reasonably estimated from its lipophilicity (eqn (6)), but a better prediction is obtained when both the size and anion binding ability of the thiourea are also taken into account (eqn (7)–(10)). Table 2 includes the R_adj² values corresponding to the linear fit of the actual versus predicted plots and are a good measure for predictability. It can be seen that the models based on the retention time on a reversed-phase HPLC column (eqn (5) and (7)) give more accurate predictions than the models based on calculated log P values (eqn (6) and (8)–(10)). However, these are not “true” predictions as the receptors of the test set had to be synthesized first and their retention time measured, before the values could be predicted. We therefore assert that the QSAR model that includes log P, molecular size and anion binding (eqn (8)–(10)) are the best models to explain and predict the anion transport activity of 1-hexyl-3-phenylthioureas, however, care must be taken when choosing the correct algorithm to calculate log P values in order to be as close to the experimental values (retention times) as possible.

Table 2 Overview of actual and predicted values for the anion association constants (log K_a) and anion transport EC₅₀ values for the test set (receptors 1, 6, 14 and 20). Errors of the experimental log(1/EC₅₀) values are given by standard deviations

	Actual values				Predicted values
	log Ka Cl^−^a	log Ka H2PO4^−^a	log Ka HCO3^−^b	log(1/EC50)^c	log Ka			log(1/EC50)
					Eqn (1)	Eqn (2)	Eqn (3)	Eqn (5)	Eqn (6)	Eqn (7)	Eqn (8)	Eqn (9)	Eqn (10)
a Anion added as TBA salt, data for the alkyl thiourea NHb is given. b Anion added as TEA salt, data for the ortho CH is given due to peak broadening of the thiourea NHs. c EC50 (in mol% transporter to lipid) is the concentration of transporter needed to obtain 50% chloride efflux in 270 s. Values obtained by means of Hill plot. d R adj ^2 value obtained from the linear fit of the actual versus predicted plot including all 22 compounds. e R adj ^2 value obtained from the linear fit of the actual versus predicted plot including the four compounds of the test set (1, 6, 14 and 22).
1 (Br)	1.27	2.67	2.65	0.03(±0.09)	1.30	2.57	2.60	0.22	0.31	0.002	0.14	0.17	0.19
6 (COMe)	1.43	2.62	2.74	−0.48(±0.01)	1.44	2.80	2.84	−0.49	−0.42	−0.53	−0.42	−0.39	−0.40
14 (OEt)	1.09	2.04	2.15	−0.28(±0.11)	1.04	2.18	2.19	−0.12	−0.02	−0.46	−0.42	−0.39	−0.40
20 (Pr)	1.12	2.20	2.27	0.88(±0.23)	1.10	2.27	2.28	0.62	0.55	0.52	0.41	0.44	0.44
R adj ^2 (all)^d	—	—	—	—	0.96	0.90	0.85	0.84	0.78	0.93	0.87	0.87	0.87
R adj ^2 (test)^e	—	—	—	—	0.98	0.77	0.94	0.86	0.74	0.95	0.79	0.79	0.77

---

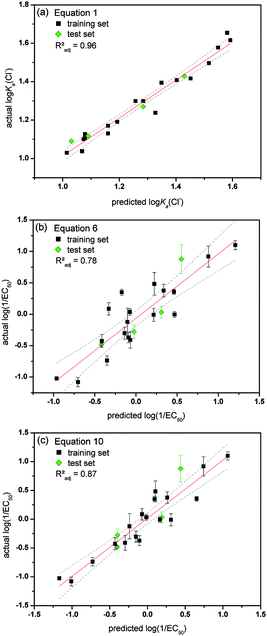Fig. 6 Overview of the actual versus predicted plots for a selection of the obtained QSAR equations. Data from the training set is shown in black and data from the test set in green. The actual log(1/EC₅₀) values are the average of a minimum of 3 repeats and error bars represent standard deviations. Linear fits are represented by a red line with 95% confidence levels shown as dotted grey lines. (a) log K_a(Cl⁻) values predicted using eqn (1) (interaction with Cl⁻); (b) log(1/EC₅₀) values predicted using eqn (6); (c) log(1/EC₅₀) values predicted using eqn (10).

Conclusions

In this paper we have reported the first attempt for a quantitative structure–activity relationship (QSAR) analysis of supramolecular anion binding and anion transport activity by simple 1-hexyl-3-phenylthioureas. It was shown that the binding constants obtained through ¹H NMR titrations with chloride, bicarbonate and phosphate correlate well with the Hammett constant of the substituent in the para-position, suggesting that anion binding by simple mono-thioureas is almost exclusively governed by hydrogen bond donor acidity. Furthermore, it has been possible to obtain a statistically relevant model that is able to explain the variety in anion transport ability observed during ISE vesicle-based experiments and is also able to predict the anion transport activity of new analogous compounds. The most relevant model highlighted the lipophilicity of a substituent as the single most important factor to increase anion transport ability, although increased anion-binding ability and decreased molecular size also contribute to anion transport. Even though the models and equations presented in this paper cannot be applied to other classes of receptors, we believe that it provides a useful guide for the design of future anion transporters and in choosing the substituent that would give the most promising result. Further QSAR analyses on other classes of anion receptors and transporters are currently being performed in our laboratory. We believe that quantitative structure–activity studies can become a powerful tool in investigating the mechanisms of supramolecular anion transport.

Acknowledgements

We thank the EPSRC for funding (MW, CJEH, LEK, SJM) and for access to the crystallographic facilities at the University of Southampton and Diamond Beamline I19. We thank the University of Southampton and A*STAR for a postgraduate scholarship (NB). IM thanks the FCT (Fundação para a Ciência e a Tecnologia) for the PhD scholarship SFRH/BD/87520/2012. PJC thanks FCT for the postdoctoral grant SFRH/BPD/27082/2006. VF acknowledges the funding from QREN-FEDER, through the Operational Program Competitiveness Factors – COMPETE and National Funds through the FCT under project PTDC/QUI-QUI/101022/2008. The authors would also like to thank Jonathan W. Essex (University of Southampton) and Russell Viner (Syngenta) for their help with calculating suitable log P values.

Notes and references

1. N. Busschaert and P. A. Gale, Angew. Chem., Int. Ed., 2013, 52, 1374.
2. P. A. Gale, Acc. Chem. Res., 2011, 44, 216.
3. J. T. Davis, O. Okunola and R. Quesada, Chem. Soc. Rev., 2010, 39, 3843.
4. A. P. Davis, D. N. Sheppard and B. D. Smith, Chem. Soc. Rev., 2007, 36, 348.
5. G. W. Gokel and N. Barkey, New J. Chem., 2009, 33, 947.
6. S. Matile, A. Vargas Jentzsch, J. Montenegro and A. Fin, Chem. Soc. Rev., 2011, 40, 2453.
7. V. Gorteau, G. Bollot, J. Mareda, A. Perez-Velasco and S. Matile, J. Am. Chem. Soc., 2006, 128, 14788.
8. P. H. Schlesinger, R. Ferdani, J. Liu, J. Pajewska, R. Pajewski, M. Saito, H. Shabany and G. W. Gokel, J. Am. Chem. Soc., 2002, 124, 1848.
9. B. A. McNally, E. J. O'Neil, A. Nguyen and B. D. Smith, J. Am. Chem. Soc., 2008, 130, 17274.
10. J. L. Seganish and J. T. Davis, Chem. Commun., 2005, 5781.
11. I.-W. Park, J. Yoo, B. Kim, S. Adhikari, S. K. Kim, Y. Yeon, C. J. E. Haynes, J. L. Sutton, C. C. Tong, V. M. Lynch, J. L. Sessler, P. A. Gale and C. H. Lee, Chem.–Eur. J., 2012, 18, 2514.
12. S. Hussain, P. R. Brotherhood, L. W. Judd and A. P. Davis, J. Am. Chem. Soc., 2011, 133, 1614.
13. A. V. Jentzsch, D. Emery, J. Mareda, S. K. Nayak, P. Metrangolo, G. Resnati, N. Sakai and S. Matile, Nat. Commun., 2012, 3, 905.
14. F. M. Ashcroft, Ion Channels and Disease, Academic Press, San Diego and London, 2000.
15. S. Matsuyama, J. Llopis, Q. L. Deveraux, R. Y. Tsien and J. C. Reed, Nat. Cell Biol., 2000, 2, 318.
16. J. L. Sessler, L. R. Eller, W.-S. Cho, S. Nicolaou, A. Aguilar, J. T. Lee, V. M. Lynch and D. J. Magda, Angew. Chem., Int. Ed., 2005, 44, 5989.
17. S. Ohkuma, T. Sato, M. Okamoto, H. Matsuya, K. Arai, T. Kataoka, K. Nagai and H. H. Wasserman, Biochem. J., 1998, 334, 731.
18. T. Sato, H. Konno, Y. Tanaka, T. Kataoka, K. Nagai, H. H. Wasserman and S. Ohkuma, J. Biol. Chem., 1998, 273, 21455.
19. N. Busschaert, P. A. Gale, C. J. E. Haynes, M. E. Light, S. J. Moore, C. C. Tong, J. T. Davis and W. A. Harrell, Jr, Chem. Commun., 2010, 46, 6252.
20. N. Busschaert, M. Wenzel, M. E. Light, P. Iglesias-Hernández, R. Pérez-Tomás and P. A. Gale, J. Am. Chem. Soc., 2011, 133, 14136.
21. C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 1997, 23, 3.
22. N. J. Andrews, C. J. E. Haynes, M. E. Light, S. J. Moore, C. C. Tong, J. T. Davis, W. A. Harrell Jr and P. A. Gale, Chem. Sci., 2011, 2, 256.
23. S. J. Moore, M. Wenzel, M. E. Light, R. Morley, S. J. Bradberry, P. Gómez-Iglesias, V. Soto-Cerrato, R. Pérez-Tomás and P. A. Gale, Chem. Sci., 2012, 3, 2501.
24. M. Wenzel, M. E. Light, A. P. Davis and P. A. Gale, Chem. Commun., 2011, 47, 7641.
25. N. Busschaert, I. L. Kirby, S. Young, S. J. Coles, P. N. Horton, M. E. Light and P. A. Gale, Angew. Chem., Int. Ed., 2012, 51, 4426.
26. B. A. McNally, A. V. Koulov, T. N. Lambert, B. D. Smith, J.-B. Joos, A. L. Sisson, J. P. Clare, V. Sgarlata, L. W. Judd, G. Magro and A. P. Davis, Chem.–Eur. J., 2008, 14, 9599.
27. V. Saggiomo, S. Otto, I. Marques, V. Félix, T. Torroba and R. Quesada, Chem. Commun., 2012, 48, 5274.
28. T. Hayashita, T. Onodera, R. Kato, S. Nishizawa and N. Teramae, Chem. Commun., 2000, 9, 755.
29. S. J. Coles and P. A. Gale, Chem. Sci., 2012, 3, 683.
30. Structures were submitted to the Cambridge Crystallographic Data Centre and were allocated the deposition numbers CCDC 927445–927460.†.
31. M. J. Hynes, J. Chem. Soc., Dalton Trans., 1993, 311.
32. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165.
33. C. D. Selassie, S. B. Mekapati and R. P. Verma, Curr. Top. Med. Chem., 2002, 2, 1357.
34. H.-J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924.
35. P. D. Beer, C. Hazlewood, D. Hesek, J. Hodacova and S. E. Stokes, J. Chem. Soc., Dalton Trans., 1993, 1327.
36. L. Nie, Z. Li, J. Han, X. Zhang, R. Yang, W.-X. Liu, F.-Y. Wu, J.-W. Xie, Y.-F. Zhao and Y.-B. Jiang, J. Org. Chem., 2004, 69, 6449.
37. F.-Y. Wu, Z. Li, L. Guo, X. Wang, M.-H. Lin, Y.-F. Zhao and Y.-B. Jiang, Org. Biomol. Chem., 2006, 4, 624.
38. G. Gil-Ramírez, E. C. Escudero-Adán, J. Benet-Buchholz and P. Ballester, Angew. Chem., Int. Ed., 2008, 47, 4114.
39. Z. Li, F.-Y. Wu, L. Guo, A.-F. Li and Y.-B. Jiang, J. Phys. Chem. B, 2008, 112, 7071.
40. C. R. Yamnitz, S. Negin, I. A. Carasel, R. K. Winter and G. W. Gokel, Chem. Commun., 2010, 46, 2838.
41. P. A. Gale, K. Navakhun, S. Camiolo, M. E. Light and M. B. Hursthouse, J. Am. Chem. Soc., 2002, 124, 11228.
42. T. Gunnlaugsson, P. E. Kruger, P. Jensen, F. M. Pfeffer and G. M. Hussey, Tetrahedron Lett., 2003, 44, 8909.
43. D. Esteban-Gòmez, L. Fabbrizzi, M. Liccelli and E. Monanzi, Org. Biomol. Chem., 2005, 70, 5717.
44. ACD/I-Lab 2.0, https://ilab.acdlabs.com/iLab2/, accessed 9 August 2012, ACD/Labs 2010–2013.
45. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96.
46. V. S. Bryantsev and B. P. Hay, Org. Lett., 2005, 7, 5031.
47. H. Hagelin, J. S. Murray, P. Politzer, T. Brinck and M. Berthelot, Can. J. Chem., 1995, 73, 483.
48. J. S. Murray, K. E. Riley, P. Politzer and T. Clark, Aust. J. Chem., 2010, 63, 1598.
49. Y. Ma, K. Gross, C. Hollingsworth, P. Seybold and J. Murray, J. Mol. Model., 2004, 10, 235.
50. F. Bulat, A. Toro-Labbé, T. Brinck, J. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679.
51. B. D. Smith and T. N. Lambert, Chem. Commun., 2003, 2261.
52. A. V. Koulov, T. N. Lambert, R. Shukla, M. Jain, J. M. Boon, B. D. Smith, H. Li, D. N. Sheppard, J.-B. Joos, J. P. Clare and A. P. Davis, Angew. Chem., Int. Ed., 2003, 42, 4931.
53. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995.
54. A. V. Hill, Biochem. J., 1913, 7, 471.
55. S. Bhosale and S. Matile, Chirality, 2006, 18, 849.
56. J. M. Boon and B. D. Smith, J. Am. Chem. Soc., 1999, 121, 11924.
57. Y. Sasaki, R. Shukla and B. D. Smith, Org. Biomol. Chem., 2004, 2, 214.
58. C. Hansch, A. Leo, D. Hoekman and S. R. Heller, Exploring QSAR, American Chemical Society, Washington, DC, 1995.
59. T. Fujita, J. Iwasa and C. Hansch, J. Am. Chem. Soc., 1964, 86, 5175.
60. C. Hansch and T. Fujita, J. Am. Chem. Soc., 1964, 86, 1616.
61. C. J. E. Haynes, S. J. Moore, J. R. Hiscock, I. Marques, P. J. Costa, V. Félix and P. A. Gale, Chem. Sci., 2012, 3, 1436.
62. VCCLAB, Virtual Computational Chemistry Laboratory, ALOGPS 2.1 and e-Dragon 1.0, http://www.vcclab.org, accessed 14 January 2013, VCCLAB 2005.
63. I. Tetko, J. Gasteiger, R. Todeschini, A. Mauri, D. Livingstone, P. Ertl, V. Palyulin, E. Radchenko, N. Zefirov, A. Makarenko, V. Tanchuk and V. Prokopenko, J. Comput.-Aided Mol. Des., 2005, 19, 453.
64. Daylight ClogP, version 4.73, Daylight Chemical Information Systems Inc., Laguna Niguel, CA, USA, 2001.
65. Accelrys Diamond Descriptors (AlogP), version 1.5, Accelrys software Inc., San Diego, CA, USA.
66. Fieldview, version 2.0.2, Cresset BMD Ltd., Hertfordshire, UK, 2011.
67. T. Braumann, J. Chromatogr., A, 1986, 373, 191.
68. JMP®, version 9.0.0, statistical software, SAS Institute Inc., Cary, NC, USA, 2010.
69. Chemdraw Ultra, version 12.0, Cambridge Soft Corporation, Cambridge, USA, 1986–2010.
70. Chemicalize, http://www.chemicalize.org/, accessed 9 August 2012, ChemAxon.
71. M. V. Volkenstein, Configurational Statistics of Polymeric Chains, Wiley-lnterscience, New York, USA, 1963.
72. R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2000.
73. SAS Institute Inc., JMP® 9 Modeling and Multivariate Methods, SAS Institute Inc., Cary, NC, USA, 2010, p. 62.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis and characterization of the receptors, details and figures about the X-ray crystal structures of the receptors, stability constant determination, stack plots and fit plots of the ¹H NMR titrations with various anions in DMSO/water solutions, various vesicle assays methods, Hill plots, overview of descriptors, details about QSAR model calculations, DFT calculations, details and figures about the prediction of anion binding and anion transport. CCDC 927445–927460. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3sc51023a

‡ Present address: School of Chemistry, Trinity Biomedical Sciences Institute, Trinity College Dublin, University of Dublin, 152-160 Pearse Street, Dublin 2, Ireland.

§ Present address: Fraunhofer IKTS, 01217, Dresden, Germany.

---