Effect of blockiness in grafted monomer sequences on assembly of copolymer grafted nanoparticles: a Monte Carlo simulation study†
Tyler B.
Martin
a,
Christopher
McKinney
b and
Arthi
Jayaraman
*a
aDepartment of Chemical and Biological Engineering, University of Colorado–Boulder, JSCBB A125, UCB 596, Boulder, CO 80309-0596. E-mail: arthi.jayaraman@colorado.edu
bDepartment of Chemical Engineering, Clarkson University, Potsdam, NY 13699
First published on 15th October 2012
Abstract
We use Monte Carlo simulations to study AB copolymer-grafted nanoparticles to elucidate the effect of blockiness (length of contiguous blocks of like-monomers) in the grafted monomer sequence on the shape, size, and structure of assembled nanoparticle clusters for a range of monomer–monomer and monomer–particle interactions. The graft sequence dictates the ease or difficulty of the grafted chains to form attractive like-monomer (A–A or B–B) contacts while minimizing repulsive unlike-monomer (A–B) contacts within an assembled cluster or a dispersed state. When A–B repulsion is negligible, with increasing blockiness at constant graft length the cluster size and average coordination number decrease in the presence of A–A or B–B attractions, and are approximately constant in the presence of A–A and B–B attractions. When A–B repulsion is strong, the cluster size and average coordination number increase with increasing blockiness for small and large particles. For small particles, with strong B–B attraction and A–B repulsion, increasing blockiness leads to increasing anisotropy in cluster shape, while strong A–A attraction produces isotropic clusters regardless of the graft sequence. The effect of graft sequence on cluster shape is reduced for large particles as compared to small particles, at constant graft length. Lastly, the extent to which monomer–particle attractive interactions change the above trends is highly dependent on the relative strength of monomer–particle to monomer–monomer interactions, in addition to the ratio of particle size to graft length, and the grafting density.
I. Introduction
Controlled nanoparticle assembly is required to create nanostructured materials for applications such as metamaterials, photovoltaics, and microelectronics. One way to tailor nanoparticle assembly is via functionalization of the nanoparticle surface with ligands such as polymers,1–31 DNA,32–36 and proteins.37,38 Polymer functionalized nanoparticles, in particular, have been studied extensively in the recent years using theory,1,13,15–17 simulation,18–21 and experiments.15,22,23 Experimental and computational studies of homopolymer grafted nanoparticles in the polymer matrix, solvent, and pure bulk (no solvent or matrix) have demonstrated the ability to tune the assembly characteristics of these grafted nanoparticles via the grafting density,2,19,26 nanoparticle size,3,17,27 graft placement,8,28,29 graft and matrix molecular weight,30 and nanoparticle shape.20,27,31 Specifically, for homopolymer grafted nanoparticles, at high grafting density in a polymer matrix, it has been shown that when the grafted chains have a higher molecular weight than the matrix chains the nanoparticles disperse. It has also been shown that, at low grafting densities, the grafted chain layer is not dense and the interactions between the particles' cores become important, causing the lightly grafted polymer functionalized nanoparticles to assemble anisotropically.Copolymer functionalization, as opposed to homopolymer functionalization, creates additional tuning parameters of the graft sequence and monomer chemistry (or interactions) which provide further control over the assembly of polymer grafted nanoparticles. In the last few years, theory13,16,17 and simulations12,24,25 have been used to study copolymers grafted onto nanoparticles. Vorselaars et al.16 have used SCFT (self-consistent field theory) to study dense layers of diblock copolymers grafted onto spherical nanoparticles. They found various domain shapes on the particle surface depending on the composition of the copolymer, and discussed the stability of the various morphologies on these highly curved nanoparticle surfaces, in contrast to the case of zero curvature. Zhu et al.17 have employed both SCFT and DFT (density fluctuation theory) to study a dense system of nanoparticles with a single diblock copolymer graft. When the particle surface was chemically neutral to the grafted chain, they observed typical block copolymer morphologies (i.e. cylinders and lamellae) determined by both the composition of the copolymer and the particle size. When the particle was repulsive to both blocks of the copolymer, they observed hierarchical morphologies, such as “lamellae with cylinders at interfaces” not typically observed with block copolymer melts. While the above studies focused on either a single copolymer grafted nanoparticle at high grafting density16 or grafted nanoparticles with a single grafted chain,17 Jayaraman and coworkers12,13,25 have conducted systematic studies of spherical copolymer grafted nanoparticles at low to intermediate grafting densities using a combination of theory and simulation techniques to better understand the effective interactions between the copolymer grafted particles and their assembly characteristics in both solvent and matrix. Using Monte Carlo simulations of a single copolymer grafted nanoparticle at low to intermediate grafting densities in an implicit solvent,25 they show that the grafted chain conformations change non-monotonically with the monomer sequence, and depend on the monomer sequence and monomer interactions. In a following study,13 Nair and Jayaraman used an integrated theory and a simulation approach (self-consistent PRISM-MC method) to study the effective interactions between two copolymer grafted nanoparticles in a homopolymer matrix as a function of the grafted monomer sequence. They found that at the same composition, particle size and grafting density, using alternating AB copolymer grafts leads to a repulsive potential of mean force (PMF) between the grafted particles at contact in both A and B homopolymer matrixes, while using diblock sequence AB copolymer grafts leads to an attractive PMF at contact and a repulsive PMF at large inter-particle distance in the B homopolymer matrix, and repulsive PMF at contact and attractive PMF at large inter-particle distance in the A homopolymer matrix. This was an interesting result because it demonstrated the isolated effect of varying the arrangement of monomers (monomer sequence) on the behavior of the grafted nanoparticles in a polymer matrix.
In recent work, we used lattice Monte Carlo simulations to study assembly of spherical nanoparticles grafted with AB alternating and diblock sequences12 in an implicit solvent at varying monomer interactions, particle size, and graft length. We found that depending on the monomer interactions, the alternating sequence either favors dispersions, or formation of smaller, isotropic clusters, while the diblock sequence favors assembly producing larger, anisotropic clusters. In this paper, we use the same approach going beyond just alternating and diblock sequences, by focusing in detail on five different graft sequences with varying “blockiness” in sequence, where blockiness is defined as the length of contiguous blocks of like-monomers. Our goal here is to study how varying AB copolymer graft sequence blockiness affects the assembly of copolymer grafted nanoparticles at varying monomer–particle and monomer–monomer interactions. We find that the total number of attractive monomer contacts in the assembled nanoparticle cluster increases with increasing blockiness in the graft sequence, with the alternating sequence being an outlier. As the graft sequence blockiness increases, attractive like monomers (A–A and/or B–B) aggregate more easily within an assembled nanoparticle cluster without having to constrain the grafted chains, thereby decreasing conformational entropic losses. The unique trend seen with the alternating sequence is explained by the alternating grafted chains forming “networks” of attractive monomer contacts within the cluster in contrast to the distinct domains of attractive monomers formed by other blockier sequences. In the case of like monomer (A–A and/or B–B) attraction in the absence of unlike (A–B) monomer repulsion, the assembled cluster size and average particle coordination number decrease with increasing blockiness. In the case of like monomer attraction in the presence of unlike monomer repulsion the clusters size and the average particle coordination number within the cluster increase with increasing blockiness. For both small and large particle sizes, we observe that the presence of B–B attraction with A–B repulsion produces the greatest range of anisotropy in clusters with varying blockiness in the grafted chains. All of the above trends are driven by how the monomer sequences enable/deter the grafted copolymer chains to bring together attractive monomer contacts for making inter-particle contacts. For the two particle sizes studied here, at constant graft length, how much the monomer–particle interactions affect the above trends are highly dependent on the particle size to graft length ratio, graft sequence, and the relative strengths of monomer–particle and monomer–monomer interactions.
Since copolymer-grafted nanoparticles are a relatively less-studied system as compared to homopolymer grafted nanoparticles in the polymer functionalized particles field, there is a need to predict how these copolymer functionalized nanoparticles assemble at a variety of parameters. Since the synthetic efforts to conduct a systematic parameter study are both time consuming and involve significant effort, we expect the results from this computational exploration to provide guidelines for synthetic chemists and other scientists attempting to create target morphologies through assembly of copolymer grafted nanoparticles.
The paper is organized as follows. In Section II we provide details of our model, the simulation method, and analysis techniques. In Section III, we present the results showing the effect of varying the monomer sequence, monomer–monomer, and monomer–particle interactions, and particle size on the shape, size and structure of assembled cluster of copolymer grafted nanoparticles. We conclude with a discussion on the observed general trends, limitations of this work, some future directions, and the impact of this computational work on experiments.
II. Approach
A. Model
We model the system of AB copolymer grafted nanoparticles as hard sphere particles of diameter D each with six grafted symmetric AB copolymers. Each grafted copolymer chain is modeled as a freely jointed chain on a cubic lattice with monomers of size d of the order 1 nm, and the first monomer is placed symmetrically 1d away from the six poles of the spherical nanoparticle. The symmetric AB copolymers of length 24 monomers, have A and B monomers arranged in one of the five sequences—(A1B1)12, (A2B2)6, (A3B3)4, (A6B6)2, (A12B12)1—displayed in Fig. 1. For all sequences the AB copolymer chains are grafted such that the first monomer attached to the particle surface is an A monomer. The identities of the second, third and higher monomers in each grafted chain depend on the chosen monomer sequence. | ||
| Fig. 1 Schematic of the monomer sequences used in this study, in the decreasing order of blockiness from top to bottom. | ||
The monomer–monomer interaction potential, Uij(r) between the ith and jth non-bonded grafted monomers is described by a square well potential shown in eqn (1)
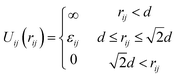 | (1) |
| Interaction set | ε AB/kT | ε AA/kT | ε BB/kT |
|---|---|---|---|
| 1 | 0.0 | −0.5 | 0.0 |
| 2 | 0.0 | −1.0 | 0.0 |
| 3 | 0.0 | 0.0 | −0.5 |
| 4 | 0.0 | 0.0 | −1.0 |
| 5 | 0.0 | −0.5 | −0.5 |
| 6 | 0.0 | −1.0 | −1.0 |
| 7 | 1.0 | −0.5 | 0.0 |
| 8 | 1.0 | −1.0 | 0.0 |
| 9 | 1.0 | 0.0 | −0.5 |
| 10 | 1.0 | 0.0 | −1.0 |
| 11 | 1.0 | −0.5 | −0.5 |
| 12 | 1.0 | −1.0 | −1.0 |
We model attractive interactions between monomer i and the grafted particle j using another square well potential:
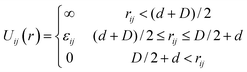 | (2) |
B. Simulation
We use Monte Carlo simulation on a cubic lattice to study the assembly of copolymer grafted nanoparticles. In this paper we focus only on dilute concentration of c ∼ 1 × 10−5 particles per nm3, obtained by using 10 particles in a 100 × 100 × 100 (nm3) simulation box with periodic boundary conditions. In the first step of the simulation we grow the initial configuration by placing the spherical nanoparticles in random positions inside the simulation box. Then for each particle, we fix the first monomers of the six grafted chains at the predetermined symmetric sites on the sphere followed by placing the second monomer of each grafted chain in one of the five unoccupied lattice sites adjacent to the first monomer of that grafted chain. During this growth process if an ith monomer cannot be grown because all neighbouring sites of the (i − 1)th monomer are occupied by other monomers, then all the monomers are subjected to local moves until a vacancy is created. This is repeated until all the grafted chains are grown to the desired chain length, Ngraft. Ngraft is maintained as 24 in this study. This process is followed for all copolymer grafted particles within the simulation box while ensuring no overlaps. After the initial configuration is grown, the simulation proceeds to the initialization stage. The initialization stage helps us avoid any bias that might arise due to the nature of the initial configuration. In the initialization stage the chains are subjected to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte Carlo (MC) steps with purely hard-sphere interactions between all monomers in the simulation. An MC time step is defined either as Ngraft × Ng random monomer moves, where Ngraft is the grafted copolymer chain length and Ng is the number of grafts (Ng = 6 in this study), or one copolymer grafted nanoparticle translate or rotate move. In one monomer move, we randomly pick a monomer (with the exception of the first monomer that is fixed) on a randomly picked grafted chain of a randomly selected nanoparticle, and then move that monomer using a randomly chosen move—“crankshaft”, “kink” and “end” (end move for the last monomer only).39 In one single copolymer grafted nanoparticle move, one copolymer grafted nanoparticle is randomly chosen and the particle along with its constituent chains is translated or rotated. The moves are accepted or rejected based on the Metropolis algorithm.40 Since interaction potentials are not turned on until the equilibration stage, all initialization-stage moves are made under athermal conditions and accepted as long as no overlaps occur during the move.
000 Monte Carlo (MC) steps with purely hard-sphere interactions between all monomers in the simulation. An MC time step is defined either as Ngraft × Ng random monomer moves, where Ngraft is the grafted copolymer chain length and Ng is the number of grafts (Ng = 6 in this study), or one copolymer grafted nanoparticle translate or rotate move. In one monomer move, we randomly pick a monomer (with the exception of the first monomer that is fixed) on a randomly picked grafted chain of a randomly selected nanoparticle, and then move that monomer using a randomly chosen move—“crankshaft”, “kink” and “end” (end move for the last monomer only).39 In one single copolymer grafted nanoparticle move, one copolymer grafted nanoparticle is randomly chosen and the particle along with its constituent chains is translated or rotated. The moves are accepted or rejected based on the Metropolis algorithm.40 Since interaction potentials are not turned on until the equilibration stage, all initialization-stage moves are made under athermal conditions and accepted as long as no overlaps occur during the move.
The initialization stage is followed by the equilibration stage. In the equilibration stage the chains go through 20 million MC steps with a temperature annealing schedule going from dimensionless temperature Tinitial = 3 to Tfinal = 1 with a temperature decrement of 0.9 at every ith stage (Ti = Ti−1 × 0.9), and 3 million MC steps per temperature stage. This annealing schedule was chosen after rigorous testing to ensure equilibrium is reached at each temperature stage, and the resulting configurations at each temperature are independent of small variations in the annealing schedule (e.g. 3 million or 4 million MC steps per stage). The moves during the equilibration stage include the monomer moves (47.5%) and grafted particle moves (47.5%) described above and cluster moves (5%). A cluster move is defined as a move of a collection of copolymer grafted nanoparticles, where every grafted particle is making at least one monomer contact with a monomer of another grafted particle in the cluster. During a cluster move we translate randomly picked clusters and accept the move only when the cluster move does not lead to an overlap or formation of a new cluster.39 If there are no clusters in the configuration the chosen cluster move is rejected. Once the simulation has reached Tfinal = 1 and our equilibrium condition has been satisfied—40 consecutive block averages of energy are within 10% of each other—we collect the ensemble average of the block averages of the equilibrated simulation. We collect data on the thermodynamic property of interest over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps and calculate the block averages for every 100
000 MC steps and calculate the block averages for every 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps. For each parameter set, described below, we repeat 5 trials of simulation where each of the trials is initialized with different random number seeds. We obtain error bars for every data point presented in the Results section from the ensemble averages collected from 5 such trials.
000 MC steps. For each parameter set, described below, we repeat 5 trials of simulation where each of the trials is initialized with different random number seeds. We obtain error bars for every data point presented in the Results section from the ensemble averages collected from 5 such trials.
C. Analysis
We employ a variety of metrics to assess the size and shape of the assembled cluster of the copolymer grafted particles, the monomer contacts within the cluster and the grafted chain configurations.We calculate the average radius of gyration of the grafted chains using equation
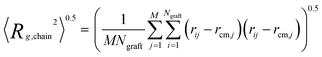 | (3) |
We also calculate the mean height of each monomer type from the center of the particle it is grafted to. We first calculate the average concentration profile for each monomer type using
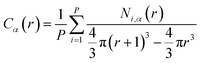 | (4) |
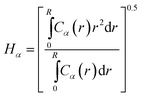 | (5) |
To quantify the shape of the assembled clusters of polymer grafted nanoparticles, we calculate relative shape anisotropy (RSA).41 The RSA of a cluster varies between 0 and 1, with 0 corresponding to perfectly isotropic (i.e. spherical symmetry) and 1 to perfectly anisotropic (i.e. rod-like) shape. Since the RSA calculation performs best when it's applied to many beads, we apply this analysis to the coordinates of the monomers of a cluster, as opposed to the coordinates of the particles of a cluster. We begin the calculation of RSA by first translating the center of mass of the monomer coordinates of a cluster to the origin and calculating the radius of gyration tensor for a cluster containing N monomers:
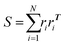 | (6) |
| S = VTSV | (7) |
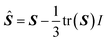 | (8) |
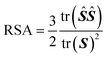 | (9) |
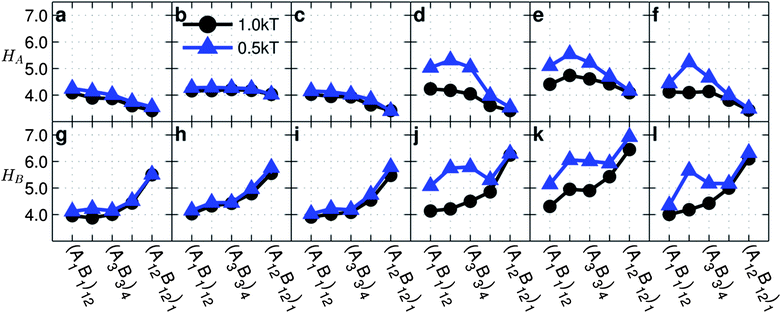
In the process of calculating RSA, we also can easily obtain the radius of gyration of a cluster which allows us to assess the size of clusters. This calculation is shown in eqn (10).
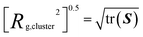 | (10) |
We also calculate the average number of particles per cluster, 〈N〉, which serves as a separate metric of the size of clusters. To quantify the structure or particle–particle connectivity within a cluster we calculate the ensemble averaged coordination number, 〈Z〉, which is defined as the average number of “neighbors” a polymer grafted particle has. We define two polymer grafted nanoparticles as “neighbors” if they have at least one monomer–monomer contact.
In an assembly/dispersion each copolymer grafted nanoparticle exhibits an effective patchiness due to aggregation of monomers. In order to quantify this “patchiness” we perform analysis on the domains of like-monomers within the assembled cluster. We define a “domain” as a set of monomers of the same type that share at least one monomer contact with another monomer in the domain. Using this criterion, we can calculate various metrics such as the average number of domains in a cluster or the average radius of gyration of these domains. We also calculate the average total number of contacts between various pairs of monomers (e.g. A–A, A–B and B–B contacts) and between particle and monomers (e.g. A–P, B–P contacts) to show how the monomers aggregate in each cluster.
In order to verify that the data and trends that we present are significant, all of the shown trends have been subject to a statistical analysis. To verify that the data points within a specific trend are statistically significant from one another, each trend line is tested using a one-way analysis of variance with an acceptance criterion of 0.05. A p-value below 0.05 indicates that the data in the trend are significantly different while a p-value above 0.05 indicates that the data are statistically the same (i.e. zero slope). To test data from different trends, for example, weak monomer attraction vs. strong monomer attraction, we employ an unequal variance, a two-tailed t-test with an acceptance criterion of 0.05. All of the data in our presented figures have error bars calculated using standard error; many of the error bars are smaller than the symbol representing the data.
D. Driving forces for assembly of grafted nanoparticles
In this section we discuss the forces that drive copolymer grafted nanoparticles to arrive at their equilibrium assembled/dispersed configuration. First, as stated earlier, the term “blockiness” is defined as the number of contiguously placed like monomers in a particular copolymer sequence. In other words, the longer the block of like monomers in a sequence is, the blockier the sequence. Therefore, in this study (A1B1)12 is the least blocky sequence (also called the alternating sequence), since it only has one like-monomer in each repeating block, while (A12B12)1 is the most blocky sequence as it has 12 like monomers contiguously placed in each block.The equilibrium configuration of the copolymer grafted nanoparticles is achieved by maximizing the enthalpic gain through maximizing the number of attractive like monomer contacts, and minimizing the number of repulsive unlike-monomer contacts, while minimizing the entropic losses associated with making or avoiding these contacts. The conformational entropy of the grafted chains and the translational entropy of nanoparticles are reduced upon assembly of the polymer grafted nanoparticles. While the translational entropy loss of the nanoparticles upon assembly should not vary with the grafted monomer sequence, the conformational entropy loss of the grafted chains upon nanoparticle assembly is strongly dependent on the monomer sequence. This is because the assembly of the nanoparticles is driven by ability of the grafted chain to (a) coil upon itself and make enthalpically favorable intra-chain contacts, and/or (b) stretch out to make enthalpically favorable inter-chain intra-particle contacts, and/or (c) stretch out towards another grafted nanoparticle and make enthalpically favorable inter-particle contacts. ESI, Fig. S1† shows schematically these different types of monomer contacts. The choice of one or more of these types of contacts is dictated by the strength of monomer attractions and repulsions, and by how the grafted chain sequence facilitates these contacts, while losing the least number of conformations or minimizing the entropic loss. For example, a highly blocky sequence, like (A12B12)1, can easily maximize the intra-chain B–B and/or A–A contacts while maintaining a high conformational entropy. The least blocky sequence, (A1B1)12, on the other hand, must seek highly compact conformations to form intra-chain contacts that lower the conformational entropy of the grafted chain. Thus, less blocky sequences could prefer to make “inter-chain intra-particle” or “inter-particle” contacts if the chain does not have to stretch too much to achieve those attractive contacts. Clearly, in addition to the sequence, the grafted chain length and the particle size also affect the above choice of types of contacts. For e.g., at constant chain length and constant number of grafts, a small nanoparticle can easily allow the formation of inter-chain intra-particle contacts as the chains are grafted closer together, but a large nanoparticle will drive mostly inter-particle or intra-chain contacts due to the increased distance between the grafts.
In summary, the equilibrium configuration of copolymer grafted nanoparticles, assembled or dispersed, tightly clustered or loosely clustered, are all based on how the above factors – grafted chain length and sequence, monomer attractive and repulsive interaction strengths, graft chain length, and particle size – balance the enthalpic gain and entropic losses. This balance is complex and non-intuitive, and motivates this computational study.
III. Results
A. Effects of monomer sequence on grafted chain conformations and monomer aggregation in the cluster
 | ||
| Fig. 2 Average radius of gyration of a grafted chain 〈Rg,chain2〉0.5, average number of total AA contacts, total BB contacts and total AB contacts as a function of the graft monomer sequence for copolymer grafted nanoparticles of size D = 4d with six grafts of length Ngraft = 24. The x-axis indices correspond to the graft sequence (A1B1)12, (A2B2)6, (A3B3)4, (A6B6)2, and (A12B12)1. The interaction sets correspond to the plot letters as follows: lines on plots a, g, m, and s correspond to interaction sets 1 (blue triangles) and 2 (black circles), lines on plots b, h, n, and t correspond to interaction sets 3 (blue triangles) and 4 (black circles), lines on plots c, i, o, and u correspond to interaction sets 5 (blue triangles) and 6 (black circles), lines on plots d, j, p, and v correspond to interaction sets 7 (blue triangles) and 8 (black circles), lines on plots e, k, q, and w correspond to interaction sets 9 (blue triangles) and 10 (black circles), and lines on plots f, l, r, and x correspond to interaction sets 11 (blue triangles) and 12 (black circles). The black lines with circle markers represent monomer–monomer attraction = 1 kT, while the blue triangles with triangle markers represent monomer–monomer attraction = 0.5 kT. All monomer–particle interactions are maintained as hard sphere interactions. | ||
In the absence of A–B repulsions, and in the presence of weak or strong A–A and/or B–B attractions (Fig. 2a–c), with increasing blockiness from (A1B1)12 to (A12B12)1, 〈Rg,chain2〉0.5 first decreases, reaches a minimum for sequences with intermediate blockiness, and then increases exhibiting the highest 〈Rg,chain2〉0.5 for the diblock sequence. The non-monotonic behavior with the graft sequence can be explained by understanding how a grafted sequence can facilitate/deter attractive like-monomer contacts both within the same particle (intra-chain and intra-particle inter-chain) as well as with chains of another particle (inter-particle contacts). At high blockiness, the grafted chains do not have to be too compact or too stretched to make these attractive contacts due to topologically favorable contiguous placement of like-monomers. In contrast, at low to intermediate blockiness, the grafted chains have to be either compact (low 〈Rg,chain2〉0.5) for intra-chain attractive contacts or stretched (high 〈Rg,chain2〉0.5) for intra-particle inter-chain or inter-particle attractive contacts because the like-monomers are dispersed along the grafted chain. Compared to strong like-monomer attractions, the weak like-monomer attractions are inferior at driving the compaction of the grafted chains, especially at lower blockiness, because the enthalpic gain from weak attractive contacts cannot overcome the entropic loss of forming smaller chain conformations, leading to slightly higher 〈Rg,chain2〉0.5 at weak attractions than strong attractions.
In the presence of A–B repulsions, when the A–A and/or B–B attractions are strong enough to dominate over the A–B repulsions (black circles in Fig. 2d–f), the results have the same trend as seen in the absence of A–B repulsion and our previous explanations for these trends hold. However, when A–A and/or B–B attractions are weak and A–B repulsions are strong (blue triangles in Fig. 2d and e), the 〈Rg,chain2〉0.5 shows a different, non-monotonic trend. The three graft sequences with the lowest blockiness—((A1B1)12, (A2B2)6, (A3B3)4)—lead to nanoparticles being dispersed (as discussed later in Fig. 5j–l) and therefore all grafted chain conformations arise from maximizing intra-particle contacts. On the other hand, for the more blocky ((A6B6)2 and (A12B12)1) sequences, the grafted nanoparticles assemble into clusters, where they are able to form inter-particle like-monomer contacts with lower stretching (i.e. lower 〈Rg,chain2〉0.5). Whether a sequence drives the copolymer grafted nanoparticles to form mostly inter-particle contacts or intra-particle contacts and how much the grafted chain has to stretch or coil up to make those contacts are dependent on the grafted sequence blockiness which governs how easy or hard it is to make attractive A–A or B–B contacts while avoiding repulsive A–B contacts.
We present the average number of total A–A, B–B, and A–B contacts in the second, third, and fourth row, respectively, in Fig. 2 and the number of inter-particle, and inter-chain intra-particle contacts in ESI Section II,† as a function of monomer sequences at varying monomer–monomer interactions listed in Table 1.
For all interaction sets, leaving aside (A1B1)12 for now, as the grafted sequence blockiness increases from (A2B2)6 to (A12B12)1, the number of like monomer (A–A and B–B) contacts increases and the number of unlike monomer (A–B) contacts decreases. This is expected because, with increasing blockiness, the like-monomers are placed closer together thereby facilitating A–A and B–B aggregation and consequently minimizing A–B contacts. We will revisit the (A1B1)12 sequence shortly to discuss why it does not fit the trend shown by the other sequences. Interestingly, we note similar trends for the number of A–A contacts for grafted nanoparticles with A–A attraction (Fig. 2g) and the number of B–B contacts for grafted nanoparticles with B–B attraction (Fig. 2n) which allude to the graft sequence and monomer–monomer interactions having a symmetric effect on chain conformations due to symmetric composition of the grafted copolymers. In other words, the A–A and B–B contact data are similar in pairs: Fig. 2g and n, h and m, i and o, j and q, k and p, l and r. Additionally, in ESI Section II,† the number of inter-particle, inter-chain, and intra-particle inter-chain contacts data further confirms these trends. They also show that, in the absence of A–B repulsion, with weak or strong A–A or B–B attraction, the total inter-particle and intra-particle inter-chain contacts decrease with increasing blockiness from (A2B2)6 to (A12B12)1. In the presence of A–B repulsion, with weak or strong A–A or B–B attraction the total inter-particle and intra-particle inter-chain contacts increase with increasing blockiness from (A2B2)6 to (A12B12)1.
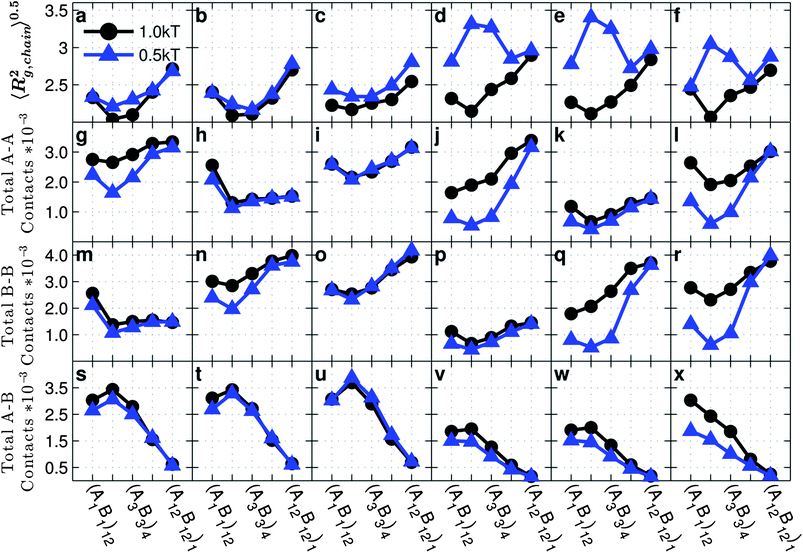
 | ||
| Fig. 3 (a–e) Snapshots of clusters for systems with interaction set 4 and no monomer–particle attraction (best viewed in color). The plots show the average number of A domains (f–k) and B domains (l–q) for copolymer grafted nanoparticles of size D = 4d each with six grafts of length Ngraft = 24. The interaction sets correspond to the plot letters as follows: lines on plots f and l correspond to interaction sets 1 (blue triangles) and 2 (black circles), lines on plots g and m correspond to interaction sets 3 (blue triangles) and 4 (black circles), lines on plots h and n correspond to interaction sets 5 (blue triangles) and 6 (black circles), lines on plots i and o correspond to interaction sets 7 (blue triangles) and 8 (black circles), lines on plots j and p correspond to interaction sets 9 (blue triangles) and 10 (black circle), and lines on plots k and q correspond to interaction sets 11 (blue triangles) and 12 (black circles). The black circles represent monomer–monomer attraction = 1 kT, while the blue triangles represent monomer–monomer attraction = 0.5 kT. All monomer–particle interactions are maintained as hard sphere interactions. | ||
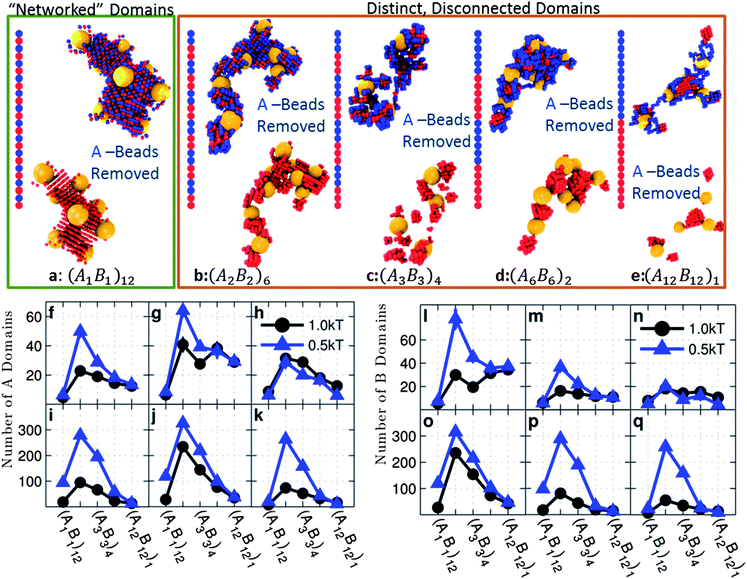
 | ||
| Fig. 4 Average height of A-monomers (top row) and B-monomers (bottom row) from the particle centers as functions of monomer sequences for copolymer grafted nanoparticles of size D = 4d with six grafts of length Ngraft = 24. The interaction sets correspond to the plot letters as follows: lines on plots a and g correspond to interaction sets 1 (blue triangles) and 2 (black circles), lines on plots b and h correspond to interaction sets 3 (blue triangles) and 4 (black circles), lines on plots c and i correspond to interaction sets 5 (blue triangles) and 6 (black circles), lines on plots d and j correspond to interaction sets 7 (blue triangles) and 8 (black circles), lines on plots e and k correspond to interaction sets 9 (blue triangles) and 10 (black circles), and lines on plots f and l correspond to interaction sets 11 (blue triangles) and 12 (black circles). The black circles represent monomer–monomer attraction = 1 kT, while the blue triangles represent monomer–monomer attraction = 0.5 kT. All monomer–particle interactions are maintained as hard sphere interactions. | ||
When A–B repulsion is negligible and the A- and/or B-monomers are attractive, we observe that HA (Fig. 4a–c) decreases slightly or is constant with increasing blockiness while HB (Fig. 4g–i) increases with increasing blockiness. At low blockiness, both A and B monomers tend to be relatively close to the particle surface because the chains must be compact (Fig. 2a–c) in order to make sufficient attractive like-monomer intrachain contacts. As blockiness increases, the monomers become more topologically separated, allowing attractive monomers to more easily aggregate either further from the surface (B-monomers) or closer to the particle surface (A-monomers). At high blockiness, the B-monomers also tend to aggregate further from the particle surface in order to increase the likelihood of inter-particle contacts and therefore the number of possible B–B contacts, while A-monomers cannot access as many of these inter-particle contacts due to the steric hindrance from the B-block.
In the presence of A–B repulsion and strong A–A and/or B–B attraction, we observe similar trends in HA and HB as discussed above for the absence of A–B repulsion. This is in line with our discussion of 〈Rg,chain2〉0.5 which showed that, when εAB = (εAA, εBB), the effect of A–B repulsion is minimal on chain conformation. Cases with irregular trends in HA and HB (Fig. 4j–l) are due to low blockiness sequences favouring dispersions and high blockiness sequences favouring assembly.
B. Effect of monomer sequence on nanoparticle arrangement in the cluster
In the absence of A–B repulsion when only A–A (Fig. 5a and g) or B–B (Fig. 5b and h) interactions are attractive, as blockiness increases, both the average number of neighbors each nanoparticle has in a cluster or the coordination number, 〈Z〉, and the average number of particles in a cluster, 〈N〉, decrease. This is because, with increasing blockiness, the grafted chains are able to form a high number of favorable intra-chain conformations without losing as much entropy, which in turn decreases the probability of forming inter-particle contacts, and hence the propensity for assembly is diminished. Using ESI, Fig. S4,† which shows the average number inter-chain contacts, and the data in Fig. 2, the approximate number of intra-chain contacts can be estimated. We also note the slightly higher 〈Z〉 and 〈N〉 for systems with B–B attraction when compared to systems with A–A attraction. This is due to the lower effective reach of the A monomers (Fig. 4g) which inhibits grafted nanoparticles with A–A attractions from aggregating as compared to grafted nanoparticles with B–B attractions. Interestingly, while 〈Z〉 and 〈N〉 decrease with increasing blockiness, the 〈Rg,cluster2〉0.5 (Fig. 5m and n) is either constant or increases slightly with increasing blockiness. This effect is a consequence of the grafts becoming less compact with increasing blockiness, as shown by 〈Rg,chain2〉0.5 in Fig. 2a and b.
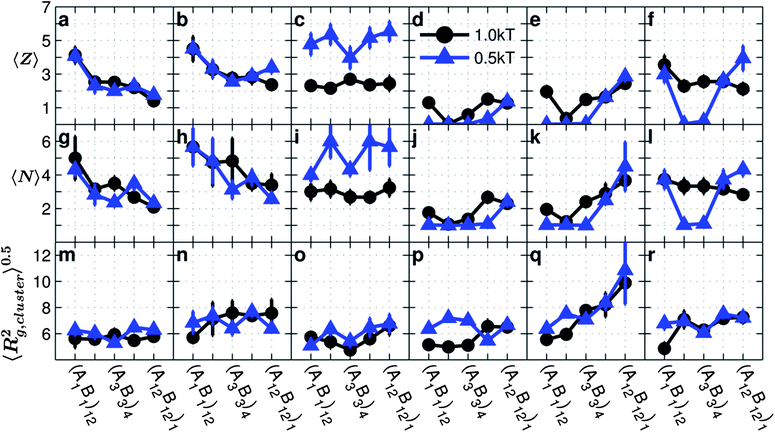 | ||
| Fig. 5 Average coordination number 〈Z〉, average number of particles per cluster 〈N〉, and average radius of gyration of a cluster 〈Rg,cluster2〉0.5 as a function of monomer sequences for copolymer grafted nanoparticles of size D = 4d with six grafts of length Ngraft = 24. The interaction sets correspond to the plot letters as follows: lines on plots a, g, and m correspond to interaction sets 1 (blue triangles) and 2 (black circle), lines on plots b, h, and n correspond to interaction sets 3 (blue triangles) and 4 (black circle), lines on plost c, i, and o correspond to interaction sets 5 (blue triangles) and 6 (black circle), lines on plots d, j, and p correspond to interaction sets 7 (blue triangles) and 8 (black circle), lines on plots e, k, and q correspond to interaction sets 9 (blue triangles) and 10 (black circle), and lines on plots f, l, and r correspond to interaction sets 11 (blue triangles) and 12 (black circle). The black circles represent monomer–monomer attraction = 1 kT, while the blue triangles represent monomer–monomer attraction = 0.5 kT. All monomer–particle interactions are maintained as hard sphere interactions. | ||
In the presence of both A–A and B–B attractions and absence of A–B repulsions (Fig. 5c, i and o), the copolymer chains seek to maximize both A–A and B–B contacts. For both strong (black circles) and weak (blue triangles) A–A and B–B attractions 〈Z〉, 〈N〉 and 〈Rg,cluster2〉0.5 are statistically constant with the monomer sequence. In effect, the presence of both like-monomer attractions causes the grafted nanoparticles to achieve similar cluster sizes and internal connectivity regardless of the monomer sequence. We also observe that the chain conformations with both A–A and B–B attractions and no A–B repulsion also show more constant trends with increasing blockiness than chains with only A–A or only B–B attraction, as evidenced by the data in Fig. 2. Due to the fact that both A–A and B–B monomers are attractive, the probability of a chain making favorable monomer–monomer contact is greatly increased, also shown by the contact profiles in Fig. 2. Due to the chains' reduced barriers to find favorable conformations, the effect of monomer sequence is diminished because the monomer sequence mainly affects chain conformations by introducing barriers to favorable enthalpic contacts. Therefore, copolymer grafted nanoparticles with both A–A and B–B monomer attractions assemble into relatively consistent configurations regardless of the graft sequence.
In the presence of A–B repulsion, when either A–A (Fig. 5d, j and p), B–B (Fig. 5e, k and q), or both are attractive (Fig. 5f, j and r), 〈Z〉, 〈N〉, and 〈Rg,cluster2〉0.5 all increase with blockiness with the exception of (A1B1)12 which tends to deviate for strong A–A or B–B attraction strength (black circles). These trends are in contrast to the behavior seen in the absence of A–B repulsion, where increasing blockiness led to decreasing or constant 〈N〉 and 〈Z〉. This is because, at low blockiness, where A and B monomers are topologically not separated, the presence of A–B repulsion lowers the propensity to assemble and in turn reduces the 〈N〉 and 〈Z〉. As blockiness increases, the A–B repulsion plays a small role because the A and B monomers are segregated topologically, and therefore the values of 〈Z〉 and 〈N〉 remain similar to that seen in the absence of A–B repulsion.
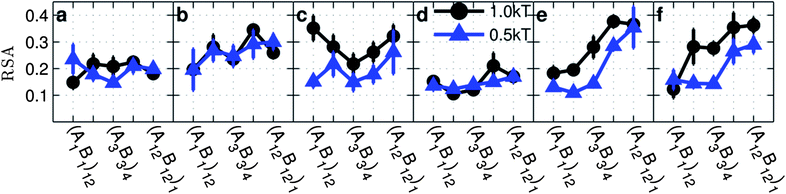 | ||
| Fig. 6 Relative shape anisotropy (RSA) as a function of the monomer sequence on copolymer grafted nanoparticles for copolymer grafted nanoparticles of size D = 4d with six grafts of length Ngraft = 24. The interaction sets correspond to the plot letters as follows: lines on plot a correspond to interaction sets 1 (blue triangles) and 2 (black circle), lines on plot b correspond to interaction sets 3 (blue triangles) and 4 (black circle), lines on plot c correspond to interaction sets 5 (blue triangles) and 6 (black circle), lines on plot d correspond to interaction sets 7 (blue triangles) and 8 (black circle), lines on plot e correspond to interaction sets 9 (blue triangles) and 10 (black circle), and lines on plot f correspond to interaction sets 11 (blue triangles) and 12 (black circle). The black lines with circle markers represent monomer–monomer attraction = 1 kT, while the blue triangles with triangle markers represent monomer–monomer attraction = 0.5 kT. All monomer–particle interactions are maintained as hard sphere interactions. | ||
In the absence of A–B repulsion and only A–A (Fig. 6a) or B–B attractions (Fig. 6b), we observe statistically constant RSA regardless of the graft sequence while strong A–A and B–B attractions (Fig. 6c) show non-monotonic trends. On comparing simulations with only A–A attraction to simulations with only B–B attraction, we observe that statistically significant differences in RSA values only appear for (A6B6)2 and (A12B12)1. Since the differences between A–A and B–B attractions can be attributed to the differing locations of the A and B monomers along the chain, which becomes more pronounced with increasing blockiness as shown by HA and HB in Fig. 4, it follows that the greatest difference in RSA between A–A and B–B attractions would be observed for the most blocky sequences. At high blockiness, when there are only A–A attractions, the attractive A-monomers aggregate close to the particle surface (Fig. 4a) which forces other grafted nanoparticles to be close in order to make inter-particle A–A contacts. This means that particles need to pack neighbors into a smaller volume (closer to the surface) leading to a more isotropic distribution (low RSA). In contrast, when there is only B–B attraction at high blockiness, the attractive B monomers tend to aggregate farther from the particle surface into few patches (low 〈Z〉 and the number of domains) leading to anisotropic cluster shapes.
In the presence of A–B repulsion and only A–A attraction (Fig. 6d) we do not see a significant effect of the sequence on RSA, since much of the cluster shape is driven by attractive A-domains being close to the surface forming isotropic clusters. Since the presence of A–B repulsion affects the height of A-monomers (Fig. 4a and d) only for sequences with the lowest blockiness, where the sequence itself drives isotropic assembly, there is no effect of A–B repulsion on RSA. In contrast, for B–B attraction (either by themselves or with A–A attraction), the presence of A–B repulsions (Fig. 6e and f) seem to amplify the effect of increasing blockiness on RSA, making the clusters span a larger range of RSA. It is interesting that, unlike the contact data in Fig. 2, there is no symmetry in the effect of A–A versus B–B attraction on cluster shape. Instead, we observe marked differences between the two types of monomer attractions. This lack of symmetry is again due to A-monomers being located much closer to the surface at high blockiness when compared to B-monomers. For B–B attraction in the presence of A–B repulsion, HB in Fig. 4k and l, and the number of B domains in Fig. 3p and q show that the B-monomers move further from particles' surfaces and become clustered into fewer domains which would cause clusters to become more “stretched” and therefore more anisotropic.
To summarize, systems with B–B monomer attraction in the presence of A–B repulsion show the greatest effect of the graft sequence on cluster shape, while systems with A–A attraction produce relatively isotropic clusters regardless of the graft sequence.
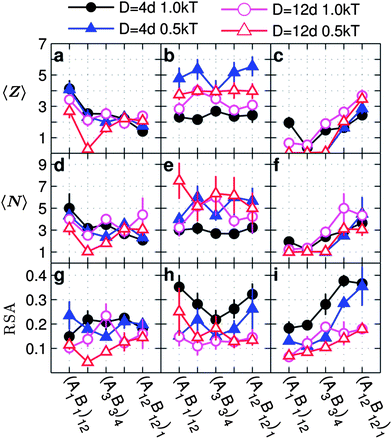 | ||
| Fig. 7 Average coordination number 〈Z〉, average number of particles per cluster 〈N〉, and relative shape anisotropy (RSA) as a function of the monomer sequence for copolymer grafted nanoparticles of size D = 4d and D = 12d with six grafts of length Ngraft = 24. The lines on plots a, d, and g correspond to interaction sets 1 (triangles) and 2 (circles), lines on plots b, e, and h correspond to interaction sets 5 (triangles) and 6 (circles), lines on plots c, f, and i correspond to interaction sets 9 (triangles) and 10 (circles). The circles represent monomer–monomer attraction = 1 kT, while the triangles represent monomer–monomer attraction = 0.5 kT. The filled symbols represent nanoparticles of size D = 4d while the open symbols represent nanoparticles of size D = 12d. All monomer–particle interactions are maintained as hard sphere interactions. | ||
In general, we expect grafted nanoparticles with higher particle-size to graft length (D/Ngraft) ratios, at a constant number of grafts, to show lowered propensity for cluster formation because the grafted chains must adopt more extended and entropically costly conformations than lower D/Ngraft to form either intra-particle inter-chain or inter-particle contacts. In particular, the barrier to intra-particle inter-chain contacts, due to large D or small Ngraft, forces the chains to assume compact conformations to maximize intra-chain contacts, which in turn minimizes probability of forming inter-particle contacts due to reduced reach of the chain. The inter-particle and intra-particle inter-chain data in ESI Section II† supports these conjectures. To summarize, increasing D/Ngraft introduces more entropic barriers to monomer aggregation by increasing the distance between intra-particle chains, and similarly reducing the number of accessible inter-particle contacts.
The differences in cluster connectivity, size and shape, between D = 4d and D = 12d, are significant only for specific combinations of interaction set and interaction strength that complement the entropic barriers introduced by the increased D/Ngraft.
With only A–A attraction (Fig. 7a and d), we see statistically indistinguishable trends in 〈Z〉 and 〈N〉 between D = 4d and D = 12d except for (A2B2)6 with weak A–A attraction. Like D = 4d, the trend in 〈Z〉 and 〈N〉 for D = 12d is non-monotonic with the graft sequence because the grafts of sequence (A1B1)12 form spatially distributed networks of like monomers as opposed to the distinct disconnected domains seen with the other sequences (Fig. 3 and ESI, Fig. S18†). Also, the dip in 〈Z〉 at (A2B2)6 for D = 12d (open symbols) is exaggerated compared to the rest of the data because the nanoparticles are in a dispersed state.
In the case of A–A and B–B attractions, in the absence of A–B repulsion, the data (second column Fig. 7) are mostly indistinguishable when comparing D = 4d and D = 12d for both weak and strong monomer attractions. As discussed above for D = 4d, for D = 12d having both types of monomer attractions diminishes the effects of monomer sequence due to the increased number of possible favorable contacts, also reducing the effect of increasing D/Ngraft.
When there is B–B attraction in the presence of A–B repulsion (third column Fig. 7) we observe only minor differences between D = 4d and D = 12d in 〈Z〉 and 〈N〉. The addition of A–B repulsion reduces the enthalpic gain from all conformations at low blockiness, regardless of particle size, forcing the nanoparticles to assume a dispersed state. As blockiness increases, the effect of the A–B repulsion diminishes and the nanoparticles assemble strongly due to the favorable placement of the B-monomers further from the particle surface (ESI, Fig. S12–S15†). Interestingly, we also observe that, at high blockiness, D = 4d produces significantly higher RSA (more anistropic cluster shapes) than D = 12d (Fig. 7i). While the outer-block attraction produces more anisotropic clusters for D = 4d due to the attractive monomers being further from the particle surface, the larger particles (D = 12d) occupies more volume and forces the nanoparticles to pack more isotropically.
C. Effects of monomer–particle interactions on assembly
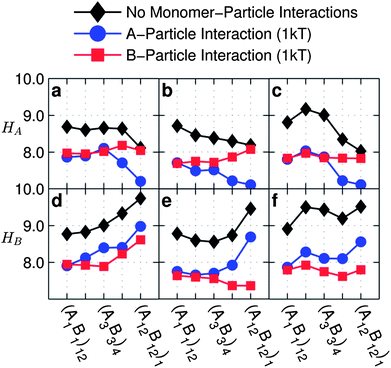
The discussion of the effect of a grafted chain's monomer sequence on the assembled nanoparticle cluster size, structure, and shape presented so far has been in the absence of any monomer–particle interactions. For the particle diameter D = 4d, we find that while monomer–particle interactions (either A-particle or B-particle) affect the local ordering of monomers, these effects do not manifest into differences in coordination number, size, or shape of the assembled cluster. This is because, for a D = 4d particle with six grafts of length Ngraft = 24 each, the small attractive surface area compared to the long grafts results in the number of monomer–monomer interactions outnumbering the possible monomer–particle interactions. See ESI Section VI† for a presentation of our full dataset on copolymer grafted nanoparticles in the presence of monomer–particle interactions. In ESI Section VII,† we also provide a discussion on the differences between monomer–monomer interactions and monomer–particle interactions in our simulation.For nanoparticles with D = 12d with the same number of grafts and graft length as D = 4d, due to an increased surface area over D = 4d, we observe a slightly increased effect of monomer–particle interactions on the chain conformations and particle assembly. In order to understand how these monomer–particle interactions affect the location of A and B monomers, we present the average heights of the A monomer (HA) and B monomer (HB) from the particle surface in the presence of A-particle or B-particle attraction in Fig. 8. We then connect this to the effect of monomer–particle interactions on assembly, via 〈Z〉, 〈N〉, 〈Rg,cluster2〉0.5, and RSA data for three interaction sets of grafted particles of D = 12d in Fig. 9. Our complete dataset for HA, HB, 〈Z〉, 〈N〉, 〈Rg,cluster2〉0.5, and RSA in the presence of A-particle or B-particle interactions for both D = 4d and D = 12d is presented in the ESI Sections II and VI.†
 | ||
| Fig. 8 Average height of A-monomers (top row) and B-monomers (bottom row) from the particle surface as a function of monomer sequences for copolymer grafted nanoparticles D = 12d with six grafts of length Ngraft = 24 for interaction sets with no particle–monomer interactions (black diamonds), A-particle attraction = 1 kT (blue circles), and B-particle attraction = 1 kT (red squares). The interaction sets correspond to the plot letters as follows (with particle–monomer interactions indicated by line color and marker shape): lines on plots a and d correspond to interaction set 4, lines on plots b and e, correspond to interaction set 1, lines on plots c and f correspond to interaction set 11. | ||
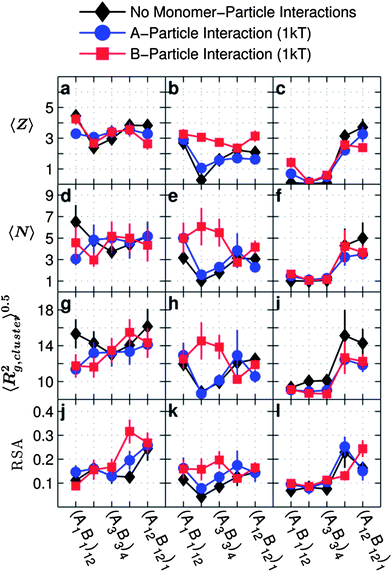 | ||
| Fig. 9 Average coordination number 〈Z〉, average number of particles per cluster 〈N〉, average radius of gyration of a cluster 〈Rg,cluster2〉0.5 and relative square anisotropy (RSA) as a function of the monomer sequence for copolymer grafted nanoparticles D = 12d with six grafts of length Ngraft = 24 for systems with no particle–monomer interactions (black diamonds), A-particle attraction = 1 kT (blue circles), and B-particle attraction = 1 kT (red squares). The interaction sets correspond to the plot letters as follows (with particle–monomer interactions indicated by line color and marker shape): lines on plots a, d, g, and j correspond to the interaction set 4, lines on plots b, e, h, and k correspond to the interaction set 1, lines on plots c, f, i, and l correspond to the interaction set 11. | ||
In Fig. 8 for all interactions presented, we observe that A-particle attraction reduces HA, and B-particle attraction reduces HB by approximately one unit for all sequences. We also see that HA decreases or is constant with increasing blockiness in the presence of A-particle attraction, while HA is relatively constant for all sequences in the presence of B-particle attraction. In contrast, HB with B-particle attraction is increasing or constant with increasing blockiness while HB with A-particle attraction is always increasing. This is because, at low blockiness, the monomers attracted to the particle drag the unlike-monomers, while at high blockiness, due to topological separation along the graft, the monomers not-attracted to the particle surface are not dragged.
Despite the significant effect of monomer–particle interactions on HA and HB, in the case of strong B–B attraction and no A–B repulsion, the monomer–particle interactions only slightly affect 〈Z〉 (Fig. 9a) and 〈N〉 (Fig. 9d) for two sequences-(A1B1)12 and (A12B12)1 and there are no statistically significant effects of monomer–particle interactions on the 〈Rg,cluster2〉0.5 for any of the sequences (Fig. 9g). As for RSA (Fig. 9j) in the presence of B-particle attraction (red line), there seems to be a significant increase in RSA at (A6B6)2 as compared to no particle–monomer attraction (black diamonds) or with A-particle attraction (blue circles). However, this sharp rise in RSA does not seem to correspond with any change in the trend for monomer position in Fig. 8a or d or monomer contacts in ESI, Fig. S2–S11.†
In Fig. 9b, e, h and k, with weak A–A attraction in the absence of A–B repulsion we see an increased effect of monomer–particle interactions on the assembled cluster as compared to the grafted nanoparticles with strong B–B attraction (Fig. 9a, d, g and j). In particular, we observe the greatest effect on the size (〈N〉 and 〈Rg,cluster2〉0.5) and connectivity (〈Z〉) of the clusters in the case of B-particle attraction, i.e. when the monomer–particle (B-particle) interactions do not compete with the monomer–monomer (A–A) interactions. When monomer–particle and monomer–monomer interactions do not compete, the monomers can easily aggregate to maximize favorable contacts both with the particle and other like monomers. Furthermore, leaving aside (A1B1)12 for its uniqueness, the effect of monomer–particle attraction is greatest at low blockiness ((A2B2)6 and (A3B3)4). Since the low blockiness sequences form tight, compact conformations (Fig. 2a–f) that make inter-particle contacts difficult, it follows that for these sequences the monomer–particle interactions would encourage particle–monomer contacts more often than in blockier sequences. (A1B1)12 does not follow this trend due to its unique domain as discussed is Section III.A. We observe that monomer–particle interactions do not have a significant effect on RSA (Fig. 9k) for this interaction set.
In the case of weak A–A and B–B attractions in the presence of A–B repulsion (Fig. 9c) either A-particle or B-particle attraction only slightly affects 〈Z〉 at low blockiness. We observe no significant effects of A-particle or B-particle attractions on 〈N〉 (Fig. 9f) or RSA (Fig. 9l), or 〈Rg,cluster2〉0.5 (Fig. 9i). The lack of an effect of particle–monomer interactions, suggests that the loss in conformational entropy by creating particle–monomer contacts cannot be overcome if the grafted chains also face enthalpic penalty due to repulsive A–B contacts made in the process of making favourable monomer–particle contacts.
Unlike the symmetry in monomer–monomer contacts seen in the absence of monomer–particle interactions (Fig. 2), there is no symmetry in the effect of switching between A-particle and B-particle interactions. With A-particle attractions, since the A-monomers are grouped closer to the surface of the nanoparticle with increasing blockiness (Fig. 8), the A-monomers collapse onto the surface of the nanoparticle they are grafted on. This only slightly affects the reach of the attractive A-block resulting in clusters with negligible changes 〈N〉 and 〈Rg,cluster2〉0.5 (blue lines: Fig. 9d, e, g and h). In contrast, B-particle contacts (either intra-particle or inter-particle) are harder to make than A-particle contacts, because B monomers are farther away from the surface and the A-monomers that are close to the particle surface sterically hinder B-particle contacts. Further compounding the complexity of monomer–particle interactions is the effect of competing or non-competing monomer–monomer interactions as was discussed above.
Overall, for particles of D = 12d, the increased surface area of the larger particle enhances the effect of monomer–particle interaction, but the effect is still limited by the lower number of possible monomer–particle contacts as compared to the number of possible non-bonded monomer–monomer contacts (see ESI Section VII† for a detailed discussion). One would expect that a significantly stronger monomer–particle attraction (≫1 kT) would overwhelm the relatively weaker monomer–monomer attraction, and lead to significant effects on the assembly. We tested this hypothesis for alternating and diblock copolymer grafted particles, and observed a drastic effect of monomer–particle interaction for grafted nanoparticles with weak monomer–monomer interactions (∼0.5 to 1 kT) and strong monomer–particle interactions of ∼16 kT (see ESI, Fig. S28†). In general, when the monomer–particle interactions are greatly increased, we see that many of the trends going from (A1B1)12 to (A12B12)1 are flipped in comparison to the case where monomer–monomer and monomer–particle attractions are equal. Thus, the relative strength of monomer–particle interactions and monomer–monomer interactions heavily dictates the extent to which monomer–particle interactions can affect characteristics of the assembled cluster.
IV. Conclusions
We have conducted Monte Carlo simulations to study copolymer grafted spherical nanoparticles placed in an implicit solvent to elucidate the effect of blockiness in the grafted copolymer sequence at varying monomer–monomer and monomer–particle interactions on size, shape and structure of assembled copolymer grafted nanoparticles. The grafted chain conformations are closely linked to how the monomer sequence facilitates the chain's ability to form energetically favorable attractive monomer contacts while minimizing unfavorable repulsive monomer contacts. As the sequence blockiness increases, attractive monomer contacts are brought together more easily due to the favorable topological placement of like monomers along the chain. Within the assembled nanocluster, the alternating sequence, (A1B1)12, forms “networks” of attractive monomer contacts in contrast to the distinct domains of attractive monomers formed by blockier monomer sequences. In the case of A–A or B–B monomer attraction without A–B repulsion, we observed decreasing cluster size and decreasing connectivity within the cluster with increasing blockiness for particle sizes D = 4d and D = 12d, with (A1B1)12 always being an outlier in these trends. With the addition of A–B repulsion to A–A or B–B monomer attraction, clusters of both particle sizes D = 4d and 12d show increasing size and increasing connectivity with increasing blockiness. For D = 4d particles, with strong B–B attraction and A–B repulsion, increasing blockiness leads to increasing anisotropy in cluster shape, while strong A–A attraction produce isotropic clusters regardless of the graft sequence. The effect of graft sequence on cluster shape is reduced for D = 12d as compared to D = 4d at constant graft length. Lastly, monomer–particle interactions only weakly affect the assembly of copolymer grafted nanoparticles when the particle size is small relative to the graft length, and the strength of particle–monomer interactions are commensurate with the monomer–monomer interactions. The effects of monomer–particle interactions on the cluster size, shape, and structure are enhanced with significantly strong particle–monomer interactions, and/or with substantially large particle sizes relative to graft lengths.The studies presented in this paper are focused only on dilute concentration of c ∼ 1 × 10−5 particles per nm3, obtained by using 10 particles in a 100 × 100 × 100 (nm3) simulation box with periodic boundary conditions. Keeping in mind that an experimentalist working at these concentrations could observe clusters with greater than 10 nanoparticles we have been careful to emphasize qualitative trends in the data with varying parameters, and not discuss specific quantitative data (especially 〈N〉). We have also carefully considered our choice of a lattice model and have tried to minimize lattice effects on our analysis, and focused on general qualitative trends that should hold true in off-lattice models as well. We have conducted off-lattice tests in some cases to ensure unique behavior of alternating copolymer (e.g. network of A and B monomers) is not an artifact of the lattice model.
The trends presented here should guide experimentalists seeking to create target morphologies of copolymer grafted nanoparticles for various applications such as metamaterials, photonics, photovoltaics and electronics. For example, in materials design for photovoltaic application, the spatial organization of the constituent chemistries dictates how well charges separate and travel to corresponding electrodes, and in turn device efficiency.42 This work shows how copolymer grafted nanoparticle assembly could be used and the sequence of grafted polymers chosen to control the number and structure of the monomer domains around the nanoparticles.
Some of the future directions of this work include investigating the dynamics during assembly of copolymer grafted particles. Also, understanding both equilibrium and dynamic behavior of these copolymer grafted nanoparticles in a polymer matrix would be useful for tailoring morphologies in polymer nanocomposites. Previous work using a self-consistent PRISM-MC scheme, has shown that the potential of mean force (PMF) between AB copolymer grafted nanoparticles in a A or B homopolymer matrix differs from that seen in homopolymer grafted nanoparticles in a homopolymer matrix (with graft and matrix chemistries being identical), and that the PMF is a function of the copolymer sequence.13 It would be interesting to study how at varying volume fractions of grafted particles, the presence of an explicit polymer matrix, and matrix chain conformations affect the grafted chain conformations, and in turn the assembly/dispersion of the particles in the matrix.
Acknowledgements
This work was partially supported by National Science Foundation under grant number CBET-0930940 and partially by National Science Foundation—Research Experience for Undergraduates (REU) for Functional Materials at University of Colorado.References
- B. Hong, A. Chremos and A. Z. Panagiotopoulos, J. Chem. Phys., 2012, 136, 204904 Search PubMed.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Soft Matter, 2012, 8, 5002–5010 RSC.
- V. Pryamtisyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, J. Chem. Phys., 2009, 131, 221102 CrossRef.
- T. A. Witten and P. A. Pincus, Macromolecules, 1986, 19, 2509–2513 CrossRef CAS.
- M. D. Clark and R. Krishnamoorti, J. Phys. Chem. C, 2009, 113, 20861–20868 CrossRef CAS.
- V. Goel, J. Pietrasik, H. Dong, J. Sharma, K. Matyjaszewski and R. Krishnamoorti, Macromolecules, 2011, 44, 8129–8135 CrossRef CAS.
- R. Krishnamoorti, MRS Bull., 2007, 32, 341–347 CAS.
- A. Jayaraman and K. S. Schweizer, Langmuir, 2008, 24, 11119–11130 CrossRef CAS.
- A. Jayaraman and K. S. Schweizer, J. Chem. Phys., 2008, 128, 164904 CrossRef.
- A. Jayaraman and K. S. Schweizer, Macromolecules, 2008, 41, 9430–9438 CrossRef CAS.
- A. Jayaraman and K. S. Schweizer, Macromolecules, 2009, 42, 8423–8434 CrossRef CAS.
- T. B. Martin, A. Seifpour and A. Jayaraman, Soft Matter, 2011, 7, 5952–5964 RSC.
- N. Nair and A. Jayaraman, Macromolecules, 2010, 43, 8251–8263 CrossRef CAS.
- N. Nair, N. Wentzel and A. Jayaraman, J. Chem. Phys., 2011, 134, 194906 CrossRef.
- K. I. Popov, R. J. Nap, I. Szleifer and M. O. de la Cruz, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 852–862 Search PubMed.
- B. Vorselaars, J. U. Kim, T. L. Chantawansri, G. H. Fredrickson and M. W. Matsen, Soft Matter, 2011, 7, 5128–5137 RSC.
- X. Zhu, L. Wang, J. Lin and L. Zhang, ACS Nano, 2010, 4, 4979–4988 CrossRef CAS.
- P. M. Dodd and A. Jayaraman, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 694–705 Search PubMed.
- A. Ghanbari, T. V. M. Ndoro, F. Leroy, M. Rahimi, M. C. Bohm and F. Muller-Plathe, Macromolecules, 2012, 45, 572–584 Search PubMed.
- S. W. Hu, Y. J. Sheng and H. K. Tsao, J. Phys. Chem. C, 2012, 116, 1789–1797 Search PubMed.
- J. X. Shen, J. Liu, Y. Y. Gao, D. P. Cao and L. Q. Zhang, Langmuir, 2011, 27, 15213–15222 CrossRef CAS.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354 CrossRef CAS.
- S. Srivastava, P. Agarwal and L. A. Archer, Langmuir, 2012, 28, 6276–6281 CrossRef CAS.
- E. R. Chan, L. C. Ho and S. C. Glotzer, J. Chem. Phys., 2006, 125, 9.
- A. Seifpour, P. Spicer, N. Nair and A. Jayaraman, J. Chem. Phys., 2010, 132, 164901 CrossRef.
- Y. Jiao and P. Akcora, Macromolecules, 2012, 45, 3463–3470 Search PubMed.
- Y. L. Lin, C. S. Chiou, S. K. Kumar, J. J. Lin, Y. J. Sheng and H. K. Tsao, J. Phys. Chem. C, 2011, 115, 5566–5577 CrossRef CAS.
- C. R. Iacovella and S. C. Glotzer, Soft Matter, 2009, 5, 4492–4498 RSC.
- S. C. Glotzer, Nature, 2012, 481, 450–452 CrossRef CAS.
- Q. Lan, L. F. Francis and F. S. Bates, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 2284–2299 CrossRef CAS.
- S. C. Glotzer and J. A. Anderson, Nat. Mater., 2010, 9, 885–887 CrossRef CAS.
- C. Knorowski and A. Travesset, Curr. Opin. Solid State Mater. Sci., 2011, 15, 262–270 Search PubMed.
- G. van Anders and S. C. Glotzer, Nat. Chem., 2012, 4, 79–80 Search PubMed.
- S. Y. Park, K. R. A. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS.
- M. R. Jones, R. J. Macfarlane, B. Lee, J. A. Zhang, K. L. Young, A. J. Senesi and C. A. Mirkin, Nat. Mater., 2010, 9, 913–917 CrossRef CAS.
- J. C. Crocker, Nature, 2008, 451, 528–529 CrossRef CAS.
- J. Kim, H. Park, B. Kang, R. Ku, C. Ham and M. Yang, J. Appl. Phys., 2011, 110, 7 Search PubMed.
- K. Keller, A. Amirian and P. Akcora, Langmuir, 2012, 28, 3807–3813 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, San Diego, 2002 Search PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1206–1214 CrossRef CAS.
- J. E. Slota, X. He and W. T. S. Huck, Nano Today, 2010, 5, 231–242 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sm26611c |
| This journal is © The Royal Society of Chemistry 2013 |
