Fast and reversible microscale formation of columns in carbon nanotube suspensions
Simon
Wongsuwarn
a,
Yan
Ji
b,
Pietro
Cicuta
a and
Eugene M.
Terentjev
*a
aCavendish Laboratory, University of Cambridge, JJ Thomson Avenue, Cambridge CB3 0HE, UK. E-mail: emt1000@cam.ac.uk
bDepartment of Chemistry, Tsinghua University, Beijing 100084, P.R. China
First published on 16th October 2012
Abstract
Homogeneous carbon nanotube suspensions are studied in the semidilute regime, which is permitted by the use of an effective polysiloxane surfactant, PySi70, as a liquid matrix. We study such suspensions under an AC electric field by optical microscopy, transient light transmission and impedance spectroscopy. Optical microscopy shows the formation of long-range microscale columnar order as a result of a fast field-induced phase separation. The aggregation process is found to be reversible and repeatable, with nanotubes re-dispersing into a homogeneous solution, in a diffusive manner, in the seconds following removal of the electric field. The suggested role of the induced dipolar forces is consistent with the relatively fast columnar formation and characteristic concentration of maximum field-response. The equilibrium columnar structure provides fast field-induced control of the transparency and dielectric response, while avoiding electrical breakdown.
1 Introduction
External fields are key to opening up fascinating behavior in soft matter, and provide a control over phase and structure formation,1 as reviewed in ref. 2. In particular, electric fields have been used for decades to manipulate neutral colloidal particles, due to dielectrophoretic forces.3 These forces can result from the distortion of the applied field in the vicinity of an induced dipole, leading to dipolar interactions. Between dipolar pairs, the strongest attraction occurs in head-to-tail alignment along the field direction. Therefore, in addition to the influence of other system-specific interactions (which may include hydrodynamic, steric, van der Waals and Brownian interactions), anisotropic dipolar interactions can lead to complex phase diagrams in the concentration/field space, as seen in the fd-virus system,4 or to structure formation. Rigid structures formed between coplanar electrodes in this way have allowed for the development of novel materials such as electrorheological fluids, where electrical signals are converted quickly into a useful change in mechanical strength,5 as well as functional microwires.6Dipolar interactions in colloids depend on the particle polarisability α, which relates the induced dipole moment p to the electric field E via p = 4πε0αE.† Carbon nanotube (CNT) suspensions present an interesting system to investigate field-induced structure, as CNTs have been shown to have a very high α value. This is both as a result of the unique electronic properties of graphene sheets, as well as the enhancement offered by the high aspect ratio of the particle and its long persistence length.7 It is known that dilute CNTs align8 and form chains9 in response to an electric field. Such a field-assisted CNT assembly, at dilute concentrations, has contributed to applications such as polymer composites10 and field emission displays.11 Structure formation in semidilute (rotationally restricted) CNT suspensions has rarely been studied, however, it is prevented mainly by poor CNT solubility: a large effective van der Waals force acts between CNTs resulting in aggregation and sedimentation, as well as percolation across electrodes causing electrical breakdown.12 As a result, the potential for complex structure formation in CNT suspensions has been overlooked despite the well-understood variety of structures underlying electrorheological and magnetorheological fluids.13,14 Simple CNT fibrillation is capable of modifying the optical,15 dielectric16 and viscoelastic17 properties of suspensions. A more complex CNT structure formation therefore holds great potential and, as with all externally directed self-assembly, especially so if the response is fast and reversible.18
A dimensionless parameter that quantifies the relative importance of dipolar interactions to the thermal energy can be introduced
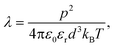 | (1) |
Progress has been recently made in the dispersion of CNTs: bile salts are successful in aqueous solvents,24 while we developed a siloxane-based pyrene surfactant (PySi70) to disperse CNTs in polysiloxane polymers.25 We found that more than 3 wt% of CNTs remained well dispersed in this surfactant after the non-polar solvent was evaporated.26 In the present paper we show semidilute suspensions of CNTs with PySi70 undergoing controlled, reversible and repeatable self-assembly into stable columnar structures. In our analysis, we focus on the optical and dielectric changes associated with the equilibrium structure and characterise the transient formation, showing fast reversibility of the effect.
2 Methods
CNT suspension preparation
Nanotubes were multi-walled CNTs (from Nanostructured & Amorphous Materials, Inc., USA) supplied with purity 95%+, diameter range 60–100 nm (average diameter a ∼ 80 nm) and length range 5–15 μm. The true density is quoted at ∼2 g cm−3, which allows for conversion between the weight and volume percent in our analysis. A 750 W ultrasonic processor (Cole-Parmer, UK), fitted with a titanium micro-tip, was used for sonication and the following sonication parameters were kept the same throughout all experiments: pulse rate 5 s on and 3 s off; probe temperature held at 15 °C and vibration amplitude 25%. We previously showed that nanotube scission as a result of cavitation occurs under these ultrasonication conditions.27 We therefore approximate the average CNT length in our present samples to be lLIM ≈ 2 μm, as previously defined,28 and, thus, the aspect ratio to be ∼20. SEM analysis also provided a persistence length of these nanotubes, lp ∼ 1 μm.29The choice of surfactant to facilitate the dispersion and stabilisation of nanotubes is very important. An extensive discussion of surfactant optimisation and the details of synthesis of the pyrene-siloxane molecule PySi70 are described in an earlier paper.25 The multi-wall CNTs were dispersed in petroleum ether (boiling point 40–60 °C) in the presence of PySi70 (PySi70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CNT = 60
CNT = 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight). A vial of the dispersion was left idle for 2 days, after which the upper 90% that contained creamed impurities was carefully removed. Following complete solvent evaporation, a stable stock of concentrated CNT suspension in liquid PySi70 was obtained. The concentration of the stock solution was measured via a calibrated UV absorption method described in detail elsewhere;30 it was found to be ca. 1.4 wt%. The CNT suspensions of lower concentration than 1.4 wt% used in this paper were prepared by diluting the concentrated suspension with further PySi70.
1 by weight). A vial of the dispersion was left idle for 2 days, after which the upper 90% that contained creamed impurities was carefully removed. Following complete solvent evaporation, a stable stock of concentrated CNT suspension in liquid PySi70 was obtained. The concentration of the stock solution was measured via a calibrated UV absorption method described in detail elsewhere;30 it was found to be ca. 1.4 wt%. The CNT suspensions of lower concentration than 1.4 wt% used in this paper were prepared by diluting the concentrated suspension with further PySi70.
Optical microscopy
ITO coated electro-optical cells (Linkam Scientific Instruments, UK) were used as optical imaging chambers across which a potential difference could be applied. The chambers were planar with a uniform height h = 20 μm and antiparallel polyimide alignment layers. The prepared CNT suspensions were imbibed into the ITO chambers by a capillary effect, at room temperature. The prepared cells were stable for many weeks since liquid PySi70 is non-volatile, and the CNT dispersion was homogeneous in equilibrium.Micrographs were collected using a Pike CCD camera (AVT, USA) attached to an LSM500 confocal microscope (Carl Zeiss, Germany) operated in bright-field mode with a 50×/0.5 NA Epiplan LD objective. To minimise non-uniform field effects around the chamber perimeter, the field of view was kept fixed at the centre of the ITO chamber. The average radius R⊥ of the densely aggregated CNT columns was found by averaging the total area below an intensity threshold judged by eye to identify the column boundaries. Their separation L was found by locating the peak in the computed structure factor.
Light transmission measurement
A basic light transmission set-up was constructed to measure the relative changes in mean sample transparency before and after structure formation and to measure the timescales of change. The ITO cell was positioned on the optical axis of a 15 mW 633 nm HeNe Laser (Melles Griot, USA) such that the beam passed through the centre of the cell; the beam spot diameter was estimated to be 2 mm, effectively averaging over a region with ∼105 columns. The chamber orientation was such that the beam propagation direction and the direction of applied field across the optical chamber were parallel. An optical density filter was used to reduce the beam intensity to a suitable level for a PDA100A-EC amplified photodetector (Thorlabs, USA), positioned on the other side of the ITO chamber, allowing the transmitted light to be measured. The photodetector operated in the range 400–1100 nm and the entire set-up was optically enclosed during measurements.Complex impedance measurement
The dielectric response of the CNT suspensions was characterised via AC impedance spectroscopy. A complex resistivity analyser 6440A (Wayne Kerr Precision Components, UK) was used to measure the in-phase and out-of-phase currents, obtaining the values of the complex impedance amplitude |Z*| and the phase angle. These experiments confirmed that no significant conductivity was encountered at any frequency in the studied range between 102 and 106 Hz.For all field-induced aggregation data, a potential difference was applied across the sample by connecting the terminals of the ITO imaging chamber to a function generator producing a square-wave alternating voltage at 10 kHz. CNT manipulation in electric fields is known to depend on both the field strength and frequency.9 We used a fixed high-frequency AC signal to avoid possible electrophoretic effects, and applied field strengths in excess of the critical field strengths required for long-range order.19 All voltages displayed in this paper are peak-to-peak values.
3 Results
Equilibrium structure
In Fig. 1A we show the typical response of a 0.7 wt% CNT–PySi70 suspension to an increasing AC field via a sequence of micrographs. The direction of the applied field is perpendicular to the image plane. Prior to field application (0 V) the CNTs are quite well-dispersed due to the PySi70 surfactant. Note that there is some residual structure even at 0 V since the sample in the image had been subject to previous cycling to test reversibility. As discussed in the next section, structure formation in the sample is almost fully reversible. When the potential difference across the ITO chamber is increased up to 20 V (E = 1 kV mm−1), the sample is observed to phase separate into a state in which dense regions are distributed homogeneously. The CNTs form structures large enough to be resolved clearly with bright-field illumination. The deep black appearance of the structures (in a chamber of height, and therefore optical path length, 20 μm) is consistent with the high optical absorption of CNTs.31 The constant position and size of the structures when the narrow focal plane of the 50× lens was moved along the optical axis confirm that the structures are columnar in form (the observed diameter of the columns is larger than the average CNT length, ruling out a spherical aggregate). Over many minutes after initial formation, the columns were not observed to move an appreciable amount.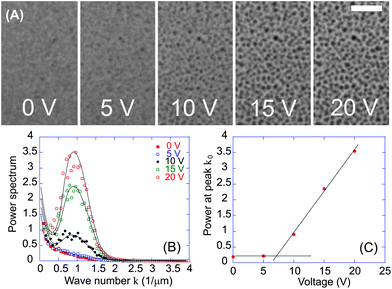 | ||
| Fig. 1 (A) Micrograph sequence of a 0.7 wt% CNT–PySi70 suspension on increasing AC field strength E, showing the formation of a microscopic structure. The field is perpendicular to the image plane and applied across an electro-optical imaging chamber of height h = 20 μm (20 V corresponds to E = 1 kV mm−1). Scale bar = h. (B) Computed structure factors S(k) show peaks at k0 ∼ 0.88 μm−1, corresponding to a column separation length scale L (2π/k0) of 7.1 μm. (C) S(k) values at peak, k = k0, suggesting that column formation begins to affect transparency at ≈7 V. | ||
To quantify the column formation, we compute the 2D Fourier transform of the image and plot the structure factor S(k), where k is the magnitude of the wavevector. Fig. 1B shows S(k) traces for several values of the applied potential difference. The increasingly defined columns correspond to the peak in S(k), which becomes more defined with increasing voltage. At 20 V, the position of the peak k0 ≈ 0.88 μm−1 corresponds to a length scale (2π/k0) of 7.1 μm. In Fig. 1C we plot the mean (interpolated) value of S(k) at k = k0, showing the that field-induced structure begins to affect the sample transparency in the range 5–10 V (E = 0.25–0.5 kV mm−1). At 20 V, R⊥ (average) ≈ 1.3 μm.
Taking the volume fraction within the dense columns being of order one, the expected column separation is estimated as L ∼ R⊥/ϕ1/2 ∼ 10 μm, comparing favourably with observations. The Halsey–Toor (HT) theory of structure formation in electrorheological fluids13,32 describes how the thermal fluctuation-induced interaction between polarised chains leads to their coarsening into columns. In the field dominated regime (λ ≫ 1) an upper limit on the column radius RHT ≤ h2/3a1/3 is predicted, giving an estimate RHT ∼ 3 μm (a ≈ 80 nm) in our case, again close to the observations of R⊥.
Aggregation time and reversibility
Fig. 2A shows the normalised sample transmission in the concentration range 0.15–0.8 wt%. An initial transmission coefficient is determined by the homogeneous concentration of dispersed CNTs in the matrix. The voltage is switched on at t = 0 and switched off at t = 10 s and the same characteristic behaviour can be identified across the concentration range. When a potential difference of 20 V is applied, the CNTs aggregate into the dense columns (visualised in Fig. 1A) leaving the rest of the fluid depleted in CNTs. The transmission rises to a plateau, and fitting the onset curves gives a reliable exponential rise ∼(1 − exp[−t/τON]) with the characteristic timescale of structure formation τON ≈ 0.3 s. Following field removal, the transmission also decayed exponentially with a longer characteristic time τOFF ≈ 5 s. It has been shown that the relaxation in such an electro-optical signal as a result of rotational diffusive decay may be approximated (to first order) as T/T0 ≈ exp[−6Drt], where Dr is the rotational diffusion coefficient.33 For the data shown in Fig. 2, Dr ≈ 0.03 s−1 is in good agreement with 0.01 s−1 calculated for rod-like particles with an aspect ratio of 20.34 A small deviation is expected since lp < lLIM therefore our CNTs may only be approximated as rods: a degree of flexibility would enhance the rotational diffusion. The dissolution of the structure is almost, but not fully, complete: a residual signature of the columns remains even after very long waiting times.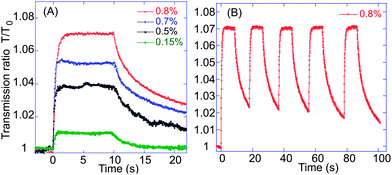 | ||
| Fig. 2 (A) Transient light transmission of CNT–PySi70 suspensions at increasing concentration, as labelled (all in wt%). A 20 V potential difference is applied between t = 0–10 s, showing a positive correlation between concentration and maximum transmission. (B) Several light transmission cycles showing reversibility of the microscopic phase separation. | ||
That the average light transmission increases when a field is applied may be understood qualitatively by considering the absorption of the homogeneously dispersed CNT solution; when nanotubes aggregate, the space between them clears and becomes transparent. The aggregated CNTs in columns shadow a much greater number of CNTs behind them, increasing the average transparency of the whole region, as we observe in Fig. 2A for increasingly dense structures. We note that other electro-optical studies of colloids35–37 have observed the same correlation and associated their observations with an increase in the photon mean free path. However, we do not suggest that mechanism here since CNTs are highly absorbing and therefore we expect changes in diffuse transmission in our system to have a minimal effect. Fig. 2B shows a typical trace of the transmission response when cycling the field (10 s on, 10 s off). Despite the faint residual structure, there is very good reproducibility in these cycles: the columns are shown to spontaneously and repeatably redisperse into an almost homogeneous suspension when the external field is switched off.
It is important to consider the effect of the high aspect ratio of CNTs: in particular, how the expected timescale of rotational alignment τR relative to the observed timescale of structure formation τON. All non-spherical particles experience a torque acting to align the axis of polarisation to the field direction. CNTs have a particularly large aspect ratio and a highly anisotropic polarisability.38 Assuming the longitudinal polarisability α‖ dominates in the case of reasonably rigid multi-wall CNTs, the dielectric torque is 4πε0α‖E2. Using E = 1 kV mm−1 (corresponding to V = 20 V in our setup) and our previously measured longitudinal polarisability α‖ ≈ 7 × 10−22 m3,30 the dielectric torque would be 4 × 10−20 J: an order of magnitude higher than kBT. This torque is opposed by the rotational viscous drag at low Reynolds number, with a rotational friction constant of the order ηl3 (omitting logarithmic corrections).39 The rotational alignment time arising from this field-driven orientation is τR ∼ ηl3/4πε0α‖E2. Taking the viscosity of PySi70 ηP ≈ 0.1 Pa s, and average nanotube length, l = lLIM ≈ 2 μm, gives τR ∼ 20 s: almost 100 times greater than the observed τON.
We may consider a number of aspects of the CNT–PySi70 system in light of the knowledge that the estimated time τR ≫ τON. Firstly, as the dielectric torque is much greater than thermal energy, the directions of the induced dipoles are not randomised by thermal fluctuations when the field is present regardless of whether a time τR has elapsed. This may be contrasted with thermally dominated systems (i.e. when λ ≪ 1) where τR ≪ τON is a requirement for structure formation.40 The fact that τR ≫ τON also suggests the observed fast aggregation occurs without significant alignment via the field-induced torque as calculated above. However, alignment may still be a factor in obtaining the columnar structure observed, as suggested by our dielectric measurements shown later in Fig. 4. As CNTs become closer to each other during the initial stages of aggregation, the dipole–dipole component of their interaction would become increasingly significant (the induced dipole p(E) was estimated in the previous paragraph, while the CNT separation changes from d0 ∼ a2/3L1/3/ϕ1/3 in the initial homogeneous state down to dcol ∼ a2/3L1/3 in dense columns). Therefore, in the semidilute regime of aggregating columns the CNT alignment may be enhanced and the speed of final stages of aggregation increased. An investigation of the effect of CNT length would provide insight into the mechanisms and timescales of structure formation.
Dielectric response
Using our standard electrooptic cell, we could monitor the change in complex impedance Z* of the parallel-plate capacitor subjected to an alternating potential difference. At a fixed frequency, Z(ω)* = ∣Z(ω)∣exp(−iθ), with ∣Z∣ being the frequency-dependent impedance modulus, θ the phase angle on the complex plane and f = 2πω the AC frequency. Taking the geometry of the cell into account, ∣Z∣ = ρ*h/A, where ρ* is the complex resistivity of the medium, A is the area of the electrodes and h is the cell gap. For a purely dielectric response, ρ* = (2πfεrε0)−1, with a characteristic 1/f frequency signature. This is precisely the response we see in Fig. 3 for all concentrations of nanotubes studied, with a maximum potential difference (V = 20 V) applied peak to peak. Furthermore, all samples have a stable phase angle around 89° over a six decade frequency range. To verify these features we have also prepared a higher-concentration CNT solution, which was sonicated at higher energies resulting in quite short CNT segments, yet even the 3 wt% solution of short multi-wall CNT segments showed no sign of conductivity. It is interesting to note that recent studies of CNTs in various fluid matrices have often registered a resistivity plateau at lowest frequencies,30 while we have a reliably non-conductive (purely capacitive) response when CNTs are fully covered by the surface-active PySi70 molecules. | ||
| Fig. 3 The dependence of the impedance amplitude of the CNT–PySi70 suspensions on frequency and concentration at an AC potential difference of 20 V peak to peak. The slope on the double-logarithmic scale is perfectly f−1 indicating therefore that CNT electrical percolation is avoided and hence that we are essentially measuring the average dielectric constant of the system. | ||
Since the frequency dependence of the complex impedance is purely dielectric, we arbitrarily chose an AC frequency of 10 kHz and investigated the change in the effective dielectric constant of the medium with increasing applied voltage. Fig. 4 shows the dependence of the impedance amplitude, across the range of CNT–PySi70 suspensions, as a function of voltage. As ∣Z∣ scales inversely with εr, a clear correlation between the CNT concentration and the dielectric constant is expected, given the known high polarisability of CNTs. The loading fraction that provides the maximum rate of change of ∣Z∣ in our system is ≈0.5 wt% (1.0 vol%). An insight may be gained as to the significance concentrations close to 1 vol% by considering that contact between dipoles allows a translational dipolar force to act as a torque about the point of contact. Since the average dielectric constant of the system depends on the level of alignment, we expect the response to be enhanced when CNT–CNT contact becomes more likely: at the transition volume between dilute and semi-dilute regimes. For interpenetrating, entangled tubes we estimate the semidilute regime is reached at a characteristic overlap volume fraction29ϕc = a7/5lp−3/5l−4/5 ∼ 1 vol% for our system (a = 80 nm, lp ∼ 1 μm, l = lLIM ≈ 2 μm).
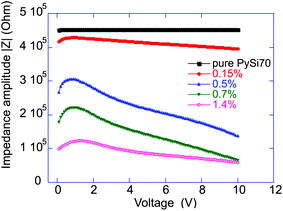 | ||
| Fig. 4 The dependence of CNT–PySi70 suspension impedance on voltage and concentration (all in wt%) at a fixed frequency f = 10 kHz. The maximum field response occurs when the loading fraction matches the characteristic overlap volume fraction ϕc as discussed in the main text. | ||
At this time, we have no model or explanation for the apparent drop in the impedance as the potential difference is reduced below 1 V in Fig. 3. Apparently, the average dielectric constant of the composite medium falls with the field, for field strengths below 50 V mm−1.
4 Discussion
In suspensions of spherical particles, the experimental observation of microscale columns in response to an external field has been documented in a few cases with varying outcomes. Dassanayake et al.23 directly visualised column formation, using confocal microscopy, in a silica/water/gycerol colloid. They identified a number of non-equilibrium structures (including sheets and crystals), prior to column formation, that were not observed by Martin et al.41 in their light scattering study of a similar silica colloid. The range of field strengths we investigated overlapped with those used in both these studies yet, with a CNT diameter of a ≈ 80 nm, we are unable to verify the formation of the debated non-equilibrium structures. However, we note that despite a CNT length comparable to that of the silica particles studied, we observe clear column formation at volume fractions less that an order of magnitude below those required for column formation in the aforementioned studies (as low as ≈1.4 vol%). Given the similarities in system parameters, this appears to be an advantageous result of the high polarisability of CNTs. In addition, we observe column formation from a non-sedimented (i.e. fully suspended) starting condition.Wen et al.22 also observed column formation at a much higher volume fraction (10 vol%) for a system of larger 35 μm glass microspheres in silicone oil. At field strengths again similar to those presented in this paper, they found that densely packed columns would only form if the field were applied slowly (30 V mm−1 s−1). This is in stark contrast to the CNT–PySi70 system, as well as those of the silica systems, highlighting that a smaller characteristic size allows for faster equilibrium structure formation.
Finally, we point out that our own quantification of the diffusive decay following removal of the field is the first observation of such a fast reversible transition from the formation of columnar structures. This result is pleasantly surprising given that CNTs are known for their strong inter-particle van der Waals forces when in suspension. In light of this result, we hope to have identified the potential for further investigation of CNT–PySi70 suspensions.
Up to now, the formation of microstructure in CNT suspensions has only been studied in dilute conditions in systems that do not reach late stage columnar formation. Additionally, field-induced columnar formation studied in colloidal systems of spherical particles has not been studied from the crucial point of view of reversibility. We have shown that a CNT–PySi70 system displays fast and reversible microscale column formation in the semidilute regime. The characteristic volume overlap concentration denotes the state of maximum dielectric response, highlighting the key role of initial CNT–CNT contact in allowing the dipolar interaction to contribute to the alignment torque. The relatively fast relaxation timescale is confirmed to be diffusive.
Acknowledgements
We acknowledge EPSRC and Kodak European Research for funding SW, European Commission FP7 NOMS project no. 228916 for funding YJ. We are grateful to Y. Y. S. Huang for many helpful discussions.References
- F. Mantegazza, M. Caggioni, M. Jiménez and T. Bellini, Nat. Phys., 2005, 1, 103 CrossRef CAS.
- H. Löwen, J. Phys.: Condens. Matter, 2001, 13, R415–R432 CrossRef CAS.
- H. Pohl, Dielectrophoresis: The Behaviour of Neutral Matter in Nonuniform Electric Fields, Cambridge University Press, Cambridge, 1978 Search PubMed.
- K. Kang and J. K. G. Dhont, Soft Matter, 2010, 6, 273–286 RSC.
- M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., 1996, 17, 57–103 Search PubMed.
- K. D. Hermanson, S. O. Lumsdon, J. P. Williams, E. W. Kaler and O. D. Velev, Science, 2001, 294, 1082–1086 CrossRef.
- C. Lin and J. W. Shan, Phys. Fluids, 2007, 19, 121702 Search PubMed.
- K. Yamamoto, S. Akita and Y. Nakayama, J. Phys. D: Appl. Phys., 1998, 31, L34–L36 CrossRef CAS.
- X. Q. Chen, T. Saito, H. Yamada and K. Matsushige, Appl. Phys. Lett., 2001, 78, 3714–3716 CrossRef CAS.
- C. Park, J. Wilkinson, S. Banda, Z. Ounaies, K. E. Wise, G. Sauti, P. T. Lillehei and J. S. Harrison, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1751–1762 CrossRef CAS.
- N. Lee, D. Chung, I. Han, J. Kang, Y. Choi, H. Kim, S. Park, Y. Jin, W. Yi, M. Yun, J. Jung, C. Lee, J. You, S. Jo, C. Lee and J. Kim, Diamond Relat. Mater., 2001, 10, 265–270 CrossRef CAS.
- C. Martin, J. Sandler, M. Shaffer, M.-K. Schwarz, W. Bauhofer, K. Schulte and A. Windle, Compos. Sci. Technol., 2004, 64, 2309–2316 CrossRef CAS.
- T. Halsey and W. Toor, Phys. Rev. Lett., 1990, 65, 2820–2823 CrossRef CAS.
- D. Andelman and R. E. Rosensweig, J. Phys. Chem. B, 2009, 113, 3785–3798 Search PubMed.
- K. Bubke, H. Gnewuch, M. Hempstead, J. Hammer and M. L. H. Green, Appl. Phys. Lett., 1997, 71, 1906–1908 CrossRef CAS.
- C. Martin, J. K. W. Sandler, A. H. Windle, M. K. Schwarz, W. Bauhofer, K. Schulte and M. S. P. Shaffer, Polymer, 2005, 46, 877–886 CrossRef CAS.
- K. Lozano, C. Hernandez, T. W. Petty, M. B. Sigman and B. Korgel, J. Colloid Interface Sci., 2006, 297, 618–624 CrossRef CAS.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS.
- R. Tao, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 423–426 CrossRef.
- J. Martin, R. A. Anderson and C. P. Tigges, J. Chem. Phys., 1998, 108, 3765–3787 CrossRef CAS.
- J. Martin, J. Odinek, T. Halsey and R. Kamien, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 756–775 CrossRef CAS.
- W. Wen, D. W. Zheng and K. N. Tu, J. Appl. Phys., 1999, 85, 530–533 Search PubMed.
- U. Dassanayake, S. Fraden and A. van Blaaderen, J. Chem. Phys., 2000, 112, 3851–3858 CrossRef CAS.
- N. Puech, E. Grelet, P. Poulin, C. Blanc and P. van der Schoot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 1–4.
- Y. Ji, Y. Huang, A. R. Tajbakhsh and E. Terentjev, Langmuir, 2009, 25, 12325–12331 CrossRef CAS.
- Y. Ji, Y. Huang, R. Rungsawang and E. Terentjev, Adv. Mater., 2010, 22, 3436–3440 CrossRef CAS.
- S. Ahir, Y. Huang and E. Terentjev, Polymer, 2008, 49, 3841–3854 CrossRef CAS.
- Y. Huang, T. P. J. Knowles and E. Terentjev, Adv. Mater., 2009, 21, 3945–3948 CrossRef CAS.
- Y. Huang, S. Ahir and E. Terentjev, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–9.
- Y. Ji, Y. Huang and E. Terentjev, Langmuir, 2011, 27, 13254–13260 Search PubMed.
- X. J. Wang, L. P. Wang, O. S. Adewuyi, B. A. Cola and Z. M. Zhang, Appl. Phys. Lett., 2010, 97, 163116 CrossRef.
- T. Halsey, Science, 1992, 258, 761–766.
- K. Baloch and T. van de Ven, J. Colloid Interface Sci., 1989, 129, 91–104 Search PubMed.
- B. van der Zande and J. K. Dhont, Langmuir, 2000, 16, 459–464 CrossRef CAS.
- J. Ginder, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 3418–3429 Search PubMed.
- X. Zhao, C. Luo and Z. Zhang, Opt. Eng., 1998, 37, 1589–1592 Search PubMed.
- K. Tanaka, K. Nakamura and R. Akiyama, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5378–5382 Search PubMed.
- L. X. Benedict, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 8541–8549 CrossRef CAS.
- M. Doi and S. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986 Search PubMed.
- A. A. Farajian, O. V. Pupysheva, H. K. Schmidt and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 205432 Search PubMed.
- J. Martin, J. Odinek and T. Halsey, Phys. Rev. Lett., 1992, 69, 1524–1527 CrossRef CAS.
Footnote |
| † Note that there are several ways to define local polarisability even within the same SI unit system, for instance via a direct p = αE; we choose a format in which the polarisability α has the dimensionality of volume (m3). |
| This journal is © The Royal Society of Chemistry 2013 |
