Wrinkling of inhomogeneously strained thin polymer films
Yu-Cheng
Chen
and
Alfred J.
Crosby
*
Polymer Science & Engineering Department, University of Massachusetts, 120 Governors Drive, Amherst, 01002, MA, USA. E-mail: crosby@mail.pse.umass.edu
First published on 3rd October 2012
Abstract
Wrinkles occur due to a mechanical instability when sufficient strain is applied to an incompressible thin film attached to a deformable substrate. For wrinkles made with a polymer film supported on a soft elastomer, the amplitude is directly proportional to the wavelength and the square root of the applied strain. This dependence has been confirmed with ideal substrates where the global strain is homogeneously distributed, but the influence of strain inhomogeneity has not been considered previously. We use the contact line wrinkling technique to prepare polystyrene thin films with periodic regions of different wrinkle amplitudes, hence strains, on soft substrates. We find that an inhomogeneously strained surface approaches amplitude homogeneity globally upon the application of sufficiently large strains. We derive relationships to describe this process, providing fundamental knowledge of the wrinkling mechanism.
Introduction
Wrinkling is a mechanical instability that has the potential to impact many advanced applications, such as optical surfaces,1,2 metrology of thin films,3–5 enhanced adhesives,6,7 and flexible electronic devices.8,9 Researchers have shown that wrinkling devices can be dynamic and “smart” due to the wrinkle dimensions, which can be uniquely tuned by varying an applied strain.9 Thus, an understanding of how wrinkles depend on strain is important for many practical applications and future developments.While it has been shown that a homogeneous strain field will result in a homogeneously wrinkled surface,10,11 it has also been shown that inhomogeneous topographical features, such as creases or folds, will develop beyond a critical strain.12,13 The onset of this secondary transition, or strain localization, has been associated with an inhomogeneity in the strain field.12,13 Such localizations have received increased attention in the recent literature due to their relevance in natural processes of morphogenesis, as well as their implications in the fidelity of thin film devices.8,14–16 Although inhomogeneities or defects have been qualitatively linked to strain localization events, a systematic understanding of pre-existing strain homogeneity has remained elusive.
Here, we use a recently developed fabrication method17 to understand the influence of strain homogeneity on wrinkling surfaces. This method allows three types of materials to be made with a single fabrication process: flat, continuously wrinkled, and periodically wrinkled films (Fig. 1). By applying global mechanical strain to each of these three types, we investigate how initial strain inhomogeneity influences amplitude growth of these wrinkling surfaces upon global compression: will the inhomogeneity lead to strain localization or will the system try to homogenize the subsequent strain globally?
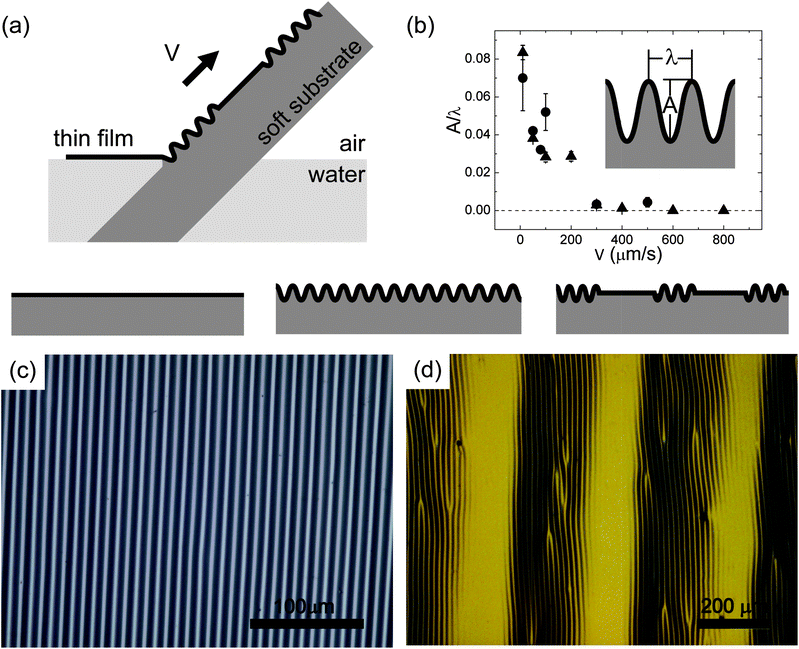 | ||
| Fig. 1 (a) Schematic diagram (not shown to scale) of the adhesion contact line technique to fabricate flat (left), continuously wrinkled (middle), and periodically wrinkled (right) surfaces. A polystyrene film is laminated on a soft substrate. The wrinkle amplitude is varied by controlling the velocity of the push in/pull out process. Mechanical compression is then applied on these structures to observe wrinkling behaviour. (b) Aspect ratio vs. pull velocity showing the dependence of process velocity V. The circle and the triangle data represent two different samples. The films are wrinkle-free (A/λ = 0) when the velocity is greater than a critical value. The inset schematic illustrates the amplitude A as the peak-to-valley height, while the wavelength λ is the peak-to-peak distance. (c) Optical image of a homogeneous wrinkled surface made with constant V. (d) Optical image of an inhomogeneous wrinkled surface made with a controlled periodic velocity profile. | ||
Experimental approach
To prepare initial structures, we apply a recently developed adhesion contact line technique.17 In brief, a soft substrate is immersed into water, and a thin film is floated onto the water surface. The deformable soft substrate is made of crosslinked polydimethylsiloxane (Dow Corning's Sylgard™ 184 elastomer) and the unstretchable thin film is made of polystyrene. One edge of the film is then attached to the substrate, creating a three-phase contact line. Since both the film and the substrate are hydrophobic, they adhere to each other easily. At the contact line, the surface tension of water and the adhesion provide a force to pull the film and cause local deformation of the substrate. The substrate as well as the film are slowly lifted from the water and the contact line sweeps across the substrate surface with a controlled velocity, V (Fig. 1a). Wrinkles form parallel to the contact line, if the deformation is larger than the critical value of wrinkling.An important feature of this method is that the magnitude of strain, hence the amplitude, strongly depends on V (Fig. 1b) due to the velocity dependence of the interfacial adhesion energy between the film and substrate. When V exceeds a critical value, the water at the contact line wets the interface between the film and substrate. The water coating prevents strain from developing due to adhesion, and the film remains wrinkle-free. This allows us to fabricate different initial structures by controlling the velocity profile. By setting the velocity beyond the critical value, films remain flat. In contrast, films form uniform wrinkles when the velocity is constant and lower than the critical value. We vary the velocity of the contact line beyond and below the critical value, fabricating initial structures with periodically wrinkled regions.
We then carefully mount each of the three types of wrinkled samples on a customized strain stage. A linear actuator on the strain stage allows us to apply uniaxial global compression (εapp) on the samples. The amplitude and wavelength at each strain step (∼0.5%) were characterized by an optical profilometer. The amplitude data are normalized by the respective wavelengths at each strain state. Both the amplitude and wavelength are averaged over 10–20 waves on an arbitrary spot far from film edges. For the inhomogeneously strained films, the data are the average values in a fixed area that is initially wrinkled or flat.
Results and discussion
For an initially flat film (Fig. 2a, open data points), we find that the aspect ratio, A/λ, increases with the square root of the applied global strain, εapp: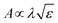 | (1) |
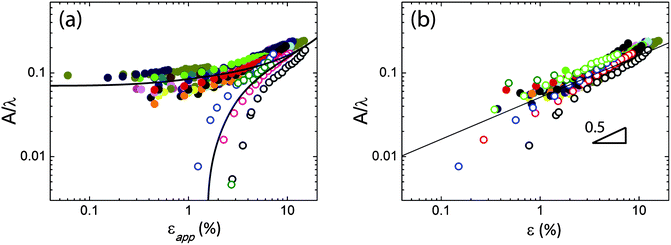 | ||
| Fig. 2 Plots of the aspect ratio as a function of applied strain and strain. The solid data points denote pre-wrinkle while the open data points denote the initially flat film. Different colours represent different samples. (a) The amplitude increases with applied strain εapp, where the aspect ratio of wrinkles from an initially flat film increase more rapidly than pre-wrinkles. The lines are guidelines for the two types of samples. (b) The same data plotted in (a) are re-plotted with respect to strain ε, demonstrating that the two types of wrinkles fall on the same scaling. The solid line is the prediction of A/λ ∝ ε, with ε defined by eqn (2). | ||
In contrast to a vanishing aspect ratio at a finite strain, materials that are pre-wrinkled homogeneously have a finite aspect ratio at infinitely small globally applied strains (Fig. 2a, solid data points). As strain is applied globally, the aspect ratio is found to increase at an initially slower rate until εapp approaches ε0, the strain applied by the contact line method for pre-wrinkling the surface. As εapp ∼ ε0, the aspect ratio grows according to ε1/2app. The continuous growth of aspect ratio over all strains can be understood according to eqn (1), if the initial strain of the pre-wrinkles is known such that
| ε = (1 − ε0)εapp + ε0 | (2) |
For inhomogeneous wrinkled surfaces that have periodically alternating pre-wrinkled regions and flat regions (width of the flat region >5λ) (Fig. 3a), the results show that the pre-wrinkle amplitude grows (Fig. 3b) while new wrinkles initiate, demonstrated by an increase in the number of wrinkles (Fig. 3c). We further find that the growth of newly formed wrinkles is identical to globally flat samples, and the growth of pre-wrinkles is identical to homogeneously wrinkled samples (Fig. 3d). In other words, eqn (1) well describes the amplitude growth regardless of initial structures on films. In addition, the wrinkle initiation and growing process is reversible as long as the materials are in their linear elastic regions. That is, when the surface is released from an applied strain, the initially flat region reverts to a wrinkle-free form and the pre-wrinkles relax to their original A/λ. Good adhesion at the film–substrate interface prevents the pre-wrinkles from re-distributing, and the homogeneity of the substrate allows the global compressive strain to be uniformly distributed.
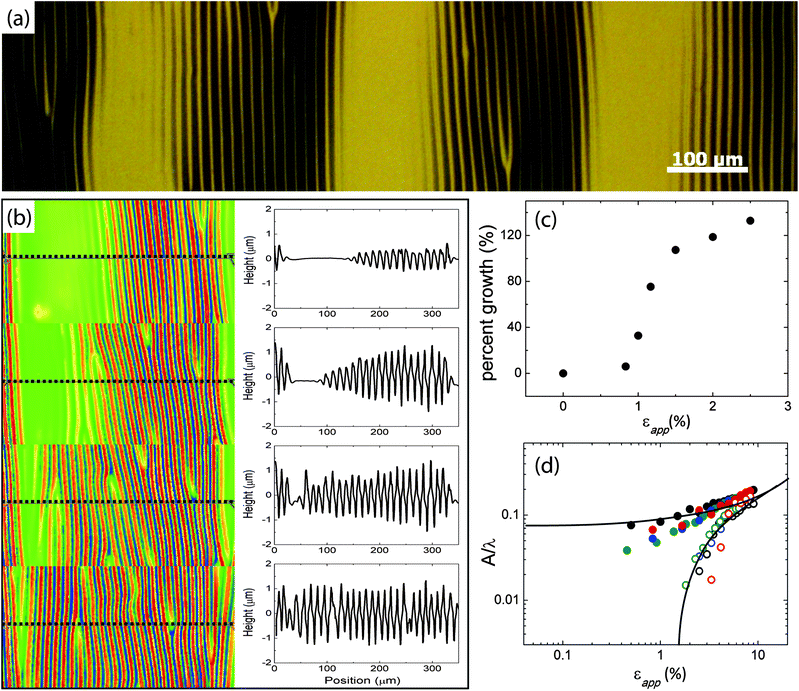 | ||
| Fig. 3 (a) Optical micrographs for a periodically wrinkled surface. (b) Optical profilometry data of the selected area of (a). Left column shows 3D contour maps for applied strain of 0%, 4.5%, 5.6%, and 6.7% from top to bottom. The image width is 350 μm. Right column shows 2D line profiles for indicated line segments in 3D contour maps. New wrinkles are initiated from the boundary of the flat and wrinkled regions. Wrinkles achieve uniform amplitude across the entire region at higher applied strain εapp. (c) The percent growth of wrinkle number over the whole film as a function of applied strain εapp. (d) Aspect ratio as a function of applied strain εapp. The solid data indicate the pre-wrinkled region; the open data indicate the initially flat region. The wrinkle amplitude growth in both pre-wrinkled regions and initially flat regions follows the classical amplitude–strain relationship. | ||
Taking the derivative to eqn (1) gives the amplitude growth rate:
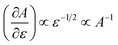 | (3) |
The growth rate is a decreasing function of amplitude. Therefore newly formed wrinkles, which are smaller in amplitude, grow faster than the pre-wrinkles, which are greater in amplitude. At a higher strain, newly formed wrinkles quickly approach the amplitude of pre-wrinkles, yielding a uniform wrinkled structure (Fig. 3b and d). It should be noted that although we expect that new wrinkles form simultaneously on an ideal flat surface, Fig. 3b indicates a progressive wrinkle formation. This is caused by a pre-existing strain gradient induced by the adhesion contact line technique.
Although the applicability of eqn (1) and (2) to the respective regimes on a periodically patterned surface implies that homogenization of the wrinkle aspect ratio is not possible, the optical profilometry data in Fig. 3b indicate that the aspect ratio of wrinkles across the entire surface becomes similar. This apparent difference can be understood by considering the rate of growth for the wrinkle aspect ratio as a function of strain. The difference between the growth rates of pre-wrinkles and newly formed wrinkles causes the system to approach a nearly homogeneous amplitude at εapp < 6%, which is significantly earlier than the predicted strain (εapp = 100%) for uniformity. Since the wrinkle growth is only governed by eqn (1) regardless of the initial structure, the homogenization strain is expected to be similar to our experimental result (6%) for surfaces with various separation distances of pre-wrinkle regions and the number of pre-wrinkles in each region. By taking advantage of this growth rate difference, surfaces can switch between homogeneous and inhomogeneous wrinkle amplitudes by only a small applied global strain.
Conclusions
In this paper, we have considered the influence of strain inhomogeneity on the formation of wrinkles under a compressive strain. A recently developed adhesion contact line technique was applied to fabricate three different initial structures: flat, continuously wrinkled, and periodically wrinkled films. By applying compressive strain to the inhomogeneous, periodically pre-wrinkled surfaces, we tracked the amplitude as a function of applied global strain. We found that the growth of both the pre-wrinkles and the newly formed wrinkles independently followed the classical amplitude–strain theory, regardless of pre-existing strains. We also observed that the total strain stored in wrinkles neither homogenized nor localized. Although the system will theoretically achieve a uniform amplitude when εapp = 1, the inhomogeneous amplitudes approach a single, uniform amplitude at small strains (<6%) due to the growth rate differences of newly formed and pre-existing wrinkles.Experimental
The stiff polymeric thin films were made with polystyrene (PS) purchased from Polymer Source Inc. (Mn = 130 kg mol−1, Mn/Mw = 1.05). An 80 nm film was made from dissolving bulk PS in toluene at 2 wt%, then spin-coated onto a silicon wafer at 3000 rpm for 30 seconds. 200 nm and 300 nm films were made from 4% solution in toluene, then spin-coated onto a silicon wafer for 30 seconds at 3000 rpm and 1000 rpm, respectively. No any further treatment such as annealing is applied. Prior to spin-coating the PS solution, the silicon wafer is cleaned with toluene and isopropanol, then treated with UV-ozone cleaner for 20 minutes. The film thickness was measured using the one point thin film profilometer (Filmetrics Optical Profilometer F-20). The Young's modulus of the film (EPS ≈ 3.4 GPa) was calculated from the wrinkle wavelength, film thickness and the substrate modulus.15Crosslinked polydimethylsiloxane (PDMS) was prepared by mixing a Dow Corning Sylgard™ 184 elastomer base and curing agent. First, a mixing ratio of base/agent 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was used as a supporting material, and the mixture was degassed for 40 minutes. It was then cured in a rectangular mold (30 × 25 × 7 mm or 44 × 25 × 7 mm) in a 70 °C oven for 1 hour. A mixing ratio of 30
1 was used as a supporting material, and the mixture was degassed for 40 minutes. It was then cured in a rectangular mold (30 × 25 × 7 mm or 44 × 25 × 7 mm) in a 70 °C oven for 1 hour. A mixing ratio of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 40
1 or 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was spin-coated (500 rpm for 60 seconds) onto the 10
1 was spin-coated (500 rpm for 60 seconds) onto the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS supporting material to make the substrate layer (∼250 μm thick). The supporting material and the substrate were again cured in a 70 °C oven for 2 hours. The substrate was then used immediately after cooling to room temperature (∼23 °C). The Young's moduli of the PDMS substrates were measured separately with thick (>5 mm) 30
1 PDMS supporting material to make the substrate layer (∼250 μm thick). The supporting material and the substrate were again cured in a 70 °C oven for 2 hours. The substrate was then used immediately after cooling to room temperature (∼23 °C). The Young's moduli of the PDMS substrates were measured separately with thick (>5 mm) 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 40
1 or 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS. A contact mechanics setup,18 which probes the force as a function of displacement of a 2 mm diameter cylindrical silica probe, provided the moduli of PDMS (EPDMS,30:1 ≈ 130 ± 10 kPa and EPDMS,40:1 ≈ 50 ± 10 kPa).
1 PDMS. A contact mechanics setup,18 which probes the force as a function of displacement of a 2 mm diameter cylindrical silica probe, provided the moduli of PDMS (EPDMS,30:1 ≈ 130 ± 10 kPa and EPDMS,40:1 ≈ 50 ± 10 kPa).
The polystyrene film was floated onto reverse osmosis (RO) water, and the substrate was placed in a plastic dish fixed on a nanopositioner (EXFO Burleigh Inchworm motor 8200). The substrate was immersed into the water and the film was attached to the substrate surface. The substrate and the film were then pulled out from water at a velocity of 10 μm s−1 and an angle of 45°. Instead of pulling continuously, a “stop-and-go” process was used, where the stopping time was 6 seconds followed by 300 μm, 500 μm, or 800 μm spacing at a velocity of 800 μm s−1 to prepare the periodically wrinkled samples.
The samples were then mounted onto a customized strain stage with a linear actuator. The contact interface of the sample and the stage was appropriately lubricated to allow the sample to slide freely. The mounting was conducted under a microscope in order to assure good alignment. Compressive strain was applied on the samples in the direction of the pre-strain by the strain stage. The amplitude, wavelength, and contour length were measured by an optical profilometer (Zygo NewView 7300, 10× and 50× objective) with MetroPro software. Optical microscopy images were taken using an optical microscope (Zeiss AxioTech Vario, 5× or 10× objective, Pixel Link CCD camera). Approximately 10% strain was applied over 2 hours. Manual and motorized stages were both used after verifying that the strain rate had little effect on the amplitude measurement results.
Acknowledgements
This work is funded by the NSF DMR-0907219 and NSF MRSEC (NSF DMR-2820506).References
- M. Ibn-Elhaj and M. Schadt, Nature, 2001, 410, 796 CrossRef CAS.
- E. P. Chan and A. J. Crosby, Adv. Mater., 2006, 18, 3238 CrossRef CAS.
- J. Huang, M. Juszkiewicz, W. H. de Jeu, E. Cerda, T. Emrick, N. Menon and T. P. Russell, Science, 2007, 317, 650 CrossRef CAS.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. VanLandingham, H.-C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3, 545 CrossRef CAS.
- E. P. Chan, S. Kundu, Q. Lin and C. M. Stafford, ACS Appl. Mater. Interfaces, 2010, 3, 331 Search PubMed.
- A. K. Geim, S. V. Dubonos, I. V. Grigorieva, K. S. Novoselov, A. A. Zhukov and S. Y. Shapoval, Nat. Mater., 2003, 2, 461 CrossRef CAS.
- E. P. Chan, E. J. Smith, R. C. Hayward and A. J. Crosby, Adv. Mater., 2008, 20, 711 CrossRef CAS.
- D.-Y. Khang, H. Jiang, Y. Huang and J. A. Rogers, Science, 2006, 311, 208 CrossRef CAS.
- H. Jiang, D.-Y. Khang, J. Song, Y. Sun, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15607 CrossRef CAS.
- X. Chen and J. W. Hutchinson, J. Appl. Phys., 2004, 71, 597 Search PubMed.
- Z. Y. Huang, W. Hong and Z. Suo, J. Mech. Phys. Solids, 2005, 53, 2101 CrossRef CAS.
- V. Trujillo, J. Kim and R. C. Hayward, Soft Matter, 2008, 4, 564 RSC.
- L. Pocivavsek, R. Dellsy, A. Kern, S. Johnson, B. Lin, K. Y. C. Lee and E. Cerda, Science, 2008, 320, 912 CrossRef CAS.
- M. Kücken and A. C. Newell, J. Theor. Biol., 2005, 235, 71 CrossRef.
- J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310 RSC.
- J. M. Harris, G. R. S. Iyer, D. O. Simien, J. A. Fagan, J. Y. Huh, J. Y. Chung, S. D. Hudson, J. Obrzut, J. F. Douglas, C. M. Stafford and E. K. Hobbie, J. Phys. Chem. C, 2011, 115, 3973 CAS.
- G. Miquelard-Garnier, A. B. Croll, C. S. Davis and A. J. Crosby, Soft Matter, 2010, 6, 5789 RSC.
- K. Kendall, J. Phys. D: Appl. Phys., 1971, 4, 1186 Search PubMed.
| This journal is © The Royal Society of Chemistry 2013 |
