High accuracy traceable Rutherford backscattering spectrometry of ion implanted samples
J. L.
Colaux
* and
C.
Jeynes
University of Surrey, Ion Beam Centre, Guildford GU2 7XH, England, UK. E-mail: j.colaux@surrey.ac.uk
First published on 7th November 2013
Abstract
There are few techniques capable of the non-destructive and model-free measurement at 1% absolute accuracy of quantity of material in thin films without the use of sample-matched standards. We demonstrate that Rutherford backscattering spectrometry can achieve this robustly, reliably and conveniently. Using 1.5 MeV He+, a 150 keV ion implant into silicon with a nominal fluence of 5 × 1015 As cm−2 has been independently measured repeatedly over a period of 2 years with a mean total combined standard uncertainty of 0.9 ± 0.3% relative to an internal standard given by the silicon stopping power (a coverage factor k = 1 is used for all uncertainties given). The stopping power factor of this beam in silicon is determined absolutely with a mean total combined standard uncertainty of 0.8 ± 0.1%, traceable to the 0.6% uncertainty of the Sb-implanted certified reference material (CRM) from IRMM, Geel. The uncertainty budget highlights the need for the accurate determination of the electronic gain of the detection system and the scattering angle, parameters conventionally regarded as trivial. This level of accuracy is equally applicable to much lower fluences since it is not dominated by any one effect; but it cannot be reached without good control of all of these effects. This analytical method is extensible to non-Rutherford scattering. The stopping power factor of 4.0 MeV lithium in silicon is also determined at 1.0% absolute accuracy traceable to the Sb-implanted CRM. This work used SRIM2003 stopping powers which are therefore demonstrated correct at 0.8% for 1.5 MeV He in Si and 1% for 4 MeV Li in Si.
Introduction
The accurate determination of quantity of material is one of the essential motivations of analytical chemistry, and its non-destructive measurement is of great importance in many circumstances, including situations where the sample is intrinsically valuable (e.g. pieces from museum collections1), or irreplaceable (e.g. forensic samples from crime scenes2), or where a full characterisation of the sample requires different complementary methods,3 or where repeated in situ measurements of it are needed.4 Full characterisation is also needed where the sample is entirely unknown, as for the impact glasses recently analysed by Total-IBA.5 Thin film materials (that is, having surface layers <∼10 μm thickness) are ubiquitous in modern technology. For example: semiconductor devices all have thin film active layers, tribological or optical coatings are frequently thin, and interface effects (including corrosion and oxidation) frequently extend beyond the near-surface region.Some analytical techniques, such as ellipsometry or XRF (X-ray fluorescence), can measure relative thin film thicknesses non-destructively and very precisely, but they depend on assumed models of the sample to obtain absolute values (and when values from XRF are given with high absolute accuracy they also depend on sample-matched standards). Other techniques, such as dynamic SIMS (secondary ion mass spectrometry) can obtain elemental thin film depth profiles with very good depth resolution (destructively, using sputtering), but heavily depend for quantification on sample-matched standards.
Rutherford backscattering spectrometry (RBS) is not deliberately destructive, although the energy deposited by the probing beam usually modifies the sample to at least some extent; we show here that it is capable of an absolute accuracy that is unusually high for thin film characterisation methods, where this accuracy does not depend on any assumptions about the sample, and where no standards related to the sample are required. The method we describe is of broad applicability, valid for a very general class of samples.
RBS has been considered a 1% technique for the measurement of quantity of material ever since Turkevich made this claim after the Moon landing of Surveyor I in 1966.6 However, the critical demonstration of this claim has proved to be unusually difficult even though the governing equation (eqn (1)) is remarkably simple, and in fact has been simplified here without any loss of generality. The signal AC (see Fig. 1) is detected from the measurand, C, and is given by the product of: the number Q of particles of the probing beam striking the target (containing C), the number density fc of the measurand present in the target, the probability σ′ of interaction of the beam with the measurand, and the probability of detection Ω of the reaction product (this is simply the detector solid angle since charged particle detection efficiencies are essentially 100%):
| AC = QfCσ′C(E, θ)Ω | (1) |
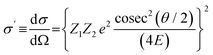 | (2) |
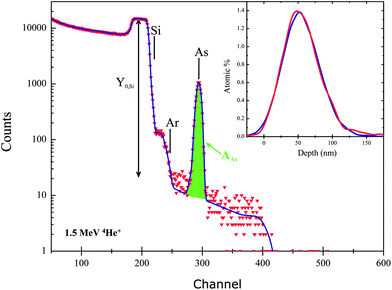 | ||
| Fig. 1 RBS energy spectrum for Det B and from (nominally) 5 × 1015 cm−2 As implant at 80 keV into silicon, together with a (nominally) 3 × 1015 cm−2 Ar implant at 150 keV. The surface signal positions for Si, Ar and As are shown together with the area AAs of the arsenic signal (see eqn (1)) and the surface yield Y0,Si of the Si substrate signal (see eqn (3)). The beam is 1.5 MeV He+ and the channel widths are about 3 keV per channel. The Si signal is high in the surface (amorphised) region and low in the deeper (crystalline) region in which the beam is channelling. The inset shows the As depth profiles derived from the spectra recorded by Det A (red) and Det B (blue). The apparent yield mismatch for channel numbers >300 is misleading: the number of counts in this region is the same for data and fit because there are many channels with no counts. | ||
It is the very simplicity of eqn (1), together with the fact that the interaction cross-section is known analytically, that underlay Turkevich's claim. In principle, the accuracy of this method is important since ion beam analysis of a sample can be effected with multiple detectors of different types, or repeated (since the method is essentially non-destructive) with ion beams of different types or energies. Thus, many different nuclear reaction spectra can be acquired for any particular sample, including RBS, non-Rutherford elastic backscattering (EBS), elastic recoil detection (ERD), or nuclear reaction analysis (NRA) which includes particle-induced γ-ray emission (PIGE). As well as these data, atomic excitation, that is, particle-induced X-ray emission (PIXE), is always present. All of these together are known as ion beam analysis (IBA),8 and the self-consistent treatment of all spectra together is known as “Total-IBA”.9 Accurate RBS has a wide significance because any Total-IBA analysis inherits the accuracy of the most accurate component of the analysis, and it is quite easy to always include RBS in any Total-IBA measurement. The literature cited earlier1–4 all use Total-IBA.
The difficulties of accurately measuring Q and Ω separately have long been recognised, but are usually sidestepped since they always appear together in the equations. Then any standard sample (for which fC is known) can be used to evaluate the product QΩ in eqn (1). This was done by l'Ecuyer et al. (1979)10 in the classical paper that established the correction to the Rutherford cross-section due to electron screening of the bare nucleus (Coulomb) potential. Their work was nominally at 1.5% accuracy, but they pointed out that an unaccounted 4% error remained. The characterisation of a Bi-implanted certified reference material (CRM) was described by Cohen et al.11 who claimed 1.6% accuracy (a coverage factor k = 1 is used throughout the present paper unless otherwise stated); this was summarised by Davies et al.12 who underline the problems of inhomogeneity suffered by this “standard”, with a fluence range over the whole set of 7% determined by Wätjen & Bax13 using the classical method of determining thin film thickness by area and weight to provide accurate (certified) standards.14 In a handbook chapter entitled “Pitfalls”, Davies et al.15 describe this work claiming only 2%. It is worth pointing out that this work was from three groups: Cohen in Paris and Wätjen in Geel used (different) weighed reference standards, whereas the Chalk River group (Davies) made absolute measurements of Q and Ω independently.
A more accurately certified CRM was established by Ecker et al.16 who determined the Sb fluence in Sb-implanted silicon. They found QΩ directly from eqn (1) using a thin evaporated gold film whose thickness was determined traceably by in situ weighing (as for the previous Bi-implanted standards). Their RBS was by the National Metrology Institutes in Berlin and Geel, each having a combined standard uncertainty of 0.9%, but the accurate balance required for traceable quantification is very special equipment (and is now dismantled). The relative uniformity of the implantation was determined separately using very precise XRF. RBS was combined with two other independent techniques, ICP-IDMS (inductively coupled plasma isotope dilution mass spectrometry) and INAA (instrumental neutron activation analysis), to obtain a combined standard uncertainty for the CRM of 0.6%.
Jeynes et al.17 subsequently used the Sb-implanted CRM indirectly to evaluate the uncertainties in an RBS analysis by three labs (Surrey, Budapest & Lisbon) of an As-implanted sample, demonstrating that, as for the work of the 1980s, each lab could achieve a combined standard uncertainty of about 1%. In the present work we will critically establish the traceability of this method (including a critical and detailed discussion of the uncertainty budget18), and demonstrate its reliability and generality in practice.
Theory
Traceability of RBS: fundamental equations
The fundamental equations for RBS, together with secondary effects, are discussed at length by Jeynes et al.;17 for convenience we here briefly review them. Eqn (1) implicitly includes an integration of the signal over the thin film thickness: thus, the stopping of the beam in the target is also implicit in this equation since the incident particles lose energy by electronic processes when penetrating the target. This stopping is related to the electron density in the target and is remarkably independent of chemical state: “Bragg's rule”,19 that the stopping in a compound is simply the linear combination of the stopping in the elements of the compound, is usually a very good approximation. The stopping powers of ion beams in elemental materials are now known fairly well.20 In this work we do not need measured stopping since we will directly determine the required values with a method traceable to certified reference materials.However, when depth information about the sample is needed, the stopping power appears at first order. Eqn (3) shows the backscattered particle yield Y (in counts per channel of the analog–digital converter, ADC, used to digitise the energy spectrum seen by the particle detector: see Fig. 1) from the surface of a target: the backscattering spectrum will contain partial spectra from each element in the target. At the surface the beam has suffered no energy loss in the target and therefore still has its full energy E0.
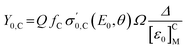 | (3) |
The difference between eqn (1) and eqn (3) is that the electronic gain Δ (in keV per channel) is involved in the yield Y, where it is not involved in the total number of counts A from a given number of atoms; clearly, the energy loss ε which governs the shape of the substrate signal (see Fig. 1) is also involved. The “stopping cross-section factor” [ε0]CM, expressed for clarity by eqn (4) in the “surface energy approximation”,21 refers to the energy lost by the particle scattered from element C of the matrix M.
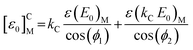 | (4) |
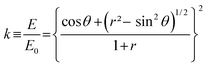 | (5) |
In eqn (4), ε(E)M is the energy loss (in eV nm−1 or equivalent units) for a beam of energy E in the matrix M, ϕi are the angles defined by the sample normal and (respectively) the incident or scattered beam directions, and kC is the so-called “kinematical factor” given for each C (in eqn (5)) by the conservation of energy and momentum; this expression is valid for any elastic interaction and depends only on the scattering angle and the ratio r of the scattering and scattered nuclear masses (that is, respectively the mass of C and the mass of the beam particles).
Again, eqn (3) has been simplified without any loss of generality and has been used directly in a hand calculation by Boudreault et al.:22 an equivalent equation can be given, mutatis mutandis, for the yield Yi,C of layer i at any given depth in the material; this is easily calculated by numerical methods, as has been reviewed by Jeynes et al.23
Analytical method
Eqn (1) makes it clear that the quantification of the numbers of counts in a spectrum depends only on the scattering cross-section and the charge-solid-angle product Q. Since the RBS cross-section is derived analytically from the Coulomb potential (eqn (2)), the accuracy of the atomic fraction (fC) determination is given directly by the accuracy of the Q determination. In fact, the integration implied by eqn (1) does also depend weakly on stopping power, but this is known well enough not to significantly affect the accuracy.The silicon substrate yield (Y in eqn (3): see Fig. 1) for this beam energy can be used as a well-defined internal standard to determine QΩ as proposed by Bianconi et al.;24 this analytical method implies that both the electronic gain Δ and the stopping cross-section factor [ε] are accurately known. Jeynes et al.17 have discussed the accurate measurement of Δ in detail, but only cite an uncritical determination of [ε].25 We here present a critical determination of [ε] for 1.5 MeV He+ in Si traceable to the Sb-implanted CRM at an accuracy much higher than is available from the SRIM database.26
Traceability of RBS: uncertainty budget
Table 1 shows a typical uncertainty budget for this analysis which includes a number of secondary effects as well as effects of spectral distortion. Counting statistics (A1 & A2) should not dominate these types of measurements, and we list ten other effects (A3–6 & B1–6) most of which are not usually considered when estimating experimental uncertainties in measurements of this type. We discuss these in turn:| Type | Det A | Det B | |
|---|---|---|---|
a
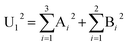 ; U2−2 = U1A−2 + U1B−2; ; U2−2 = U1A−2 + U1B−2; 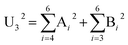 ; U42 = U22 + U32. Measurement uncertainties of type A (statistical estimate available) and type B (estimate made by other methods) are defined in GUM,56 and see ref. 18. See text for discussion of Ai and Bi. The reduced uncertainty (U5; this is the measurement precision shown in Fig. 2) for a given beam is given by U4 less the systematic contributions (B3–6 & A5,6) in quadrature. ; U42 = U22 + U32. Measurement uncertainties of type A (statistical estimate available) and type B (estimate made by other methods) are defined in GUM,56 and see ref. 18. See text for discussion of Ai and Bi. The reduced uncertainty (U5; this is the measurement precision shown in Fig. 2) for a given beam is given by U4 less the systematic contributions (B3–6 & A5,6) in quadrature.
|
|||
| Pileup correction (As signal), % | 0.3 | 0.8 | |
| Pileup uncertainty (10% of total correction), % | B1 | 0.03 | 0.08 |
| Counting statistics, implant signal, % | A1 | 1.60 | 0.85 |
| Counting statistics, a-Si signal, % | A2 | 0.25 | 0.13 |
| Scattering angle ∼1/sin4(θ/2) and 1/cos(θ), % | B2 | 0.08 | 0.41 |
| Electronics calibration uncertainty, % | A3 | 0.26 | 0.14 |
| Relative uncertainty (dataset), % | U1 | 1.64 | 0.97 |
| Relative uncertainty of average of 2 detectors (dataset), % | U2 | 0.83 | |
| Beam energy, % | B3 | 0.20 | |
| Disagreement between both detectors, % | A4 | 0.00 | |
| Pileup uncertainty (from model), % | B4 | 0.20 | |
| Code uncertainty, % | B5 | 0.20 | |
| Rutherford cross-section (screening uncertainty), % | B6 | 0.16 | |
| Si stopping power (uncertainty on the a-Si yield), % | A5 | 0.80 | |
| Si stopping power (uncertainty on the implant counts), % | A6 | 0.03 | |
| Combined extra systematic uncertainty, % | U3 | 0.89 | |
| Total combined standard uncertainty (accuracy), % | U4 | 1.22 | |
| Reduced uncertainty | U5 | 0.83 | |
The first thing to consider concerning a signal from a noise-level system is the issue of the signal/noise ratio. The signal background in this case is due to pulse pileup (see Fig. 1), which is roughly linear with counting rate and can never be eliminated. It can be reduced by reducing the count rate, but then the counting time must be increased and questions of cost & benefit become important. It can be systematically reduced by increasing the time resolution of the pileup rejection circuit, and this would dramatically improve our sensitivity. However, in any given experiment the pileup must be modelled, which can be done with various algorithms (see ref. 27 and 28 and references therein), none of which have any free parameters. That these models are good can be seen from Fig. 1. Provided the calculated pileup is well clear of large signals, we estimate that it can be fitted with an accuracy of about 10% (B1 in Table 1): this is because although the model parameters are not strictly free it is not clear precisely what they are, and in practice the modelled pileup is normalised to the signal. Added to this is an extra uncertainty of the model itself (B4) since the various models give slightly different answers.
The uncertainty in the scattering angle (B2) affects measured fluence both through the scattering cross-section (eqn (1) & (2)) and the exit pathlength in the material (eqn (3) & (4)).
The beam energy of electrostatic ion accelerators is usually determined by the energy calibration achieved through standard nuclear techniques such as (p,n) threshold reactions,29 resonant (p,γ) and (p,αγ) nuclear reactions,30 or direct capture (p,γ) reactions.31 In principle, these high precision techniques lead to a very precise energy calibration (for instance, Demarche et al. claimed a precision of 0.03% (ref. 32)). However, to the best of our knowledge, no critical uncertainty budget has yet been assigned to these techniques and their accuracy still needs to be critically addressed in the literature. Moreover, these techniques are quite time consuming due to the low reaction-cross-sections involved,31 and the necessity of measuring several excitation curves.29,30 In this work, we took advantage of the 16O(α,α)16O resonance at 3037.9 ± 2.3 keV to calibrate our accelerator, with the resonance energy determined at 0.08% from a critical analysis of the literature (see ref. 32 and references therein). The procedure is to measure a Au/Ni/SiO2/Si calibration sample33 at different energies near the resonance: the nominal incident energy is increased from 3020 keV to 3110 keV in 10 keV steps. The actual energy of the incident beam is derived from the peak shape of the 16O signal through the shape of the 16O(α,α)16O cross-section (modelled with appropriate nuclear parameters34), with a precision of 0.02% and an accuracy of 0.1% (B3 in Table 1) dominated by the uncertainty on the energy of the resonance. This same method was used in an approximate way by Andrade et al.35
The electronic gain Δ of the acquisition system as well as the so-called “pulse-height defect” (PHD) of the detector are determined simultaneously from the calibration sample by obtaining the scattered particle energy from the kinematics and using the electronics offset (which is set to zero beforehand) of the acquisition system. It is worth stressing the value of performing the measurements at several incident energies to properly determine the PHD of the detector, which is done here since 3 MeV is used to determine the beam energy. Lennard et al.36 also emphasise the distinction between “energy” spectra (for which the PHD is neglected) and pulse-height spectra. Particular attention must be paid to the PHD determination since the electronic gain derived from the data processing is largely related to the PHD chosen.37 The electronics calibration uncertainty (A3 in Table 1) is evaluated from the standard deviation of the electronic gains Δ used to properly fit the set of spectra acquired on the calibration sample at various incident energies; in particular, it is the upper limit of the confidence interval (considering 99% of confidence) given for this standard deviation by the one-tailed probability of the χ2-distribution.
The simultaneous use of two independent detectors for performing the RBS measurements allows an independent check of the estimates of uncertainty and hence the internal consistency of the calibration parameters (see inset in Fig. 1). Moreover, the ratio of the apparent implant fluences measured by each detector should equal unity, with an uncertainty given by:
| UDetA/DetB2 = (UDetA1)2 + (UDetB1)2 | (6) |
If this is not the case there must be doubt about the value of the average fluence; the contribution A4 reported in the uncertainty budget (Table 1) is an attempt to take account of such a discrepancy:
 | (7) |
The first term in eqn (7) is a weighted average of the uncertainties U1: for an unweighted average this term is simply equal to 1/2. The second term of this equation represents the apparent divergence between both detectors taking into account the uncertainty that applies to the ratio FluenceDetA/FluenceDetB (eqn (6)). We are comparing the difference observed with the most probable expected difference, and estimating the measurement bias simply as a difference of variances. If this difference is negative (giving an imaginary A4) clearly the difference is less than the expected (most probable) difference – that is, there is no bias (A4 = 0). In this case the discrepancy is consistent with what is expected from the statistics. It is worth noting that the apparent disagreement between both detectors (A4) can easily reach several percent if the electronics are not accurately calibrated.
The uncertainty of the analysis code used (DataFurnace38) was evaluated as 0.2% in an IAEA-sponsored intercomparison39 (B5 in Table 1). The uncertainty of the screening correction on the (Rutherford) scattering cross-section (eqn (2)) was taken conservatively as the standard deviation of the screening correction factors obtained using the approximations of Molière and Thomas–Fermi:10 that is, considering a 1.5 MeV He beam, and using a cover factor k = 2 to estimate this important quantity conservatively, we obtain 0.50% for Bi, 0.27% for Sb (B6′ in Table 2) and 0.16% for As (B6 in Table 1).
| Type | Det A | Det B | |
|---|---|---|---|
| Pileup correction (Sb signal), % | C′1 | 0.16 | 0.36 |
| Pileup uncertainty (10% of total correction), % | B′1 | 0.02 | 0.04 |
| Counting statistics, implant signal, % | A′1 | 0.12 | 0.06 |
| Counting statistics, a-Si signal, % | A′2 | 0.08 | 0.05 |
| Scattering angle ∼1/sin4(θ/2) and 1/cos(θ), % | B′2 | 0.07 | 0.40 |
| Electronics calibration uncertainty, % | A′3 | 0.29 | 0.17 |
| Relative uncertainty (dataset), % | U′1 | 0.33 | 0.44 |
| Relative uncertainty of average of 2 detectors (dataset), % | U′2 | 0.27 | |
| Beam energy, % | B′3 | 0.20 | |
| Disagreement between both detectors, % | A′4 | 0.00 | |
| Pileup uncertainty (from model), % | B′4 | 0.20 | |
| Code uncertainty, % | B′5 | 0.20 | |
| Rutherford cross-section (screening uncertainty), % | B′6 | 0.27 | |
| Si stopping power (uncertainty on the a-Si yield), % | A′5 | — | |
| Si stopping power (uncertainty on the implant counts), % | A′6 | — | |
| Combined extra systematic uncertainty, % | U′3 | 0.44 | |
| Total combined standard uncertainty (accuracy), % | U′4 | 0.52 | |
The accuracy of the stopping power used to determine the QΩ product (through eqn (3)) dominates the final uncertainty. Consequently, we have measured the stopping power factor [ε] for this beam in silicon with the reverse process, that is, using the Sb-CRM to determine the QΩ product from eqn (1), and then determining [ε] from eqn (3) (see Table 2). The evaluated uncertainty on this determination of [ε] is A5 in Table 1, which is the uncertainty of the CRM certification (0.6%) and U′4 from Table 2 added in quadrature.
There is also a second-order effect of the stopping power since the Rutherford differential cross-section depends on the energy E of the scattered particles (eqn (2)), and therefore the uncertainty on the matrix stopping power will also induce an uncertainty on the probability of a scattering event occurring at a given depth in the material. This extra uncertainty has been evaluated for the particles backscattered by the implanted material at its maximum of distribution (A6 in Table 1).
Channelling effects
We will use the alpha particle backscattering yield from the silicon substrate (see Y0,Si in Fig. 1 and discussion of eqn (3)) as an internal standard determining QΩ in these measurements. But we have to avoid distortion of this yield due to the crystallinity of the silicon: the atoms are very highly correlated to each other and therefore can shadow each other from the highly collimated alpha beam; this is due to the so-called “channelling” effect. Efforts to “randomise” the backscattering yield by choosing pseudo-random directions40 or rotating the sample under the beam41 are effective only at the 4% level (see the extended discussion of channelling in Lulli et al.42,43). For accurate work, amorphisation of crystalline samples is essential to eliminate channelling effects.24Experimental section
In April 2010, two 100 mm Si wafers (##20, 21) were amorphised with a (nominally) 3 × 1015 Ar cm−2 implant at 150 keV, and subsequently implanted by (nominally) 5 × 1015 As cm−2 at 80 keV. The uniformity over the wafers was verified by RBS to be better than 1%, and four-point-probe resistivity measurements on comparable implants (annealed appropriately) show a uniformity of about 0.5%; since this is the precision of the technique, the real uniformity is probably better. The measured Ar fluence was (3.075 ± 0.030) × 1015 Ar cm−2 where the ratio of Ar content between the two wafers was 1.010 ± 0.014. The ratio of As fluences between wafers was determined by RBS as 1.004 ± 0.003: that is, the wafers are indistinguishable. In this work we repeatedly measured samples from wafer #20 over a period of 2 years.The Sb-implant CRM is a 15 mm square piece of the certified reference material IRMM0001/BAML003, provided by the European Institute for Reference Materials and Measurements.16 This sample was produced by a Sb implantation into a (100) Si wafer, and subsequently amorphised at Surrey to a depth of about 630 nm with an “Epifab” implant,44 that is, a 5 × 1015 28Si cm−2 cold implant at 500 keV on a liquid-nitrogen-cooled stage. Such implants are widely used in defect-engineering applications, and are well known. The implanted fluence of the CRM is 48.1 × 1015 Sb cm−2 certified at an absolute accuracy of 0.6%. The implant was mixed 121Sb and 123Sb such that assuming natural abundance introduces a systematic error of 0.06% which we neglect.
All RBS measurements were performed on a 2 MV tandem accelerator in a chamber containing a six-axis goniometer45 and two “passivated implanted planar silicon” (PIPS) detectors set at 172.8 ± 0.2° (DetA) and 148.6 ± 0.2° (DetB) with nominal subtended solid angles of 1.3 and 3.9 msr, respectively. The scattering angles were measured directly using a beam-line laser and the six-axis goniometer. The nominal beam size was 2 mm with a typical beam intensity of 2–25 nA, whatever beam was used (3.0 MeV 1H+, 1.5 MeV 4He+, 4.0 MeV 7Li2+ or 9.6 MeV 12C4+).
For the helium, lithium and carbon RBS measurements, the energy of the incident beam was calculated using an energy calibration factor determined less than three months before performing the experiment. For the proton beam measurements, the latest energy calibration factor determined following the 16O(α,α)16O procedure described above was more than 6 months. Subsequently, we checked the calibration of our accelerator by using the 27Al(p,γ)28Si, 13C(p,γ)14N and 32S(p,p′γ)32S nuclear resonances occurring respectively at (991.9 ± 0.1), (1747.6 ± 0.9) and (3379 ± 1) keV.46 The stability of the energy calibration factor, over this period of six months, was found to be better than 0.04 ± 0.12%.
The experimental conditions used for the analysis of the Sb-implant CRM and the As-implant samples are reported in Table 3. All spectra analysed in Surrey used the DataFurnace software (NDF47 version 9.4 h). The electronic gain and PHD of both detectors were fitted from the calibration sample (Au/Ni/SiO2/Si) spectra collected at various incident energies33,48 by assuming a linear calibration with a null offset, which was initially verified using a high precision electronic pulser. The Molodtsov & Gurbich pileup correction27 was used together with the pileup rejection capability of the shaping amplifiers. The electron screening factors given by Andersen et al.49 were used.
| Sample | Ion beam | Ion beam energy (MeV) | Ion beam intensity (nA) | Total collected charge (μC) | Date of measurement |
|---|---|---|---|---|---|
| Sb-implant CRM | 1H+ | 3.0 | 2 | 190 | Jan 13 |
| Sb-implant CRM | 4He+ | 1.5 | 15 | 300 | Jun 13 |
| Sb-implant CRM | 7Li2+ | 4.0 | 2 | 10 | Oct 12 |
| As-implant | 4He+ | 1.5 | 25 | 850 | Feb 11 |
| As-implant | 4He+ | 1.5 | 7 | 10 | Jun 12 |
| As-implant | 4He+ | 1.5 | 5 | 30 | Jul 12 |
| As-implant | 4He+ | 1.5 | 14 | 29 | Jun 13 |
| As-implant | 4He+ | 1.5 | 13 | 27 | Jun 13 |
| As-implant | 4He+ | 1.5 | 13 | 45 | Jul 13 |
| As-implant | 4He+ | 1.5 | 12 | 40 | Jul 13 |
| As-implant | 7Li2+ | 4.0 | 2 | 23 | Oct 12 |
| As-implant | 12C4+ | 9.6 | 5 | 25 | Mar 12 |
| As-implant | 12C4+ | 9.6 | 5 | 72 | Mar 12 |
Results
The As-implant sample has been independently measured repeatedly over a period of 2 years using a 4He+ beam at 1.5 MeV and the Si substrate yield as an internal standard. A typical uncertainty budget obtained for an As fluence determination using this ion beam is reported in Table 1, and the measured fluences with their uncertainties are tabulated in Table 4 and shown as a function of time in Fig. 2. The error bars given in this figure are the “reduced uncertainties” (U5 in Table 1): this is, for each measurement, the total combined standard uncertainty (penultimate column of Table 4) less the contribution of all systematic errors (i.e. B3–6 & A5,6) which are identical for each dataset measured with the 1.5 MeV He+ beam. The reduced uncertainties were used to calculate the weighted average, (4.647 ± 0.014) × 1015 As cm−2, also shown in Fig. 2.| Ion beam | Target | Date of measurement | Measured fluence (1015 cm−2) | Total combined uncertainty U′4 or U4 (%) | Stopping power factor uncertainty (%) |
|---|---|---|---|---|---|
| a The uncertainty on the stopping power factor used is traceable to the CRM for all cases except for the C-beam analysis, for which it is traceable to Helmut Paul's compilation.50 The weighted average for the measurements of the As implant fluence with a He beam is 4.647 ± 0.043 × 1015 As cm−2. | |||||
| 3.0 MeV 1H+ | Sb-CRM | Jan 13 | 41.0 | 1.2 | — |
| 1.5 MeV 4He+ | Sb-CRM | Jun 13 | 48.0 | 0.56 | 0.8 |
| 4.0 MeV 7Li2+ | Sb-CRM | Oct 12 | 48.4 | 0.82 | 1.0 |
| 1.5 MeV 4He+ | As-implant | Feb 11 | 4.632 | 1.09 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jun 12 | 4.699 | 1.55 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jul 12 | 4.673 | 1.17 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jun 13 | 4.680 | 1.39 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jun 13 | 4.574 | 1.40 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jul 13 | 4.648 | 1.08 | 0.8 |
| 1.5 MeV 4He+ | As-implant | Jul 13 | 4.635 | 1.10 | 0.8 |
| 4.0 MeV 7Li2+ | As-implant | Oct 12 | 4.595 | 1.92 | 1.0 |
| 9.6 MeV 12C4+ | As-implant | Mar 12 | 4.626 | 3.22 | 3.0 |
| 9.6 MeV 12C4+ | As-implant | Mar 12 | 4.721 | 3.23 | 3.0 |
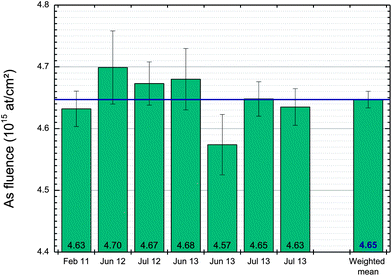 | ||
| Fig. 2 As-implant fluences measured by a 1.5 MeV 4He+ beam over a two year period. The error bars are given as the “reduced uncertainty” (U5, k = 1; see Table 1). The weighted mean of the measurements is calculated using Wi = 1/U5i. | ||
The Sb-implanted CRM was measured similarly, to derive the uncertainty of the stopping power factor for Si “[ε]Si” from the certified Sb fluence. The results are shown in Table 4. The uncertainty budget is constructed similarly to Table 1 and is shown in Table 2; the total combined uncertainty U′4 from Table 2 is therefore combined with the uncertainty of the CRM certification (0.6%) to evaluate the uncertainty on [ε]Si used in Table 1 (A5).
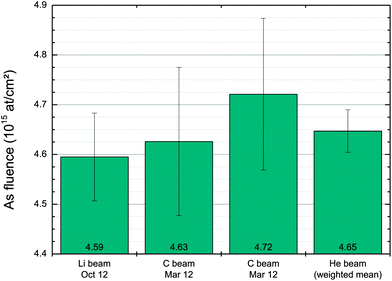
Table 4 also tabulates the measured fluences with their uncertainties for H, Li and C beams, which are shown in Fig. 3. In this case, the error bars represent the total combined standard uncertainty (U4 in Table 4) since we are comparing the results obtained with different ion beams. The combined uncertainty of the weighted average obtained for the 1.5 MeV alpha beam measurements is 0.9%.
Discussion
Stopping power factor
The uncertainty of the silicon stopping power factor for the 1.5 MeV 4He+ beam (A5 and see Table 2) was critically estimated through the Sb-implant CRM analysis. The measured Sb fluence was found to be 48.0 × 1015 Sb cm−2 with a standard uncertainty of 0.52% (U′4 in Table 2) derived from our uncertainty budget disregarding the silicon stopping power uncertainties (A′5 & A′6). The ratio between the certified and measured Sb fluences is therefore equal to 1.002 with an uncertainty of 0.8% derived from the combination of the uncertainties that apply to the measured (0.52%) and certified (0.6%) values. Since this ratio is closer to unity (0.2%) than its combined uncertainty (0.8%), we can conclude that the error on [ε] (obtained from the SRIM2003 database) is lower than 0.8% (A5 in Table 1), which is about 3 times lower than the uncertainty estimated from the experimental measurements of [ε] for this target and beam (see the SRIM and other databases26,50).This method measures the stopping power factor for a material directly for a particular beam and can be used for any beam and any material. Similar measurements were made for the 4 MeV Li beam, again finding that the SRIM2003 database was accurate (this time at 1%). If measurements are made at a series of beam energies, then the stopping power itself can be extracted (see Barradas et al.51 for example). This has not yet been done, but is clearly feasible at accuracies much higher than are possible with direct methods.
Robustness of the analytical method
The relative uncertainty of the average of 2 detectors (U2 in Table 1) is dominated by the counting statistics in the case shown, but it is easy to count longer so that no one effect dominates the uncertainty. We deliberately have detectors with significantly different solid angles so that with greatly different counting rates (and consequently with different counting statistics and pileup background) the effect that dominates the combined uncertainty differs between detectors. For much smaller fluences (the Surrey implantation QA protocol uses 1 × 1015 As cm−2) the dominating effects are usually pileup for the large detector and counting statistics for the small one. Note that Table 2 shows that for some cases the uncertainty from the scattering angle dominates: we have reached an accuracy for which there are many similarly sized contributions to the uncertainty. It will not be easy to improve significantly on this.Therefore, using two detectors gives robustness to the method since, apart from having two independent data channels which ought to agree, we also have data channels which should be subject to different types of uncertainty. The method consequently has in-built self-consistency checks which should be able to signal the presence of extra error.
Fig. 2 shows that each measurement agrees with the weighted mean within the error bars given by the reduced uncertainty (U5, see Table 1; k = 1) except the second point of measurement performed in June 13 that requires one to consider a coverage factor k = 2. This is nevertheless expected since the reduced uncertainty is largely dominated by the counting statistics on the implant signal. The weighted mean presented in this work (4.647 ± 0.013 1015 As cm−2) is about 1.2% higher than the average reported by Jeynes et al.17 We believe that this difference, if indeed a difference equivalent to k = 1.2 is significant, is mainly related to the electronic gain determination which directly changes the As-fluence measured through the a-Si yield (see eqn (3)). We have reprocessed the Surrey data used previously17 by paying extra attention to the PHD and electronics gain determination, finding a value of (4.632 ± 0.029) 1015 As cm−2 which is in much better agreement with the weighted means presented both in this and the previous work. This shows how difficult it is to determine the electronics gain with accuracy better than 0.5%: in particular, the determination of the PHD and the electronics offset is crucial for that level of precision. A careful processing of the spectra acquired on the Au/Ni/SiO2/Si sample at various incident energies (see calibration method described above) nevertheless allows one to determine these parameters with that level of accuracy. The details of the procedure required will be published elsewhere.
Generalisation to other ion beams
The uncertainty budget reported in Table 1 for the 1.5 MeV 4He+ beam can be easily extended to any other ion beam. Indeed, only the contributions A5 and A6 are directly related to the ion beam properties (i.e. energy and ion type) through the uncertainty in the silicon stopping power factor. This stopping factor can always be estimated from the semi-empirical data compilations,26,50 but where it can be determined directly from the CRM the uncertainty can be dramatically reduced. For heavier beams the screening correction on the Rutherford scattering cross-section is larger but still known to a good approximation, with an uncertainty (B6) directly deduced from the comparison between the screening factors obtained in the Molière and Thomas–Fermi approximations.10 The very good agreement between the measurements performed with 1.5 MeV 4He+, 4.0 MeV 7Li2+ and 9.6 MeV 12C4+ is shown in Fig. 3. For the lithium beam the stopping power factor is evaluated directly from the CRM with an uncertainty of 1% and an Uncertainty Budget directly comparable to Table 2; but for the carbon beam the uncertainty in the stopping power factor is evaluated directly from Helmut Paul's compilation.50For higher energy beams the Rutherford approximation breaks down. Non-Rutherford scattering needs a full quantum mechanical treatment to harmonise datasets of measured cross-sections (which are often strong functions of scattering angle), and determining the uncertainty (which may be large) of such “evaluated” cross-section datasets is difficult52 and has not been done for the evaluated scattering cross-sections for H on silicon.53 We expect that this uncertainty accounts for the very large observed discrepancy (17.3 ± 1.6%) between the certified and the measured Sb fluence of the Sb-CRM when measured with 3.0 MeV 1H+ even though the measurement is precise (with a small uncertainty of 1.3%), with the expected error in the silicon stopping power evaluated by SRIM03 expected to be quite small. For this non-Rutherford case the uncertainty assigned to the cross-section (B6) is entirely different from the Rutherford case: but the other uncertainties are also evaluated quite differently. Since the kinematics are different (see eqn (5)) the elemental edges are much closer together in energy, affecting both the pileup background (B1) and the pileup model (B4). The variation of cross-section with angle (B2) is a different function, and the code uncertainty is also larger (B5). All of these effects are outside the scope of the present work. Here we restrict ourselves to pointing out that the method remains valid, but the construction of the Uncertainty Budget is very considerably harder.
Future developments
The present method depends for its traceable accuracy on an internal standard from which the QΩ product can be obtained, where this internal standard is independently determined absolutely. Here we have relied on the silicon stopping which has been measured traceable to the Sb-implanted CRM.However, in principle, measured charge (Q) could be used directly as the reference quantity if it could be determined sufficiently accurately, a problem on which there has been relatively little critical published work so far. It is not easy to measure charged particle beam fluences at sub-1% absolute accuracy because the electronic environment of the scattering chamber is very complex. This is very widely acknowledged in the ion implantation community: even research implanters with relatively low beam currents, simple beam lines and comprehensive instrumentation cannot currently be specified at better than 2% (and that is challenging!), and Gries' suggestion of “Quantitative Ion-Implantation”54 has not been taken up in practice. Nevertheless, it is possible to determine Q at quite high accuracy by a variety of methods, and it may even be practical to directly determine the ion beam current with intrinsically traceable methods based on SQUIDs.55
Conclusion
In this work, we have demonstrated, by performing multiple independent measurements of an implanted sample over a period of 2 years, that the implant fluence can be reliably determined at a traceable accuracy of about 1% for reasonable acquisition times (Q ≅ 30 μC), and that the measured fluences have the agreement expected from the estimated global uncertainty. Moreover, measurement precision (for extended measurement times) has been demonstrated at 0.3%, showing that the accuracy is currently limited by the uncertainty in stopping power used (or, equivalently, by the uncertainty in the measurement of the charge solid-angle product).This method has a general applicability: the same measurement protocol was successfully applied to various ion beams, and comparable methods can be constructed for almost any type of sample, although 1% accuracy is not always available.
Whatever the incident beam, it is clear that the uncertainty of the material stopping power usually dominates the best accuracy of this analytical method. In the present work, we have critically determined this uncertainty for a helium beam and silicon-based samples essentially by directly measuring the stopping power factor using an Sb-implanted silicon sample certified at 0.6%, with a consequent uncertainty on the measured fluence in this case of 0.8%. This direct stopping power measurement method can be extended to any ion-matter couple, provided that appropriate certified reference materials are available.
It should be emphasised that we have here substituted traceability based on the stopping power factor (a physical constant) for traceability based on an artefact (the Sb-implanted CRM). By determining the stopping power factor (through the CRM) we have dramatically generalised the availability and usability of this particular measurement protocol, since although creating and certifying a CRM is very difficult, anyone with an ion implanter can make an amorphised silicon wafer for themselves.
In general, of the non-destructive thin film characterisation techniques available, ion beam analysis (including RBS) is the most quantitative (that is, traceably accurate) while not requiring either sample-matched standards or further information about the sample. All of the many and very powerful methods available today have their own strengths, and modern materials analysis should make full use of the toolbox of complementary techniques; Total-IBA has a significant place in this toolbox.
References
- L. de Viguerie, L. Beck, J. Salomon, L. Pichon and P. Walter, Composition of Renaissance Paint Layers: Simultaneous Particle Induced X-ray Emission and Backscattering Spectrometry, Anal. Chem., 2009, 81, 7960–7966 CrossRef CAS PubMed.
- M. E. Christopher, J.-W. Warmenhoeven, F. S. Romolo, M. Donghi, R. P. Webb, C. Jeynes, N. I. Ward, K. J. Kirkby and M. J. Bailey, A New Quantitative Method for Gunshot Residue Analysis by Ion Beam Analysis, Analyst, 2013, 138, 4649–4655 RSC.
- D. Krecar, M. Rosner, M. Draxler, P. Bauer and H. Hutter, Quantitative analysis of the Ge concentration in a SiGe quantum well: comparison of low-energy RBS and SIMS measurements, Anal. Bioanal. Chem., 2006, 384, 525–530 CrossRef CAS PubMed.
- J. Demeulemeester, D. Smeets, C. M. Comrie, C. Van Bockstael, W. Knaepen, C. Detavernier, K. Temst and A. Vantomme, The influence of Pt redistribution on Ni(1-x)Pt(x)Si growth properties, J. Appl. Phys., 2010, 108, 043505 CrossRef.
- K. T. Howard, M. J. Bailey, D. Berhanu, P. A. Bland, G. Cressey, L. E. Howard, C. Jeynes, R. Mathewman, Z. Martins, M. Sephton, V. Stolojan and S. Verchovsky, Biomass preservation in impact melt ejecta, Nat. Geosci., 2013 DOI:10.1038/ngeo1996.
- A. L. Turkevich, E. J. Franzgrote and J. H. Patterson, Chemical Analysis of Moon at Surveyor V Landing Site, Science, 1967, 158, 635–637 CAS.
- E. Rutherford, The Scattering of Alpha and Beta Particles by Matter and the Structure of the Atom, Philos. Mag., 1911, 21, 669–688 CrossRef CAS.
- C. Jeynes, R. P. Webb and A. Lohstroh, Ion Beam Analysis: A Century of Exploiting the Electronic and Nuclear Structure of the Atom for Materials Characterisation, Reviews of Accelerator Science and Technology, 2011, 4, 41–82 CrossRef.
- C. Jeynes, M. J. Bailey, N. J. Bright, M. E. Christopher, G. W. Grime, B. N. Jones, V. V. Palitsin and R. P. Webb, Total IBA – Where are we?, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 271, 107–118 CrossRef CAS PubMed.
- J. L'Ecuyer, J. A. Davies and N. Matsunami, How Accurate Are Absolute Rutherford Backscattering Yields, Nucl. Instrum. Methods Phys. Res., 1979, 160, 337–346 CrossRef CAS.
- C. Cohen, J. A. Davies, A. V. Drigo and T. E. Jackman, Intercomparison of Absolute Standards for RBS Studies, Nucl. Instrum. Methods Phys. Res., 1983, 218, 147–148 CrossRef CAS.
- J. A. Davies, T. E. Jackman, H. L. Eschbach, W. Dobma, U. Wätjen and D. Chivers, Calibration of the Harwell Series-II Bi-Implanted RBS Standards, Nucl. Instrum. Methods Phys. Res., Sect. B, 1986, 15, 238–240 CrossRef.
- U. Wätjen and H. Bax, Bi-Implanted Silicon Reference Material Revisited - Uniformity of the Remaining Batch, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 85, 627–632 CrossRef.
- U. Wätjen, H. Bax and P. Rietveld, Evaporated and Implanted Reference Layers for Calibration in Surface-Analysis, Surf. Interface Anal., 1992, 19, 253–258 CrossRef.
- J. A. Davies, W. N. Lennard and I. V. Mitchell, in Handbook of Ion Beam Materials Analysis, ed. J. R. Tesmer and M. Nastasi, Materials Research Society, Pittsburgh, 1992 Search PubMed.
- K. H. Ecker, U. Wätjen, A. Berger, L. Persson, W. Pritzkow, M. Radtke and H. Riesemeier, RBS, SY-XRF, INAA and ICP-IDMS of antimony implanted in silicon - a multi-method approach to characterize and certify a reference material, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 188, 120–125 CrossRef CAS.
- C. Jeynes, N. P. Barradas and E. Szilágyi, Accurate Determination of Quantity of Material in Thin Films by Rutherford Backscattering Spectrometry, Anal. Chem., 2012, 84, 6061–6069 CrossRef CAS PubMed.
- K. A. Sjoland, F. Munnik and U. Wätjen, Uncertainty budget for ion beam analysis, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 161, 275–280 CrossRef.
- W. H. Bragg and M. A. Elder, On the alpha particles of radium, and their loss of ranae in passing through various atoms and molecules, Philos. Mag., 1905, 10, 318–340 CrossRef CAS.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, SRIM - The stopping and range of ions in matter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS PubMed.
- W. K. Chu, J. W. Mayer and M. A. Nicolet, Backscattering Spectrometry, Academic Press, New York, 1978 Search PubMed.
- G. Boudreault, C. Jeynes, E. Wendler, A. Nejim, R. P. Webb and U. Wätjen, Accurate RBS measurement of ion implant doses in a silicon, Surf. Interface Anal., 2002, 33, 478–486 CrossRef CAS.
- C. Jeynes, N. P. Barradas, P. K. Marriott, G. Boudreault, M. Jenkin, E. Wendler and R. P. Webb, Elemental thin film depth profiles by ion beam analysis using simulated annealing - a new tool, J. Phys. D: Appl. Phys., 2003, 36, R97–R126 CrossRef CAS.
- M. Bianconi, F. Abel, J. C. Banks, A. C. Font, C. Cohen, B. L. Doyle, R. Lotti, G. Lulli, R. Nipoti, I. Vickridge, D. Walsh and E. Wendler, The Si surface yield as a calibration standard for RBS, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 161, 293–296 CrossRef.
- N. P. Barradas, K. Arstila, G. Battistig, M. Bianconi, N. Dytlewski, C. Jeynes, E. Kotai, G. Lulli, M. Mayer, E. Rauhala, E. Szilágyi and M. Thompson, Summary of IAEA intercomparison of IBA software, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1338–1342 CrossRef CAS PubMed.
- J. F. Ziegler, SRIM website, http://www.srim.org/.
- S. L. Molodtsov and A. F. Gurbich, Simulation of the pulse pile-up effect on the pulse-height spectrum, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 3484–3487 CrossRef CAS PubMed.
- N. P. Barradas and M. A. Reis, Accurate calculation of pileup effects in PIXE spectra from first principles, X-Ray Spectrom., 2006, 35, 232–237 CrossRef CAS.
- R. O. Bondelid and E. E. D. Whiting, (p,n) Threshold-Curve Shapes and Measurements of Threshold Energy with 1H+ Beams, Phys. Rev. B: Solid State, 1964, 134, B591–B594 Search PubMed.
- C. Jeynes and N. P. Barradas, in Handbook of Modern Ion Beam Materials Analysis, ed. Y. W. a. M. Nastasi, Materials Research Society, Warrendale, Pennsylvania, 2009, pp. 347–383 Search PubMed.
- C. Rolfs, W. S. Rodney, S. Durrance and H. Winkler, New Method for Measurement of Proton-Beam Energies, Nucl. Phys. A, 1975, 240, 221–234 CrossRef.
- J. Demarche and G. Terwagne, Precise measurement of the differential cross section from the 16O(α,α)16O elastic reaction at 165 degrees and 170 degrees between 2.4 and 6.0 MeV, J. Appl. Phys., 2006, 100, 124909 CrossRef.
- C. Jeynes, N. P. Barradas, M. J. Blewett and R. P. Webb, Improved ion beam analysis facilities at the University of Surrey, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 136, 1229–1234 CrossRef.
- A. F. Gurbich, Evaluation of non-Rutherford proton elastic scattering cross section for oxygen, Nucl. Instrum. Methods Phys. Res., Sect. B, 1997, 129, 311–316 CrossRef CAS.
- E. Andrade, C. Solis and M. F. Rocha, Application of the SIMNRA code to calibrate the analyzing magnet associated with a Van de Graaff accelerator, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 553–556 CrossRef CAS PubMed.
- W. N. Lennard, H. Xia and J. K. Kim, Revisiting the stopping powers of Si and SiO2 for He-4 ions: 0.5–2.0 MeV, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 215, 297–307 CrossRef CAS PubMed.
- A. F. Gurbich and C. Jeynes, Evaluation of non-Rutherford proton elastic scattering cross-section for magnesium, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 265, 447–452 CrossRef CAS PubMed.
- N. P. Barradas, C. Jeynes and R. P. Webb, Simulated annealing analysis of Rutherford backscattering data, Appl. Phys. Lett., 1997, 71, 291–293 CrossRef CAS.
- N. P. Barradas, K. Arstila, G. Battistig, M. Bianconi, N. Dytlewski, C. Jeynes, E. Kotai, G. Lulli, M. Mayer, E. Rauhala, E. Szilágyi and M. Thompson, International Atomic Energy Agency intercomparison of ion beam analysis software, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 262, 281–303 CrossRef CAS PubMed.
- A. L'Hoir, D. Schmaus, J. Cawley and O. Jaoul, Depth Profiling Light-Nuclei in Single-Crystals - a Combined Nuclear-Reaction and Rbs Technique to Minimize Unwanted Channeling Effects, Nucl. Instrum. Methods Phys. Res., 1981, 191, 357–366 CrossRef CAS.
- M. Kokkoris, A. Spyrou, G. Perdikakis, R. Vlastou, C. T. Papadopoulos, A. Lagoyannis, E. Simoen and S. Kossionides, On the radiation damage effects in semiconductors beyond the end of range of implanted protons at high energies and fluences, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 240, 168–173 CrossRef CAS PubMed.
- G. Lulli, E. Albertazzi, M. Bianconi, R. Nipoti, M. Cervera, A. Camera and C. Cellini, Stopping and damage parameters for Monte Carlo simulation of MeV implants in crystalline Si, J. Appl. Phys., 1997, 82, 5958–5964 CrossRef CAS.
- G. Lulli, E. Albertazzi, M. Bianconi, G. G. Bentini, R. Nipoti and R. Lotti, Determination of He electronic energy loss in crystalline Si by Monte-Carlo simulation of Rutherford backscattering-channeling spectra, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 170, 1–9 CrossRef CAS.
- J. P. Zhang, R. J. Wilson, P. L. F. Hemment, A. Claverie, F. Cristiano, P. Salles, J. Q. Wen, J. H. Evans, A. R. Peaker and G. J. Parker, Regrowth Behavior of Si1-XGex/Si Structures Formed by Ge+ Ion-Implantation and Post Amorphization, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 84, 222–228 CrossRef CAS.
- A. Simon, C. Jeynes, R. P. Webb, R. Finnis, Z. Tabatabian, P. J. Sellin, M. B. H. Breese, D. F. Fellows, R. van den Broek and R. M. Gwilliam, The new Surrey ion beam analysis facility, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 219, 405–409 CrossRef PubMed.
- J. B. Marion, Accelerator Calibration Energies, Rev. Mod. Phys., 1966, 38, 660–668 CrossRef CAS.
- N. P. Barradas and C. Jeynes, Advanced physics and algorithms in the IBA Data Furnace, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1875–1879 CrossRef CAS PubMed.
- C. Pascual-Izarra and N. P. Barradas, Introducing routine pulse height defect corrections in IBA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 1866–1870 CrossRef CAS PubMed.
- H. H. Andersen, F. Besenbacher, P. Loftager and W. Möller, Large-angle scattering of light ions in the weakly screened Rutherford region, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 21, 1891–1901 CrossRef CAS.
- P. Helmut, Stopping Power for Light Ions, http://www.exphys.uni-linz.ac.at/stopping/stopp_bot.htm.
- N. P. Barradas, E. Alves, Z. Siketić and I. Bogdanović Radović, Stopping power of He, C and O in TiO2, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 273, 22–25 CrossRef CAS PubMed.
- E. V. Gai and A. F. Gurbich, Evaluated C-12(He-4,He-4)C-12 cross-section and its uncertainty, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 296, 87–91 CrossRef CAS PubMed.
- A. F. Gurbich, Evaluated differential cross-sections for IBA, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1703–1710 CrossRef CAS PubMed.
- W. H. Gries, Quantitative Ion-Implantation - Theoretical Aspects, Int. J. Mass Spectrom., 1979, 30, 97–112 CrossRef CAS.
- L. Hao, J. C. Macfarlane, C. Carr and J. C. Gallop, HTS current concentrator for remote sensing of charged particle beams, IEEE Trans. Appl. Supercond., 2003, 13, 739–742 CrossRef CAS.
- Guide to the Expression of Uncertainty in Measurement, International Organization for Standardization, Geneva, Switzerland, 1995 Search PubMed.
| This journal is © The Royal Society of Chemistry 2014 |