Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density-functional description of electrides
Stephen G.
Dale
,
Alberto
Otero-de-la-Roza
and
Erin R.
Johnson
Chemistry and Chemical Biology, School of Natural Sciences, University of California, Merced, 5200 North Lake Road, Merced, California 95343, USA. E-mail: sdale@ucmerced.edu; aoterodelaroza@ucmerced.edu; ejohnson29@ucmerced.edu
First published on 11th April 2014
Abstract
Electrides are a unique class of ionic solids in which the anions are stoichiometrically replaced by electrons localised within the crystal voids. There are only nine electrides with known crystal structures and their study represents a challenge for theory. A systematic investigation of their electronic structure is conducted using semilocal density-functional theory (DFT) in this article. The band structure is calculated for each electride and a range of techniques including plots of the valence densities, procrystal densities, non-covalent interaction isosurfaces, and Bader's quantum-chemical topology are applied. All of these methods provide consistent results, confirming the presence of localised interstitial electrons and demonstrating that these crystals display a characteristic electronic structure.
I. Introduction
Electrides are a relatively-unexplored class of materials derived from research into solvated electrons. An electride is an ionic substance in which a confined electron, localised within crystal voids, acts as the anion. The localised electron arises from spontaneous ionisation of an alkali metal coordinated to electron-rich, cage-like ligands, such as crown ethers and cryptands.1 Packing of the alkali–metal complexes leaves large voids within the crystal structure, in which the localised electron can reside. The energetic penalty incurred in moving the electron away from the nuclear potential well is offset by the lowering of its kinetic energy contribution,2 which is related to the ionisation potential of the metal complex. Currently, there are only nine stoichiometric electrides with known crystal structures, of which seven are organic and two are inorganic. Eight of these electrides are investigated in this work and comparisons made to the ninth, most recently identified electride,3 which was yet undiscovered at the commencement of this study. The structure of the simplest organic electride is shown in Fig. 1.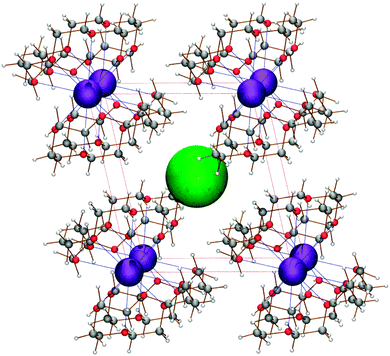 | ||
| Fig. 1 The structure of the Cs+(15-crown-5)2e− electride.4 The green sphere represents the electron trapped within the crystal void. | ||
The localised electrons give the electrides unique properties, such as high hyperpolarisabilities, high magnetic susceptibilities, highly variable conductivities, extremely low workfunctions, low-temperature thermionic emission, and very strong reducing character.1,5 Unfortunately, reduction processes cause the electrides to decompose at low temperatures,1 which makes their study challenging and limits their applicability. However, the first room-temperature-stable organic electride was synthesised recently,6 an achievement in which density-functional theory (DFT) played a role in predicting ligand–metal binding energies.
While electrides have recently attracted some interest for use in synthetic7,8 and photonics9,10 applications, there have been relatively few theoretical studies of these materials. Of the two previous DFT studies, Singh et al.2 considered the simplest organic electride with known crystal structure, Cs+(15-crown-5)2e−, and Sushko et al.11 examined the single inorganic electride [Ca24Al28O68]4+4e−. The most comprehensive study, conducted by Dye et al.,12 did not consider the electronic structure, but instead used isosurfaces constructed from a sum of van der Waals radii to predict the electride crystal-void shapes, under the assumption that the localised electron must reside in these voids. This analysis enabled connections between the macroscopic properties of electrides and their crystal structures to be made, but actual electronic-structure calculations are necessary to ascertain the presence of the caged electron and study its role in the experimental behavior of the electride.
In the present work, we conduct a systematic DFT study of the electronic structure of the eight electrides with known crystal structures. In particular, the band structure is calculated and compared with experimental conductivity measurements. Localised regions of electron density within the crystal voids are detected and visualised by calculating the valence-band densities and by using the recently-developed non-covalent interactions (NCI) index.13–15 The results from each of these approaches are compared with procrystal isosurfaces16 similar to those plotted by Dye et al. to detect the interstitial regions. Additionally, the void volumes and integrated void charges are evaluated using Bader's quantum theory of atoms in molecules (QTAIM).17–20 We show that the organic electrides all share a characteristic electronic structure that is readily detected with each of these analyses. This article may serve as a first step in the computational design of electrides with controlled experimental behavior.
II. Computational methods
Calculations on the eight studied electrides used geometries taken directly from the experimental crystal structures.4,6,21–27 For [Cs+(15-crown-5)(18-crown-6)e−]6, two caesium atoms were deleted since they represent a defect that exists in very small concentrations throughout the crystal.22 Also, for K+(cryptand-2.2.2)e−, we found that a hydrogen atom was missing from the crystal structure and was added using the mercury program.28 Finally, we used the crystal structure for [Ca24Al28O68]4+2O2−, which is identical to [Ca24Al28O68]4+4e−, except with the extra O2− dianions removed. The removal of the oxide anions allows us to use a smaller primitive cell with two caged electrons and six voids ([Ca12Al14O34]2+2e−).Calculations under periodic-boundary conditions were performed using the planewaves/pseudopotentials (PW/PS) approach and the Projected Augmented Wave (PAW) formalism29 with the Quantum Espresso program.30 Single-point, spin-polarised calculations for each electride used a 50 Ry cut-off energy, a variable number of k-points chosen depending on the unit-cell size (see Table 1), and cold smearing31 with a smearing temperature of 0.01 Ry. The PBE functional32 was used in all cases to calculate the electron density and band structure. For each electride, the charge density of the highest of the valence bands was visualised (using an iso-surface plot) to confirm the presence of the localised electron within the crystal void.
| Electride | CSD code | k-points (k × k × k) | Metal atoms per unit cell | Total atoms per unit cell |
|---|---|---|---|---|
| Cs+(15C5)2e− | TAGFEM | 4 | 1 | 71 |
| Cs+(18C6)2e− | DUBCIM | 4 | 2 | 170 |
| [Cs+(15C5)(18C6)e−]6(18C6) | WIHFIC | 2 | 6 | 518 |
| Li+(cryptand-2.1.1)e− | ROGDAS | 4 | 4 | 196 |
| Na+(tri-pip-aza-2.2.2)e− | DAWCIO | 2 | 4 | 324 |
| K+(cryptand-2.2.2)e− | GAVFIS | 4 | 4 | 248 |
| Rb+(cryptand-2.2.2)e− | EBEWOX | 4 | 2 | 126 |
| [Ca24Al28O68]4+4e− | 4 | 12 | 58 |
All the electride crystals were calculated at their experimental structures because it is too computationally expensive to relax the cell geometry. For the sake of comparison, we optimised the geometry of the smallest organic electride (Cs+(15C5)2e−, TAGFEM) using the PBE-XDM functional.33,34 Upon relaxation, the cell contracted from 733.1 Å3 to 714.5 Å3 (a 2.5% reduction in volume). The changes to the band structure, band gap and valence properties are small, except for the volume and charge of the voids (the population of the Bader non-nuclear maximum decreases from 0.361 to 0.132, for instance). Also, the DFT calculation converges to a non-magnetic state at the PBE-XDM equilibrium structure in contrast to what happens at the experimental structure (ferromagnetic, see Section III). The zero-magnetisation solution is also found for the rest of the electrides and an explanation of the sensitivity of the solution to the starting magnetisation is provided in Section III.
Since PW/PS calculations necessitate the use of generalised-gradient approximation (GGA) functionals, such as PBE, we must consider whether delocalisation error35–42 is expected to adversely affect the results. We recently investigated the role of delocalisation error for a small “model electride” using a range of GGA, hybrid, and range-separated functionals.43 It was found that delocalisation error serves to spread out any accumulation of charge. As the fraction of Hartree–Fock exchange increases and the delocalisation error is reduced, the electron becomes increasingly localised and the amount of fractional charge decreases. Range-separated functionals maintain integer charges and correctly localise the electron. However, despite the substantial delocalisation error seen with GGAs for this model system, an informative and insightful analysis of electrides is still possible. In particular, it was found that GGA calculations predict a tenfold increase in the amount of localised, interstitial charge in Cs+(15-crown-5)2e−, relative to the finite model system.43 Furthermore, even the most accurate method used to treat the electride model system and recent studies of solvated electrons in solution44,45 each showed extensive delocalisation of the excess electron over neighbouring moieties. It can then be expected that fractional charges will be observed within the crystal void irrespective of the choice of functional.
In addition to the valence-band densities, we investigated several alternative approaches to detect and visualise the localised interstitial electron. The simplest approach is to plot low-density isosurfaces, below some threshold value, to view the crystal voids. This can be done with the self-consistent field (SCF) density, or even with a sum of free atomic densities, termed the promolecular or procrystal density,16 the latter of which gives results equivalent to Dye's original representation of the voids (vide infra). While this approach can not distinguish between a vacant void and one inhabited by a confined electron, it is much faster computationally than the self-consistent DFT calculation of the electron density.
A more sophisticated approach uses the DFT density and the non-covalent interactions (NCI) index13–15 to visualise the localised electron. This approach is capable of mapping real-space regions where non-covalent interactions are important, using the electron density and reduced density gradient. Specifically, NCI plots represent low reduced-gradient isosurfaces in regions that also have low electron density, and can provide information regarding the strength and extent of non-covalent interactions in real space. In the case of electrides, the localised electron in the void manifests as a non-nuclear maximum in the density, which is also characterised by a region of low density and reduced gradient. Thus, NCI should be an ideal tool to reveal the confined electron; unlike low-density isosurfaces, the appearance of an NCI surface in a void is directly related to its electron occupation. For the eight electride crystals, NCI plots were generated from the PBE densities using the critic2 program.46 Only intermolecular interactions within the voids, and not intramolecular interactions within each metal complex, are visualised to simplify the resulting plots.
Finally, the amount of charge localised within each crystal void is determined to facilitate comparison between the different electrides. This problem is well suited to QTAIM analysis, since the localised electron (usually) corresponds to a non-nuclear maximum in the electron density.43,47 The density and volumes of the Bader basins corresponding to the non-nuclear maxima were calculated using the critic2 program46 with the Yu–Trinkle algorithm.48
III. Band structures of the electride crystals
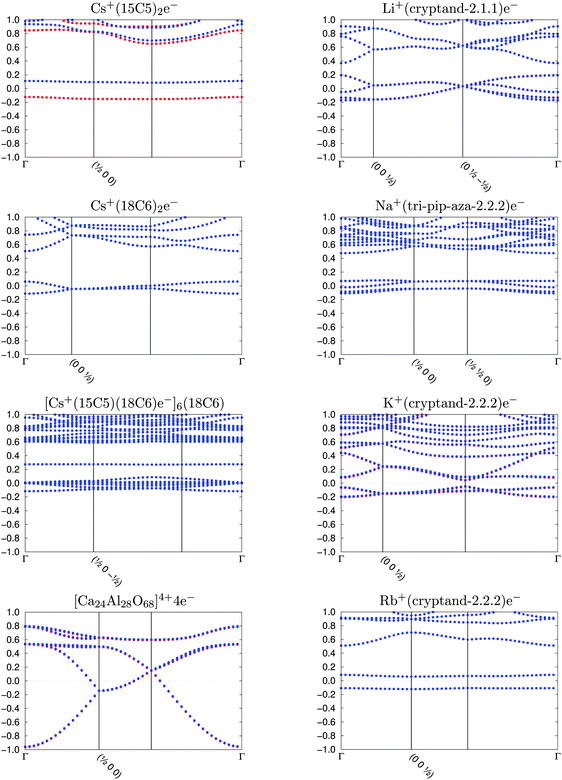
The sole previous DFT study of an organic electride confirmed the presence of a localised electron within the crystal void.2 The Cs+(15-crown-5)2e− crystal was shown to have a high-lying, half-occupied band near the Fermi level. This “electride” state is responsible for many of the observed electride properties, principally the strong reducing character and small band gap. Singh et al. observed the valence density of this band to be located within the crystal void, demonstrating that caged electrons do act as anions in electrides.The band structures of the eight studied electrides, calculated in this work, are shown in Fig. 2. The band structure of almost all electrides consists of a valence band that is occupied by the loose electrons (two one-electron states per metal atom), which is energetically separated from the rest of the underlying occupied bands. This picture, which is consistent with previous observations,2 is valid for all organic electrides.
 | ||
| Fig. 2 Band structure of the organic electrides. The blue and red dots correspond to the α and β spins, respectively. The plot shows energies (in eV) of each band along the k-path. | ||
Cs+(15-crown-5)2e−, which is the only electride with an odd number of metal atoms (and consequently of interstitial electrons) in the unit cell is the only crystal with distinct α and β bands and a non-zero magnetisation (a ferromagnetic state). For the rest of the electrides, our calculations converge to a zero-magnetisation situation, sometimes with the electride states crossing the Fermi level and each crystal void occupied by the same fraction of α and β density.
The fractional-spin behavior of the loose electron and its relation to the SCF procedure deserves some comment. Our DFT calculations were run with spin-polarisation, that is, the α and β electrons were not forced to occupy the same bands. In order to achieve a particular electron distribution (ferromagnetic or antiferromagnetic), the usual procedure is to assign a certain magnetisation to some atoms in the unit cell at the beginning of the SCF calculation. Since the electride state is not associated with any atom, in practice, we have little control over the final magnetic state to which the SCF converges.
The starting magnetisation for our calculations is a ferromagnetic state on all metal atoms although, as shown in Fig. 2, most electrides converge to the non-magnetic solution. The case of TAGFEM is particular, since the SCF finds the ferromagnetic minimum. However, if the calculation is repeated at the equilibrium structure (after the geometry relaxation described in Section II), or if the unit cell is doubled and an initial antiferromagnetic density is used, the non-magnetic state is found (see Fig. 3). The geometry relaxation does not affect the qualitative features of the band structure. If a magnetic solution were to be found, the electride state would split into an occupied α band and an unoccupied β band. The ferromagnetic state corresponds to a crystal where every void is occupied by a single α electron. The antiferromagnetic electron distribution is, likewise, not accessible in our calculations.
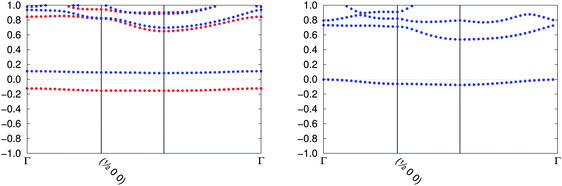 | ||
| Fig. 3 The band structure plots for TAGFEM at the experimental geometry (ferromagnetic, left) and at the relaxed geometry (non-magnetic, right) are shown. Red and blue label different spins. | ||
The energy separation between the electride state and the unoccupied conduction band is related to the experimental (optical) band gap. Since the spin state needs to be conserved during an optical transition, the observed band gap is related to the same-spin direct gap. In the non-magnetic electrides, we expect that the electride states are split in the magnetic state, so we estimate the optical gap by calculating the difference between the bottom of the conduction band and the Fermi level. The experimental and the calculated band gaps are reported in Table 2.
| Electride | Band gap (obs) | Band gap (exp) | Conductivity |
|---|---|---|---|
| Cs+(15C5)2e− | 0.64 | 0.6 | 10−8 |
| Cs+(18C6)2e− | 0.57 | 0.9 | 10−8 |
| [Cs+(15C5)(18C6)e−]6(18C6) | 0.27 | 0.069 | 2 × 10−3 |
| Li+(cryptand-2.1.1)e− | 0.42 | 0.22 | 4 × 10−7 |
| Na+(tri-pip-aza-2.2.2)e− | 0.49 | — | — |
| K+(cryptand-2.2.2)e− | 0.38 | 0.086 | 5 |
| Rb+(cryptand-2.2.2)e− | 0.62 | — | — |
| [Ca24Al28O68]4+4e− | 0.00 | — | 100 |
Fig. 2 shows two types of band gaps, consistent with the experimental results: Cs+(15-crown-5)2e− and Cs+(18-crown-6)2e− show slightly larger gaps than the rest of the electrides. Naturally, the band gaps are only in qualitative agreement with the experimental values. Conductivity in electrides occurs by void-hopping of the electrons and the experimental conductivity values (also in Table 2) qualitatively correlate with the experimental and calculated band gaps.
The inorganic electride [Ca24Al28O68]4+4e− has a completely different band structure than the organic electrides. This is reasonable because all the organic electrides have a stoichiometry of one localised electron per crystal void, while in [Ca24Al28O68]4+4e− there are 4 electrons that spread over 12 crystal voids.27 In the organic electrides all voids are fully occupied and the crystal behaves as a semiconductor, whereas the band dispersion of the inorganic electride resembles the electronic structure of a free-electron metal. As we shall see, this difference also impacts the electron density distribution with a density that is more flat than in the organic crystals, and no non-nuclear maximum. This result, however, may be an artifact of the semilocal functional, since non-nuclear maxima have been observed in a recent experimental study.51
The differences in the band structure of [Ca24Al28O68]4+4e− can be rationalised. The crystal void sizes in the inorganic electride are significantly smaller than those of the organic crystals. The smaller void size permits electron tunneling while the increased number of empty voids prevents the localised electrons from excluding each other from neighbouring void sites. Both of these properties allow [Ca24Al28O68]4+4e− to be an efficient conductor and indeed the best conductor of the eight considered electrides.27 The band structure for [Ca24Al28O68]4+4e− is consistent with the LDA band structure reported by Sushko et al.11 and with the experimental observation that this electride behaves like a metallic conductor.11 The band structure is, however, different from the B3LYP band structure reported in the same work, although the calculation by Sushko et al. was carried out with the linear combination of atomic orbitals (LCAO) approach, which may also introduce artifacts related to the basis set choice.
The band structure for the newest electride, [Ca2N]e−, is reported by Lee et al.3 This electride shows similar band motifs as [Ca24Al28O68]4+4e−, this time due to 2D layer structure of the electride, which is discussed in detail by the authors. The high lying “electride” state is still present and consistent with the electrides examined here.
For each material, the density of the highest valence band was plotted to examine the location of the electride state within the crystal, as shown in Fig. 4. The appearance of the valence densities for Cs+(15-crown-5)2e− and [Ca24Al28O68]4+4e− show good agreement with previous literature.2,11 Moreover, all of the valence-density plots show the electride state to be located within the crystal voids, as expected.
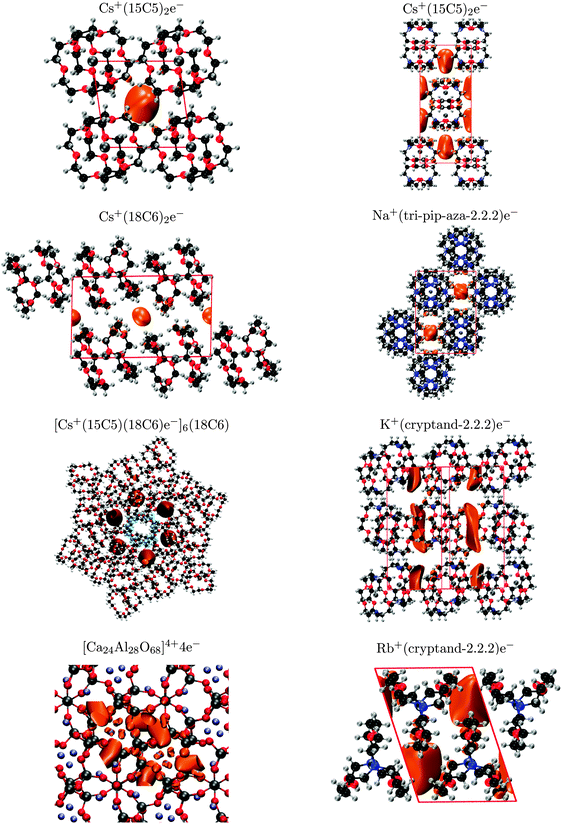 | ||
| Fig. 4 Valence-band densities for the eight electride crystals, plotted using a 0.001 a.u. isosurface, except for K+(cryptand-2.2.2)e− (0.0008 a.u.). | ||
IV. Visualisation of the interstitial electron
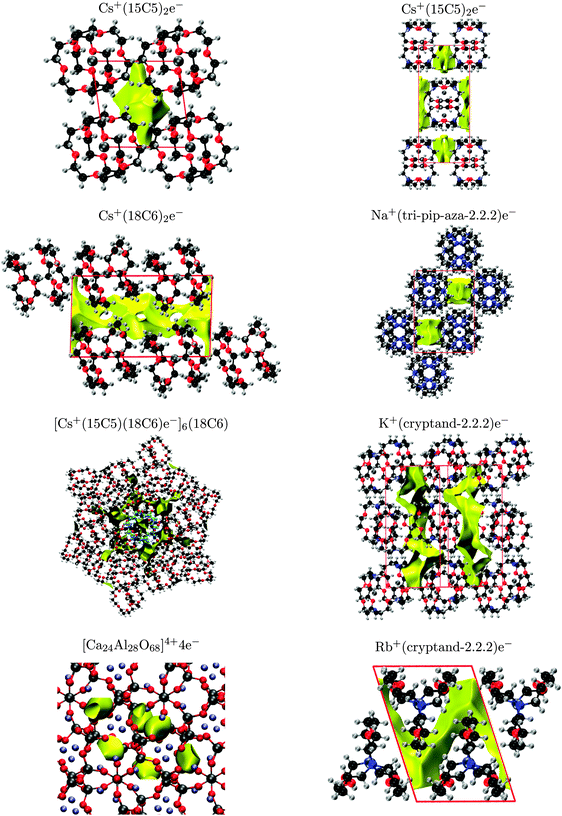
The most extensive theoretical study of electrides, conducted by Dye et al.,12 identified crystal voids by considering the regions excluded by the molecular van der Waals surface. However, the van der Waals surfaces and resulting void shapes are only dependent on the arrangement of the unit cell and not on the electron density. While it can only be assumed that the localised electron exists within the voids, this analysis does provide a rapid method of identifying crystal motifs that might be conducive to electride formation. The van der Waals surfaces were also used to rationalise differences in magnetic susceptibility and conductivity by identifying trends in cavity and channel diameters and proximities (which might allow 2-D and 3-D electron hopping). In this work, we examine the crystal voids using the procrystal density,52 which provides similar information as the van der Waals surfaces.53The procrystal density is the sum of spherically-averaged atomic electron densities for all atoms belonging to the crystal. We define the procrystal void to be the unit-cell region with lower than a threshold electron density.16 This analysis is similar to the van der Waals radii approach used by Dye et al. although, unlike the procrystal, the van der Waals surface method does not sum the densities of each atom and will therefore give slightly larger surfaces for the same isodensity value. The procrystal voids of each electride are shown in Fig. 5. The surfaces for Li+(cryptand-2.1.1)e−, K+(cryptand-2.2.2)e−, Cs+(15-crown-5)2e−, Cs+(18-crown-6)2e−, and [Cs+(15-crown-5)(18-crown-6)e−]6(18-crown-6) all show good agreement with the results of Dye et al. with the remaining electrides included for completeness.
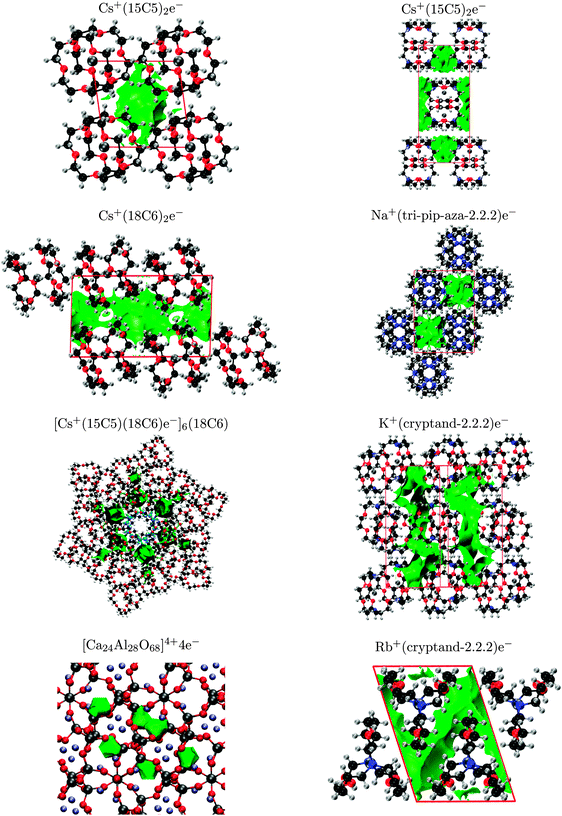
The NCI index is also used to detect and visualise the localised, interstitial electron and can be readily compared with the valence and procrystal densities. This method is more computationally expensive than the procrystal approach since it uses the DFT densities, but it is therefore capable of detecting any interstitial accumulation of electron density, giving rise to a non-nuclear maximum. The NCI plots of the eight studied electrides are shown in Fig. 6 and, with the exception of [Cs+(15-crown-5)(18-crown-6)e−]6(18-crown-6), show good agreement with the procrystal densities from Fig. 5. Additionally, while the shape of the valence-band densities from Fig. 4 are different than the NCI surfaces, the predicted location of the electron is always within the same crystal voids. Therefore, all three visualisation methods are consistent, with the single exception of [Cs+(15-crown-5)(18-crown-6)e−]6(18-crown-6) demonstrating that localised electrons indeed exist within the electride crystal voids.
The results of the NCI and promolecular methods differ for the mixed crown either electride [Cs+(15-crown-5)(18-crown-6)e−]6(18-crown-6). This crystal contains an extra solvated crown ether at the centre of the unit cell, highlighted in blue in Fig. 6. Six Cs+(15-crown-5)(18-crown-6) complexes coordinate to the crown ether, both above and below the ring, in an alternating fashion. This results in formation of six equivalent crystal voids, surrounded by the caesium complexes in the hexagonal unit cell. According to the procrystal approach, the solvated crown ether forms two extra crystal voids, above and below the ring, in which an electron should be able to reside. However, the NCI and valence density calculations both predict that the electron is excluded from these central voids in favour of the surrounding six-fold symmetric voids. The reason electrons prefer not to occupy the central voids is clear from consideration of the electrostatics. The crown ether has six oxygen atoms, all with lone pairs pointed towards the centre of the ring, creating a region of relatively-high electron density and the repulsive potential discourages interstitial electrons from occupying these voids, which correspond to the single, unoccupied electride band ca. 0.3 eV above the Fermi level in Fig. 2. This is an example in which the assumption that the electron can occupy any void space within the crystal falters. It demonstrates the additional information that can be gained from DFT study of the electronic structure rather than simple geometric analysis of the voids.
V. Quantifying the localised electron
The calculated QTAIM void charges and volumes of the eight considered electrides are collected in Table 3. Non-nuclear maxima (NNM) were identified for all the electrides, with the single exception of [Ca24Al28O68]4+4e−. The organic electrides have charges of ca. 0.13–0.36 electrons within the Bader basin corresponding to the non-nuclear maximum. These fractional charge values are consistent with recent studies of solvated electrons.45| Electride | Ionisation potential | Bader charge | Bader volume | Number of NNM |
|---|---|---|---|---|
| Cs+(15C5)2e− | 1.53 | 0.361 | 316.2 | 1 |
| Cs+(18C6)2e− | 1.37 | 0.260 | 324.3 | 8 |
| [Cs+(15C5)(18C6)e−]6(18C6) | 1.45 | 0.185 | 166.4 | 6 |
| Li+(cryptand-2.1.1)e− | 2.08 | 0.135 | 127.0 | 4 |
| Na+(tri-pip-aza-2.2.2)e− | 1.97 | 0.196 | 189.7 | 4 |
| K+(cryptand-2.2.2)e− | 1.88 | 0.171 | 218.6 | 8 |
| Rb+(cryptand-2.2.2)e− | 1.66 | 0.249 | 196.3 | 3 |
| [Ca24Al28O68]4+4e− | — | 0 | 0 | 0 |
The vertical ionisation potentials (IPs) of the neutral alkali–metal complexes were calculated at the B3LYP level of theory54,55 using the Gaussian 09 program.56 The metal atoms were assigned either the 6-31+G* basis set (Li, Na, and K) or Stuttgart effective-core potentials and accompanying basis sets (Rb and Cs).57 The 6-31G* basis set was used for all other atoms. The IPs increase down the alkali group, with decreasing electronegativity of the metal. However, there is no clear correlation between the IPs and Bader charges or volumes, indicating that the three-dimensional structure of the electride crystal, and not just the identity of the alkali–metal complex, is important in determining electride properties.
The number of NNM critical points for each electride are also reported in Table 3. Cs+(15-crown-5)2e−, [Cs+(15-crown-5)(18-crown-6)e−]6(18-crown-6), Li+(cryptand-2.1.1)e−, and Na+(tri-pip-aza-2.2.2)e− all have the same number of NNM as interstitial electrons, implying that the electrons are well localised in isolated crystal voids for these electrides. Conversely, Cs+(18-crown-6)2e−, K+(cryptand-2.2.2)e−, and Rb+(cryptand-2.2.2)e− each have more NNM than interstitial electrons, implying that the electrons occupy delocalised channels rather than separate voids in these crystals. The overall appearance of the NCI surfaces in Fig. 6 matches these findings, showing either voids or channels as predicted.
The Bader charges for [Ca24Al28O68]4+4e− are negligible as no non-nuclear maxima in the electron density are present, even though all other applied methods in this work predict it to have localised electrons. However, QTAIM analysis only detects critical points, which are not a strict requirement for the presence of localised electrons. Thus, for the inorganic electride, the QTAIM results do not necessarily contradict our other results and there are two plausible explanations as to why a NNM is not observed. The small cages within the unit cell, and the increased ratio of cages to electrons, may cause the localised electrons to be too dispersed through the unit cell to form non-nuclear maxima. Also, any accumulation of charge within the void may be drowned out by its proximity to the more electron-rich species in the crystal.
In order to test whether the absence of non-nuclear maxima in the inorganic electride is an artifact of delocalisation error from PBE, we recalculated the system using the Hybrid-Scuseria–Ernzerhof (HSE) functional,58 which contains Coulomb-screened short-range exact exchange, as implemented in VASP.59,60 No non-nuclear maxima were found either. This is not surprising considering the sensitivity of the non-nuclear maxima to the calculation level in metallic conductors due to the extremely-flat profile of the electron density.47,61
VI. Conclusion
In this work, we have systematically examined the band structure of eight electrides with known crystal structures. All electrides show the high lying electride state first observed by Singh et al. with corresponding valence densities located within the crystal voids, confirming the electride nature of these materials. The conductivity of the electrides is related to the occupation of the voids and the band structure. For the inorganic electride, the voids are only partially occupied and the band structure resembles that of a free-electron metal. For the organic electrides, the voids are fully occupied and these solids behave like semiconductors. Our calculations qualitatively agree with the experimentally-observed band gaps and conductivities.A number of different analyses to detect and visualise the localised electrons have been applied, including procrystal and NCI surfaces, and QTAIM. However, the procrystal density requires the assumption that the localised electron will exist within the voids, while the NCI, QTAIM, or valence-density calculations all use the DFT density and allow one to distinguish between occupied and unoccupied voids. This is illustrated for the mixed crown-ether electride, where the DFT-based analyses show that only the six-fold symmetric voids are occupied, while the central void remains vacant. With this single exception, all of the methods considered herein provide consistent results, reproducibly revealing characteristic electride properties, such as distinguishing between localised crystal voids and delocalised electron channels. These theoretical tools should aid future design of more stable electride materials with targeted electronic properties.
Acknowledgements
We acknowledge Mark Spackman for helpful comments and discussions.References
- J. L. Dye, Acc. Chem. Res., 2009, 42, 1564 CrossRef CAS PubMed.
- D. J. Singh, H. Krakauer, C. Haas and W. E. Pickett, Nature, 1993, 365, 39 CrossRef CAS.
- K. Lee, S. W. Kim, Y. Toda, S. Matsuishi and H. Hosono, Nature, 2013, 494, 336 CrossRef CAS PubMed.
- S. B. Dawes, J. L. Eglin, K. J. Moeggenborg, J. Kim and J. L. Dye, J. Am. Chem. Soc., 1991, 113, 1605 CrossRef CAS.
- H.-L. Xu, Z.-R. Li, D. Wu, B.-Q. Wang, Y. Li, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2007, 129, 2967 CrossRef CAS PubMed.
- M. Y. Redko, J. E. Jackson, R. H. Huang and J. L. Dye, J. Am. Chem. Soc., 2005, 127, 12416 CrossRef CAS PubMed.
- H. Buchammagari, Y. Toda, M. Hirano, H. Hosono, D. Takeuchi and K. Osakada, Org. Lett., 2007, 9, 4287 CrossRef CAS PubMed.
- J. Li, B. Yin, T. Fuchigami, S. Inagi, H. Hosono and S. Ito, Electrochem. Commun., 2012, 17, 52 CrossRef CAS PubMed.
- H. Yanagi, K.-B. Kim, I. Koizumi, M. Kikuchi, H. Hiramatsu, M. Miyakawa, T. Kamiya, M. Hirano and H. Hosono, J. Phys. Chem. C, 2009, 113, 18379 CAS.
- S. Watanabe, T. Watanabe, K. Ito, N. Miyakawa, S. Ito, H. Hosono and S. Mikoshiba, Sci. Technol. Adv. Mater., 2011, 12, 034410 CrossRef.
- P. V. Sushko, A. L. Shluger, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2007, 129, 942 CrossRef CAS PubMed.
- J. L. Dye, M. J. Wagner, G. Overney, R. H. Huang, T. F. Nagy and D. Tomanek, J. Am. Chem. Soc., 1996, 118, 7329 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- J. Contreras-Garca, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625 CrossRef PubMed.
- A. Otero-de-la Roza, E. R. Johnson and J. Contreras-García, Phys. Chem. Chem. Phys., 2012, 14, 12165 RSC.
- M. J. Turner, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystEngComm, 2011, 13, 1804 RSC.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- Topology and properties of the electron density in solids, ed. R. Boyd and C. Matta, Wiley-VCH, Weinheim, Germany, 2007 Search PubMed.
- C. Gatti, Z. Kristallogr., 2005, 220, 399 CrossRef CAS.
- S. B. Dawes, D. L. Ward, R. H. Huang and J. L. Dye, J. Am. Chem. Soc., 1986, 108, 3534 CrossRef CAS.
- M. J. Wagner, R. H. Huang, J. L. Eglin and J. L. Dye, Nature, 1994, 368, 726 CrossRef CAS.
- R. H. Huang, M. J. Wagner, D. J. Gilbert, K. A. Reidy-Cedergren, D. L. Ward, M. K. Faber and J. L. Dye, J. Am. Chem. Soc., 1997, 119, 3765 CrossRef CAS.
- R. Huang, M. Faber, K. Moeggenborg, D. Ward and J. Dye, Nature, 1988, 331, 599 CrossRef CAS.
- Q. Xie, R. H. Huang, A. S. Ichimura, R. C. Phillips, W. P. Pratt and J. L. Dye, J. Am. Chem. Soc., 2000, 122, 6971 CrossRef CAS.
- H. Bartl and T. Scheller, Neues Jahrb. Mineral., Monatsh., 1970, 35, 547 Search PubMed.
- S. Matsuishi, Y. Toda, M. Miyakawa, K. Hayashi, T. Kamiya, M. Hirano, I. Tanaka and H. Hosono, Science, 2003, 301, 626 CrossRef CAS PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380 CrossRef PubMed.
- P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- N. Marzari, D. Vanderbilt, A. De Vita and M. C. Payne, Phys. Rev. Lett., 1999, 82, 3296 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109 CrossRef CAS PubMed.
- A. Otero-de-la Roza and E. R. Johnson, J. Chem. Phys., 2013, 138, 204109 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, J. Chem. Phys., 1998, 109, 2604 CrossRef CAS PubMed.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943 CrossRef CAS PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 194112 CrossRef PubMed.
- P. Mori-Sanchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sanchez and W. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902 CrossRef CAS.
- G. Sini, J. S. Sears and J.-L. Bredas, J. Chem. Theory Comput., 2011, 7, 602 CrossRef CAS.
- S. N. Steinmann, C. Piemontesi, A. Delacht and C. Corminboeuf, J. Chem. Theory Comput., 2012, 8, 1629 CrossRef CAS.
- E. R. Johnson, A. Otero de la Roza and S. G. Dale, J. Chem. Phys., 2013, 139, 184116 CrossRef PubMed.
- R. E. Larsen, W. J. Glover and B. J. Schwartz, Science, 2010, 329, 65 CrossRef CAS PubMed.
- F. Uhlig, O. Marsalek and P. Jungwirth, J. Phys. Chem. Lett., 2012, 3, 3071 CrossRef CAS.
- A. Otero-de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018, DOI:10.1016/j.cpc.2013.10.026.
- A. M. Pendás, M. A. Blanco, A. Costales, P. M. Sánchez and V. Luaña, Phys. Rev. Lett., 1999, 83, 1930 CrossRef.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- K. J. Moeggenborg, J. Papaioannou and J. L. Dye, Chem. Mater., 1991, 3, 514 CrossRef CAS.
- M. J. Wagner and J. L. Dye, J. Solid State Chem., 1995, 117, 309 CrossRef CAS.
- L. Palacios, A. Cabeza, S. Bruque, S. García-Granda and M. A. Aranda, Inorg. Chem., 2008, 47, 2661 CrossRef CAS PubMed.
- M. A. Spackman and E. N. Maslen, J. Phys. Chem., 1986, 90, 2020 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09 Revision A.1, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- M. Dolg, H. Stoll, H. Preuss and R. M. Pitzer, J. Phys. Chem., 1993, 97, 5852 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- V. Luaña, P. Mori-Sánchez, A. Costales, M. A. Blanco and A. Pendás, J. Chem. Phys., 2003, 119, 6341 CrossRef PubMed.
| This journal is © the Owner Societies 2014 |